Nonlinear Control Applied in Jump Attenuation of a Non-ideal System

Abstract

This work proposes the attenuation of the Sommerfeld effect (jump phenomenon) present in a non-ideal oscillator thought the use of different nonlinear controllers. The non-ideal system is composed of a beam-like mechanical structure excited by a limited power supply, in this case an unbalanced direct current motor. Two different control techniques are considered. The first controller has its feedback gain obtained through the SDRE (State-Dependent Riccati Equation) technique in conjunction with a feedforward gain. The second controller is based in the SMC (Sliding Mode Control) technique. Numerical simulations show that the two proposed control strategies are effective in suppressing the jump phenomenon, and thus keeping the structure vibration of the studied system at desirable levels.

1 Introduction

The Sommerfeld effect is a resonance phenomenon that arises from the interaction between a non-ideal energy source with the mechanical structure. The energy source influences the mechanical structure, which in turn influences and exchanges energy with the source, in a two-way effect. The nomenclature of non-ideal energy source comes from the fact that the power supply provides limited energy to the system, thus being a characteristic of all real energy sources [1,2,3,4,5,6].

The first researcher who studied this phenomenon was Arnould Sommerfeld in 1902 [7]. Through a simple experiment, which consisted of an unbalanced DC electric motor fixed on a table, Sommerfeld realized that as the motor rotational speed approached the critical speed of the mechanical structure, the increase in voltage no longer corresponded to the increase in motor speed, but the vibration amplitudes continued to increase. This behavior was not expected, as direct current motors have their angular speed directly proportional to the armature voltage. Moreover, this behavior quickly changes when the system reaches a critical point, where the vibration amplitudes suddenly drop to low levels and the motor speed increases return to the values corresponding to the applied voltage, thus generating a jump phenomenon in the vibration amplitude graphs in relation to the motor angular velocity [2, 4, 8,9,10]

Some works have proposed methodologies to suppress the jump effect, because this effect if is unwanted as it represents a loss of system energy, as well as resulting in an amplification of the mechanical vibrations. Reference [11] proposed to include a friction element in a non-ideal structural system to eliminate the Sommerfeld effect. In [4] is considered a semi-active control using a magnetorheological damper for reducing the resonance vibrations of a non-ideal structure in an active way. Reference [12] considered a shape-memory alloy to attenuate the vibration and Sommerfeld effect of a non-ideal type oscillator. In [13] is considered a snap-through truss absorber for attenuation of the jump phenomenon in an oscillator under excitation of an electric motor with an eccentricity and limited power.

In this work is proposed the use of an active control in order to attenuate the Sommerfeld effect and the vibration amplitudes of a non-ideal mechanical oscillator. The NIS studied is composed of a beam and an unbalanced electric motor with limited power supply. For the active control of the system are considered two techniques. The first being a controller that uses a portion of feedback gain and another portion of feedforward gain and the second controller is based in the sliding mode control technique.

2 Mathematical Model

Figure 1a shows the mechanical part of the non-ideal system. In this figure, ${m}_{1}$ is the mass of the cart with the motor, ${m}_{2}$ is the motor unbalance mass, $r$ is the length of the unbalance axis and $\varphi$ is the position angle of the motor shaft. $k$ and $c$ represent the stiffness and damping of the mechanical structure, respectively. Motor unbalance will cause vibration, with displacement $x$ [4, 9, 14, 15].

Fig. 1

a Non-ideal mechanical system (NIS). b electrical schematic representation of the DC motor

The mathematical model that represents the dynamics of the system shown in Fig. 1 is developed using Lagrange’s energy method, where the Lagrange’s function is expressed as:

$$ L = E_k - E_p $$

(1)

where E_k is the kinetic energy, and E_p is the potential energy. The equations of motion can be obtained through the Euler–Lagrange equation, given by:

$$ \frac{d}{dt}\left( {\frac{\partial L}{{\partial \dot{Q}_i }}} \right) - \frac{\partial L}{{\partial Q_i }} = \mathfrak{I}_i $$

(2)

where i = 1, 2,..., N. N is the number of degrees-of-freedom, $\mathfrak{I}_i$’s are the non-conservatives forces, Q_i’s are the generalized coordinates, being that $Q_1 = x$, and $Q_2 = \varphi$.

The kinetic energy is given by:

$$ E_k = \frac{1}{2}m_1 \dot{x}^2 + \frac{1}{2}J\dot{\varphi }^2 + \frac{1}{2}m_2 \left( {\left( {\dot{x} - \dot{\varphi }r\sin (\varphi )} \right)^2 + \left( {\dot{\varphi }r\cos (\varphi )} \right)^2 } \right) $$

(3)

where: $J$ is the moment of inertia, $\dot{\varphi }$ is the rotational speed, ${m}_{2}$ is the unbalanced mass.

The potential energy is given by:

$$ E_p = \frac{1}{2}kx^2 $$

(4)

The non-conservatives forces are given by:

$$ \mathfrak{I}_1 = - c\dot{x} $$

(5)

Substituting Eqs. (3), (4) into Eq. (1), and substituting the result accounting for Eq. (5) into Eq. (2), we obtain:

$$ \begin{aligned} & M\ddot{x} + c\dot{x} + kx = mr(\dot{\varphi }^2 \sin (\varphi ) + \ddot{\varphi }\cos (\varphi )) \\ & (J + mr^2 )\ddot{\varphi } = mrx\cos (\ddot{\varphi }) + T_e \\ \end{aligned} $$

(6)

where: $M = m_1 + m_2$

The electrical part, shown in Fig. 1b, refers to the circuit of a direct current motor. In this circuit, ${V}_{a}$ is the applied armature voltage, $I$ is the armature current. ${R}_{a}$ and ${L}_{a}$ are the resistance and inductance of the armature, respectively. ${E}_{A}$ is the counter-electromotive force (CEMF) and in the case of constant flux can be directly related to the rotational speed of the motor as $E_a = k_e \dot{\varphi }$, where $k_e$ is the electrical constant. Using the Kirchhoff's circuit laws will have:

$$ V_a = R_a I + L{}_a\dot{I} + E_a $$

(7)

This is the voltage equation for the armature circuit of a DC motor. To obtain the motor torque equation, it is necessary to analyze its mechanical structure, where the torque experienced by the motor windings $T_e$ can be directly related to the armature current as $T_e = k_t I$, where $k_t$ is the torque constant. The equation of motion for a DC motor is given by:

$$ T_e = J\ddot{\varphi } + b\dot{\varphi } + T_l $$

(8)

where: J is the inertia, b is the coefficient of viscous friction and $T_l$ is the load torque. In this paper $T_l$ will be neglected.

Coupling the elements of inertia, as well as relating the displacement of the mechanical structure to the angular displacement of the motor, it is possible to obtain the following set of equations, this being the set of dynamic nonlinear equations for the non-ideal system shown in Fig. 1.

$$ \begin{aligned} & M\ddot{x} + c\dot{x} + kx = mr(\dot{\varphi }^2 \sin (\varphi ) + \ddot{\varphi }\cos (\varphi )) \\ & (J + mr^2 )\ddot{\varphi } = mrx\cos (\ddot{\varphi }) + k_t I \\ & L_a \dot{I} = R_a I - k_e I + V_a \\ \end{aligned} $$

(9)

Equation (9) can be written in state-space notation as follows:

$$ \begin{aligned} \dot{x}_1 & = x_2 \\ \dot{x}_2 & = \Delta \left( {\alpha_1 x_5 \cos (x_3 ) - \alpha_2 x_4^2 \sin (x_3 ) - \alpha_3 x_2 - \alpha_4 x_1 } \right) \\ \dot{x}_3 & = x_4 \\ \dot{x}_4 & = \Delta \left( { - \beta_1 x_4^2 \sin (x_3 )\cos (x_3 ) - \beta_2 x_2 \cos (x_3 ) - b_3 x_1 \cos (x_3 ) + \beta_4 x_5 } \right) \\ \dot{x}_5 & = - c_1 x_5 - c_2 x_4 + c_3 \\ \end{aligned} $$

(10)

where: $x_1 = x$, $x_2 = \dot{x}$, $x_3 = \varphi$, $x_4 = \dot{\varphi }$, $x_5 = I$, $\alpha_1 = k_t mr$, $\alpha_2 = m^2 r^3 + Jmr$, $\alpha_3 = cmr^2 + cJ$, $\alpha_4 = kmr^2 + kJ$, $\alpha_5 = Mmr^2 + JM$, $\beta_1 = m^2 r^2$, $\beta_2 = cmr$, $\beta_3 = kmr$, $\beta_4 = Mk_t$, $c_1 = \frac{R_a }{{L_a }}$, $c_2 = \frac{k_e }{{L_a }}$, $c_3 = \frac{V}{L_a }$ and $\Delta = \frac{1}{{ - \beta_1 \cos \left( {x_3 } \right)^2 + \alpha_5 }}$.

3 Numerical Simulations

The numerical simulations are carried out accounting for the following parameters: $m_1 = 0.13$, $m_2 = 0.005$, $k = 399$, $c = 0.077$, $t = 0.015$, $R_a = 51$, $J = 9 \times 10^{ - 7}$, $J = 2.82 \times 10^{ - 6}$, $L_a = 0.004$, $k_t = 0.0663$ and $k_m = 0.0663$.

Figure 2 shows the results for the jump phenomenon according to the motor shaft angular frequency and the voltage applied to the armature.

Fig. 2

Jump phenomenon. a Frequency response diagram. b Jump phenomenon due to the applied voltage in the DC motor. c Angular frequency response by voltage

Considering the process of increasing the electrical voltage (V), the jump phenomenon occurs when the motor reaches 56 rad/s and 8.5 V. After this point, if the voltage increase is maintained, the system returns to the linear and normal operation expected. Due to the effect of the coupling between the motor and the mechanical structure, the system has its operation weakened and it is realized that between 3.5 and 8.5 V all the increase of voltage in the motor serves almost solely to increase the amplitudes of vibration and not the rotation of the motor. This disruption of the direct relationship between electrical voltage and motor rotation can be clearly seen in Fig. 2c. The effect of converting electrical energy into mechanical vibration can also be observed during the process of decreasing the electrical voltage. However, as this is a non-linear system and that it depends on its initial conditions, the Sommerfeld effect of the voltage decrease process occurs at a different point than that of the increasing voltage process, in this case occurring when the motor reaches 55.5 rad/s and 5.3 V. This conversion of electrical energy into mechanical vibration energy is one of the biggest problems of this type of system, being responsible for reducing the efficiency of the electric motor, as well as reducing the angular frequencies available for the project.

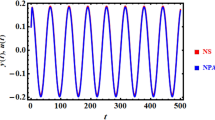
In Fig. 3 it is possible to observe the behavior of the system (11), considering a voltage of 3 V applied to the DC motor.

Fig. 3

Dynamics of the systems considering x₁. a Time history. b Phase plane for x₁ versus x₂

As can be seen in Fig. 3, when the motor is powered with 3 V, the vibrations of the structure are low, showing a periodic behavior with a unit period after the transient period.

Considering the behavior of x₁ shown in Fig. 3, the following displacement equation for x₁ can be determined:

$$ \begin{aligned} \tilde{x}_1 & = 0.001113\sin (44.88t) \\ \tilde{x}_2 & = 0.05\cos (44.88t) \\ \end{aligned} $$

(11)

3.1 Nonlinear Control Project

Considering that the objective is to eliminate the Somerfield effect observed in x₁, the following control signal (U) can be introduced in Eq. (10) [9, 14, 16, 17]:

$$ \begin{aligned} \dot{x}_1 & = x_2 \\ \dot{x}_2 & = \Delta \left( {\alpha_1 x_5 \cos (x_3 ) - \alpha_2 x_4^2 \sin (x_3 ) - \alpha_3 x_2 - \alpha_4 x_1 } \right) + U \\ \dot{x}_3 & = x_4 \\ \dot{x}_4 & = \Delta \left( { - \beta_1 x_4^2 \sin (x_3 )\cos (x_3 ) - \beta_2 x_2 \cos (x_3 ) - b_3 x_1 \cos (x_3 ) + \beta_4 x_5 } \right) \\ \dot{x}_5 & = - c_1 x_5 - c_2 x_4 + c_3 \\ \end{aligned} $$

(12)

Since the objective of the control signal (U) is to control the displacement of x₁, the control design can be obtained by considering only the first two equations of (12). In addition, the states x₃, x₄ and x₅ will be considered disturbances in the system [9].

$$ \begin{aligned} \dot{x}_1 & = x_2 \\ \dot{x}_2 & = \Delta \left( {\alpha_1 x_5 \cos (x_3 ) - \alpha_2 x_4^2 \sin (x_3 ) - \alpha_3 x_2 - \alpha_4 x_1 } \right) + U \\ \end{aligned} $$

(13)

3.2 Proposed SDRE Control

The vector control U for the Optimal Linear feedback control consists of two parts: $U = \tilde{u} + u$, where u is the optimal feedback control and $\tilde{u}$ is the feedforward control gain, the last one responsible for maintaining the system in the desired trajectory. The feedforward gain is given by:

$$ \tilde{u} = - \Delta \left( {\alpha_1 x_5 \cos (x_3 ) - \alpha_2 x_4^2 \sin (x_3 ) - \alpha_3 \tilde{x}_2 - \alpha_4 \tilde{x}_1 } \right) $$

(14)

Substituting Eq. (14) into Eq. (13), and defining the deviation of the desired trajectory as:

$$ e = \left[ {\begin{array}{*{20}c} {x_1 - \tilde{x}_1 } \\ {x_2 - \tilde{x}_2 } \\ \end{array} } \right] $$

(15)

where $\tilde{x}_1$ and $\tilde{x}_2$ are the trajectories desired. The system can be represented in the following form:

$$ \begin{aligned} \dot{e}_1 & = e_2 \\ \dot{e}_2 & = - \Delta \alpha_3 e_2 - \Delta \alpha_4 e_1 + u \\ \end{aligned} $$

(16)

Or in matrix form as:

$$ {\bf{\dot{e}}} = {\bf{Ae}} + {\bf{Bu}} $$

(17)

The control u is optimal and it transfers the nonlinear system of Eq. (16) from any initial state to the final state ${\bf{e}}\left( \infty \right) = 0$.

Minimizing the cost functional to:

$$ J = \int_0^\infty {\left( {{\bf{e}}^T {\bf{Qe}} + {\bf{u}}^T {\bf{Ru}}} \right)} \,dt $$

(18)

the control u can be found solving the following equation:

$$ {\bf{u}} = - {\bf{R}}^{ - 1} {\bf{B}}^T {\bf{Pe}} $$

(19)

Being P a symmetric matrix, the Algebraic Riccati Equation is developed, denoted by:

$$ {\bf{PA}} + {\bf{A}}^T {\bf{P}} - {\bf{PBR}}^{ - 1} {\bf{B}}^T {\bf{P}} + {\bf{Q}} = {\bf{0}} $$

(20)

The matrices A and B may be represented by:

${\bf{A}} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - \Delta \alpha_4 } & { - \Delta \alpha_3 } \\ \end{array} } \right]$, ${\bf{B}} = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right]$ and by definition: ${\bf{Q}} = 10^4 \left[ {\begin{array}{*{20}c} {10^3 } & 0 \\ 0 & 1 \\ \end{array} } \right]$ and ${\bf{R}} = 10^{ - 4}$.

In Figs. 4, it is observed the jump phenomenon suppression using the proposed control $U = \tilde{u} + u$, considering $\tilde{x}_1$ and $\tilde{x}_2$ obtained in the Eq. (11).

Fig. 4

Jump phenomenon suppression by SDRE control. a Frequency response diagram. b Jump phenomenon due to the applied voltage in the DC motor. c Angular frequency response by voltage

As can be seen in the results presented in Fig. 4, using the proposed control ($U = \tilde{u} + u$), it is possible to eliminate the jump effect, keeping the displacements in the desired amplitude and frequency.

3.3 Proposed Sliding Mode Control

For the sliding mode control, the sliding surface is generally given by [18, 19]:

$$ s = e_2 + \lambda e_1 $$

(21)

The existence of the sliding mode requires the following conditions to be satisfied:

$$ \begin{aligned} s & = e_2 + \lambda e_1 \\ \dot{s} & = \dot{e}_2 + \lambda e_1 \\ \end{aligned} $$

(22)

where $\lambda$ represents a real number.

Equation (21) defines the output of the sliding mode control, while the reaching law is given by [18, 19]:

$$ U = \left\{ {\begin{array}{*{20}c} {U_{\max } } & {if\quad \frac{s}{\mu } < - 1} \\ { - U_{\max } } & {if\quad \frac{s}{\mu } > 1} \\ {K_{smc} s} & {if\quad - 1 < \frac{s}{\mu } < 1} \\ \end{array} } \right. $$

(23)

where $\mu$ is the layer thickness of the control, $K_{smc}$ is a proportional gain, and $U_{\max }$ is related to the saturation value. The parameters $\mu$ and $K_{smc}$ are positive constants [18, 19].

In Figs. 5, it is observed the jump phenomenon suppression using the Proposed sliding mode control for parameters: $\mu = 10^{ - 3}$, $K_{smc} = 10^3$ and $U_{\max } = 100$.

Fig. 5

Jump phenomenon suppression by Sliding Mode control. a Frequency response diagram. b Jump phenomenon due to the applied voltage in the DC motor. c Angular frequency response by voltage

It can be seen in Fig. 5 that the proposed control using the sliding mode control was also efficient in suppressing the jump effect, keeping the displacements in the desired amplitude and frequency.

4 Conclusions

This work presented two control techniques for suppression of the Sommerfeld effect of a non-ideal system, i.e., a system where the excitation source is influenced by its own performance, losing energy in the process that serves only to amplify the vibration amplitudes.

The numerical results showed that both the SDRE and SMC controls are efficient in suppressing the jump effect, keeping the vibration amplitudes at desired levels as well as the motor voltage.