Robust Adaptive Sliding Mode Control for Nonlinear Uncertain Neutral Markovian Jump Systems

Abstract

This paper investigates the robust adaptive sliding mode control problem for a class of nonlinear uncertain neutral Markovian jump systems. In this study, the system state is unmeasurable and the upper norm bounds of the nonlinear functions are unavailable. An observer-based adaptive sliding mode controller is synthesized to render the resulting error system stochastically stable with a prescribed disturbance attenuation level. Finally, a numerical example is exploited to demonstrate the effectiveness of the control scheme.

1 Introduction

In practice, unpredictable structural changes may occur unexpectedly due to repairs of sudden environment disturbances, random failures, etc. [11, 39, 46, 47]. The use of neutral Markovian jump systems (MJSs) consisting of Markovian parameters is one of the appropriate ways to describe and model these types of dynamical systems. MJSs refer to a class of hybrid systems with multiple system modes where each mode corresponds to a deterministic subsystem, and the mode switching is dominated by a Markov process [25]. In the past few years, stochastic stability, stochastic stabilization, $H_{\infty }$ filtering and $H_{\infty }$ control of neutral MJSs have been investigated [5, 6, 9, 18, 23, 24, 30, 34, 41, 43, 44]. In [9], the authors investigated $H_{\infty }$ sliding mode control (SMC) for uncertain stochastic systems with input nonlinearity and Markovian switching. In [43], the authors considered the stability analysis of neutral MJSs with both time-varying delay and partially unknown transition probabilities, but they did not include the parameter uncertainties, unknown nonlinearity or $H_{\infty }$ performance. In [23], the authors investigated the problem of $H_{\infty }$ control and passive filter design for Markovian jump impulsive networked control systems with uncertainties and random packet dropouts . The effects of nonlinearity, time delay and SMC control strategy, however, have not been considered.

Because of its robustness against model uncertainties, parameter variations and external disturbances, SMC has been proven to be an effective control algorithm for a variety of both linear and nonlinear systems [1–4, 7, 8, 29, 31, 40, 42, 48, 49]. To mention a few, in [4], the authors investigated the problem of SMC for stochastic MJSs with possible actuator degradation. Besides, $H_{\infty }$ SMC has also been widely studied in [17, 38]. In particular, the authors presented a sliding mode controller for uncertain time-delay systems with $H_{\infty }$ performance in [17] . Extensive attention has been paid to the observer-based SMC problem [17, 28, 45]. The authors in [28] proposed an SMC scheme based on the state estimation to stabilize a series of Itô stochastic time-delay systems. The SMC problem was considered by [33] in the case of Markovian jump linear systems with parameter uncertainties and disturbances. It appears, however, that the issue of SMC with $H_{\infty }$ performance for uncertain neutral MJSs with unmeasured states and unknown nonlinearity has still not been adequately researched and this is the motivation for the study.

In this paper, we investigate the robust adaptive SMC problem for uncertain neutral MJSs with unmeasured states and unknown nonlinearity. In this design, the upper bounds of the nonlinear term are unknown and the parameter uncertainties are norm-bounded. An appropriate integral sliding mode surface is constructed such that the resultant sliding motion equation system is stochastically stable. The designed observer-based adaptive sliding mode controller can adapt the unknown upper bounds of nonlinearity, and then the reachability of system state trajectories and error trajectories can be satisfied. A sufficient condition of stochastic stability of the closed-loop system can be achieved by using the technique of linear matrix inequality (LMI). Finally, a numerical example is shown to validate the effectiveness of the proposed control scheme.

The organization of this paper is given as follows. The main problems are formulated in Sect. 2. In Sect. 3, an observer with $H_{\infty }$ performance and integral sliding mode surface is presented and Sect. 4 presents an adaptive sliding mode controller. Section 5 presents a numerical example to prove the feasibility of the mentioned method, and Sect. 6 concludes this paper.

Notations: The superscript “T” represents the matrix transposition. $\mathbb {R}^{n}$ shows the n -dimensional Euclidean space. A matrix $X>0$ means that X is real symmetric and positive definite. $\left\| \cdot \right\| _{1}$ and $\left\| \cdot \right\|$ refer to the 1-norm and usual Euclidean vector norm, respectively. The notation ($\varOmega ,\mathcal {F},\mathcal {P}$) denotes the probability space. $\varOmega$, $\mathcal {F}$ and $\mathcal {P}$ represent the sample space, $\sigma$-algebra of subsets of the sample space and probability measure on $\mathcal {F}$, respectively. $L_{2}[0,\infty )$ stands for the space of square integral vector functions. $\mathbf {E}\{\cdot \}$ indicates the mathematical expectation operator on the given probability $\mathcal {P}$. The symbol “$*$” denotes a term induced by symmetry.

2 Problem Formulation

Let $\{r_{t},$ $t\ge 0\}$ be a right-continuous Markov process taking values in the finite discrete space $S=\{1,2,\ldots ,s\}$ with generator $\varPi =(\pi _{ij})$ (i,  $j\in S)$ given by

$$\begin{aligned} \Pr \{r_{t+\bigtriangleup t}=j|r_{t}=i\}=\left\{ \begin{array}{l} \pi _{ij}\triangle t+o\left( \triangle t\right) ,{\ }i\ne j \\ 1+\pi _{ii}\triangle t+o\left( \triangle t\right) ,{\ }i=j \end{array} \right. \end{aligned}$$

(1)

where $\bigtriangleup t>0$ and $\lim _{\bigtriangleup t\rightarrow 0}\frac{ o(\bigtriangleup t)}{\bigtriangleup t}=0.$ $\pi _{ij}$ is the transition rate from mode i to j if $i\ne j$ and $\pi _{ii}=-\sum _{j\ne i}\pi _{ij}$. Consider a class of uncertain neutral MJSs with nonlinearity on a complete probability ($\varOmega ,\mathcal {F},\mathcal {P}$) as follows:

$$\begin{aligned} \dot{x}(t)-D\dot{x}(t-\tau ) =\,&(A(r_{t})+\bigtriangleup A(r_{t},t))x(t)\nonumber \\&+(A_{d}(r_{t})+\bigtriangleup A_{d}(r_{t},t))x(t-d) \nonumber \\&+B(u(t)+f(x,t)+d(t)), \\ y(t) =\,&C(r_{t})x(t), \nonumber \\ x(t,r_{0}) =\,&\phi (t,r_{0}),\qquad t\in \left[ -\bar{d},0\right] , \quad r_{0}\in S \nonumber \end{aligned}$$

(2)

where $x(t)\in \mathbb {R}^{n}$ denotes the state vector, $u(t)\in \mathbb {R}^{m}$ denotes control input, $y(t)\in \mathbb {R}^{p}$ denotes measured output, $f(x,t)\in \mathbb {R}^{m}$ and $d(t)\in \mathbb {R}^{m}$ indicate nonlinearity and external disturbance, respectively. $\phi (t,r_{0})$ is an initial vector-valued continuous function, which is defined in the interval $\left[ - \bar{d},0\right]$. $A(r_{t})\in \mathbb {R}^{n\times n},$ $A_{d}(r_{t})\in \mathbb {R}^{n\times n},$ $B\in \mathbb {R}^{n\times m},$ $C(r_{t})\in \mathbb { R}^{p\times n}$ and $D\in \mathbb {R}^{n\times n}$ are constant system matrices with appropriate dimensions. $\bigtriangleup A(r_{t},t)$ and $\bigtriangleup A_{d}(r_{t},t)$ are parameter uncertainties. $\tau$ and d denote the constant time delay. Besides, $\bar{d}=\max \{\tau ,d\}$ and the input matrix B has full column rank in this paper. For notional simplicity, when the uncertain neutral MJSs operate in the i-th mode, system (2) can be rewritten as

$$\begin{aligned} \dot{x}(t)-D\dot{x}(t-\tau )= & {} (A_{i}+\bigtriangleup A_{i}(t))x(t) \nonumber \\&+\,(A_{di}+\bigtriangleup A_{di}(t))x(t-d) \nonumber \\&+\,B(u(t)+f(x,t)+d(t)), \\ y(t)= & {} C_{i}x(t), \nonumber \\ x(t,r_{0})= & {} \phi (t,r_{0}),\qquad t\in \left[ -\bar{d},0\right] , \quad r_{0}\in S \nonumber \end{aligned}$$

(3)

where $A(r_{t})$, $\bigtriangleup A(r_{t},t)$, $A_{d}(r_{t})$, $\bigtriangleup A_{d}(r_{t},t)$ and $C(r_{t})$ are denoted by $A_{i}$, $\bigtriangleup A_{i}(t)$, $A_{di}$, $\bigtriangleup A_{di}(t)$ and $C_{i}$, respectively.

In the following, we define the two operators as follows:

$$\begin{aligned}&\mathcal {\bar{D}:}\mathcal {C}\left( [-\tau , 0], \mathbb {R} ^{n}\right) \longrightarrow \mathbb {R} ^{n}: \mathcal {\bar{D}}\left( \hat{x}_{t}\right) =\hat{x}(t)-D\hat{x} (t-\tau ), \\&\mathcal {D:}\mathcal {C}\left( [-\tau \hbox {, }0]\hbox {, } \mathbb {R} ^{n}\right) \longrightarrow \mathbb {R} ^{n}: \mathcal {D}\left( e_{t}\right) =e(t)-De(t-\tau ). \end{aligned}$$

We assume that the admissible uncertainties

$$\begin{aligned} \left[ \bigtriangleup A_{i}(t)\hbox {, }\bigtriangleup A_{di}(t)\right] =M_{i}F_{i}(t)\left[ N_{i}\hbox {, }N_{di}\right] , \qquad \forall i\in S \end{aligned}$$

(4)

where $M_{i}$, $N_{i}$ and $N_{di}$ are the real constant matrices with appropriate dimensions, and $F_{i}(t)$ is an unknown time-varying matrix function satisfying

$$\begin{aligned} F_{i}^{T}(t)F_{i}(t)\le I, \qquad \forall i\in S. \end{aligned}$$

(5)

The following definitions, assumption and lemmas are necessary in this paper.

Definition 1

[26] Let $V(x(t), r_{t}, t\ge 0)=V(x(t), i)$ be a stochastic positive functional candidate, which has twice differentiable on x(t). Define its infinitesimal operator $\mathcal {L}V(x(t), i)$ as

$$\begin{aligned} \mathcal {L}V(x(t), i) =\lim _{\bigtriangleup t\rightarrow 0^{+}}\frac{ 1}{\bigtriangleup t}\left[ \mathbf {E}\{V(x(t+\bigtriangleup t),r_{t+\bigtriangleup t})\ |\ x(t), r_{t}=i\}-V(x(t), i)\right] . \end{aligned}$$

(6)

Definition 2

[33] For the closed-loop system with $u(t)=0$, the equilibrium point 0 is stochastically stable, if for any x(0) and $i\in S$

$$\begin{aligned} \int _{0}^{\infty }\mathbf {E}\{\left\| x(t,x(0))\right\| ^{2}\}dt<+\infty . \end{aligned}$$

(7)

Assumption 1

The nonlinear function f(x, t) satisfies

$$\begin{aligned} \parallel f(x,t)\parallel \le \alpha +\beta \parallel y(t)\parallel , \end{aligned}$$

(8)

where $\alpha >0$ and $\beta >0$ are unknown constants.

Lemma 1

[10] (Schur complement) Let symmetric matrices W,  R and S with appropriate dimensions, then $R<0$, $W-S^{T}R^{-1}S<0$ is equivalent to

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c} W &{} S \\ S^{T} &{} R \end{array} \right] <0. \end{aligned}$$

Lemma 2

[10] Let $E\in \mathbb {R} ^{n}$, $G\in \mathbb {R} ^{n}$ and a positive scalar $\varepsilon .$ Then we have $E^{T}G+G^{T}E\le \varepsilon G^{T}G+\varepsilon ^{-1}E^{T}E.$

3 Observer-Based Sliding Mode Control

In practice, the bounds of the nonlinearity are generally not available. This means that the two unknown constant parameters $\alpha$ and $\beta$ are estimated by $\hat{\alpha }(t)$ and $\hat{\beta }(t)$, respectively. The estimation error of each parameter is defined as $\tilde{ \alpha }(t)=\hat{\alpha }(t)-\alpha$, $\tilde{\beta }(t)=\hat{\beta }(t)-\beta$ , respectively. Our purpose is to design a state observer to estimate unmeasured state components for the uncertain neutral MJSs (3) such that the resultant closed-loop system is stochastically stable despite the presence of uncertainties, Markovian switching and external disturbance.

3.1 Observer Design

In this subsection, we design a state observer of the controlled plant (3),

$$\begin{aligned} \dot{\hat{x}}(t)-D\dot{\hat{x}}(t-\tau )= & {} A_{i}\hat{x}(t)+A_{di}\hat{x} (t-d) \nonumber \\&+\,L_{i}(y(t)-C_{i}\hat{x}(t)) \nonumber \\&+\,Bu(t)+Bu_{s}(t)\hbox {,} \\ \hat{y}(t)= & {} C_{i}\hat{x}(t), \nonumber \end{aligned}$$

(9)

where $L_{i}\in \mathbb {R} ^{n\times p}$ is the observer gain to be designed and $\hat{x}(t)$ represents the estimation of x(t). The robust control term $u_{s}(t)$ is designed to remove the impact of the unknown nonlinear term. In the following derivations, assume $S_{e}(t)=B^{T}X_{i}\mathcal {D}\left( e_{t}\right)$. Besides, it is assumed that the positive symmetric matrix $X_{i}$ satisfies the constraint

$$\begin{aligned} B^{T}X_{i}=NC_{i}. \end{aligned}$$

(10)

The robust control term $u_{s}(t)$ is designed as

$$\begin{aligned} u_{s}(t)=(\hat{\alpha }(t)+\hat{\beta }(t)\left\| y(t)\right\| +\epsilon )\hbox {sgn}(S_{e}(t))\hbox {,} \end{aligned}$$

(11)

with the adaptive laws

$$\begin{aligned} \dot{\hat{\alpha }}(t)=c_{\alpha }\left\| S_{e}(t)\right\| \hbox {, } \dot{\hat{\beta }}(t)=c_{\beta }\left\| S_{e}(t)\right\| \left\| y(t)\right\| \hbox {,} \end{aligned}$$

(12)

where $\epsilon$ is a small positive constant, $c_{\alpha }$ and $c_{\beta }$ are positive constants chosen by the designer. Define the error $e(t)=x(t)-\hat{x}(t),$ and then the estimation error dynamics is derived from (3) subtracting (9) as:

$$\begin{aligned} \dot{e}(t)-D\dot{e}(t-\tau )= & {} (A_{i}+\bigtriangleup A_{i}(t)-L_{i}C_{i})e(t)+\bigtriangleup A_{i}(t)\hat{x}(t) \nonumber \\&+\,(A_{di}+\bigtriangleup A_{di}(t))e(t-d) \nonumber \\&+\,\bigtriangleup A_{di}(t)\hat{x}(t-d) \nonumber \\&-\,B(u_{s}(t)-f(x,t)-d(t)), \\ y_{e}(t)= & {} C_{i}e(t), \nonumber \end{aligned}$$

(13)

where $y_{e}(t)$ denotes the output of the error system. Now we introduce the $H_{\infty }$ performance index as follows:

$$\begin{aligned} J=\mathbf {E}\left\{ \int _{0}^{\infty }\left( y_{e}^{T}(\theta )y_{e}(\theta )-\gamma ^{2}d^{T}(\theta )d(\theta )\right) d\theta \right\} . \end{aligned}$$

(14)

The performance $J<0$ is converted into the following condition:

$$\begin{aligned} \mathbf {E}\left( \sup _{0\ne d(t)\in L_{2}}\frac{\left\| y_{e}(t)\right\| }{\left\| d(t)\right\| }\right) <\gamma . \end{aligned}$$

(15)

3.2 Sliding Mode Surface Design

Define the integral sliding mode surface in the state-estimate space as follows:

$$\begin{aligned} S(t)=F(\hat{x}(t)-D\hat{x}(t-\tau ))-F\int _{0}^{t}(A_{i}+BK_{i})(\hat{x}(s)-D \hat{x}(s-\tau ))ds, \end{aligned}$$

(16)

where $F\in \mathbb {R} ^{m\times n}$ is a given constant matrix and $K_{i}\in \mathbb {R} ^{m\times n}$ is a coefficient matrix, which is designed such that $A_{i}+BK_{i}$ is Hurwitz and FB is positive definite symmetric matrix and nonsingular.

Remark 1

Note that the linear term $F\hat{x}(t)$ is continuous in integral sliding mode surface (16). Moreover, although $F(A_{i} + BK_{i})$ is switching in different mode i, the integral term $F\int _{0}^{t}(A_{i}+BK_{i})x(s)ds$ is still continuous in the jump point. Then, the pre-defined integral sliding mode surface is continuous when the uncertain neutral MJSs states switch.

To obtain the sliding mode dynamics of system (3), we utilize the equivalent control method in the following. Taking the derivative of S(t), we have

$$\begin{aligned} \dot{S}(t)= & {} F(\dot{\hat{x}}(t)-D\dot{\hat{x}}(t-\tau ))-F(A_{i}+BK_{i})( \hat{x}(t)-D\hat{x}(t-\tau )) \nonumber \\= & {} F(A_{di}\hat{x}(t-d)+Bu(t)+Bu_{s}(t)+FA_{i}D\hat{x}(t-\tau ) \nonumber \\&+\,L_{i}C_{i}e(t))-FBK_{i}\hat{x}(t)+FBK_{i}D\hat{x}(t-\tau )\hbox {.} \end{aligned}$$

(17)

From $\dot{S}(t)=0$, we obtain the following equivalent control law

$$\begin{aligned} u_{eq}(t)= & {} K_{i}\hat{x}(t)-(FB)^{-1}FA_{di}\hat{x}(t-d)-u_{s}(t) \nonumber \\&-\,(FB)^{-1}FL_{i}C_{i}e(t)-(FB)^{-1}FA_{i}D\hat{x}(t-\tau )-K_{i}D\hat{x} (t-\tau )\hbox {.} \end{aligned}$$

(18)

Substituting the equivalent control law (18) into observer (9 ), the sliding mode dynamics can be obtained as follows:

$$\begin{aligned} \dot{\hat{x}}(t)-D\dot{\hat{x}}(t-\tau )= & {} (A_{i}+BK_{i})\hat{x}(t)+\bar{B} A_{di}\hat{x}(t-d) \nonumber \\&+\,\bar{B}L_{i}C_{i}e(t)-B(K_{i}+(FB)^{-1}FA_{i})D\hat{x}(t-\tau )\hbox {,} \end{aligned}$$

(19)

where $\bar{B}=I-B(FB)^{-1}F$. Thus, the stochastic stability of the overall closed-loop system composed of (13) and (19) will be analyzed in the following theorem.

3.3 Analysis of Stochastic Stability

A sufficient condition of stochastic stability of the resulting closed-loop system composed of (13) and (19) with Markovian parameters, and a disturbance attenuation level is given in the following theorem.

Theorem 1

Consider the overall closed-loop system composed of estimation error dynamics (13) and sliding mode dynamics (19), given a scalar $\gamma >0$, the integral sliding mode surface is given by (16). If there exist matrices $X_{i}\in \mathbb {R} ^{n\times n}>0$, $P_{1}\in \mathbb {R}^{n\times n}>0,$ $P_{2}\in \mathbb {R} ^{n\times n}>0$, $Q_{1}\in \mathbb {R}^{n\times n}>0$, $Q_{2}\in \mathbb {R} ^{n\times n}>0$, $Y_{i}\in \mathbb {R}^{n\times p}$ and scalars $\varepsilon _{il}$ $(l=1,2,3,4)$ for any $i\in S$ such that the following LMIs and equality constraint hold,

$$\begin{aligned}&\left[ \begin{array}{cccccc} \varLambda _{i11} &{}\quad \varLambda _{i12} &{}\quad X_{i}A_{di} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ *&{}\quad \varLambda _{i22} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ *&{}\quad *&{}\quad \varLambda _{i33} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ *&{}\quad *&{}\quad *&{}\quad \varLambda _{i44} &{}\quad \varLambda _{i45} &{}\quad X_{i}\bar{B}A_{di} \\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad \varLambda _{i55} &{}\quad 0 \\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad \varLambda _{i66} \\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *\end{array} \right. \nonumber \\&\left. \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} J_{2} &{} C_{i}^{T}Y_{i}^{T} &{} 0 &{} 0 &{} X_{i}B \\ 0 &{} 0 &{} D_{i}C_{i}^{T}Y_{i}^{T} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \sqrt{2}X_{i}\bar{B} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ J_{1} &{} 0 &{} 0 &{} 0 &{} 0 \\ *&{} -X_{i} &{} 0 &{} 0 &{} 0 \\ *&{} *&{} -X_{i} &{} 0 &{} 0 \\ *&{} *&{} *&{} -X_{i} &{} 0 \\ *&{} *&{} *&{} *&{} -\gamma ^{2}I \end{array} \right] <0, \end{aligned}$$

(20)

$$\begin{aligned}&B^{T}X_{i}=NC_{i}\hbox {,} \end{aligned}$$

(21)

where

$$\begin{aligned} \varLambda _{i11}= & {} X_{i}A_{i}+A_{i}^{T}X_{i}+P_{1}+P_{2}+\varepsilon _{i1}N_{i}^{T}N_{i} \\&-\,C_{i}^{T}Y_{i}^{T}-Y_{i}C_{i}+\sum _{j=1}^{s}\pi _{ij}X_{j}+C_{i}^{T}C_{i},\\ \varLambda _{i12}= & {} (X_{i}A_{i}+P_{1}+P_{2}-Y_{i}C_{i})D+\varepsilon _{i1}N_{i}^{T}N_{i}D+C_{i}^{T}C_{i}D, \\ \varLambda _{i22}= & {} D^{T}(P_{1}+P_{2})D-P_{1}+\varepsilon _{i1}D^{T}N_{i}^{T}N_{i}D+D^{T}C_{i}^{T}C_{i}D, \\ \varLambda _{i33}= & {} \varepsilon _{i2}N_{di}^{T}N_{di}-P_{2}, \\ \varLambda _{i44}= & {} X_{i}(A_{i}+BK_{i})+(A_{i}+BK_{i})^{T}X_{i} \\&+\,\varepsilon _{i3}N_{i}^{T}N_{i}+Q_{1}+Q_{2}+\sum _{j=1}^{s}\pi _{ij}X_{j}, \\ \varLambda _{i45}= & {} X_{i}(A_{i}+BK_{i})D+(Q_{1}+Q_{2})D+\varepsilon _{i3}N_{i}^{T}N_{i}D \\&-\,X_{i}B(K_{i}+(FB)^{-1}FA_{i})D\hbox {,} \\ \varLambda _{i55}= & {} \varepsilon _{i3}D^{T}N_{i}^{T}N_{i}D+D^{T}(Q_{1}+Q_{2})D-Q_{1}, \\ \varLambda _{i66}= & {} \varepsilon _{i4}N_{di}^{T}N_{di}-Q_{2}, \\ J_{1}= & {} -diag (\varepsilon _{i1}I,\varepsilon _{i2}I, \varepsilon _{i3}I,\varepsilon _{i4}I), \\ J_{2}= & {} (X_{i}M_{i},X_{i}M_{i},X_{i}M_{i},X_{i}M_{i}). \end{aligned}$$

Moreover, the observer gain can be obtained as

$$\begin{aligned} L_{i}=X_{i}^{-1}Y_{i}, \end{aligned}$$

(22)

and then the system (3) with Markovian parameters is stochastically stable under observer (9) and integral sliding mode surface (16) with a disturbance attenuation level $\gamma .$

Proof

Choose the Lyapunov functional of each subsystem as follows:

$$\begin{aligned} V_{1}(i,t)= & {} \mathcal {D}^{T}\left( e_{t}\right) X_{i}\mathcal {D}\left( e_{t}\right) +\int _{t-\tau }^{t}e^{T}(\theta )P_{1}e(\theta )d\theta \nonumber \\&+\int _{t-d}^{t}e^{T}(\theta )P_{2}e(\theta )d\theta +\mathcal {\bar{D}} ^{T}\left( \hat{x}_{t}\right) X_{i}\mathcal {\bar{D}}\left( \hat{x}_{t}\right) \nonumber \\&+\int _{t-\tau }^{t}\hat{x}^{T}(\theta )Q_{1}\hat{x}(\theta )d\theta +\int _{t-d}^{t}\hat{x}^{T}(\theta )Q_{2}\hat{x}(\theta )d\theta \nonumber \\&+\,c_{\alpha }^{-1}\tilde{\alpha }^{2}(t)+c_{\beta }^{-1}\tilde{\beta }^{2}(t). \end{aligned}$$

(23)

Then, based on Definition 1, we take the time derivative of Lyapunov functional $V_{1}(i,t)$ along the trajectories of sliding mode dynamics and state error dynamics with $d(t)=0$ as follows:

$$\begin{aligned} \mathcal {L}{V}_{1}(i,t)= & {} 2\mathcal {D}^{T}\left( e_{t}\right) X_{i}[(A_{i}+\bigtriangleup A_{i}(t)-L_{i}C_{i})e(t)+\bigtriangleup A_{i}(t)\hat{x}(t) \nonumber \\&+\,(A_{di}+\bigtriangleup A_{di}(t))e(t-d)+\bigtriangleup A_{di}(t)\hat{x} (t-d) \nonumber \\&-\,B(u_{s}(t)-f(x,t))]+e^{T}(t)P_{1}e(t)+e^{T}(t)P_{2}e(t) \nonumber \\&-\,e^{T}(t-\tau )P_{1}e(t-\tau )-e^{T}(t-d)P_{2}e(t-d) \nonumber \\&+\,\hat{x}^{T}(t)Q_{1}\hat{x}(t)-\hat{x}^{T}(t-\tau )Q_{1}\hat{x}(t-\tau ) \nonumber \\&+\,2\mathcal {\bar{D}}^{T}\left( \hat{x}_{t}\right) X_{i}[(A_{i}+BK_{i})\hat{x }(t)+\bar{B}A_{di}\hat{x}(t-d) \nonumber \\&+\,\bar{B}L_{i}C_{i}e(t)-B(K_{i}+(FB)^{-1}FA_{i})D\hat{x}(t-\tau )] \nonumber \\&+\,\hat{x}^{T}(t)Q_{2}\hat{x}(t)-\hat{x}^{T}(t-d)Q_{2}\hat{x}(t-d) \nonumber \\&+\,2c_{\beta }^{-1}\dot{\tilde{\beta }}(t)\tilde{\beta }(t)+\mathcal {D} ^{T}\left( e_{t}\right) \sum _{j=1}^{s}\pi _{ij}X_{j}\mathcal {D}\left( e_{t}\right) \nonumber \\&+\,2c_{\alpha }^{-1}\dot{\tilde{\alpha }}(t)\tilde{\alpha }(t)+\mathcal {\bar{D} }^{T}\left( \hat{x}_{t}\right) \sum _{j=1}^{s}\pi _{ij}X_{j}\mathcal {\bar{D}} \left( \hat{x}_{t}\right) . \end{aligned}$$

(24)

Using Lemma 2 and Assumption 1, it follows from (24) that

$$\begin{aligned}&2\mathcal {D}^{T}\left( e_{t}\right) X_{i}\bigtriangleup A_{i}(t)e(t) \nonumber \\&\quad \le \varepsilon _{i1}^{-1}\mathcal {D}^{T}\left( e_{t}\right) X_{i}M_{i}M_{i}^{T}X_{i}\mathcal {D}\left( e_{t}\right) +\varepsilon _{i1}e(t)N_{i}^{T}N_{i}e(t) \nonumber \\&\quad \le \varepsilon _{i1}^{-1}\mathcal {D}^{T}\left( e_{t}\right) X_{i}M_{i}M_{i}^{T}X_{i}\mathcal {D}\left( e_{t}\right) +\varepsilon _{i1} \mathcal {D}^{T}\left( e_{t}\right) N_{i}^{T}N_{i}\mathcal {D}\left( e_{t}\right) \nonumber \\&\qquad +\,2\varepsilon _{i1}\mathcal {D}^{T}\left( e_{t}\right) N_{i}^{T}N_{i}De(t-\tau )+\varepsilon _{i1}e^{T}(t-\tau )D^{T}N_{i}^{T}N_{i}De(t-\tau )\hbox {,} \end{aligned}$$

(25)

$$\begin{aligned}&2\mathcal {D}^{T}\left( e_{t}\right) X_{i}\bigtriangleup A_{di}(t)e(t-d) \nonumber \\&\quad \le \varepsilon _{i2}^{-1}\mathcal {D}^{T}\left( e_{t}\right) X_{i}M_{i}M_{i}^{T}X_{i}\mathcal {D}\left( e_{t}\right) +\varepsilon _{i2}e(t-d)N_{di}^{T}N_{di}e(t-d)\hbox {,} \end{aligned}$$

(26)

$$\begin{aligned}&2\mathcal {D}^{T}\left( e_{t}\right) X_{i}\bigtriangleup A_{i}(t)\hat{x}(t) \nonumber \\&\quad \le \varepsilon _{i3}^{-1}\mathcal {D}^{T}\left( e_{t}\right) X_{i}M_{i}M_{i}^{T}X_{i}\mathcal {D}\left( e_{t}\right) +\varepsilon _{i3} \hat{x}^{T}(t)N_{i}^{T}N_{i}\hat{x}(t) \nonumber \\&\quad \le \varepsilon _{i3}^{-1}\mathcal {D}^{T}\left( e_{t}\right) X_{i}M_{i}M_{i}^{T}X_{i}\mathcal {D}\left( e_{t}\right) +\varepsilon _{i3} \mathcal {D}^{T}\left( \hat{x}_{t}\right) N_{i}^{T}N_{i}\mathcal {D}\left( \hat{x}_{t}\right) \nonumber \\&\qquad +\,2\varepsilon _{i3}\mathcal {D}^{T}\left( \hat{x}_{t}\right) N_{i}^{T}N_{i}D \hat{x}(t-\tau )+\varepsilon _{i3}\hat{x}^{T}(t-\tau )D^{T}N_{i}^{T}N_{i}D \hat{x}(t-\tau )\hbox {,} \end{aligned}$$

(27)

$$\begin{aligned}&2\mathcal {D}^{T}\left( e_{t}\right) X_{i}\bigtriangleup A_{di}(t)\hat{x} (t-d) \nonumber \\&\quad \le \varepsilon _{i4}^{-1}\mathcal {D}^{T}\left( e_{t}\right) X_{i}M_{i}M_{i}^{T}X_{i}\mathcal {D}\left( e_{t}\right) +\varepsilon _{i4} \hat{x}^{T}(t-d)N_{di}^{T}N_{di}\hat{x}(t-d)\hbox {,} \end{aligned}$$

(28)

$$\begin{aligned}&\qquad -\,2\mathcal {D}^{T}\left( e_{t}\right) X_{i}B(u_{s}(t)-f(x,t))+2c_{\alpha }^{-1}\dot{\tilde{\alpha }}(t)\tilde{\alpha }(t)+2c_{\beta }^{-1}\dot{\tilde{ \beta }}(t)\tilde{\beta }(t) \nonumber \\&\quad \le -2\epsilon \left\| S_{e}(t)\right\| <0\hbox {,} \end{aligned}$$

(29)

$$\begin{aligned}&2\mathcal {\bar{D}}^{T}\left( \hat{x}_{t}\right) X_{i}\bar{B}L_{i}C_{i}e(t) \nonumber \\&\quad =2\mathcal {\bar{D}}^{T}\left( \hat{x}_{t}\right) X_{i}\bar{B}L_{i}C_{i}( \mathcal {D}\left( e_{t}\right) +De(t-\tau )) \nonumber \\&\quad \le 2\mathcal {\bar{D}}^{T}\left( \hat{x}_{t}\right) X_{i}\bar{B}X_{i}^{-1} \bar{B}^{T}X_{i}\mathcal {\bar{D}}\left( \hat{x}_{t}\right) +\mathcal {D} ^{T}\left( e_{t}\right) C_{i}^{T}Y_{i}^{T}X_{i}^{-1}Y_{i}C_{i}\mathcal {D} \left( e_{t}\right) \nonumber \\&\qquad +\,e^{T}(t-\tau )D^{T}C_{i}^{T}Y_{i}^{T}X_{i}^{-1}Y_{i}C_{i}De(t-\tau ). \end{aligned}$$

(30)

Substituting (25)–(30) into (24), one can obtain:

$$\begin{aligned} \mathcal {L}{V}_{1}(i,t)\le \eta ^{T}(t)\varPhi _{i}\eta (t), \end{aligned}$$

(31)

where $\eta ^{T}(t)=\left[ \begin{array}{cccccc} \mathcal {D}^{T}\left( e_{t}\right)&e^{T}(t-\tau )&e^{T}(t-d)&\mathcal { \bar{D}}^{T}\left( \hat{x}_{t}\right)&\hat{x}^{T}(t-\tau )&\hat{x} ^{T}(t-d) \end{array} \right] ^{T}$, and

$$\begin{aligned} \varPhi _{i}=\left[ \begin{array}{cccccc} \varPhi _{i11} &{}\quad \varPhi _{i12} &{}\quad X_{i}A_{di} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ *&{}\quad \varPhi _{i22} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ *&{}\quad *&{}\quad \varPhi _{i33} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ *&{}\quad *&{}\quad *&{}\quad \varPhi _{i44} &{}\quad \varPhi _{i45} &{}\quad X_{i}\bar{B}A_{di} \\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad \varPhi _{i55} &{}\quad 0 \\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad \varPhi _{i66} \end{array} \right] , \end{aligned}$$

where

$$\begin{aligned} \varPhi _{i11}= & {} X_{i}A_{i}+A_{i}^{T}X_{i}+P_{1}+P_{2}+C_{i}^{T}Y_{i}^{T}X_{i}^{-1}Y_{i}C_{i} \\&+\,(\varepsilon _{i1}^{-1}+\varepsilon _{i2}^{-1}+\varepsilon _{i3}^{-1}+\varepsilon _{i4}^{-1})X_{i}M_{i}M_{i}^{T}X_{i} \\&-\,C_{i}^{T}Y_{i}^{T}-Y_{i}C_{i}+\varepsilon _{i1}N_{i}^{T}N_{i}+\sum _{j=1}^{s}\pi _{ij}X_{j}\hbox {,} \\ \varPhi _{i12}= & {} (X_{i}A_{i}+P_{1}+P_{2}-Y_{i}C_{i})D+\varepsilon _{i1}N_{i}^{T}N_{i}D, \\ \varPhi _{i22}= & {} D^{T}(P_{1}+P_{2})D-P_{1} \\&+\,\varepsilon _{i1}D^{T}N_{i}^{T}N_{i}D+D^{T}C_{i}^{T}Y_{i}^{T}X_{i}^{-1}Y_{i}C_{i}D, \\ \varPhi _{i33}= & {} \varepsilon _{i2}N_{di}^{T}N_{di}-P_{2}, \\ \varPhi _{i44}= & {} X_{i}(A_{i}+BK_{i})+(A_{i}+BK_{i})^{T}X_{i} \\&+\,2X_{i}\bar{B}X_{i}^{-1}\bar{B}^{T}X_{i}+\varepsilon _{i3}N_{i}^{T}N_{i}+Q_{1} \\&+\,Q_{2}+\sum _{j=1}^{s}\pi _{ij}X_{j}, \\ \varPhi _{i45}= & {} X_{i}(A_{i}+BK_{i})D+(Q_{1}+Q_{2})D \\&+\,\varepsilon _{i3}N_{i}^{T}N_{i}D-X_{i}B(K_{i}+(FB)^{-1}FA_{i})D\hbox {,} \\ \varPhi _{i55}= & {} \varepsilon _{i3}D^{T}N_{i}^{T}N_{i}D+D^{T}(Q_{1}+Q_{2})D-Q_{1}, \\ \varPhi _{i66}= & {} \varepsilon _{i4}N_{di}^{T}N_{di}-Q_{2}\hbox {.} \end{aligned}$$

It can be seen that LMIs (20) are obtained if the condition $\varPhi _{i}<0$ holds by Lemma 1. Then $\mathcal {L}{V}_{1}(i,t)<0$ for $\forall \eta (t)\ne 0$. The resulting closed-loop system with $d(t)=0$ is stochastically stable by the above proof.

In the following, we will demonstrate that the uncertain neutral MJSs (3) with Markovian parameters are stochastically stable under the observer (9) and the integral sliding mode surface (16) with a disturbance attenuation level $\gamma ,$ that is to say, external disturbance $d(t)\ne 0.$ Then, the stochastic Lyapunov functional ${V} _{1}(i,t)$ as in (23). Thus

$$\begin{aligned} \mathcal {L}{V}_{1}(i,t)=\eta ^{T}(t)\varPhi _{i}\eta (t)+2\mathcal {D}^{T}\left( e_{t}\right) X_{i}Bd(t). \end{aligned}$$

(32)

According to the above proof and $\mathbf {E}{V}_{1}(i,t)=\mathbf {E} \int _{0}^{\infty }\mathcal {L}{V}_{1}(i,t)dt>0$, for $d(t)\in L_{2}[0,\infty )$, the system performance J can be converted into

$$\begin{aligned} J\le & {} \mathbf {E}\left\{ \int _{0}^{\infty }[y_{e}^{T}(t)y_{e}(t)-\gamma ^{2}d^{T}(t)d(t)+\mathcal {L}{V} _{1}(i,t)]dt\right\} \nonumber \\= & {} \mathbf {E}\int _{0}^{\infty }\xi ^{T}(t)\varXi _{i}\xi (t)dt, \end{aligned}$$

(33)

where $\xi ^{T}(t)=\Big [ \mathcal {D}^{T}\left( e_{t}\right) \, e^{T}(t-\tau ) \, e^{T}(t-d) \, \mathcal { \bar{D}}^{T}\left( \hat{x}_{t}\right) \, \hat{x}^{T}(t-\tau ) \, \hat{x} ^{T}(t-d) \, d^{T}(t) \Big ] ^{T}.$

By utilizing Lemma 1 and LMIs (20), it is straightforward that $\varXi _{i}<0,$ which implies that $J<0$. Thus, it results in

$$\begin{aligned} \mathbf {E}\left( \sup _{0\ne d(t)\in L_{2}}\frac{\left\| y_{e}(t)\right\| }{\left\| d(t)\right\| }\right) <\gamma . \end{aligned}$$

Notice that the linear equality condition (21) is equivalent to

$$\begin{aligned} \hbox {tr}[(B^{T}X_{i}-NC_{i})^{T}(B^{T}X_{i}-NC_{i})]=0. \end{aligned}$$

We introduce the condition

$$\begin{aligned} (B^{T}X_{i}-NC_{i})^{T}(B^{T}X_{i}-NC_{i})<\sigma I, \end{aligned}$$

(34)

where $\sigma >0$ is a parameter to be designed. Then, by Lemma 1, we have

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c} -\sigma I &{} (B^{T}X_{i}-NC_{i})^{T} \\ *&{} -I \end{array} \right] <0. \end{aligned}$$

(35)

Hence, the observer-based adaptive SMC problem is changed to the following minimization problem:

$$\begin{aligned} \min \sigma ,\,\text {subject to}\, (20)\,\text {and}\, (35). \end{aligned}$$

(36)

Then the resulting closed-loop system composed of (13) and (19) is stochastically stable with a disturbance attenuation level $\gamma$. This completes the proof.

Remark 2

It should be noted that (36) is a minimization problem with linear objective and LMIs constraints, and it admits a global infimum. Then, the observed-based adaptive SMC problem can be solved if this infimum equals zero.

4 Adaptive Sliding Mode Controller Design

In this section, an adaptive SMC law will be designed to guarantee the reachability of state trajectories of the system (3) such that it can start sliding motion. The state trajectories of system (3) can be driven onto the designed integral sliding mode surface $S(t)=0$ in finite time.

Theorem 2

For any $i\in S$, suppose that there exists positive definite symmetric matrix $X_{i}$ such that Theorem 1 holds, thus, the reachability of state trajectories of the uncertain neutral MJSs (3) can be guaranteed by synthesizing the following adaptive SMC law

$$\begin{aligned} u(t)= & {} -l_{i}S(t)+K_{i}\hat{x}(t)-(FB)^{-1}FA_{di}\hat{x}(t-d) \\&-\,(\hat{\alpha }(t)+\hat{\beta }(t)\left\| y(t)\right\| +\epsilon +\delta _{i}(t))sgn (S(t)) \nonumber \\&-\,(FB)^{-1}FA_{i}D\hat{x}(t-\tau )-K_{i}D\hat{x}(t-\tau ), \nonumber \end{aligned}$$

(37)

where the above two adaptive gains are designed as in (12), $l_{i}$ is a small positive constant and $\delta _{i}(t)$ satisfies

$$\begin{aligned} \delta _{i}(t)=\max _{i\in S}\left\{ \left\| (FB)^{-1}FL_{i}y(t)\right\| +\left\| (FB)^{-1}FL_{i}C_{i}\hat{x}(t)\right\| \right\} . \end{aligned}$$

The synthesized adaptive SMC law (37) can not only drive the state trajectories of the uncertain neutral MJSs (3) onto the integral sliding mode surface (16) but also keep them on the integral sliding mode surface for all subsequent time.

Proof

Choose the following Lyapunov functional

$$\begin{aligned} V_{2}(t)=\frac{1}{2}S^{T}(t)(FB)^{-1}S(t). \end{aligned}$$

(38)

Then, along with the solution to sliding mode dynamics (19), we have

$$\begin{aligned} \mathcal {L}V_{2}(t)&=S^{T}(t)(FB)^{-1}\dot{S}(t) \nonumber \\&=S^{T}(t)(FB)^{-1}[F(A_{di}\hat{x}(t-d)+Bu(t)+Bu_{s}(t) \nonumber \\&\quad +L_{i}C_{i}e(t))-FBK_{i}\hat{x}(t)+(FBK_{i}+FA_{i})D\hat{x} (t-\tau )]. \end{aligned}$$

(39)

Substituting (37) into (39),  we have

$$\begin{aligned} \mathcal {L}V_{2}(t)= & {} -l_{i}S^{T}(t)S(t)-S^{T}(t)(FB)^{-1}FL_{i}C_{i}e(t) \nonumber \\&+\,S^{T}(t)(\hat{\alpha }(t)+\hat{\beta }(t)\left\| y(t)\right\| +\epsilon )\hbox {sgn}(S_{e}(t)) \nonumber \\&-\,S^{T}(t)(\hat{\alpha }(t)+\hat{\beta }(t)\left\| y(t)\right\| +\epsilon +\delta _{i}(t))\hbox {sgn}(S(t)). \end{aligned}$$

(40)

Noting that $S^{T}(t)\hbox {sgn}(S_{e}(t))\le \left\| S(t)\right\| _{1}.$ Then, (40) can be simplified as

$$\begin{aligned} \mathcal {L}V_{2}(t)\le -l_{i}S^{T}(t)S(t)+\left\| S(t)\right\| \left\| (FB)^{-1}FL_{i}C_{i}e(t)\right\| -\delta _{i}(t)\left\| S(t)\right\| . \end{aligned}$$

Therefore, (39) can be transformed to the following form

$$\begin{aligned} \mathcal {L}V_{2}(t)\le -\left\| S(t)\right\| (\delta _{i}(t)-\varTheta _{i}\left\| e(t)\right\| )-l_{i}\left\| S(t)\right\| ^{2}\le 0. \end{aligned}$$

(41)

Define $\varTheta _{i}=\left\| (FB)^{-1}FL_{i}C_{i}\right\| ,$ then it can be shown from (41) that,

$$\begin{aligned} \delta _{i}(t)=\max _{i\in S}\left\{ \left\| (FB)^{-1}FL_{i}y(t)\right\| +\left\| (FB)^{-1}FL_{i}C_{i}\hat{x}(t)\right\| \right\} . \end{aligned}$$

Thus, we have

$$\begin{aligned} \mathcal {L}V_{2}(t)\le -l_{i}\left\| S(t)\right\| ^{2}<0\hbox {, } \forall \left\| S(t)\right\| \ne 0. \end{aligned}$$

(42)

From (42), it is straightforward that $\mathcal {L}V_{2}(t)\le -l_{i}\left\| S(t)\right\| ^{2}<0$ ($\forall \left\| S(t)\right\| \ne 0$). Therefore, the state trajectories of the uncertain neutral MJSs (3) can be attained onto the integral sliding mode surface S(t) under the adaptive SMC law (37) in finite time. The proof is finished.

Remark 3

When the system is in mode i, the system state trajectories will be attracted to the i-th integral sliding mode surface (16) due to the fact that the system switching method is determined by a Markov process. If system mode i $(i\ne j)$ switches to another mode j before the system state trajectories reach the i-th sliding mode surface, then the system state still can be attracted to the j-th integral sliding mode surface since the integral sliding mode surface is always continuous (see Remark 1), which implies that the system state will be driven onto any sliding mode function. Thus, when the system state reaches onto the defined integral sliding mode surface, the state will reach within one sliding mode surface all the subsequent time.

If $D=0$, the uncertain neutral MJSs (3) with Markovian switching parameters and unknown nonlinear function become uncertain time-delay systems such that state observer, state estimation error dynamics and sliding mode dynamics have the same forms as (9), (13) and (19) with $D=0$, respectively, for the uncertain time-delay systems. So, based on Theorem 2, we have the following result for the uncertain time-delay systems.

The overall closed-loop uncertain time-delay MJSs (i.e., system 9 and 13 with $D=0$) are stochastically stable with a disturbance attenuation level $\gamma ,$ if there exist $X_{i}>0$, $P_{2}>0$, $Q_{2}>0$ and scalars $\varepsilon _{il}$ $(l=1,2,3,4)$ for any $i\in S$ such that the following LMIs and equality constraint hold,

$$\begin{aligned}&\left[ \begin{array}{cccccccc} \varOmega _{i11} &{}\quad X_{i}A_{di} &{}\quad 0 &{}\quad 0 &{}\quad J_{4} &{}\quad C_{i}^{T}Y_{i}^{T} &{}\quad 0 &{}\quad X_{i}B \\ *&{}\quad \varOmega _{i22} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ *&{}\quad *&{}\quad \varOmega _{i33} &{}\quad X_{i}\bar{B}A_{di} &{}\quad 0 &{}\quad 0 &{}\quad X_{i}\bar{B} &{}\quad 0 \\ *&{}\quad *&{}\quad *&{}\quad \varOmega _{i44} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad J_{3} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad -X_{i} &{}\quad 0 &{}\quad 0 \\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad -X_{i} &{} 0 \\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad -\gamma ^{2}I \end{array} \right] <0\hbox {, } \end{aligned}$$

(43)

$$\begin{aligned}&B^{T}X_{i}=NC_{i}\hbox {,} \end{aligned}$$

(44)

where

$$\begin{aligned} \varOmega _{i11}= & {} X_{i}A_{i}+A_{i}^{T}X_{i}+P_{2}+\varepsilon _{i1}N_{i}^{T}N_{i} \\&-\,C_{i}^{T}Y_{i}^{T}-Y_{i}C_{i}+\sum _{j=1}^{s}\pi _{ij}X_{j}+C_{i}^{T}C_{i} \hbox {,} \\ \varOmega _{i22}= & {} \varepsilon _{i2}N_{di}^{T}N_{di}-P_{2}\hbox {,} \\ \varOmega _{i33}= & {} X_{i}(A_{i}+BK_{i})+(A_{i}+BK_{i})^{T}X_{i} \\&+\,\varepsilon _{i3}N_{i}^{T}N_{i}+Q_{2}+\sum _{j=1}^{s}\pi _{ij}X_{j}\hbox {,} \\ \varOmega _{i44}= & {} \varepsilon _{i4}N_{di}^{T}N_{di}-Q_{2}\hbox {,} \\ J_{3}= & {} -\hbox {diag}(\varepsilon _{i1}I,\varepsilon _{i2}I, \varepsilon _{i3}I,\varepsilon _{i4}I)\hbox {,} \\ J_{4}= & {} (X_{i}M_{i},X_{i}M_{i},X_{i}M_{i},X_{i}M_{i})\hbox {.} \end{aligned}$$

Moreover, the state observer gain can be then obtained by $L_{i}=X_{i}^{-1}Y_{i}$.

Proof

The proof of this corollary is very similar to the techniques used in Theorem 1. It is omitted.

Remark 4

It is noted that there are few results on the robust adaptive SMC of networked systems, fuzzy systems and switched systems with Markovian parameters. Besides, the proposed approaches in this paper can be also applied to the networked systems, fuzzy systems and switched systems with Markovian parameters which have been studied in [12–16, 19–22, 27, 32, 35–37, 50, 51]. Thus, in future work, it is worth studying the research topic.

5 A Numerical Example

In this section, a numerical example is provided to demonstrate the feasibility of the presented method. The parameter matrices of uncertain neutral MJSs (2) with two subsystems are given as follows:

$$\begin{aligned} A_{1}= & {} \left[ \begin{array}{c@{\quad }c@{\quad }c} -4.5 &{} 0.1 &{} 0.2 \\ 0 &{} -5.6 &{} 2 \\ 0.1 &{} 0.2 &{} -5 \end{array} \right] ,B=\left[ \begin{array}{c} -2 \\ -1 \\ -1 \end{array} \right] \hbox {, }A_{d1}=\left[ \begin{array}{c@{\quad }c@{\quad }c} -1.6 &{} 0 &{} 1.2 \\ -1.8 &{} -1.5 &{} -1.2 \\ -0.4 &{} -0.5 &{} -2 \end{array} \right] \hbox {, } \\ M_{1}= & {} \left[ \begin{array}{c} 0.2 \\ 0.2 \\ 0.1 \end{array} \right] , N_{1}=\left[ \begin{array}{c} 0.2 \\ 0 \\ 0.1 \end{array} \right] ^{T}, C_{1}=\left[ \begin{array}{c@{\quad }c@{\quad }c} 0.5 &{} 0 &{} 0 \\ 0 &{} 0.5 &{} 0 \\ 0 &{} 0 &{} 0.5 \end{array} \right] , N_{d1}=\left[ \begin{array}{c} -0.3 \\ -0.3 \\ -0.3 \end{array} \right] ^{T}\hbox {,} \\ D= & {} \left[ \begin{array}{c@{\quad }c@{\quad }c} 0.5 &{} 0 &{} 0.1 \\ 0 &{} 0.5 &{} 0.1 \\ 0.1 &{} 0.1 &{} 0.5 \end{array} \right] , A_{2}=\left[ \begin{array}{c@{\quad }c@{\quad }c} -4 &{} 0.2 &{} 0 \\ 0 &{} -5 &{} 0.1 \\ 0.5 &{} 0.425 &{} -5.6 \end{array} \right] \hbox {,}M_{2}=\left[ \begin{array}{c} 0 \\ -0.3 \\ -0.3 \end{array} \right] \hbox {,} \\ A_{d2}= & {} \left[ \begin{array}{c@{\quad }c@{\quad }c} -2 &{} 0 &{} 0.1 \\ -0.9 &{} -1.2 &{} -0.1 \\ 0 &{} 0 &{} -2 \end{array} \right] \hbox {,}N_{d2}=\left[ \begin{array}{c} 0.2 \\ 0.2 \\ 0.2 \end{array} \right] ^{T}\hbox {,}\\ N_{2}= & {} \left[ \begin{array}{c} 0 \\ 0.2 \\ 0.2 \end{array} \right] ^{T}\hbox {,}C_{2}=\left[ \begin{array}{c@{\quad }c@{\quad }c} 0.5 &{} 0 &{} 0 \\ 0 &{} 0.5 &{} 0 \\ 0 &{} 0 &{} 0.5 \end{array} \right] \hbox {.} \end{aligned}$$

We select the coefficient matrices $K_{1}$ and $K_{2}$ as

$$\begin{aligned} K_{1}=\left[ \begin{array}{c@{\quad }c@{\quad }c} -0.7468&-0.2911&-0.1313 \end{array} \right] \hbox {,}K_{2}=\left[ \begin{array}{c@{\quad }c@{\quad }c} -0.4683&-0.5531&-0.5602 \end{array} \right] \hbox {.} \end{aligned}$$

The time-varying matrix function $F_{i}(t)$ $(i=1,2),$ the nonlinear function f(x, t) and the external disturbance d(t) of two subsystems are given, respectively, as follows:

$$\begin{aligned} F_{1}(t)= & {} F_{2}(t)= \begin{array}{c} 0.02\sin (200t) \end{array} , \\ f(x,t)= & {} \begin{array}{c} 0.028+0.02\sin (200t)x_{1}(t) \end{array} ,d(t)= \begin{array}{c} 2\exp (-100t) \end{array} . \end{aligned}$$

Then the constant matrix F and probabilities transition matrix $\varPi ,$ respectively, are given as

$$\begin{aligned} F=\left[ \begin{array}{c@{\quad }c@{\quad }c} -0.3&-0.1&-0.1 \end{array} \right] \hbox {, }\varPi =\left[ \begin{array}{cc} -7 &{} 7 \\ 8 &{} -8 \end{array} \right] \hbox {.} \end{aligned}$$

The initial states of original system (2) and state observer (9), respectively, are set as $x(t)=\left[ \begin{array}{c@{\quad }c@{\quad }c} 0.5&-0.5&0.2 \end{array} \right] ^{T}$ and $\hat{x}(t)=\left[ \begin{array}{c@{\quad }c@{\quad }c} 0.2&-0.1&0.1 \end{array} \right] ^{T}$ for $t\in [-4,0]$. The parameters of the adaptive laws are selected as $\hat{\alpha }(0)=0.027$ and $\hat{\beta }(0)=0.012,$ and $c_{\alpha }=0.75$, $c_{\beta }=2.5.$ The adaptive SMC law is designed in (37) with $l_{1}=0.85,$ $l_{2}=0.80,$ and $\epsilon =1.$ The constant time delays $\tau$ and d are chosen as $\tau =4$ and $d=2.5$, respectively. The minimum disturbance attenuation $\gamma =1.3256.$ To restrain the control signals from chattering, we replace $\hbox {sgn}(S(t))$ and $\hbox {sgn}(S_{e}(t))$ with $\frac{S(t)}{\left\| S(t)\right\| +0.02}$ and $\frac{S_{e}(t)}{\left\| S_{e}(t)\right\| +0.02},$ respectively. By solving the LMIs in (36), we have

$$\begin{aligned} L_{1}=\left[ \begin{array}{c@{\quad }c@{\quad }c} 0.5914 &{} 0.1982 &{} -0.1188 \\ 0.8065 &{} 1.2528 &{} -0.2627 \\ -0.7962 &{} 0.0782 &{} 1.3376 \end{array} \right] ,L_{2}=\left[ \begin{array}{c@{\quad }c@{\quad }c} 1.6862 &{} 0.2745 &{} -1.0859 \\ 0.0968 &{} 1.8497 &{} -1.7177 \\ 0.0824 &{} -0.0984 &{} 0.7299 \end{array} \right] . \end{aligned}$$

Fig. 1

Trajectory of r(t)

Fig. 2

State estimation error e(t)

Fig. 3

State estimation responses of the uncertain neutral MJSs

Fig. 4

The trajectory of integral sliding mode surface S(t)

Fig. 5

Estimation $\hat{\alpha }(t)$

Fig. 6

Estimation $\hat{\beta }(t)$

Besides, the integral sliding mode function can be computed as

$$\begin{aligned} S(t)=\left\{ \begin{array}{l} {\left[ \begin{array}{c@{\quad }c@{\quad }c} -0.3&-0.1&-0.1 \end{array} \right] \hat{x}(t)}\quad {-\left[ \begin{array}{c@{\quad }c@{\quad }c} -0.16 &{} -0.06 &{} -0.09 \end{array} \right] \hat{x}(t-\tau )}\\ {-\left[ \begin{array}{c@{\quad }c@{\quad }c} 0.7425 &{} 0.2771 &{} 0.1349 \end{array} \right] \int _{0}^{t}\hat{x}(s)ds}\\ {+\left[ \begin{array}{c@{\quad }c@{\quad }c} 0.3848 &{} 0.1520 &{} 0.1694 \end{array} \right] \int _{0}^{t}\hat{x}(s-\tau )ds,}\qquad \quad i=1, \\ \left[ \begin{array}{c@{\quad }c@{\quad }c} -0.3 &{} -0.1 &{} -0.1 \end{array} \right] \hat{x}(t)\quad -\left[ \begin{array}{c@{\quad }c@{\quad }c} -0.16 &{} -0.06 &{} -0.09 \end{array} \right] \hat{x}(t-\tau ) \\ -\left[ \begin{array}{c@{\quad }c@{\quad }c} 0.7753 &{} -0.0450 &{} 0.1018 \end{array} \right] \int _{0}^{t}\hat{x}(s)ds\\ {+\left[ \begin{array}{c@{\quad }c@{\quad }c} 0.3978 &{} -0.0123 &{} 0.1239 \end{array} \right] \int _{0}^{t}\hat{x}(s-\tau )ds},\qquad \quad i=2. \end{array} \right. \end{aligned}$$

(45)

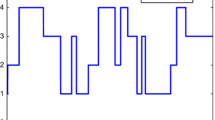
The simulation results are provided in Figs. 1, 2, 3, 4, 5 and 6. Figure 1 shows the switching signal r(t), and Fig. 2 plots the state responses of the error estimation system under adaptive SMC law (37). The state estimation responses and the integral sliding mode surface are shown in Figs. 3, 4. Figures 5, 6 depict the estimated values $\hat{\alpha }(t)$ and $\hat{\beta }(t)$, respectively. It can be seen from Figs. 5, 6 that $\hat{ \alpha }(t)$ and $\hat{\beta }(t)$ are bounded and the trajectories of e(t) are convergent, which can demonstrate the validity of the proposed method.

6 Conclusion

The problem of robust adaptive SMC for uncertain neutral MJSs with unknown nonlinearity and unmeasured states has been investigated in this paper. The upper bounds of the nonlinear term are unknown for control design in this study. An appropriate integral sliding mode surface has been constructed such that the reduced-order equivalent sliding motion can adjust the effect of the chattering phenomenon in the plant. A sufficient condition of stochastic stability of the overall closed-loop system can be achieved in terms of LMIs based on SMC strategy. Finally, a numerical example has illustrated the effectiveness of the proposed scheme.