Abstract
We study price formation in intraday electricity markets in the presence of asymmetric information and intermittent generation. We use stochastic control theory to identify optimal strategies of agents with market impact and exhibit the Nash equilibrium in closed form for a finite number of agents as well as in the asymptotic setting of Mean field games. We show that our model is able to reproduce some empirical facts observed in the market (price impact, volatility), and allows producers to deal with risks and costs related to intermittent renewable generation.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The world electricity markets are presently undergoing a major transformation driven by the transition towards a carbon-free energy system. The intraday markets are increasingly used by the renewable producers to compensate forecast errors. This improves market liquidity and at the same time creates feedback effects of the renewable generation on the market price, leading to negative correlations between renewable infeed and prices, and, negative impact on the revenues of renewable producers.
The aim of this paper is to build an equilibrium model for the intraday electricity market, to understand the price formation and identify optimal strategies for renewable producers in the setting where renewable generation forecasts may affect market prices. We consider renewable producers, optimizing their revenues based on imperfect forecasts of terminal production. The actions of each agent impact the market, leading to a stochastic game where players interact through the market price. We exhibit a closed-form Nash equilibrium for this game in the linear-quadratic setting, first for a finite number of agents with perfect information, and then in the asymptotic Mean field game setting, with imperfect information. We then show by numerical simulations that our model reproduces the observed stylized features of the market price, such as the volatility patterns and the market impact.
Correlations between renewable infeed and intraday market prices have been studied by a number of authors. Kiesel and Paraschiv [10] perform an econometric analysis of the German intraday market and show that a deeper penetration of renewable energies increases market liquidity and price-infeed correlations. Karanfil and Li [9] draw similar conclusions on the Danish market, and exhibit the impact of renewable energies on price and volatility. Gruet, Rowińska and Veraart [14] establish a negative correlation between the wind energy penetration and the day ahead market prices. Jonsson et al. [8] show not only prices are negatively correlated with the penetration of intermittent energies but also that the latter modifies significantly the spot price distribution.
Optimal strategies in the intraday market for a single wind energy producer have already been studied. In the price-taker setting, Garnier and Madlener [6] solve a discrete optimal trading problem to arbitrate between immediate and delayed trading when price and production forecast are uncertain. In [13], Morales et al. consider a multimarket setting to derive an optimal bidding strategy in the day ahead and adjustment markets while minimizing the cost in the balancing market. This approach has been enhanced by Madsen et al., [16] and then by Delikaraoglou et al. [5] , where the wind energy producer is first a price maker in the balancing market , and then in both the spot and balancing markets. Still in the price-maker setting, continuous approaches have also been developed. Aïd, Gruet and Pham [1], consider the optimal trading rate and power generation for producer with uncertain terminal residual demand. Tan and Tankov [15] develop an optimal trading model with a quantified evolution of forecast uncertainty and exhibit optimal strategies depending on forecast updates. We differ from the latter by considering an equilibrium setting with many agents and determining the market price as the result of their interactions.
Explicit results for dynamic equilibria are often difficult to obtain. In particular, Nash equilibria often lead to coupled Partial Differential Equation (PDE) systems. In the imperfect information setting, the problem may be simplified by assuming a continuum of agents and using the Mean field game (MFG) approach.
The Mean field games are stochastic differential games with a large number of symmetric agents, which were originally studied by Lions and Lasry [12] and Huang, Caines, and Malhamé [7]. The equilibrium of such a game is characterized through a coupled system of a Hamilton-Jacobi-Bellman and a Fokker-Planck equation. Carmona and Delarue [3] proposed an alternative way to formalize the system inspired by the Pontryagin principle and relating the Mean field game solution to a McKean-Vlasov Forward Backward Stochastic Differential Equation (FBSDE). From the Mean field game solution one can derive an \(\varepsilon \)-Nash equilibrium of the corresponding N-player game.
Financial markets and energy systems are a natural domain of applications of MFG. Alasseur, Tahar and Matoussi [2] develop a model for the optimal management of energy storage and distribution in a smart grid system through an extended MFG. Casgrain and Jaimungal [4] apply it to optimal trade execution with price impact and deterministic terminal liquidation condition. They dealt with incomplete information and heterogeneous sub-populations of agents.
The paper is organized as follows. Section 2 describes the main elements of the model. Section 3 is devoted to the setting of complete information, where each agent observes the production forecast of all other agents. In Sect. 4, we consider a more realistic setting, where each agent observes only its own production forecast as well as the national production forecast. In Sect. 5 we perform empirical analysis of intraday market and confront it to the theoretical results obtained. Section 6 concludes the paper.
2 The Model
We place ourselves in the intraday market for a given delivery hour starting at time T, where time 0 corresponds to the opening time of the market. We assume that market participants can trade during the entire period [0, T].
To model the price and the forecasts, we introduce a filtered probability space \((\varOmega , \mathcal {F}, \mathbb {F}:=(\mathcal {F}_t)_{t \in [0,T]} ,\mathbb {P})\) to which all processes are adapted. As the agents’ strategies may impact the market price, we distinguish the price without price impact or fundamental price \(S:=(S_t)_{t \in [0,T]}\) from the market price \(P:=(P_t)_{t \in [0,T]}\), where the market impact is included.
We consider small renewable energy producers that use the intraday market to manage the volume risk associated to the imperfect production forecast. They observe a common national production forecast. In addition, each agent has access to the individual production forecast, which may or may not be observed by other agents. We assume that the forecast process of \(i^{th}\) renewable producer at time t is given by \(X^i_t := \overline{X}_t + \check{X}_t^i\), where \(\overline{X}: = (\overline{X}_t)_{t \in [0,T]}\) is common for all agents (one can see this component as the national forecast), and the processes \(\check{X}^i := (\check{X}_t^i)_{t\in [0,T]}\) for \(i = 1, \dots , N\) represent the individual production forecast of each renewable producer. Each small renewable producer aims to maximise her gain from trading in the market where they take their positions denoted \(\phi ^i := (\phi ^{i}_t)_{t \in [0,T]}\) for \(i = 1, \dots , N\). The agents control their positions by choosing the trading rate, denoted by \(\dot{\phi }^i_t\), \(i = 1, \dots ,N\), at time t. They also face a terminal volume constraint \(\phi ^i_T = X^i_T\), which is enforced as a penalty. In Sects. 4, we use a generic agent to model the renewable producers in the Mean field setting. The agent has the same characteristics and goals as the ones of the small renewable energy producers above. The forecast process of this producer at time t is denoted \(X_t = \overline{X}_t + \check{X}_t\), her state process position is given by \(\phi :=(\phi _t)_{t \in [0,T]}\) and controlled by \(\dot{\phi }:=(\dot{\phi }_t)_{t \in [0,T]}\).
In the following sections, we say that a strategy \(\dot{\phi }^{i}\), \(i = 1, \dots , N\) (resp \(\dot{\phi }\)), is admissible if it is \(\mathbb F\)-adapted and square integrable.
3 A Complete Information Game
In this section we place ourselves in a complete information setting to find the unique Nash equilibrium. We assume that there are N identical agents in the market and they all observe the individual production forecast of the other agents. The filtration \( \mathbb {F}:=(\mathcal {F}_t)_{t \in [0,T]}\) models the information available to all of them. Without loss of generality, we assume that the initial position is \(\phi ^i_{0} = 0\) for all \(i = 1, \dots , N\), so that the position of the \(i^{th}\) agent at time t is given by \(\phi ^i_t = \int _{0}^{t}\dot{\phi ^i_s}ds\). The strategies impact the market price P as follows:
where \(\bar{\phi }^N_t = \frac{1}{N}\sum _{i=1}^N \phi ^i_t\) is the average position of the agents and a is a constant. The agents trading in the market at time t incur an instantaneous cost,
for \(i^{th}\) agent. The first term represents the actual cost of buying the electricity, and the second term represents the cost of trading, where \(\alpha (.)\) is a continuous strictly positive function on [0, T] reflecting the variation of market liquidity at the approach of the delivery date.
The processes S and \((X^i)_{i=1}^N\) satisfy the following assumption.
Assumption 1
The processes S and \((X^i)_{i=1}^N\) are square integrable martingales with respect to the filtration \(\mathbb F\).
Each producer wishes to maximize the objective function:
where \(\lambda \) determines the strength of the imbalance penalty and \(\phi ^{-i}:= (\phi ^1,\dots , \phi ^{i-1}, \phi ^{i+1}, \dots , \phi ^N)\) is the vector of all positions except \(i^{th}\) agent’s one.
The optimal strategy of each player depends on other players’ actions and we want to describe the resulting dynamical equilibrium, which we define formally below.
Definition 1 (Nash equilibrium)
We say that \((\dot{\phi }^{i*})_{i = 1}^N\) is a Nash equilibrium for the N-player game if it is a vector of admissible strategies, and for each \(i=1,\dots , N\),
for any other admissible strategy \(\dot{\phi }^{i}\) of player i in the market.
The following theorem characterizes the Nash equilibrium of the N-player game. In the theorem, we denote the average forecast process by \(\overline{X}^N_t:= \frac{1}{N}\sum _{i=1}^N X^i_t\) and use the following shorthand notation:
Theorem 2
Under Assumption 1, the unique Nash equilibrium in the complete information N-player game is given by
The equilibrium price has the following shape:
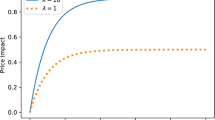
From the expression of the equilibrium price (5) in Theorem 2, we observe that the price impact is composed of a deterministic part, a path dependent stochastic part relying on the past values of S and \(\overline{X}\). These processes both play a symmetric role in the price impact up to some coefficients.
Let us consider a finite number of players and let the penalization parameter \(\lambda \) go to infinity. Then, from the expression (5) of \(\overline{\phi }^{N*}\), we can derive, that the price impact depends only on the aggregate production forecast and the final aggregate position matches exactly with the final production forecast:
The complete information setting is questionable since one could argue that, in practice, the producers do not observe the individual forecasts of other players. The complexity of determining a Nash equilibrium in a partial information setting motivates us to consider the partial information problem in the Mean field setting.
4 An Incomplete Information Game
In this section we assume that the agents do not observe each other’s individual production forecasts and consider the associated Mean field game. We then investigate on the existence of an \(\varepsilon \)-Nash equilibrium approximation in the N-player incomplete information game.
We consider a generic agent, and the filtration \(\mathbb F\) contains the information available to this agent. In addition we introduce a smaller filtration, containing the common noise and denoted by \(\mathbb F^0\). This filtration contains the information about the fundamental price and common part of the production forecast of the generic agent.
Throughout the paper and for any \(\mathbb {F}\)-adapted process \((\zeta _t)_{t \in [0,T]}\), we will denote \(\bar{\zeta }_t = \mathbb {E}[\zeta _t |\mathcal {F}^0_t]\). The game is now modeled by the interaction of agents through the conditional distribution flow \(\mu ^{\phi }_t:= \mathcal {L}(\phi _t|\mathcal {F}^0_t)\) of the state process. In the price impact function defined in the previous section, expectation with respect to the empirical measure, will be replaced by an integral with respect to the measure flow such that the market price is now given by:
The generic agent wants to maximize the objective function:
We now define what is meant be a Mean field equilibrium and make some additional assumptions:
Definition 2 (Mean field equilibrium)
An admissible strategy \(\dot{\phi }^*\) is a Mean field equilibrium if it maximizes (7) and \(\bar{\phi } = \bar{\phi }^*\).
Assumption 3
-
The process X is a square integrable martingale with respect to the filtration \(\mathbb F\).
-
The process S and the process \(\overline{X}\), defined by \(\overline{X}_t := \mathbb E[X_t|\mathcal F^ 0_t]\) for \(0\le t\le T\), are square integrable martingales with respect to the filtration \(\mathbb F^0\).
Note that if X is an \(\mathbb F\)-martingale, then \(\overline{X}\) is by construction an \(\mathbb F^0\)-martingale, but it may not necessarily be a martingale in the larger filtration \(\mathbb F\).
The following theorem characterizes the Mean field equilibrium in our setting. In the theorem we use the same shorthand notation (4) as before.
Theorem 4
Under Assumption 3, the unique Mean field equilibrium is given by
The equilibrium price has the following shape:
We now would like to construct an approximate equilibrium in the N-player setting and quantify how close this approximate equilibrium will be to the true solution. To address this question, both the N-agent problem and the Mean field problem must be defined on the same probability space.
Assumption 5
-
The process S is a square integrable martingale with respect to the filtration \(\mathbb F^0\).
-
The process \(\bar{X}\) and the processes \((X^i)_{i=1}^N\) are square integrable martingale with respect to the filtration \(\mathbb F\).
-
For \(i=1,\dots ,N\), almost surely, \(\mathbb E[X_t|\mathcal F^0_t] = \mathbb E[X^i_t|\mathcal F^0_t]:=\overline{X}_t\), \(i=1,\dots ,N\).
-
The processes \((\check{X}^i)_{i=1}^N\) defined by \(\check{X}^i_t = X^i_t - \overline{X}_t\) for \(t\in [0,T]\), are orthogonal square integrable martingales with respect to the filtration \(\mathbb F\), which are identically distributed.
Definition 3
(\(\varepsilon \)-Nash equilibrium). We say that a strategy \((\dot{\phi }^{i*})^N_{i = 1}\) is an \(\varepsilon \)-Nash equilibrium for the N-player game if it is admissible and:
for any other admissible control \(\dot{\phi }^{i}\).
Proposition 1
Under assumption 5, we define an admissible strategy for the N-player game as follows.
Then, for any \(\varepsilon >0\), there exists \(N_\varepsilon \) with \(N_\varepsilon = \mathcal {O}(\frac{1}{\varepsilon ^2})\), such that for all N with \(N\ge N_\varepsilon \), this strategy is an \(\varepsilon \)-Nash equilibrium of the N-player game.
To complete the analysis led in the previous part, we would like to numerically confront the model results to some empirical findings.
5 Numerical Illustration
Volatility and price impact showed to be characteristics of interest in empirical studies. As they affect strategies of the agents, we want the model to capture these patterns in order to manage the risks and costs related to renewable production uncertainty.
5.1 Data Presentation
We use the limit order book data from the intraday EPEX market of January 2017 for the Germany delivery zone to perform the analyses on the market price. To exhibit a linear price impact and calibrate the volatility of the market price P defined in the theoretic model, we used the observed midquote price that we denote \(\tilde{P}\). The volatility of the production forecast that we denote \(\tilde{X}\), is also calibrated from empirical wind energy forecasts over January 2015.
In order to conduct these empirical studies we assume the following dynamics for \(\tilde{P}\) and \(\tilde{X}\):
where \(W^{\tilde{P}}, W^{\tilde{X}}\) are \(\mathbb {F}\)-Brownian motions, and \(\mu \), \(\sigma \), \(\tilde{\sigma }\) are \(\mathbb {F}\)-adapted processes. For the simulated data, we assume all through Sect. 5 the following dynamics:
where \(\sigma ^s\),\(\sigma ^0\) and \(\sigma ^x\) are deterministic functions and \(W^0,B^0, B^i\) are \(\mathbb {F}\)-Brownian motions in the complete information setting (respectively \(\mathbb {F}^0\) for \(W^0, B^0\) and \(\mathbb {F}^i\) for \(B^i\) in the incomplete setting). We also assume all through Sect. 5 the liquidity function \(\alpha (.)\) is given by:
The model parameters are specified in Table 1.
5.2 Price Impact
In this section, we compare the simulated price impact of the model to the empirical one. In the empirical data, the market price is identified to the observed midquote price, and we make the simplifying assumption that we can derive the price impact from this single variable. We regress the midquote price shift just before and just after a transaction on the traded volumes:
as the empirical analogous of the linear price impact in the model given by expression (1). The volume sign corresponds to the side of the order that trigger the transaction: if it is sell order then the sign is −, if it is a buy order it is \(+\).
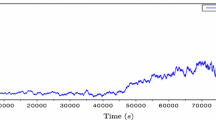
The results of this study are available in Fig. 1. We present the price impact for several delivery hours, the regression was made over more than 4750 data points for each of them. The price shifts are heteroscedastic and seem to be less significant for small volumes. Despite the small volume effect, the p-value and the \(R^2\) indicate a significant regression coefficient and are coherent with the price impact assumption. In Fig. 2, we draw a trajectory of the fundamental price S starting from \(t = 0\) an hour before the delivery time, to the delivery time T. We also draw the market price P associated with the different homogeneous settings studied in the paper: the N-player Nash equilibrium, the \(\varepsilon \)-Nash equilibrium, and the Mean field one.
The price impact matches with the production forecast changes. If producers think they have underestimated their production forecast with respect to their supply commitment (negative values of the production forecast changes process), there will be an excess of sell positions in the market, thus the price impact is negative. On the contrary, if they think they overestimated the final production forecast, there will be a lack of supply in the market and a negative price impact.
5.3 Volatility
We want to investigate whether or not the uncertain production forecast has an impact on the market price variations, and show that the volatility observed empirically in the intraday market can be explained by this phenomenon.
We are interested in estimating the instantaneous volatility \(\sigma \) of \(\tilde{P}\), introduced in the dynamics (8). Following [11], we use a kernel-based non parametric estimator of the instantaneous volatility:
where \(K_h(x)= \frac{1}{h}K(\frac{x}{h})\) and K(.) is the Epanechnikov kernel. We used a generic choice: \(h = 0.1\) hour for all the delivery dates and hours of January. We also estimate the volatility \(\tilde{\sigma }\) of the empirical wind production forecast \(\tilde{X}\) introduced in the dynamic (8) using the same method with \(h = 1\) hour, and use it to calibrate the volatility of the production forecasts \(\sigma ^0\) and \(\sigma ^x\) in the model.
In Fig. 3, the first graph and the second graph represent respectively the empirical volatility of the midquote \(\tilde{P}\) and the estimated variations of the Nash equilibrium market price P, for different hours in function of the time to delivery. During peak hours, activity and thus liquidity in the market is more important. In order to adapt the liquidity to the delivery hour considered in the model, we chose different levels of the liquidity coefficients \(\alpha \) and \(\beta \) for the function \(\alpha (.)\) defined in (9), available in Table 2. Apart from these coefficients, all the other parameters are the same as in Table 1. The model reproduces the increasing shape of the empirical market price volatility when we approach the delivery time. Moreover, by adapting the liquidity coefficients, the model also captures the different levels of volatility according to the delivery hour.
6 Conclusion
We developed a linear quadratic model and derived a dynamic price equilibrium in the intraday electricity market. We focused on the integration of renewable energies in the energy supply system. We considered intermittent energy producers first in a complete information setting, then, in a more realistic incomplete information one.
The model provides closed form optimal strategies for agents taking into account their own incertitude. It leads to a dynamic equilibrium on the market, and reproduces some important empirical patterns such as the price impact and the volatility. For these reasons, a practical use of this mathematical tool might help to better optimize the renewable furniture system.
References
Aïd, R., Gruet, P., Pham, H.: An optimal trading problem in intraday electricity markets. Math. Financ. Econ. 10(1), 49–85 (2016). https://doi.org/10.1007/s11579-015-0150-8
Alasseur, C., Ben Tahar, I., Matoussi, A.: An extended mean field game for storage in smart grids. J. Optim. Theory Appl. 184(2), 644–670 (2020)
Carmona, R., Delarue, F.: Probabilistic Theory of Mean Field Games with Applications I. Springer, Cham (2018)
Casgrain, P., Jaimungal, S.: Mean field games with partial information for algorithmic trading. Technical report, arXiv.org (2019)
Delikaraoglou, S., Papakonstantinou, A., Ordoudis, C., Pinson, P.: Price-maker wind power producer participating in a joint day-ahead and real-time market. In: 2015 12th International Conference on the European Energy Market (EEM), pp. 1–5. IEEE (2015)
Garnier, E., Madlener, R.: Balancing forecast errors in continuous-trade intraday markets. Energy Syst. 6(3), 361–388 (2015). https://doi.org/10.1007/s12667-015-0143-y
Huang, M., Malhamé, R.P., Caines, P.E., et al.: Large population stochastic dynamic games: closed-loop mckean-vlasov systems and the nash certainty equivalence principle. Commun. Inf. Syst. 6(3), 221–252 (2006)
Jónsson, T., Pinson, P., Madsen, H.: On the market impact of wind energy forecasts. Energy Econ. 32(2), 313–320 (2010)
Karanfil, F., Li, Y.: Wind up with continuous intraday electricity markets? The integration of large-share wind power generation in denmark. Chaire European Electricity Markets working paper (2015)
Kiesel, R., Paraschiv, F.: Econometric analysis of 15-minute intraday electricity prices. Energy Econ. 64, 77–90 (2017)
Kristensen, D.: Nonparametric filtering of the realized spot volatility: a kernel-based approach. Econom. Theor. 26(1), 60–93 (2010)
Lasry, J.M., Lions, P.L.: Mean field games. Japan. J. Math. 2(1), 229–260 (2007)
Morales, J.M., Conejo, A.J., Pérez-Ruiz, J.: Short-term trading for a wind power producer. IEEE Trans. Power Syst. 25(1), 554–564 (2010)
Rowińska, P.A., Veraart, A., Gruet, P.: A multifactor approach to modelling the impact of wind energy on electricity spot prices (2018). SSRN 3110554
Tan, Z., Tankov, P.: Optimal trading policies for wind energy producer. SIAM J. Financ. Math. 9(1), 315–346 (2018)
Zugno, M., Morales, J.M., Pinson, P., Madsen, H.: Pool strategy of a price-maker wind power producer. IEEE Trans. Power Syst. 28(3), 3440–3450 (2013)
Acknowledgements
Financial support from LABEX ECODEC (ANR-11-IDEX-0003/Labex Ecodec/ANR-11-LABX-0047), FIME Research Initiative and Agence Nationale de Recherche (ANR project EcoREES) is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
A Appendix
A Appendix
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Féron, O., Tankov, P., Tinsi, L. (2021). Price Formation and Optimal Trading in Intraday Electricity Markets. In: Lasaulce, S., Mertikopoulos, P., Orda, A. (eds) Network Games, Control and Optimization. NETGCOOP 2021. Communications in Computer and Information Science, vol 1354. Springer, Cham. https://doi.org/10.1007/978-3-030-87473-5_26
Download citation
DOI: https://doi.org/10.1007/978-3-030-87473-5_26
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-87472-8
Online ISBN: 978-3-030-87473-5
eBook Packages: Computer ScienceComputer Science (R0)