An optimal trading problem in intraday electricity markets

Abstract

We consider the problem of optimal trading for a power producer in the context of intraday electricity markets. The aim is to minimize the imbalance cost induced by the random residual demand in electricity, i.e. the consumption from the clients minus the production from renewable energy. For a simple linear price impact model and a quadratic criterion, we explicitly obtain approximate optimal strategies in the intraday market and thermal power generation, and exhibit some remarkable properties of the trading rate. Furthermore, we study the case when there are jumps on the demand forecast and on the intraday price, typically due to error in the prediction of wind power generation. Finally, we solve the problem when taking into account delay constraints in thermal power production.

1 Introduction

The development of renewable energy sources in Europe as a response to global climate change has led to an increase of exchange in the intraday electricity markets. For instance, the exchanged volume on the European Energy Exchange (EEX) for Germany has grown from 2 TWh in 2008 to 25 TWh in 2013. This increase is mainly due to the level of forecasting error of wind production, which leads power producers owning a large share of wind production to turn more than ever to intraday markets in order to adjust their position and avoid penalties for their imbalances. The accuracy of forecasts for renewable power production from wind and solar may vary considerably depending on the agreggation level (local vs regional forecast) and the time horizon. For a complete survey on this problem, the reader can consult Giebel et al. [5], and may have in mind that the root mean square error (RMSE) of the error forecast for the production of a wind farm in 6 h can reach 20 % of its installed capacity. Many different intraday markets have been designed and are subject to different sets of regulation. But, in all cases, intraday markets offer power producer the possibility to buy or sell power for the next (say) 9–32 h (case of the French electricity market of EpexSpot). These trades can occur after the closing of the day-ahead market or during the clearing phase of the day-ahead market. Moreover, there is a clear evidence that traders take the existence of some market impact into account. Indeed, for a given hour of delivery, the average volume sold or purchased in 2014 is of order of magnitude 340 MW while the average trade order volume is of approximate size 20 MW (source: Epexspot). This point indicates that traders split their sales or their purchases into small quantities to reduce their impact.

The problem of trading management in the intraday electricity market for a balancing purpose has already drawn the attention in the literature. Henriot [7] studied the problem of how the intraday market can help a power producer to deal with the wind production error forecast in a stylized discrete time model. In his model, the power producer is a wind producer who is trying to minimize her sourcing cost on the intraday market while maintaining a balance position between her forecast production and her sales. Henriot’s model takes into account the impact of the wind power producer on the intraday price with a deterministic inverse demand function, and the intraday price is not a risk factor. The only risk factor comes from the error forecast of the wind production and its auto-correlation. Garnier and Madlener [4] studies the trade-off between entering into a deal in the intraday market right now and postponing it in a discrete time decision model where intraday prices follow a geometric Brownian model and wind production error forecast follows an arithmetic Brownian motion. In their framework, the power producer is supposed to have no impact on intraday prices. Liquidity risk is taken into account as a probability of not finding a counter-party at the next trading window.

In this paper, we consider a power producer having at disposal some renewable energy sources (e.g. wind and solar), and thermal plants (e.g. coal, gas, oil, and nuclear sources), and who can buy/sell energy in the intraday markets. Her purpose is to minimize the imbalance cost, i.e. the cost induced by the difference between the demand of her clients minus the electricity produced and traded, plus the production and trading costs. In contrast with thermal power plants whose generation can be controlled, the power generated from renewable sources is subject to non controllable fluctuations or risks (wind speed, weather forecast) and is then considered here as a random factor just like the demand. We then call the residual demand the demand minus the energy generated by renewable energy. Thus, the problem of the power producer is to minimize the imbalance costs arising from her residual demand by relying both on her own controllable thermal assets and on the intraday market. As in [4], we assume that the power producer has access to a continuously updated forecast of the residual demand to be satisfied at terminal date T and that this forecast evolves randomly. Moreover, the intraday price for delivery at time T evolves also randomly and is correlated with the residual demand forecast. However, compared with [4], the intraday market can be used for optimization purposes. We develop a model that allows us to study how power producers can take advantage of the interaction between the dynamics of the residual demand forecast and the dynamics of the intraday prices.

Our model shares some links with optimal order execution problems, as introduced in the seminal paper by Almgren and Chriss [2], and then largely studied in the recent literature, see e.g. the survey paper [10]. In our context, the original feature with respect to this literature is the consideration of a random demand target and the possibility for the agent to use her thermal power production. This connection with optimal execution is fruitful in the sense that it allows us to take into account several features of intraday markets while maintaining the tractability of the model sufficiently high to allow analytical solutions. Hence, we take into account liquidity risk through a market impact, both permanent and temporary, on the electricity price generated by a power producer when trading in the intraday market. As in optimal execution problems, this impact is always in the adverse direction: when the producer sells, the price decreases and when she buys, the price increases. Our setting is a continuous-time decision problem representing the possibility for the producer to make a deal at each time she wants and not only at pre-specified windows. Moreover, it is general enough as it permits us to study the limiting cases of a pure retailer (no production function), a pure trader (no demand commitment) and an integrated player (player owning both clients and generation), small or large.

The main goal of this paper is to derive analytical results, which provide explicit solutions for the (approximate) optimal control, hence giving enlightening economic interpretations of the optimal trading strategies. In order to achieve such analytical tractability, we have to make some simplifying assumptions on the dynamics of the price process and of the residual demand forecast, as well as on the cost function, assumed to be of quadratic form meaning a simple linear growth of the marginal cost of production with respect to the production level. We first consider a simple model for a continuous price process with linear impact, and demand forecast driven by an arithmetic Brownian motion, and neglect in a first step the delay of production when using thermal power plants. We then study an auxiliary control problem by relaxing the nonnegativity constraint on the generation level, for which we are able to derive explicit solutions. The approximation error induced by this relaxation constraint is analyzed. In next steps, we consider more realistic situations and investigate two extensions: (i) On one hand, we incorporate the case where the residual demand forecast is subject to sudden changes, related to prediction error for wind or solar power production, which may be quite important due to the difficulties for estimating wind speed and forecasting weather, see [3]. This is formalized by jumps in the dynamics of the demand process, and consequently also on the price process. Again, we are able to obtain explicit solutions. Actually, the key tool in the derivation of all these analytical results is a suitable treatment of the linear-quadratic structure of our stochastic control problem. (ii) On the other hand, we introduce natural delay constraints in the production, and show how the optimal decision problem can be explicitly solved by a suitable reduction to a problem without delay.

Our (approximate) optimal trading strategies present some remarkable properties. When the intraday price process is a martingale, the optimal trading rate inherits the martingale property, which implies in particular that the net position of electricity shares has a constant growth rate on average. Moreover, the optimal strategy consists in making at each time the forecast marginal cost equal to the forecast intraday price. This property follows the common sense of intraday traders. Consequently, if the producer has made sales or purchases on the day-ahead such that her forecast marginal cost equals the day-ahead price and if the initial condition of the intraday price is the day-ahead price, thus, on average, the producer optimal trading rate is zero. This fact is no longer true when the demand forecast and the price follow processes with jumps. In this case, the optimal trading rate is a supermartingale or a submartingale depending on the relative probability and size of positive and negative jumps on the price process. For this reason, contrary to the case without jumps, the power producer may need to have a non-zero initial trading rate even if she has made sales or purchases on the day-ahead such that her forecast marginal cost equals the day-ahead price and if the initial condition of the intraday price is the day-ahead price. We also quantify explicitly the impact of delay in production on the trading strategies. When the price process is a martingale, the net inventory in electricity shares grows linearly on average, with a change of slope (which is smaller) at the time decision for the production.

The outline of the paper is organized as follows. We formulate the optimal trading problem in Sect. 2. In Sect. 3, we study the optimal trading problem without delay. We first solve explicitly the auxiliary optimal execution problem, and then study the approximation on the solution to the original problem, by focusing in particular on the error asymptotics. We illustrate our results with some numerical tests and simulations. We extend in Sect. 4 our results to the case where jumps in demand forecast may arise. In Sect. 5, we show how the optimal trading problem with delay in production can be reduced to a problem without delay, and then leads to explicit solutions. Finally, the Appendix collects the explicit derivations of our solutions, which are justified by verification theorems.

2 Problem formulation

We consider an agent on an intraday energy market, who is required to guarantee her equilibrium supply/demand for a given fixed time T: she has to satisfy the demand of her customers by purchase/sale of energy on the intraday market at time T and also by means of her thermal power generation. We denote by $X_t$ the net position of sales/purchases of electricity at time $t \le T$ for a delivery at terminal time T, assumed to be described by an absolutely continuous trajectory up to time T, and by $q_t = \dot{X}_t$ the trading rate: $q_t > 0$ means an instantaneous purchase of electricity, while $q_t < 0$ represents an instantaneous sale at time t:

$$\begin{aligned} X_t= & {} X_0 + \int _0^t q_s ds, \quad 0 \le t \le T. \end{aligned}$$

(2.1)

Given the trading rate, the transactions occur with a market price impact:

$$\begin{aligned} P_t(q)= & {} {\hat{P}}_t + \int _0^t g(q_s) ds + f(q_t). \end{aligned}$$

Here, $({\hat{P}}_t)_t$ is the unaffected intraday electricity price process on a filtered probability space $(\Omega ,\mathcal {F},\mathbb {F}=(\mathcal {F}_t)_{t\in [0,T]},\mathbb {P})$, carrying some part of randomness of the market, and following the terminology in the seminal paper by Almgren and Chriss [2], the term $f(q_t)$ refers to the temporary price impact, while $\int _0^t g(q_s)ds$ describes the permanent price impact. The price $(\hat{P}_t)_t$ may be seen as a forward price, evolving in real time, for delivery at time T. Let us then denote by Y the intraday electricity price impacted by the past trading rate q of the agent, defined by:

$$\begin{aligned} Y_t:= & {} {\hat{P}}_t + \int _0^t g(q_s) ds. \end{aligned}$$

We assume that $Y_t$ is observable and quoted, which means actually that the agent is a large trader and electricity producer, whose actions directly impact the intraday electricity price. The case where the agent is a small producer can be also dealt with by simply considering a zero permanent impact function $g \equiv 0$. Notice that the transacted price is equal to the sum of the quoted price Y and the temporary price impact:

$$\begin{aligned} P_t(q)= & {} Y_t + f(q_t). \end{aligned}$$

(2.2)

The residual demand $D_T$ is the consumption of clients of the agent minus the production from renewable energy at terminal date T, and we assume that the agent has access to a continuously updated forecast $(D_t)_t$ of the residual demand. The agent can use her thermal power production with a quantity $\xi$ at cost $c(\xi )$ in order to match as close as possible the target demand $D_T$. In practice, generation of electricity cannot be obtained instantaneously and needs a delay to reach a required level of production. Hence, the decision to produce a quantity $\xi$ should be taken at time $T-h$, where $h \in [0,T]$ is the delay. Thus, for a controlled trading rate $q = (q_t)_t \in \mathcal {A}$, the set of real-valued $\mathbb {F}$-adapted processes satisfying some integrability conditions to be precised later, a production quantity $\xi \in L^0_+(\mathcal {F}_{T-h})$, the set of nonnegative $\mathcal {F}_{T-h}$-measurable random variables, the total cost is:

$$\begin{aligned} \int _0^T q_t P_t(q) dt + C(D_T-X_T,\xi ):= & {} \int _0^T q_t P_t(q) dt + c(\xi ) + \frac{\eta }{2} (D_T-X_T - \xi )^2. \end{aligned}$$

(2.3)

The first term in (2.3) represents the total running cost arising from the trading in the intraday electricity market, and the last term, where $\eta > 0$, represents the quadratic penalization when the net position in sales/purchases of electricity $X_T + \xi$ (including the production quantity $\xi$ at cost $c(\xi )$) at terminal date T does not fit the effective demand $D_T$. The objective of the agent is then to minimize over q and $\xi$ the expected total cost:

$$\begin{aligned} \hbox { minimize over } q \in \mathcal {A}, \; \xi \in L^0_+(\mathcal {F}_{T-h})&\mathbb {E}\Big [ \int _0^T q_t P_t(q) dt + C(D_T-X_T,\xi ) \Big ]. \end{aligned}$$

(2.4)

Remark 2.1

• (1) The imbalance of the agent ($D_T-X_T - \xi$) is penalized by the transport system operator (TSO) because if a producer generates less power than her demand, then the TSO has to buy the energy from another producer to insure that the total production of all producers is equal to the total demand of the electric system. When the producer generates too much power, she is not truly penalized, but this excess of energy is bought back by the TSO at a price that is lower than the marginal cost of the producer. The penalization term in the objective function above is a simplification of the effective penalization process that can be found in real electricity markets. For instance, the penalization of imbalances in the French electricity market depends both on the sign of the imbalance of the electricity system and on the price of imbalances (see [1, chap 2, Sec. 2.2.1]). Nevertheless, the positive coefficient $\eta$ captures the main objective of the penalization process. The agent has no incentive of being either too long or too short.

• (2) On real markets, trading ends some time before the date of delivery, at which the agent has to ensure equilibrium (e.g. on the French electricity market, there is a delay of 45  mins). We do not include that practical fact in our framework, by considering that the delay is null for the sake of clarity. There is no mathematical consequence: it is enough to have in mind that the delivery and production do not really take place at T, but at T plus some delay.

• (3) The larger is $\eta$, the stronger is the incentive for the agent to be as close as possible to the equilibrium supply-demand. At the limit, when $\eta$ goes to infinity, the agent is formally constrained to fit supply and demand. However, the limiting problem when $\eta = \infty$ is not mathematically well-posed since such perfect equilibrium constraint is in general not achievable. Indeed, the demand at terminal date T is random, typically modelled via a Gaussian noise, and the inventory X which is of finite variation, may exceed or underperform with positive probability the demand $D_T$ at terminal date T. Hence, in the scenario where $X_T > D_T$, and since by nature the production quantity $\xi$ is nonnegative, it is not possible to realize the equilibrium $X_T +\xi = D_T$, even if there is no delay. In the sequel, we fix $\eta > 0$ (which may be large, but finite), and study the stochastic control problem (2.4).

• (4) The optimization problem (2.4) shares somes similarities with the optimal execution problem in limit order book studied in the seminal paper by Almgren and Chriss [2], and then extended by many authors in the literature, see e.g. the survey paper [10]. The main difference is that in the execution problem of equities, the target is to buy or sell a certain number of shares, i.e. lead $X_T$ to a fixed constant (meaning formally that $\eta$ goes to infinity) while in our intraday electricity markets context, the target is to realize the equilibrium with the random demand $D_T$, eventually with the help of production leverage $\xi$. However, in contrast with the case of constant target, it is not possible in presence of random target $D_T$ to achieve perfectly the equilibrium, which justifies the introduction of the penalty factor $\eta$ as pointed out above. $\square$

The main aim of this paper is to provide explicit (or at least approximate explicit) solutions to the optimization problem (2.4), which are easily interpreted from an economic point of view, and also allow to measure the impact of the various parameters of the model. In order to achieve this goal, we shall adapt our modeling as close as possible to the linear-quadratic framework of stochastic control, and make the following assumptions: The energy production cost function is in the quadratic form:

$$\begin{aligned} c(x)= & {} \frac{\beta }{2} x^2, \end{aligned}$$

for some $\beta > 0$. Although simple, a quadratic cost function represents the increase of the marginal cost of production with the level of production.

Remark 2.2

(Pure retailer) In the limiting case when $\beta$ goes to infinity, meaning an infinite cost of production, this corresponds to the framework where the agent never uses the production leverage and only trades in the intraday-market by solving the optimal execution problem:

$$\begin{aligned} \hbox { minimize over } q \in \mathcal {A}&\mathbb {E}\Big [ \int _0^T q_t P_t(q) dt + C(D_T-X_T,0) \Big ]. \end{aligned}$$

(2.5)

$\square$

As in Almgren and Chriss, we assume that the price impact (both permanent and temporary) is of linear form, i.e.

$$\begin{aligned} g(q) = \nu q, \qquad f(q) = \gamma q, \end{aligned}$$

for some constants $\nu \ge 0$ and $\gamma > 0$. The unaffected intraday electricity price is taken as a Bachelier model:

$$\begin{aligned} {\hat{P}}_t= & {} {\hat{P}}_0 + \sigma _0 W_t, \end{aligned}$$

(2.6)

where W is a standard Brownian motion, and $\sigma _0 > 0$ is a positive constant. Such assumption might seem a shortcoming at first sight since it allows for negative values of the unaffected price. However, in practice, for our intraday execution problem within few hours, negative prices occur only with negligible probability. This issue has been addressed in several works, see for instance Footnote 8 in [2], the comments in [10], or [6]. The martingale assumption is also standard in the market impact literature since drift effects can often be ignored due to short trading horizon. The quoted price Y, impacted by the past trading rate $q \in \mathcal {A}$, is then governed by the dynamics:

$$\begin{aligned} dY_t= & {} \nu q_t dt + \sigma _0 dW_t. \end{aligned}$$

(2.7)

The dynamics of the residual demand forecast is given by

$$\begin{aligned} dD_t= & {} \mu dt + \sigma _d dB_t, \end{aligned}$$

(2.8)

where $\mu$, $\sigma _d$ are constants, with $\sigma _d > 0$, and B is a Brownian motion correlated with W: $d<W,B>_t = \rho dt$, $\rho \in [-1,1]$.

From (2.2), one can then define the value function associated to the dynamic version of the optimal execution problem (2.4) by:

$$\begin{aligned} v(t,x,y,d):= & {} \inf _{q \in \mathcal {A}_t,\xi \in L_+^0(\mathcal {F}_{T-h})} J(t,x,y,d;q,\xi ) \end{aligned}$$

(2.9)

with

$$\begin{aligned} J(t,x,y,d;q,\xi ):= & {} \mathbb {E}\Big [ \int _t^T q_s (Y_s^{t,y} + \gamma q_s) ds + C\left( D_T^{t,d}- X_T^{t,x},\xi \right) \Big ], \end{aligned}$$

(2.10)

for $(t,x,y,d) \in [0,T]\times \mathbb {R}\times \mathbb {R}\times \mathbb {R}$, where $\mathcal {A}_t$ denotes the set of real-valued processes $q = (q_s)_{t\le s\le T}$ s.t. $q_s$ is $\mathcal {F}_s$-adapted and $\mathbb {E}\big [\int _t^T q_s^2 ds] < \infty$, $D^{t,d}$ is the solution to (2.8) starting from d at t, and given a control $q \in \mathcal {A}_t$, $Y^{t,y}$ denotes the solution to (2.7) starting from y at time t, and $X^{t,x}$ is the solution to (2.1) starting from x at t.

In a first step, we shall consider the case when there is no delay in the production, and then show in the last section of this paper how to reduce the problem with delay to a no delay problem. We shall also study the case when there are jumps in the residual demand forecast.

3 Optimal execution without delay in production

In this section, we consider the case when there is no delay in production, i.e. $h = 0$. In this case, we notice that the optimization over q and $\xi$ in (2.4) is done separately. Indeed, the production quantity $\xi \in L_+^0(\mathcal {F}_T)$ is chosen at the final date T, after the decision over the trading rate process $(q_t)_{t\in [0,T]}$ is achieved (leading to an inventory $X_T$). It is determined optimally through the optimization a.s. at T of the terminal cost $C(D_T-X_T,\xi )$, hence in feedback form by $\xi _T^* = {\hat{\xi }}^{tr+}(D_T-X_T)$ where

$$\begin{aligned} {\hat{\xi }}^{tr+}(d):= & {} \mathop {\mathrm{arg}\,\mathrm{min}}_{\xi \ge 0}\, C(d,\xi ) = \mathop {\mathrm{arg}\,\mathrm{min}}_{\xi \ge 0} \Biggl [ \frac{\beta }{2} \xi ^2 + \frac{\eta }{2} (d- \xi )^2 \Biggr ] \nonumber \\= & {} \frac{\eta }{\eta + \beta } d 1\!\!1_{d \ge 0}, \end{aligned}$$

(3.1)

the notation “$tr+$” indicating that some truncation of the negative part has been performed. The value function of problem (2.9) may then be rewritten as

$$\begin{aligned} v(t,x,y,d)= & {} \inf _{q \in \mathcal {A}_t} \mathbb {E}\Biggl [ \int _t^T q_s \left( Y_s^{t,y} + \gamma q_s\right) ds + C^+\left( D_T^{t,d}- X_T^{t,x}\right) \Biggr ], \end{aligned}$$

(3.2)

where

$$\begin{aligned} C^+(d):= & {} C(d,{\hat{\xi }}^{tr+}(d)) \nonumber \\= & {} \frac{1}{2} \frac{\eta \beta }{\eta + \beta } d^2 1\!\!1_{d\ge 0} + \frac{\eta }{2} d^2 1\!\!1_{d< 0}. \end{aligned}$$

(3.3)

and the optimal trading rate $q^*$ is derived by solving (3.2).

Due to the indicator function in $C^+$, caused by the non negativity constraint on the production quantity, there is no hope to get explicit solutions for the problem (3.2), i.e. solve explicitly the associated dynamic programming Hamilton-Jacobi-Bellman (HJB) equation. We shall then consider an auxiliary execution problem by relaxing the sign constraint on the production quantity, for which we are able to provide explicit solution. Next, we shall see how one can derive an approximate solution to the original problem in terms of this auxiliary explicit solution, and we evaluate the error and illustrate the quality of this approximation by numerical tests.

3.1 Auxiliary optimal execution problem

We consider the optimal execution problem with relaxation on the non negativity constraint of the production leverage, and thus introduce the auxiliary value function

$$\begin{aligned} {\tilde{v}}(t,x,y,d):= & {} \inf _{q \in \mathcal {A},\xi \in L^0(\mathcal {F}_T)} J(t,x,y,d;q,\xi ), \end{aligned}$$

for $(t,x,y,d) \in [0,T]\times \mathbb {R}\times \mathbb {R}\times \mathbb {R}$. By same arguments as for the derivation of (3.2), we have

$$\begin{aligned} {\tilde{v}}(t,x,y,d)= & {} \inf _{q \in \mathcal {A}} \mathbb {E}\Big [ \int _t^T q_s (Y_s^{t,y} + \gamma q_s) ds + {\tilde{C}}\left( D_T^{t,d}-X_T^{t,x}\right) \Big ], \end{aligned}$$

(3.4)

where

$$\begin{aligned} {\hat{\xi }}(d):= & {} \mathop {\mathrm{arg}\,\mathrm{min}}_{\xi \in \mathbb {R}} C(d,\xi ) = \frac{\eta }{\eta + \beta } d, \nonumber \\ {\tilde{C}}(d):= & {} C(d,{\hat{\xi }}(d)) = \frac{1}{2} \frac{\eta \beta }{\eta + \beta } d^2 = : \frac{1}{2} r(\eta ,\beta ) d^2. \end{aligned}$$

(3.5)

The function in (3.5) can be interpreted as a reduced cost function. Because the production cost function and the penalization are both quadratic, they can be reduced to a single production function where the imbalances are internalized by the producer.

The auxiliary problem (3.4)–(3.5) can be interpreted as a situation where it would be necessary to increase the demand. Allowing for negative generation is equivalent to include the possibility either to increase the demand through a price signal or to sell at a negative price on the intraday market. Those two possibilities exist on electricity markets.

By exploiting the linear-quadratic structure of the stochastic control problem (3.4), we can obtain explicit solutions for this auxiliary problem.

Theorem 3.1

The value function to (3.4) is explicitly equal to:

$$\begin{aligned} {\tilde{v}}(t,x,y,d)= & {} \frac{r(\eta ,\beta ) \left( \frac{\nu }{2}(T-t)+\gamma \right) }{ (r(\eta ,\beta ) + \nu )(T-t)+2\gamma } \big ( (d-x)^2+2\mu (T-t)(d-x)\big ) \\&+ \, \frac{T-t}{ (r(\eta ,\beta ) + \nu )(T-t)+2\gamma } \Biggl (-\frac{y^2}{2} + r(\eta ,\beta )\mu (T-t)y\Biggr ) \\&+ \, \frac{r(\eta ,\beta )(T-t)}{ (r(\eta ,\beta ) + \nu )(T-t)+2\gamma } (d-x)y \\&+ \, \gamma \frac{\sigma _0^2 + \sigma _d^2r^2(\eta ,\beta ) - 2 \rho \sigma _0\sigma _dr(\eta ,\beta )}{\big (r(\eta ,\beta ) + \nu \big )^2}\ln \Biggl ( 1 + \frac{(r(\eta ,\beta ) + \nu )(T-t)}{2\gamma }\Biggr ) \\&+ \, \frac{\sigma _d^2r(\eta ,\beta )\nu +2\rho \sigma _0\sigma _dr(\eta ,\beta ) - \sigma _0^2}{2\big (r(\eta ,\beta ) + \nu \big )}(T-t) \\&+ \, \frac{r(\eta ,\beta )\mu ^2(T-t)^2\left( \frac{\nu }{2}(T-t)+\gamma \right) }{ (r(\eta ,\beta ) + \nu )(T-t)+2\gamma }, \end{aligned}$$

for $(t,x,y,d) \in [0,T]\times \mathbb {R}\times \mathbb {R}\times \mathbb {R}$, with an optimal trading rate given in feedback form by:

$$\begin{aligned} {\hat{q}}_s= & {} {\hat{q}}\left( T-s,D_s^{t,d}-{\hat{X}}_s^{t,x,y,d},{\hat{Y}}_s^{t,x,y,d}\right) , \quad t\le s\le T \nonumber \\ {\hat{q}}(t,d,y):= & {} \frac{ r(\eta ,\beta ) (\mu t + d) - y}{(r(\eta ,\beta ) + \nu )t + 2 \gamma }. \end{aligned}$$

(3.6)

Here $({\hat{X}}^{t,x,y,d},{\hat{Y}}^{t,x,y,d},D^{t,d})$ denotes the solution to (2.1)–(2.7)–(2.8) when using the feedback control ${\hat{q}}$, and starting from (x, y, d) at time t. Finally, the optimal production leverage is given by:

$$\begin{aligned} {\hat{\xi }}_T= & {} {\hat{\xi }}\left( D_T^{t,d}-{\hat{X}}_T^{t,x,y,d}\right) = \frac{\eta }{\eta + \beta } \big (D_T^{t,d} - {\hat{X}}_T^{t,x,y,d}\big ). \end{aligned}$$

(3.7)

Proof

We look for a candidate solution to (3.4) in the quadratic form:

$$\begin{aligned} {\tilde{w}}(t,x,y,d)= & {} A(T-t) (d-x)^2 + B(T-t) y^2 + F(T-t) (d-x)y \\&+ \, G(T-t) (d-x) + H(T-t) y + K(T-t), \end{aligned}$$

for some deterministic functions A, B, F, G, H and K. Plugging this ansatz into the Hamilton-Jacobi-Bellman (HJB) equation associated to the stochastic control problem (3.4), we find that these deterministic functions should satisfy a system of Riccati equations, which can be explicitly solved. Then, by a classical verification argument, we check that this ansatz ${\tilde{w}}$ is indeed equal to ${\tilde{v}}$, with an optimal feedback control derived from the argmax in the HJB equation. The details of the proof are reported in Appendix. $\square$

Remark 3.1

(Pure trader) By sending $\beta$ to infinity in the expression of the value function ${\tilde{v}}$ and of the optimal feedback control ${\hat{q}}$, and observing that $r(\eta ,\beta )$ goes to $\eta$, we obtain the solution to the optimal execution problem (2.5) without leverage production:

$$\begin{aligned} v_{_{NP}}(t,x,y,d):= & {} \inf _{q \in \mathcal {A}} \mathbb {E}\Biggl [ \int _t^T q_s \left( Y_s^{t,y} + \gamma q_s\right) ds + C\left( D_T^{t,d}-X_T^{t,x},0\right) \Biggr ] \nonumber \\= & {} \frac{\eta \left( \frac{\nu }{2}(T-t)+\gamma \right) }{ (\eta + \nu )(T-t)+2\gamma } \big ( (d-x)^2+2\mu (T-t)(d-x)\big ) \nonumber \\&+ \, \frac{T-t}{ (\eta + \nu )(T-t)+2\gamma } \left( -\frac{y^2}{2} + \eta \mu (T-t)y\right) \nonumber \\&+ \, \frac{\eta (T-t)}{ (\eta + \nu )(T-t)+2\gamma } (d-x)y \nonumber \\&+ \, \gamma \frac{\sigma _0^2 + \sigma _d^2\eta ^2 - 2\rho \sigma _0\sigma _d\eta }{\big (\eta +\nu \big )^2} \ln \Biggl ( 1 + \frac{(\eta + \nu )(T-t)}{2\gamma }\Biggr ) \nonumber \\&+ \, \frac{\sigma _d^2\eta \nu +2\rho \sigma _0\sigma _d\eta - \sigma _0^2}{2\big (\eta + \nu \big )}(T-t) \nonumber \\&+ \, \frac{\eta \mu ^2(T-t)^2\left( \frac{\nu }{2}(T-t)+\gamma \right) }{ (\eta + \nu )(T-t)+2\gamma }, \end{aligned}$$

(3.8)

for $(t,x,y,d) \in [0,T]\times \mathbb {R}\times \mathbb {R}\times \mathbb {R}$, with an optimal trading rate given in feedback form by:

$$\begin{aligned} {\hat{q}}_s^{NP}= & {} {\hat{q}}^{NP}\left( T-s,D_s^{t,d}-{\hat{X}}_s^{t,x,y,d},{\hat{Y}}_s^{t,x,y,d}\right) , \quad t\le s\le T \\ {\hat{q}}^{NP}(t,d,y):= & {} \frac{ \eta (\mu t + d) - y}{(\eta + \nu )t + 2 \gamma }. \end{aligned}$$

$\square$

Interpretation:

• 1. The optimal trading rate ${\hat{q}}_s$ at time $s \in [t,T]$, given in feedback form by (3.6), is decomposed in two terms: the first one

  $$\begin{aligned} \frac{ r(\eta ,\beta )}{(r(\eta ,\beta ) + \nu )(T-t) + 2 \gamma } \left( \mu (T-s) + D_s^{t,d} -{\hat{X}}_s^{t,x,y,d}\right) \end{aligned}$$

  is related to the trading rate in order to follow the trend of the demand, and to the incentive to invest when the forecast of the residual demand is larger than the current inventory. The second term

  $$\begin{aligned} - \frac{1}{(r(\eta ,\beta ) + \nu )(T-t) + 2 \gamma } {\hat{Y}}_s^{t,x,y,d} \end{aligned}$$

  represents the negative impact of the quoted price on the investment strategy: the higher the price is, the more the agent decreases her trading rate until she reaches negative value meaning a resale of electricity shares. These effects are weighted by the constant denominator term depending on the penalty factor $\eta$, the marginal cost production factor $\beta$, the temporary and permanent price impact parameters $\gamma$, $\nu$, and the time to maturity $T-t$.

• 2. By introducing the marginal cost function: $c'(x) = \beta x$, and the process

  $$\begin{aligned} {\hat{\xi }}_s:= & {} \frac{\eta }{\eta + \beta } \left( D_s^{t,d} + \mu (T-s) - {\hat{X}}_s^{t,x,y,d} - {\hat{q}}_s (T-s) \right) , \quad t \le s \le T, \end{aligned}$$

  which is interpreted as the forecast production for the final time T (recall expression (3.7) of the final production), we notice from the expression of the optimal trading rate that the following relation holds:

  $$\begin{aligned} {\hat{Y}}_s^{t,x,y,d} + \nu {\hat{q}}_s (T-s) + 2 \gamma {\hat{q}}_s= & {} c'\left( {\hat{\xi }}_s\right) , \quad t \le s \le T. \end{aligned}$$

  (3.9)

  This relation means that at each time, the optimal trading rate is to make the forecast intraday price plus marginal temporary impact (left hand side), which can be seen as the marginal cost of electricity on the intraday market at time T, equal to the forecast marginal cost of production. Here, the instantaneous impact $\gamma$ appears as a marginal cost of buying or selling, and the forecast at time s supposes that the optimal trading rate ${\hat{q}}_s$ is held constant between s and T. $\square$

We complete the description of the optimal trading rate by pointing out a remarkable martingale property.

Proposition 3.1

The optimal trading rate process $({\hat{q}}_s)_{t\le s \le T}$ in (3.6) is a martingale.

Proof

By applying Itô’s formula to ${\hat{q}}_s = {\hat{q}}(T-s,D_s^{t,d}-{\hat{X}}_s^{t,x,y,d},{\hat{Y}}_s^{t,x,y,d})$, $t\le s\le T$, and since ${\hat{q}}$ is linear in d and y, we have:

$$\begin{aligned} d{\hat{q}}_s= & {} \Biggl [ - \displaystyle \frac{\partial {\hat{q}}}{\partial t} + \left( \mu - {\hat{q}}\right) \displaystyle \frac{\partial {\hat{q}}}{\partial d} + \nu {\hat{q}} \displaystyle \frac{\partial {\hat{q}}}{\partial y} \Biggr ] \left( T-s,D_s^{t,d}-{\hat{X}}_s^{t,x,y,d},{\hat{Y}}_s^{t,x,y,d}\right) ds \\&+ \, \displaystyle \frac{\partial {\hat{q}}}{\partial d}\left( T-s,D_s^{t,d}-{\hat{X}}_s^{t,x,y,d},{\hat{Y}}_s^{t,x,y,d}\right) \sigma _d dB_s \\&+ \, \displaystyle \frac{\partial {\hat{q}}}{\partial y}\left( T-s,D_s^{t,d}-{\hat{X}}_s^{t,x,y,d},{\hat{Y}}_s^{t,x,y,d}\right) \sigma _0 dW_s, \end{aligned}$$

from the dynamics (2.1), (2.8), and (2.7) of ${\hat{X}}^{t,x,y,d}$, $D^{t,d}$ and ${\hat{Y}}^{t,x,y,d}$. Now, from the explicit expression of the function ${\hat{q}}(t,y,d)$, we see that

$$\begin{aligned} - \displaystyle \frac{\partial {\hat{q}}}{\partial t} + \left( \mu - {\hat{q}}\right) \displaystyle \frac{\partial {\hat{q}}}{\partial d} + \nu {\hat{q}} \displaystyle \frac{\partial {\hat{q}}}{\partial y}= & {} 0, \end{aligned}$$

and so:

$$\begin{aligned} d{\hat{q}}_s= & {} \frac{r(\eta ,\beta )\sigma _d }{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } dB_s - \frac{\sigma _0 }{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } dW_s, \end{aligned}$$

(3.10)

which shows the required martingale property. $\square$

Remark 3.2

Recall that in the classical optimal execution problem as studied in [2], the optimal trading rate is constant. We retrieve this result in their framework which corresponds to the case where $\sigma _d = 0$ (constant demand target), $\beta = \infty$ (there is no production), and $\eta = \infty$ (constraint to lead $X_T$ to the fixed target), see Remark 2.1 4). Indeed, in these limiting regimes, we see from (3.10) that $d{\hat{q}}_s = 0$, meaning that $\{{\hat{q}}_s,t\le s\le T\}$ is constant. In our framework, this is generalized to the martingale property of the optimal trading rate process, which implies that the optimal inventory $\{{\hat{X}}_s^{t,x,y,d}$, $t\le s\le T\}$ has a constant growth rate in mean, i.e. $\frac{d \mathbb {E}[{\hat{X}}_s^{t,x,y,d}]}{ds}$ is constant equal to the initial trading rate at time t given by ${\hat{q}}(T-t,d-x,y)$.

As a consequence of this martingale property, if the producer already satisfies the relation (3.9) in the day-ahead market, and if the initial intraday price is the day-ahead price, her initial trading rate on the intraday market will be zero. And thus, on average, her trading rate will be zero.

The martingale property of the trading rate process is actually closely related to the martingale dynamics of the unaffected price ${\hat{P}}$ in (2.6). As we shall see in Sect. 4 where we consider jumps on price, making $\hat{P}$ a sub or super martingale, the optimal trading rate will inherit the converse sub or super martingale property. $\square$

3.2 Approximate solution

We go back to the original execution problem with the non negativity constraint on the production quantity. As pointed out above, there is no explicit solution in this case, due to the form of the terminal cost function $C^+$. The strategy is then to use the explicit control consisting in the trading rate ${\hat{q}}$ derived in (3.6), and of the truncated nonnegative production quantity:

$$\begin{aligned} {\tilde{\xi }}_T^*:= & {} {\hat{\xi }}_T 1\!\!1_{_{{\hat{\xi }}_T \ge 0}} = {\hat{\xi }}^{tr+}(D_T^{t,d} - {\hat{X}}_T^{t,x,y,d}), \end{aligned}$$

(3.11)

with ${\hat{\xi }}_T$ defined in (3.7) from the auxiliary problem. In other words, we follow the trading rate strategy ${\hat{q}}$ determined from the problem without constraint on the final production quantity, and at the terminal date use the production leverage if the final inventory ${\hat{X}}_T^{t,x,y,d}$ is below the terminal demand $D_T^{t,d}$, by choosing a quantity proportional to this spread $D_T^{t,d}-{\hat{X}}_T^{t,x,y,d}$. The aim of this section is to measure the relevance of this approximate strategy $({\hat{q}},{\tilde{\xi }}_T^*) \in \mathcal {A}\times L_+^0(\mathcal {F}_T)$ with respect to the optimal execution problem (2.9) by estimating the induced error:

$$\begin{aligned} \mathcal {E}_1(t,x,y,d):= & {} J\left( t,x,y,d;{\hat{q}},{\tilde{\xi }}_T^*\right) - v(t,x,y,d), \end{aligned}$$

for $(t,x,y,d) \in [0,T]\times \mathbb {R}\times \mathbb {R}\times \mathbb {R}$. We also measure the approximation error on the value functions:

$$\begin{aligned} \mathcal {E}_2(t,x,y,d):= & {} v(t,x,y,d) - {\tilde{v}}(t,x,y,d). \end{aligned}$$

Notice that if ${\hat{\xi }}_T \ge 0$ a.s., i.e. $D_T^{t,d} \ge {\hat{X}}_T^{t,x,y,d}$ a.s. (which is not true), and so ${\tilde{\xi }}_T^* = {\hat{\xi }}_T$, then clearly $({\hat{q}},{\hat{\xi }}_T)$ would be the solution to (2.9), and so $\mathcal {E}_1(t,x,y,d) = \mathcal {E}_2(t,x,y,d) = 0$. Actually, these errors depend on the probability of the event: $\{{\hat{X}}_T^{t,x,y,d} > D_T^{t,d}\}$, and we have the following estimate:

Proposition 3.2

For all $(t,x,y,d) \in [0,T]\times \mathbb {R}\times \mathbb {R}\times \mathbb {R}$, we have

$$\begin{aligned} 0 \le \mathcal {E}_i(t,x,y,d)\le & {} \frac{\eta r(\eta ,\beta )}{2\beta } V(T-t) \psi \Biggl ( \frac{m(T-t,d-x,y)}{\sqrt{V(T-t)}}\Biggr ), \quad i=1,2, \end{aligned}$$

(3.12)

where

$$\begin{aligned} \psi (z):= & {} (z^2 + 1) \Phi (-z) - z\phi (z), \quad z \in \mathbb {R}, \end{aligned}$$

with $\phi = \Phi '$ the density of the standard normal distribution, and

$$\begin{aligned} m(t,d,y):= & {} \frac{(\nu t+2\gamma )(\mu t+d) + y t}{(r(\eta ,\beta ) + \nu )t + 2 \gamma }, \end{aligned}$$

(3.13)

$$\begin{aligned} V(t):= & {} \int _0^t \frac{\sigma _0^2 s^2 + \sigma _d^2(\nu s + 2 \gamma )^2 + 2 \rho \sigma _0\sigma _ds (\nu s + 2 \gamma )}{\big [(r(\eta ,\beta ) + \nu )s + 2 \gamma \big ]^2} ds \ge 0. \end{aligned}$$

(3.14)

Proof

By definition of the value functions v and ${\tilde{v}}$, recalling that $({\hat{q}},{\hat{\xi }}_T)$ is an optimal control for ${\tilde{v}}$, and since $({\hat{q}},{\tilde{\xi }}_T^*) \in \mathcal {A}\times L_+^0(\mathcal {F}_T)$, we have:

$$\begin{aligned} J(t,x,y,d;{\hat{q}},{\hat{\xi }}_T) = {\tilde{v}}(t,x,y,d) \le v(t,x,y,d)\le & {} J(t,x,y,d;{\hat{q}},{\tilde{\xi }}_T^*), \end{aligned}$$

for all $(t,x,y,d) \in [0,T]\times \mathbb {R}\times \mathbb {R}\times \mathbb {R}$. This clearly implies that both errors $\mathcal {E}_1$ and $\mathcal {E}_2$ are nonnegative, and

$$\begin{aligned}&\max (\mathcal {E}_1(t,x,y,d),\mathcal {E}_2(t,x,y,d) )\\&\quad \le \mathcal {E}(t,x,y,d) := J(t,x,y,d;{\hat{q}},{\tilde{\xi }}_T^*) - J(t,x,y,d;{\hat{q}},{\hat{\xi }}_T). \end{aligned}$$

We now focus on the upper bound for $\mathcal {E}$. By definition of J in (2.10), ${\hat{\xi }}_T$ and ${\tilde{\xi }}_T^*$ in (3.7) and (3.11), we have

$$\begin{aligned} \mathcal {E}(t,x,y,d)= & {} \mathbb {E}\Big [ C\left( D_T^{t,d} - {\hat{X}}_T^{t,x,y,d},{\tilde{\xi }}_T^*\right) - C\left( D_T^{t,d} - {\hat{X}}_T^{t,x,y,d},{\hat{\xi }}_T\right) \Big ] \nonumber \\= & {} \mathbb {E}\Big [ C\left( D_T^{t,d} - {\hat{X}}_T^{t,x,y,d}, {\hat{\xi }}^+\left( D_T^{t,d} - {\hat{X}}_T^{t,x,y,d}\right) \right) \nonumber \\&- \, C\left( D_T^{t,d} - {\hat{X}}_T^{t,x,y,d},{\hat{\xi }}\left( D_T^{t,d} - {\hat{X}}_T^{t,x,y,d}\right) \right) \Big ] \nonumber \\= & {} \mathbb {E}\Big [ C^+\left( D_T^{t,d} - {\hat{X}}_T^{t,x,y,d}\right) - {\tilde{C}}\left( D_T^{t,d} - {\hat{X}}_T^{t,x,y,d}\right) \Big ] \nonumber \\= & {} \frac{\eta r(\eta ,\beta )}{2\beta } \mathbb {E}\Big [ \left( D_T^{t,d} - {\hat{X}}_T^{t,x,y,d} \right) ^2 1\!\!1_{D_T^{t,d} - {\hat{X}}_T^{t,x,y,d} < 0} \Big ], \end{aligned}$$

(3.15)

from the definitions and expressions of $C^+$ and ${\tilde{C}}$ in (2.3), (3.3) and (3.5). Now, from (3.10) and by integration, we obtain the explicit (path-dependent) form of the optimal trading rate control:

$$\begin{aligned} {\hat{q}}_s= & {} {\hat{q}}_t + \int _t^s \frac{r(\eta ,\beta ) \sigma _d}{(r(\eta ,\beta ) + \nu )(T-u) + 2 \gamma } dB_u \\&- \, \int _t^s \frac{ \sigma _0}{(r(\eta ,\beta ) + \nu )(T-u) + 2 \gamma } dW_u, \quad t \le s \le T, \end{aligned}$$

with ${\hat{q}}_t = {\hat{q}}(T-t,d-x,y)$. We then obtain the expression of the final spread between demand and inventory:

$$\begin{aligned} D_T^{t,d} - {\hat{X}}_T^{t,x,y,d}= & {} d- x + \mu (T-t) + \int _t^T \sigma _d dB_s - \int _t^T {\hat{q}}_s ds \\= & {} m(T-t,d-x,y) + \int _t^T \frac{\sigma _d(\nu (T-s)+2\gamma )}{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } dB_s \\&+\, \int _t^T \frac{\sigma _0 (T-s)}{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } dW_s, \end{aligned}$$

by Fubini’s theorem, and with

$$\begin{aligned} m(t,d,y):= & {} d + \mu t - t {\hat{q}}(t,d,y), \end{aligned}$$

which is explicitly written as in (3.13) from the expression (3.6) of ${\hat{q}}$. Thus, $D_T^{t,d} - {\hat{X}}_T^{t,x,y,d}$ follows a normal distribution law with mean $m(T-t,d-x,y)$ and variance $V(T-t)$ given by (3.14), and from (3.15), we deduce that

$$\begin{aligned} \mathcal {E}(t,x,y,d)= & {} \frac{\eta r(\eta ,\beta )}{2\beta } V(T-t) \psi \Big ( \frac{m(T-t,d-x,y)}{\sqrt{V(T-t)}}\Big ), \end{aligned}$$

while the probability that the final inventory is larger than the terminal demand is:

$$\begin{aligned} \mathbb {P}\big [ D_T^{t,d} - {\hat{X}}_T^{t,x,y,d} < 0 \big ]= & {} \Phi \Big ( - \frac{m(T-t,d-x,y)}{\sqrt{V(T-t)}}\Big ). \end{aligned}$$

(3.16)

$\square$

Error asymptotics. We now investigate the accuracy of the upper bound in (3.12)

$$\begin{aligned} {\bar{\mathcal {E}}}(T-t,d-x,y):= & {} \frac{\eta r(\eta ,\beta )}{2\beta } V(T-t) \psi \Big ( \frac{m(T-t,d-x,y)}{\sqrt{V(T-t)}}\Big ). \end{aligned}$$

It is well-known (see e.g. Sect. 14.8 in [11]) that

$$\begin{aligned} z \Phi (-z)\le & {} \phi (z), \quad \forall z \in \mathbb {R}, \end{aligned}$$

(3.17)

from which we easily see that $\psi$ is non increasing, convex, and $\psi (\infty ) = 0$. Thus, ${\bar{\mathcal {E}}}(T-t,d-x,y)$ decreases to zero for large $m(T-t,d-x;y)$ or small $V(T-t)$. We shall study its asymptotics in three limiting cases (i) the time to maturity $T-t$ is small, (ii) the initial demand spread $d-x$ is large, (iii) the initial quoted price y is large. We prove that the error bound ${\bar{\mathcal {E}}}(T-t,d-x,y)$, and thus $\mathcal {E}_1(t,x,y,d)$, $\mathcal {E}_2(t,x,y,d)$, converge to zero at least with an exponential rate of convergence in these limiting regimes:

Proposition 3.3

• (i) For all $(x,y,d) \in \mathbb {R}\times \mathbb {R}\times \mathbb {R}$ with $d > x$, we have

  $$\begin{aligned} \limsup _{T-t\downarrow 0} (T-t) \ln {\bar{\mathcal {E}}}(T-t,d-x,y)\le & {} - \frac{1}{2} \Big (\frac{d-x}{\sigma _d} \Big )^2. \end{aligned}$$

  (3.18)

• (ii) For all $(t,y) \in [0,T)\times \mathbb {R}$, we have

  $$\begin{aligned} \limsup _{d-x\rightarrow \infty } \frac{1}{(d-x)^2} \ln {\bar{\mathcal {E}}}(T-t,d-x,y)\le & {} - \frac{1}{2} \frac{m_\infty ^2(T-t)}{V(T-t)}, \end{aligned}$$

  (3.19)

  where

  $$\begin{aligned} m_\infty (t)= & {} \frac{\nu t+2\gamma }{\big ( r(\eta ,\beta ) + \nu \big )t + 2 \gamma } \end{aligned}$$

• (iii) For all $(t,x,d) \in [0,T)\times \mathbb {R}\times \mathbb {R}$, we have

  $$\begin{aligned} \limsup _{ y \rightarrow \infty } \frac{1}{y^2} \ln {\bar{\mathcal {E}}}(T-t,d-x,y)\le & {} - \frac{1}{2} \frac{n_\infty ^2 (T-t)}{V(T-t)}, \end{aligned}$$

  (3.20)

  where

  $$\begin{aligned} n_\infty (t)= & {} \frac{t}{(r(\eta ,\beta ) + \nu )t + 2 \gamma }. \end{aligned}$$

Proof

From (3.17), we have:

$$\begin{aligned} 0 \le&\psi (z)&\le z^{-1} \phi (z), \quad \forall z >0. \end{aligned}$$

Notice that in the three asymptotic regimes (i) (with $d-x > 0$), (ii), and (iii), the quantity $m(T-t,d-x,y)$ is positive, and we thus have:

$$\begin{aligned} {\bar{\mathcal {E}}}(T-t,d-x,y)\le & {} \frac{\eta r(\eta ,\beta )}{2\beta } \frac{V(T-t)^{\frac{3}{2}}}{m(T-t,d-x,y)} \phi \Big ( \frac{m(T-t,d-x,y)}{\sqrt{V(T-t)}}\Big ). \end{aligned}$$

(3.21)

• (i) For small time to maturity $T-t$, we see that $m(T-t,d-x,y)$ converges to $d-x > 0$, while $V(T-t) \sim \sigma _d^2(T-t)$, i.e. $V(T-t)/\sigma ^2_d(T-t)$ converges to 1. This shows from (3.21) that, when $T-t$ goes to zero, the error bound ${\bar{\mathcal {E}}}(T-t,d-x,y)$, converges to zero at least with an exponential rate of convergence, namely the one given by (3.18).

• (ii) For large demand spread $d-x$, we see that $m(T-t,d-x,y) \sim$ $m_\infty (T-t) (d-x)$, i.e. the ratio $m(T-t,d-x,y)/m_\infty (T-t)(d-x)$ converges to 1 when $d-x$ goes to infinity. This shows from (3.21) that, when $d-x$ goes to infinity, the error bound ${\bar{\mathcal {E}}}(T-t,d-x,y)$, converges to zero at least with an exponential rate of convergence, namely the one given by (3.19).

• (iii) For large y, we see that $m(T-t,d-x,y) \sim n_\infty (T-t) y$, i.e. the ratio $m(T-t,d-x,y)/n_\infty (T-t)y$ converges to 1 when y goes to infinity. This shows from (3.21) that, when $d-x$ goes to infinity, the error bound ${\bar{\mathcal {E}}}(T-t,d-x,y)$ converges to zero at least with an exponential rate of convergence, namely the one given by (3.20). $\square$

Interpretation. Recall from (3.16) that

$$\begin{aligned} \mathbb {P}\left[ D_T^{t,d} < {\hat{X}}_T^{t,x,y,d} \right]= & {} \Phi \Big ( - \frac{m(T-t,d-x,y)}{\sqrt{V(T-t)}}\Big ), \end{aligned}$$

and thus following the same arguments as in the above proof, we have:

• (i)
  $$\begin{aligned} \limsup _{T-t\downarrow 0} (T-t) \ln \mathbb {P}\left[ D_T^{t,d} < {\hat{X}}_T^{t,x,y,d} \right]= & {} - \frac{1}{2} \left( \frac{d-x}{\sigma _d} \right) ^2, \end{aligned}$$

  (3.22)

  for all $(x,y,d) \in \mathbb {R}\times \mathbb {R}\times \mathbb {R}$ with $d > x$. We observe that the rate in the rhs of (3.18) or (3.22) depends only on the demand volatility $\sigma _d$ and the initial demand spread $d-x$. Moreover, it is all the larger, the smaller $\sigma _d$ is, and the larger $d-x$ is. This means that the terminal demand will stay with very high probability above the final inventory once we are near from the maturity with a low volatile demand, initially larger than the inventory, in which case, the explicit strategy $({\hat{q}},{\tilde{\xi }}_T^*)$ approximates very accurately the optimal strategy $(q^*,\xi _T^*)$.

• (ii)
  $$\begin{aligned} \limsup _{d-x\rightarrow \infty } \frac{1}{(d-x)^2} \ln \mathbb {P}\left[ D_T^{t,d} < {\hat{X}}_T^{t,x,y,d} \right]= & {} - \frac{1}{2} \frac{m_\infty ^2(T-t)}{V(T-t)}, \end{aligned}$$

  (3.23)

  for all $(t,y) \in [0,T)\times \mathbb {R}$, The rate in the rhs of (3.19) (or (3.23)) is all the larger, the smaller the volatilities $\sigma _0$ and $\sigma _d$ of the electricity price and demand are. Again, we have the same interpretation than in the asymptotic regime (i), and this means that the explicit strategy $({\hat{q}},{\tilde{\xi }}_T^*)$ approximates very accurately the optimal strategy $(q^*,\xi _T^*)$ in the limiting regime when the initial demand spread is large, and the volatilities are small.

• (iii)
  $$\begin{aligned} \limsup _{ y \rightarrow \infty } \frac{1}{y^2} \ln \mathbb {P}\left[ D_T^{t,d} < {\hat{X}}_T^{t,x,y,d} \right]= & {} - \frac{1}{2} \frac{n_\infty ^2 (T-t)}{V(T-t)}, \end{aligned}$$

  (3.24)

  for all $(t,x,d) \in [0,T)\times \mathbb {R}\times \mathbb {R}$. In the limiting regime where the initial quoted price y is large, the agent has a strong incentive to sell energy on the intraday market, which leads to a final inventory staying under the final demand with high probability, and thus to a very accurate approximate strategy $({\hat{q}},{\tilde{\xi }}_T^*)$. As in case (ii), this accuracy is strengthened for small volatilities $\sigma _0$ and $\sigma _d$ of the electricity price and demand. $\square$

3.3 Numerical results

3.3.1 Numerical tests

We measure quantitatively the accuracy of the error bound derived in the previous paragraph with some numerical tests. Let us fix the following parameter values: $\sigma _0=1/60$ € $\cdot (\hbox {MW})^{-1}\cdot s^{-1/2}$, $\sigma _d=1000/60\hbox { MW}\cdot s^{-1/2}$, $\beta =0.002$ € $\cdot (\hbox {MW})^{-2}$, $\eta =200$ € $\cdot (\hbox {MW})^{-2}$, $\mu =0\hbox { MW}\cdot s^{-1}$, $\nu =10^{-10}$ € $\cdot (\hbox {MW})^{-2}$, $\gamma =10^{-10}$ € $\cdot s\cdot (\hbox {MW})^{-2}$ and $\rho =0.8$.

We start from the initial time $t = 0$, with a zero inventory $X_0 = 0$, and vary respectively the maturity T, the initial demand $D_0$ and the initial price $Y_0$. We compute the probability for the final inventory to exceed the final demand $\mathbb {P}[{\hat{X}}_T > D_T]$, the approximate value function $\tilde{v}(0,X_0,Y_0,D_0)$, and the error bound ${\bar{\mathcal {E}}}(T,D_0-X_0,Y_0)$. The results are reported in Table 1 when varying T, in Table 2 when varying $D_0$ and in Table 3 when varying $Y_0$.

Table 1 $Y_0=50$ € $\cdot (\hbox {MW})^{-1}$ and $D_0=$50,000MW

Table 2 $T=24$ h and $Y_0=50$ € $\cdot (\hbox {MW})^{-1}$

Table 3 $T=24$ h and $D_0=50{,}000$ MW

Table 1 shows that for time to maturity less than $T = 24\hbox {h}$, the probability for the final inventory to exceed the final demand is very small, and consequently the error bound is rather negligible. When the time horizon increases, the agent has the possibility to spread over time her trading strategies for reducing the price impact, and purchase more energy, in which case the probability for the final inventory to exceed the demand increases.

Table 2 shows that the probability for the final inventory to exceed the final demand, and the error bound are not much sensitive to the variations of the initial positive demand $D_0$. Actually, the main impact is caused by the initial stock price, as observed in Table 3.

For small initial electricity price $Y_0$, the agent will buy more energy in the intraday market and produce less. Therefore, the inventory will overtake with higher probability the demand, in which case the approximate value function can be significantly different from the original one, as observed from the error bound in Table 3 for $Y_0 =$ 20.

3.3.2 Simulations

We plot trajectories of some relevant quantities that we simulate with the following set of parameters: $\sigma _0=1/60$ € $\cdot (\hbox {MW})^{-1}\cdot s^{-1/2}$, $\sigma _d=1000/60$ MW$\cdot s^{-1/2}$, $\beta =0.002$ € $\cdot \,(\hbox {MW})^{-2}$, $\eta =100$ € $\cdot (\hbox {MW})^{-2}$, $\mu =0$ MW$\cdot s^{-1}$, $\rho =0.8$, $\nu =4.00\times 10^{-5}$ € $\cdot (\hbox {MW})^{-2}$, $\gamma =2.22$ € $\cdot s\cdot (\hbox {MW})^{-2}$, $T = 24\hbox {h}$, $X_0 = 0$, $D_0=50,000$ MW and $Y_0=50$ € $\cdot (\hbox {MW})^{-1}$.

For such parameter values, the probability $\mathbb {P}[{\hat{X}}_T > D_T]$ is bounded above by $10^{-16}$, the error ${\bar{\mathcal {E}}}(0,D_0 -X_0,Y_0)$ is bounded by $2.82\times 10^{-10}$ €, and

The executed strategy $({\hat{q}},{\hat{\xi }}_T^*)$ can then be considered as very close to the optimal strategy.

Figure 1 represents the evolution of the trading rate control $({\hat{q}}_t)_{t\in [0,T]}$ derived in (3.6) for a given trajectory of price and demand, and this is consistent with the martingale property as shown in Proposition 3.1. Figure 2 represents a simulation of the quoted price ${\hat{Y}}_t$ with impact and of the unaffected price ${\hat{P}}_t$. Due to the buying strategy, i.e. positive ${\hat{q}}$, we observe that the quoted price ${\hat{Y}}$ is larger than $\hat{P}$. In Fig. 3, we plot the evolution of the optimal inventory $({\hat{X}}_t)_{t\in [0,T)}$, and of the forecast residual demand $(D_t)_{t\in [0,T]}$. We see that ${\hat{X}}_t$ is increasing, with a growth rate which looks constant as pointed out in Remark 3.2. At final time, if ${\hat{X}}_T < D_T$ (which is the case in our simulation), the agent uses her production leverage ${\hat{\xi }}_T$, and achieves a final inventory: ${\hat{X}}_T + {\hat{\xi }}_T$, which is represented by the peak at time T. From the expression (3.7) of ${\hat{\xi }}_T$, the final imbalance cost is equal to

$$\begin{aligned} D_T - {\hat{X}}_T - {\hat{\xi }}_T= & {} \frac{\beta }{\eta +\beta } (D_T - {\hat{X}}_T), \end{aligned}$$

and is then positive, as shown in Fig. 3.

Fig. 1

Evolution of the trading rate control ${\hat{q}}$

Fig. 2

Simulation of the quoted impacted price ${\hat{Y}}$ and of the unaffected price $\hat{P}$

Fig. 3

Evolution of the inventory ${\hat{X}}$ and of the forecast residual demand D

4 Jumps in the residual demand forecast

In this section, we incorporate the case where the residual demand forecast is subject to sudden changes induced by prediction errors on renewable production, which may be quite large. Our aim is to study the impact on the strategies obtained in the previous section, and we shall also neglect the delay in thermal plants production.

The sudden changes in the demand forecast are modeled via a compound Poisson process $N_t = (N_t^+,N_t^-)_{t\ge 0}$ with intensity $\lambda > 0$, where $N_t^+$ is the counting process associated to positive jumps of the demand forecast with size $\delta ^+ > 0$, occurring with probability $p^+ \in [0,1]$, while $N_t^-$ is the counting process associated to negative jumps of the demand forecast with size $\delta ^- < 0$, occurring with probability $p^- = 1-p^+$. We denote by $\delta := \delta ^+ p^+ + \delta ^- p^-$ the mean of the jump size of the demand forecast. The dynamics of the residual demand forecast D is then given by:

$$\begin{aligned} dD_t= & {} \mu dt + \sigma _d dB_t + \delta ^+ dN_t^+ + \delta ^- dN_t^-, \end{aligned}$$

(4.1)

where we add a jump component with respect to the model in (2.8). Moreover, as soon as a jump in the residual demand forecast occurs, this is impacted into the intraday electricity price since the main producers are assumed to have access to the whole updated forecast. We thus model the unaffected electricity price by:

$$\begin{aligned} {\hat{P}}_t= & {} {\hat{P}}_0 + \sigma _0 W_t + \pi ^+ N_t^+ + \pi ^- N_t^-, \end{aligned}$$

(4.2)

where we add with respect to the Bachelier model in (2.6) a jump component of size $\pi ^+ >$ 0 (resp. $\pi ^- < 0$) when the jump on residual demand is positive (resp. negative), which means that a higher (resp. lower) demand induces an increase (resp. drop) of price. We denote by $\pi := \pi ^+ p^+ + \pi ^- p^-$ the mean of the jump size of the intraday price. Given a trading rate $q \in \mathcal {A}$, the dynamics of the quoted price Y is then governed by

$$\begin{aligned} dY_t= & {} \nu q_t dt + \sigma _0 dW_t + \pi ^+ dN_t^+ + \pi ^- dN_t^-. \end{aligned}$$

(4.3)

By considering this simplified modeling of demand forecast subject to sudden shift in terms of a Poisson process, we do not have additional state variables with respect to the no jump case of the previous section. Let us then denote by $v = v^{(\lambda )}(t,x,y,d)$ the value function to the optimal execution problem (2.4) with cost functional $J = J^{(\lambda )}(t,x,y,d,q,\xi )$, where we stress the dependence in $\lambda$ for taking into account jumps in demand forecast. The value function in the no jump case derived in the previous section is denoted by $v = v^{(0)}$.

As in the case with no jumps, there is no explicit solution to $v^{(\lambda )}$ due to the non negativity constraint on the final production: we shall first study the auxiliary execution problem without sign constraint on the final production, then provide an approximate solution to the original one with an estimation of the induced error approximation, and with some numerical illustrations. We compare the results with the no jump case by focusing on the impact of the jump components.

4.1 Auxiliary optimal execution problem

Similarly as in Subsect. 3.1, we consider the optimal execution problem without non negativity constraint on the final production, denoted by ${\tilde{v}} = {\tilde{v}}^{(\lambda )}(t,x,y,d)$.

As in Theorem 3.1 for the case of the value function ${\tilde{v}}^{(0)}$ without jumps, we have an explicit solution to this auxiliary problem.

Theorem 4.1

The value function to the auxiliary optimization problem is explicitly given by:

$$\begin{aligned}&{\tilde{v}}^{(\lambda )}(t,x,y,d)\\&\quad = {\tilde{v}}^{(0)}(t,x,y,d) \\&\qquad + \frac{\lambda }{2} \frac{r(\eta ,\beta ) (T-t) \big ( \pi (T-t) + 2 \delta (\nu (T-t) + 2\gamma ) \big )}{\big (r(\eta ,\beta ) + \nu \big )(T-t) + 2 \gamma } (d-x) \\&\qquad - \frac{\lambda }{2} \frac{(T-t)^2\big ( \pi - 2 r(\eta ,\beta ) \delta \big )}{\big (r(\eta ,\beta ) + \nu \big )(T-t) + 2 \gamma } y \\&\qquad + \, \lambda \gamma \frac{p^+(\pi ^+ - r(\eta ,\beta )\delta ^+)^2+p^-(\pi ^- - r(\eta ,\beta )\delta ^-)^2}{\big (r(\eta ,\beta ) + \nu \big )^2} \ln \Big ( 1 + \frac{(r(\eta ,\beta ) + \nu )(T-t)}{2\gamma }\Big ) \\&\qquad - \frac{\lambda }{2} \frac{p^+((\pi ^+)^2- r(\eta ,\beta ) \delta ^+(2\pi ^++\nu \delta ^+)) +p^-((\pi ^-)^2- r(\eta ,\beta ) \delta ^-(2\pi ^- +\nu \delta ^-))}{r(\eta ,\beta ) + \nu } (T-t)\\&\qquad + \frac{\lambda r(\eta ,\beta )}{2}\frac{2\nu \mu \delta +\lambda ((p^+)^2\delta ^+(\pi ^++\nu \delta ^+)+(p^-)^2\delta ^-(\pi ^-+\nu \delta ^-))}{ r(\eta ,\beta ) + \nu }(T-t)^2 \\&\qquad +\, \lambda ^2 \gamma r(\eta ,\beta ) \frac{r(\eta ,\beta )\delta ^2 +2\nu p^+p^-\delta ^+\delta ^- -((p^+)^2\delta ^+\pi ^++(p^-)^2\delta ^-\pi ^-)}{(r(\eta ,\beta )+ \nu )\big ((r(\eta ,\beta )+\nu )(T-t) + 2 \gamma \big )}(T-t)^2 \\&\qquad + \frac{2\lambda \gamma r^2(\eta ,\beta ) \mu \delta }{(r(\eta ,\beta )+ \nu )\big ((r(\eta ,\beta )+\nu )(T-t) + 2 \gamma \big )}(T-t)^2 - \frac{\lambda ^2\pi ^2}{48\gamma }(T-t)^3 \\&\qquad + \frac{\lambda ^2p^+p^-r(\eta ,\beta )}{2}\frac{2\nu \delta ^+\delta ^-+\delta ^-\pi ^++\delta ^+\pi ^-}{(r(\eta ,\beta )+\nu )(T-t) + 2\gamma }(T-t)^3\\&\qquad + \frac{1}{8}\frac{4r(\eta ,\beta ) \mu \lambda \pi - \lambda ^2\pi ^2}{(r(\eta ,\beta )+\nu )(T-t) + 2\gamma }(T-t)^3, \end{aligned}$$

for $(t,x,y,d) \in [0,T]\times \mathbb {R}\times \mathbb {R}\times \mathbb {R}$, with an optimal trading rate given in feedback form by:

$$\begin{aligned} {\hat{q}}_s^{(\lambda )}= & {} {\hat{q}}^{(\lambda )} \left( T-s,D_s^{t,d} - {\hat{X}}_s^{t,x,y,d},{\hat{Y}}_s^{t,x,y,d}\right) , \quad t \le s \le T \nonumber \\ {\hat{q}}^{(\lambda )}(t,d,y):= & {} {\hat{q}}^{(0)}(t,d,y) + \lambda \frac{r(\eta ,\beta )\delta t + \frac{\pi }{4\gamma }(r(\eta ,\beta )+ \nu )t^2}{(r(\eta ,\beta )+\nu )t + 2\gamma } \nonumber \\= & {} {\hat{q}}^{(0)}\left( t,d+\lambda \delta t,y+ \frac{\lambda }{2}\pi t\right) + \frac{\lambda \pi }{4\gamma }t, \end{aligned}$$

(4.4)

where ${\hat{q}}^{(0)}$ is the optimal trading rate given in (3.6) in the case with no jump in the demand forecast. Here $({\hat{X}}^{t,x,y,d},{\hat{Y}}^{t,x,y,d},D^{t,d})$ denotes the solution to (2.1)-(4.3)-(4.1) when using the feedback control ${\hat{q}}^{(\lambda )}$, and starting from (x, y, d) at time t. Finally, the optimal production quantity is given by:

$$\begin{aligned} {\hat{\xi }}_T^{(\lambda )}= & {} \frac{\eta }{\eta + \beta } \left( D_T^{t,d} - {\hat{X}}_T^{t,x,y,d}\right) . \end{aligned}$$

(4.5)

Proof

See Appendix.$\square$

Interpretation. The expression of the optimal trading rate ${\hat{q}}_s^{(\lambda )}$, $s \in [t,T]$, as

$$\begin{aligned} {\hat{q}}_s^{(\lambda )}= & {} {\hat{q}}_s^{(0)} + \lambda \frac{r(\eta ,\beta )\delta (T-s) + \frac{\pi }{4\gamma }(r(\eta ,\beta )+ \nu )(T-s)^2}{(r(\eta ,\beta )+\nu )(T-s)+ 2\gamma }, \end{aligned}$$

where ${\hat{q}}_s^{(0)} = {\hat{q}}^{(0)}\left( T-s,D_s^{t,d}-{\hat{X}}_s^{t,x,y,d},{\hat{Y}}_s^{t,x,y,d}\right)$ represents the optimal trading rate that the agent would use if she believes that the demand forecast will not jump, shows that under the information knowledge about jumps, the agent will purchase more (resp. less) electricity shares and this impact is all the larger, the larger the intensity $\lambda$ of jumps, and the positive (resp. negative) mean $\delta$ and $\pi$ of jump size in demand forecast and price are. On the other hand, the expression of ${\hat{q}}_s^{(\lambda )}$ as the sum of two terms:

$$\begin{aligned} {\hat{q}}_s^{(\lambda )}= & {} {\hat{q}}^{(0)}\big (T-s,D_s^{t,d}+ \lambda \delta (T-s),{\hat{Y}}_s^{t,x,y,d} + \frac{\lambda }{2} \pi (T-s) \big ) + \frac{\lambda \pi }{4\gamma }(T-s), \end{aligned}$$

(4.6)

can be interpreted as follows. The first term is analog to the optimal trading rate in the no jump case, with an adjustment $\lambda \delta (T-s)$ in the demand, which represents the expectation of the demand jump size up to the final horizon, and an adjustment $\frac{\lambda }{2} \pi (T-s)$ on the price, which represents half of the expectation of the price jump size up to the final horizon. The second term, $\frac{\lambda \pi }{4\gamma }(T-s)$, is deterministic, and linear in time, and we shall see on the simulations for some parameter values that it can be dominant with respect to the first stochastic term. Moreover, as in (3.9), we can write an equilibrium relation which indicates that this control aims at making the forecast intraday price and the forecast cost of production equal, in particular at terminal date T:

$$\begin{aligned} {\hat{Y}}_T^{t,x,y,d} + 2\gamma {\hat{q}}_T^{(\lambda )}= & {} c'\left( {\hat{\xi }}_T^{(\lambda )}\right) . \end{aligned}$$

(4.7)

The unaffected price ${\hat{P}}$ in (4.2) is no more a martingale in presence of jumps, except when $\pi = 0$. It is actually a supermartingale when $\pi < 0$ (predominant negative jumps), and submartingale when $\pi > 0$ (predominant positive jumps). The next result shows that the optimal trading rate inherits the converse submartingale or supermartingale property of the price process.

Proposition 4.1

The optimal trading rate process $({\hat{q}}_s^{(\lambda )})_{t\le s \le T}$ in (4.4) is a supermartingale if $\pi > 0$, and a submartingale if $\pi < 0$. More precisely, the process $\{{\hat{q}}_s^{(\lambda )} + \frac{\lambda \pi }{2\gamma }(s-t), t\le s\le T\}$ is a martingale.

Proof

Notice that $N_t^\pm$ is a Poisson process with intensity $\lambda p^\pm$, and let us introduce the compensated martingale Poisson process ${\tilde{N}}_t^\pm = N_t - \lambda p^\pm t$. By applying Itô’s formula to the trading rate process ${\hat{q}}_s^{(\lambda )} = {\hat{q}}^{(\lambda )}(T-s,D_s^{t,d}-{\hat{X}}_s^{t,x,y,d},{\hat{Y}}_s^{t,x,y,d})$, $t\le s\le T$, and from the dynamics (2.1), (4.1) and (4.3), we have:

$$\begin{aligned} d{\hat{q}}_s^{(\lambda )}= & {} \Biggl [ - \displaystyle \frac{\partial {\hat{q}}^{(\lambda )}}{\partial t} + (\mu - {\hat{q}}^{(\lambda )})\displaystyle \frac{\partial {\hat{q}}^{(\lambda )}}{\partial d} + \nu {\hat{q}}^{(\lambda )}\displaystyle \frac{\partial {\hat{q}}^{(\lambda )}}{\partial y} + \lambda p^+\big ( {\hat{q}}^{(\lambda )}(.,.+\delta ^+, . + \pi ^+) - {\hat{q}}^{(\lambda )}\big ) \nonumber \\&+ \, \lambda p^-\big ( {\hat{q}}^{(\lambda )}(.,.+\delta ^-, . + \pi ^-) - {\hat{q}}^{(\lambda )}\big ) \Biggr ] (T-s,D_s^{t,d} -{\hat{X}}_s^{t,x,y,d},{\hat{Y}}_s^{t,x,y,d}) ds \nonumber \\&+ \, \displaystyle \frac{\partial {\hat{q}}^{(\lambda )}}{\partial d}\left( T-s,D_s^{t,d}-{\hat{X}}_s^{t,x,y,d},{\hat{Y}}_s^{t,x,y,d}\right) \sigma _d dB_s \nonumber \\&+ \, \displaystyle \frac{\partial {\hat{q}}^{(\lambda )}}{\partial y}\left( T-s,D_s^{t,d}-{\hat{X}}_s^{t,x,y,d},{\hat{Y}}_s^{t,x,y,d}\right) \sigma _0 dW_s \nonumber \\&+ \, \big [ {\hat{q}}^{(\lambda )}\left( T-s,D_{s^-}^{t,d} + \delta ^+ - {\hat{X}}_s^{t,x,y,d},{\hat{Y}}_{s^-}^{t,x,y,d} + \pi ^+\right) \nonumber \\&- \, {\hat{q}}^{(\lambda )}\left( T-s,D_{s^-}^{t,d} - {\hat{X}}_s^{t,x,y,d},{\hat{Y}}_{s^-}^{t,x,y,d}\right) \big ] d {\tilde{N}}_s^+ \nonumber \\&+ \, \left[ {\hat{q}}^{(\lambda )}\left( T-s,D_{s^-}^{t,d} + \delta ^- - {\hat{X}}_s^{t,x,y,d},{\hat{Y}}_{s^-}^{t,x,y,d} + \pi ^-\right) \right. \nonumber \\&\left. -\, {\hat{q}}^{(\lambda )}\left( T-s,D_{s^-}^{t,d} - {\hat{X}}_s^{t,x,y,d},{\hat{Y}}_{s^-}^{t,x,y,d}\right) \right] d {\tilde{N}}_s^-. \nonumber \end{aligned}$$

Now, from the expression (4.4) of ${\hat{q}}^{(\lambda )}(t,d,y)$, we see that:

$$\begin{aligned}&- \displaystyle \frac{\partial {\hat{q}}^{(\lambda )}}{\partial t} + \Big (\mu - {\hat{q}}^{(\lambda )}\Big )\displaystyle \frac{\partial {\hat{q}}^{(\lambda )}}{\partial d} + \nu {\hat{q}}^{(\lambda )} \displaystyle \frac{\partial {\hat{q}}^{(\lambda )}}{\partial y} \\&\quad +\lambda \big ( p^+{\hat{q}}^{(\lambda )}(.,.+\delta ^+, . + \pi ^+) + p^-{\hat{q}}^{(\lambda )}(.,.+\delta ^-, . + \pi ^-) - {\hat{q}}^{(\lambda )}\big ) = - \frac{\lambda \pi }{2\gamma }, \end{aligned}$$

and then:

$$\begin{aligned} d{\hat{q}}_s^{(\lambda )}= & {} - \frac{\lambda \pi }{2\gamma } ds \nonumber \\&+ \, \frac{r(\eta ,\beta )\sigma _d }{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } dB_s - \frac{\sigma _0 }{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } dW_s \nonumber \\&+ \, \frac{r(\eta ,\beta )\delta ^+ - \pi ^+}{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } d {\tilde{N}}_s^+ + \frac{r(\eta ,\beta )\delta ^- - \pi ^-}{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } d {\tilde{N}}_s^-. \end{aligned}$$

(4.8)

This proves the required assertions of the proposition. $\square$

Remark 4.1

The above supermartingale (or submartingale) property implies in particular that the mean of the optimal trading rate process $({\hat{q}}_s^{(\lambda )})_{0\le s\le T}$ is decreasing (or increasing) in time, and so that the trajectory of the optimal inventory mean $\mathbb {E}[{\hat{X}}_s^{0,x,y,d}]$, $0\le s\le T$, is concave (or convex). Moreover, from the martingale property of ${\hat{q}}_s^{(\lambda )}+\frac{\lambda \pi }{2\gamma }s$, $0\le s\le T$, we have: $\mathbb {E}[{\hat{q}}_s^{(\lambda )}] =$ ${\hat{q}}^{(\lambda )}(T,d-x,y) - \frac{\lambda \pi }{2\gamma }s$ for $0\le s\le T$. Fix d, x, y, and let us then denote by $\bar{s}^{(\lambda )} := \frac{2\gamma }{\lambda \pi }{\hat{q}}^{(\lambda )}(T,d-x,y)$, which is explicitly written as:

$$\begin{aligned} {\bar{s}}^{(\lambda )} = \frac{T}{2} + \frac{1}{\lambda \pi } \frac{\big (r(\eta ,\beta )\mu + \lambda (r(\eta ,\beta )\delta - \frac{\pi }{2}) \big )T + r(\eta ,\beta ) (d-x) - y}{1 + \frac{(r(\eta ,\beta )+\nu )T}{2\gamma }} \end{aligned}$$

We have the following cases:

• ${\bar{s}}^{(\lambda )} \le 0$ and $\pi > 0$: this may arise for large y, or $d << x$, or $r(\eta ,\beta )\delta << \pi /2$. In this extreme case, $\frac{d \mathbb {E}[{\hat{X}}_s^{0,x,y,d}]}{ds} =$ $\mathbb {E}[{\hat{q}}_s^{(\lambda )}] \le 0$ for $0\le s\le T$, i.e. the trajectory of $\mathbb {E}[{\hat{X}}_s^{0,x,y,d}]$, $0\le s \le T$, is decreasing, which means that the agent will “always” sell electricity shares since she takes advantage of high price, in order to decrease her inventory for approaching the demand, and because in average, the jump size of the demand is much lower than the positive jump size of the price.

• ${\bar{s}}^{(\lambda )} \le 0$ and $\pi < 0$: this may arise for small y, or $d >> x$, or $r(\eta ,\beta )\delta >> \pi /2$. In this extreme case, $\frac{d \mathbb {E}[{\hat{X}}_s^{0,x,y,d}]}{ds} =$ $\mathbb {E}[{\hat{q}}_s^{(\lambda )}] \ge 0$ for $0\le s\le T$, i.e. the trajectory of $\mathbb {E}[{\hat{X}}_s^{0,x,y,d}]$, $0\le s \le T$, is increasing, which means that the agent will “always” buy electricity shares since she takes advantage of low price, in order to increase her inventory for approaching the demand, and because in average, the jump size of the price is much lower than the jump size of the demand.

• ${\bar{s}}^{(\lambda )} \ge T$ and $\pi > 0$: this may arise for $r(\eta ,\beta )\delta >> \pi /2$, $d>>x$ or small y. In this other extreme case, the trajectory of $\mathbb {E}[{\hat{X}}_s^{0,x,y,d}]$, $0\le s \le T$, is increasing, which means that the agent will “always” buy electricity shares at low price in order to approach the residual demand at final time.

• ${\bar{s}}^{(\lambda )} \ge T$ and $\pi < 0$: this may arise for $r(\eta ,\beta )\delta << \pi /2$, $d<<x$ or large y. The trajectory of $\mathbb {E}[{\hat{X}}_s^{0,x,y,d}]$, $0\le s \le T$, is decreasing, which means that the agent will “always” sell electricity shares at high price in order to approach the residual demand at final time.

• $0 < {\bar{s}}^{(\lambda )} < T$: in this regular case, it is interesting to comment on the two subcases:

  • if $\pi > 0$, the trajectory of $s \mapsto \mathbb {E}[{\hat{X}}_s^{0,x,y,d}]$ is increasing for $s \le {\bar{s}}^{(\lambda )}$ and then decreasing for ${\bar{s}}^{(\lambda )} < s \le T$. This means that the agent starts by purchasing electricity shares for taking profit of the positive price jumps (which have more impact than the negative price jumps as $p^+\pi ^++p^-\pi ^->0$), and then resells shares in order to achieve the equilibrium relation (4.7).

  • if $\pi < 0$, i.e. the negative jumps have more impact than the positive ones: the agent starts by selling electricity shares and then purchases shares.$\square$

4.2 Approximate solution

We turn back to the original optimal execution problem with the non negativity constraint on the final production, and as in Sect. 3.2, we use the approximate strategy consisting in the trading rate ${\hat{q}}^{(\lambda )}$ derived in (4.4), and of the truncated nonnegative final production:

$$\begin{aligned} {\tilde{\xi }}_T^{(\lambda ),*}:= & {} {\hat{\xi }}_T^{(\lambda )} 1\!\!1_{_{{\hat{\xi }}_T^{(\lambda )} \ge 0}} = {\hat{\xi }}^{tr+}(D_T^{t,d} - {\hat{X}}_T^{t,x,y,d}), \end{aligned}$$

with ${\hat{\xi }}_T^{(\lambda )}$ given in (4.5). We measure the relevance of this strategy $({\hat{q}}^{(\lambda )},{\tilde{\xi }}_T^{(\lambda ),*}) \in \mathcal {A}\times L_+^0(\mathcal {F}_T)$ by estimating the induced error:

$$\begin{aligned} \mathcal {E}_1^{(\lambda )}(t,x,y,d):= & {} J^{(\lambda )}(t,x,y,d;{\hat{q}}^{(\lambda )},{\tilde{\xi }}_T^{(\lambda ),*}) - v^{(\lambda )}(t,x,y,d), \end{aligned}$$

for $(t,x,y,d) \in [0,T]\times \mathbb {R}\times \mathbb {R}\times \mathbb {R}$, and also measure the approximation error on the value functions:

$$\begin{aligned} \mathcal {E}_2^{(\lambda )}(t,x,y,d):= & {} v^{(\lambda )}(t,x,y,d) - {\tilde{v}}^{(\lambda )}(t,x,y,d). \end{aligned}$$

Proposition 4.2

For all $(t,x,y,d) \in [0,T]\times \mathbb {R}\times \mathbb {R}\times \mathbb {R}$, we have

$$\begin{aligned} 0 \le \mathcal {E}_i^{(\lambda )}(t,x,y,d)\le & {} \frac{\eta r(\eta ,\beta )}{2\beta } V(T-t) \mathbb {E}\Big [ \psi \Big ( \frac{m^{(\lambda )}(T-t,d-x,y) + \Sigma _T^{-,t}}{\sqrt{V(T-t)}}\Big ) \Big ] \end{aligned}$$

(4.9)

for $i = 1,2$, where $\psi$, m, V are defined in Proposition 3.2,

$$\begin{aligned} m^{(\lambda )}(t,d,y)= & {} m\Big (t,d,y + \lambda \big (\frac{\pi }{2} - r(\eta ,\beta )\delta \big )t \Big ) \nonumber \\&+ \, \lambda \frac{ r(\eta ,\beta )\delta - \pi }{r(\eta ,\beta )+\nu } \Big [ t - \frac{2\gamma }{r(\eta ,\beta )+\nu } \ln \Big ( 1 + \frac{r(\eta ,\beta ) + \nu }{2\gamma }t\Big ) \Big ], \end{aligned}$$

(4.10)

and

$$\begin{aligned} \Sigma _T^{-,t}= & {} \int _t^T \frac{\delta ^- ( \nu (T-s)+2\gamma ) + \pi ^-(T-s) }{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } dN_s^- \le 0, \;\; a.s. \end{aligned}$$

Proof

By the same arguments as in Proposition 3.2, we have

$$\begin{aligned} 0\le & {} \mathcal {E}_i^{(\lambda )}(t,x,y,d) \le \mathcal {E}^{(\lambda )}(t,x,y,d) \\:= & {} J^{(\lambda )}(t,x,y,d;{\hat{q}}^{(\lambda )},{\tilde{\xi }}_T^{(\lambda ),*}) - J^{(\lambda )}(t,x,y,d;{\hat{q}}^{(\lambda )},{\hat{\xi }}_T^{(\lambda )}), \end{aligned}$$

for $i = 1,2$, and

$$\begin{aligned} \mathcal {E}^{(\lambda )}(t,x,y,d)= & {} \frac{\eta r(\eta ,\beta )}{2\beta } \mathbb {E}\Big [ \big (D_T^{t,d} - {\hat{X}}_T^{t,x,y,d} \big )^2 1\!\!1_{D_T^{t,d} - {\hat{X}}_T^{t,x,y,d} < 0} \Big ], \end{aligned}$$

(4.11)

for $(t,x,y,d) \in [0,T]\times \mathbb {R}\times \mathbb {R}\times \mathbb {R}$. Now, recall from (4.8) that:

$$\begin{aligned} d{\hat{q}}_s^{(\lambda )}= & {} - \lambda \Big [ \frac{\pi }{2\gamma } + \frac{r(\eta ,\beta )\delta - \pi }{(r(\eta ,\beta )+\nu )(T-s) + 2 \gamma } \Big ] ds \\&+ \, \frac{r(\eta ,\beta )\sigma _d }{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } dB_s - \frac{\sigma _0 }{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } dW_s \\&+ \, \frac{r(\eta ,\beta )\delta ^+ - \pi ^+}{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } dN_s^+ + \frac{r(\eta ,\beta )\delta ^- - \pi ^-}{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } dN_s^-, \end{aligned}$$

where we write the dynamics directly in terms of the Poisson processes $N^\pm$. By integration, we deduce the (path-dependent) expression of ${\hat{q}}_s^{(\lambda )}$, $t\le s \le T$:

$$\begin{aligned} {\hat{q}}_s^{(\lambda )}= & {} {\hat{q}}_t^{(\lambda )} - \frac{\lambda \pi }{2\gamma } (s-t) +\frac{\lambda \big (r(\eta ,\beta )\delta - \pi \big )}{r(\eta ,\beta ) + \nu } \ln \Big ( \frac{(r(\eta ,\beta )+\nu )(T-s) + 2 \gamma }{(r(\eta ,\beta )+\nu )(T-t) + 2 \gamma }\Big ) \\&+ \, \int _t^s \frac{r(\eta ,\beta )\sigma _d }{(r(\eta ,\beta ) + \nu )(T-u) + 2 \gamma } dB_u - \int _t^s \frac{\sigma _0 }{(r(\eta ,\beta ) + \nu )(T-u) + 2 \gamma } dW_u \\&+ \, \int _t^s \frac{r(\eta ,\beta )\delta ^+ - \pi ^+}{(r(\eta ,\beta ) + \nu )(T-u) + 2 \gamma } dN_u^+ + \int _t^s \frac{r(\eta ,\beta )\delta ^- - \pi ^-}{(r(\eta ,\beta ) + \nu )(T-u) + 2 \gamma } dN_u^-, \end{aligned}$$

with ${\hat{q}}_t^{(\lambda )} = {\hat{q}}^{(\lambda )}(T-t,d-x,y)$. We thus obtain the expression of the final spread between demand and inventory:

$$\begin{aligned} D_T^{t,d} - {\hat{X}}_T^{t,x,y,d}= & {} d - x + \mu (T-t) + \int _t^T \sigma _d dB_s + \int _t^T \delta ^+ dN_s^+ + \int _t^T \delta ^- dN_s^- - \int _t^T {\hat{q}}_s^{(\lambda )} ds \nonumber \\= & {} m^{(\lambda )}(T-t,d-x,y) \nonumber \\&+ \, \int _t^T \frac{\sigma _d(\nu (T-s)+2\gamma )}{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } dB_s \nonumber \\&+ \, \int _t^T \frac{\sigma _0 (T-s)}{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } dW_s \nonumber \\&+ \, \int _t^T \frac{\delta ^+ ( \nu (T-s)+2\gamma ) + \pi ^+(T-s) }{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } dN_s^+ \nonumber \\&+ \, \int _t^T \frac{\delta ^- ( \nu (T-s)+2\gamma ) + \pi ^-(T-s) }{(r(\eta ,\beta ) + \nu )(T-s) + 2 \gamma } dN_s^-, \end{aligned}$$

(4.12)

by Fubini’s theorem, and where

$$\begin{aligned} m^{(\lambda )}(t,d,y):= & {} d + \mu t - t {\hat{q}}^{(\lambda )}(t,d,y) + \frac{\lambda \pi }{2\gamma } \int _0^t s ds \\&- \, \frac{\lambda \big (r(\eta ,\beta )\delta - \pi \big )}{r(\eta ,\beta ) + \nu } \int _0^t \ln \Big ( \frac{(r(\eta ,\beta )+\nu ) s + 2 \gamma }{(r(\eta ,\beta )+\nu ) t + 2 \gamma }\Big ) ds, \end{aligned}$$

is explicitly written as in (4.10) after some straightforward calculation. Denoting by $\Delta _T^{t,x,y,d}$ the continuous part of $D_T^{t,d} - {\hat{X}}_T^{t,x,y,d}$ consisting in the three first terms in the rhs of (4.12), and by $\Sigma _T^{+,t}$, $\Sigma _T^{-,t}$ the jump parts consisting in the two last terms of (4.12), so that

$$\begin{aligned} D_T^{t,d} - {\hat{X}}_T^{t,x,y,d}= & {} \Delta _T^{t,x,y,d} + \Sigma _T^{+,t} + \Sigma _T^{-,t}, \end{aligned}$$

we notice that $\Delta _T^{t,x,y,d}$ follows a normal distribution law with mean $m^{(\lambda )}(T-t,d-x,y)$ and variance $V(T-t)$, independent of $\Sigma _T^{\pm ,t}$. Then, conditionally on $\Sigma _T^{\pm ,t}$, $D_T^{t,d} - {\hat{X}}_T^{t,x,y,d}$ follows a normal distribution law with mean $m^{(\lambda )}(T-t,d-x,y) + \Sigma _T^{+,t} + \Sigma _T^{-,t}$, and variance $V(T-t)$, and this implies from (4.11) that:

$$\begin{aligned} \mathcal {E}^{(\lambda )}(t,x,y,d)= & {} \frac{\eta r(\eta ,\beta )}{2\beta } V(T-t) \mathbb {E}\Big [ \psi \Big ( \frac{m^{(\lambda )}(T-t,d-x,y) + \Sigma _T^{+,t} + \Sigma _T^{-,t}}{\sqrt{V(T-t)}}\Big ) \Big ] \\\le & {} \frac{\eta r(\eta ,\beta )}{2\beta } V(T-t) \mathbb {E}\Big [ \psi \Big ( \frac{m^{(\lambda )}(T-t,d-x,y) + \Sigma _T^{-,t} }{\sqrt{V(T-t)}}\Big ) \Big ], \end{aligned}$$

since $\Sigma _T^{+,t} \ge 0$ a.s. and $\psi$ is non-increasing. $\square$

Comments on the approximation error. Let us discuss about the accuracy of the upper bound in (4.9):

$$\begin{aligned} {\bar{\mathcal {E}}}^{(\lambda )}(T-t,d-x,y):= & {} \frac{\eta r(\eta ,\beta )}{2\beta } V(T-t) \mathbb {E}\Big [ \psi \Big ( \frac{m^{(\lambda )}(T-t,d-x,y) + \Sigma _T^{-,t} }{\sqrt{V(T-t)}}\Big ) \Big ], \end{aligned}$$

First, notice that $m^{(\lambda )}(T-t,d-x,y) + \Sigma _T^{-,t}$ $\sim \, m(T-t,d-x,y)$ a.s. in the limiting regimes where $T-t$ goes to zero, $d-x$ or y goes to infinity. Therefore, by dominated convergence theorem, ${\bar{\mathcal {E}}}^{(\lambda )}(T-t,d-x,y)$ converges to zero in these limiting regimes as in the no jump case. However, we are not able to derive an asymptotic limit as in the no jump case of Proposition 3.3, except when $\Sigma _T^{-,t} = 0$, i.e. $\delta ^- = \pi ^- = 0$, fo which we get the same asymptotic limit. Actually, in the presence of negative jumps on the demand, it is intuitively clear that our approximation should be less accurate than in the no jump case since the probability for the residual demand to stay above the final inventory is decreasing. Anyway, the explicit strategies $({\hat{q}}^{(\lambda )},{\tilde{\xi }}_T^{(\lambda ),*})$ still provide a very accurate approximation of the optimal strategies at least in these limiting regimes, as illustrated in the next paragraph.

4.3 Numerical results

We plot trajectories of some relevant quantities that we simulate with the same set of parameters as in Paragraph 3.3.2: $\sigma _0=1/60$ € $\cdot (\hbox {MW})^{-1}\cdot s^{-1/2}$, $\sigma _d=1000/60$ MW$\cdot s^{-1/2}$, $\beta =0.002$ € $\cdot (\hbox {MW})^{-2}$, $\eta =200$ € $\cdot (\hbox {MW})^{-2}$, $\mu =0$ MW$\cdot s^{-1}$, $\rho =0.8$, $\nu =4.00\cdot 10^{-5}$ € $\cdot (\hbox {MW})^{-2}$, $\gamma =2.22$ € $\cdot s\cdot (\hbox {MW})^{-2}$, $T = 24\hbox {h}$, $X_0 = 0$, $D_0=50000$ MW and $Y_0=50$ € $\cdot (\hbox {MW})^{-1}$. Moreover, we fix the probability of positive jumps, $p^+=1$ (then all jumps are positive: $p^-=0$), and the following values for the jump components: $\lambda =1.5/(3600\cdot 24) s^{-1}$, $\pi ^+=10$ € $\cdot (\hbox {MW})^{-1}$, $\delta ^+=1500$ MW.

For such parameter values, we observe two occurrences of jumps on the trajectories of the demand of price. Moreover, the probability $\mathbb {P}[{\hat{X}}_T > D_T]$ is bounded above by $2.92\times 10^{-16}$, the error ${\bar{\mathcal {E}}}^{(\lambda )}(0,D_0 -X_0,Y_0)$ is bounded by $2.66\times 10^{-5}$ €, and

The executed strategy $({\hat{q}}^{(\lambda )},{\hat{\xi }}_T^{(\lambda ),*})$ can then be considered as very close to the optimal strategy. This has to be compared with the numerical result obtained in the previous section in the no jump case where we obtained a lower expected total cost: ${\tilde{v}}(0,X_0,Y_0,D_0) = 1{,}916{,}700$€.

Figure 4 represents the evolution of the trading rate $({\hat{q}}_t^{(\lambda )})_{t\in [0,T]}$, and we see that it is decreasing consistently with the supermartingale property in Proposition 4.1. Actually, we observe that the deterministic part in (4.6), which is linear in time, dominates the stochastic part. The interpretation of the strategy is the following: since positive price jumps are expected, the agent purchases a large number of shares in electricity with the hope to sell it later at a higher price thanks to the possible occurrence of a positive jump. At the price jump times, which can be visualized in Fig. 5, we notice that the control ${\hat{q}}^{(\lambda )}$ reacts by a decrease in the trading rate. The reaction to the second jump is more sensible than to the first jump since it occurs a short time before the final horizon T, where the objective is also to achieve the equilibrium relation (4.7) between price and marginal cost. Finally, we observe clearly in Fig. 6 the concavity of the trajectory of the optimal inventory process $({\hat{X}}_t)_{t\in [0,T)}$, as expected from Remark 4.1. This emphasizes the double objective of the agent: on one hand, the purchase of electricity shares for taking profit of the positive price jumps, and on the other hand the resale of electricity shares for attaining the equilibrium relation between price and marginal cost at terminal date. We also plot the production ${\hat{\xi }}_T$ at the final time T on Fig. 6, and observe as in the no jump case that the imbalance cost $D_T - {\hat{X}}_T -{\hat{\xi }}_T$ is positive.

Fig. 4

Evolution of the trading rate control ${\hat{q}}^{(\lambda )}$

Fig. 5

Simulation of the quoted impacted price ${\hat{Y}}$ and of the unaffected price ${\hat{P}}$

Fig. 6

Evolution of the inventory ${\hat{X}}$ and of the forecast residual demand D

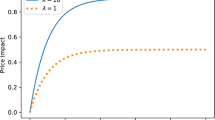
Next, we plot trajectories with the same set of parameters, but with $p^+=0.3$ (i.e. $p^-=0.7$), $\pi ^-=-10$ € $\cdot (\hbox {MW})^{-1}$, $\delta ^-=-1500$ MW. There are, in average, more negative than positive jumps. Now

Figure 7 shows that the trading rate $({\hat{q}}_t^{(\lambda )})_{t\in [0,T]}$ is increasing, which is consistent with the submartingale property in Proposition 4.1: the deterministic part in (4.6) dominates the stochastic part. Since negative jumps are more expected than negative jumps are, the agent first sells a large number of shares in electricity with the hope to buy it later at a lower price thanks to the possible occurrence of jumps, that should be mainly negative. Here, the control reacts to the negative price jumps by an increase in the trading rate. Finally, in Fig. 9 we observe the convexity of the trajectory of the optimal inventory $({\hat{X}}_t)_{t\in [0,T)}$ process, as expected from Remark 4.1. We also plot the production ${\hat{\xi }}_T$ at the final time T on that figure (Figs. 8, 9).

Fig. 7

Evolution of the trading rate control ${\hat{q}}^{(\lambda )}$

Fig. 8

Simulation of the quoted impacted price ${\hat{Y}}$ and of the unaffected price ${\hat{P}}$

Fig. 9

Evolution of the inventory ${\hat{X}}$ and of the forecast residual demand D

5 Delay in production

In this section, we consider the more realistic situation when there is delay in the production, assumed to be fixed equal to $h \in [0,T]$, and we denote by $v = v_{h}$ the value function to the associated optimal execution problem, as defined in (2.9), where we stress the dependence in the delay h. Our aim is to show how one can reduce the problem with delay to a suitable problem without delay, and then solve it explicitly. We shall consider the problem without jumps on demand forecast and price, but the same argument also works for the case with jumps.

5.1 Explicit solution with delay

For simplicity of presentation, and without loss of generality, we shall focus on the derivation of the value function $v_h(t,x,y,d)$ for an initial time $t = 0$, and fixed $(x,y,d) \in \mathbb {R}\times \mathbb {R}\times \mathbb {R}$. Given a control trading rate $q \in \mathcal {A}$, and from pathwise uniqueness for the solution to the dynamics (2.1), (2.7), (2.8), we observe that for any $\xi \in L^0(\mathcal {F}_{T-h})$:

$$\begin{aligned} {\left\{ \begin{array}{ll} X_T^{0,x} + \xi = X_T^{T-h,X_{T-h}^{0,x} + \xi } \; a.s. \\ Y_T^{0,y} = Y_T^{T-h,Y_{T-h}^{0,y}}, \quad D_T^{0,d} = D_T^{T-h,D_{T-h}^{0,d}} \; a.s. \end{array}\right. } \end{aligned}$$

(5.1)

To alleviate notations, we shall omit the dependence in the fixed initial conditions (x, y, d), and simply write $X_s = X_s^{0,x}$, $Y_s = Y_s^{0,y}$, $D_s = D_s^{0,d}$, for $s \ge 0$, $v_h = v_h(0,x,y,d)$, and $J(0;q,\xi ) = J(0,x,y,d;q,\xi )$ for the the cost functional in (2.10). By the tower property of conditional expectations and from (5.1), the cost functional can be written, for all $q \in \mathcal {A}$, $\xi \in L^0(\mathcal {F}_{T-h})$, as:

$$\begin{aligned}&J(0;q,\xi ) \nonumber \\&\quad = \mathbb {E}\Big [ \int _0^{T-h} q_s \big ( Y_s + \gamma q_s) ds + c(\xi ) + J(T-h,X_{T-h} + \xi ,Y_{T-h},D_{T-h};q,0) \Big ] \nonumber \\&\quad \ge \mathbb {E}\Big [ \int _0^{T-h} q_s \big ( Y_s + \gamma q_s) ds + c(\xi ) + v_{_{NP}}(T-h,X_{T-h} + \xi ,Y_{T-h},D_{T-h}) \Big ], \end{aligned}$$

(5.2)

by definition (3.8) of the value function $v_{_{NP}}$ for the optimal execution problem without production, i.e. the pure retailer problem. Since q is arbitrary in $\mathcal {A}$, this shows that:

$$\begin{aligned}&\inf _{q \in \mathcal {A}} J(0;q,\xi ) \nonumber \\&\quad \ge \inf _{q \in \mathcal {A}} \mathbb {E}\Big [ \int _0^{T-h} q_s \big ( Y_s + \gamma q_s) ds + c(\xi ) + v_{_{NP}}(T-h,X_{T-h} + \xi ,Y_{T-h},D_{T-h}) \Big ], \end{aligned}$$

(5.3)

for all $\xi \in L^0(\mathcal {F}_{T-h})$. Now, given $q \in \mathcal {A}$, and $\xi \in L^0(\mathcal {F}_{T-h})$, let us consider the trading rate ${\hat{q}}^{NP,\xi }$ in $\mathcal {A}_{T-h}$ solution to the pure retailer problem: $v_{_{NP}}(T-h,X_{T-h} + \xi ,Y_{T-h},D_{T-h})$, hence starting at time $T-h$ from an inventory $X_{T-h}+\xi$. By considering the process ${\tilde{q}} \in \mathcal {A}$ defined by: ${\tilde{q}}_s = q_s$ for $0\le s< T-h$, and ${\tilde{q}}_s = {\hat{q}}_s^{NP,\xi }$, for $T-h\le s \le T$, we then obtain from (5.2):

$$\begin{aligned}&J(0;{\tilde{q}},\xi ) \nonumber \\&\quad = \mathbb {E}\Big [ \int _0^{T-h} q_s \big ( Y_s + \gamma q_s) ds + c(\xi ) + v_{_{NP}}(T-h,X_{T-h} + \xi ,Y_{T-h},D_{T-h}) \Big ], \end{aligned}$$

(5.4)

which proves together with (5.3) the equality:

$$\begin{aligned}&\inf _{q \in \mathcal {A}} J(0;q,\xi ) \nonumber \\&\quad = \inf _{q \in \mathcal {A}} \mathbb {E}\Big [ \int _0^{T-h} q_s \big ( Y_s + \gamma q_s) ds + c(\xi ) + v_{_{NP}}(T-h,X_{T-h} + \xi ,Y_{T-h},D_{T-h}) \Big ], \end{aligned}$$

(5.5)

for all $\xi \in L^0(\mathcal {F}_{T-h})$. Therefore, $v_h = \inf _{q\in \mathcal {A},\xi \in L_+^0(\mathcal {F}_{T-h})} J(0;q,\xi )$ can be written as:

$$\begin{aligned} v_h= & {} \inf _{q \in \mathcal {A},\xi \in L_+^0(\mathcal {F}_{T-h})} \mathbb {E}\Big [ \int _0^{T-h} q_s \big ( Y_s + \gamma q_s) ds \nonumber \\&+ \, c(\xi ) + v_{_{NP}}(T-h,X_{T-h} + \xi ,Y_{T-h},D_{T-h}) \Big ]. \end{aligned}$$

(5.6)

In other words, the original problem with delay in production is formulated as an optimal execution problem without delay, namely with final horizon $T-h$, and terminal cost function:

$$\begin{aligned} C_h(x,y,d,\xi ):= & {} c(\xi ) + v_{_{NP}}(T-h,x+\xi ,y,d). \end{aligned}$$

Notice from the explicit expression of $v_{_{NP}}$ in Remark 3.1 that this cost function $C_h$ does not depend on T, and is in the form:

$$\begin{aligned} C_h(x,y,d,\xi )= & {} C_h(0,y,d-x-\xi ,0) = c(\xi ) + v_{_{NP}}(T-h,0,y,d-x-\xi ). \end{aligned}$$

The optimization over q and $\xi$ in (5.6) is done separately: the production $\xi \in L^0_+(\mathcal {F}_{T-h})$ is decided at time $T-h$, after the choice of the trading rate $(q_s)$ for $0\le s\le T-h$ (leading to an inventory $X_{T-h}$), and is determined optimally from the optimization a.s. at $T-h$ of the terminal cost $C_h(X_{T-h},Y_{T-h},D_{T-h},\xi )$. It is then given in feedback form by $\xi _{T-h}^* =$ ${\hat{\xi }}^{h,tr+}(D_{T-h} - X_{T-h},Y_{T-h})$ where

$$\begin{aligned} {\hat{\xi }}^{h,tr+}(d,y):= & {} \mathop {\mathrm{arg}\,\mathrm{min}}_{\xi \ge 0} C_h(0,y,d-\xi ,0) = \mathop {\mathrm{arg}\,\mathrm{min}}_{\xi \ge 0} \big [ c(\xi ) + v_{_{NP}}(T-h,0,y,d-\xi ) \big ], \end{aligned}$$

hence explicitly given from the expression of $v_{_{NP}}$ in Remark 3.1 by:

$$\begin{aligned} {\hat{\xi }}^{h,tr+}(d,y)= & {} {\hat{\xi }}^h(d,y) 1\!\!1_{{\hat{\xi }}^h(d,y)\ge 0}, \nonumber \\ {\hat{\xi }}^h(d,y):= & {} \frac{\eta }{\eta +\beta } \Big [ \frac{(\nu h + 2 \gamma )(\mu h + d) + hy}{(r(\eta ,\beta )+\nu )h + 2 \gamma } \Big ]. \end{aligned}$$

(5.7)

The problem (5.6) is then rewritten as

$$\begin{aligned} v_h= & {} \inf _{q\in \mathcal {A}} \mathbb {E}\Big [ \int _0^{T-h} q_s \big ( Y_s + \gamma q_s) ds + C_h^+(D_{T-h}-X_{T-h},Y_{T-h}) \Big ], \end{aligned}$$

(5.8)

where

$$\begin{aligned} C_h^+(d,y):= & {} C_h(0,y,d-{\hat{\xi }}^{h,tr+}(d),0). \end{aligned}$$

Notice that when $h = 0$, we retrieve the expressions in the no delay case: ${\hat{\xi }}^{0,tr+} = {\hat{\xi }}^{tr+}$ in (3.1), $C_0^+ = C^+$ in (3.3) and $v_0 = v$ in (3.2). As in the no delay case, there is no explicit solution to the HJB equation associated to the stochastic control problem (5.8). We then consider the approximate control problem where we relax the non negativity constraint on the production, i.e. ${\tilde{v}}_h = \inf _{q\in \mathcal {A},\xi \in L^0(\mathcal {F}_{T-h})} J(0;q,\xi )$. Therefore by following the same arguments as above, the corresponding value function is written as:

$$\begin{aligned} {\tilde{v}}_h= & {} \inf _{q\in \mathcal {A}} \mathbb {E}\Big [ \int _0^{T-h} q_s \big ( Y_s + \gamma q_s) ds + {\tilde{C}}_h(D_{T-h}-X_{T-h},Y_{T-h}) \Big ], \end{aligned}$$

(5.9)

where

$$\begin{aligned} {\tilde{C}}_h(d,y):= & {} C_h(0,y,d-{\hat{\xi }}^h(d),0). \end{aligned}$$

From the explicit expressions of ${\hat{\xi }}^h$ in (5.7) and $v_{_{NP}}$ in Remark 3.1, it appears after some tedious but straightforward calculations that the auxiliary terminal cost function ${\tilde{C}}_h$ simplifies remarkably into:

$$\begin{aligned} {\tilde{C}}_h(d,y)= & {} {\tilde{v}}_0(T-h,0,y,d) + K_h, \end{aligned}$$

where ${\tilde{v}}_0$ is the auxiliary value function without delay explicitly obtained in Theorem 3.1, and $K_h$ is a constant depending only on the delay h and the parameters of the model, given explicitly by

$$\begin{aligned} K_h= & {} \frac{\eta ^2}{2}\frac{\sigma _0^2+\sigma _d^2\nu ^2+2\rho \sigma _0\sigma _d\nu }{(\eta +\beta )(\eta +\nu )(r(\eta ,\beta )+\nu )}h\\&+ \, \gamma \frac{\sigma _0^2+\sigma _d^2\eta ^2-2\rho \sigma _0\sigma _d\eta }{(\eta +\nu )^2}\ln \Big (1+\frac{(\eta +\nu )h}{2\gamma }\Big )\\&- \, \gamma \frac{\sigma _0^2+\sigma _d^2 r^2(\eta ,\beta )-2\rho \sigma _0\sigma _dr(\eta ,\beta )}{(r(\eta ,\beta )+\nu )^2} \ln \Big (1+\frac{(r(\eta ,\beta )+\nu )h}{2\gamma }\Big ). \end{aligned}$$

One easily checks that $K_h = 0$ for $h = 0$, and $K_h$ is increasing with h (actually the derivative of $K_h$ w.r.t. h is positive), hence in particular $K_h$ is nonnegative. Plugging into (5.9), we then get

$$\begin{aligned} {\tilde{v}}_h= & {} \inf _{q\in \mathcal {A}} \mathbb {E}\Big [ \int _0^{T-h} q_s \big ( Y_s + \gamma q_s) ds + {\tilde{v}}_0(T-h,X_{T-h},Y_{T-h},D_{T-h}) \Big ] + K_h. \end{aligned}$$

(5.10)

Therefore, by using the dynamic programming principle for the control problem ${\tilde{v}}_0 = {\tilde{v}}_0(0,x,y,d)$ in (3.4), we obtain this remarkable relation

$$\begin{aligned} {\tilde{v}}_h= & {} {\tilde{v}}_0 + K_h, \end{aligned}$$

(5.11)

which explicitly relates the (approximate) value function with and without delay. As expected from the very definition of ${\tilde{v}}_h$, this relation implies that ${\tilde{v}}_h-{\tilde{v}}_0$ is nonnegative, and is increasing in h. This is consistent with the intuition that when making the production choice in advance, we do not take into account the future movements of the price and of the residual demand, which should therefore lead to an average positive correction of the cost. More precisely, the relation (5.11) gives an explicit quantification of the delay impact via the term $K_h$ (which does not depend on the state variables x, y, d) in function of the various model parameters. Moreover, the optimal control of the stochastic control problem (5.10) over $[0,T-h)$ is explicitly given by the optimal control $({\hat{q}}_s)_{0\le s \le T-h}$ of problem ${\tilde{v}}_0$ without delay in Theorem 3.1.

Let us now consider the following strategy $({\hat{q}}^{h,+},{\tilde{\xi }}_{T-h}^{h,*}) \in \mathcal {A}\times L_+^0(\mathcal {F}_{T-h})$ for the original problem $v_h$ with delay:

• Before $T-h$, follow the trading strategy ${\hat{q}}^{h,+}_s = {\hat{q}}_s$, $s < T-h$, corresponding to the solution of the auxiliary problem without delay as if production choice is made at time T, and leading to an inventory ${\hat{X}}_{T-h}$, and an impacted price ${\hat{Y}}_{T-h}$.

• At time $T-h$, choose the production quantity:

  $$\begin{aligned} {\tilde{\xi }}_{T-h}^{h,*}:= & {} {\hat{\xi }}^{h,{tr+}}(D_{T-h} - {\hat{X}}_{T-h},{\hat{Y}}_{T-h}). \end{aligned}$$

• Between time $T-h$ and T, follow the trading strategy ${\hat{q}}^{h,+}_s = {\hat{q}}_s^{NP,{\tilde{\xi }}_{T-h}^{h,*}}$, $T-h\le s\le T$, corresponding to the solution of the problem without production, and starting at $T-h$ from an inventory ${\hat{X}}_{T-h} + {\tilde{\xi }}_{T-h}^{h,*}$.

In order to estimate the quality of this approximate strategy with respect to the optimal trading problem $v_h$, measured by

$$\begin{aligned} \mathcal {E}_1^h:= & {} J(0;{\hat{q}}^{h,+},{\tilde{\xi }}_{T-h}^{h,*}) - v_h, \end{aligned}$$

we shall compare it with the following strategy $({\hat{q}}^h,{\hat{\xi }}_{T-h}^h)$ $\in \mathcal {A}\times L^0(\mathcal {F}_{T-h})$:

• Before $T-h$, follow the trading strategy ${\hat{q}}^{h}_s = {\hat{q}}_s$, $s < T-h$, corresponding to the solution of the auxiliary problem without delay as if production choice is made at time T, and leading to an inventory ${\hat{X}}_{T-h}$, and an impacted price ${\hat{Y}}_{T-h}$.

• At time $T-h$, choose the “production” quantity (which can be negative):

  $$\begin{aligned} {\hat{\xi }}_{T-h}^h= & {} {\hat{\xi }}^h(D_{T-h} - {\hat{X}}_{T-h},{\hat{Y}}_{T-h}). \end{aligned}$$

• Between time $T-h$ and T, follow the trading strategy ${\hat{q}}^{h}_s = {\hat{q}}_s^{NP,{\hat{\xi }}_{T-h}^h}$, $T-h\le s \le T$, corresponding to the solution of the problem without production, and starting at $T-h$ from an inventory ${\hat{X}}_{T-h} + {\hat{\xi }}_{T-h}^h$.

Then, by construction and following the arguments (see in particular (5.4), (5.9), (5.10)) leading to the expression (5.11) of ${\tilde{v}}_h$, we see that $({\hat{q}}^h,{\hat{\xi }}_{T-h}^h)$ is the optimal solution for ${\tilde{v}}_h$, i.e. ${\tilde{v}}_h = J(0;{\hat{q}}^h,{\hat{\xi }}_{T-h}^h)$. On the other hand, since ${\tilde{v}}_h \le v_h \le J(0;{\hat{q}}^{h,+},{\tilde{\xi }}_{T-h}^{h,*})$, we deduce that

$$\begin{aligned} \max (v_h-{\tilde{v}}_h , \mathcal {E}_1^h)\le & {} {\bar{\mathcal {E}}}^h := J(0;{\hat{q}}^{h,+},{\tilde{\xi }}_{T-h}^{h,*}) - J(0;{\hat{q}}^h,{\hat{\xi }}_{T-h}^h). \end{aligned}$$

Now, from the expression (5.4) of J, and by same arguments as in the proof of Proposition 3.2 (see the derivation of relation (3.15)), we have

$$\begin{aligned} {\bar{\mathcal {E}}}^h= & {} \mathbb {E}\Big [ C_h^+(D_{T-h}-{\hat{X}}_{T-h},{\hat{Y}}_{T-h}) - {\tilde{C}}_h(D_{T-h}-{\hat{X}}_{T-h},{\hat{Y}}_{T-h}) \Big ] \\= & {} \mathbb {E}\Big [ v_{_{NP}}(T-h, 0, \hat{Y}_{T-h}, D_{T-h}-\hat{X}_{T-h}-\tilde{\xi }_{T-h}^{h,*})+c(\tilde{\xi }_{T-h}^{h,*})\\&-\, v_{_{NP}}(T-h, 0, \hat{Y}_{T-h}, D_{T-h}-\hat{X}_{T-h}-\hat{\xi }_{T-h}^h)-c(\hat{\xi }_{T-h}^h) \Big ]\\= & {} \frac{\eta r(\eta ,\beta )}{2\beta } \frac{(r(\eta ,\beta )+\nu )h+2\gamma }{(\eta +\nu )h+2\gamma } V_h(T) \psi \Big ( \frac{m(T,d-x,y)}{\sqrt{V_h(T)}}\Big ) \end{aligned}$$

where m and $\psi$ are defined as in (3.12), and

$$\begin{aligned} V_h(T)= & {} \int _h^T \frac{\sigma _0^2 s^2 + \sigma _d^2(\nu s + 2 \gamma )^2 + 2 \rho \sigma _0\sigma _ds (\nu s + 2 \gamma )}{\big [(r(\eta ,\beta ) + \nu )s + 2 \gamma \big ]^2} ds. \end{aligned}$$

We recover when $h = 0$ the expression in Proposition 3.2 of the error in the no delay case, and notice that ${\bar{\mathcal {E}}}^h$ decreases when the delay increases: indeed, the error comes from the trading procedure before deciding how much to produce, which is dictated by the auxiliary problem, in which the final “production” can be negative. After $T-h$, the followed control is optimal, as there remains no production decision at some further date. The shorter the period before making the production decision is, the weaker the error is.

Let us finally discuss some properties of the (approximate) optimal trading strategy ${\hat{q}}^{h,+}$. Recalling from Proposition 3.1 that the optimal trading rate is a martingale in the no delay case, we see by construction of $({\hat{q}}_s^{h,+})_{0\le s\le T}$ that it is a martingale on $[0,T-h)$ and a martingale on $[T-h,T]$. Moreover, for any $s \in [T-h,T]$, and $t \in [0,T-h)$, we have

$$\begin{aligned} \mathbb {E}\big [ {\hat{q}}_s^{h,+} | \mathcal {F}_t \big ]= & {} \mathbb {E}\big [ \mathbb {E}\big [ {\hat{q}}_s^{NP,{\tilde{\xi }}_{T-h}^{h,*}} | \mathcal {F}_{T-h} \big ] | \mathcal {F}_t \big ] = \mathbb {E}\big [ {\hat{q}}_{T-h}^{NP,{\tilde{\xi }}_{T-h}^{h,*}} | \mathcal {F}_t \big ] \nonumber \\= & {} \mathbb {E}\Big [ \frac{\eta (\mu h + D_{T-h} - {\hat{X}}_{T-h} - {\tilde{\xi }}_{T-h}^{h,*}) - {\hat{Y}}_{T-h}}{(\eta +\nu )h + 2\gamma } \big | \mathcal {F}_t \Big ] \nonumber \\= & {} \mathbb {E}\Big [ \frac{\eta (\mu h + D_{T-h} - {\hat{X}}_{T-h} - {\hat{\xi }}_{T-h}^h) - {\hat{Y}}_{T-h}}{(\eta +\nu )h + 2\gamma } \big | \mathcal {F}_t \Big ] \nonumber \\&+ \, \frac{\eta }{(\eta +\nu )h + 2\gamma } \mathbb {E}\Big [ {\hat{\xi }}_{T-h}^h - {\tilde{\xi }}_{T-h}^{h,*} \big | \mathcal {F}_t \Big ] \nonumber \\= & {} \mathbb {E}\Big [ \frac{r(\eta ,\beta )(\mu h + D_{T-h} - {\hat{X}}_{T-h}) - {\hat{Y}}_{T-h}}{(r(\eta ,\beta )+\nu )h + 2\gamma } \big | \mathcal {F}_t \Big ] \nonumber \\&\quad + \, \frac{\eta }{(\eta +\nu )h + 2\gamma } \mathbb {E}\Big [ {\hat{\xi }}_{T-h}^h - {\tilde{\xi }}_{T-h}^{h,*} \big | \mathcal {F}_t \Big ] \nonumber \\= & {} \mathbb {E}\big [ {\hat{q}}_{T-h} | \mathcal {F}_t \big ] + \frac{\eta }{(\eta +\nu )h + 2\gamma } \mathbb {E}\Big [ {\hat{\xi }}_{T-h}^h - {\tilde{\xi }}_{T-h}^{h,*} \big | \mathcal {F}_t \Big ] \nonumber \\= & {} {\hat{q}}_t + \frac{\eta }{(\eta +\nu )h + 2\gamma } \mathbb {E}\Big [ {\hat{\xi }}_{T-h}^h 1\!\!1_{{\hat{\xi }}_{T-h}^h<0} \big | \mathcal {F}_t \Big ] \le {\hat{q}}_t = {\hat{q}}_t^{h,+}. \end{aligned}$$

(5.12)

where we used the tower rule for conditional expectations, the martingale property and the explicit expression of $q^{NP,{\tilde{\xi }}_{T-h}^{h,*}}$ in Remark 3.1, the definition of ${\hat{\xi }}_{T-h}^h$, the martingale property and explicit expression of ${\hat{q}}$ in Theorem 3.1, and finally the fact that ${\tilde{\xi }}_{T-h}^{h,*} = {\hat{\xi }}_{T-h}^h1\!\!1_{{\hat{\xi }}_{T-h}^h\ge 0}$. This shows in particular the supermartingale property of ${\hat{q}}^{h,+}$ over the whole period [0, T]. Notice that the same arguments as for the derivation of (5.12) shows the martingale property over the whole period [0, T] of the optimal trading strategy ${\hat{q}}^h$ associated to the auxiliary problem ${\tilde{v}}_h$. Moreover, by the martingale property of ${\hat{q}}^{h,+}$ on $[0,T-h)$, and relation (5.12), we see that the (approximate) optimal inventory process ${\hat{X}}^{h,+}$ with trading rate ${\hat{q}}^{h,+}$ has on average, a growth rate $\frac{d\mathbb {E}[{\hat{X}}^{h,+}_s]}{ds}$, which is piecewise constant, equal to:

$$\begin{aligned} \mathbb {E}[{\hat{q}}_s^{h,+}]= & {} \left\{ \begin{array}{l@{\quad }l} {\hat{q}}_0, &{} \hbox { for } \; 0 \le s < T-h \\ \textstyle {\hat{q}}_0^{(h)} := {\hat{q}}_0 + \frac{\eta }{(\eta +\nu )h + 2\gamma } \mathbb {E}\big [ {\hat{\xi }}_{T-h}^h 1\!\!1_{{\hat{\xi }}_{T-h}^h<0} \big ] < {\hat{q}}_0, &{} \hbox { for } \; T-h \le s \le T, \end{array} \right. \end{aligned}$$

with ${\hat{q}}_0 = \frac{r(\eta ,\beta ))(\mu T + d-x)-y}{(r(\eta ,\beta )+\nu )T +2\gamma }$, and

$$\begin{aligned} {\hat{q}}_0^{(h)}= & {} {\hat{q}}_0 - \frac{\eta r(\eta ,\beta )}{\beta ((\eta +\nu )h+2\gamma )}\sqrt{V_h(T)}\tilde{\psi }\Big (\frac{m(T,d-x,y)}{\sqrt{V_h(T)}}\Big ), \end{aligned}$$

where

$$\begin{aligned} \tilde{\psi }(z):= & {} \phi (z) - z\Phi (-z), \quad z \in \mathbb {R}\end{aligned}$$

is a nonnegative function, as pointed out in (3.17).

5.2 Numerical results

We plot figures showing relevant trajectories with the same parameters as in Sect. 3.3.2. We add a delay $h=4$ h: the production choice has to be made 4 h before the end of the trading period. We have

which is slightly higher than the value ${\tilde{v}}_0(0,X_0,Y_0,D_0) = 1{,}916{,}700$€ without delay.

On Fig. 10, we see that at time $T-h$, the positive production choice $\tilde{\xi }_{T-h}^{h,*}$ is made, and then we go on buying shares on the intraday market in order to go nearer to the demand forecast, with a smaller slope of trading rate. On Fig. 11, which represents the control process without the last hour of trading (because oscillations then become overwhelming), we see that after date $T-h$, as we do not plan to use final production leverage any more, the approximate optimal control process ${\hat{q}}^{h,+}$ oscillates a lot as we are approaching the end of trading time. We can compare with Fig. 1 to assert that qualitatively, the control in the problem with no production oscillates more than the one in the problem with final production, as in the former problem, the intraday market is the only way to seek to reach the equilibrium.

Fig. 10

Evolution of the inventory ${\hat{X}}$ (with production choice at time $T-h$) and of the forecast residual demand D

Fig. 11

Evolution of the trading rate control ${\hat{q}}^{h,+}$ without the last hour

Appendix

1.1 Proof of Theorem 3.1

The Hamilton-Jacobi-Bellman (HJB) equation arising from the dynamic programming associated to the stochastic control problem (3.4) is:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial {\tilde{v}}}{\partial t} + \inf _{q \in \mathbb {R}} \left[ q \displaystyle \frac{\partial {\tilde{v}}}{\partial x} + \nu q \displaystyle \frac{\partial {\tilde{v}}}{\partial y} + \mu \displaystyle \frac{\partial {\tilde{v}}}{\partial d} + \frac{1}{2} \sigma _0^2 \displaystyle \frac{\partial ^2 {\tilde{v}}}{\partial y^2} + \frac{1}{2} \sigma _d^2 \displaystyle \frac{\partial ^2 {\tilde{v}}}{\partial d^2} + \rho \sigma _0\sigma _d \displaystyle \frac{\partial ^2 {\tilde{v}}}{\partial y \partial d} + q(y+\gamma q) \right] = 0, \nonumber \\ {\tilde{v}}(T,x,y,d) = {\tilde{C}}(d-x) = \frac{1}{2} r(\eta ,\beta ) (d-x)^2. \end{array}\right. } \end{aligned}$$

The argmin in HJB is attained for

$$\begin{aligned} {\tilde{q}}(t,x,y,d)= & {} - \frac{1}{2\gamma }\left[ \displaystyle \frac{\partial {\tilde{v}}}{\partial x} + \nu \displaystyle \frac{\partial {\tilde{v}}}{\partial y} + y \right] , \end{aligned}$$

and the HJB equation is rewritten as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial {\tilde{v}}}{\partial t} + \mu \displaystyle \frac{\partial {\tilde{v}}}{\partial d} + \frac{1}{2} \sigma _0^2 \displaystyle \frac{\partial ^2 {\tilde{v}}}{\partial y^2} + \frac{1}{2} \sigma _d^2 \displaystyle \frac{\partial ^2 {\tilde{v}}}{\partial d^2} + \rho \sigma _0\sigma _d \displaystyle \frac{\partial ^2 {\tilde{v}}}{\partial y \partial d} - \frac{1}{4\gamma }\left[ \displaystyle \frac{\partial {\tilde{v}}}{\partial x} + \nu \displaystyle \frac{\partial {\tilde{v}}}{\partial y} + y \right] ^2 = 0, \\ {\tilde{v}}(T,x,y,d) = \frac{1}{2} r(\eta ,\beta ) (d-x)^2. \end{array}\right. } \end{aligned}$$

(6.1)

We look for a candidate solution to HJB in the form

$$\begin{aligned} {\tilde{w}}(t,x,y,d)= & {} A(T-t) (d-x)^2 + B(T-t) y^2 + F(T-t) (d-x)y \nonumber \\&+ \, G(T-t) (d-x) + H(T-t) y + K(T-t), \end{aligned}$$

(6.2)

for some deterministic functions A, B, F, G, H and K. Plugging the candidate function $\tilde{w}$ into equation (6.1), we see that ${\tilde{w}}$ is solution to the HJB equation iff the following system of ordinary differential equations (ODEs) is satisfied by A, B, F, G, H and K:

$$\begin{aligned} \left\{ \begin{array}{r} \textstyle A'+\frac{1}{4\gamma }(-2A+\nu F)^2 = 0 \\ \textstyle B'+\frac{1}{4\gamma }(2\nu B-F+1)^2 = 0 \\ \textstyle F'+\frac{1}{2\gamma } (-2A+\nu F) (2\nu B-F+1) = 0 \\ \textstyle G'-2\mu A +\frac{1}{2\gamma }(-2A+\nu F)(-G+\nu H) = 0 \\ \textstyle H'-\mu F +\frac{1}{2\gamma }(2\nu B-F+1)(-G+\nu H) = 0 \\ \textstyle K'-\mu G -(\sigma _0^2B+\sigma _d^2 A + \rho \sigma _0\sigma _d F)+\frac{1}{4\gamma }(-G+\nu H)^2 = 0 \end{array} \right. \end{aligned}$$

with the initial conditions $A(0)=\frac{1}{2}r(\eta , \beta )$, $B(0)=0$, $F(0)=0$, $G(0)=0$, $H(0)=0$, $K(0)=0$. We first solve the Riccati system relative to the triple (A, B, F), and obtain:

$$\begin{aligned} {\left\{ \begin{array}{ll} \textstyle A(t) = \frac{r(\eta ,\beta )(\frac{\nu }{2}t+\gamma )}{(r(\eta ,\beta )+\nu )t+2\gamma } , \\ \textstyle B(t) = -\frac{1}{2}\frac{t}{(r(\eta ,\beta )+\nu )t+2\gamma }, \quad F(t) = \frac{r(\eta ,\beta )t}{(r(\eta ,\beta )+\nu )t+2\gamma }. \end{array}\right. } \end{aligned}$$

(6.3)

Then we solve the first-order linear system of ODE relative to the pair (G, H), which leads to the explicit solution:

$$\begin{aligned} G(t) = 2\mu t A(t), \;\;&\hbox { and }&\; H(t) = -2 r(\eta ,\beta )\mu t B(t). \end{aligned}$$

(6.4)

Finally, we explicitly obtain K from the last equation:

$$\begin{aligned} K(t)= & {} \gamma \frac{\sigma _0^2 + \sigma _d^2r^2(\eta ,\beta ) - 2\rho \sigma _0\sigma _dr(\eta ,\beta )}{\big (r(\eta ,\beta ) + \nu \big )^2} \ln \Big ( 1 + \frac{(r(\eta ,\beta ) + \nu )t}{2\gamma }\Big ) \nonumber \\&+ \, \frac{\sigma _d^2r(\eta ,\beta )\nu +2\rho \sigma _0\sigma _dr(\eta ,\beta ) - \sigma _0^2}{2\big (r(\eta ,\beta ) + \nu \big )}t + \frac{r(\eta ,\beta )\mu ^2 t^2(\frac{\nu }{2}t+\gamma )}{ (r(\eta ,\beta ) + \nu )t+2\gamma }. \end{aligned}$$

(6.5)

By construction, ${\tilde{w}}$ in (6.2) with A, B, F, G, H and K explicitly given by (6.3)–(6.4)–(6.5), is a smooth solution with quadratic growth condition to the HJB equation (6.1). Moreover, the argmin in HJB equation for ${\tilde{w}}$ is attained for

$$\begin{aligned} {\tilde{q}}(t,x,y,d)= & {} - \frac{1}{2\gamma }\left[ \displaystyle \frac{\partial {\tilde{w}}}{\partial x} + \nu \displaystyle \frac{\partial {\tilde{w}}}{\partial y} + y \right] \\= & {} \frac{r(\eta ,\beta )(\mu (T-t)+d-x)-y}{(r(\eta ,\beta )+\nu )(T-t)+2\gamma } =: {\hat{q}}(T-t,d-x,y). \end{aligned}$$

Notice that ${\hat{q}}$ is linear, and Lipschitz in x, y, d, uniformly in time t, and so given an initial state (x, y, d) at time t, there exists a unique solution $({\hat{X}}^{t,x,y,d},{\hat{Y}}^{t,x,y,d},D^{t,d})_{t\le s\le T}$ to (2.1)–(2.7)–(2.8) with the feedback control ${\hat{q}}_s = {\hat{q}}(T-s,D_s^{t,d}-{\hat{X}}_s^{t,x,y,d},{\hat{Y}}_s^{t,x,y,d})$, which satisfies: $\mathbb {E}[\sup _{t\le s\le T} |{\hat{X}}_s^{t,x,y,d}|^2 + |{\hat{Y}}_s^{t,x,y,d}|^2 + |D_s^{t,d}|^2] < \infty$. This implies in particular that $\mathbb {E}[\int _t^T |{\hat{q}}_s|^2 ds] < \infty$, hence ${\hat{q}} \in \mathcal {A}_t$. We now call on a classical verification theorem (see e.g. Theorem 3.5.2 in [9]), which shows that ${\tilde{w}}$ is indeed equal to the value function ${\tilde{v}}$, and ${\hat{q}}$ is an optimal control. Finally, once the optimal trading rate ${\hat{q}}$ is determined, the optimal production is obtained from the optimization over $\xi \in \mathbb {R}$ of the terminal cost $C(D_T^{t,d}-{\hat{X}}_T^{t,x,y,d},\xi )$, hence given by: ${\hat{\xi }}_T = \frac{\eta }{\eta +\beta }(D_T^{t,d}-{\hat{X}}_T^{t,x,y,d})$. $\square$

1.2 Proof of Theorem 4.1

The Hamilton-Jacobi-Bellman (HJB) integro-differential equation arising from the dynamic programming associated to the stochastic control problem ${\tilde{v}} = {\tilde{v}}^{(\lambda )}$ with jumps in the dynamics of Y and D is:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial {\tilde{v}}^{(\lambda )}}{\partial t} + \inf _{q \in \mathbb {R}} \Bigg [ q \displaystyle \frac{\partial {\tilde{v}}^{(\lambda )}}{\partial x} + \nu q \displaystyle \frac{\partial {\tilde{v}}^{(\lambda )}}{\partial y} + \mu \displaystyle \frac{\partial {\tilde{v}}^{(\lambda )}}{\partial d} + \frac{1}{2} \sigma _0^2 \displaystyle \frac{\partial ^2 {\tilde{v}}^{(\lambda )}}{\partial y^2}\\ + \frac{1}{2} \sigma _d^2 \displaystyle \frac{\partial ^2 {\tilde{v}}^{(\lambda )}}{\partial d^2} + \rho \sigma _0\sigma _d \displaystyle \frac{\partial ^2 {\tilde{v}}^{(\lambda )}}{\partial y \partial d} + q(y+\gamma q) \Bigg ]\nonumber \\ + \lambda \big [ p^+{\tilde{v}}^{(\lambda )} (t,x,y+\pi ^+,d+\delta ^+) + p^- {\tilde{v}}^{(\lambda )}(t,x,y+\pi ^-,d +\delta ^-) - {\tilde{v}}^{(\lambda )}(t,x,y,d) \big ] = 0 \nonumber \\ {\tilde{v}}^{(\lambda )}(T,x,y,d) = {\tilde{C}}(d-x) = \frac{1}{2} r(\eta ,\beta ) (d-x)^2. \nonumber \end{array}\right. } \end{aligned}$$

Notice that with respect to the no jump case, there is in addition a linear integro-differential term in the HJB equation (which does not depend on the control), and the argmin is attained as in the no jump case for

$$\begin{aligned} {\tilde{q}}^{(\lambda )}(t,x,y,d)= & {} - \frac{1}{2\gamma }\left[ \displaystyle \frac{\partial {\tilde{v}}^{(\lambda )}}{\partial x} + \nu \displaystyle \frac{\partial {\tilde{v}}^{(\lambda )}}{\partial y} + y \right] . \end{aligned}$$

The HJB equation is then rewritten as

$$\begin{aligned} \!{\left\{ \begin{array}{ll}\! \displaystyle \frac{\partial {\tilde{v}}^{(\lambda )}}{\partial t} + \mu \displaystyle \frac{\partial {\tilde{v}}^{(\lambda )}}{\partial d} + \frac{1}{2} \sigma _0^2 \displaystyle \frac{\partial ^2 {\tilde{v}}^{(\lambda )}}{\partial y^2} + \frac{1}{2} \sigma _d^2 \displaystyle \frac{\partial ^2 {\tilde{v}}^{(\lambda )}}{\partial d^2} + \rho \sigma _0\sigma _d \displaystyle \frac{\partial ^2 {\tilde{v}}^{(\lambda )}}{\partial y \partial d} - \frac{1}{4\gamma }\left[ \displaystyle \frac{\partial {\tilde{v}}^{(\lambda )}}{\partial x} + \nu \displaystyle \frac{\partial {\tilde{v}}^{(\lambda )}}{\partial y} + y \right] ^2 \\ + \lambda \big [ p^+{\tilde{v}}^{(\lambda )}(t,x,y+\pi ^+,d +\delta ^+) + p^- {\tilde{v}}^{(\lambda )}(t,x,y +\pi ^-,d+\delta ^-) - {\tilde{v}}^{(\lambda )}(t,x,y,d) \big ] = 0 \\ {\tilde{v}}^{(\lambda )}(T,x,y,d) = \frac{1}{2} r(\eta ,\beta ) (d-x)^2. \end{array}\right. } \end{aligned}$$

(6.6)

We look again for a candidate solution to (6.6) in the form

$$\begin{aligned} {\tilde{w}}^{(\lambda )}(t,x,y,d)= & {} A_{\lambda }(T-t) (d-x)^2 + B_{\lambda }(T-t) y^2 + F_{\lambda }(T-t) (d-x)y \nonumber \\&+ \, G_{\lambda }(T-t) (d-x) + H_{\lambda }(T-t) y + K_{\lambda }(T-t), \end{aligned}$$

(6.7)

for some deterministic functions $A_{\lambda }$, $B_{\lambda }$, $F_{\lambda }$, $G_{\lambda }$, $H_{\lambda }$ and $K_{\lambda }$. Plugging the candidate function ${\tilde{w}}^{(\lambda )}$ into equation (6.6), we see that ${\tilde{w}}^{(\lambda )}$ is solution to the HJB equation iff the following system of ordinary differential equations (ODEs) is satisfied by $A_{\lambda }$, $B_{\lambda }$, $F_{\lambda }$, $G_{\lambda }$, $H_{\lambda }$ and $K_{\lambda }$:

$$\begin{aligned} \left\{ \begin{array}{r} A_{\lambda }'+\frac{1}{4\gamma }(-2A_{\lambda }+\nu F_{\lambda })^2 = 0 \\ B_{\lambda }'+\frac{1}{4\gamma }(2\nu B_{\lambda }-F_{\lambda }+1)^2 = 0 \\ F_{\lambda }'+\frac{1}{2\gamma } (-2A_{\lambda }+\nu F_{\lambda }) (2\nu B_{\lambda }-F_{\lambda }+1) = 0 \\ G_{\lambda }'-2\mu A_{\lambda } +\frac{1}{2\gamma }(-2A_{\lambda }+\nu F_{\lambda })(-G_{\lambda }+\nu H_{\lambda })-\lambda (2\delta A_{\lambda }+\pi F_{\lambda }) = 0 \\ H_{\lambda }'-\mu F_{\lambda } +\frac{1}{2\gamma }(2\nu B_{\lambda }-F_{\lambda }+1)(-G_{\lambda }+\nu H_{\lambda })-\lambda (2\pi B_{\lambda } +\delta F_{\lambda }) = 0 \\ K_{\lambda }'-\mu G_{\lambda } -(\sigma _0^2 B_{\lambda } + \sigma _d^2 A_{\lambda } + \rho \sigma _0\sigma _d F_{\lambda })+\frac{1}{4\gamma }(-G_{\lambda } + \nu H_{\lambda })^2 \qquad \quad \\ \quad -\lambda [(p^+(\delta ^+)^2+p^-(\delta ^-)^2) A_{\lambda } + (p^+(\pi ^+)^2+p^-(\pi ^-)^2) B_{\lambda }\qquad \quad \\ +(p^+\delta ^+\pi ^++p^-\delta ^-\pi ^-) F_{\lambda } + \delta G_{\lambda } + \pi H_{\lambda }] = 0 \end{array} \right. \end{aligned}$$

with the initial conditions $A_{\lambda }(0)=\frac{1}{2}r(\eta , \beta )$, $B_{\lambda }(0)=0$, $F_{\lambda }(0)=0$, $G_{\lambda }(0)=0$, $H_{\lambda }(0)=0$, $K_{\lambda }(0)=0$. We first solve the Riccati system relative to the triple $(A_{\lambda },B_{\lambda },F_{\lambda })$, which is the same as in the no jump case, and therefore obtain: $A_{\lambda } = A$, $B_{\lambda } = B$, $F_{\lambda } = F$ as in (6.3). Then we solve the first-order linear system of ODE relative to the pair $(G_{\lambda },H_{\lambda })$, which involves the jump parameters $\lambda$, $\pi$ and $\delta$, and get:

$$\begin{aligned} G_{\lambda }(t)= & {} G(t) +\frac{\lambda }{2}\frac{r(\eta ,\beta )t(\pi t +2\delta (\nu t+2\gamma ))}{(r(\eta ,\beta )+\nu )t+2\gamma }, \\ H_{\lambda } (t)= & {} H(t) - \frac{\lambda }{2}\frac{(\pi - 2r(\eta ,\beta )\delta )t^2}{(r(\eta ,\beta )+\nu )t+2\gamma }, \end{aligned}$$

where G and H are given from the no jump case (6.4). Finally, after some tedious but straightforward calculations, we explicitly obtain $K_{\lambda }$ from the last equation:

$$\begin{aligned} K_{\lambda }(t)= & {} K(t)+ \lambda \gamma \frac{p^+(\pi ^+ - r(\eta ,\beta )\delta ^+)^2 +p^-(\pi ^- - r(\eta ,\beta )\delta ^-)^2}{\big (r(\eta ,\beta ) + \nu \big )^2} \ln \Big ( 1 + \frac{(r(\eta ,\beta ) + \nu )t}{2\gamma }\Big ) \\&- \, \frac{\lambda }{2} \frac{p^+((\pi ^+)^2 - r(\eta ,\beta ) \delta ^+(2\pi ^++\nu \delta ^+)) +p^-((\pi ^-)^2- r(\eta ,\beta ) \delta ^-(2\pi ^- +\nu \delta ^-))}{r(\eta ,\beta ) + \nu } t \\&+ \, \frac{\lambda r(\eta ,\beta )}{2}\frac{2\nu \mu \delta +\lambda ((p^+)^2\delta ^+(\pi ^++\nu \delta ^+)+(p^-)^2\delta ^-(\pi ^-+\nu \delta ^-))}{ r(\eta ,\beta ) + \nu }t^2 \\&+ \, \lambda ^2 \gamma r(\eta ,\beta ) \frac{r(\eta ,\beta )\delta ^2 +2\nu p^+p^-\delta ^+\delta ^- -((p^+)^2\delta ^+\pi ^++(p^-)^2\delta ^-\pi ^-)}{(r(\eta ,\beta )+ \nu )\big ((r(\eta ,\beta )+\nu )t + 2 \gamma \big )}t^2 \\&+ \, \frac{2\lambda \gamma r(\eta ,\beta )^2 \mu \delta }{(r(\eta ,\beta )+ \nu )\big ((r(\eta ,\beta )+\nu )t + 2 \gamma \big )}t^2 - \frac{\lambda ^2\pi ^2}{48\gamma }t^3 \\&+ \, \frac{\lambda ^2p^+p^-r(\eta ,\beta )}{2}\frac{2\nu \delta ^+\delta ^-+\delta ^-\pi ^++\delta ^+\pi ^-}{(r(\eta ,\beta )+\nu )t + 2\gamma }t^3\\&+ \, \frac{1}{8}\frac{4r(\eta ,\beta ) \mu \lambda \pi - \lambda ^2\pi ^2}{(r(\eta ,\beta )+\nu )t + 2\gamma }t^3, \end{aligned}$$

with K in (6.5). The function ${\tilde{w}}^{(\lambda )}$ in (6.7) may thus be rewritten as the sum of ${\tilde{w}}$ in (6.2) and another function of t, $d-x$ and y, and is by construction a smooth solution with quadratic growth condition to the HJB equation (6.6). Moreover, the argmin in HJB equation for ${\tilde{w}}^{(\lambda )}$ is attained for

$$\begin{aligned} {\tilde{q}}^{(\lambda )}(t,x,y,d)= & {} - \frac{1}{2\gamma }\left[ \displaystyle \frac{\partial {\tilde{w}}^{(\lambda )}}{\partial x} + \nu \displaystyle \frac{\partial {\tilde{w}}^{(\lambda )}}{\partial y} + y \right] \\= & {} \frac{r(\eta ,\beta )(\mu (T-t)+d-x)-y}{(r(\eta ,\beta )+\nu )(T-t)+2\gamma } \\&+ \, \lambda \frac{r(\eta ,\beta )\delta (T-t) + \frac{\pi }{4\gamma }(r(\eta ,\beta )+ \nu )(T-t)^2}{(r(\eta ,\beta )+\nu )(T-t) + 2\gamma } \\=: & {} {\hat{q}}^{(\lambda )}(T-t,d-x,y). \end{aligned}$$

Again, notice that ${\hat{q}}^{(\lambda )}$ is linear, and Lipschitz in x, y, d, uniformly in time t, and so given an initial state (x, y, d) at time t, there exists a unique solution $({\hat{X}}^{t,x,y,d},{\hat{Y}}^{t,x,y,d},D^{t,d})_{t\le s\le T}$ to (2.1)–(4.3)–(4.1) with the feedback control ${\hat{q}}_s^{(\lambda )} = {\hat{q}}^{(\lambda )}(T-s,D_s^{t,d}-{\hat{X}}_s^{t,x,y,d},{\hat{Y}}_s^{t,x,y,d})$, which satisfies: $\mathbb {E}[\sup _{t\le s\le T} |{\hat{X}}_s^{t,x,y,d}|^2 + |{\hat{Y}}_s^{t,x,y,d}|^2 + |D_s^{t,d}|^2] < \infty$, see e.g. Theorem 1.19 in [8]. This implies that $\mathbb {E}[\int _t^T |{\hat{q}}_s^{(\lambda )}|^2 ds] < \infty$, hence ${\hat{q}}^{(\lambda )} \in \mathcal {A}_t$. We now call on a classical verification theorem for stochastic control of jump-diffusion processes (see e.g. Theorem 3.1 in [8]), which shows that ${\tilde{w}}^{(\lambda )}$ is indeed equal to the value function ${\tilde{v}}^{(\lambda )}$, and ${\hat{q}}^{(\lambda )}$ is an optimal control. Finally, once the optimal trading rate ${\hat{q}}^{(\lambda )}$ is determined, the optimal production is obtained from the optimization over $\xi \in \mathbb {R}$ of the terminal cost $C(D_T^{t,d}-{\hat{X}}_T^{t,x,y,d},\xi )$, hence given by: ${\hat{\xi }}_T^{(\lambda )} = \frac{\eta }{\eta +\beta }(D_T^{t,d}-{\hat{X}}_T^{t,x,y,d})$. $\square$