Keywords

1 Introduction

The centrifugation process has a wide range of applications in scientific research, medical and industrial sectors. The first scientific studies conducted by Knight in 1806 [1], where primary forecasts were made of the effect of the angle of inclination of the glass on the separation process. Also, the foundations of theoretical and experimental studies of centrifuges are laid in the works of de Laval, Svedberg, Pickels, Brakke, Anderson, G.I. Bremer, V.I. Sokolov, P.G. Romankov, N.N. Lipatov, E.M. Goldin. Research Yu.N. Bochkov, S.A. Plyushkin, E.V. Semenov, A. V. Schlau significantly deepened the theory of centrifugation processes and contributed to the creation of new effective centrifuges [2, 3].

Today, centrifuges are commonly used in a wide variety of fields, from large-scale commercial applications to laboratory research. The number of designs and con-figurations of centrifuges used in the mineral, petrochemical, chemical, medical, pharmaceutical, industrial, dairy, food, polymer, energy and agricultural industries is numerous [4, 5]. Emerging new trends in centrifugal technology have led to the emergence of diverse designs of centrifuges, some of which are difficult to evaluate using a known calculation method [6, 7]. Numerous scientific works are devoted to this topic, patents, copyright certificates are obtained, methods for mechanically separating solid particles from liquids using centrifugation, and devices for their implementation are proposed [8,9,10,11]. At the present time there are two ways of separation the liquid heterogeneous systems: centrifugal filtration and centrifugal sedimentation. The centrifugal filtration method is widely applied in the sugar industry for separating raw sugar under the action of the centrifugal forces field. As a consequence of the filtration centrifugation the solid particles accumulate on the inner wall of the rotor. The centrifugal sedimentation that is as well widely applied in the modern industry is divided into two methods of separation heterogeneous systems: centrifugal clarification and precipitation centrifugation. As compared with the centrifugal clarification by using which occurs removing impurities that are in the liquid in small quantities, the precipitation centrifugation implies the separation of the suspensions that contain the most amount of the solid particles. It should be noted that the separation of the suspensions, at applying the centrifugal deposition method, is carried out in the following way: particles of the solid phase, which have a weight greater than the particles of the liquid phase, are deposited on the inner wall of the rotor under the action of the centrifugal force in the form of a ring layer, whereas particles of the liquid phase further in the form of the ring layer are located closer to the axis of rotation of the rotor [3, 5, 12,13,14,15,16,17,18]. Currently, great attention is paid to micro and nanoobjects, nanostructures and nanoparticles, and, consequently, there is a question of their experimental separation. In this regard, the problem of finding ways to differentiate nanoparticles by size is important. One of the possible and promising ways to solve this problem is application of the centrifugation method for description the process of the sedimentation of the nanoparticles in the centrifugal forces field [19,20,21,22].

In this paper, we study the spatial motion of a particle and the time of its deposition in a vertical centrifuge, where, for a complete assessment of the process of separation of solid particles from a liquid, it is taken into account that the angular velocity of rotation of the rotor, tubes and their angle of inclination are time-dependent variables, which also complicates the search for a general solution to the differential equations of motion of the particle and the mechanical system as a whole. Particular cases that take place in industrial production are given and analyzed. An analytical research technique used in the industry of the separation method for the technical rotary unit used for processing the suspension was developed and presented in [17].

2 Statement of the Problem

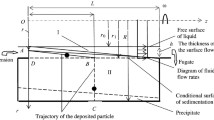
The rotor system consists of a flexible, symmetrical relative to the shaft supports and a disk mounted on the shaft, on which tubes with emulsion are mounted symmetrically. The tubes can rotate around their own horizontal axis with an angular velocity Ω (Fig. 1). The angular velocity of rotation of the shaft ω. The angle of rotation of the tubes from the vertical α, then \(\Omega = \dot{\alpha }\) – the angular speed of rotation of the containers, Ls – distance from the rotor axis to the axis of rotation of containers, Lm – distance to the particles of the suspension with a mass Δm, r – containers radius, g – acceleration of gravity, L – containers length.

Fig. 1.
figure 1

The rotor system: shaft and disc with containers (test tube)

Full size image

The rotor position is determined relative to a fixed coordinate system Ox1y1z1 (see Fig. 1). The position of the studied particles M(x,y,z) is determined by the relative moving coordinate system Oxyz. Oy axis is directed along the axis of symmetry of the container bottom, an Oz axis directed along the rotational axis of the container. In the calculation the following assumptions were used: the angular speed of the rotor is large enough so that we can ignore the force of gravity suspension (g  ≪ ω2r), spherical shape of particles assumed, particle mean free path is much larger its size, no turbulence suspension (laminar flow), the interaction forces between the particles and the walls of the container (test tube) absent, container (test tube) is rather narrow radius is much smaller than its length (r0 ≪  L), after deposition of the particles on the wall of the container stop moving, the friction force between the containers and their axes of rotation, as well as a change in gravity from the suspensions disregarded containers, the force of friction between the solid particles and the container wall disregarded.

3 The Equations of Motion

To compile the equation of motion of a particle, it is necessary to determine transfer \(\bar{F}_{e}\) and Coriolis inertia \(\bar{F}_{c}\) forces of the suspension particle. The transport acceleration of a particle M is determined by the formula.

$$ \bar{a}_{{e\,}} = \left( {\bar{\omega } + \bar{\Omega }} \right)\left( {\left( {\bar{\omega } + \bar{\Omega }} \right) \cdot \bar{r}} \right) - \bar{r}\left( {\bar{\omega } + \bar{\Omega }^{2} } \right) + \bar{\varepsilon } \times \bar{r}, $$
(1)

Projecting the vector of transfer acceleration defined by Eq. (1) onto the moving coordinate axes Ox, Oy, Oz, we obtain:

$$ \begin{array}{*{20}l} \begin{gathered} a_{ex\,} = \,\, - \left( {L_{s} \cos \alpha + x} \right)\left( {\omega^{2} + \Omega^{2} } \right)\, + \,\omega^{2} \sin \alpha \left( {x\sin \alpha - y\cos \alpha } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, + \dot{\Omega }\left( {L_{s} \sin \alpha + y} \right) - \dot{z}\omega \cos \alpha , \hfill \\ \end{gathered} \hfill \\ \begin{gathered} a_{ey\,} = \,\, - \left( {L_{s} \sin \alpha + y} \right)\left( {\omega^{2} + \Omega^{2} } \right)\, - \,\omega^{2} \cos \alpha \left( {x\sin \alpha - y\cos \alpha } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, - \dot{\Omega }\left( {L_{s} \cos \alpha + x} \right) - \dot{z}\omega sin\alpha , \hfill \\ \end{gathered} \hfill \\ {a_{ez\,} = \,\dot{\omega }\left( {L_{s} + y\sin \alpha + x\cos \alpha } \right)\left( {\omega^{2} + \Omega^{2} } \right)\, - \,2\omega \Omega \left( {x\sin \alpha - y\cos \alpha } \right) - z\omega^{2} .} \hfill \\ \end{array} $$
(2)

The transfer and Coriolis inertia forces are equal respectively.

$$ \bar{F}_{e} = - \Delta m\bar{a}_{e} ,\,\bar{F}_{c} = - \Delta m\bar{a}_{c} . $$

Coriolis acceleration of the particle M of the suspension, taking into account the fact that \(\Omega _{{ox}} = \omega \sin \alpha ,\;\Omega _{{oy}} = - \omega \cos \alpha ,\;\Omega _{{oz}} = - \Omega ,\) has the form

$$ a_{{cx}} = - 2\left( {\dot{z}\omega \cos \alpha - \dot{y}\Omega } \right),\,a_{{cy}} = - 2\left( {\dot{z}\omega \sin \alpha + \dot{x}\Omega } \right),\,a_{{cz}} = 2\omega \left( {\dot{y}\sin \alpha + \dot{x}\cos \alpha } \right). $$
(3)

After using Eq. (2) and Eq. (3) , taking into account the accepted assumptions, the equations of motion of the particle M of the suspension have the form:

$$ \begin{aligned} \ddot{x} + 6\pi \eta _{1} r_{0} \dot{x} &= - g\sin \alpha + \left( {L_{s} \cos \alpha + x} \right)\left( {\omega ^{2} + \Omega ^{2} } \right) - \omega ^{2} \sin \alpha \left( {x\sin \alpha - y\cos \alpha } \right) \\ & \quad+ z\dot{\omega }\cos \alpha - \dot{\Omega }\left( {L_{s} \sin \alpha + y} \right) + 2\left( {\dot{z}\omega \cos \alpha - \dot{y}\Omega } \right), \\ \ddot{y} + 6\pi \eta _{1} r_{0} \dot{y} & = g\cos \alpha + \left( {L_{s} \sin \alpha + y} \right)\left( {\omega ^{2} + \Omega ^{2} } \right) + \omega ^{2} \cos \alpha \left( {x\sin \alpha - y\cos \alpha } \right)\\ & \quad- \dot{\Omega }\left( {L_{s} \cos \alpha + x} \right) + 2\left( {\dot{z}\omega \sin \alpha - \dot{x}\Omega } \right) + z\dot{\omega }\cos \alpha , \\ \ddot{z} + 6\pi \eta _{1} r_{0} \dot{z} &= \omega ^{2} z + 2\Omega \omega \left( {x\sin \alpha - y\cos \alpha } \right) - \dot{\omega }\left( {L_{s} + y\sin \alpha + x\cos \alpha } \right) \\ & - 2\omega \left( {\dot{y}\sin \alpha + \dot{x}\cos \alpha } \right) \\ \end{aligned} $$
(4)

There r0 – particle radius M of suspension Δm =  4πr03ρp, η1 = η/Δm =  3η/4πr03ρp = 3ρf ν/4πr03ρp, ρf – particle density, ρp – fluid density; ν – kinematic viscosity of a liquid (suspension); η = ρf ν – dynamic viscosity of the liquid (suspension); 6πηr0 – the coefficient of friction of a particle M (the coefficient of resistance force of a liquid of a medium) during its motion. The system of Eq. (4) is nonlinear, since ω = ω(t), α = α(t), Ω = Ω(t), and the rotation angle α is an argument of trigonometric functions. In addition, the coefficients of the functions with coordinates and their derivatives are variables. In this regard, Eq. (4) has no exact solution. The rotor is rotated at a constant angular speed, ω = const, that is,. At first we define the dependence of the angle of the angular speed of the rotor. For this purpose, we draw up the balance of forces acting on the container (see Fig. 2). Projecting force in the direction of ττ we get

$$ g\sin \alpha = \omega ^{2} \left( {L_{{cm}} + l\sin \alpha } \right)\cos \alpha $$
(5)

Where l − distance from the axis of rotation to center of gravity of the container with a suspension of. From here it follows that

$$ \omega \, = \,\sqrt {\frac{{g \cdot tg\alpha }}{{L_{s} \, + \,l\sin \alpha}}}. $$
(6)

If \(\omega \to \infty ,\alpha \to \pi /2\;or\;\alpha \to \pi /2,\omega \to \infty\) which follows from the physical meaning of the problem.

Fig. 2.
figure 2

Determination of forces

Full size image

From Eq. (6) it is obvious that if the angular velocity ω of the rotor is constant, then the angle of rotation of the cups α is also constant. Each value of ω corresponds to a specific defined value of α (see Table 1).

Table 1. The relationship between the angular velocity and the angle of the tubes.
Full size table

Accordingly, the faster the angular velocity of rotation, the faster the process of sedimentation of particles. But since in the general case it is better to avoid acceleration of the rotor system to huge angular velocities, it is necessary to determine the optimal angle of inclination of the tubes and the corresponding rotation speeds that would satisfy the conditions of the problem of sedimentation of solid particles of the emulsion. Hence, each value of ω corresponds to the specific value of α. Then Eq. (4) as ω = const, α = const, Ω = 0, ε = 0 we will have.

$$ \begin{gathered} \ddot{x} + 2n\dot{x} - x\omega ^{2} \cos ^{2} \alpha = - g\sin \alpha + \left( {L_{s} + y\sin \alpha } \right)\omega ^{2} \cos \alpha + 2\omega \cos \alpha \dot{z}, \\ \ddot{y} + 2n\dot{y} - y\omega ^{2} \sin ^{2} \alpha = g\cos \alpha + \left( {L_{s} + x\cos \alpha } \right)\omega ^{2} \sin \alpha + 2\omega \sin \alpha \dot{z}, \\ \ddot{z} + 2n\dot{z} - \omega ^{2} z = - 2\omega \left( {\dot{y}\sin \alpha = \dot{x}\cos \alpha } \right) \\ \end{gathered} $$
(7)

where 2n = 6πη1r0 or n = 9νρf/4r02ρp – friction coefficient. Equation (7) can be solved analytically, making some assumptions, which was done in [17]. In this case, taking into account the spatial motion of the deposited substance in the cavity, one can calculate the particle trajectory by a numerical method, estimate the time and trajectory of the sedimentation of particles in suspension for different values of the slope of the tube, particle size and resistance coefficient.

4 Results

In the calculation, three basic parameters vary, namely the particle radius, the angle of the tubes and the coefficient of resistance of the medium, which are the most important and fundamental in industrial production. Figure 3 shows the results of calculations for different tilt of the glasses (test tubes). As shown above, when the angular velocity of rotation of the rotor tends to an infinitely large value, the angle of inclination of the tubes tends to an absolutely horizontal position, i.e. to a value of 90°. It is impossible to achieve an absolutely horizontal position in industry, which is confirmed by a mathematical model. Therefore, it is necessary to determine the angle of inclination, which would provide a sufficient degree of cleaning and at the same time would be optimal from a structural point of view. For industrial centrifuges with operating speeds from 1500 rpm, angles from 80° are suitable. When tilted at 88°, particles settle faster (see Table 2) than at smaller bevel angles (tubes). We do not consider cases with a greater slope in connection with structural changes, which, for given parameters, can lead to a decrease in productivity, which follows from Eq. (6) . To achieve a tilt angle of 88°, it is necessary that the rotor rotates at a speed of 1640 rpm. Thus, if the centrifuge’s working speed is 3000 rpm or more, as in many modern centrifuges of this class, the separation goal is achieved at much lower speeds. This will obviously reduce certain economic costs for centrifuges with a specified degree of purification. For an approximate estimate of the sedimentation time of particles T, one can use the expression obtained by the analytical method earlier in [17], i.e.

$$ T\, = \,{\text{ln}}\xi /b, $$

where

$$ \xi = - \frac{p}{2} + \sqrt {\frac{{p^{2} }}{4} - q} ,p = - \frac{{2(L + A_{0} )b}}{{b(y_{0} + A_{0} ) + \dot{y}_{0} }},q = \frac{{b(y_{0} + A_{0} ) - \dot{y}_{0} }}{{b(y_{0} + A_{0} ) + \dot{y}_{0} }}, $$
$$ b_{1} = b_{2} = \sqrt {n^{2} + \omega ^{2} \sin ^{2} \alpha } = b,b_{1} + b_{2} = 2b,\begin{array}{*{20}c} {} & {A_{0} = \frac{{g\cos \alpha }}{{\omega ^{2} \sin ^{2} \alpha }}} \\ \end{array} + \frac{{L_{s} }}{{\sin \alpha }}. $$

In cases where the inclination angles are less than 80°, the sedimentation process proceeds more slowly and sedimentation occurs along spatial curves with increasing amplitudes due to an increase in the centrifugal force (see Fig. 3 and Table 2).

Table 2. The dependence of the separation time on the angle of the tube
Full size table

The sedimentation rate of particles also depends on the nature of the multiphase fluid, and therefore it is advisable to consider the resistance of the medium as the next important parameter. For the calculation, drag coefficients for crude oil and some more viscous liquids were used. As expected, the higher the resistance index, the longer the separation time, respectively, the lower the resistance coefficient, the shorter the settling time of particles (see Fig. 4 and Table 3), which confirms the correctness of the proposed mathematical model.

Fig. 3.
figure 3

Particle movement at different slope of the tube

Full size image

The magnitude of the resulting resistance depends mainly on the mode of motion and the shape of the streamlined body. The mode of deposition of a solid phase particle can be taken as laminar until the condition Re < 1–1.6 is fulfilled. In practical cases of centrifugation, the Reynolds number is less than the transition value from laminar to turbulent. During laminar motion, the body is surrounded by a boundary layer of fluid and flows smoothly around it. If the particle being deposited, having reached a certain distance from the axis of rotation, continued to experience the action of a constant centrifugal inertia force during further deposition, then the particle deposition rate would soon become constant. In this case, the fluid resistance would increase to the value of centrifugal force. The increase in resistance is caused by the fact that the liquid molecules in the layer adjacent to the body become denser, and with a decrease in the distance between them, the energy of mutual repulsion increases. But in reality, the centrifugal inertia force of a particle is always greater than the resistance force of a liquid medium due to its increase (force) as the particle moves away from the axis of rotation.

Table 3. The dependence of the separation time on the resistance of the medium
Full size table
Fig. 4.
figure 4

Particle motion at different values of the drag coefficient of the medium

Full size image

The third parameter is the dispersed composition of the particles, which must be separated. This characteristic is crucial when choosing a centrifuge. For a separator of this configuration, its required productivity is all the less, the smaller the particles of the solid phase in the treated suspension, which leads to a higher separation factor, which formally represents the Froude number. Since it is initially assumed that the particles have the shape of a sphere, their radius changes accordingly to consider different sizes of particles. It should be noted that in this model in one cycle of the system, the particle sizes were taken equal, i.e., in each case, all solid fractions in the suspension have the same size. Also, colloidal disperse systems are not taken into account, since it was found that for a certain range the particle size does not play the most important role in the separation process (see Fig. 5). For example, particles of size r0 = 0.01 – 0.05 m settle along almost the same curved path, although here the particle size increases by 5 times (see Fig. 5). Initially, all particles up to the fourth second of the working regime of a fixed rotor have almost very close trajectories of subsidence. Up to the ninth second, particles of size r0 = 0.01 – 0.05 m move along very close curves. Particles of size r0 = 5·10–3 – 1·10–6 m up to the ninth second settle along more curved paths, which further diverge even more (see Table 4).

Table 4. Separation time versus particle radius
Full size table

For these particles, these sedimentation curves are natural, since they are small in size, which means the need for higher operating speeds for micro- and nanoparticles. Since the separability of the suspension largely depends on the degree of dispersion, it becomes necessary to use the sedimentometric method to assess the nature of the particle distribution. When applying this method, the deposition time is plotted on the abscissa axis, and the total amount of solid phase deposited on the bottom of the centrifuge cup or passed through the reference level in a certain time is plotted along the ordinate axis. This amount consists of particles that have completely precipitated and are still precipitated [3]. This method requires the availability of experimental data, which is not always possible. At a certain stage of research, using the above sedimentation data for a qualitative assessment, the need for an experiment can be avoided.

Fig. 5.
figure 5

Particle motion at different particle radius values

Full size image

5 Conclusions

A qualitative analysis of the results based on classical numerical methods for solving differential equations is carried out. The time of particle deposition was estimated for different values ​​of the angle of the tubes, the drag coefficients, and the size of these particles, taking into account spatial motion. The optimal parameters of the operating modes for the case of a fixed rotor, i.e. when each specific value of the angle of inclination corresponds to a specific angular speed of rotation of the disk on the flexible shaft. The results of the work performed confirm the physical meaning of the task, which can serve as a rationale for the use and implementation of this mathematical model in industrial production. The obtained dependences with sufficient accuracy for engineering practice allow us to determine such process characteristics as sedimentation time, deposition trajectory and the dependence of rotational speeds on inclination angles, as well as to predict the centrifuge operation efficiency. In addition, these results avoid the need to use the sedimentometric method and eliminate the need for additional costly experimental work.