Many studies, including [1,2,3,4,5,6,7,8,9], are dedicated to quantitative analysis of suspension separation processes in centrifuging devices, development of mathematical description of the process of centrifugal separation of the liquid phase of the emulsions in circulating flows, sedimentation of suspensions in centrifuges (for treating heterogeneous fluid systems with phases differing in density), etc. Emulsions (heterogeneous systems consisting of two mutually insoluble liquid phases with a tendency to separate into layers), particularly water-oil emulsion with globules (floccules) of dispersed oil 10−1–103 μm in size, are used in chemical, food, and other production technologies.

Various methods, including mechanical, are used to reduce emulsion stability (to facilitate separation of water from the emulsion), such as treatment of the emulsion in a gravitational force field (in a gravity sedimentation tank) or in a centrifugal force field (in a centrifuge). In this regard, centrifugal treatment method, which ensures maximum emulsion separation rate, is preferred most.

There is a multiplicity of computing devices based on the proposed models and used for practical purposes [1,2,3,4,5,6,7,8,9] for analysis of the state of scientific problems of physicomathematical modeling of the process of separation of heterogeneous fluid systems (suspensions and emulsions), which (including) is explained also by the complexity of the studied phenomenon. The physicomathematical modeling problem has been studied most deeply for the case where suspension density is low (volume content of the disperse phase is not more than 1%) and can only be studied approximately.

In many cases, the rationale for calculation of the operation parameters of centrifuges for separation of disperse systems is based on the scientific postulate that the kinetics of motion of the first phase (generally a liquid or a gas) is independent of the second phase (generally finely dispersed particles of low volume concentration suspended in a liquid or a gas), which can be the foundation for effective use of hydrodynamic problems relating to the kinetics of motion of the first phase that is independent of the motion of the second phase.

If, however, the calculated hydrodynamic parameters of the first phase (velocity and pressure fields) are used to calculate the kinetics of the second phase (suspension particles), such approach to solution of the problem makes it difficult to take account of the factor of influence of the kinetics of one phase on the kinetics of another phase (especially when volume concentrations of the phases of the fluid system are commensurable).

In calculations of process parameters of hydrocyclones and centrifuges [2, 6], one also notices the peculiarities (either disregard for interaction of particles or attempt to take account of collisions of particles without regard for their hydrodynamic interaction), which considerably limits the area of application of the proposed models.

In this paper, we formulate and quantitatively analyze the problem of simultaneous motion of the phases in the process of their separation in a batch-operated centrifuge using a model of interpermeating and interacting media [10].

Formulation of the Problem

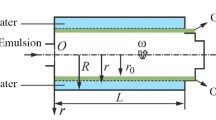
Let us assume that there is a heterogeneous fluid system consisting of two phases differing in density (water and oil particles in the form of floccules), i.e., a water-oil emulsion that needs to be separated in a centrifugal force field. The adopted assumptions are the following: the aqueous phase of the emulsion is a Newtonian liquid with dynamic viscosity μ1 and density \( {\uprho}_1^{\circ } \), an oil phase with density \( {\uprho}_2^{\circ } \) is monodisperse, and oil floccules with diameter δ are spherical particles isolated from each other. Let us also assume the following: the emulsion flow (confined by the wall of the rotor with diameter R and the free surface with radius r0 ) is layered and axisymmetric; the emulsion flow rotates with the rotor as a semisolid body with angular velocity ω (Fig. 1); the floccule moves in axial and circular directions as a suspended particle (does not lag behind the flow and does not outpaces it).

Fig. 1.
figure 1

Scheme for calculation of water-oil emulsion separation process in batch-operated centrifuge rotor.

Full size image

With due regard for the adopted assumptions, it is essential to establish the dependencies of stratification of volume concentration of the phases (in radial direction), velocity of floccule floating up in the flow, and emulsion separation process time on the physicomechanical and geometric parameters of the emulsion.

It is expedient to solve the formulated problem in a cylindrical system of coordinates rϑz rigidly connected with the rotating cylinder that simulates the rotor wall. Taking account of the assumptions that the ratio of floccule and water densities \( \upvarepsilon ={\uprho}_2^{\mathrm{v}}/{\uprho}_1^{\mathrm{v}}<1, \) the floccule size is not too large and the radial floccule velocity vr = v2 is negligible, the Reynolds number in relative motion should be considered small.

Then (according to the law of mass conservation for each emulsion phase), the system of flow continuity equations is valid:

$$ \frac{\partial {c}_1}{\partial t}+\frac{1}{r}\frac{\partial \left(r{c}_1{v}_1\right)}{\partial r}=0,\kern1em \frac{\partial {c}_2}{\partial t}+\frac{1}{r}\frac{\partial \left(r{c}_2{v}_2\right)}{\partial r}=0, $$
(1)
$$ {c}_1+{c}_2=1, $$
(2)

where c1, c2 − volume concentrations of the first (heavy) and second (light) phases; v1, v2 − velocities of the first (heavy) and second (light) phases; t − time.

In turn, if the inertial and Coriolis forces (minor in comparison with other forces acting on water and oil particles) are ignored, then under conditions of equilibrium of pressure and interphase forces (according to momentum conservation law), the system of differential equations of motion of a two-phase medium in the chosen system of coordinates will take the form

$$ -{c}_1\frac{\partial p}{\partial r}-{K}_{\upmu}^{\ast }{c}_1{c}_2\left({v}_1-{v}_2\right)-{\uprho}_1^{\mathrm{v}}{c}_1{\upomega}^2r=0, $$
(3)
$$ -{c}_2\frac{\partial p}{\partial r}-{K}_{\upmu}{c}_1{c}_2\left({v}_1-{v}_2\right)-{\uprho}_2^{\mathrm{v}}{c}_2{\upomega}^2r=0, $$
(4)

where p − pressure; ω − angular speed of the rotor; r − radial coordinate of the floccule (Fig. 1);

$$ {K}_{\upmu}^{\ast }=\frac{18{\upmu}_1}{\updelta^2}\uppsi \left({c}_2\right), $$
(5)
$$ \uppsi \left({c}_2\right)={\left(1-{c}_2\right)}^{-3} $$
(6)

is a correction for the exponential pattern of particle motion;

$$ {\displaystyle \begin{array}{c}{K}_{\upmu}=\frac{54{\upmu}_1}{\updelta^2}{C}_{\upmu}\frac{{\operatorname{Re}}_{12}}{10},\\ {}{C}_{\upmu}={C}_{\upmu}^{\mathrm{v}}{\uppsi}_{\mathrm{c}},\\ {}{C}_{\upmu}^{\mathrm{v}}\left({\operatorname{Re}}_{12}\right)=\frac{24}{{\operatorname{Re}}_{12}}+4{\left({\operatorname{Re}}_{12}\right)}^{-1/2}+0.4,\end{array}} $$

where \( {\operatorname{Re}}_{12}={\uprho}_1^{\mathrm{v}}{w}_{12}\updelta /{\upmu}_1 \) − Reynolds number referred to the sliding rate of the phases w12 = v1 − v2; δ − floccule diameter; ψc − a coefficient that takes account of the influence of individuality of dispersed particles [10].

Solution of the Problem

Summing up equation (1) and allowing for (2) we get

$$ \frac{\partial \left(r{c}_1{v}_1+r{c}_2{v}_2\right)}{\partial r}=0, $$

whence, by integration we get

$$ {c}_1{v}_1+{c}_2{v}_2=\frac{W(t)}{r}, $$
(7)

where W(t) − arbitrary time function.

In turn, summing up equations (3) and (4) we get

$$ \frac{\partial p}{\partial r}=-{\uprho \upomega}^2r, $$
(8)

where \( \uprho ={c}_1{\uprho}_1^{\mathrm{v}}+{c}_2{\uprho}_2^{\mathrm{v}} \) − emulsion density averaged over the emulsion volume.

Putting equations (5) and (8) in equation (3) we get the following expression for the rate of sliding of one phase relative to the other phase:

$$ {w}_{12}={v}_2-{v}_1=\frac{w_0}{\uppsi \left({c}_2\right)}, $$
(9)

where

$$ {w}_0={w}_{00}r, $$
(10)
$$ {w}_{00}=\frac{\left({\uprho}_1^{\mathrm{v}}-{\uprho}_2^{\mathrm{v}}\right){\upomega}^2{\updelta}^2}{18{\upmu}_1}>0, $$
(11)

ψ(c2 ) is determined by equation (6).

Equations (7) and (9) can be used to determine the velocity of floccule floating:

$$ {v}_2=\frac{W(t)}{r}+\frac{w_0{c}_1}{\uppsi \left({c}_2\right)}, $$
(12)

where w0 is obtained by equation (10).

Since unsteady motion of globules with concentrations c2 is studied, the task boils down to solution relating to c2 of the second (quasilinear) differential equation of system (1) of the first order

$$ \frac{\partial {c}_2}{\partial t}+\frac{1}{r}\frac{\partial {W}_2}{\partial r}=0, $$
(13)

where

$$ {W}_2\left(t,r\right)={c}_2W(t)+\frac{w_0{c}_1{c}_2r}{\uppsi \left({c}_2\right)}. $$
(14)

Let us transform equation (13) to the form

$$ \frac{\partial {c}_2}{\partial t}+\frac{1}{r}\frac{\partial {W}_2}{\partial {c}_2}\frac{\partial {c}_2}{\partial r}=0 $$
(15)

then, in conformity with equation (14), equation (13) will take the form

$$ \frac{\partial {c}_2}{\partial }+\frac{1}{r}\left[W(t)+\frac{w_0 rdJ\left({c}_2\right)}{d{c}_2}\right]\frac{\partial {c}_2}{\partial r}=0, $$
(16)

where, with due regard for (6),

$$ J\left({c}_2\right)=\frac{c_1{c}_2}{\uppsi \left({c}_2\right)}. $$
(17)

If, however, the studied emulsion separation condition is provisionally considered as quasisteady and all process parameters are time independent, the referred emulsion separation conditions are determined by coordinate-and time-specified volume flow rates of the phases and the mixture (reduced velocities) [10]:

$$ {\displaystyle \begin{array}{c}{c}_1{v}_1=\frac{W_{10}}{r},\kern1em {c}_2{v}_2=\frac{W_{20}}{r},\\ {}{W}_0={W}_{10}+{W}_{20},\kern1em {W}_{10},{W}_{20}=\mathrm{const}.\end{array}} $$
(18)

Then, taking account of the adopted assumption about the nature of the separation condition and proceeding from equation (16) we get the ordinary differential equation with respect to the sought current concentration c2 of the second phase:

$$ W(t)+\frac{w_0 rdJ\left({c}_2\right)}{d{c}_2}=0 $$

the general integral of which is the expression

$$ {c}_2W(t)+{w}_0 rJ\left({c}_2\right)=D, $$
(19)

where D − arbitrary constant.

Taking c2 = 1 in equation (19) and, consequently, according to equation (2), c1 = 0 and according to equation (18), W0 = W20 and considering equation (17), we get D = W20 . Since the target particle (floccule) moves toward the rotor rotation axis (opposite to the direction of the coordinate axis r ), with due regard for (10) and (19) is taken that

$$ {W}_{20}-{c}_2{W}_0=-{w}_0 rJ\left({c}_2\right). $$
(20)

Let us introduce the characteristic parameters L (length) and T (time) in accordance with the formulas

$$ L=R,\kern1em T=\frac{1}{w_{00}}, $$

where w00 is determined by equation (11), then equation (20) is transformed to the dimensionless form

$$ {U}_{20}-{c}_2{U}_0=-{\upxi}^2J\left({c}_2\right), $$
(21)

where U20 = W20 /(w0R); U0 = W0 /(w0R); ξ = r/R and, in accordance with equations (6) and (17) it is taken in explicit form that

$$ J\left({c}_2\right)={c}_2{\left(1-{c}_2\right)}^4, $$
(22)

Thus, preliminarily, the formulated problem is reduced to determination of the root c2(U20,U0 ) of the algebraic equation (21) as a function of two process control parameters specified by equations (18), which are dimensionless volume flow rates of the phases U20 and U0 = U10 +U20.

The roots of equation (21) are determined by the standard computational procedure (smallest value of root is chosen).

Then, based on the found c2 value and the set U20 value the floccule floating velocity is expressed by the equation

$$ {v}_2={u}_2{w}_0, $$
(23)

where u2 = U20 /c2(U20,U0 ) − dimensionless floccule velocity; w0 is determined by equation (10).

Then, the rate of sedimentation v1 of the first (heavy) phase is determined in accordance with equations (9) and (2).

We can get an estimate of the time τ (duration of the emulsion separation process) provisionally assuming that after completion of this process the floccule will move from the rotor shell (r = R) to the free surface (r = r0 ) of the emulsion flow (Fig. 1).

Taking account of the function v2 = dr/dt , we can calculate the time τ by the equation

$$ \tau \left({U}_{20}\right)=\frac{1-{\upxi}_0}{\int_{\upxi_0}^1{u}_2\left({U}_{20},\upxi \right)d\upxi {w}_0\cdot 60}, $$
(24)

where ξ0 = r0 /R; u2 is linked with v2 by equation (23); w0 is given by equation (10).

Equations (23) and (24) are the foundation of quantitative analysis of water-oil emulsion separation process in a batch-operated centrifuge.

Numerical Experiment

The subject of the study was an analog of 1251L-09 sugar plant centrifuge (rotor diameter 1250 mm, nominal angular speed ω = 150 rad/sec (Fig. 1). To calculate the dependencies of the volume concentration of the phases, floccule floating velocity, and emulsion separation time on the physicomechanical and geometric parameters of the emulsion, the following parameters were chosen: water density ρ1 = 1000 kg/m3, oil density ρ2 = 850 kg/m3, dynamic viscosity coefficient of water μ1 = 0.001 Pa·sec, and oil floccule diameter δ = 10−5m.

In calculations of volume concentration of the light phase of the emulsion c2, volume concentration of heavy phase of the emulsion c1 = 1− c2 , velocity v2 of the floating floccule, and emulsion separation time τ, the process control parameter U20 (reduced floccule floating velocity) was varied (in per cents) in the region of values [0; 50%] and the second process control parameter U0 (full reduced velocity) was taken as 50, 60, 70, and 80% (Figs. 2–5).

Fig. 2.
figure 2

Dependence of light phase volume concentration c2 in emulsion on dimensionless partial (with respect to light phase) U20 and full U0 process control parameters (R = 0.625 m, ω = 150 rad/sec, δ = 10−5m, and ξ = 50%): U0 = 50% (1), 60% (2), 70% (3), and 80% (4).

Full size image
Fig. 3.
figure 3

Dependence of light phase volume concentration c2 on specific (with respect to rotor radius) radial distance ξ at different values of dimensionless partial U20 and total U0 process control parameters: 1 − U20 = 10%, U0 = 50%; 2 − U20 = 10%, U0 = 70%; 3 − U20 = 20%, U0 = 50%; 4 − U20 = 20%, U0 = 70%.

Full size image
Fig. 4.
figure 4

Dependence of velocity v2 of floccule floating in emulsion on dimensionless partial U20 and full U0 process control parameters at ξ = 50%: U0 = 50% (1), 60% (2), 70% (3), and 80% (4).

Full size image
Fig. 5.
figure 5

Dependence of time τ of emulsion separation on dimensionless partial U20 and full U0 process control parameters: U0 = 50% (1), 60% (2), 70% (3), and 80% (4).

Full size image

In analysis of the results of the performed calculations (for definiteness), the velocities v1 and v2 of the emulsion phases are taken as fixed in expressions of the cited dimensionless velocities U20 and U0 . Then, analysis of the dependencies of concentration c2, velocity v2 of floccule floating, and emulsion separation time τ on the parameter U20 (Figs. 2–5) boils down to the study of these dependencies.

It is evident from the graphs in Figs. 2 and 3 that (in congruence with the physical interpretation of the studied phenomenon) calculated values of concentration c2 increase with increase of the control parameter U20 and decrease with increase of specific radial distance ξ. In turn, since oil floccule floating velocity v2 is determined by equations (23) and (24) and emulsion separation time is unambiguously determined from expression (21) by the concentration c2 of the oil in the emulsion, the graphs in Figs. 4 and 5 qualitatively and quantitatively express the characteristics of the graph in Fig. 2.

In particular, for example, at fixed control parameter U20 (in congruence, concentration c20), in Fig 2, curve 1 (corresponding to control parameter U0 = 50%) lies above curve 4 (corresponding to control parameter U0 = 80%), the reason for which is that the water phase concentration in the emulsion is higher at U0 = 80% than at U0 = 50%.

In turn, from the v2 (floccule floating velocity) values calculated at ξ = 50% (Fig. 4) it follows that the light phase of the emulsion (oil) floats up more slowly at U0 = 50% (Fig. 4, curve 1 − average water concentration in the emulsion) than at U0 = 90% (Fig. 4, curve 4 − high water concentration in the emulsion), i.e., as expected, floccule floating accelerates in the centrifuge when dilution of the emulsion with water is high).

For the same reason, in keeping with equation (23), water-diluted emulsion is clarified from oil faster than emulsion with a higher content of the oil phase (Fig. 5, curve 4 lies below curve 1).

The noted peculiarities of the water-oil emulsion clarification process in a centrifugal force field conform to the physical foundations of the studied phenomenon.

Thus, the mechanisms of mutual influence of each phase of the emulsion treated in a centrifugal force field are disclosed qualitatively and quantitatively and relationships for calculation of emulsion separation parameters are obtained within the confines of the scientific postulates of the theory of interpermeating and interacting media adopted for the fluid system (water-oil emulsion) separation process. An algorithm is derived from the obtained relationships for calculating the emulsion separation process (aggregation of particles suspended in water) in a batch-operated centrifuge, taking account of the emulsion density.