Efficient Improved Estimation Method for Non-Gaussian Regression from Discrete Data

Abstract

We study a robust adaptive nonparametric estimation problem for periodic functions observed in discrete fixed time moments with non-Gaussian Ornstein–Uhlenbeck noises. For this problem we develop a model selection method, based on the shrinkage (improved) weighted least squares estimates. We found constructive sufficient conditions for the observations frequency under which sharp oracle inequalities for the robust risks are obtained. Moreover, on the basis of the obtained oracle inequalities we establish for the proposed model selection procedures the robust efficiency property in adaptive setting. Then, we apply the constructed model selection procedures to estimation problems in Big Data models in continuous time. Finally, we provide Monte - Carlo simulations confirming the obtained theoretical results.

1 Introduction

In this paper we consider the following nonparametric regression model in continuous time

$$\begin{aligned} \mathrm {d}y_t=S(t)\mathrm {d}t+\mathrm {d}\xi _t, \quad 0\le t\le T, \end{aligned}$$

(1)

where S is an unknown 1-periodic $\mathbb {R}\rightarrow \mathbb {R}$ function from , the duration of observations T is integer and is defined by a Ornstein – Uhlenbeck – Lévy defined as

(2)

Here is a standard Brownian motion, is a pure jump Lévy process defined through the stochastic integral with respect to the compensated jump measure $\mu (\mathrm {d}s,\,\mathrm {d}x)$ with deterministic compensator $\widetilde{\mu }(\mathrm {d}s\,\mathrm {d}x)=\mathrm {d}s\Pi (\mathrm {d}x)$, i.e.

$\Pi (\cdot )$ is the Lévy measure on , (see, for example in [2]), such that

We assume that the unknown parameters $a\le 0$, and are such that

(3)

Moreover, we assume that the bounds , $\underline{\varrho }$ and $\varsigma ^{*}$ are functions of T, i.e. , and , for which for any $\epsilon >0$

(4)

We denote by the family of all distributions of process (1)–(2) on the Skorokhod space $\mathbf{D}[0,n]$ satisfying the conditions (3)–(4). It should be noted that the process (2) is conditionally-Gaussian square integrated semimartingale with respect to which is generated by the jump process $(z_t)_{t\ge 0}$.

The problem is to estimate the unknown function S in the model (1) on the basis of observations

(5)

where $n=Tp$ and the observations frequency p is some fixed integer number. For this problem we use the quadratic risk, which for any estimate $\widehat{S}$, is defined as

(6)

where stands for the expectation with respect to the distribution of the process (1) with a fixed distribution Q of the noise and a given function S. Moreover, in the case when the distribution Q is unknown we use also the robust risk

(7)

Note that if is a Brownian motion, then we obtain the well known white noise model (see, for example, [7] and [13]). Later, to take into account the dependence structure in the papers [6] and [10] it was proposed to use the Ornstein – Uhlenbeck noise processes, so called color Gaussian noises. Then, to study the estimation problem for non-Gaussian observations (1) in the papers [9, 11] and [12] it was introduced impulse noises defined through the compound Poisson processes with unknown impulse distributions. However, compound Poisson processes can describe the impulse influence of only one fixed frequency and, therefore, such models are too restricted for practical applications. In this paper we consider more general pulse noises described by the Ornstein – Uhlenbeck – Lévy processes.

Our main goal in this paper is to develop improved estimation methods for the incomplete observations, i.e. when the process (1) is available for observations only in the fixed time moments (5). To this end we propose adaptive model selection method based on the improved weighted least squares estimates. For nonparametric estimation problem such approach was proposed in [15] for Lévy regression model.

2 Improved Estimation Method

First, we chose the trigonometric basis in , i.e. and for $j\ge 2$

(8)

where [a] denotes the integer part of a. Note that if p is odd, then for any $1\le i,j\le p$

(9)

We use this basis to represent the function S on the lattice $\mathcal{T}_p=\{t_1,...,t_p\}$ in the Fourier expansion form

The coefficients can be estimated from the discrete data (5) as

We note that the system of the functions is orthonormal in $\mathbf{L}_2[0,1]$. Now we set weighted least squares estimates for S(t) as

(10)

with weights $\gamma =(\gamma (j))_{1\le j\le p}$ from a finite set $\varGamma \subset [0,\,1]^p$. Now for the weight coefficients we introduce the following size characteristics

where $\#(\varGamma )$ is the number of the vectors $\gamma$ in $\varGamma$.

Definition 1

Function $\mathbf{g}(T)$ is called slowly increasing as $T\rightarrow \infty$, if for any $\epsilon >0$

For any vector $\gamma \in \varGamma$ there exists some fixed integer $7\le d=d(\gamma )\le p$ such that their first d components are equal to one, i.e. $\gamma (j)=1$ for $1\le j\le d$ . Moreover, we assume that the parameters $\nu$ and are functions of T, i.e. $\nu =\nu (T)$ and , and the functions $\nu (T)$ and are slowly increasing as $T\rightarrow \infty$.

Using this condition, we define the shrinkage weighted least squares estimates for S

(11)

where

and the radius $\mathbf{r}>0$ may be dependent of T, i.e. as a slowly increasing function for $T\rightarrow \infty$. To compare the estimates (10) and (11) we set

Now we can compare the estimators (10) and (11) in mean square accuracy sense.

Theorem 1

Assume that the condition holds with . Then for any $p\ge d$ and $T\ge 3$

(12)

Remark 1

The inequality (12) means that non-asymptotically, uniformly in $p\ge d$ the estimate (11) outperforms in square accuracy the estimate (10). Such estimators are called improved. Note that firstly for parametric regression models in continuous time similar estimators were proposed in [14] and [12]. Later, for Lévy models in nonparametric setting these methods were developed in [15].

3 Adaptive Model Selection Procedure

To obtain a good estimate from the class (11), we have to choose a weight vector $\gamma \in \varGamma$. The best way is to minimize the empirical squared error

with respect to $\gamma$. Since this quantity depends on the unknown function S and, hence, depends on the unknown Fourier coefficients , the weight coefficients cannot be found by minimizing one. Then, one needs to replace the corresponding terms by their estimators. For this change in the empirical squared error, one has to pay some penalty. Thus, one comes to the cost function of the form

(13)

Here $\rho$ is some positive penalty coefficient, is the penalty term is defined as

where is the estimate for the variance which is chosen for $\sqrt{T}\le p\le T$ in the following form

(14)

The substituting the weight coefficients, minimizing the cost function (13), in (11) leads to the improved model selection procedure, i.e.

(15)

It will be noted that $\gamma ^*$ exists because $\varGamma$ is a finite set. If the minimizing sequence $\gamma ^*$ is not unique, one can take any minimizer. Unlike Pinsker’s approach [16], here we do not use the regularity property of the unknown function to find the weights sequence $\gamma ^*$, i.e. the procedure (15) is adaptive.

Now we study non-asymptotic property of the estimate (15). To this end we assume that

The observation frequency p is a function of T, i.e. $p = p(T)$ such that $\sqrt{T} \le p \le T$ and for any $\epsilon > 0$

First, we study the estimate (14).

Proposition 1

Assume that the conditions and hold and the unknown function S has the square integrated derivative $\dot{S}$. Then for $T\ge 3$ and $\sqrt{T}<p\le T$

(16)

where the term is slowly increasing as $T\rightarrow \infty$.

Using this Proposition, we come to the following sharp oracle inequality for the robust risk of proposed improved model selection procedure.

Theorem 2

Assume that the conditions – hold and the function S has the square integrable derivative $\dot{S}$. Then for any $T\ge 3$ and $0<\rho <1/2$ the robust risk (7) of estimate (15) satisfies the following sharp oracle inequality

where the rest term is slowly increasing as $T\rightarrow \infty$.

We use the condition to construct the special set $\varGamma$ of weight vectors as it is proposed in [4] and [5] for which we will study the asymptotic properties of the model selection procedure (15). For this we consider the following grid

where $r_i=i\delta$, $i=\overline{1,\,m}$ with $m=[1/\delta ^2]$. We assume that the parameters $\mathbf{k}\ge 1$ and $0<\delta \le 1$ are functions of T, i.e. and $\delta =\delta (T)$, such that

for any $\epsilon >0$. One can take, for example,

where is a fixed constant.

For we define the weights as

where ,

Finally, we set

(17)

Remark 2

It should be noted, that in this case the condition holds true with (see, for example, [15]). Therefore, the model selection procedure (15) with the coefficients (17) satisfies the oracle inequality obtained in Theorem 2.

4 Asymptotic Efficiency

To study the efficiency properties we use the approach proposed by Pinsker in [16], i.e. we assume that the unknown function S belongs to the functional Sobolev ball defined as

(18)

where $\mathbf{r}>0$ and $k\ge 1$ are some unknown parameters, is the space of k times differentiable 1-periodic $\mathbb {R}\rightarrow \mathbb {R}$ functions such that for any $0\le i \le k-1$ the periodic boundary conditions are satisfied, i.e. $f^{(i)}(0)=f^{(i)}(1)$. It should be noted that the ball can be represented as an ellipse in $\mathbb {R}^{\infty }$ through the Fourier representation in for S, i.e.

In this case we can represent the ball (18)

(19)

where .

To compare the model selection procedure (15) with all possible estimation methods we denote by the set of all estimators based on the observations . According to the Pinsker method, firstly one needs to find a lower bound for risks. To this end, we set

(20)

Using this coefficient we obtain the following lower bound.

Theorem 3

The robust risks (7) are bounded from below as

(21)

where .

Remark 3

The lower bound (21) is obtained on the basis of the Van - Trees inequality obtained in [15] for non-Gaussian Lévy processes.

To obtain the upper bound we need the following condition.

The parameter $\rho$ in the cost function (13) is a function of T , i.e. $\rho = \rho (T)$ , such that and

for any $\epsilon > 0$

Theorem 4

Assume that the conditions – hold. Then the model selection procedure (15) constructed through the weights (17) has the following upper bound

It is clear that these theorems imply the following efficient property.

Theorem 5

Assume that the conditions of Theorems 3 and 4 hold. Then the procedure (15) is asymptotically efficient, i.e.

and

(22)

Remark 4

Note that the parameter (20) defining the lower bound (21) is the well-known Pinsker constant, obtained in [16] for the model (1) with the Gaussian white noise process . For general semimartingale models the lower bound is the same as for the white noise model, but generally the normalization coefficient is not the same. In this case the convergence rate is given by while in the white noise model the convergence rate is $\left( T\right) ^{-2k/(2k+1)}$. So, if the upper variance threshold tends to zero, the convergence rate is better than the classical one, if it tends to infinity, it is worse and, if it is a constant, the rate is the same.

Remark 5

It should be noted that the efficiency property (22) is shown for the procedure (15) without using the Sobolev regularity parameters $\mathbf{r}$ and k, i.e. this procedure is efficient in adaptive setting.

5 Statistical Analysis for the Big Data Model

Now we apply our results for the high dimensional model (1), i.e. we consider this model with the parametric function

(23)

where the parameter dimension q more than number of observations given in (5), i.e. $q>n$, the functions are known and orthonormal in . In this case we use the estimator (11) to estimate the vector of parameters as

Moreover, we use the model selection procedure (15) as

(24)

It is clear that

and

Therefore, Theorem 2 implies

Theorem 6

Assume that conditions - hold and the function (23) has the square integrable derivative $\dot{S}$. Then for any $T\ge 3$ and $0<\rho <1/2$

where the term is slowly increasing as $T\rightarrow \infty$.

Theorems 3 and 4 imply the efficiency property for the estimate (24) based on the model selection procedure (15) constructed on the weight coefficients (17) and the penalty threshold satisfying the condition ).

Theorem 7

Assume that the conditions ) – ) hold. Then the estimate (24) is asymptotically efficient, i.e.

(25)

and

where is the set of all possible estimators for the vector $\beta$.

Remark 6

In the estimator (15) doesn’t use the dimension q in (23). Moreover, it can be equal to $+\infty$. In this case it is impossible to use neither LASSO method nor Dantzig selector which are usually applied to similar models (see, for example, [17] and [1]). It should be emphasized also that the efficiency property (25) is shown without using any sparse conditions for the parameters usually assumed for such problems (see, for example, [3]).

6 Monte-Carlo Simulations

In this section we give the results of numerical simulations to assess the performance and improvement of the proposed model selection procedure (15). We simulate the model (1) with 1-periodic functions S of the forms

$$\begin{aligned} S_1(t)=t\,\sin (2\pi t)+t^2(1-t)\cos (4\pi t) \end{aligned}$$

(26)

and

(27)

on $[0,\,1]$ and the Ornstein – Uhlenbeck – Lévy noise process is defined as

where is a homogeneous Poisson process of intensity $\lambda =1$ and is i.i.d. $\mathcal{N}(0,\,1)$ sequence (see, for example, [11]). We use the model selection procedure (15) constructed through the weights (17) in which $\mathbf{k}=100+\sqrt{\ln (T+1)}$,

and $\varsigma ^*=0.5$ We define the empirical risk as

where and is the deviation for the l-th replication. In this example we take $p=T/2$ and $N = 1000$.

Table 1. The sample quadratic risks for different optimal weights

Table 2. The sample quadratic risks for the same optimal weights

Tables 1 and 2 give the sample risks for the improved estimate (15) and the model selection procedure based on the weighted least squares estimates (10) from [11] for different observation period T. One can observe that the improvement increases as T increases for the both models (26) and (27).

Fig. 1.

Behavior of the regression functions and their estimates for $T=200$ (a) – for the function $S_1$ and b) – for the function $S_2$).

Fig. 2.

Behavior of the regressions function and their estimates for $T=500$ (a) – for the function $S_1$ and b) – for the function $S_2$).

Fig. 3.

Behavior of the regression functions and their estimates for $T=1000$ (a) – for the function $S_1$ and b) – for the function $S_2$).

Fig. 4.

Behavior of the regression functions and their estimates for $T=10000$ (a) – for the function $S_1$ and b) – for the function $S_2$).

Remark 7

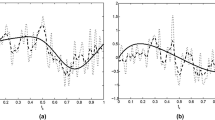
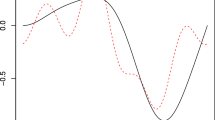
The figures show the behavior of the procedures (10) and (11) in the depending on the observation time T. The continuous lines are the functions (26) and (27), the dotted lines are the model selection procedures based on the least squares estimates $\widehat{S}$ and the dashed lines are the improved model selection procedures $S^*$. From the Table 2 for the same $\gamma$ with various observations numbers T we can conclude that theoretical result on the improvement effect (12) is confirmed by the numerical simulations. Moreover, for the proposed shrinkage procedure, from the Table 1 and Figs. 1, 2, 3 and 4, one can be noted that the gain is significant for finite periods T.

7 Conclusion

In the conclusion we would like emphasized that in this paper we studied the following issues:

• we considered the nonparametric estimation problem for continuous time regression model (1) with the noise defined by non-Gaussian Ornstein–Uhlenbeck process with unknown distribution under the condition that this process can be observed only in the fixed discrete time moments (5);

• we proposed adaptive robust improved estimation method via model selection approach and we developed new analytical tools to provide the improvement effect for the non-asymptotic estimation accuracy. It turns out that in this case the accuracy improvement is much more significant than for parametric models, since according to the well-known James–Stein result [8] the accuracy improvement increases when dimension of the parameters increases. It should be noted, that for the parametric models this dimension is always fixed, while for the nonparametric models it tends to infinity, that is, it becomes arbitrarily large with an increase in the number of observations. Therefore, the gain from the application of improved methods is essentially increasing with respect to the parametric case;

• we found constructive conditions for the observation frequency under which we shown sharp non-asymptotic oracle inequalities for the robust risks (7). Then, through the obtained oracle inequalities we provide the efficiency property for the developed model selection methods in adaptive setting, i.e. when the regularity of regression function is unknown;

• we apply the developed model selection procedure to the estimation problem for the Big Data model in continuous time without using the parameter dimension and without assuming any sparse condition for the model parameters ;

• finally, we give Monte - Carlo simulations which confirm the obtained theoretical results.