Keywords

1 Introduction

Given an undirected connected graph \(G=(V,E)\), edge costs \(c: E \rightarrow \mathbb {Q}_{> 0}\) and a set \(T \subseteq V\) of terminals, the Steiner tree problem in graphs (SPG) is to find a tree \(S\subseteq G\) with \(T \subseteq V(S)\) that minimizes c(E(S)). The SPG is a classic \(\mathcal {NP}\)-hard problem [15], and one of the most studied problems in combinatorial optimization. Part of its theoretical appeal might be attributed to the fact that the SPG generalizes two other classic combinatorial optimization problems: Shortest paths, and minimum spanning trees. On the practical side, many applications can be modeled as SPG or closely related problems, see e.g. [4, 19].

The SPG has seen numerous theoretical advances in the last 10 years, bringing forth significant improvements in complexity and approximability. See e.g. [3, 10] for approximation, and [16, 34] for complexity results. However, when it comes to (practical) exact algorithms, the picture is bleak. After flourishing in the 1990s and early 2000s, algorithmic advances came to a staggering halt with the joint PhD theses of Polzin and Vahdati Daneshmand almost 20 years ago [21, 33]. The authors introduced a wealth of new results and algorithms for SPG, and combined them in an exact solver that drastically outperformed all previous results from the literature. Their work is also published in a series of articles [22,23,24,25,26]. However, their solver is not publicly available.

The 11th DIMACS Challenge in 2014, dedicated to Steiner tree problems, brought renewed interest to the field of exact algorithms. In the wake of the challenge, several new exact SPG solvers were introduced in the literature, e.g. [8, 9, 20]. Overall, the 11th DIMACS Challenge brought notable progress on the solution of notoriously hard SPG instances that had been designed to defy known solution techniques, see [18, 30]. However, on the vast majority of instances from the literature, [21, 33] stayed out of reach: For many benchmark instances, their solver is even two orders of magnitude or more faster, and it can furthermore solve substantially more instances to optimality—including those introduced at the DIMACS Challenge [27]. In 2018, the 3rd PACE Challenge [2] took place, dedicated to fixed-parameter tractable algorithms for SPG. Thus, the PACE Challenge considered mostly instances with a small number of terminals, or with small tree-width. Still, even for these special problem types, the solver by [21, 33] remained largely unchallenged, see e.g. [13].

The following article aims to once again advance the state of the art in exact SPG solution.

1.1 Contribution

This article is based on a combination of three concepts: Implications, conflicts, and reductions. As a result, various new SPG techniques are conceived. The main contributions are as follows.

  • By using a new implication concept, a distance function is conceived that provably dominates the well-known bottleneck Steiner distance. As a result, several reduction techniques that are stronger than results from the literature can be designed.

  • We show how to derive conflict information between edges from the above methods. Further, we introduce a new reduction operation whose main purpose is to introduce additional conflicts. Such conflicts can for example be used to generate cuts for the IP formulation.

  • We introduce a more general version of the powerful so-called extended reduction techniques. We furthermore enhance this framework by using both the previously introduced new distance concept, and the conflict information.

  • Finally, we integrate the components into a branch-and-cut algorithm. Besides preprocessing, domain propagation, and cuts, also primal heuristics can be improved (by using the new implication concept). The practical implementation is realized as an extension of the branch-and-cut based Steiner tree solver SCIP-Jack  [9].

The resulting exact SPG solver outperforms the current state-of-the-art solver from [21, 33] on a wide range of well-established benchmark sets from the literature. Furthermore, it can solve several instances for the first time to optimality. Proofs of the new results are given in the extended version of this article [28].

1.2 Preliminaries and Notation

We write \(G := (V,E)\) for an undirected graph, with vertices V and edges E. We set \(n := |V|\) and \(m := |E|\). For \(S \subseteq G\) write V(S) and E(S) for its vertices and edges. For a walk W we write V(W) and E(W) for the set of included vertices and edges. For \(U \subseteq V\) we define \(\delta (U):=\{ \{u,v\} \in E \mid u\in U, v\in V\setminus U\}\). We define the neighborhood of \(v \in V\) as \(N(v) := \{ w \in W \mid \{v,w\} \in \delta (v) \}\). Note that \(v \notin N(v)\).

Given edge costs \(c: E \mapsto \mathbb {Q}_{\ge 0}\), the triplet (V, E, c) is referred to as network. By d(v, w) we denote the cost of a shortest path (with respect to c) between vertices \(v, w \in V\). For any (distance) function \(\tilde{d}: \genfrac(){0.0pt}1{V}{2} \mapsto \mathbb {Q}_{\ge 0}\), and any \(U \subseteq V\) we define the \(\tilde{d}\)-distance graph on U as the network

$$\begin{aligned} D_G(U, \tilde{d}) := ( U, \left( {\begin{array}{c}U\\ 2\end{array}}\right) , \tilde{c}), \end{aligned}$$
(1)

with \(\tilde{c}( \{v,w\} ) := \tilde{d}(v,w)\) for all \(v,w \in U\). If \( \tilde{d} =d\), we write \(D_G(U)\) instead of \(D_G(U, {d})\). If a given \(\tilde{d}: \genfrac(){0.0pt}1{V}{2} \mapsto \mathbb {Q}_{\ge 0}\) is symmetric, we occasionally write \(\tilde{d}(e)\) instead of \(\tilde{d}(v,w)\) for an edge \(e=\{v,w \}\).

2 From Implications to Reductions

Reduction techniques have been a key ingredient in exact SPG solvers, see e.g. [5, 17, 23, 32]. Among these techniques, the bottleneck Steiner distance introduced in [7] is arguably the most important one, being the backbone of several powerful reduction methods.

2.1 The Bottleneck Steiner Distance

Let P be a simple path with at least one edge. The bottleneck length [7] of P is

$$\begin{aligned} bl(P) := \max _{e \in E(P)} c(e). \end{aligned}$$
(2)

Let \(v,w \in V\). Let \(\mathcal {P}(v,w)\) be the set of all simple paths between v and w. The bottleneck distance [7] between v and w is defined as

$$\begin{aligned} b(v,w) := \inf \{ bl(P) \mid P \in \mathcal {P}(v,w) \}, \end{aligned}$$
(3)

with the common convention that \(\inf \emptyset = \infty \). Consider the distance graph \(D := D_G(T \cup \{v,w\})\). Let \(b_D\) be the bottleneck distance in D. Define the bottleneck Steiner distance [7] between v and w as

$$\begin{aligned} s(v,w) := b_D(v,w). \end{aligned}$$
(4)

The arguably best known bottleneck Steiner distance reduction method is based on the following criterion, which allows for edge deletion [7].

Theorem 1

Let \(e = \{v,w\} \in E\). If \(s(v,w) < c(e)\), then no minimum Steiner tree contains e.

2.2 A Stronger Bottleneck Concept

Initially, for an edge \(e = \{v,w\}\) define the restricted bottleneck distance \(\overline{b}(e)\) [23] as the bottleneck distance between v and w on \((V,E \setminus \{e\},c)\).

The basis of the new bottleneck Steiner distance concept is formed by a node-weight function that we introduce below. For any \(v \in V \setminus T\) and \(F \subseteq \delta (v)\) define

$$\begin{aligned} p^+(v, F) = \max \left\{ 0, \sup \left\{ \overline{b}(e) - c(e) \mid e \in \delta (v) \cap F, e \cap T \ne \emptyset \right\} \right\} . \end{aligned}$$
(5)

We call \(p^+(v, F)\) the F-implied profit of v. The following observation motivates the subsequent usage of the implied profit. Assume that \(p^+(v, \{ e \})>0\) for an edge \(e \in \delta (v)\). If a Steiner tree S contains v, but not e, then there is a Steiner tree \(S'\) with \(e \in E(S')\) such that \(c(E(S')) + p^+(v, \{ e \}) \le c(E(S))\).

Let \(v, w \in V\). Consider a finite walk \(W = (v_{1},e_{1}, v_{2},e_{2},...,e_{r}, v_{r})\) with \(v_{1} = v\) and \(v_{r} = w\). We say that W is a (v, w)-walk. For any \(k,l \in \mathbb {N}\) with \(1 \le k \le l \le r\) define the subwalk \(W({k}, {l}) := (v_{k}, e_{k},v_{{k+1}}, e_{{k+1}},...,e_{l}, v_{l})\). W will be called Steiner walk if \(V(W) \cap T \subseteq \{v,w\}\) and v, w are contained exactly once in W. The set of all Steiner walks from v to w will be denoted by \(\mathcal {W}_T(v,w)\). With a slight abuse of notation we define \(\delta _W(u) := \delta (u) \cap E(W)\) for any walk W and any \(u \in V\). Define the implied Steiner cost of a Steiner walk \(W \in \mathcal {W}_T(v,w)\) as

(6)

Further, set

$$\begin{aligned} P^+_W := \{ u \in V(W) \mid p^+\big (u, \delta (u) \setminus \delta _W(u) \big ) > 0 \} \cup \{v,w\}. \end{aligned}$$
(7)

Define the implied Steiner length of W as

$$\begin{aligned} l_{p}^+(W) := \max \{c_p^+(W(v_{k},v_{l})) \mid 1 \le k \le l \le r,~ v_{k},v_{l} \in P^+_W\}. \end{aligned}$$
(8)

Define the implied Steiner distance between v and w as

$$\begin{aligned} d_{p}^+(v,w) := \min \{ l_{p}^+(W) \mid W \in \mathcal {W}_{T}(v,w)\}. \end{aligned}$$
(9)

Note that \(d_{p}^+(v,w) = d_{p}^+(w,v)\). At last, consider the distance graph \(D^+ := D_G(T \cup \{v,w\}, d_{p}^+)\). Let \(b_{D^+}\) be the bottleneck distance in \(D^+\). Define the implied bottleneck Steiner distance between v and w as

$$\begin{aligned} s_p(v,w) := b_{D^+}(v,w). \end{aligned}$$
(10)
Fig. 1.
figure 1

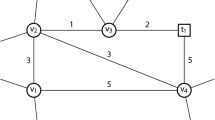
Segment of a Steiner tree instance. Terminals are drawn as squares. The dashed edge can be deleted by employing Theorem 2.

Full size image

Note that \(s_p(v,w) \le s(v,w)\) and that \(\tfrac{s(v,w)}{s_p(v,w)}\) can become arbitrarily large. Thus, the next result provides a stronger reduction criterion than Theorem 1.

Theorem 2

Let \(e = \{v,w\} \in E\). If \(s_p(v,w) < c(e)\), then no minimum Steiner tree contains e.

Figure 1 shows a segment of an SPG instance for which Theorem 2 allows for the deletion of an edge, but Theorem 1 does not. The implied bottleneck Steiner distance between the endpoints of the dashed edge is 1—corresponding to a walk along the four non-terminal vertices. The edge can thus be deleted. In contrast, the (standard) bottleneck Steiner distance between the endpoints is 1.5 (corresponding to the edge itself). Unfortunately, already computing the implied Steiner distance is hard:

Proposition 1

Computing the implied Steiner distance is \(\mathcal {NP}\)-hard.

Despite this \(\mathcal {NP}\)-hardness, one can devise heuristics that provide useful upper bounds on \(s_p\), as discussed in the extended version of this article.

2.3 Bottleneck Steiner Reductions Beyond Edge Deletion

This section discusses applications of the implied bottleneck Steiner distance that allow for additional reduction operations: Edge contraction and node replacement. We start with the former. For an edge e and vertices v, w define \({b}_e(v,w)\) as the bottleneck distance between v and w on \((V,E \setminus \{e\},c\restriction _{E \setminus \{e\}} )\). With this definition, we define a generalization of the classic NSV reduction test from [6].

Proposition 2

Let \(\{v,w\} \in E\), and \(t_1,t_2 \in T\) with \(t_1 \ne t_2\). If

$$\begin{aligned} s_p(v,t_1) + c(\{v,w\}) + s_p(w,t_2) \le b_{\{v,w\}}(t_1,t_2), \end{aligned}$$
(11)

then there is a minimum Steiner tree S with \(\{v,w\} \in E(S)\).

If criterion (11) is satisfied, one can contract edge \(\{v,w\}\) and make the resulting vertex a terminal. Note that in the original criterion by [6] the standard distance is used, and no strengthening is achieved when the (standard) bottleneck Steiner distance is used instead.

This section closes with a new reduction criterion based on the standard bottleneck Steiner distance. This result also serves to highlight the complications that arise if one attempts to formulate similar conditions based on the implied bottleneck Steiner distance.

Proposition 3

Let \(D:= D_G(T, d)\). Let Y be a minimum spanning tree in D. Write its edges \(\{e^Y_1,e^Y_2,..., e^Y_{|T|-1}\} := E(Y)\) in non-ascending order with respect to their weight in D. Let \(v \in V \setminus T\). If for all \(\varDelta \subseteq \delta (v)\) with \(|\varDelta | \ge 3\) it holds that:

$$\begin{aligned} \sum _{i = 1}^{|\varDelta | - 1} d(e^Y_i) \le \sum _{e \in \varDelta } c(e), \end{aligned}$$
(12)

then there is at least one minimum Steiner tree S such that \(|\delta _S(v)| \le 2\).

If the conditions (12) are satisfied for a vertex \(v \in V \setminus T\), one can pseudo-eliminate [6] or replace [21] vertex v, i.e., delete v and connect any two vertices \(u, w \in N(v)\) by a new edge \(\{u,w\}\) of weight \(c(\{v, u\}) + c(\{v, w\})\).

The SPG depicted in Fig. 2 exemplifies why Proposition 3 cannot be formulated by using the implied bottleneck Steiner distance. The weight of the minimum spanning tree Y for \(D_G(T, d)\) is 4, but the weight of a minimum spanning tree with respect to \(s_p\) is 2. Similarly also the \(BD_m\) reduction technique from [6] cannot be directly formulated by using the implied bottleneck Steiner distance.

Fig. 2.
figure 2

SPG instance. Terminals are drawn as squares

Full size image

3 From Reductions to Conflicts

In this section we use the concept of conflicts between edges. We say that a set \(E' \subset E\) with \(|E'|\ge 2\) is in conflict if no minimum Steiner tree contains more than one edge of \(E'\). Recall that we have seen three types of reductions so far: Edge deletion, edge contraction, and node replacement. For simplicity, we assume in the following that a reduction is only performed if it retains all optimal solutions. We say that such a reduction is valid. We start with an SPG instance \(I = (G,T,c)\), and consider a series of subsequent, valid reductions (of one of the three above types) that are applied to I. In each reduction step \(i \ge 0\), the current instance \(I^{(i)} = (G^{(i)},T^{(i)},c^{(i)})\) is transformed to instance \(I^{(i+1)} = (G^{(i+1)},T^{(i+1)},c^{(i+1)})\). We set \(I^{(0)} := I\).

3.1 Node Replacement

In [24] the authors observe that two edges that originate from a common edge by a series of replacements cannot both be contained in a minimum Steiner tree. We introduce an edge conflict criterion that is strictly stronger. For a series of \(i = 0,1,...,k\) valid reductions, we define sets of replacement ancestors \(\varLambda ^{(i)}: E^{(i)} \rightarrow \mathcal {P}(\{1,...,k\})\), and \(\varLambda ^{(i)}_{FIX} \in \mathcal {P}(\{1,...,k\})\). We set \(\varLambda ^{(0)}(e) := \emptyset \) for all \(e \in E\), and \(\varLambda ^{(0)}_{FIX} := \emptyset \). Further, we define \(\lambda ^{(0)} := 0\). Consider a reduced instance \(I^{(i)}\). If we contract an edge \(e \in E^{(i)}\), we set \(\varLambda ^{(i + 1)}_{FIX} := \varLambda ^{(i)}_{FIX} \cup \varLambda ^{(i)}(e)\). If we replace a vertex \(v \in V^{(i)}\), we set \(\lambda ^{(i + 1)} := \lambda ^{(i)} + 1\). Further, we define for each newly inserted edge \(\{u,w\}\), with \(u, w \in N(v)\):

$$\begin{aligned} \varLambda ^{(i+1)}(\{u,w\}) := \varLambda ^{(i)}(\{v,u\}) \cup \varLambda ^{(i)}(\{v,w\}) \cup \{\lambda ^{(i)}\}. \end{aligned}$$

If no node replacement is performed, we set \(\lambda ^{(i + 1)} := \lambda ^{(i)}\).

Proposition 4

Let I be an SPG and let \(I^{(k)}\) be the SPG obtained from performing a series of k valid reductions on I. Further, let \(e_1,e_2 \in E^{(k)}\). If \(\varLambda ^{(k)}(e_1) \cap \varLambda ^{(k)}(e_2) \ne \emptyset \), then no minimum Steiner tree \(S^{(k)}\) for \(I^{(k)}\) contains both \(e_1\) and \(e_2\).

Corollary 1

Let I, \(I^{(k)}\) as in Proposition 4, and let \(e \in E^{(k)}\). If \(\varLambda ^{(k)}(e) \cap \varLambda ^{(k)}_{FIX} \ne \emptyset \), then no minimum Steiner tree \(S^{(k)}\) for \(I^{(k)}\) contains e.

Note that any edge e as in Corollary 1 can be deleted.

3.2 Edge Replacement

This subsection introduces a new replacement operation, whose primary benefit lies in the conflicts it creates.

Proposition 5

Let \(e = \{v,w\} \in E\) with \(e \cap T = \emptyset \). Define

$$\begin{aligned} \mathcal {D} := \left\{ \varDelta \subseteq \left( \delta (v) \cup \delta (w)\right) \setminus \{e\} \mid \varDelta \cap \delta (v) \ne \emptyset , \varDelta \cap \delta (w) \ne \emptyset \right\} . \end{aligned}$$

For any \(\varDelta \in \mathcal {D}\) let

$$\begin{aligned} U_{\varDelta } := \left\{ u \in V \mid \{u,v\} \in \varDelta \vee \{u,w\} \in \varDelta \right\} . \end{aligned}$$

If for all \(\varDelta \in \mathcal {D}\) with \(|\varDelta | \ge 3\) the weight of a minimum spanning tree on \(D_G(U_{\varDelta }, s)\) is smaller than \(c(\varDelta )\), then each minimum Steiner tree S satisfies \(|\delta _S(v)| \le 2\) and \(|\delta _S(w)| \le 2\).

If the condition of Proposition 5 is successful, we can perform what we will call a path replacement of e: We delete e and add for each pair \(p,q \in V\) with \(p \in N(v) \setminus \{w\}\), \(q \in N(w)) \setminus \{v\}\), \(p \ne q\) an edge \(\{p,q\}\) with weight \(c(\{p,v\}) + c(\{v,w\}) + c(\{q,w\})\). The apparent increase in the number of edges by this operations seems highly disadvantageous. However, due to the increased weight, the new edges can often be deleted by using the criterion from Theorem 2. We only perform a path replacement if at most one of the new edges needs to be inserted. If exactly one new edge remains, we create new replacement ancestors as follows: Let \(\hat{e} = \{p,q\}\) be the newly inserted edge. Initially, set \(\lambda ^{(i+1)} := \lambda ^{(i)}\) and \(\varLambda ^{(i+1)}(\hat{e}) := \varLambda ^{(i)}(\{p,v\}) \cup \varLambda ^{(i)}(\{v,w\}) \cup \varLambda ^{(i)}(\{v,q\})\). Next, for each \(e' \in \left( \delta (v) \cup \delta (w)\right) \setminus \{e\}\) increment \(\lambda ^{(i+1)}\), and add \(\lambda ^{(i+1)}\) to \(\varLambda ^{(i+1)}(\hat{e})\) and \(\varLambda ^{(i+1)}(e')\). One can show that Proposition 4 remains valid if path replacement is added to the list of valid reduction operations. As we will see in the remainder of this article, conflicts cannot only be used for further reductions, but also for generating cuts in an IP model.

4 From Steiner Distances and Conflicts to Extended Reduction Techniques

At the end of the last section we have seen a reduction method that inspects a number of trees (of depth 3) that extend an edge considered for replacement. This section continues along this path, based on the reduction concepts introduced so far. In the following, we introduce new so-called extended reduction algorithms that (provably) dominate the strongest ones from the literature, due to [24].

4.1 The Framework

For a tree Y in G, let \(L(Y) \subseteq V(Y)\) be the set of its leafs. We start with several definitions from [24]. Let \(Y'\) be a tree with \(Y' \subseteq Y\). The linking set between Y and \(Y'\) is the set of all vertices \(v \in V(Y')\) such that there is a path \(Q \subseteq Y\) from v to a leaf of Y with \(V(Q) \cap V(Y') = \{v\}\). Note that Q can consist of a single vertex. \(Y'\) is peripherally contained in Y if the linking set between Y and \(Y'\) is \(L(Y')\). For any \(P \subseteq V(Y)\) with \(|P| > 1\) let \(Y_P\) be the union of the (unique) paths between any \(v,w \in P \cup V(Y)\) in Y. Note that \(Y_P\) is a tree, and that \(Y_P \subseteq Y\) holds. P is called pruning set if it contains the linking set between \(Y_P\) and Y. Additionally, we will use the following new definition: P is called strict pruning set if it is equal to the linking set between \(Y_P\) and Y.

Additionally, we define a stronger, and new, inclusion concept. Consider a tree \(Y \subseteq G\), and a subtree \(Y'\). Let P be a pruning set for \(Y'\). We say that \(Y'\) is P-peripherally contained in Y if P is a pruning set for Y. Now let P be a strict pruning set for \(Y'\). We say that \(Y'\) is strictly P-peripherally contained in Y if P is a strict pruning set for Y. One obtains the following important property.

Observation 1

Let \(Y \subseteq G\) be a tree, let \(Y' \subseteq Y\) be a subtree, and let P be a pruning set for \(Y'\). If \(Y'\) is peripherally contained in Y, then \(Y'\) is also P-peripherally contained in Y.

Note that an equivalent property holds for strict pruning sets. Given a tree Y and a set \(E' \subseteq E\), we write with a slight abuse of notation \(Y + E'\) for the subgraph with the edge set \(E(Y) \cup E'\). Algorithm 1 shows a high level description of the extended reduction framework used in this article. The framework is similar to the one introduced in [24], but more general. A possible input for Algorithm 1 is an SPG instance together with a single edge. If the algorithm returns true, the edge can be deleted. Besides ExtensionSets, which is described in Algorithm 2, the extended reduction framework contains the following subroutines, with SPG \(I =(G,T,c)\), tree \(Y \subseteq G\), and a pruning set P for Y.

  • RuledOut(I ,  Y ,  P) returns true if Y is shown to not be P-peripherally contained in any minimum Steiner tree. Otherwise, returns false.

  • RuledOutStrict(I ,  Y ,  P) same as above, but with strict pruning set P.

  • StrictPruningSets(I ,  Y) returns a subset of all strict pruning sets for Y.

  • Truncate(I ,  Y) returns true if no further extensions of Y should be performed; otherwise returns false.

  • Promising(I ,  Y ,  v) is given additionally a vertex \(v \in L(Y)\). Returns true if further extensions of Y from v should be performed; otherwise returns false.

figure a
figure b

In Lines 1–2 of Algorithm 1, we try to peripherally rule-out tree Y. If that is not possible, we try to recursively extend Y in Lines 4–11. Since (given positive edge weights) no minimum Steiner tree has a non-terminal leaf, we can extend from any of the non-terminal leaves of Y. Note that ruling-out all extensions along one single leaf is sufficient to rule-out Y.

4.2 Reduction Criteria

In this section we introduce several elimination criteria used within RuledOut and RuledOutStrict. Note that any criterion that is valid for RuledOut is also valid for RuledOutStrict. We also note that several of the criteria in this section are similar to results from [21, 24], but are all stronger. Throughout this section we consider a graph \(G =(V,E)\) and an SPG instance \(I =(G,T,c)\).

Consider a tree \(Y \subseteq G\), and a pruning set P for Y such that \(V(Y_P) \cap T \subseteq L(Y_P)\). For each \(p \in P\) let \(\overline{Y}_p \subset Y\) such that \(V(\overline{Y}_p)\) is exactly the set of vertices \(v \in V(Y_P)\) that satisfy the following: For any \(q \in P \setminus \{p\}\) the (unique) path in Y from v to q contains p. Note that when removing \(E(Y_P)\) from Y, each non-trivial connected component equals one \(\overline{Y}_p\). Further, note that \(p \in V(\overline{Y}_p)\) for all \(p \in P\). Let \(G_{Y,P} = (V_{Y,P}, E_{Y,P})\) be the graph obtained from \(G = (V,E)\) by contracting for each \(p \in P\) the subtree \(\overline{Y}_p\) into p. For any parallel edges, we keep only one of minimum weight. We identify the contracted vertices \(V(\overline{Y}_p)\) with the original vertex p. Overall, we thus have \(V_{Y,P} \subseteq V\). Let \(c_{Y,P}\) be the edge weights on \(G_{Y,P}\) derived from c. Let

$$\begin{aligned} T_{Y,P} := \big (T \cap V_{Y,P}\big ) \cup \{ p \in P \mid T \cap V(\overline{Y}_p) \ne \emptyset \}. \end{aligned}$$
(13)

Finally, let \(s_{Y,P}\) be the bottleneck Steiner distance on \((G_{Y,P}, T_{Y,P}, c_{Y,P})\). The next theorem generalizes a number of results from the literature. See [11, 21] for similar, but weaker, conditions.

Theorem 3

Let \(Y \subseteq G\) be a tree, and let P be a pruning set for Y such that \(V(Y_P) \cap T \subseteq L(Y_P)\). Let \(I_{Y,P}\) be the SPG on the distance network \(D_{G_{Y,P}}\big (V_{Y,P}, s_{Y,P}\big )\) with terminal set P. If the weight of a minimum Steiner tree for \(I_{Y,P}\) is smaller than \(c(E(Y_P))\), then Y is not P-peripherally contained in any minimum Steiner tree for I.

If computing (or even approximating) a minimum Steiner tree on \(D_{G_{Y,P}}\big (V_{Y,P}, s_{Y,P}\big )\) is deemed to expensive, one can use the weight of a minimum spanning tree on \(D_{G_{Y,P}}\big (P, s_{Y,P}\big )\) instead.

Next, let \(Y \subseteq G\) be a tree with pruning set P, and let \(v,w \in V(Y)\) and let Q be the path between v, w in Y. We define a pruned tree bottleneck between v and w as a subpath Q(a, b) of Q that satisfies \(|\delta _Y(u)| = 2|\) and \(u \notin P\) for all \(u \in V(Q(a,b)) \setminus \{a,b\}\), \(V(Q(a,b)) \cap T \subseteq \{a,b\}\), and maximizes c(V(Q(a, b))). The weight c(V(Q(a, b))) of such a pruned tree bottleneck is denoted by \(b_{Y,P}(v,w)\). Using this definition and the implied bottleneck Steiner distance, we obtain the following result.

Proposition 6

Let Y be a tree, let P be a pruning set for Y, and let \(v,w \in V(Y)\). If \(s_p(v,w)< b_{Y,P}(v,w)\), then Y is not P-peripherally contained in any minimum Steiner tree.

In the extended version of this article we also give an reduction criteria based on reduced costs of an IP formulation, which can only be used for the RuledOutStrict routine. Finally, another important reduction criteria is constituted by edge conflicts between edges of an enumerated tree.

5 Exact Solution

This section describes the usage of the previous techniques for exact SPG solution. They have been implemented as an extension of the solver SCIP-Jack  [9].

5.1 Branch-and-cut

We enhance several vital components of branch-and-cut algorithms. The most natural application of reduction methods is within presolving. However, we also use (limited versions of) them for domain propagation during branch-and-bound, translating the deletion of edges into variable fixings in the integer programming model. The edge conflicts described in this article can be used for generating clique cuts [1]. Note that SCIP-Jack also separates the Steiner cuts from the bidirected cut formulations, as well as the flow-balance constraints from [17]. Finally, also primal heuristics are improved. First, the stronger reduction methods enhance primal heuristics that involve the solution of auxiliary SPG instances, such as from the combination of several Steiner trees. Second, the implication concept introduced in this article can be used to directly improve a classic SPG heuristic by [31], as shown in the extended version of this article.

5.2 Computational Results

This section provides computational results for the new solver. In particular, we compare its performance with the updated results of the solver by [21, 33] published in [27]. The computational experiments were performed on Intel Xeon CPUs E3-1245 with 3.40 GHz and 32 GB RAM. This machine obtains a score of 488.993589 with the benchmark software of the 11th DIMACS Challenge (with the same compiler as [27]). Thus, this computer is roughly 1.59 times faster than the machine used in [27]. We have scaled the run-times reported in the following accordingly. We use the same LP solver as [27]: CPLEX 12.6 [12]. For the comparison we use a diverse range of well-established benchmark sets from the SteinLib  [18] and the 11th DIMACS Challenge.

Table 1 provides results of the two solvers for a time limit of two hours. The second column shows the number of instances in the test-set. Column three shows the mean time taken by the solver of [21, 33], column four shows the mean time of the new solver. The next column gives the relative speedup of the new solver. The next three columns provide the same information for the maximum run-time, the last two columns give the number of solved instances. For the mean time we use the well-established shifted geometric mean [1] with a shift of 10.

Table 1. Comparison of the new solver and the solver by [21, 33].
Full size table

Overall, the new solver performs better on eight of the ten test-sets. Often by a significant margin, such as for GEO-adv or SP. Only on ALUE the new solver performs significantly worse. A possible reason is the existence of small node-separators on these instances. These separators are heavily exploited by partitioning methods in [21, 33]. However, our solver includes no algorithms yet to exploit such separators. It should be noted that the same behavior can be observed for the related test-set ALUT which is not included in Table 1. On the other hand, there are also several other benchmark sets for which the new solver is faster, but which are not contained in Table 1, since they are similar to already included ones (e.g. GEO-org, 1R, WRP3, LIN). We also note that in [27] specialized settings are used for individual test-sets. In contrast, we run all test-sets with default settings, although a considerable speed-up (usually more than 50 percent) could be achieved when using specialized settings.

For most of the test-sets in Table 1, the new solver is around one order of magnitude or more faster than the previous version of SCIP-Jack described in [29], both with respect to the mean and maximum time. Even if one merely considers the enhancements described in this article (as compared to methods already known in the literature), the speed-up is still huge, as shown in the extended version of this article. In particular, the \(s_p\)-based methods have a significant impact, as we demonstrate in the following. To this end, we use three benchmark sets from the DIMACS Challenge, and three from the SteinLib. Table 2 shows in the first column the name of the test-set, followed by its number of instances. The next columns show the percentual average number of nodes and edges of the instances after the preprocessing without (column three and four), and with (columns five and six) the \(s_p\) based methods. The last two columns reports the percentual relative change between the previous results. It can be seen that the \(s_p\) methods allow for a significant additional reduction of the problem size. This behavior is rather remarkable, given the variety of powerful reduction methods already included in SCIP-Jack. Furthermore, the instances from the GEO-adv set come already in preprocessed form; by means of the reduction package from [32]. We note that the overall run-time of the preprocessing notably decreases when the \(s_p\) based methods are used.

Table 2. Average remaining nodes and edges after preprocessing.
Full size table

Finally, we provide results for several large-scale Euclidean Steiner tree problems. For solving such problems, the bottleneck is usually the full Steiner tree concatanation [14]. This concatanation can also be solved as an SPG, however [25]. We report results for Euclidean instances from [14] with 25 thousand (EST-25k) and 50 thousand (EST-50k) points in the plane. Both test-sets contain 15 instances. For EST-25k the mean and maximum times of the new solver are 66.2 and 92.4 s—between one and two orders of magnitude faster than those of the well-known geometric Steiner tree solver GeoSteiner 5.1 [14]. The EST-50k instances can also be solved quickly, with a mean of 286.1 s. Moreover, 7 of the 15 instances are solved for the first time to optimality—in at most 390 s. On the other hand, GeoSteiner cannot solve these instances even after seven days of computation. Unfortunately, [27] does not report results for these instances. However, the solver by [20], which won the heuristic SPG category at the 11th DIMACS Challenge, does not reach the upper bounds from GeoSteiner on any of the EST-25k and EST-50k instances.

6 Outlook

There are several promising routes for further improvement. First, one could enhance the newly introduced methods. For example, by using full-backtracking in the extended reduction methods, by improving the approximation of the implied bottleneck Steiner distance, or by adapting the latter for replacement techniques. Second, several powerful methods described in [21, 33] could be added to the new solver, e.g. a stronger IP formulation realized via price-and-cut, or additional reduction techniques via partitioning.

Unlike the solver by [21, 33], the new SCIP-Jack will be made freely available for academic use—as part of the next SCIP release.