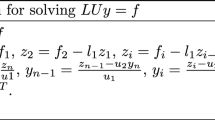Fast Rational Lanczos Method for the Toeplitz Symmetric Positive Semidefinite Matrix Functions

Abstract

In this paper, we use the rational Lanczos method to approximate Toeplitz matrix functions, in which the matrices are symmetric positive semidefinite (SPSD). In order to reduce the computational cost, we use the inverse of the Toeplitz matrix and the fast Fourier transform (FFT). Then, we apply this method to solve a heat equation. Numerical examples are given to show the effectiveness of the rational Lanczos method.

Supported by the “Peiyu” Project from Xuzhou University of Technology (Grant Number XKY2019104).

1 Introduction

Recently, many authors have been interested in exponential integrators which are widely used in various fields [15, 16, 27, 32]. In the exponential integrators, one needs to compute some products of $\varphi _{i}$ matrix functions and vectors:

$$\begin{aligned} y_{i}(t)=\varphi _{i}(-tA_{m})\text {v},~~i=0,1,2,\ldots ,s_1, \end{aligned}$$

(1)

where $A_{m}$ is an $m\times m$ matrix, $s_1$, t are given parameters, and $\text {v}$ is a vector. And $\varphi _{i}$-functions are of the following form

$$\begin{aligned} \varphi _{0}(x)=\mathrm{exp}(x),\varphi _{i}(x)={\int _0^1 \frac{\mathrm{exp}\big ((1-\xi )x\big )\xi ^{i-1}}{(i-1)!}d\xi }, i\in \mathbb {Z^{+}}. \end{aligned}$$

(2)

Furthermore, the $\varphi _{i}$-functions satisfy the following relations

$$\begin{aligned} \varphi _{i}(x)=x\varphi _{i+1}(x)+\frac{1}{i},\quad i\in \mathbb {Z^{+}}. \end{aligned}$$

(3)

Toeplitz matrices have various applications [5, 6]. Based on the importance of Toeplitz matrices, we want to approximate the products of the $\varphi _{i}$ matrix functions and vectors (TMF), in which the matrices are the SPSD Toeplitz matrix. That is, in (1), the matrix $A_{m}$ is the SPSD Toeplitz matrix. TMF can be applied to practical calculation problems; see [12, 36] for example. Recently, some new techniques are proposed to improve network routing and performance measurement [17, 39]. Based on effective user behavior and traffic analysis approaches [19, 20], we can design more effective scheduling strategies to raise resources utilization [22, 26] and energy-efficiency [23, 24]. To test new scheduling strategies, traffic must be reconstructed in test bed [18, 21, 25, 34, 38]. Fluid model is effective model to reconstruct the bursty data traffic. In this situation, TMF can also be used to build the fluid model.

Classical methods for solving $\varphi _{i}$ matrix functions require very high complexity [2]. Recently, Krylov subspace method has been widely studied in large-scale sparse matrix due to its high efficiency [1, 3, 4, 7,8,9, 29, 30, 40]. In this method, we only need to compute the smaller matrix functions instead of computing the large matrix functions. Moreover, rational technique could be exploited to speed up Krylov subspace method [10, 11].

It is known that we can calculate Toeplitz matrix-vector products by the fast Fourier transform [5, 6], and one can calculate the explicit inverse of the Toeplitz matrix by the Gohberg-Semencul formula (GS) [13, 14]. These important properties can be used to accelerate the rate of convergence of the computation of TMF. In this work, we use the rational Lanczos method to compute the TMF and reduce the computational cost by using the GS.

2 Toeplitz Matrix

An $m\times m$ Toeplitz matrix $T_{m}$ satisfies $(T_{m})_{i,j}=t_{i-j}$ for $1\le i,j \le m$. A circulant matrix $C_{m}((C_{m})_{i,j}=c_{i-j})$ satisfies $c_{i}=c_{i-m}$, $1\le i \le m-1$. According to [5], we know that the complexity is $\mathcal {O}(m\log m)$, if one computes the products $C_{m}\text {u}$ and $C^{-1}_{m}\text {u}$ for a given vector $\text {u}$ by the FFT.

A skew-circulant matrix $S_{m}((S_{m})_{i,j}=s_{i-j})$ satisfies $s_{i}=-s_{i-m}$ for $1\le i \le m-1$. Similarly, the computational complexity of the products of $S_{m}\text {u}$ and $S^{-1}_{m}\text {u}$ is also $\mathcal {O}(m\log m)$ by the FFT.

In addition, by constructing a proper circulant matrix, we can compute $T_{m}\text {u}$ in $\mathcal {O}(2m\log ( 2m))$ complexity by the FFT; see [5, 6].

The GS for the inverse of a Toeplitz matrix $T_{m}$ which is SPD is as follows [13]

$$\begin{aligned} T_m^{-1}=\frac{1}{a_{1}}(A_{m}A_{m}^\intercal -\hat{A}_{m}\hat{A}_{m}^\intercal ), \end{aligned}$$

(4)

where the matrices $A_{m}$ and $\hat{A}_{m}$ are of the following forms

$$\begin{aligned} \ A_{m}=\left[ \begin{array}{cccc} a_{1}&{} 0&{}\cdots &{}0\\ a_{2}&{} a_{1}&{}\ddots &{}\vdots \\ \vdots &{}\ddots &{}\ddots &{}0\\ a_{m}&{}\ldots &{}a_{2}&{}a_{1} \end{array}\right] \end{aligned}$$

and

$$\begin{aligned} \ \hat{A}_{m}=\left[ \begin{array}{cccc} 0&{} 0&{}\cdots &{}0\\ a_{m}&{} 0&{}\ddots &{}\vdots \\ \vdots &{}\ddots &{}\ddots &{}0\\ a_{2}&{}\ldots &{}a_{m}&{}0 \end{array}\right] . \end{aligned}$$

Denote $\mathbf {a}=[a_{1},a_{2},\ldots ,a_{m}]^\intercal$, then we can get $\mathbf {a}$ by solving the following linear system

$$\begin{aligned} T_{m}\mathbf {a}=\text {e}_{1}=[1,0,\ldots ,0]^\intercal . \end{aligned}$$

(5)

According to [31, 33], by using (4), one can obtain

$$\begin{aligned} T_{m}^{-1}\text {u}=Re(\text {p})+\hat{J}Im(\text {p}) \end{aligned}$$

(6)

and

$$\begin{aligned} \text {p}=\frac{1}{2a_{1}}\left[ (A_{m}+\hat{A}_{m}^\intercal )(A_{m}^\intercal -\hat{A}_{m})\right] (\text {u}+\mathbf {i}\hat{J}\text {u}), \end{aligned}$$

(7)

where $\mathbf {i}$ is the imaginary unit and $\hat{J}$ is the anti-identity matrix, and $Re(\text {p})$ is the real part of $\text {p}$ and $Im(\text {p})$ is the imaginary part of $\text {p}$. Thus, we can compute $T_{m}^{-1}\text {u}$ in ${\mathcal {O}}(m \log m)$ operations. To construct $T_{m}^{-1}$ by the GS, we need to solve the Toeplitz linear system (5). We use the PCG with Strang’s preconditioner to solve (5) in this paper.

3 Rational Lanczos Method

In this section, we first introduce the Lanczos method for solving $y_{i}(t)=\varphi _{i}(-tT_{m})\text {v}$. By using the Lanczos algorithm for a symmetric matrix $T_{m}$, we can get a basis of a Krylov subspace

$$\mathcal {K}_{n}(T_{m},\text {v})=\text {span}\{\text {v},T_{m}\text {v},T_{m}^{2}\text {v},\ldots ,T_{m}^{n-1}\text {v}\}.$$

Please see [35] for the details of this algorithm.

The following formulation can be obtained by the Lanczos algorithm [35]

$$\begin{aligned} T_mU_{n}=U_nH_n+h_{n+1,n}\text {v}_{n+1}\text {e}^\intercal _n, \end{aligned}$$

(8)

where $U_n=[\text {u}_{1},\text {u}_{2},\ldots ,\text {u}_{n}]$ is an $m\times n$ matrix. $H_n$ is an $n\times n$ symmetric tri-diagonal matrix, and $\text {e}_n$ is the n-th column of the identity matrix. Therefore, we can give the following approximation

$$\varphi _{i}(-tT_{m})\text {v}\approx \hat{\beta } U_n \varphi _{i}(-tH_{n})\text {e}_1,~\hat{\beta }=\Vert \text {v}\Vert _{2}.$$

Therefore, the computation of large matrix functions $\varphi _{i}(-tT_{m})$ are replaced by the computation of the small matrix functions $\varphi _{i}(-tH_{n})$. In addition, $\varphi _{i}(-tH_{n})$ can be effectively calculated by the function “phipade” in the software package EXPINT [2].

According to [35], we note that, for approximating $\varphi _{i}(-tT_{m})\text {v}$, the rate of convergence of the Lanczos algorithm is very slow when the 2-norm of $tT_m$ gets larger. In order to overcome this drawback, the rational Krylov subspace method is proposed [10, 11, 30, 40].

Let $I_m$ be the identity matrix and $\hat{\sigma }$ is a parameter. We give the rational Lanczos algorithm as follows:

Similar to (8), we have the following formulation

$$\begin{aligned} (I_m+\hat{\sigma } T_{m})^{-1}U_{n}=U_nH_n+h_{n+1,n}\text {u}_{n+1}\text {e}^\intercal _n, ~U^\intercal _nU_n=I_n. \end{aligned}$$

(9)

Therefore, we can approximate $\varphi _{i}(-tT_{m})\text {v}$ by

$$\begin{aligned} \varphi _{i}(-tT_{m})\text {v}\approx \hat{\beta } U_n \varphi _{i}(-tB_{n})\text {e}_1,~\hat{\beta }=\Vert \text {v}\Vert _{2}, \end{aligned}$$

(10)

where

$$B_n=\frac{1}{\hat{\sigma }}(H^{-1}_n-I_n)+h^{2}_{n+1,n}\left( \frac{1}{\hat{\sigma }}+\text {u}_{n+1}^\intercal T_{m}\text {u}_{n+1}\right) H^{-1}_n\text {e}_n\text {e}^\intercal _nH^{-1}_n=U^\intercal _nT_mU_n.$$

In [11], the following error bound for approximating (10) is given.

Theorem 1

Let $A_{m}=P^\intercal _mT_mP_m$, where $P_m$ is the projection operator of $T_m$ on the subspace $\mathcal {K}_{n}((I_m+\sigma T_{m})^{-1},\mathrm {v})$, then the approximation of $\varphi _{i}(-tT_{m})\mathrm {v}$ on the subspace $\mathcal {K}_{n}((I_m+\hat{\sigma } T_{m})^{-1},\mathrm {v})$ has the following error bound

$$\begin{aligned} \Vert \varphi _{i}(-tT_{m})\mathrm {v}-\varphi _{\textit{i}}(-\textit{t}A_{\textit{m}})\mathrm {v}\Vert \le \frac{\textit{D}}{\textit{m}^{\textit{i}/2}}\Vert \mathrm {v}\Vert , \end{aligned}$$

(11)

where D is a constant which depends on $\hat{\sigma }$ and i.

For the rational Lanczos algorithm, $P_m=U_nU^\intercal _n$, and

$$\varphi _{i}(-tA_{m})\text {v}=\varphi _{i}(-tP_mT_{m}P_m)\text {v}$$

$$=U_n\varphi _{i}(-tU^\intercal _nT_{m}U_n)U^\intercal _n\text {v}$$

$$=\hat{\beta } U_n\varphi _{i}(-tB_{n})\text {e}_1.$$

The error bound of Theorem 1 shows: Firstly, the error bound of the rational Lanczos method (11) does not depend on the 2-norm of the matrix $tT_n$. Secondly, if the i increases, the rate of convergence of the approximation $\varphi _{i}(-tT_{m})\text {v}$ will increase.

3.1 Implementation for the TMF Algorithm

In this section, we give the implementation of the algorithm for approximating the TMF. We note that if a Toeplitz matrix $T_{m}$ is a SPSD, then $I_m+\hat{\sigma } T_{m}$ ($\hat{\sigma }>0$) is a SPD Toeplitz matrix. Therefore, the GS can be used to solve the inverse of the Toeplitz matrix $I_m+\hat{\sigma } T_{m}$. For the computation of the TMF, the rational Lanczos algorithm using the GS is as follows:

Algorithm 2: Rational Lanczos algorithm for the TMF

1. Solve $(I_m+\hat{\sigma } T_{m})\mathbf {a}=\text {e}_{1}$

2. Run Algorithm 1, where $(I_m+\hat{\sigma } T_{m})^{-1}\text {u}_j$ is computed by (6) and (7)

3. Calculate $\tilde{y}_i(t)=\hat{\beta } U_n \varphi _{i}(-tB_{n})\text {e}_1$

In step 1 of Algorithm 2, the cost of solving $(I_m+\hat{\sigma } T_{m})\mathbf {a}=\text {e}_{1}$ is ${\mathcal {O}}(m \log m)$ [5, 6]. Then, the matrix-vector products $(I_m+\hat{\sigma } T_{m})^{-1}\text {u}_j$ in step 2 of Algorithm 2 can be computed by using (6) and (7), and the cost of computation is ${\mathcal {O}}(m \log m)$. In step 3 of Algorithm 2, we need to approximate $\varphi _{i}(-tB_{n})\text {e}_1$. From [37], we know that $n \ll m$ in general. Therefore, $\varphi _{i}(-tB_{n})\text {e}_1$ can be fast approximated by the function “phipade” in the software package EXPINT [2], the computation amount is ${\mathcal {O}}(n^{3})$. As a consequence, the computation amount of Algorithm 2 is ${\mathcal {O}}(nm \log m)$.

4 Numerical Examples

In this section, we show the effectiveness of the rational Lanczos algorithm to approximate $\varphi _{i}(-tT_{m})\text {v}$ by two numerical examples. In Example 1, we use MATLAB command “phipade” to calculate the exact solution $\hat{y}(t)$. In the tables of numerical examples, “m” is the size of the matrix $T_{m}$, and “Itol” is the accuracy of the error

$$\frac{\Vert \hat{y}(t)-\hat{y}_n(t)\Vert _{2}}{\Vert \hat{y}(t)\Vert _{2}}<Itol,$$

where $\hat{y}_n(t)$ is the approximation of $\hat{y}(t)$. “IStand” and “IRL” denote the Lanczos method and rational Lanczos method, respectively. The parameter $\hat{\sigma }$ in Algorithm 2 is $\hat{\sigma }=\frac{t}{10}$ [28].

Example 1

In the first example, we study the SPD Toeplitz matrix. The elements of the SPD Toeplitz matrix are as follows [6].

$$t_i=\frac{1}{2\pi }\int ^{\pi }_{-\pi }x^{4}\exp (-\mathbf{i} ix)dx, i=0,\pm 1,\pm 2,\ldots ,\pm (m-1).$$

The elements of the vector $\text {v}$ are all 1. We approximate $\varphi _{i}(-tT_{m})\text {v}$ ($i=1,2,3$). In this example, the order of the matrix $T_{m}$ is $2^{10}$ and the value of t changes.

It can be seen from Tables 1, 2 and 3 that the numbers of iterations of the IRL are much less than these of the IStand, especially when the 2-norm of $tT_{m}$ gets larger. In addition, for the IRL, the numbers of iterations do not change. This indicates that the rate of convergence of the IRL does not depend on the 2-norm of $tT_{m}$ compared with the IStand.

Table 1. Numerical results for Example 1 ($i=1$)

Table 2. Numerical results for Example 1 ($i=2$)

Table 3. Numerical results for Example 1 ($i=3$)

To compare the computational time of the IStand and the IRL, we give the results of the numbers of iterations and computational time in seconds of the IStand and the IRL in Table 4, where $Itol=10^{-9}$ and $m=2^{10}$. It can be seen from Table 4: Firstly, the computational times and the numbers of iterations of the IRL are much less than these of the IStand. Furthermore, if the size of the matrix $T_{m}$ gets larger, the superiority of the IRL will become more obvious. Secondly, if t is fixed, as i increases, the iteration numbers of the IRL decreases, which also validates the result of (11) in Theorem 1.

Table 4. Numerical results of the IRL and the IStand for Example 1

Example 2

In the second example, we study a heat equation [12]. Please refer to [12] for the detailed equation. Numerically solving the heat equation leads to a matrix function problem

$$\hat{v}(t)=(-tT_m)\varphi _1(-tT_m)v_0+v_0,$$

where

$$\hat{v}(t)=[\hat{v}_1(t),\hat{v}_2(t),\ldots ,\hat{v}_m(t)]^\intercal $$

is an approximation solution, $T_m$ is a SPD Toeplitz matrix, and $v_0$ is an initial vector. We solve $\hat{v}(t)$ by the IStand and the IRL, respectively. Table 5 lists the numbers of iterations and computational times of the IStand and the IRL for different m and t.

Table 5. Numerical results for Example 2

According to Table 5, it is seen that the IRL needs fewer numbers of iterations and calculation times to reach the final accuracies than these of the IStand. In addition, for the large matrix size, the IStand becomes unacceptable due to a lot of iteration numbers, while the IRL still works well.

5 Conclusion and Future Work

In this work, we use the rational Lanczos algorithm to approximate the TMF, and this method is applied to the numerical calculation. Using the GS, we can avoid the use of internal iterations to implement the rational Lanczos algorithm. In addition, due to the Toeplitz matrix, the amount of computation can be reduced. Numerical results show the advantage of the new method.