Poynting–Robertson and Oblateness Effects on the Equilibrium Points of the Perturbed R3BP: Application on Cen X-4 Binary System

Abstract

We examine the dynamical effects of Poynting–Robertson (P–R) drag and oblateness together with small perturbations in the Coriolis and centrifugal forces on the existence, location and stability of equilibrium points in the photogravitational restricted three-body problem. It is found that under constant P–R drag effect, collinear equilibrium points cease to exist numerically and of course analytically. The problem admits five non-collinear equilibrium points and it is found that the positions of these points depend on all the system parameters except small perturbation in the Coriolis force. Finally, we justify the relevance of the model in astronomy by applying it to Cen X-4 binary system, for which all the equilibrium points have been seen to be unstable.

1 Introduction

The restricted three-body problem (R3BP) consists of two finite bodies, known as primaries which rotate in circular orbits around their common center of mass and a massless body which moves in the plane of motion of the primaries under their gravitational attraction and does not affect their motion. The study of the R3BP is still an active field of research because of its applications in dynamics of the solar and stellar systems, artificial satellites and lunar theory. The circular restricted three-body problem (CR3BP) has been the well known studied problem in celestial mechanics. In this problem there are five equilibrium points; three of them lie on the x-axis and are called collinear while the other two are away from the x-axis and are called triangular equilibrium points. The three collinear points are generally unstable while the triangular points are generally stable for the mass ratio $\mu \leqslant 0.03850\ldots$ [30]. These equilibrium points are extensively used in space mission (see [1, 3, 12, 31] and references therein).

In celestial mechanics, many scientists and astronomers over the years have made modifications to the classical CR3BP (e.g. [6, 8, 13, 17,18,19, 22, 23, 29, 32,33,34]). Some of the modifications made, include the consideration of one or both primaries as oblate spheroids and/or radiation sources with small change in Coriolis and centrifugal forces and/or under the effect of different kinds of dissipation (Stokes and/or Poynting–Robertson drags). The studying of these issues enable us to get real and accurate data about the dynamical features of the system. For example, Oberti and Vienne [15] showed that the addition of oblateness effects leads to improved approximations of real orbits of certain satellites in the Solar System. Singh [28] examined out-of-plane equilibria by considering effect of a small change in Coriolis and centrifugal forces, when the primaries are both radiating and oblate spheroids. Chernikov [4] studied the existence and stability of equilibrium points under the influence of radiation and Poynting–Robertson drag. He found that six equilibrium points exist at most and pointed out that the collinear points are not positioned on the axis connecting the primaries any more while the triangular points are not symmetrical with respect to this axis. It was found that the triangular points are unstable for P–R effect. Schuerman [21] studied the triangular points of the problem and found that the points are unstable due to P–R effect. Furthermore, Ragos and Zafiropoulos [20] extended the problem to the case that both main bodies are radiation sources and studied the existence and stability of the equilibrium points. The P–R effect renders unstable those equilibrium points which are conditionally stable in the classical case. Murray [14] has discussed the dynamical effect of different kinds of dissipation (nebular drag, gas drag, and P–R drag) in the circular restricted three body problem and found the collinear points are not positioned on the axis joining the two masses while the displaced triangular points L ₄ and L ₅ are asymptotically stable for certain classes of drag forces.

Kushvah [11] studied numerically the existence of equilibrium points of the perturbed R3BP, where the bigger and smaller primaries are considered radiation sources and oblate spheroids, respectively, and discussed the P–R effect which is caused due to the radiation pressure. They observe that the collinear points deviate from the axis joining the two primaries, while the triangular points are not symmetrical due to radiation pressure. The P–R effect ruins the stability of equilibrium points known to be conditionally stable in the gravitational case. When the primaries are radiation sources, Singh and Aminu [24] investigated the influences of small perturbations in the Coriolis and centrifugal forces together with P–R drag from both primaries on the triangular points. They found that the positions of these points are affected from the radiation pressure, P–R drag and small perturbation in the centrifugal force. They also discovered that these perturbing forces do not influence the nature of the stability of the points in the presence of P–R drag as they remain unstable for the binary systems Luyten 726–8 and Kruger 60.1. In the same vein, Singh and Amuda [25] studied the triangular equilibrium points when the effect of radiation pressure from the smaller primary and its Poynting Robertson (P–R) drag are taken into account and the bigger primary as an oblate spheroid. They found numerically that the equilibrium points of the binary RXJ 0450.1–5856 are unstable. Later, Singh and Amuda [26] investigated the three dimensional case of the problem studied in [25] and they pointed out that the out-of-plane equilibria of the binary Cen X-4 system are unstable. By taking into consideration the P–R effect and Stellar wind drag, Chakraborty and Narayan [5] investigated the photogravitational elliptic restricted three-body problem and found that the equilibrium points are unstable due to the effect of the drag. Recently, Kalantonis et al. [10] studied the stability of the triangular equilibrium points in the elliptic R3BP with radiation and oblateness and showed that the positions of the triangular equilibrium points are given by an analytical formulae in which the parameters of the problem are only involved.

In this work, we aim to make an extension to the work of Singh and Amuda [25] by also taking small perturbations in the Coriolis and centrifugal forces and continue to study numerically the existence and location of the equilibrium points. As an application in this study, we consider the Cen X-4 binary system. The paper is organized as follows: In Section 2, the dynamical equations that involve the parameters of the infinitesimal particle in the binary system under consideration are obtained. In Section 3, we determine the existence and locations of the equilibrium points numerically and verify them graphically for values of the parameters of the problem, while their linear stability is analyzed in Section 4. A numerical application of these results is given in Section 5 while Section 6 summarizes the discussion and conclusion of our study.

2 Equations of Motion

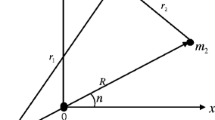
The dynamical system consists of two bodies (known as the primaries) which move on circular orbits. We consider a barycentric coordinate system Oxyz rotating relative to an inertial reference system with angular velocity ω about a common z-axis. The two finite bodies P ₁ (bigger primary) and P ₂ (smaller primary) have masses m ₁ = 1 − μ and $m_2 = \mu \ (0<\mu \leqslant 1/2)$, respectively, with μ being the mass ratio parameter while the test particle P is considered to have a mass m, which is significantly smaller than the masses of the primaries and therefore it does not affect their motion. Also, the bigger primary body is considered to be an oblate spheroid while the smaller one is a source of radiation with its P–R drag. The equations of motion of the test particle in the three-dimensional restricted three-body problem with the origin resting at the center of mass, in a barycentric rotating coordinate system take the form [25]:

$$\displaystyle \begin{aligned} \begin{array}{lll} && \displaystyle \ddot x - 2n\dot y = n^2 x - \frac{(1-\mu )(x+\mu)}{r_1^3} - \frac{\mu (x+\mu -1) q_2}{r_2^3} - \frac{3(1-\mu)(x+\mu)A_1}{2r_1^5} - \\[1.0pc] && \displaystyle\hspace{1.4cm} \frac{W_2}{r_2^2} \left\{\frac{x+\mu-1}{r_2^2} \left[(x+\mu-1)\dot x + y\dot y + z\dot z \right]+\dot x - ny \right\}, \\[1.0pc] && \displaystyle \ddot y + 2n \dot x = n^2 y - \frac{(1-\mu )y}{r_1^3} - \frac{\mu q_2 y}{r_2^3} -\frac{3(1-\mu)A_1 y}{2r_1^5} - \\[1.0pc] && \displaystyle\hspace{1.4cm} \frac{W_2}{r_2^2} \left\{\frac{y}{r_2^2} \left[(x+\mu -1) \dot x + y\dot y + z\dot z \right]+\dot y + n(x+\mu -1) \right\}, \\[1.0pc] && \displaystyle \ddot z \hspace{0.9cm} = -\frac{(1-\mu )z}{r_1^3} - \frac{\mu q_2 z}{r_2^3} - \frac{3A_1 (1-\mu)z}{2r_1^5} - \\[0.9pc] && \displaystyle\hspace{1.4cm} \frac{W_2}{r_2^2} \left\{\frac{z}{r_2^2} \left[(x+\mu-1) \dot x + y\dot y + z\dot z \right] + \dot z \right\}, \end{array} \end{aligned} $$

(1)

with

$$\displaystyle \begin{aligned} r_1^2 = (x+\mu)^2 + y^2 + z^2, \quad r_2^2 = (x+\mu -1)^2 + y^2 + z^2, \quad W_2 = \frac{\mu (1-q_2)}{c_d}, \end{aligned} $$

(2)

where r _i, i = 1, 2 are the distances of the test particle from the bigger and smaller primaries, respectively, q ₂ ∈ (0, 1], W ₂ ≪ 1 stand for radiation pressure and P–R drag of the smaller body, respectively, c _d is the dimensional velocity of light which depends on the physical masses of the two bodies and the distance between them, chosen to the value c _d = 299792458 (see [25]) while the dots denote differentiation with respect to time t. Also, A ₁ is the oblateness coefficient of the bigger primary body defined by the formula $A_1 = (A_E^2 - A_P^2)/5R^2 \ll 1$ where A _E and A _P are the equatorial and polar radii of the said primary body, respectively, and R is the distance between the primaries. On account of the oblateness of the primary body m ₁, the mean perturbed motion n is defined by $n^2 = 1 + \frac {3}{2}A_1$. Additionally, perturbations on the Coriolis and centrifugal forces are included with the help of the parameters α and β, respectively, such that α = 1 + ε ₁, β = 1 + ε ₂, |ε _i|≪ 1, i = 1, 2. The unperturbed value of each is taken as unity. Restricting ourselves to the plane Oxy and following the work of Singh and Aminu [24], the pertinent equations of motion (1) are finally written in the form:

$$\displaystyle \begin{aligned} \begin{array}{lll} && \displaystyle \ddot x - 2n\alpha\dot y {=} n^2 \beta x {-} \frac{(1-\mu )(x+\mu)}{r_1^3} {-} \frac{\mu (x+\mu -1) q_2}{r_2^3} {-} \frac{3(1-\mu)(x+\mu)A_1}{2r_1^5} {-} \\[1.0pc] && \displaystyle\hspace{1.4cm} \frac{W_2}{r_2^2} \left\{\frac{x+\mu-1}{r_2^2} \left[(x+\mu-1)\dot x + y\dot y \right] + \dot x - ny \right\}, \\[1.0pc] && \displaystyle \ddot y + 2n \alpha\dot x = n^2 \beta y - \frac{(1-\mu )y}{r_1^3} - \frac{\mu q_2 y}{r_2^3} -\frac{3(1-\mu)A_1 y}{2r_1^5} - \\[1.0pc] && \displaystyle\hspace{1.4cm} \frac{W_2}{r_2^2} \left\{\frac{y}{r_2^2} \left[(x+\mu -1) \dot x + y\dot y \right] + \dot y + n(x+\mu -1) \right\}, \end{array} \end{aligned} $$

(3)

while now

$$\displaystyle \begin{aligned} r_1^2 = (x+\mu)^2 + y^2, \quad r_2^2 = (x+\mu -1)^2 + y^2. \end{aligned} $$

(4)

The physical parameters of the binary Cen X-4 system are shown in Table 1 (see [2, 25, 26]).

3 Existence and Positions of Equilibrium Points

The equilibrium (or Lagrangian) points are obtained when the acceleration $(\ddot x, \ddot y)$ and velocity $(\dot x, \dot y)$ components of the test particle are zero. So, we obtain the coordinates (x ₀, y ₀) of equilibrium points as solutions of the equations:

$$\displaystyle \begin{aligned} \begin{array}{ll} & \displaystyle n^2 \beta \ x - \frac{(1-\mu)(x+\mu)}{r_1^{3}} {-} \frac{\mu (x+\mu -1) q_2}{r_2^{3}} {-} \frac{3(1-\mu )(x+\mu ) A_1}{2r_1^5} {+} \frac{W_2 ny}{r_2^2} = 0, \\ & \displaystyle n^2 \beta \ y - \frac{(1-\mu )y}{r_1^3} - \frac{\mu yq_2}{r_2^3} - \frac{3y(1-\mu )A_1}{2r_1^5} - \frac{W_2 n(x+\mu -1)}{r_2^2} = 0. \end{array} \end{aligned} $$

(5)

It is interesting to note that for A ₁ = 0, q ₂ = β = 1, the classical case of the R3BP is recovered while the case β = 1 leads to the equations of motion presented in [25]. It is well known that in the classical R3BP there are two types of equilibria or solutions, depending on whether y = 0 or y≠0. Points for which y = 0 are called collinear equilibrium points and they lie on the line connecting the primaries, the x-axis of the synodic system, while points for which y≠0 are called triangular (non-collinear) equilibrium points and they lie away from the x-axis of the synodic system.

In the perturbed R3BP where the radiation pressure coupled with P–R drag terms appear, the existence of collinear equilibria as well as the total number of the equilibrium points depend on the particular values of the radiation pressure (see, for example, [4, 14]). Ragos and Zafiropoulos [20] have shown numerically that in the photogravitational CR3BP including the P–R effect there are at most five equilibrium points (with no collinear points), depending on the values of radiation factors q ₁ and q ₂. Following the lead of above paper, we resort to a numerical study in this case of the problem since the system of Equations (5) which provides the (x ₀, y ₀) coordinates of the points of equilibrium cannot be solved analytically. In this premise, the equilibrium points are obtained by solving Equations (5) simultaneously using any well-known iterative method for finding roots of non-linear algebraic equations. The aforementioned method has been successfully applied in [16, 27] and [7] (see also references therein) for the determination of equilibrium points in a different model problem of Celestial Mechanics. We observe that our problem admits five non-collinear equilibrium points, L _i, i = 1, 2, …, 5, which positions are independent of the Coriolis force but dependent upon the centrifugal force and the remaining involved parameters.

Generally, to obtain the positions for the collinear equilibrium points we solve Equations (5) for y = 0 but due to the existence of the dissipative term defined by the P–R drag, it is obvious that collinear equilibrium solution does not exist anymore. This is also easy to show geometrically by plotting the contours of the two implicit functions presented in system (5) (see Figure 1). We observe from this figure that the y components of the equilibrium points L _1,2,3 are close to zero but not zero. Moreover, this can be easily seen from bottom-left and right frames in Figure 1 where we enlarge the area close to L _1,2 and L ₃, respectively. Therefore, we can conclude that under the effect of P–R drag, induced by the radiation pressure of the smaller primary, there are no equilibrium points that lie exactly on the x-axis, called collinear equilibrium points. This result agrees with [14, 20] and [11].

Fig. 1

The five non-collinear equilibrium points and the position of the primary bodies for μ = 0.03852, β = 1.01, A ₁ = 0.0005, q ₂ = 0.9999 and c _d = 299792458. Bottom frames depict zoomed images of L _1,2 and L ₃, respectively, with intersections of the curves. Black dots indicate the positions of the bodies m _i, i = 1, 2 while the positions of the equilibrium points L _i, i = 1, 2, …, 5 are denoted by green dots

So, for the non-collinear equilibrium points, the second Equation (5) holds and the equilibria are obtained by solving both Equations (5) simultaneously. Figure 1 depicts the five non-collinear equilibrium points, L _i, i = 1, 2, …, 5 of the problem in the xy-plane, along with the associated primaries, which have been found by solving numerically the aforementioned system for assumed values of μ = 0.03852, β = 1.01, A ₁ = 0.0005, q ₂ = 0.9999 and c _d = 299792458. We denote here that the equilibria in the xy-plane are given by the mutual intersections of the two coloured curves where blue and brown lines in the figure correspond to the first and second equation of (5), respectively. Here we also note that the intersection points of these curves show the coordinates (x ₀, y ₀) of the equilibria on the xy-plane. It is seen that under the combined effects of the parameters, there exist five non-collinear equilibrium points for which the ordinates of L ₁, L ₂ and L ₃ are close to zero but not zero. Therefore, from Figure 1, it is observed that under the combined effects of radiating smaller primary with it P–R drag, and oblateness of the bigger primary, the equilibria positions are different from those of the classical R3BP. All these results tally with [20].

4 Stability of the Non-collinear Equilibrium Points

To study analytically the solutions in the neighborhood of the non-collinear equilibrium points L _i, i = 1, 2, …, 5, following Ragos and Zafiropoulos [20] as well as Singh and Amuda [25], we consider small displacements ξ and η given to the coordinates of an equilibrium point (x ₀, y ₀) such that ξ = x − x ₀, η = y − y ₀ and denote the right-hand side of equations of motion (3) by Ω _x = ∂Ω∕∂x and Ω _y = ∂Ω∕∂y, respectively. Then the variational form of the equations of motion is derived as:

$$\displaystyle \begin{aligned} \begin{array}{ll} & \displaystyle\ddot{\xi} - 2n\alpha \dot{\eta} = \varOmega_{x\dot{x}}^{(0)} \dot{\xi} + \varOmega_{x\dot{y}}^{(0)} \dot{\eta} + \varOmega_{xx}^{(0)} \xi + \varOmega_{xy}^{(0)} \eta , \\[0.5pc] & \displaystyle\ddot{\eta} + 2n\alpha \dot{\xi} = \varOmega_{y\dot{x}}^{(0)} \dot{\xi} + \varOmega_{y\dot{y}}^{(0)} \dot{\eta} + \varOmega_{yx}^{(0)} \xi + \varOmega_{yy}^{(0)} \eta , \end{array} \end{aligned} $$

(6)

where the dots are the derivatives with respect to time t and only the linear terms in ξ and η have been taken. Now, we assume solutions of the variational equations of the form

$$\displaystyle \begin{aligned} \xi = B_1 e^{\lambda t} , \qquad \eta = B_2 e^{\lambda t}, \end{aligned} $$

(7)

where A _i, i = 1, 2, are arbitrary constants and λ is a parameter. Substituting Equations (7) in Equations (6) and simplifying, we obtain:

$$\displaystyle \begin{aligned} \begin{array}{ll} & (\lambda^2 - \lambda\varOmega_{x\dot{x}}^{(0)} - \varOmega_{xx}^{(0)})B_1 + (-2n\alpha\lambda - \lambda\varOmega_{x\dot{y}}^{(0)} - \varOmega _{xy}^{(0)})B_2 = 0, \\[0.5pc] & (2n\alpha\lambda - \lambda\varOmega_{y\dot{x}}^{(0)} - \varOmega _{yx}^{(0)})B_1 + (\lambda^2 - \lambda\varOmega_{y\dot{y}}^{(0)} - \varOmega _{yy}^{(0)})B_2 = 0. \end{array} \end{aligned} $$

(8)

Now, for the nontrivial solution the determinant of the coefficients matrix of the above system must be zero, namely:

$$\displaystyle \begin{aligned} \left| \begin{array}{ll} \lambda^2 - \lambda\varOmega_{x\dot{x}}^{(0)} - \varOmega _{xx}^{(0)} & -2n\alpha\lambda - \lambda\varOmega_{x\dot{y}}^{(0)} - \varOmega _{xy}^{(0)} \\ 2n\alpha\lambda - \lambda\varOmega_{y\dot{x}}^{(0)} - \varOmega _{yx}^{(0)} & \lambda^2 - \lambda\varOmega_{y\dot{y}}^{(0)} - \varOmega_{yy}^{(0)} \end{array} \right| =0. \end{aligned} $$

(9)

Simplifying Equation (9) we obtain the characteristic polynomial corresponding to the system (6) as:

$$\displaystyle \begin{aligned} \lambda^4 + a\lambda^3 + b\lambda^2 + c\lambda + d = 0, \end{aligned} $$

(10)

with

$$\displaystyle \begin{aligned} \begin{array}{lll} a &=& -(\varOmega_{y\dot{y}}^{(0)} + \varOmega_{x\dot{x}}^{(0)}), \\[0.4pc] b &=& 4n^2 \alpha^2 + \varOmega_{x\dot{x}}^{(0)} \varOmega_{y\dot{y}}^{(0)} - \varOmega_{xx}^{(0)} - \varOmega_{yy}^{(0)} - [\varOmega_{x\dot{y}}^{(0)}]^2, \\[0.4pc] c &=& \varOmega_{x\dot{x}}^{(0)} \varOmega_{yy}^{(0)} + \varOmega_{xx}^{(0)} \varOmega_{y\dot{y}}^{(0)} + 2n\alpha\varOmega_{xy}^{(0)} - 2n\alpha\varOmega_{yx}^{(0)} - \varOmega_{y\dot{x}}^{(0)} \varOmega_{xy}^{(0)} - \varOmega_{yx}^{(0)} \varOmega_{x\dot{y}}^{(0)}, \\[0.4pc] d &=& \varOmega_{xx}^{(0)} \varOmega_{yy}^{(0)} - \varOmega_{yx}^{(0)} \varOmega_{xy}^{(0)}, \end{array} \end{aligned} $$

(11)

and the obtained eigenvalues determine the stability or instability of the respective equilibrium point. The second order partial derivative of Ω are denoted by subscripts while the superscript “0” means that the corresponding derivatives have been evaluated at the equilibrium points (x ₀, y ₀) and are given by the following analytical formulas:

$$\displaystyle \begin{aligned} & \displaystyle\varOmega _{xx}^{(0)} = n^2 \beta - \frac{(1-\mu)}{r_{10}^3} - \frac{q_2\mu}{r_{20}^3} - \frac{3A_1 (1-\mu)}{2r_{10}^5} + \frac{3(1-\mu )(x_0+\mu)^2}{r_{10}^5}\\ &\qquad + \frac{3q_2\mu (x_0+\mu -1)^2}{r_{20}^5} + \\ & \displaystyle\hspace{2.1cm} \frac{15A_1 (1-\mu)(x_0+\mu)^2}{2r_{10}^7} - \frac{2nW_2 y_0 (x_0+\mu-1)}{r_{20}^4}, \end{aligned} $$

(12)

$$\displaystyle \begin{aligned} & \displaystyle\varOmega_{yy}^{(0)} = n^2 \beta - \frac{(1-\mu)}{r_{10}^3} - \frac{q_2 \mu}{r_{20}^3} + \frac{3(1-\mu)y_0^2}{r_{10}^5} - \frac{3(1-\mu )A_1}{2r_{10}^5} + \frac{3q_2 \mu y_0^2}{r_{20}^5} + \\ & \displaystyle\hspace{2.05cm} \frac{15A_1 (1-\mu )y_0^2}{2r_{10}^7} + \frac{2nW_2 y_0 (x_0+\mu -1)}{r_{20}^4}, \end{aligned} $$

(13)

$$\displaystyle \begin{aligned} & \displaystyle\varOmega_{xy}^{(0)} = \frac{nW_2}{r_{20}^2} - \frac{2nW_2 y_0^2}{r_{20}^4} + \frac{3(1-\mu) (x_0+\mu )y_0}{r_{10}^5} + \frac{3q_2 \mu (x_0+\mu-1) y_0}{r_{20}^5} + \\ & \displaystyle\hspace{2.13cm} \frac{15A_1 (1-\mu)(x_0+\mu)y_0}{2r_{10}^7} , \end{aligned} $$

(14)

$$\displaystyle \begin{aligned} & \displaystyle\varOmega_{yx}^{(0)} = - \frac{nW_2}{r_{20}^2} + \frac{2nW_2 (x_0+\mu -1)^2}{r_{20}^4} + \frac{3(1-\mu)(x_0+\mu)y_0}{r_{10}^5} + \\ & \displaystyle\hspace{2.4cm} \frac{3q_2\mu (x_0+\mu -1) y_0}{r_{20}^5} + \frac{15A_1 (1-\mu)(x_0+\mu)y_0}{2r_{10}^7}, \end{aligned} $$

(15)

$$\displaystyle \begin{aligned} & \displaystyle\varOmega_{x\dot{x}}^{(0)} = -\frac{W_2}{r_{20}^2} (1+\frac{1}{r_{20}^2}) + \frac{W_2 x_0}{r_{20}^4} (2-x_0) + \frac{W_2 \mu}{r_{20}^4} (2(1-x_0)-\mu), \end{aligned} $$

(16)

$$\displaystyle \begin{aligned} \varOmega_{y\dot{y}}^{(0)} = -\frac{W_2}{r_{20}^2} (1+\frac{y_{0}^2}{r_{20}^2}), \qquad \varOmega_{x\dot{y}}^{(0)} = \frac{W_2 y_0}{r_{20}^4} (1-(x_0+\mu)) = \varOmega_{y\dot{x}}^{(0)}, \end{aligned} $$

(17)

with

$$\displaystyle \begin{aligned} r_{10}^2 = (x_0+\mu)^2 + y_0^2, \qquad r_{20}^2 = (x_0+\mu-1)^2 + y_0^2. \end{aligned} $$

(18)

An equilibrium point (x ₀, y ₀) is said to be stable in the sense of Lyapunov if and only if all the four roots of the characteristic polynomial, given by Equation (10), are either negative real numbers or distinct imaginary; asymptotically stable if roots are complex with negative real parts and unstable, otherwise.

5 Numerical Application

In this section, we compute and examine graphically and numerically the positions of the non-collinear equilibrium points for the binary Cen X-4 system using the astrophysical parameters presented in Table 1 for some assumed oblateness and centrifugal force parameters. As pointed out in Section 2, the adjective non-collinear is due to the fact that L ₁, L ₂ and L ₃ do not lie exactly on the x-axis. In order to visualize the evolution of the equilibria we consider region of the oblateness coefficient A ₁ is [0, 0.2] (see [9]). The investigated region for the values of the Coriolis and centrifugal forces are α, β ∈ [1, 1.2] (see, e.g. [28]) while we the value of the dimensional velocity of light is kept fixed to c _d = 988.323 for all numerical calculations.

Table 1 Numerical data for the binary Cen X-4 system

Solving Equations (5), using parameters in Table 1, we present in Figures 2 and 3 the positions of the equilibria for the binary system as the two parameters A ₁ and β vary in the absence and presence of the P–R drag effect, respectively. For better understanding the evolution of the equilibria, in both figures, we use colour codes to indicate the set of pairs (A ₁, β), while green dots signify the positions of the equilibria. So, the intersections of blue-magenta, black-magenta, and red-magenta curves correspond to three specific pairs of values of A ₁ and β; particularly to (0, 1), (0.1, 1.04) and (0.2, 1.1), respectively. It is necessary to note that, although the curves are identical, their behaviours are different as we observe completely different results regarding the movement of the equilibrium points. From Figure 2 it can be observed that for varying oblateness factor and varying centrifugal force we have five equilibrium points (as in the classical restricted problem), three collinear L _1,2,3 and two triangular L _4,5, where equilibria L ₁ and L ₂ both approach the radiating primary m ₂, while L ₃ moves toward the oblate primary m ₁ and point L ₄ (the situation is same at the symmetric point L ₅) moves closer to the point L ₁. For clarity purposes, the top-right, bottom-left, and bottom-right frames are enlargements of the top-left frame of Figure 2 (first frame) close to L _1,2, L ₃, and L ₄₍₅₎ points, respectively.

Fig. 2

Effect of oblateness and centrifugal force parameters on the collinear L _1,2,3 and the triangular L _4,5 points of Cen X-4 system without P–R effect (i.e., q ₂ = 1, W ₂ = 0) for A ₁ = 0, β = 1 (blue, magenta); A ₁ = 0.1, β = 1.04 (black, magenta) and A ₁ = 0.2, β = 1.1 (red, magenta). Top-right, bottom-left and right frames: Zoomed areas close to L _1,2, L ₃ and L ₄ points, respectively. Black dots represent the primaries while green dots represent the positions of the equilibria

Fig. 3

Effect of oblateness and centrifugal force parameters on the non-collinear equilibrium points of Cen X-4 system with P–R effect (i.e., q ₂ = 0.993, W ₂ = 2.72790 × 10⁻⁷) for A ₁ = 0, β = 1 (blue, magenta); A ₁ = 0.1, β = 1.04 (black, magenta) and A ₁ = 0.2, β = 1.1 (red, magenta). Top-right, bottom-left and right frames: Zoomed areas close to L _1,2, L ₃ and L ₄ points, respectively. Black dots represent the primaries while green dots represent the positions of the equilibria

In Table 2, we have evaluated numerically the coordinates of the five equilibrium points for different values of the parameters A ₁ and β for the binary system. One can observe in this table that the variational trend of the equilibria is similar to the scenario presented in Figure 2. However, the situation is different in the presence of P–R drag effect as we observe that for increasing values of the oblateness and centrifugal force parameters, there exist five non-collinear equilibrium points positioned off the Ox-axis. In addition L _1,3,4 have y > 0, while points L _2,5 have y < 0. It can be observed that the equilibria L ₁ and L ₂ approach the radiating primary body m ₂ in opposite directions while L ₃ approaches the oblate primary m ₁, and the two non symmetric equilibria L ₄ and L ₅ approach the displaced L ₁ in opposite directions. Tables 3 and 4 provide the locations of the equilibrium points L _i, i = 1, 2, …, 5 for varying oblateness and centrifugal force parameters in the presence of P–R drag for same fixed values of the parameters. One can see from these tables that the variational trend of the equilibria is similar to the behaviour presented in Figure 3.

Table 2 Positions of the five equilibrium points for varying oblateness and varying centrifugal force in the absence of P–R (i.e. q ₂ = 1,W ₂ = 0) for the binary Cen X-4 system

Table 3 Positions of L _1,2,3 non-collinear equilibrium points for varying oblateness and varying centrifugal force in the presence of P–R for the binary Cen X-4 system

Table 4 Positions of L _4,5 non-collinear equilibrium points for varying oblateness and varying centrifugal force in the presence of P–R for the binary Cen X-4 system (continuation of Table 3)

Next, since we have already found the coordinates (x ₀, y ₀) of the equilibrium points presented in Tables 2, 3, and 4), we can insert them into the characteristic Equation (10) and thus derive their linear stability numerically. In Tables 5 and 6, we show the nature of the stability of the equilibrium points for various values of oblateness, Coriolis and centrifugal forces in the absence and presence of the P–R effect, respectively, for the binary Cen X-4 system. Analysis of Tables 5 and 6 reveals the non existence of pure imaginary roots except in the classical case (i.e. q ₂ = 1, W ₂ = 0, α = β = 1). In all cases for all the assumed values of oblateness and perturbations in Coriolis and centrifugal forces with and without P–R effect, there exists at least a positive real root and/or a complex root with positive real part. Consequently the motion of the infinitesimal body is unbounded and thus unstable around all these equilibrium points.

Table 5 Stability of Cen X-4 system for small assumed values of oblateness and perturbations in Coriolis and centrifugal forces in the absence of P–R drag effect (see Table 2)

Table 6 Stability of Cen X-4 system for small assumed values of oblateness and perturbations in Coriolis and centrifugal forces in the presence of P–R drag effect (see Table 3)

6 Discussion and Conclusion

The location and stability of the equilibrium points in the photogravitational restricted three-body problem that accounts for Poynting–Robertson (P–R) drag force with oblateness of the first primary together with small perturbations in the Coriolis and centrifugal forces were studied. It was found both analytically and numerically that in the presence of P–R drag effect the well-known collinear equilibrium points of the circular restricted three-body problem cease to exist while the respective triangular equilibrium points do not form equilateral triangles.

Using the astrophysical parameters of the Cen X-4 binary system we performed a numerical study for its equilibrium points and showed that in the case where P–R drag was considered five non-collinear equilibrium points exist whereas in the absence of P–R drag force there are also five equilibrium points but three of them are located on the axis joining the primaries and the rest two form in the plane of motion equilateral triangles with the primaries, as in the circular restricted three-body problem. It was also found that the equilibrium points are independent of the effect of small perturbation in the Coriolis force but are affected by the small perturbation in centrifugal force. For the stability of the five equilibria, the four roots of the characteristic polynomial were determined numerically and found that are unstable due to the existence of at least one positive real root or a complex root with positive real part. The instability of the equilibrium points agrees with the results existing in the literature when the primaries are not oblate spheroids and small perturbations in the Coriolis and centrifugal forces are not considered (for details we refer to [4, 21])