Updated rotating mass dipole with oblateness of one primary (I): equilibria in the equator and their stability

Abstract

The rotating mass dipole is possibly used to approximate the potential distribution of nearly axisymmetrical elongated celestial bodies. To increase the accuracy of the approximation, an updated dipole system is proposed by taking the oblateness of one primary into account. The system is composed with a point mass and a spheroid with oblateness connected with a massless rod. Dynamic equations of the updated dipole system in body-fixed frame are derived in canonical system units. The potential distribution is determined with three parameters, including the mass ratio, the force ratio and the oblateness of the primary. Equilibrium points along with zero-velocity curves are given in the equatorial plane. The influence of the above three parameters on the distribution of equilibria are illustrated via numerical simulations. The stability of the system equilibria is discussed under linearized dynamic equations around each equilibrium point.

1 Introduction

The Philae probe was successfully landed on the nucleus of Comet 67P/Churyumov–Gerasimenko as the first time in the world on November 12, 2014. The Rosetta mission launched by ESA on 2004 aimed to explore the physical properties, materials and environments of the comet which undoubtedly stimulate the development of deep space explorations. For these missions around minor celestial bodies, the estimation and construction of the central body’s gravitational potential are of great importance for the success of missions (Cui and Qiao 2014). The accurate gravitational model is usually obtained by orbiting the central body with a spacecraft for a period of time, like the Rosetta or Hayabusa launched by JAXA in 2003. The orbiting data is used to amend the initial model based on the ground-based observation and laboratory analysis. The widely adopted method to generate the initial model is the polyhedral method proposed by Werner and Scheeres (Werner 1994; Werner and Scheeres 1997). The accuracy of the approximation highly depends on the number of faces and vertices by discretizing the geometrical surface of the concerned body. Although the method is suitable for specific missions, it may not be used to obtain some common characteristics of minor celestial bodies due to their different shape and compositions.

Aiming to understand common properties around irregular shaped bodies, the dynamics around some simple bodies have been studies for the past decades, including but not limited to disks (Eckhardt and Pestaña 2002), homogeneous cube (Liu et al. 2011), dumbbell-shaped bodies (Li et al. 2013), ellipsoids (Guibout and Scheeres 2003) and material segments (Bartczak and Breiter 2003; Breiter et al. 2005; Bartczak et al. 2006). The simplest model should be the rotating mass dipole with an explicit expression of the potential function. This dipole system is a generalization of the circular restricted three body problem (CRTBP) (Szebehely 1967; Battin 1999) since there is a massless rod connecting the two point masses. The rotating dipole was proposed by Chermnykh (1987) to approximate the rotating dumbbell. Following researches were conducted by Kokoriev and Kirpichnikov (1988) and Kirpichnikov and Kokoriev (1988) by considering a rotating system consisted with a spheroid and a dumbbell. Goździewski and Maciejewski (1998, 1999) and Goździewski (2003) made an extensive study on the rotating system with a point mass and a rigid body.

In 1994, Prieto-Llanos and Gómez-Tierno (1994) revisited the dipole system focusing on the stability of equilibrium points and orbital control around collinear equilibria. Based on their work, Hirabayashi et al. (2010) found there is linearly stable region at the collinear equilibrium point $E_{1}$ (locating between the two primaries) with small values of the force ratio. Recently, Zeng et al. (2015) proposed a method to approximate the external potential distribution of natural elongated bodies by using the rotating mass dipole. There are only two independent parameters of the dipole system, i.e., the mass ratio between the two primaries and the force ratio between the gravitational force and the centrifugal force. Consequently, some inherent errors between the relatively accurate model and the dipole can not be eliminated by increasing the accuracy of the two parameters.

An updated rotating mass dipole (abbreviated as ‘URMDP’ hereafter throughout this paper) is introduced in this paper to improve the accuracy of the classical rotating mass dipole (CRMDP), such as the distribution of equilibrium points. The URMDP is composed with a point mass and a spheroid with oblateness. The spheroid can be oblate or prolate which guarantees the stable spinning state of the system. A massless rod connects the point mass and the spheroid, which can provide cohesive or compressive strengths to keep a constant distance between the two primaries. The equatorial plane of the spheroid is consistent with the plane of the rotating system.

In fact, the problem with one oblate primary (or even both oblate spheroids) for the CRTBP has been studied since 1970s, including Vidyakin (1974), and Sharma and Subba Rao (1975). Sharma and Subba Rao (1976, 1978), Sharma (1981) and Subba Rao and Sharma (1997) made a series of contributions on this problem by considering the oblateness of the more massive body whose equatorial plane coincides with the plane of the rotating primaries. Such theoretical discussions (Arredondo et al. 2012) seem of no practical applications before the publication of Oberti and Vienne (2003). In their work, the consideration of Saturn’s oblateness on the motion of its moons, including Helene, Telesto and Calypso, has shown great significance of the theory which is also useful for some certain satellites. Recent investigations in terms of the oblateness have been extended to realistic applications, such as Saturn system (Beevi and Sharma 2012) and binary asteroid system (Taylor and Margot 2014).

In this study, the consideration of the oblateness of one primary gives another freedom of the system, i.e., the gravitational potential of the URMDP is determined by three independent parameters, including the mass ratio, the force ratio and the oblateness. Section 2 derives the dynamic equations of the URMDP along with its Jacobi integral. The distribution of equilibrium points are analyzed in Sect. 3 where numerical examples are presented to clearly show the location of each equilibrium point. Some new equilibrium points are obtained due to the oblateness of the primary based on numerical simulations. Section 4 discusses the influence of the three parameters on the equilibrium points in a parametric way. Finally, the stability of collinear and non-collinear equilibria will be investigated via numerical simulations in Sect. 5.

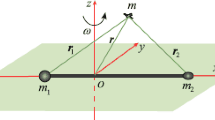
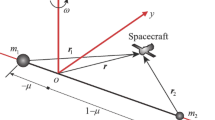
2 Dynamical model of the updated rotating mass dipole

The rotating mass dipole is composed of two primaries $m_{1}$ and $m_{2}$ with total system mass of $M = m_{1} + m_{2}$. The characteristic distance between these two primaries is fixed in a constant value of $d$. The dynamics for a massless particle is usually described in a synodic reference frame $\mathit{oxyz}$ with origin at the barycenter of the system. The plane $\mathit{oxy}$ contains the two primaries whereas axis $\mathit{ox}$ is collinear with the two primaries pointing from $m_{1}$ to $m_{2}$ (naturally assuming $m_{1} \geq m_{2}$). The axis $oz$ is aligned with the angular velocity of the rotating system $\boldsymbol{\omega} = \omega \boldsymbol{z}$, and axis $\mathit{oy}$ is determined with the right-handed frame. The equations of motion for the massless particle in the synodic frame with uniformly rotating can be written as

$$ \ddot{\boldsymbol{r}} + 2\boldsymbol{\omega} \times \dot{\boldsymbol{r}} + \boldsymbol{\omega} \times ( \boldsymbol{\omega} \times \boldsymbol{r} ) = - \nabla U $$

(1)

where $\boldsymbol{r} = [x, y, z]^{\mathrm{T}}$ is the position vector from the barycenter of the system to the particle, and $\nabla U$ is the gradient of the gravitational potential of the central body.

To enhance the computational efficiency, dimensionless units are usually applied to the above system. The mass unit is set to be $M$, the length unit is taken as the characteristic distance $d$, and the time unit is $\omega^{-1}$ resulting in that the periodic time of the spinning primaries is $2 \pi$. Define the mass ratio $\mu = m_{2} / M$ so that $m_{1}$ and $m_{2}$ remain fixed positions at $[- \mu, 0, 0]^{\mathrm{T}}$ and $[1 - \mu, 0, 0]^{\mathrm{T}}$, respectively. The admissible region for $\mu$ in this study is $(0, 0.5]$ by neglecting the trivial case of $\mu = 0$ (recalling $m_{1} \geq m_{2}$). The position vector of the particle with respect to the two primaries can be expressed as

$$ \textstyle\begin{cases} \boldsymbol{r}_{1} = [x + \mu, \ y, \ z ]^{\mathrm{T}} \\ \boldsymbol{r}_{2} = [ x + \mu - 1,\ y, \ z ]^{\mathrm{T}} \end{cases} $$

(2)

Since the centrifugal term in Eq. (1) is conservative, a reduced dynamical equation in dimensionless units can be introduced with

$$ \ddot{\boldsymbol{r}} + 2\boldsymbol{\omega} \times \dot{\boldsymbol{r}} = - \nabla V $$

(3)

where the new co-rotating potential is

$$ V = U - \frac{1}{2}\Vert \boldsymbol{\omega} \times \boldsymbol{r} \Vert ^{2} $$

(4)

For the case of both oblate primaries, the effective potential can be explicitly given as

$$\begin{aligned} V_{12} &= - \frac{\omega^{2}}{2} \bigl( x^{2} + y^{2} \bigr) - \kappa \omega^{2} \biggl\{ \frac{1 - \mu}{r_{1}} \biggl[ 1 + \frac{A_{1}}{2r_{1}^{2}} \biggl( 1 - \frac{3z^{2}}{r_{1}^{2}} \biggr) \biggr] \\ &\quad {}+ \frac{\mu}{r_{2}} \biggl[ 1 + \frac{A_{2}}{2r_{2}^{2}} \biggl( 1 - \frac{3z^{2}}{r_{2}^{2}} \biggr) \biggr] \biggr\} \end{aligned}$$

(5)

where the parameters $r_{1}$ and $r_{2}$ are the respective magnitude of position vectors in Eq. (2). Here, $A_{1}$ and $A_{2}$ are the oblateness coefficient of $m_{1}$ and $m_{2}$, respectively. The perturbed mean motion of the rotating mass dipole in Eq. (5) is given by

$$ \omega = \sqrt{1 + \frac{3}{2} ( A_{1} + A_{2} )} $$

(6)

The definition of the oblateness coefficient $A_{i}$ ($i = 1, 2$) based on Sharma and Subba Rao (1976) is

$$ A_{i} = \frac{ ( \rho_{i}^{e} )^{2} - ( \rho_{i}^{p} )^{2}}{5d^{2}}, \quad i = 1,2 $$

(7)

where $\rho^{e}$ and $\rho^{p}$ are the dimensionless equatorial and polar radii of the oblate primary. For major planets in the solar system, all of them are oblate spheroids rotating about its minor axis in the relatively stable state of lowest energy, even their large moons, such as the Moon and Tethys. Consequently, the value of $A_{i}$ ($i = 1, 2$) should be positive for both primaries. However, for the rotating mass dipole connected with the massless rod, the fixed primaries without spinning can be prolate spheroids corresponding to a stable system. It indicates that the value of $A_{i}$ ($i = 1, 2$) for the dipole system can be less than zero. More detailed discussions about the value of $A_{i}$ will be given in the next section.

The definition of the dimensionless parameter $\kappa$ in Eq. (5) is

$$ \kappa = \frac{GM}{\omega^{2}d^{3}} $$

(8)

representing the ratio between the gravitational force and the centrifugal force, referred to as ‘the force ratio’. The parameter $G$ is the gravitational constant ($6.674 \times 10^{-11}\ \mbox{m}^{3}\, \mbox{kg}^{-1} \,\mbox{s}^{-2}$). When $\kappa$ is exactly equal to one, only the gravitational attraction is between the two primaries (Prieto-Llanos and Gómez-Tierno 1994). If the value of $\kappa$ is greater than unity, there should be compressive stress in the massless rod to keep the constant distance between the primaries. On the contrary, the rod would provide tensile stress to overcome the extra centrifugal force tending to separate the two primaries.

In this paper, the oblateness of the second primary is considered where the first primary is treated as a point mass. In such a case the value of $A_{1}$ is zero and $A_{2} \neq 0$, the effective potential of Eq. (5) can be reduced to

$$\begin{aligned} W& = - \frac{\omega^{2}}{2} \bigl( x^{2} + y^{2} \bigr) - \kappa \omega^{2} \biggl\{ \frac{1 - \mu}{r_{1}} \\ &\quad {}+ \frac{\mu}{r_{2}} \biggl[ 1 + \frac{A_{2}}{2r_{2}^{2}} \biggl( 1 - \frac{3z^{2}}{r_{2}^{2}} \biggr) \biggr] \biggr\} \end{aligned}$$

(9)

and through the following transformation $[ \mu,\ r_{1},\ r_{2},\ A_{2}]^{\mathrm{T}} \rightarrow [1 - \mu,\ r_{2},\ r_{1},\ A_{1}]^{\mathrm{T}}$, the above equation can give the effective potential with oblate primary $m_{1}$. Therefore, the above equation is actually a representation of the case where the oblateness of only one primary is considered for the rotating dipole system. Particularly, if both primaries are point masses, the model will be degenerated into the simple rotating mass dipole (Prieto-Llanos and Gómez-Tierno 1994). Furthermore, if the force ratio $\kappa$ is unity, the model corresponds to the classical CRTBP.

Substituting Eq. (9) into Eq. (3), one can obtain the componential form of the dynamical equations in dimensionless units

$$\begin{aligned} & \begin{bmatrix} \ddot{x} & \ddot{y} & \ddot{z} \end{bmatrix}^{\mathrm{T}} + \begin{bmatrix} - 2\omega \dot{y} & 2\omega \dot{x} & 0 \end{bmatrix} ^{\mathrm{T}} \\ &\quad = - \begin{bmatrix} \nabla W_{x} & \nabla W_{y} & \nabla W_{z} \end{bmatrix}^{\mathrm{T}} \end{aligned}$$

(10)

where the gradients of the effective potential are listed below:

$$\begin{aligned} & \begin{aligned}[b] \nabla W_{x}& = - \omega^{2} \biggl\{ x - \kappa \biggl[ \frac{ ( 1 - \mu ) ( x + \mu )}{r_{1}^{3}} \\ &\quad {}+ \frac{\mu ( x + \mu - 1 )}{r_{2}^{3}} \biggl( 1 + \frac{3A_{2}}{2r_{2}^{2}} - \frac{15A_{2}z^{2}}{2r_{2}^{4}} \biggr) \biggr] \biggr\} \end{aligned} \end{aligned}$$

(11)

$$\begin{aligned} & \begin{aligned}[b] \nabla W_{y} &= - \omega^{2}y \biggl\{ 1 - \kappa \biggl[ \frac{ ( 1 - \mu )}{r_{1}^{3}}\\ &\quad {} + \frac{\mu}{r_{2}^{3}} \biggl( 1 + \frac{3A_{2}}{2r_{2}^{2}} - \frac{15A_{2}z^{2}}{2r_{2}^{4}} \biggr) \biggr] \biggr\} \end{aligned} \end{aligned}$$

(12)

$$\begin{aligned} &\nabla W_{z} = \kappa \omega^{2}z \biggl[ \frac{ ( 1 - \mu )}{r_{1}^{3}} + \frac{\mu}{r_{2}^{3}} \biggl( 1 + \frac{9A_{2}}{2r_{2}^{2}} - \frac{15A_{2}z^{2}}{2r_{2}^{4}} \biggr) \biggr] \end{aligned}$$

(13)

where the dimensionless term of $\omega^{2}$ is given by $1 + 3A_{2}/2$ as $A_{1}$ is assumed to be zero. Equation (10) admits the well-known Jacobi integral

$$ C = \frac{1}{2}\dot{\boldsymbol{r}}\dot{\boldsymbol{r}} + W $$

(14)

which defines the admissible region for possible motions. In other words, for a given set of initial conditions, the orbit of the infinitesimal particle can not exceed the boundary determined by the zero-velocity surface of $C = V_{2}$.

3 Equilibrium points of the updated dipole system

For the classical CRTBP there are five equilibrium points in the equatorial plane, i.e., three points (Euler libration points) collinear with the two primaries and two triangular points (Lagrange points) equidistant from both primaries. In this section, the equilibrium points in the equatorial plane of the dipole system are first investigated in terms of their locations. The influence of oblateness of the primary on the equilibrium points is illustrated via numerical examples.

3.1 Locations of the equilibrium points

The equilibrium points in the equatorial plane must satisfy the condition of $z = 0$. Equation (10) can be degenerated into two dimensional equations as

$$\begin{aligned} & \begin{aligned}[b] \ddot{x} - 2\omega \dot{y} & = \omega^{2}x - \kappa \omega^{2} \biggl[ \frac{ ( 1 - \mu ) ( x + \mu )}{r_{1}^{3}} \\ &\quad {}+ \frac{\mu ( x + \mu - 1 )}{r_{2}^{3}} \biggl( 1 + \frac{3A_{2}}{2r_{2}^{2}} \biggr) \biggr] \end{aligned} \end{aligned}$$

(15)

$$\begin{aligned} &\ddot{y} + 2\omega \dot{x} = \omega^{2}y \biggl\{ 1 - \kappa \biggl[ \frac{ ( 1 - \mu )}{r_{1}^{3}} + \frac{\mu}{r_{2}^{3}} \biggl( 1 + \frac{3A_{2}}{2r_{2}^{2}} \biggr) \biggr] \biggr\} \end{aligned}$$

(16)

where the equilibria can be obtained with $\dot{x} = \dot{y} = \ddot{x} = \ddot{y} = 0$ by setting the right terms of Eqs. (15) and (16) to be zero. Consequently, the equilibrium points in the equatorial plane are determined by the following equations

$$\begin{aligned} &x - \kappa \biggl[ \frac{ ( 1 - \mu ) ( x + \mu )}{r_{1}^{3}} + \frac{\mu ( x + \mu - 1 )}{r_{2}^{3}} \biggl( 1 + \frac{3A_{2}}{2r_{2}^{2}} \biggr) \biggr] = 0 \end{aligned}$$

(17)

$$\begin{aligned} &y \biggl\{ 1 - \kappa \biggl[ \frac{ ( 1 - \mu )}{r_{1}^{3}} + \frac{\mu}{r_{2}^{3}} \biggl( 1 + \frac{3A_{2}}{2r_{2}^{2}} \biggr) \biggr] \biggr\} = 0 \end{aligned}$$

(18)

When $y = 0$ corresponding to the vanishment of Eq. (18), Eq. (17) gives the locations of the collinear points with

$$ x - \kappa \biggl[ \frac{ ( 1 - \mu )s_{1}}{ ( x + \mu )^{2}} + \frac{\mu s_{2}}{ ( x + \mu - 1 )^{2}} + \frac{3\mu A_{2}s_{2}}{2 ( x + \mu - 1 )^{4}} \biggr] = 0 $$

(19)

where the sign functions are

$$ s_{1} = \operatorname{sign} ( x + \mu ), \qquad s_{2} = \operatorname{sign} ( x + \mu - 1 ) $$

(20)

After some derivations, Eq. (19) can be rewritten as

$$ \sum_{i = 0}^{7} c_{i}x^{i} = 0 $$

(21)

whose coefficients are

$$ \textstyle\begin{cases} c_{7} = 1 \\ c_{6} = 6\mu - 4 \\ c_{5} = 15\mu^{2} - 20\mu + 6 \\ c_{4} = 20\mu^{3} - 40\mu^{2} + 24\mu - 4 - \sigma_{4} \\ c_{3} = 15\mu^{4} - 40\mu^{3} + 36\mu^{2} - 12\mu + 1 - 4\mu \sigma_{4} - \sigma_{3} \\ c_{2} = 6\mu^{5} - 20\mu^{4} + 24\mu^{3} - 12\mu^{2} + 2\mu \\ \qquad {}- 6\mu^{2}\sigma_{4} - 3\mu \sigma_{3} - \sigma_{2} \\ c_{1} = \mu^{6} - 4\mu^{5} + 6\mu^{4} - 4\mu^{3} + \mu^{2} - 4\mu^{3}\sigma_{4} - 3\mu^{2}\sigma_{3} \\ \qquad {}- 2\mu \sigma_{2} - \sigma_{1} \\ c_{0} = - \sum_{j = 0}^{4} \mu^{j}\sigma_{j} \end{cases} $$

(22)

where the auxiliary parameters $\sigma_{j}$ ($j = 0, 1, \ldots, 4$) in the above equation are given as

$$ \textstyle\begin{cases} \sigma_{4} = \kappa ( 1 - \mu )s_{1} + \kappa \mu s_{2} \\ \sigma_{3} = - 4\kappa ( 1 - \mu )s_{1} - 2\kappa \mu s_{2} \\ \sigma_{2} = 6\kappa ( 1 - \mu )s_{1} + \kappa \mu s_{2} + 3\kappa \mu A_{2}s_{2} / 2 \\ \sigma_{1} = - 4\kappa ( 1 - \mu )s_{1} \\ \sigma_{0} = \kappa ( 1 - \mu )s_{1} \end{cases} $$

(23)

According to the definition specified in Eq. (7), the cases of $A_{2} > 0$, $A_{2} = 0$ and $A_{2} < 0$ correspond to oblate, spherical and prolate bodies, respectively. Since physical planets (such as the Earth, Mars or Jupiter) are oblate bodies with the stable spinning state, the value of $A_{2}$ in previous analyses is never less than zero. However, such a constraint can be also removed in the current study. Because even the second primary is a prolate body, the rotating dipole system can also keep a stable spinning with the maximum momentum of inertial along axis $\mathit{oz}$. Moreover, the magnitude of $A_{2}$ is not necessary to be small in the level of $10^{-8}{\sim} 10^{-3}$ as in the physical planet systems (Arredondo et al. 2012), such as the systems of Earth-Moon, Saturn-Phoebe or Jupiter-Ganymede (Sharma and Subba Rao 1976) where the influence of $A_{1}$ was discussed on the restricted three body problem.

When $y \neq$ 0, after some derivations by combining Eq. (17) and Eq. (18), one can get (Idrisi 2014)

$$ r_{1}^{3} = \kappa $$

(24)

and

$$ 2r_{2}^{5} - 2\kappa r_{2}^{2} - 3 \kappa A_{2} = 0 $$

(25)

where the value of $r_{2}$ can be obtained by solving the above quintic polynomial. Equation (24) indicates that the non-collinear equilibrium points lie on the cycle whose center is $m_{1}$ and its radius is $\sqrt[3]{\kappa}$. It also illuminates that the distances of the triangular equilibria with respect to the second primary are only relevant to the parameters $[ \kappa,\ A_{2}]$ and independent of the mass ratio. According to the Descartes’ rule of signs, the above equation has only one positive solution for $A_{2} > 0$ since $\kappa$ is always positive. As for $A_{2}$ is negative, there are two positive roots for the above equation. If these two roots are not multiple roots, it indicates that additional equilibrium points exist for this updated rotating dipole system. After obtaining $r_{2}$, combining Eq. (2) with the values of $r_{1}$ and $r_{2}$, the $x$-coordinate of the triangular equilibrium point can be given by

$$ x_{\mathrm{T}} = \frac{r_{1}^{2} - r_{2}^{2}}{2} + \frac{1}{2} - \mu $$

(26)

where the subscript ‘T’ denotes the triangular equilibrium points. Then the corresponding $y$-coordinate of the equilibrium point can be easily determined with

$$ y_{\mathrm{T}} = \pm \sqrt{r_{2}^{2} - ( x_{\mathrm{T}} + \mu - 1 )^{2}} $$

(27)

For the CRTBP without oblateness, Eq. (26) and Eq. (27) will be deduced to $[1/2 - \mu,\ \pm \sqrt{}3/2]$ which coincides with previous investigations (Prieto-Llanos and Gómez-Tierno 1994; Szebehely 1967). Additionally, if $A_{2} = 0$ for the classical rotating mass dipole, Eq. (25) will be degenerated into $r_{2}^{3} = \kappa$ which indicates that Eq. (26) is always $1/2 - \mu$. With the possibility of two roots of Eq. (25), there will be two pairs of equilibrium points symmetrical with respect to the axis $\mathit{ox}$. Although these equilibrium points may be not equidistant with the two primaries, they are also termed as ‘triangular equilibrium points’ throughout this study.

3.2 Numerical examples

Numerical examples are presented with respect to the simplest case where the force ratio $\kappa$ is set to be unity and the mass ratio is 0.5. Both positive and negative values of $A_{2}$ are considered for the updated dipole system. The limiting case for the oblate spheroid is a circular disk locating in the equatorial plane. The limiting case for the prolate spheroid should be a massive straight segment perpendicular to the massless rod in the plane $\mathit{oxz}$. The barycenter of the massive segment must be at the axis $\mathit{ox}$ and also coincides with its geometric midpoint. The radius of the circular disk and the length of the massive segment determine the values of $A_{2}$ for the two different cases. For instance, if the radius of the disk is $0.5d$ with equal mass to the first primary, the value of $A_{2}$ is 0.05 based on Eq. (7). Similarly, if the length of the perpendicular massive segment is $d$, the value of $A_{2}$ is −0.05. For convenience, the physical dimension of the oblate/prolate primary is not discussed hereafter.

The first scenario is for the oblate primary with $A_{2} = 0.05$. The equilibrium points along with some zero-velocity curves in the equatorial plane are shown in Fig. 1. The sketch of the updated dipole system is also illustrated in the figure whose physical dimensions are neglected. Five equilibrium points $E_{i}$ ($i = 1, 2, \ldots, 5$), i.e., two triangular points ($i = 4, 5$) and three collinear points ($i = 1, 2, 3$) are obtained at similar locations with respect to the traditional five Lagrange points. The coordinates of these equilibria will be compared to the CRMDP in later discussions.

Fig. 1

Zero-velocity curves and equilibrium points of the updated rotating mass dipole with $A_{2} = 0.05$

The second case is for the prolate primary with $A_{2} = -0.05$. Figure 2 illustrates the distributions of the equilibrium points of the system and zero-velocity curves. It is found that there are two pair of new equilibrium points besides the classical equilibria $E_{1} {\sim} E_{5}$. All these four new equilibrium points are near the prolate spheroid. The two collinear equilibria, i.e., $E_{8}$ and $E_{9}$ are on either side of the prolate primary between $E_{1}$ and $E_{2}$. As for the other two points $E_{6}$ and $E_{7}$, they are on the circle with a radius of unity and centered at the first primary. These two equilibria are also referred to as ‘triangular equilibrium points’. The locations of the new equilibria $E_{i}$ ($i = 6, 7, 8, 9$) in this particular case are listed in Table 1 in dimensionless length unit.

Fig. 2

Zero-velocity curves and equilibrium points of the updated rotating mass dipole with $A_{2} = -0.05$

Table 1 Locations of new equilibrium points ${E_{6}} {\sim} {E_{9}}$ of the updated rotating mass dipole due to the prolate primary $m_{2}$ with $A_{2} = -0.05$

To investigate the influence of oblateness of the second primary on the locations of the classical five equilibrium points, the coordinates of the equilibria are summarized in Table 2 for three cases, including $A_{2} = 0.05,\ 0.0,\ -0.05$. Compared to the dipole system without oblateness, all equilibria get shifted away from $m_{2}$ for the case of $A_{2} = 0.05$. On the contrary, all equilibria move towards $m_{2}$ for $A_{2} = -0.05$ corresponding to the prolate primary. As for the $x$-coordinate of each equilibrium point, the change is in the level of $10^{-2}$ except $E_{3}$ whose change is approximately $10^{-3}$. The change of the $y$-coordinate for $E_{4}$ and $E_{5}$ is also in the level of $10^{-2}$. Therefore, the influence of the oblate primary is greater on $E_{1}$, $E_{2}$, $E_{4}$ and $E_{5}$ than on $E_{3}$. Such an observation is consistent with the results given by Sharma and Subba Rao (1976) with respect to the CRTBP with oblateness. In fact, it should be easy to understand as $E_{3}$ is the farthest equilibrium point away from $m_{2}$.

Table 2 Locations of the five classical equilibrium points ${E_{1}}{\sim}{E_{5}}$ of the updated rotating mass dipole with respect to three different cases of $A_{2} = 0.05,\ 0.0,\ -0.05$

From the above discussions, it can be seen that the oblateness of one primary has changed the topological structure of the potential distribution of the rotating dipole system. On the one hand, there are new equilibrium points for both oblate and prolate cases. On the other hand, the locations of the classical five equilibrium points (corresponding to the Lagrange points) are also changed based on Table 2.

4 Parametric study

Besides the above qualitative study about the URMDP, quantitative investigations will be made in a parametric way to illustrate the relationship between the equilibria distribution and the system parameters. There are total three parameters $\kappa$, $\mu$ and $A_{2}$ determining the potential distribution of the URMDP. In the following studies, two of them are fixed and the other is a free parameter. The admissible regions for the first two parameters are specified as: $\kappa \in (0, +\infty)$ and $\mu \in (0, 0.5]$. Note that the value of $\kappa$ for a realistic rotating dipole system can not be too large since it represents the force ratio between the gravitational and centrifugal terms. The investigated region of $A_{2}$ is set to be $[-0.05, 0.05]$ which should be enough to analyze its influence on the dipole system.

4.1 Influence of $[\kappa,\ \mu]$ on equilibrium points

The influence of the parameters $[ \kappa,\ \mu ]$ on the classical five equilibrium points $E_{1}$ to $E_{5}$ has been well investigated by Prieto-Llanos and Gómez-Tierno (1994) as well as the linearized stabilities of these equilibria. Some conclusive remarks in terms of the classical rotating mass dipole (CRMDP) are summarized as a reference to the current study. The CRMDP involves only two parameters $[ \kappa,\ \mu ]$ which fully determine the potential distribution of the system. With the increasing of $\kappa$ with a fixed $\mu$, the equilibria $E_{i}$ ($i = 2, \ldots, 5$) shift away from the dipole and vice versa where $E_{1}$ is kept at a fixed position. For the case of decreasing $\mu$ with a fixed $\kappa$, the variational trend of the equilibria is more complicated than the former scenario. All equilibria $E_{i}$ ($i = 1, 2, \ldots, 5$) move right along the direction of axis $\mathit{ox}$. At the same time, $E_{1}$ and $E_{2}$ move towards the smaller primary while $E_{3}$ shifts away from $m_{2}$. The two triangular equilibrium points $E_{4}$ and $E_{5}$ remain at a fixed position relative to the dipole system.

For the URMDP with a fixed value of $A_{2}$, the variation trend of the locations of equilibria should be similar to that of the CRMDP. Some particular cases, such as the vanishment of the triangular equilibria relevant to the parameters of the URMDP, are the focus of this section. Moreover, the influence of the parameters $[ \kappa,\ \mu,\ A_{2}]$ on the new equilibria $E_{i}$ ($i = 6, 7, 8, 9$) will be studies to better understand the properties of the URMDP. Prieto-Llanos and Gómez-Tierno (1994) investigated the properties of the CRMDP for $\kappa \geq 1$ in detail. Hirabayashi et al. (2010) extended their work by focusing on the case of $\kappa < 1$. They have pointed out that the triangular equilibria will vanish when $\kappa \leq 0.125$ for the CRMDP. Due to the oblateness of the second primary, the critical value of $\kappa$ corresponding to the equilibrium bifurcation of $E_{4}$ and $E_{5}$ is first investigated.

From the geometrical point of view, the equilibria $E_{4}$ and $E_{5}$ are the intersection points of two specific circles. The center of the first circle is at the first primary with a radius of $\rho_{1}$ satisfying Eq. (24), while the center of the second circle is at the barycenter of the second primary with a radius of $\rho_{2 1}$ satisfying Eq. (25). When the sum of $\rho_{1}$ and $\rho_{2 1}$ is not greater than the characteristic distance $d$, the equilibria $E_{4}$ and $E_{5}$ will vanish. Therefore, the critical value of $\kappa$ corresponds to $\rho_{2 1} = d - \rho_{1}$. Combining Eq. (24) and Eq. (25), one can get the polynomial equation involving only $\kappa$ and $A_{2}$ as

$$ \bigl( 1 - \sqrt[3]{\kappa}\, \bigr)^{5} - \kappa \bigl( 1 - \sqrt[3]{ \kappa}\, \bigr)^{2} - \frac{3}{2}\kappa A_{2} = 0 $$

(28)

When $A_{2}$ is given, the critical value of $\kappa$ can be determined by solving the above equation. For example, when $A_{2}$ is zero, the value of $\kappa$ is 0.125 as is known for the CRDMP. When $A_{2}$ is 0.05, the value of $\kappa$ is approximately 0.1104 whereas $\kappa$ is approximately 0.1536 for $A_{2} = -0.05$. Based on numerical simulations, the critical value of $\kappa$ (resulting in the vanishment of $E_{4}$ and $E_{5}$) decreases with positive $A_{2}$ and increases with negative $A_{2}$ compared to the CRMDP.

For the case with a negative $A_{2}$ and a fixed $\kappa$, $E_{8}$ and $E_{9}$ move towards the prolate primary while $E_{6}$ and $E_{7}$ are fixed relative to the prolate primary by decreasing $\mu$. To investigate the influence of $\kappa$ on the equilibria variation for the negative $A_{2}$, both values of $A_{2}$ and $\mu$ are fixed. Figure 3 gives an example with $A_{2} = -0.05$ and $\mu = 0.5$ by varying $\kappa$ in the region of $[0.36,\ 2.16]$ with a step of 0.1. A schematic map of the rotating mass dipole is also shown by neglecting the physical size of the prolate primary. By increasing $\kappa$ the equilibria $E_{8}$ and $E_{9}$ move to approach $m_{2}$ with relatively small amplitude change.

Fig. 3

Equilibria variation of the updated rotating mass dipole by varying $\kappa \in [0.36,\ 2.16]$ with $A_{2} = -0.05$ and $\mu = 0.5$

Significant changes in terms of the bifurcation of $E_{6}$ and $E_{7}$ can be seen from Fig. 3, including generation, variation and vanishment. The critical value $\kappa_{\mathrm{g}}$ is approximately 0.37 corresponding to the equilibria generation. With the increase of $\kappa$, $E_{6}$ and $E_{7}$ move along the circle centered at the prolate primary with a radius of $\rho_{2 2}$. When $\rho_{1}$ satisfies $\rho_{1} = d + \rho_{22}$, $E_{6}$ and $E_{7}$ will be degenerated into a single point corresponding to $\kappa_{\mathrm{v}} = 2.07$. If $\kappa$ still increases, this equilibrium point vanishes as there is no intersection point between the two circles with respect radius of $\rho_{1}$ and $\rho_{22}$. Half circles centered at $m_{1}$ with radius of $\rho_{1}$ are plotted to show the relationships between the two pair of triangular equilibria.

The variational trend of the two pairs of triangular equilibria can be intuitively explained by Fig. 4. Since the existence of triangular equilibria only depends on the parameters $[ \kappa,\ A_{2}]$ involving Eqs. (24) and (25). Assuming $Q$ to be functional value of Eq. (25), Fig. 4 illustrates the variational trend of $Q$ as a function of $\kappa$ with $A_{2} = -0.05$. For a fixed $A_{2}$, the radius of $\rho_{2 2}$ is a fixed value with variation of $\kappa$. That is why the two equilibria $E_{6}$ and $E_{7}$ move on a circle. Another root of Eq. (25) $\rho_{2 1}$ increases along the increase of $\kappa$ corresponding to the movement of $E_{4}$ and $E_{5}$ given in Fig. 3.

Fig. 4

Variation trend of $Q$ and the two roots of Eq. (25) as a function of $\kappa$ with $A_{2} = -0.05$ and $\mu = 0.5$

4.2 Variation of equilibria $E_{1} {\sim} E_{5}$ by varying $A_{2}$

Without loss of generality, the parameters $[ \kappa,\ \mu ]$ of the updated rotating dipole are still assumed to be $[1,\ 0.5]$ which admit the existence of system equilibria. The investigated region for the oblateness coefficient $A_{2}$ is $[-0.05,\ 0.05]$. The variation of coordinates of each equilibrium point is studied by varying the value of $A_{2}$ in its admissible region. The definition of the coordinate variation of each equilibrium point is

$$ \Delta q ( E_{i} ) = q ( E_{i} ) - q_{0} ( E_{i} ), \quad \textstyle\begin{cases} q = x,y \\ i = 1,2,\ldots,5 \end{cases} $$

(29)

Figure 5 summarizes the coordinate variations of $E_{1}$ to $E_{4}$ since $E_{5}$ is symmetrical with $E_{4}$ with respect to the axis $\mathit{ox}$. The intersection point is $[0,\ 0]$ corresponding to the case of $A_{2} = 0$. For each of the five coordinates, the coordinate variation depends nearly linearly on the value of $A_{2}$ in the domain of $[-0.05,\ 0.05]$. But in fact, the influence of the negative $A_{2}$ is slightly greater than its positive case for these five classical equilibria. The coordinates of each equilibrium point at the boundaries with $A_{2} = \pm 0.05$ are the same as given in Table 2. It is intuitively noted that the variation of the collinear equilibria $\Delta x(E_{1})$ and $\Delta x(E_{2})$ is the biggest whereas $\Delta x(E_{3})$ is nearly zero. Particularly, the value of $|\Delta x(E_{4})|$ is slightly greater than its corresponding $|\Delta y(E_{4})|$ for the same value of $A_{2}$.

Fig. 5

Influence of $A_{2} \in [-0.05,\ 0.05]$ on the equilibria $E_{1}$ to $E_{5}$ of the URMDP compared to the CRMDP with $\kappa = 1$ and $\mu = 0.5$

4.3 Dependence of $E_{6} {\sim} E_{9}$ on negative $A_{2}$

Figure 6 shows the equilibria variation along with the variation of $A_{2}$ from 0 to −0.05 for the case of prolate primary. The values of $[ \kappa,\ \mu ]$ are taken to be $[1,\ 0.5]$, respectively. The variational step of $A_{2}$ is −0.005 which is enough to illustrate the variational trend of the equilibria. $E_{3}$ seems to be a fixed point due to the artifact of the scale of the figure. Thus, zoomed-in views about $E_{3}$ and $E_{4}$ are given with higher resolution. The overall trend for $E_{1}$ to $E_{5}$ is to approach the prolate primary by decreasing $A_{2}$. Conversely, the equilibria $E_{6}$ to $E_{9}$ shift away from the prolate primary. Moreover, in terms of the magnitude of equilibriums’ position change due to the variation of $A_{2}$, the four equilibria $E_{6}$ to $E_{9}$ change most whereas $E_{3}$ is the last which coincide with the results summarized in Fig. 5.

Fig. 6

Equilibria variation of the updated rotating mass dipole with $\kappa = 1$ and $\mu = 0.5$ by decreasing $A_{2}$ from 0 to −0.05

Based on the above discussions, it is necessary to make a brief summary with respect to the equilibria variations of the URMDP. Variational trends of $E_{1}$ to $E_{5}$ dependent on $[ \kappa,\ \mu,\ A_{2}]$ are specified as follows:

• (a) $[ \mu,\ A_{2}]$ are fixed: By increasing $\kappa$, $E_{1}$ moves towards the prolate primary ($A_{2} < 0$) while away from the oblate primary ($A_{2} > 0$). Other equilibria $E_{2}$ to $E_{5}$ shift away from the barycenter of the dipole system.

• (b) $[\kappa,\ A_{2}]$ are fixed: By decreasing $\mu$, $E_{1}$ and $E_{2}$ approach the second primary $m_{2}$ (i.e., the oblate or prolate primary) whereas $E_{3}$ is away from $m_{2}$. $E_{4}$ and $E_{5}$ keep at respective fixed points relative to the barycenter of the dipole system.

• (c) $[\kappa,\ \mu ]$ are fixed: By decreasing $A_{2}$, $E_{1}$ to $E_{5}$ move towards $m_{2}$.

  As for the four new equilibria $E_{6}$ to $E_{9}$ due to the prolate primary, their variational trends and bifurcation conditions are also given here:

• (d) $[\mu,\ A_{2}]$ are fixed: There are two boundary values $\kappa_{\mathrm{g}}$ (lower value) and $\kappa_{\mathrm{v}}$ (upper value) corresponding to the case that $E_{6}$ and $E_{7}$ merge into a single point. When $\kappa_{\mathrm{g}} < \kappa < \kappa_{\mathrm{v}}$, $E_{6}$ and $E_{7}$ move to the right along axis $ox$ along a circle centered at $m_{2}$ by increasing $\kappa$. If $\kappa < \kappa_{\mathrm{g}}$ or $\kappa > \kappa_{\mathrm{v}}$, the equilibria $E_{6}$ and $E_{7}$ will vanish. $E_{8}$ and $E_{9}$ move towards $m_{2}$ along with the increase of $\kappa$.

• (e) $[\kappa,\ A_{2}]$ are fixed: By decreasing $\mu$, $E_{8}$ and $E_{9}$ move towards the prolate primary while $E_{6}$ and $E_{7}$ keep at respective fixed points relative to the barycenter of the dipole system.

• (f) $[\kappa,\ \mu]$ are fixed: By decreasing $A_{2}$, $E_{6}$ to $E_{9}$ are all away from $m_{2}$.

5 Stability of the equilibrium points

To investigate the motion around an equilibrium point $[x_{E},\ y_{E}]^{\mathrm{T}}$ in the equatorial plane, let an initial perturbing vector $[\xi,\ \eta ]^{\mathrm{T}}$ add to the nominal position as $\xi = x - x_{E}$ and $\eta = y - y_{E}$. Then the linearized equations of motion in dimensionless units can be derived from Eqs. (15) and (16):

$$ \textstyle\begin{cases} \ddot{\xi} - 2\omega \dot{\eta} = - W_{xx}\xi - W_{xy}\eta \\ \ddot{\eta} + 2\omega \dot{\xi} = - W_{yx}\xi - W_{yy}\eta \end{cases} $$

(30)

where the coefficients of the right terms are

$$\begin{aligned} & \begin{aligned}[b] W_{xx} = \frac{\partial W_{x}}{\partial x} &= - \omega^{2} + \kappa \omega^{2}\biggl[ \frac{1 - \mu}{r_{1}^{3}} - \frac{3 ( 1 - \mu ) ( x + \mu )^{2}}{r_{1}^{5}} \\ &\quad {}+ \frac{\mu}{r_{2}^{3}} - \frac{3\mu ( x + \mu - 1 )^{2}}{r_{2}^{5}} +\ldots \frac{3\mu A_{2}}{2r_{2}^{5}}\\ &\quad {} - \frac{15\mu A_{2} ( x + \mu - 1 )^{2}}{2r_{2}^{7}} \biggr] \end{aligned} \end{aligned}$$

(31)

$$\begin{aligned} & \begin{aligned}[b] W_{yy} = \frac{\partial W_{y}}{\partial y} &= - \omega^{2} + \kappa \omega^{2} \biggl[ \frac{1 - \mu}{r_{1}^{3}} - \frac{3 ( 1 - \mu )y^{2}}{r_{1}^{5}} + \frac{\mu}{r_{2}^{3}} \\ &\quad {}- \frac{3\mu y^{2}}{r_{2}^{5}} + \frac{3\mu A_{2}}{2r_{2}^{5}} - \frac{15\mu A_{2}y^{2}}{2r_{2}^{7}} \biggr] \end{aligned} \end{aligned}$$

(32)

$$\begin{aligned} & \begin{aligned}[b] W_{xy} = W_{yx} = \frac{\partial W_{x}}{\partial y} &= - 3\kappa \omega^{2}y \biggl[ \frac{ ( 1 - \mu ) ( x + \mu )}{r_{1}^{5}}\\ &\quad {} + \frac{\mu ( x + \mu - 1 )}{r_{2}^{5}} \\ &\quad {}+ \frac{5\mu A_{2} ( x + \mu - 1 )}{2r_{2}^{7}} \biggr] \end{aligned} \end{aligned}$$

(33)

By introducing the state variable vector $\boldsymbol{\chi} = [ \xi, \eta,\dot{\xi},\dot{\eta} ]^{\mathrm{T}}$, the variational equations (30) can be transformed into a set of first-order equations $\dot{\boldsymbol{\chi}} = \varPhi \boldsymbol{\chi}$ where the state transition matrix $\varPhi$ is (Szebehely 1967)

$$ \varPhi = \begin{bmatrix} \mathbf{0}_{2 \times 2} & \mathbf{I}_{2 \times 2} \\ - \nabla^{2}W & - \varOmega \end{bmatrix}_{4 \times 4} $$

(34)

whose eigenvalues are specified as $\lambda_{j}$ ($j = 1, 2, 3, 4$). The equilibrium point is linearly stable if and only if $\operatorname{Re}\lambda_{j} < 0$ while unstable if and only if $\operatorname{Re} \lambda_{j} > 0$ ($j = 1, 2, 3, 4$). When $\operatorname{Re} \lambda_{j} = 0$ the system of Eq. (30) yields asymptotic stability. Here, $\mathbf{0}_{2\times2}$ and $\mathbf{I}_{2\times2}$ are the second-order zero matrix and identity matrix, respectively. The well-known Hessian matrix $\nabla^{2}W$ and the skew symmetric matrix $\varOmega$ in Eq. (34) are defined as

$$ \nabla^{2}W = \begin{bmatrix} W_{xx} & W_{xy} \\ W_{xy} & W_{yy} \end{bmatrix}; \qquad \varOmega = \begin{bmatrix} 0 & - 2\omega \\ 2\omega & 0 \end{bmatrix} $$

(35)

The characteristic equation of Eq. (30) is

$$ \lambda^{4} + \bigl( 4\omega^{2} + W_{xx} + W_{yy} \bigr)\lambda^{2} + \bigl( W_{xx} \cdot W_{yy} - W_{xy}^{2} \bigr) = 0 $$

(36)

where the above quartic equation in the variable $\lambda_{j}$ ($j = 1, 2, 3, 4$) is also a quadratic equation in $\lambda^{2}$. Let $\lambda_{\mathrm{a}} = \lambda_{1}^{2} = \lambda_{2}^{2}$ and $\lambda_{\mathrm{b}} = \lambda_{3}^{2} = \lambda_{4}^{2}$ where $\lambda_{1} = - \lambda_{2}$ and $\lambda_{3} = - \lambda_{4}$. According to Murray and Dermott (1999), the equilibrium point is stable if all the eigenvalues are purely imaginary indicating that $\lambda_{\mathrm{a}}$ and $\lambda_{\mathrm{b}}$ ($\lambda_{\mathrm{a}} \neq \lambda_{\mathrm{b}}$) must be negative. Such a condition is the same as that given by using Eq. (34) with non-positive eigenvalues.

5.1 Collinear equilibrium points

For collinear equilibrium points, one can immediately know that the term $W_{xy}$ is zero with $y = 0$. Equation (31) and Eq. (32) can be reduced to

$$\begin{aligned} &W_{xx} = - \omega^{2} \biggl\{ 1 + 2\kappa \biggl[ \frac{1 - \mu}{r_{1}^{3}} + \frac{\mu}{r_{2}^{3}} + \frac{3\mu A_{2}}{r_{2}^{5}} \biggr] \biggr\} \end{aligned}$$

(37)

$$\begin{aligned} &W_{yy} = - \omega^{2} \biggl\{ 1 - \kappa \biggl[ \frac{1 - \mu}{r_{1}^{3}} + \frac{\mu}{r_{2}^{3}} + \frac{3\mu A_{2}}{2r_{2}^{5}} \biggr] \biggr\} \end{aligned}$$

(38)

where $r_{1} = |x + \mu |$ and $r_{2} = |x + \mu - 1|$ for collinear equilibrium points. Combining Eqs. (35), (37) with (38), the eigenvalues of Eq. (34) can be determined via numerical simulations. For the case of $A_{2} = 0$, it has been proved that the equilibria $E_{2}$ and $E_{3}$ are unstable (Prieto-Llanos and Gómez-Tierno 1994) whereas $E_{1}$ is conditionally stable for $k \leq 0.125$ (Hirabayashi et al. 2010).

Through our numerical simulations, there is no case where the roots are all imaginary for $E_{2}$ and $E_{3}$ with $\mu \in (0, 0.5]$, $A_{2} \in [0, 0.05]$ and a wide range of $\kappa \in (0, 100]$. Consequently, $E_{2}$ and $E_{3}$ are unstable in the case of oblate second primary. Figure 7 shows the stable region at $E_{1}$ in the cases of $A_{2} = 0$ and $A_{2} = 0.05$ with $\mu \in (0, 0.5]$. The closed area with boundaries of solid lines is the stable region for $A_{2} = 0$ and the other with boundaries of dashed lines is for $A_{2} = 0.05$. The shapes of these two areas are similar to each other. It should be emphasized that there is still stable region for $E_{1}$ with oblateness of the second primary. Due to the oblateness the stable region shifts down where the maximum value of $\kappa$ drops down from 0.125 to approximately 0.11.

Fig. 7

Stable region at $E_{1}$ by varying $\mu \in (0, 0.5]$ and $\kappa$ with respect to $A_{2} = 0$ and $A_{2} =0.05$

In Fig. 8, the closed area with boundaries of solid line is still the stable region at $E_{1}$ with $A_{2} = 0$ which is the same as that given in Fig. 7. The stable region corresponding to $A_{2} = -0.05$ is given by dashed-line boundaries with $\mu \in (0, 0.5]$. Obviously, the stable region is enlarged due to the prolate primary compared to the CRMDP. Particularly, the variational trend of the lower boundary along with the increase of $\mu$ with $A_{2} = -0.05$ is different from the case of $A_{2} = 0$. Taking $\mu = 0.5$ as an example, the stable domain is approximately 0.055 for $\kappa$ with $A_{2} = -0.05$ while it is only 0.015 with $A_{2} = 0$. The stable region at $E_{1}$ with other values of $A_{2}$ can be determined by using the same method. Moreover, according to the simulations, it is found that the upper boundary for the stable region at $E_{1}$ is always constant with a fixed $A_{2}$ by varying the mass ratio. The above cases with small values of $\kappa$ regarding the stability of $E_{1}$ may be helpful to understand dynamical properties of elongated minor celestial bodies.

Fig. 8

Stable region at $E_{1}$ by varying $\mu \in$ (0, 0.5] and $\kappa$ with respect to $A_{2} = 0$ and $A_{2} = -0.05$

There are another two collinear equilibria $E_{8}$ and $E_{9}$ for the case of prolate primary. Taking $A_{2} = -0.05$ as an example, the stable region at $E_{8}$ is given in Fig. 9 with filled area. The lower boundary is a constant value of approximately 0.369 starting from the left point of $\mu \approx$ 0.097. When $\mu$ is greater than 0.175, the maximum value of $\kappa$ goes up sharply from 10 to 50 which is relatively a very high value for a realistic spinning system. Thus, higher values of $\kappa$ corresponding to the upper boundary of the stable area are not presented in the figure. According to numerical simulations, the lower boundary of the stable region shifts up along with the decrease of $|A_{2}|$ while the left boundary is towards the axis $oy$. Additionally, the stable region at $E_{9}$ is nearly the same as that at $E_{8}$ as well as variational trends as a function of system parameters. Therefore, the stability of $E_{9}$ is not discussed any more.

Fig. 9

Stable region at $E_{8}$ by varying $\mu \in$ (0, 0.5] and $\kappa$ with respect to $A_{2} = -0.05$

5.2 Stability of the non-collinear equilibrium points

The stability regarding $E_{4}$ and $E_{5}$ is investigated based on the Eqs. (31) to (34). For the CRMDP with $A_{2} = 0$, the stable condition for $E_{4} (E_{5})$ can be explicitly given as (Prieto-Llanos and Gómez-Tierno 1994)

$$ 9\mu ( 1 - \mu ) \cdot \kappa^{ - 2 / 3} \cdot \bigl( 4 - \kappa^{ - 2 / 3} \bigr) \le 1 $$

(39)

corresponding to the scenario that all eigenvalues of Eq. (34) are purely imaginary. Particularly, when $\kappa$ is unity, Eq. (39) illustrates the stability of the triangular equilibrium points in the CRTBP. Due to the oblateness of the primary, the stable condition for $E_{4} (E_{5})$ of the URMDP can not be deduced to an explicit form as simple as Eq. (39). Consequently, numerical simulations are performed to identify the stable region at $E_{4} (E_{5})$.

Figure 10 shows the stable region at $E_{4} (E_{5})$ with different values of $A_{2}$. The filled area with short dashed-line boundary is the region of unstable motion for the case of $A_{2} = -0.05$, the solid line is for $A_{2} = 0$ and the long dashed-line is for $A_{2} = 0.05$. The values of $A_{2} = -0.05$ and 0.05 are taken as representatives to illustrate the influence of $A_{2}$ on the stable region. With a negative $A_{2}$ (prolate primary), the unstable area reduces compared to the case of $A_{2} = 0$. Conversely, the unstable area increases with a positive $A_{2}$ (oblate primary). Particularly, there is a small area next to the axis $\mathit{oy}$ where no triangular equilibria $E_{4} (E_{5})$ exist. A zoom-in plotting is given in Fig. 10(b) to show the details around the axis $\mathit{oy}$. $\mathit{By}$ increasing $A_{2}$ from negative to positive, the boundary value of $\kappa$ for the existence of $E_{4} (E_{5})$ decreases whose line moves to the left. Except the unstable region and the area where $E_{4} (E_{5})$ can not exist, other regions are linearly stable areas for $E_{4} (E_{5})$.

Fig. 10

Stable region at $E_{4} (E_{5})$ by varying $\mu \in (0, 0.5]$ and $\kappa$ with respect to $A_{2} = 0,\ 0.05,\ -0.05$

The existence of the other two triangular equilibria $E_{6} (E_{7})$ is within $\kappa \in [0.37,\ 2.07]$ according to Sect. 3.1 which is independent of the mass ratio. The eigenvalues of Eq. (34) are calculated with $\kappa \in [0.37, 2.07]$ and $\mu \in (0, 0.5]$. Neglecting the truncation error of the calculations, there are always a pair of pure imaginaries and a pair of real numbers. Therefore, $E_{6}$ and $E_{7}$ are unstable based on the numerical evidence.

A brief summary regarding the stability of the equilibria is given. The collinear equilibrium point $E_{1}$ is conditionally stable with small values of the force ratio $\kappa$. The maximum value of $\kappa$ corresponding to the upper boundary of the stable region increases along with the decrease of the oblateness $A_{2}$ from positive to negative. The triangular equilibria $E_{4}$ and $E_{5}$ are conditionally stable. With the increase of $A_{2}$ from negative to positive, the stable region at $E_{4} (E_{5})$ enlarges slightly whereas the minimum value of $\kappa$ determining the existence of $E_{4} (E_{5})$ decreases. The non-collinear equilibria $E_{8}$ and $E_{9}$ are conditionally stable while all other equilibria of the URMDP, including $E_{2}$, $E_{3}$, $E_{6}$ and $E_{7}$, are unstable according to our numerical results.

6 Conclusions

Dynamic properties of the updated rotating mass dipole have been studied in this paper. The updated dipole system is composed of a point mass and a spheroid with oblateness which corresponds to the less massive primary. The gravitational potential of this system depends on three free parameters, i.e., the mass ratio, the force ratio and the oblateness. There are five equilibrium points for the updated dipole with an oblate spheroid, including three collinear points and two triangular points. Besides the above five equilibria, there are up to four new equilibrium points around the primary of a prolate spheroid. The boundary values of the oblateness in this study are taken to be −0.05 to 0.05.

The non-collinear equilibria $E_{6}$ and $E_{7}$ exist when the force ratio is approximately in the region of $[0.37,\ 2.07]$ which are independent of the mass ratio. The variation trend in terms of the locations of equilibria is categorized into six cases by varying the three independent parameters. Particularly, when the mass ratio and the force ratio are fixed, the equilibria $E_{1}$ to $E_{5}$ move towards the oblate or prolate primary where $E_{6}$ to $E_{9}$ away from it along with the decrease of the oblateness. The collinear equilibrium point $E_{1}$ is conditionally stable with small values of the force ratio. The triangular equilibria $E_{4}$ and $E_{5}$ are also conditionally stable whose stable region increases along with the decrease of the oblateness. All other equilibrium points are unstable based on the numerical simulations.