Bias Detection and Prediction of Mapping Errors in Camera Calibration

Abstract

Camera calibration is a prerequisite for many computer vision applications. While a good calibration can turn a camera into a measurement device, it can also deteriorate a system’s performance if not done correctly. In the recent past, there have been great efforts to simplify the calibration process. Yet, inspection and evaluation of calibration results typically still requires expert knowledge.

In this work, we introduce two novel methods to capture the fundamental error sources in camera calibration: systematic errors (biases) and remaining uncertainty (variance). Importantly, the proposed methods do not require capturing additional images and are independent of the camera model. We evaluate the methods on simulated and real data and demonstrate how a state-of-the-art system for guided calibration can be improved. In combination, the methods allow novice users to perform camera calibration and verify both the accuracy and precision.

1 Introduction

In 2000 Zhang published a paper [19] which allowed novice users to perform monocular camera calibration using only readily available components. Several works, including systems for guided calibration, improved upon the original idea [10, 12, 13]. However, we believe that a central building block is still missing: a generic way to evaluate the quality of a calibration result. More precisely, a way to reliably quantify the remaining biases and uncertainties of a given calibration. This is of critical importance, as errors and uncertainties in calibration parameters propagate to applications such as visual SLAM [9], ego-motion estimation [3, 17, 20] and SfM [1, 4]. Despite this importance, typical calibration procedures rely on relatively simple metrics to evaluate the calibration, such as the root mean squared error (RMSE) on the calibration dataset. Furthermore, many frequently used metrics lack comparability across camera models and interpretability for non-expert users.

In general, the error sources of camera calibration can be divided into underfit (bias) and overfit (high variance). An underfit can be caused by a camera projection model not being able to reflect the true geometric camera characteristics, an uncompensated rolling shutter, or non-planarity of the calibration target. An overfit, on the other hand, describes that the model parameters cannot be estimated reliably, i.e. a high variance remains. A common cause is a lack of images used for calibration, bad coverage in the image, or a non-diversity in calibration target poses. In this paper, we address the challenge of quantifying both types of errors in target-based camera calibration, and provide three main contributions:

• A method to detect systematic errors (underfit) in a calibration. The method is based on estimating the variance of the corner detector and thereby disentangles random from systematic errors in the calibration residual (Fig. 1).

• A method to predict the expected mapping error (EME) in image space, which quantifies the remaining uncertainty (variance) in model parameters in a model-independent way. It provides an upper bound for the precision that can be achieved with a given dataset (Fig. 1).

• The application of our uncertainty metric EME in calibration guidance, which guides users to poses that lead to a maximum reduction in uncertainty. Extending a recently published framework [10], we show that our metric leads to further improvement of suggested poses.

In combination, these methods allow novice users to perform camera calibration and verify both the accuracy and precision of the result. Importantly, the work presented here explicitly abstracts from the underlying camera model and is therefore applicable in a wide range of scenarios. We evaluate the proposed methods with both simulations and real cameras.

Fig. 1.

Proposed camera calibration procedure, including the detection of systematic errors (biases) and the prediction of the expected mapping error.

2 Fundamentals

Camera Projection Modeling. From a purely geometric point of view, cameras project points in the 3D world to a 2D image [6]. This projection can be expressed by a function $\varvec{p}:\mathbb {R}^3\rightarrow \mathbb {R}^2$ that maps a 3D point $\varvec{x}=(x, y, z)^T$ from a world coordinate system to a point $\bar{\varvec{u}}=(\bar{u}, \bar{v})^T$ in the image coordinate system. The projection can be decomposed into a coordinate transformation from the world coordinate system to the camera coordinate system $\varvec{x} \rightarrow \varvec{x_{c}}$ and the projection from the camera coordinate system to the image $\varvec{p_C}:\varvec{x_{c}}\rightarrow \bar{\varvec{u}}$:

$$\begin{aligned} \bar{\varvec{u}} = \varvec{p}(\varvec{x}, \varvec{\theta }, \varvec{\varPi }) = \varvec{p_C}(\varvec{x_{c}}, \varvec{\theta }) = \varvec{p_C}(\varvec{R} \varvec{x} + \varvec{t}, \varvec{\theta }), \end{aligned}$$

(1)

where $\varvec{\theta }$ are the intrinsic camera parameters and $\varvec{\varPi }$ and are the extrinsic parameters describing the rotation $\varvec{R}$ and translation $\varvec{t}$. For a plain pinhole camera, the intrinsic parameters are the focal length f and the principal point $(\mathrm {ppx, ppy})$, i.e. $\varvec{\theta } = (f,\mathrm { ppx, ppy})$. For this case, the projection $\varvec{p_C}(\varvec{x_{c}}, \varvec{\theta })$ is given by $u =f/z_{c}\cdot x_{c} + \mathrm {ppx}$, $v = f/z_{c}\cdot y_{c} + \mathrm {ppy}$. In the following, we will consider more complex camera models, specifically, a standard pinhole camera model (S) with radial distortion $\varvec{\theta }_S = (f_x, f_y, \mathrm {ppx}, \mathrm {ppy}, r_1, r_2)$, and the OpenCV fisheye model (F) $\varvec{\theta }_F = (f_x, f_y, \mathrm {ppx}, \mathrm {ppy}, r_1, r_2, r_3, r_4)$ [8].

Calibration Framework. We base our methods on target-based camera calibration, in which planar targets are imaged in different poses relative to the camera. Without loss of generality, we assume a single chessboard-style calibration target and a single camera in the following. The calibration dataset is a set of images $\mathcal {F}=\{\text {frame}_i\}_{i=1}^{N_\mathcal {F}}$. The chessboard calibration target contains a set of corners $\mathcal {C}=\{\text {corner}_i\}_{i=1}^{N_\mathcal {C}}$. The geometry of the target is well-defined, thus the 3D coordinates of chessboard-corner i in the world coordinate system are known as $\varvec{x}_{i}=(x_i, y_i, z_i)^T$. The image coordinates $\varvec{u}_i=(u_i, v_i)^T$ of chessboard-corners are determined by a corner-detector with noise $\sigma _d$. Thus, the observed coordinates $\varvec{u}_i$ are assumed to deviate from the true image points $\varvec{\bar{u}}_i$ by an independent identically distributed (i.i.d.) error $\epsilon _d \sim \mathcal {N}(0, \sigma _d)$. Estimation is performed by minimizing a calibration cost function, typically defined by the quadratic sum over reprojection errors

$$\begin{aligned} \epsilon _{\mathrm {res}}^2 = \sum _{j\in \mathcal {F}} \sum _{i \in \mathcal {C}} ||\varvec{u}_{ij} - \varvec{p}(\varvec{x}_{ij}, \varvec{\theta }, \varvec{\varPi }_j)||^2. \end{aligned}$$

(2)

For the sake of simplicity, we present formulas for non-robust optimization here. Generally, we advise robustification, e.g. using a Cauchy kernel. Optimization is performed by a non-linear least-squares algorithm, which yields parameter estimates $(\varvec{\hat{\theta }}, \varvec{\hat{\varPi }}) = \text {argmin}(\epsilon _{\mathrm {res}}^2)$.

A common metric to evaluate the calibration is the root mean squared error (RMSE) over all N individual corners coordinates (observations) in the calibration dataset $\mathcal {F}$ [6, p. 133]:

$$\begin{aligned} \mathrm {RMSE} = \sqrt{\frac{1}{N} \sum _{j\in \mathcal {F}} \sum _{i \in \mathcal {C}} ||\varvec{u}_{ij} - \varvec{p}(\varvec{x}_{ij}, \varvec{\hat{\theta }}, \varvec{\hat{\varPi }}_j)||^2}, \end{aligned}$$

(3)

The remaining uncertainty in estimated model parameters $\varvec{\hat{\theta }}, \varvec{\hat{\varPi }}$ is given by the parameter’s covariance matrix $\varvec{\varSigma }$. The covariance matrix can be computed by backpropagation of the variance of the corner detector $\sigma _d^2$:

$$\begin{aligned} \varvec{\varSigma } = ( \varvec{J}_{\mathrm {calib}}^T \varvec{\varSigma }_d^{-1} \varvec{J}_{\mathrm {calib}})^{-1} = \sigma _d^2( \varvec{J}_{\mathrm {calib}}^T \varvec{J}_{\mathrm {calib}})^{-1}, \end{aligned}$$

(4)

where $\varvec{\varSigma _d} = \sigma _d^2 \varvec{I}$ is the covariance matrix of the corner detector and $\varvec{J}_{\mathrm {calib}}$ is the Jacobian of calibration residuals [6]. The covariance matrix of intrinsic parameters $\varvec{\varSigma _{\theta }}$ can be extracted as a submatrix of the full covariance matrix.

3 Related Work

Approaches to evaluating camera calibration can be divided into detecting systematic errors and quantifying the remaining uncertainty in estimated model parameters. Typical choices of uncertainty metrics are the trace of the covariance matrix [10], or the maximum index of dispersion [13]. However, given the variety of camera models, from a simple pinhole model with only three parameters, up to local camera models, with around $10^5$ parameters [2, 15], parameter variances are difficult to interpret and not comparable across camera models. To address this issue, the parameter’s influence on the mapping can be considered. The metric maxERE [12] quantifies uncertainty by propagating the parameter covariance into pixel space by means of a Monte Carlo simulation. The value of maxERE is then defined by the variance of the most uncertain image point of a grid of projected 3D points. The observability metric [16] weights the uncertainty in estimated parameters (here defined by the calibration cost function’s Hessian) with the parameters’ influence on a model cost function. Importantly, this model cost function takes into account a potential compensation of differences in the intrinsics by adjusting the extrinsics. The observability metric is then defined by the minimum eigenvalue of the weighted Hessian.

While both of these metrics provide valuable information about the remaining uncertainty, there are some shortcomings in terms of how uncertainty is quantified. The observability metric does not consider the whole uncertainty, but only the most uncertain parameter direction. Furthermore, it quantifies uncertainty in terms of an increase in the calibration cost, which can be difficult to interpret. maxERE quantifies uncertainty in pixel space and is thus easily interpretable. However, it relies on a Monte Carlo Simulation instead of an analytical approach and it does not incorporate potential compensations of differences in the intrinsics by adjusting the extrinsics.

The second type evaluation metrics aims at finding systematic errors. As camera characteristics have to be inferred indirectly through observations, there is a high risk of introducing systematic errors in the calibration process by choosing an inadequate projection model, neglecting rolling-shutter effects, or using an out-of-spec calibration target, to give a few examples. If left undetected, these errors will inevitably introduce biases into the application.

Historically, one way to detect systematic errors is to compare the resulting RMSE or reconstruction result against expected values obtained from earlier calibrations or textbooks [7]. However, these values vary for different cameras, lenses, calibration targets, and marker detectors and, hence, only allow capturing gross errors in general. Professional photogrammetry often makes use of highly accurate and precisely manufactured 3D calibration bodies [11]. Images captured from predefined viewpoints are then used to perform a 3D reconstruction of the calibration body. Different length ratios and their deviation from the ground truth are then computed to assess the quality of the calibration by comparing against empirical data. While these methods represent the gold standard due to the accuracy of the calibration body and repeatability, they are often not feasible or too expensive for typical research and laboratory settings and require empirical data for the camera under test. The methods presented in the following relax these requirements but can also be seen as a complement to this standard.

4 Detecting Systematic Errors

In the following, we derive the bias ratio (BR), a novel metric for quantifying the fraction of systematic error contribution to the mean squared reprojection error (MSE). Following the assumptions made in Sect. 2 one finds that asymptotically (by augmentation of [6, p. 136])

$$\begin{aligned} \mathrm {MSE_{\mathrm {calib}}} = \underbrace{\sigma _d^2 (1-\frac{N_\mathcal {P}}{N})}_{\begin{array}{c} \mathrm {random \ error} \end{array}} + \underbrace{\ \epsilon _{\mathrm {bias}}^2\ }_{\begin{array}{c} \mathrm {systematic\ error\ contribution} \end{array}}, \end{aligned}$$

(5)

where $N_\mathcal {P}$ is the total number of free intrinsic and extrinsic parameters and $\epsilon _{\mathrm {bias}}$ denotes the bias introduced through systematic errors. The variance $\sigma _d^2$ is generally camera dependent and not known a priori. To disentangle stochastic and systematic error contributions to the MSE, we need a way to determine $\sigma _d^2$ independently: The rationale behind many calibration approaches, and in particular guided calibration, is to find most informative camera-target configurations (cf. Fig. 1). For bias estimation, we propose the opposite. We explicitly use configurations which are less informative for calibration but at the same time also less likely to be impacted by systematic errors. More specifically, we decompose the calibration target virtually into several smaller calibration targets $\mathcal {V} = \{\text {target}_i\}_{i=1}^{N_\mathcal {V}}$, usually consisting of exclusive sets of the four corners of a checker board tile (cf. Fig. 2a). The poses of each virtual calibration target in each image are then estimated individually while keeping the camera intrinsic parameters fixed. Pose estimation is overdetermined with a redundancy of two (four tile corners and six pose parameters). From the resulting MSE values, $\mathrm {MSE}_v$ with $v \in \mathcal {V}$, we compute estimates of $\sigma _d^2$ via (5) assuming the bias is negligible within these local image regions

$$\begin{aligned} \widehat{\sigma }_{d_v}^2 = \frac{\mathrm {MSE}_v}{1-\frac{6}{8}} = 4~\mathrm {MSE}_v. \end{aligned}$$

(6)

To obtain an overall estimate of $\widehat{\sigma }_d^2$, we compute the MSE in (6) across the residuals of all virtual targets, using the MAD as a robust estimator¹. Finally, we use $\widehat{\sigma }_d^2$ to determine $\epsilon _{\mathrm {bias}}^2$ using (5) and compute the bias ratio as

$$\begin{aligned} \mathrm {BR} = \frac{\epsilon _{\mathrm {bias}}^2}{\mathrm {MSE}_{\mathrm {calib}}}. \end{aligned}$$

(7)

The bias ratio is zero for unbiased calibration and close to one if the results are dominated by systematic errors. The bias ratio is an intuitive metric that quantifies the fraction of bias introduced by systematic errors. A bias ratio below a certain threshold $\tau _{BR}$ is a necessary condition for a successful calibration and a precondition for uncertainty estimation.² Generally, this kind of analysis can be performed for any separable³ calibration target.

Fig. 2.

Detecting systematic errors. a Illustration of the virtual decomposition of the calibration target into smaller targets used to estimate the corner detector variance. b Exemplary image of the same scene with the two test cameras. c Results of the bias ratio (BR) and the robust estimate of the RMSE (MAD) for one simulated and the two real cameras, using models of different complexities. For details see Sect. 7.

Practical Implementation. Computation of the bias ratio for target-based calibration procedures:

• 1. Perform robust camera calibration and extract a robust estimate of $\mathrm {MSE}_{\mathrm {calib}}$ and the optimal parameters $\varvec{\hat{\theta }}$ and $\varvec{\hat{\varPi }}$.

• 2. Compute the residuals for all $v \in \mathcal {V}$:

  • Decompose the calibration targets found in each image into a total of $N_\mathcal {V}$ exclusive virtual calibration targets.

  • Optimize their pose independently leaving $\varvec{\hat{\theta }}$ unchanged.

• 3. Compute a robust estimate of the MSE over all residuals and determine $\widehat{\sigma }_d^2$ using (6).

• 4. Use $\widehat{\sigma }_d^2$ to determine the bias contribution $\epsilon _{\mathrm {bias}}^2$ via (5).

• 5. Finally, compute the bias ratio as $\mathrm {BR} = \epsilon _{\mathrm {bias}}^2/\mathrm {MSE}_{\mathrm {calib}}$ and test the result against the threshold $\tau _{BR}$.

5 The Expected Mapping Error (EME)

The second type of error source, in addition to biases, is a high remaining uncertainty in estimated model parameters. We will now derive a novel uncertainty metric, the expected mapping error (EME), which is interpretable and comparable across camera models. It quantifies the expected difference between the mapping of a calibration result $\varvec{p_C}(\varvec{x}; \hat{\varvec{\theta }})$ and the true (unknown) model $\varvec{p_C}(\varvec{x}; \bar{\varvec{\theta }})$.

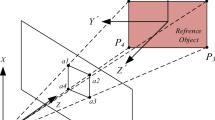
Inspired by previous works [5, 12], we quantify the mapping difference in image space, as pixel differences are easily interpretable: we define a set of points in image space $\mathcal {G}=\{\varvec{u}_i\}_{i=1}^{N_\mathcal {G}}$, which are projected to space via the inverse projection $\varvec{p_C}^{-1}(\varvec{u}_i; \bar{\varvec{\theta }})$ using one set of model parameters and then back to the image using the other set of model parameters [2]. The mapping error is then defined as the average distance between original image coordinates ${\varvec{u}_i}$ and back-projected image points $\varvec{p_C}(\varvec{x}_i; \hat{\varvec{\theta }})$ (see Fig. 3):

$$\begin{aligned} \tilde{K}(\hat{\varvec{\theta }}, \bar{\varvec{\theta }}) = \frac{1}{N} \sum _{i\in \mathcal {G}} ||\varvec{u_i} - \varvec{p_C}(\varvec{p_C}^{-1}(\varvec{u_i}; \bar{\varvec{\theta }}); \hat{\varvec{\theta }})||^2, \end{aligned}$$

(8)

where $N=2N_\mathcal {G}$ is the total number of image coordinates. Since small deviations in intrinsic parameters can oftentimes be compensated by a change in extrinsic parameters [16], we allow for a virtual compensating rotation $\varvec{R}$ of the viewing rays. Thus, we formulate the effective mapping error as follows:

$$\begin{aligned} K(\hat{\varvec{\theta }}, \bar{\varvec{\theta }}) = \underset{\varvec{R}}{\text {min}}~ \frac{1}{N} \sum _{i\in \mathcal {G}} ||\varvec{u}_i - \varvec{p_C}(\varvec{R}~ \varvec{p_C}^{-1}(\varvec{u}_i; \bar{\varvec{\theta }}); \hat{\varvec{\theta }})||^2. \end{aligned}$$

(9)

We now show that for an ideal, bias-free calibration, the effective mapping error $K(\hat{\varvec{\theta }}, \bar{\varvec{\theta }})$ can be predicted by propagating parameter uncertainties. Note that the following derivation is independent of the particular choice of K, provided that we can approximate K with a Taylor expansion around $\hat{\varvec{\theta }}=\bar{\varvec{\theta }}$ up to second order:

$$\begin{aligned} \begin{aligned} K(\hat{\varvec{\theta }}, \bar{\varvec{\theta }})&\approx K(\bar{\varvec{\theta }}, \bar{\varvec{\theta }}) + \mathrm {grad}(K) \varvec{\varDelta \theta } + \frac{1}{2} \varvec{\varDelta \theta }^T \varvec{H}_K \varvec{\varDelta \theta } \\&\approx \frac{1}{N}\varvec{\varDelta \theta }^T (\varvec{J_{\mathrm {res}}}^T \varvec{J_{\mathrm {res}}}) \varvec{\varDelta \theta } \\&\approx \varvec{\varDelta \theta }^T \varvec{H} \varvec{\varDelta \theta }, \end{aligned} \end{aligned}$$

(10)

where $\varvec{\varDelta \theta }=\bar{\varvec{\theta }}- \hat{\varvec{\theta }}$ is the difference between true and estimated intrinsic parameters, $\varvec{\mathrm {res}}_i(\hat{\varvec{\theta }}, \bar{\varvec{\theta }}) = \varvec{u}_i - \varvec{p_C}(\varvec{R}~ \varvec{p_C}^{-1}(\varvec{u}_i; \bar{\varvec{\theta }}); \hat{\varvec{\theta }})$ are the mapping residuals and $\varvec{J_{\mathrm {res}}}=d\varvec{\mathrm {res}}/d\varvec{\varDelta \theta }$ is the Jacobian of the residuals. Furthermore, we defined the model matrix $\varvec{H} := \frac{1}{N}\varvec{J_{\mathrm {res}}}^T \varvec{J_{\mathrm {res}}}$. For a more detailed derivation of the second step in (10), see Supplementary.

Fig. 3.

Predicting the mapping error based on parameter uncertainties. a Schematic of the derived uncertainty metric $\mathrm {EME}=\mathrm {trace}( \varvec{\varSigma _{\theta }}^{1/2} \varvec{H} \varvec{\varSigma _{\theta }}^{1/2})$. b Evaluation in simulation and experiments. The simulation results validate the derived relation (5). For real cameras, the EME is a lower bound to the error, as non-ideal behavior can lead to higher absolute errors. Error bars are 95% bootstrap confidence intervals.

Estimated model parameters $\hat{\varvec{\theta }}$ obtained from a least squares optimization are a random vector, asymptotically following a multivariate Gaussian with mean $\varvec{\mu _{\theta }} = \bar{\varvec{\theta }}$ and covariance $\varvec{\varSigma _{\theta }}$ [18, p. 8]. Likewise, the parameter error $\varvec{\varDelta \theta }=\bar{\varvec{\theta }}- \hat{\varvec{\theta }}$ follows a multivariate Gaussian, with mean $\varvec{\mu _{\varDelta \theta }} = \varvec{0}$ and covariance $\varvec{\varSigma _{\varDelta \theta }} = \varvec{\varSigma _{\theta }}$. We propagate the distribution of the parameter error $\varvec{\varDelta \theta }$ to find the distribution of the mapping error $K(\hat{\varvec{\theta }}, \bar{\varvec{\theta }})$. In short, we find that the mapping error $K(\hat{\varvec{\theta }}, \bar{\varvec{\theta }})$ can be expressed as a linear combination of $\chi ^2$ random variables:

$$\begin{aligned} \begin{aligned} K(\hat{\varvec{\theta }}, \bar{\varvec{\theta }})&= \varvec{\varDelta \theta }^T \varvec{H} \varvec{\varDelta \theta } \\&= \sum _{i=1}^{N_{\varvec{\theta }}} \lambda _i Q_i, \quad \text {with} \quad Q_i\sim \chi ^2(1). \end{aligned} \end{aligned}$$

(11)

The coefficients $\lambda _i$ are the eigenvalues of the matrix product $\varvec{\varSigma _{\theta }}^{1/2} \varvec{H} \varvec{\varSigma _{\theta }}^{1/2}$ and $N_{\varvec{\theta }}$ is the number of eigenvalues which equals the number of parameters $\varvec{\theta }$. The full derivation of relation (11) is shown in the Supplementary. Importantly, based on expression (11), we can derive the expected value of $K(\hat{\varvec{\theta }}, \bar{\varvec{\theta }})$:

$$\begin{aligned} \begin{aligned} \mathbb {E}[K(\hat{\varvec{\theta }}, \bar{\varvec{\theta }})]&= \mathbb {E}[\sum _{i=1}^{N_{\varvec{\theta }}} \lambda _i Q_i] \nonumber = \sum _{i=1}^{N_{\varvec{\theta }}} \lambda _i \mathbb {E}[Q_i] = \sum _{i=1}^{N_{\varvec{\theta }}} \lambda _i \\&= \mathrm {trace}(\varvec{\varSigma _{\theta }}^{1/2} \varvec{H} \varvec{\varSigma _{\theta }}^{1/2}), \end{aligned} \end{aligned}$$

where we used that the $\chi ^2$-distribution with n degrees of freedom $\chi ^2(n)$ has expectation value $\mathbb {E}[\chi ^2(n)]=n$. We therefore propose the expected mapping error $\mathrm {EME}=\mathrm {trace}(\varvec{\varSigma _{\theta }}^{1/2} \varvec{H} \varvec{\varSigma _{\theta }}^{1/2})$ as a model-independent measure for the remaining uncertainty.

Practical Implementation. The expected mapping error $\mathrm {EME}$ can be determined for any given bundle-adjustment calibration:

• 1. Run the calibration and extract the RMSE, the optimal parameters $\varvec{\hat{\theta }}$ and the Jacobian $\varvec{J}_{\mathrm {calib}}$ of the calibration cost function.

• 2. Compute the parameter covariance matrix $\varvec{\varSigma }=\sigma _d^2 ( \varvec{J}_{\mathrm {calib}}^T \varvec{J}_{\mathrm {calib}})^{-1}$ and extract the intrinsic part $\varvec{\varSigma _{\theta }}$.

• 3. Determine the model matrix $\varvec{H}$:

  • Implement the mapping error (Eq. (9)) as a function of the parameter estimate $\varvec{\hat{\theta }}$ and a parameter difference $\varvec{\varDelta \theta }$.

  • Numerically compute the Jacobian $\varvec{J_{\mathrm {res}}} = d\varvec{\mathrm {res}}/d\varvec{\varDelta \theta }$ at the estimated parameters $\varvec{\hat{\theta }}$ and compute $\varvec{H} = \frac{1}{N}\varvec{J_{\mathrm {res}}}^T \varvec{J_{\mathrm {res}}}$.

• 4. Compute $\mathrm {EME}=\mathrm {trace}( \varvec{\varSigma _{\theta }}^{1/2} \varvec{H} \varvec{\varSigma _{\theta }}^{1/2})$.

6 Experimental Evaluation

Simulations. We simulated 3D world coordinates of a single planar calibration target in different poses relative to the camera (random rotations $\varphi _x, \varphi _y, \varphi _z \in [-\frac{\pi }{4}, \frac{\pi }{4}]$, translations $t_z\in [0.5~\text {m}, 2.5~\text {m}]$, $t_x, t_y\in [-0.5~\text {m}, 0.5~\text {m}]$). We then computed the resulting image coordinates using different camera models. To simulate the detector noise, we added Gaussian noise with $\sigma _d = 0.1$ px to all image coordinates. To validate the bias ratio, we simulated a pinhole camera with two radial distortion parameters, but ran calibrations with different models, including insufficiently complex models (underfit). To validate the uncertainty measure $\mathrm {EME}=\mathrm {trace}(\varvec{\varSigma _{\theta }}^{1/2} \varvec{H} \varvec{\varSigma _{\theta }}^{1/2})$, we ran calibrations with different numbers of simulated frames ($N_{\mathcal {F}}\in [3,20]$) and $n_r=50$ noise realizations for each set of frames. After each calibration, we computed the true mapping error K with respect to the known ground-truth (Eq. 9) and the EME.

Evaluation with Real Cameras. We tested the metrics for two different real cameras (see Fig. 2b). For each camera, we collected a total of $n=500$ images of a planar calibration target. As reference, we performed a calibration with all 500 images. To test the bias metric, we ran calibrations with camera models of different complexities (Fig. 2c). To test the uncertainty metric EME, we ran calibrations with different numbers of randomly selected frames ($N_{\mathcal {F}}\in [3,20]$, 50 randomly selected datasets for each $N_{\mathcal {F}}$). For each calibration, we computed both the true mapping error K with respect to the reference and the EME.

7 Results

Validating the Bias Ratio. Figure 2c shows the robust estimate of the RMSE (median absolute deviation, MAD) and the bias ratio for the calibrations of three cameras (one simulated camera and the two real cameras shown in Fig. 2b) for varying numbers of non-zero intrinsic calibration parameters, representing different camera models. In detail, the individual parameter sets are $\varvec{\theta }_{S(3)} = (f, \mathrm {ppx}, \mathrm {ppy})$, $\varvec{\theta }_{S(4)} = (f_x, f_y, \mathrm {ppx}, \mathrm {ppy})$, $\varvec{\theta }_{S(5)} = (f_x, f_y, \mathrm {ppx}, \mathrm {ppy}, r_1)$, $\varvec{\theta }_{S(6)} = (f_x, f_y, \mathrm {ppx}, \mathrm {ppy}, r_1, r_2)$, and $\varvec{\theta }_{F(8)} = (f_x, f_y, \mathrm {ppx}, \mathrm {ppy}, r_1, r_2, r_3, r_4)$ (cf. Sect. 2).

For all cameras, the MAD and BR can be reduced by using a more complex camera model which is to be expected, since the projections are not rectilinear and thus necessitate some kind of (nonlinear) distortion modeling. For the simulated camera and camera 1, a bias ratio below $\tau _{BR} = 0.2$ is reached using the standard camera model (S) with two radial distortion parameters. For camera 2, a low bias ratio cannot be reached even when using OpenCV’s fisheye camera model with 8 parameters. This highlights the advantage of the bias ratio over the RMSE: the low RMSE could wrongfully be interpreted as low bias – the bias ratio of $\mathrm {BR} \approx 0.6$, however, demonstrates that some sort of systematic error remains and a more complex model should be tried.

Validating the Uncertainty Metric. To validate the uncertainty metric EME in simulations, we ran calibrations with different numbers of images using a pinhole with radial distortion S(6) and a fisheye camera F(8). Figure 3b shows the uncertainty metric $\mathrm {EME}=\mathrm {trace}(\varvec{\varSigma _{\theta }}^{1/2} \varvec{H} \varvec{\varSigma _{\theta }}^{1/2})$ and the real average mapping error. Consistent with Eq. (5), the EME predicts the average mapping error. For the real camera, the EME is highly correlated with the true mapping error, however the absolute values of the real errors are higher, which is to be expected in practice. It reflects that (i) the ground-truth is only approximated by the reference calibration, (ii) deviations from the ideal assumptions underlying the covariance matrix (Eq. (4)), and (iii) deviations from the i.i.d. Gaussian error assumption. This limitation affects all metrics that are based on the covariance matrix computed via Eq. (4). The EME therefore provides an upper bound to the precision that can be achieved for a given dataset.

Fig. 4.

Comparison of state-of-the-art metrics for real camera 1. On average, the true error K decreases with the number frames. For comparability with maxERE, we show $\sqrt{K}$ and $\sqrt{EME}$ in units of pixels. All metrics are correlated with the true error, but absolute values and the scaling differ. Values are medians across 50 random samples, error bars are 95% bootstrap confidence intervals.

Comparison with State-of-the-Art. We compare the EME with the other state-of-the-art uncertainty metrics introduced in Sect. 3. We focus on $\mathrm {trace}(\varvec{\varSigma _{\theta }})$, maxERE [12] and observability [16], as these are the metrics closest to ours (Fig. 4). All metrics provide information about the remaining uncertainty and are correlated with the true error. However, the metrics quantify uncertainty in very different ways: $\mathrm {trace}(\varvec{\varSigma _{\theta }})$ quantifies the uncertainty in model parameters, and thus inherently differs depending on the camera model. The observability metric accounts for the parameter’s effect of the mapping and for compensations via different extrinsics. However, it does not incorporate the full uncertainty, but just the least observable direction. Furthermore, the absolute values are comparatively difficult to interpret, as they measure an increase in the calibration cost. maxERE quantifies the maximum expected reprojection error in image space and is therefore easily interpretable. Similar to maxERE, the EME predicts the expected error in image space and is therefore easily interpretable. Instead of a maximum error, the EME reflects the average error. In contrast to maxERE, the EME does not require a Monte Carlo simulation. Furthermore, the EME can account for a compensation via different extrinsics, which we consider a reasonable assumption in many scenarios.

8 Application in Calibration Guidance

To demonstrate the practical use of the EME, we apply it in calibration guidance. Calibration guidance refers to systems that predict most informative next observations to reduce the remaining uncertainty and then guide users towards these measurements. We choose an exitisting framework, called calibration wizard [10] and extend it with our metric. Calibration wizard predicts the next best pose by minimizing the trace of the intrinsic parameter’s covariance matrix $\mathrm {trace}(\varvec{\varSigma _{\theta }})$. However, depending on the camera model, parameters will affect the image in very different ways. High variance in a given parameter will not necessarily result in a proportionally high uncertainty in the image. To avoid such an imbalance, we suggest to minimize the uncertainty in image space, instead of parameters, i.e. to replace $\mathrm {trace}(\varvec{\varSigma _{\theta }})$ with $\mathrm {trace}(\varvec{\varSigma _{\theta }}^{1/2} \varvec{H} \varvec{\varSigma _{\theta }}^{1/2})$.

To compare the methods, we use images of camera 1 (see Fig. 2b). Starting with two random images, the system successively selectes the most informative next image with (i) the original metric $\mathrm {trace}(\varvec{\varSigma _{\theta }})$, (ii) our metric $\mathrm {trace}(\varvec{\varSigma _{\theta }}^{1/2} \varvec{H} \varvec{\varSigma _{\theta }}^{1/2})$ and (iii) randomly. Using the pinhole model with radial distortion, the poses suggested by $\mathrm {trace}(\varvec{\varSigma _{\theta }})$ and $\mathrm {trace}(\varvec{\varSigma _{\theta }}^{1/2} \varvec{H} \varvec{\varSigma _{\theta }}^{1/2})$ are similarly well suited, both leading to a significantly faster convergence than random images (Fig. 5). However, when changing the camera model, e.g. by parameterizing the focal length in millimeters instead of pixels, simulated here by a division by 100 ($f \rightarrow 0.01\cdot f$), the methods differ: the poses proposed by $\mathrm {trace}(\varvec{\varSigma _{\theta }}^{1/2} \varvec{H} \varvec{\varSigma _{\theta }}^{1/2})$ reduce uncertainty significantly faster than $\mathrm {trace}(\varvec{\varSigma _{\theta }})$. This can be explained by the fact that when minimizing $\mathrm {trace}(\varvec{\varSigma _{\theta }})$, the variance of less significant parameters will be reduced just as much as the variance of parameters with large effect on the mapping. This example shows that the performance of $\mathrm {trace}(\varvec{\varSigma _{\theta }})$ can be affected by the choice of the model, while $\mathrm {trace}(\varvec{\varSigma _{\theta }}^{1/2} \varvec{H} \varvec{\varSigma _{\theta }}^{1/2})$ remains unaffected.

Fig. 5.

Application of EME for calibration guidance. a For the original model, both metrics lead to a similarly fast reduction in uncertainty. Rescaling the model to a different unit of the focal length results in a reduced performance of $\mathrm {trace}(\varvec{\varSigma _{\theta }})$, while $\mathrm {trace}(\varvec{\varSigma _{\theta }}^{1/2} \varvec{H} \varvec{\varSigma _{\theta }}^{1/2})$ remains unaffectd. Uncertainty is quantified by the average of the uncertainty map proposed by calibration wizard [10]. b Examples of suggested poses.

9 Conclusion and Future Research

In this paper, we proposed two metrics to evaluate systematic errors and the remaining uncertainty in camera calibration. We have shown that the bias ratio (BR) reliably captures underfits, which can result from an insufficiently complex model. Furthermore, we have shown that it is possible to predict the expected mapping error (EME) in image space, which provides an upper bound for the precision that can be achieved with a given dataset. Both metrics are model-independent and therefore widely applicable. Finally, we have shown that the EME can be applied for calibration guidance, resulting in a faster reduction in mapping uncertainty than the existing parameter-based approach.

In future, we will extend the metrics to multi-camera systems and extrinsic calibration. Furthermore, we would like to incorporate an analysis of the coverage of the camera field of view into our evaluation scheme.