Four points: one-pass geometrical camera calibration algorithm

Abstract

Conventional geometrical camera calibration algorithms are usually based on running some iterative algorithms on test images obtained carefully from reference objects with precisely known pattern. Providing these test images and running the iterative algorithms are often time-consuming and sometimes costly. In addition, they are usually very sensitive to image distortions. To overcome these problems, an efficient and practical camera calibration method using a single rectangular reference object is proposed. The reference object can be as simple as an A4-size paper placed on a table. Using the coordinate of four corner points of reference image, generate eight equations. This paper first describes an analytical method to solve the equations and then provides a step-by-step algorithm. The proposed algorithm is evaluated using simulated images generated with both Autodesk 3ds Max software and Microsoft Camera Calibration data set. The results show that the accuracy of the proposed method is very close to the best ones available, while its sensitivity to distortion and computational load is the least. In addition, the required reference object is the simplest one.

1 Introduction

Camera calibration is often used as an essential early stage in computer vision to derive metric information from 2-D images. The task of camera calibration is to estimate the parameters that govern the relationship between the 2-D image perceived by a camera and the 3-D information of the photographed object [1]. Camera intrinsic parameters describe the camera model, and extrinsic parameters define the relative location and orientation of the camera in the real world. Camera calibration is an indispensable step in a wide spectrum of applications, such as metrology, video surveillance, augmented reality presentation, virtual content insertion and 3-D reconstruction to provide the geometric mapping between 2-D image positions and 3-D real-world coordinates [2,3,4]. Several methods have been proposed to accomplish this task.

Camera calibration methods that use collinear points on a 1-D object with rotation, planar motion, general motion and non-collinear points under special motion require two or more images of the reference object, while it would be more practical if the calibration method required only a single image. One common technique is to take 2-D images of a reference object and then estimate both intrinsic and extrinsic parameters from the 2-D images based on a camera model [1]. Using an accurate 3-D reference point, one can obtain precise camera parameters by applying 3-D reference object-based calibration algorithms [5,6,7]. A 2-D plane-based calibration method [8,9,10] is more desired because the 2-D paper on which a checker pattern is sketched is easily available, compared to a precise 3-D reference object. A camera calibration scheme that uses a simple reference object is more preferred in the real world, as it results in systems with quickly response to various camera configurations in both outdoor and indoor applications.

Self-calibration is discussed in many previous works [11,12,13,14]. It estimates camera parameters from feature points in an image scene without any reference object. However, it needs many reliable feature points and multiple image views in order to extract accurately camera parameters, as a drawback.

An important type of techniques that usually use a stick consisting of at least three points to calibrate camera parameters is 1-D calibration techniques. The method using 1-D object proposed by Zhang [15] has a simpler structure than the 2-D model plane. This calibration technique uses a terminal point as a fixed reference point and rotates a 1-D object around it. For this calibration technique, at least six views of the 1-D object are required with three collinear points as reference.

Many other researchers have been inspired by Zhang’s algorithm. The degenerate cases or critical motions, where the above 1-D object-based calibration fails, are studied by Hammarstedt et al. [16]. In [17], it has been shown that the rotating 1-D object is in essence equivalent to a 2-D planar calibration object, and also shown that when the object undergoes planar motion, the calibration principle still holds. Although the 1-D reference object is constrained to rotation and planar motion, Qi et al. [18] developed a camera calibration method using a 1-D object with general motion. Wang et al. [19] proposed a multi-camera calibration algorithm with a 1-D object under general motion. de Francca et al. [20] proposed a linear algorithm with the normalized image points, which significantly improved the accuracy of the calibration introduced in [15].

To avoid possible non-positive-definite values of the image of absolute conic (IAC), Wang et al. [21] minimized the norm of algebraic residuals considering to the constraint that the solution was positive definite. In [22], a calibration method using a single image and a special combination of two orthogonal 1-D objects is proposed. Each object has three collinear points, sharing a common one. The discussed calibration algorithm uses the five points to estimate the extrinsic parameters. This algorithm is very sensitive to distortion and its accuracy decreases dramatically as the distortion level increases. In [23], a more accurate algorithm based on weighted similarity invariant for camera calibration is proposed. However, it needs multiple images of rotated object to obtain the result which increases its overhead and complexity. Recently, Zhao et al. [24] have studied a camera calibration method using three non-collinear points. The algorithm needs some image of precisely rotated object to work. The final accuracy is strongly related to these rotations. The human body as a 1-D reference object also was used in order to estimate camera parameters from images of human faces [25] and walking humans [26].

It is important that the system operators have a flexible and simple calibration method to handle camera configurations and obtain camera parameters smoothly even out of laboratory. Such methods should offer a camera calibration technique using just one single simple object as reference. A well-known approach that uses a single image is the camera calibration based on vanishing points [1]. In [27], a calibration method has been discussed that uses vanishing points to estimate intrinsic parameters from a single camera and extrinsic parameters from a pair of cameras. Next, in [28] a method for measuring intrinsic parameters using vanishing points from one image of model planes has been developed. Cipolla et al. [29] proposed a method to compute both intrinsic and extrinsic parameters from three vanishing points and two reference points from two views. The vanishing points computed from static scene structures are used for camera calibration in [30, 31]. It is possible to use orthogonal 2-D model planes as one of the means to obtain both intrinsic and extrinsic parameters by using vanishing points from a single image. That is, one can estimate the intrinsic parameters from the vanishing points detected in the image and obtain the extrinsic parameters using plane homographies [7]. All above-mentioned algorithms suffer from the lack of accuracy and high complexity.

There has been a proliferation of research on sports video analysis in the recent years [32,33,34]. Camera calibration also plays a vital role in sports video analysis, enabling a variety of applications, such as semantic/tactic analysis [35], 3-D ball trajectory reconstruction [36] and free viewpoint video synthesis [37]. For sports videos, instead of setting up a calibration object, a passive object such as the court with a known 3-D model is often exploited to compute the camera projection matrix. One classical way is based on the detection of corresponding points, the reference points whose coordinates are known in both the 3-D real-world and the 2-D image, such as intersection points of court lines and characteristic points on court objects (e.g., a net post in tennis or badminton). Then by solving a set of linear equations obtained from these corresponding points, the camera projection matrix is computed [35]. In [38], a calibration technique based on geometric analysis is proposed. This method can estimate the camera parameters from just one view of only five corresponding points. Geometric analysis is used to realize camera calibration from four coplanar corresponding points and a fifth non-coplanar one. For applications of sports video analysis, it is also easy to find four planar points (e.g., intersections of court lines) and a non-planar one (e.g., a point on a court object).

In [39] and [40], a simple rectangular reference object is used for camera calibration. The proposed technique in [39] requires a single image having two vanishing points. Using four points of the object and the two vanishing points, it provides just the intrinsic parameters of camera. In [40], a single image of a scene rectangle of an unknown aspect ratio is used for camera calibration. It uses the vanishing points to center the quad and then rectifies the image to get a rectangle. The intrinsic and extrinsic parameters of camera are then extracted with the cost of using some iterative solutions.

In this paper, a new calibration algorithm using just one image and a simple 2-D reference object with four corner points is proposed. It is absolutely practical and one can even use an A4-size paper as the reference object and is very fast as it uses just one single image. The proposed method is of high applicability in many types of scenes. For example, in an indoor scene, one will be able to set four reference points on the floor (e.g., corners of ceramic tiles) to conduct our calibration method. In an outdoor scene, one can simply choose four preselected (vs. premarked) points on the ground as reference points. For applications of sports video analysis, it is also easy to find four reference points (e.g., intersections of court lines). The proposed method is very accurate, and compared to the other ones, it has less distortion sensitivity.

This paper is organized as follows: Sect. 2 describes the calculation of camera parameters based on four corner points of a 2-D reference object. The camera calibration algorithm is discussed in Sect. 3. Section 4 provides simulations and experimental results, and finally, Sect. 5 provides conclusions.

2 Mathematic fundamental of propose method

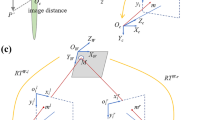
Suppose points $P_{1}^{\prime }$ to $P_{4}^{\prime }$ are the corner points of the reference object in $X^{\prime } ,Y^{\prime } ,Z^{\prime }$ coordinate system as in Fig. 1. The corresponding points on the image plane are named as $a_{1}$ to $a_{4}$. The relation between these eight points can be described by:

Fig. 1

Space location of camera and reference object

$$ \begin{array}{*{20}l} {a_{j} = \left[ {\begin{array}{*{20}c} {x_{j} } \\ {y_{j} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {U_{j} } \\ {V_{j} } \\ {S_{j} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} f & 0 & {x_{0 } } \\ 0 & f & {y_{0 } } \\ 0 & 0 & {1 } \\ \end{array} \begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} R & T \\ 0 & 1 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {X^{{\prime }}_{j} } \\ {Y^{{\prime }}_{j} } \\ {\begin{array}{*{20}c} {Z^{{\prime }}_{j} } \\ 1 \\ \end{array} } \\ \end{array} } \right]} \hfill \\ {x_{j} = \frac{{U_{j} }}{{S_{j} }}\quad y_{j} = \frac{{V_{j} }}{{S_{j} }},\quad {\text{for}} \; j = 1,2,3,4} \hfill \\ \end{array} $$

(1)

$$\begin{aligned} R &= R_{X} \times R_{Y} \times R_{Z} = \left[ {\begin{array}{*{20}c} 1 &\quad 0 &\quad 0 \\ 0 &\quad {\cos \left( {\theta_{x} } \right)} &\quad { - \sin \left( {\theta_{x} } \right)} \\ 0 &\quad {\sin \left( {\theta_{x} } \right)} &\quad {\cos \left( {\theta_{x} } \right)} \\ \end{array} } \right] \\ & \quad \times \left[ {\begin{array}{*{20}c} {\cos \left( {\theta_{y} } \right)} &\quad 0 &\quad {\sin \left( {\theta_{y} } \right)} \\ 0 &\quad 1 &\quad 0 \\ { - \sin \left( {\theta_{y} } \right)} &\quad 0 &\quad {\cos \left( {\theta_{y} } \right)} \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {\cos \left( {\theta_{z} } \right)} &\quad { - \sin \left( {\theta_{z} } \right)} &\quad 0 \\ {\sin \left( {\theta_{z} } \right)} &\quad {\cos \left( {\theta_{z} } \right)} &\quad 0 \\ 0 &\quad 0 &\quad 1 \\ \end{array} } \right] \end{aligned}$$

(2)

$$ T = \left[ {\begin{array}{*{20}c} {T_{X} } \\ {T_{Y} } \\ {T_{Z} } \\ \end{array} } \right] $$

(3)

in which f is the camera focal length, R is rotation matrix and T is camera translation vector into space coordinates (Eqs. 2, 3). We will consider that f is equal in x and y directions, principal point is projection center and there is no lens distortion to simplify equations.

It is desired to obtain extrinsic parameters of camera in space coordinates from intrinsic parameters of it. With today’s technology, the image center coordinates of the camera are available and we take them as initial values.

To solve this problem, suppose that reference object is moved to the center of camera coordinates which is ($X,Y,Z$) by rotation matrix of R and translation matrix of T, as shown in Fig. 2. The camera coordinates of the corner points of the reference object is now as follows:

Fig. 2

Reference object transferred to camera origin coordinates

$$\begin{aligned} P_{1}^{{\prime }} &= \left[ {\begin{array}{*{20}c} {l_{1} } \\ {l_{2} } \\ 0 \\ \end{array} } \right]\quad P_{2}^{{\prime }} = \left[ {\begin{array}{*{20}c} { - l_{1} } \\ {l_{2} } \\ 0 \\ \end{array} } \right]\quad P_{3}^{{\prime }} = \left[ {\begin{array}{*{20}c} { - l_{1} } \\ { - l_{2} } \\ 0 \\ \end{array} } \right]\\ & \quad P_{4}^{{\prime }} = \left[ {\begin{array}{*{20}c} {l_{1} } \\ { - l_{2} } \\ 0 \\ \end{array} } \right] \end{aligned}$$

(4)

in which $l_{1}$ and $l_{2}$ are halves of reference object dimensions.

Equation (5) shows the relation between $P_{j}^{{\prime }}$ and $P_{j}$ points.

$$ P_{j} = \left[ {\begin{array}{*{20}c} {X_{{P_{j} }} } \\ {Y_{{P_{j} }} } \\ {Z_{{P_{j} }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R^{\text{T}} } & { - R^{\text{T}} T} \\ 0 & 1 \\ \end{array} } \right] \times P_{j} ^{{\prime }} \quad j = 1,2,3,4 $$

(5)

As a result, the coordinates of image points is calculated as:

$$ \begin{aligned} & {\left[ {\begin{array}{*{20}c} {U_{j} } \\ {V_{j} } \\ {S_{j} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} f & {\quad 0} & {\quad x_{0} } & {\quad 0} \\ 0 & {\quad f} & {\quad y_{0} } & {\quad 0} \\ 0 & {\quad 0} & {\quad 1} & {\quad 0} \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {X_{{P_{j} }} } \\ {Y_{{P_{j} }} } \\ {Z_{{P_{j} }} } \\ \end{array} } \\ 1 \\ \end{array} } \right]} \hfill \\ & a_{j} = \left[ {\begin{array}{*{20}c} {x_{{a_{j} }} } \\ {y_{{a_{j} }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{U_{j} }}{{S_{j} }}} \\ {\frac{{V_{j} }}{{S_{j} }}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{f \times X_{{P_{j} }} }}{{Z_{{P_{j} }} }} + x_{0} } \\ {\frac{{f \times Y_{{P_{j} }} }}{{Z_{{P_{j} }} }} + y_{0} } \\ \end{array} } \right] ,\\ & \quad {\text{for}}\; j = 1,2,3,4 \end{aligned} $$

(6)

Having the image of reference object, the $a_{j}$, and actual reference object corners, the $P_{j}^{{\prime }}$, using (5), (6) ($l_{1}$, $l_{2}$ and $a_{1}$ to $a_{4}$ are known) one can calculate unknown $R$, $T$ and $f$ as follows.

Defining $B_{j} ,a,b,c,D_{2j} ,D_{1j}$ as in Eq. (7) to (2).

$$ B_{j} = \left( {\frac{{x_{{a_{j} }} - x_{0} }}{f}} \right)/\left( {\frac{{y_{{a_{j} }} - y_{0} }}{f}} \right),\quad {\text{for}}\; j = 1 \;{\text{to}}\; 4 $$

(7)

$$ a = { \cos }\left( {\theta_{y} } \right) \times { \cos }\left( {\theta_{z} } \right) $$

(8)

$$ b = { \sin }\left( {\theta_{x} } \right) \times { \sin }\left( {\theta_{y} } \right) \times { \cos }\left( {\theta_{z} } \right) $$

(9)

$$ c = { \cos }\left( {\theta_{x} } \right) \times { \sin }\left( {\theta_{z} } \right) $$

(10)

$$ D_{2j} = B_{j} \times \cot \left( {\theta_{z} } \right) - 1,\quad {\text{for}} \;j = 1 \;{\text{to }}\;4 $$

(11)

$$ D_{1j} = - 1 - B_{j} \times \tan \left( {\theta_{z} } \right),\quad {\text{for}}\; j = 1\; {\text{to}}\; 4 $$

(12)

These abstract equations are concluded:

$$\begin{aligned} &\left( {l_{1} - T_{X} } \right)a + \left( {l_{2} - T_{Y} } \right)\left[ {b + c\frac{{D_{21} }}{{D_{11} }}} \right] \\ & \quad - T_{Z} \left[ { - b\cot \left( {\theta_{x} } \right) + c{ \tan }\left( {\theta_{x} } \right)\frac{{D_{21} }}{{D_{11} }}} \right] = 0 \end{aligned}$$

(13)

$$ \begin{aligned} &\left( { - l_{1} - T_{X} } \right)a + \left( {l_{2} - T_{Y} } \right)\left[ {b + c\frac{{D_{22} }}{{D_{12} }}} \right]\\ & \quad - T_{Z} \left[ { - b\cot \left( {\theta_{x} } \right) + c{ \tan }\left( {\theta_{x} } \right)\frac{{D_{22} }}{{D_{12} }}} \right] = 0 \end{aligned}$$

(14)

$$\begin{aligned} & \left( { - l_{1} - T_{X} } \right)a + \left( { - l_{2} - T_{Y} } \right)\left[ {b + c\frac{{D_{23} }}{{D_{13} }}} \right]\\& \quad - T_{Z} \left[ { - b\cot \left( {\theta_{x} } \right) + c{ \tan }\left( {\theta_{x} } \right)\frac{{D_{23} }}{{D_{13} }}} \right] = 0 \end{aligned}$$

(15)

$$ \begin{aligned} &\left( {l_{1} - T_{X} } \right)a + \left( { - l_{2} - T_{Y} } \right)\left[ {b + c\frac{{D_{24} }}{{D_{14} }}} \right] \\ & \quad - T_{Z} \left[ { - b\cot \left( {\theta_{x} } \right) + c{ \tan }\left( {\theta_{x} } \right)\frac{{D_{24} }}{{D_{14} }}} \right] = 0 \end{aligned}$$

(16)

Solving the above equations will result in:

$$ Q_{1} = \frac{{D_{21} }}{{D_{11} }} - \frac{{D_{22} }}{{D_{12} }} - \frac{{D_{23} }}{{D_{13} }} + \frac{{D_{24} }}{{D_{14} }} $$

(17)

$$ Q_{2} = \frac{{D_{21} }}{{D_{11} }} - \frac{{D_{22} }}{{D_{12} }} + \frac{{D_{23} }}{{D_{13} }} - \frac{{D_{24} }}{{D_{14} }} $$

(18)

$$ K_{1} = \frac{{Q_{1} }}{{Q_{2} }} $$

(19)

$$ K_{2} = \frac{{4 \times l_{1} }}{{l_{2} \times \left( {K_{1}^{2} - 1} \right) \times Q_{2} }} $$

(20)

$$ K_{3} = - \frac{{K_{2} }}{2}\left( {\frac{{D_{23} }}{{D_{13} }} + \frac{{D_{22} }}{{D_{12} }}} \right) - \frac{{K_{1} \times K_{2} }}{2}\left( {\frac{{D_{23} }}{{D_{13} }} - \frac{{D_{22} }}{{D_{12} }}} \right) $$

(21)

$$ K_{4} = - { \tan }\left( {\theta_{x} } \right) $$

(22)

$$ K_{5} = l_{2} \times K_{1} $$

(23)

$$ K_{6} = K_{3} \times \left[ {\cot \left( {\theta_{x} } \right) + { \tan }\left( {\theta_{x} } \right)} \right] $$

(24)

$$\begin{aligned} K_{7} &= \frac{{l_{2} }}{2}\left[ {K_{2} \left( {\frac{{D_{21} }}{{D_{11} }} - \frac{{D_{23} }}{{D_{13} }}} \right)}\right. \\ & \quad \left.{- K_{1} \left[ {2 \times K_{3} + K_{2} \left( {\frac{{D_{21} }}{{D_{11} }} + \frac{{D_{23} }}{{D_{13} }}} \right)} \right]} \right] \end{aligned}$$

(25)

$$ T_{Y} = K_{4} \times T_{Z} + K_{5} $$

(26)

$$ c = K_{2} \times a $$

(27)

$$ b = K_{3} \times a $$

(28)

$$ T_{X} = K_{6} \times T_{Z} + K_{7} $$

(29)

Define $g_{j}$ variables for j = 1–4 as Eq. (30) and parameters $H_{1}$ and $H_{2}$ as in Eqs. (31) and (32).

$$ g_{j} = x_{aj} - x_{0} ,\quad {\text{for}} j = 1 \;{\text{to}}\; 4 $$

(30)

$$ H_{1} = \frac{{l_{1} + l_{2} \times \left( {K_{2} + K_{3} } \right)\left( {1 - K_{1} } \right) - K_{7} }}{{g_{1} }} $$

(31)

$$ H_{2} = \frac{{ - l_{1} + l_{2} \times \left( {K_{2} + K_{3} } \right)\left( {1 - K_{1} } \right) - K_{7} }}{{g_{2} }} $$

(32)

Now substituting $g_{j}$, $H_{1}$ and $H_{2}$ in Eqs. (5) and (6), one can reach Eqs. (33) and (34).

$$\begin{aligned} H_{1} \times f {\text{cos}}\left( {\theta_{z} } \right) &= \left( {l_{1} - T_{X} } \right){ \tan }\left( {\theta_{y} } \right) - \left( {l_{2} - T_{Y} } \right)\\ & \quad \times \sin \left( {\theta_{x} } \right) - T_{z} { \cos }\left( {\theta_{x} } \right) \end{aligned}$$

(33)

$$\begin{aligned} H_{2} \times f {\text{cos}}\left( {\theta_{z} } \right) &= \left( { - l_{1} - T_{X} } \right){ \tan }\left( {\theta_{y} } \right) - \left( {l_{2} - T_{Y} } \right)\\ & \quad \times \sin \left( {\theta_{x} } \right) - T_{z} { \cos }\left( {\theta_{x} } \right) \end{aligned}$$

(34)

Subtracting (34) from (33), $\theta_{y}$ can be obtained as:

$$ \theta_{y} = { \arctan }\left( {\frac{{\left( {H_{1} - H_{2} } \right)f{ \cos }\left( {\theta_{z} } \right)}}{{2 \times l_{1} }}} \right) $$

(35)

Using (27) and (8) and (10), $\theta_{x}$ is calculated as:

$$ \theta_{x} = { \arccos }\left( {K_{2} \frac{{{ \cos }\left( {\theta_{y} } \right){ \cos }\left( {\theta_{z} } \right)}}{{{ \sin }\left( {\theta_{z} } \right)}}} \right) $$

(36)

In the next step, using Eqs. (26), (29) and (33) will result in $T_{Z}$ as:

$$ T_{Z} = \frac{{H_{1} f{ \cos }\left( {\theta_{z} } \right) + \left( {K_{7} - l_{1} } \right)\tan \left( {\theta_{y} } \right) + \left( {K_{5} - l_{2} } \right){ \sin }\left( {\theta_{x} } \right)}}{{ - K_{6} \tan \left( {\theta_{y} } \right) + K_{4} \sin \left( {\theta_{x} } \right) - { \cos }\left( {\theta_{x} } \right)}} $$

(37)

Till now, the rotation angle values, $\theta_{x}$ and $\theta_{y}$, and translation vectors ($T_{X}$$T_{Y}$$T_{Z}$) have been obtained based on the $\theta_{z}$ value. Assume $H_{3}$ defined as in Eqs. (38):

$$ H_{3} = \frac{{ - l_{1} + l_{2} \times \left( {K_{2} + K_{3} } \right)\left( { - 1 - K_{1} } \right) - K_{7} }}{{g_{3} }} $$

(38)

Rewriting Eq. (33) for j = 3, we have:

$$ \begin{aligned}H_{3} \times f {\text{cos}}\left( {\theta_{z} } \right) &= \left( { - l_{1} - T_{X} } \right){ \tan }\left( {\theta_{y} } \right) - \left( { - l_{2} - T_{Y} } \right)\\ & \quad \times \sin \left( {\theta_{x} } \right) - T_{z} { \cos }\left( {\theta_{x} } \right) \end{aligned}$$

(39)

Considering (28), (33), (34) and (39), one can show that

$$ \left( {H_{1} - H_{2} } \right)\left( {H_{2} - H_{3} } \right)f^{2} { \cos }^{2} \left( {\theta_{z} } \right) + 4l_{1} l_{2} K_{3} = 0 $$

(40)

Now the focal length $f$ can be calculated as:

$$ f = \sqrt {\frac{{ - 4l_{1} l_{2} K_{3} }}{{\left( {H_{1} - H_{2} } \right)\left( {H_{2} - H_{3} } \right){ \cos }^{2} \left( {\theta_{z} } \right)}}} $$

(41)

To calculate $\theta_{z}$, we can follow the same routine. Rewriting Eq. (33) for j = 4 and assuming that $H_{4}$ is defined as in Eqs. (42), we reach Eq. (43).

$$ H_{4} = \frac{{l_{1} + l_{2} \times \left( {K_{2} + K_{3} } \right)\left( { - 1 - K_{1} } \right) - K_{7} }}{{g_{4} }} $$

(42)

$$\begin{aligned} H_{4} \times f {\text{cos}}\left( {\theta_{z} } \right) &= \left( {l_{1} - T_{X} } \right){ \tan }\left( {\theta_{y} } \right) - \left( { - l_{2} - T_{Y} } \right)\\ & \quad \times \sin \left( {\theta_{x} } \right) - T_{z} { \cos }\left( {\theta_{x} } \right) \end{aligned}$$

(43)

Considering Eqs. (33), (34), (41) and (43), one can show that:

$$ H_{1} - H_{4} = H_{2} - H_{3} $$

(44)

To simplify Eq. (44), assume that $m_{1}$ to $m_{4}$ are as in Eqs. (45)–(48).

$$ m_{1} = g_{1} g_{2} B_{3} B_{4} \left( {B_{1} - B_{2} } \right) $$

(45)

$$ m_{2} = g_{3} g_{4} B_{1} B_{2} \left( {B_{3} - B_{4} } \right) $$

(46)

$$ m_{3} = m_{1} \left( {\frac{{g_{4} }}{{B_{4} }} - \frac{{g_{3} }}{{B_{3} }}} \right) + m_{2} \left( {\frac{{g_{1} }}{{B_{1} }} - \frac{{g_{2} }}{{B_{2} }}} \right) $$

(47)

$$ m_{4} = m_{1} \left( {g_{3} - g_{4} } \right) + m_{2} \left( {g_{2} - g_{1} } \right) $$

(48)

Solving Eq. (48) now leads to the following equation which gives us the $\theta_{z}$ value:

$$ m_{3} - m_{4} \times \tan \left( {\theta_{z} } \right) = 0 $$

(49)

After finding the $\theta_{z}$ value, it is now possible to find all the camera extrinsic parameters.

3 Proposed computing algorithm

We summarize a calibration algorithm based on the above-derived equations as follows.

• 1. Determining corner points of the rectangular plane from image.

• 2. $B_{j}$ calculation using (7) and $g_{j}$ calculation using (30).

• 3. $\theta_{z}$ calculation using (49).

• 4. $D_{1j}$ and $D_{2j}$ calculation using (11) and (12).

• 5. $K_{1} , K_{2}$, $K_{3}$ and $K_{7}$ calculation using (19)–(21) and (25).

• 6. $H_{1}$, $H_{2}$ and $H_{3}$ calculation using (31), (32) and (38) and then $f$ calculation using (41).

• 7. Determining $\theta_{y}$ using (35).

• 8. Determining $\theta_{x}$ using (36).

• 9. $K_{4} , K_{5}$ and $K_{6}$ calculation using (22)–(24).

• 10. $T_{Z}$ calculation using (37).

• 11. $T_{Y}$ and $T_{X}$ calculation using (26) and (29).

Using the previous mentioned algorithm, all of the variables are calculated. Note that if $\theta_{z}$ is zero or $\frac{\pi }{2}$, Eqs. (11) and (12) will not result in $D_{1j}$ and $D_{2j}$, so the rest of the parameters will not be obtained and the algorithm will not work. This is not important because with careful choosing 2-D reference object position in 3-D space, it can be avoided.

So far, the camera is calibrated in relation to 2-D reference object coordinates. If the space coordinates is not the same as to 2-D reference object one, the camera should be calibrated in relation to space coordinates. To achieve this, it is sufficient to rotate and transform the space coordinates in relation to the 2-D reference object coordinates which are considered as follows:

$$ \left[ {\begin{array}{*{20}c} R &\quad T \\ 0 &\quad 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R_{S2} } &\quad {T_{S2} } \\ 0 &\quad 1 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {R^{{\prime }} } &\quad {T^{{\prime }} } \\ 0 &\quad 1 \\ \end{array} } \right] $$

(50)

in which $R_{S2}$ is the rotation matrix and $T_{S2}$ is the translation vector both calculated in above and $R^{{\prime }}$ and $T^{{\prime }}$ are the rotation matrix and the translation vector of the space coordinates in relation to 2-D reference object coordinates, respectively. Note that while the position of the 2-D reference object is available, $T^{{\prime }}$ and $R^{{\prime }}$ are available. So the camera is calibrated in relation to space coordinates.

The previous mentioned algorithm could be used for a multi-camera system. Since in a multi-camera system, all the cameras will not see the object necessarily, calculation of the extrinsic parameters will be a problem [41]. Considering that the 2-D plane used for the calibration is seen with all cameras or several 2-D planes are used in such a way that all of the cameras see one 2-D plane at least, the proposed algorithm could be used for all of the cameras of the multi-camera system. Since every camera has its own coordination system, the extrinsic parameters of each camera should be transformed to the multi-camera coordination system. To accomplish this job, the method used in [22] could be used.

4 Simulation and experimental results

4.1 Computer-aided simulation

The 1-D and 2-D calibration methods presented in [22] and [7] have been used in comparison with our proposed method. An ASUS N501VW laptop with 12 GB DDRIV RAM and a core i7 6700HQ CPU is used to run the algorithms. For the 2-D algorithm of Ref [7], a uniform two-dimensional array of $8 \times 8$ points in a rectangle of $70 \times 70 \;{\text{cm}}^{2}$ is considered as in Fig. 3, with h1 = 70 cm, h2 = 35 cm, d3 = 70 cm, d4 = 35 cm for the proposed object of [22]. It is assumed that camera has a focal length of 1700, unity aspect ratio, zero skew and lens distortion with the principle point at (500, 500). The image resolution is $1000 \times 1000$. The extrinsic parameters of camera are given in Table 1.

Fig. 3

Chessboard as a reference object

Table 1 Extrinsic parameters for simulation

To evaluate the effect of distortion, a Gaussian noise with zero mean and different values of STD, between 1 and 6 pixels, is added to the position of $8 \times 8$ reference points in the image.

For each value of injected distortion, the algorithm is performed 1000 times and the absolute average error and total simulation time per each method are measured. Table 2 shows the results and it is clear that by increasing the distortion STD, our proposed method outperforms the rivals and in STD = 6, the maximum angle error of our algorithm is almost less than the minimum of [22] algorithm with STD = 1.

Table 2 Simulation results for different values of distortion STD

In addition, the proposed algorithm is three times faster than [22] and seven times faster than [7].

The results in Table 2 are used to draw graphs in Figs. 4 and 5 in which the vertical axes are logarithmic to present the difference. Figure 5a and b shows the average attitude measurement error, consisting of location error and orientation error, respectively. The focal length measuring error is reported in Fig. 5c. Again one can see that the present method has least distortion sensitivity especially when the distortion increases.

Fig. 4

Comparison of our method to the existing methods

Fig. 5

Comparison of our method to the existing methods. a Average location error; b orientation error; c focal length error

4.2 Data calculated using Autodesk 3ds Max 2013

Here Autodesk 3ds Max 2013 is used to generate reference images as in Figs. 6, 7 and 8. In these images, the chessboard size is $30 \times 40\;{\text{cm}}^{2}$. For Ref. [22], parameters are h1 = 30 cm, h2 = 15 cm, d3 = 40 cm, d4 = 20 cm, while Ref. [7] uses the 64 points in the chessboard as before. Calibration result comparison of three calibration methods with the image produced with Autodesk 3ds Max 2013 (Fig. 6) is given in Table 3.

Fig. 6

Generated image by 3ds Max software for calibration

Fig. 7

Rotated image generated by 3ds Max software for calibration algorithm comparison

Fig. 8

Third image generated by 3ds Max software required for calibration proposed in [7]

Table 3 Calibration result comparison for image 6

Considering the previous explanations for our algorithm and its disability near $\theta_{z} = 0$, now we rotate the image in respect to z-axis which is shown in Fig. 7. Calibration result comparison is given in Table 4. The third image required for calibration method in [7] is shown in Fig. 8.

Table 4 Calibration result comparison for image 7

As given in Table 4, the proposed algorithm is practically more accurate than other algorithms.

4.3 Experimental results

In this section, the validity of the proposed method is assessed by the experimental results. For this purpose, Microsoft Camera Calibration data set is applied [42].

In this data set, the reference object which is like a chessboard has dimensions of 17 cm × 17 cm. Ref [7] uses all the 256 corner points in the reference object, while ref [22] uses just five points, three corner points and two on the outside edges. For this algorithm, we have h1 = 17 cm, h2 = 10.256 cm, d3 = 17 cm, d4 = 10.256 cm.

Ref [7] needs at least three reference images, and the images shown in Figs. 9, 10 and 11 are used for this method. Our proposed method and Ref [22] need just one image to work. Tables 5 and 6 show the results of three calibration methods of images in Figs. 9 and 10. Ref [7] corresponding data in Tables 5 and 6 have similar intrinsic parameters, while there are extrinsic data in Figs. 9 and 10.

Fig. 9

Selected image from Microsoft Camera Calibration data set for calibration

Fig. 10

Rotated image selected from Microsoft Camera Calibration data set for calibration algorithm comparison

Fig. 11

Third image selected from Microsoft Camera Calibration data set required for calibration proposed in [7]

Table 5 Calibration result comparison for image 9

Table 6 Calibration result comparison for image 10

Looking carefully at Tables 5 and 6, we can say that our proposed method accuracy is somewhere between Refs [7] and [22]. When the reference object normal is not along the camera z-axis, our algorithm works better and the results are similar to those of Ref [7] as given in Table 6 which is related to Fig. 10. We must consider that the image used in data set has a lot of lens distortion which reduces the accuracy of our method.

5 Conclusion

In these papers, a mathematic calibration method to find all extrinsic and intrinsic parameters of a camera using just one 2-D reference object is proposed. Then the accuracy of the method during different distortions is evaluated. Using images obtained with 3ds Max software, the algorithm is simulated. Finally the method is applied to Microsoft Camera Calibration data set for obtaining experimental results. For comparison, works in [7, 22] are considered.

Considering the results, the proposed method has the least distortion sensitivity and computational load, while its accuracy is slightly less than the 2-D calibration method and much better than 1-D ones. In addition, the used reference object is the most simple and available among other rivals and so the proposed method has suitable for applications of sports video analysis.

Appendix

1.1 How to get a relationship from (13)–(16) to (17)–(35)

Summing Eqs. (13) and (14), we have:

$$\begin{aligned} &- 2T_{X} a + \left( {l_{2} - T_{Y} } \right)\left[ {2b + c\left( {\frac{{D_{21} }}{{D_{11} }} + \frac{{D_{22} }}{{D_{12} }}} \right)} \right] \\ & \quad - T_{Z} \left[ { - 2b\cot \left( {\theta_{x} } \right) + c{ \tan }\left( {\theta_{x} } \right)\left( {\frac{{D_{21} }}{{D_{11} }} + \frac{{D_{22} }}{{D_{12} }}} \right)} \right] = 0 \end{aligned}$$

(51)

Summing Eqs. (13) and (15), we have:

$$\begin{aligned} &- 2T_{X} a + l_{2} c\left( {\frac{{D_{21} }}{{D_{11} }} - \frac{{D_{23} }}{{D_{13} }}} \right) - T_{Y} \left[ {2b + c\left( {\frac{{D_{21} }}{{D_{11} }} + \frac{{D_{23} }}{{D_{13} }}} \right)} \right]\\ & \quad - T_{Z} \left[ { - 2b\cot \left( {\theta_{x} } \right) + c{ \tan }\left( {\theta_{x} } \right)\left( {\frac{{D_{21} }}{{D_{11} }} + \frac{{D_{23} }}{{D_{13} }}} \right)} \right] = 0 \end{aligned}$$

(52)

Summing Eqs. (13) and (16), we have:

$$\begin{aligned} &2\left( {l_{1} - T_{X} } \right)a + l_{2} c\left( {\frac{{D_{21} }}{{D_{11} }} - \frac{{D_{24} }}{{D_{14} }}} \right) \\ & \quad - T_{Y} \left[ {2b + c\left( {\frac{{D_{21} }}{{D_{11} }} + \frac{{D_{24} }}{{D_{14} }}} \right)} \right] \\ & \quad - T_{Z} \left[ { - 2b\cot \left( {\theta_{x} } \right) + c{ \tan }\left( {\theta_{x} } \right)\left( {\frac{{D_{21} }}{{D_{11} }} + \frac{{D_{24} }}{{D_{14} }}} \right)} \right] = 0 \end{aligned}$$

(53)

Summing Eqs. (14) and (15), we have:

$$\begin{aligned} &2\left( { - l_{1} - T_{X} } \right)a + l_{2} c\left( {\frac{{D_{22} }}{{D_{12} }} - \frac{{D_{23} }}{{D_{13} }}} \right) \\ & \quad - T_{Y} \left[ {2b + c\left( {\frac{{D_{22} }}{{D_{12} }} + \frac{{D_{23} }}{{D_{13} }}} \right)} \right] \\ & \quad - T_{Z} \left[ { - 2b\cot \left( {\theta_{x} } \right) + c{ \tan }\left( {\theta_{x} } \right)\left( {\frac{{D_{22} }}{{D_{12} }} + \frac{{D_{23} }}{{D_{13} }}} \right)} \right] = 0 \end{aligned}$$

(54)

Summing Eqs. (14) and (16), we have:

$$ \begin{aligned}&- 2T_{X} a + l_{2} c\left( {\frac{{D_{22} }}{{D_{12} }} - \frac{{D_{24} }}{{D_{14} }}} \right) - T_{Y} \left[ {2b + c\left( {\frac{{D_{22} }}{{D_{12} }} + \frac{{D_{24} }}{{D_{14} }}} \right)} \right] \\ & \quad - T_{Z} \left[ { - 2b\cot \left( {\theta_{x} } \right) + c{ \tan }\left( {\theta_{x} } \right)\left( {\frac{{D_{22} }}{{D_{12} }} + \frac{{D_{24} }}{{D_{14} }}} \right)} \right] = 0 \end{aligned}$$

(55)

Now subtracting Eq. (52) from (55) and keeping in mind that $Q_{1} ,Q_{2} ,K_{1} ,K_{2} ,K_{4} ,K_{5}$ are defined as Eqs. (17–20) and (22–23), we reach Eq. (26). In the same way, Eq. (27) is obtained from subtracting Eq. (53) from (54).

Substituting Eqs. (22), (23), (26) and (27) in Eqs. (51) and (52), one can reach Eqs. (56) and (57), respectively.

$$ \begin{aligned}&- 2T_{X} a + l_{2} \left( {1 - K_{1} } \right)\left[ {2b + K_{2} a\left( {\frac{{D_{21} }}{{D_{11} }} + \frac{{D_{22} }}{{D_{12} }}} \right)} \right] \\ & \quad+ 2bT_{Z} \left[ {\cot \left( {\theta_{x} } \right) + {\text{tan}}\left( {\theta_{x} } \right)} \right] = 0 \end{aligned}$$

(56)

$$\begin{aligned} &- 2T_{X} a + l_{2} K_{2} a\left( {\frac{{D_{22} }}{{D_{12} }} - \frac{{D_{24} }}{{D_{14} }}} \right)\\ & \quad - l_{2} K_{1} \left[ {2b + K_{2} a\left( {\frac{{D_{22} }}{{D_{12} }} + \frac{{D_{24} }}{{D_{14} }}} \right)} \right] \\ & \quad + 2bT_{Z} \left[ {\cot \left( {\theta_{x} } \right) + {\text{tan}}\left( {\theta_{x} } \right)} \right] = 0 \end{aligned}$$

(57)

Again subtracting Eq. (56) from (57) and keeping in mind that $K_{3}$ is defined as Eq. (21), we reach Eq. (28). Finally with the assumption that $K_{6 ,} K_{7}$ as defined in Eqs. (24, 25), substituting Eq. (28) in Eq. (57) one can reach Eq. (29).