Nodal Discretization of Two-Phase Discrete Fracture Matrix Models

Abstract

This chapter reviews the nodal Vertex Approximate Gradient (VAG) discretization of two-phase Darcy flows in fractured porous media for which the fracture network is represented as a manifold of co-dimension one with respect to the surrounding matrix domain. Different types of models and their discretizations are considered depending on the transmission conditions set at matrix fracture interfaces accounting for fractures acting either as drains or both as drains or barriers. Difficulties raised by nodal discretizations in heterogeneous media are investigated and solutions to solve these issues are discussed. It includes the adaptation of the porous volumes at nodal unknowns and discontinuous saturations accounting for the jumps induced by the discontinuity in space of the capillary pressure functions. A new Multi-Point upwind scheme is also introduced for the approximation of the mobilities at matrix fracture interfaces to address the issue of fluxes not defined at faces. The most accurate approach is based on the extension of the discontinuous pressure model to two-phase Darcy flows taking into account the discontinuities of both the pressures and saturations at matrix fracture interfaces. As opposed to single phase flows, It improves the accuracy even in the case of fracture acting as drains. On the other hand this approach can still exhibit a robustness issue in terms of nonlinear convergence.

3.1 Introduction

Many real life applications in the geosciences like oil and gas recovery, basin modelling, energy storage, geothermal energy or hydrogeology involve two-phase Darcy flows in heterogeneous porous media. Such models are governed by nonlinear partial differential equations typically coupling elliptic and degenerate parabolic equations. Next to the inherent difficulties posed by such equations, further challenges are due to the heterogeneity of the medium and the presence of discontinuities like fractures. This has a strong impact on the complexity of the models, challenging the development of efficient simulation tools.

This work focuses on the numerical modelling of two-phase Darcy flows in fractured porous media, for which the fracture network is represented as a manifold of co-dimension one with respect to the matrix domain. These reduced models are obtained by averaging the physical unknowns as well as the conservation equations along the fracture width. They are termed hybrid-dimensional or also Discrete Fracture Matrix (DFM) Darcy flow models. Given the high geometrical complexity of real life fracture networks, the main advantages of these hybrid-dimensional compared with equi-dimensional models are both to facilitate the mesh generation and the discretisation of the model, and to reduce the computational cost of the resulting schemes. This type of hybrid-dimensional models is the object of intensive researches since the last 15 years due to the ubiquity of fractures in geology and their considerable impact on the flow and transport in the porous medium.

DFM models are closed with appropriate transmission conditions at matrix fracture (mf) interfaces which differ for fractures acting as drains or as barriers. For single-phase flows there are two major approaches. The first, designed for modelling highly conductive fractures and referred to as continuous pressure model [7, 17], assumes the continuity of the fluid pressure at the mf interfaces. The second approach, referred to as discontinuous pressure model [10, 15, 24, 32, 33, 39, 41], allows to represent fractures acting as permeability barriers by imposing Robin-type transmission conditions at mf interfaces.

When the modelling of two-phase flow is concerned, three major types of models can be distinguished. The first and most common type is based on a straightforward adaptation of the single-phase continuous pressure model to the two-phase setting (see [13, 14, 20, 38, 43, 44]), it assumes the continuity of each phase pressure at mf interfaces which allows to capture the saturation jump for fractures acting as drains and matrix as barrier. As for single-phase flow, this approach cannot account for fractures acting as barriers. In contrast to the single-phase context, let us stress that, due to heterogeneous capillary pressures, fractures having a large absolute permeability may still act as barriers for a given phase, typically for the wetting phase for fractures filled by the non-wetting phase (see [1]). Another existing type of models, accounting for both drains or permeability barriers, is based on the linear (without mobility but including gravity) single-phase Darcy flux conservation equation imposed at mf interfaces for each phase. It is usually combined with Two-Point [1, 41] or Multi-Point [4, 5, 36, 46, 51, 52] cell-centred finite volume schemes for which the interfacial discontinuous pressures are eliminated when building the single phase Darcy flux transmissibilities. These models account for the discontinuity of the pressures but not of the mobilities at mf interfaces. Both previous types of models are based on linear mf transmission conditions. The last type of models considers nonlinear mf transmission conditions which are based on the nonlinear (including mobility) two-phase normal flux continuity equations at mf interfaces. This type of models is considered in [1, 2, 6, 16, 25, 26] using a two-point flux approximation in the fracture width with upwinding of the mobilities, and in [3, 40] using a global pressure formulation. Such nonlinear transmission conditions account for the discontinuity of both the phase pressures and the mobilities at mf interfaces. A comparison of these three types of models using reference equi-dimensional solutions can be found in [1, 16].

Having in mind that tetrahedral meshes are commonly used to cope with the geometrical complexity of fracture networks, nodal discretizations of DFM two-phase Darcy flow models have a clear advantage over cell-centred or face based discretizations thanks to their much lower number of degrees of freedom (d.o.f.). This is in particular the case when considering fully coupled implicit time integration which are necessary to avoid severe time step restrictions in high velocity regions such as fractures and to account for the strong coupling between the pressure and saturation unknowns at mf interfaces [9]. Alternatively, cell centred discretizations have been considered for DFM two-phase flow models using the Two-Point Flux Approximation (TPFA) as in [1, 6, 41] or Multi-Point Flux Approximations (MPFA) as in [5, 36, 52]. Face based discretizations have been considered in [3, 38] using the Mixed Hybrid Finite Element (MHFE) method and in [2, 37] using the Hybrid Finite Volume (HFV) scheme. Non conforming discretizations have also been developed for this type of models using XFEM discretizations as in [34] or Embedded Discrete Fracture Models as in [50].

Nodal discretizations, such as the Control Volume Finite Element (CVFE) method, have been first introduced in [20, 35, 43, 44] for DFM two-phase Darcy flow models with continuous pressures at mf interfaces accounting for fractures acting as drains. In this work, we review the Vertex Approximate Gradient (VAG) discretization introduced in [13, 14, 53] for continuous pressure models and in [16, 25] for discontinuous pressure models. The VAG scheme is based on nodal d.o.f. like CVFE methods but it also includes the cell d.o.f. which are eliminated at the linear algebra level at each Newton iteration without any fill-in. These cell d.o.f. provide an additional flexibility in the design of the discretization allowing to cope with traditional issues raised at mf interfaces by nodal discretizations of the transport equation. On practical meshes, for which the cell sizes at mf interfaces are much larger than the fracture width, these issues are induced by the use of dual control volumes combined with heterogeneous petrophysical and hydrodynamical properties defined on the primal mesh.

The outline of the remaining of this article is as follows. Section 3.2 describes the DFM continuous and discontinuous pressure two-phase Darcy flow models as introduced in [13, 16]. Section 3.3 presents the VAG discretizations of DFM continuous pressure two-phase Darcy flow models. Several techniques to cope with the issues raised by nodal discretizations at mf interfaces are discussed, including the adaptation of the control volumes at mf interfaces, a new Multi-Point upwind approximation of the mobilities in Sect. 3.3.3, and taking into account the saturation jump for general capillary pressure curves in Sect. 3.3.5. Section 3.4 reviews the VAG discretizations of the three types of DFM discontinuous pressure two-phase Darcy flow models as presented in [16, 25]. For each type of model and its VAG discretization, numerical experiments are exhibited on 2D and 3D DFM models including comparisons of the VAG discretizations to a face based scheme, as well as the comparison between the hybrid-dimensional DFM models and the reference equi-dimensional model.

3.2 Two-Phase DFM Discontinuous and Continuous Pressure Models

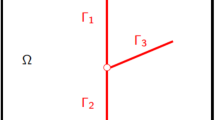
Let $\Omega$ be a bounded domain of $\mathbb {R}^d$, $d=2,3$ assumed to be polyhedral for $d=3$ and polygonal for $d=2$. To fix ideas, the dimension will be fixed to $d=3$ when it needs to be specified, for instance in the naming of the geometrical objects or for the space discretization. The adaptations to the case $d=2$ are straightforward. Let $\overline{\Gamma }= \bigcup _{i\in I} \overline{\Gamma }_i$ denotes the network of fractures $\Gamma _i\subset \Omega$, $i\in I$, such that each $\Gamma _i$ is a planar polygonal simply connected open domain included in some plane of $\mathbb {R}^d$ (see Fig. 3.1).

Fig. 3.1

Example of a 2D DFM with the matrix domain $\Omega$ and 3 intersecting fractures $\Gamma _i,i=1,2,3$

In the matrix domain $\Omega$, we denote by $\phi _m(\mathbf{x})$ the porosity and by $\Lambda _m(\mathbf{x})$ the permeability tensor. Along the fracture network $\mathbf{x}\in {\Gamma }$, we denote by $\phi _f(\mathbf{x})$ the porosity averaged on the fracture width and by $d_f(\mathbf{x})$ the fracture aperture. The permeability tensor is assumed constant along the width of the fracture and the normal vector to the fracture is assumed to be a principal direction. It results that we can define along the fracture network $\mathbf{x}\in {\Gamma }$, the tangential permeability tensor $\Lambda _f(\mathbf{x})$ and the normal permeability $\lambda _{n,f}(\mathbf{x})$.

It is assumed, for the sake of simplicity, that the matrix (resp. the fracture network) has a single rock type. Hence, for each phase $\alpha \in \{nw,w\}$ (where nw stands for the non-wetting phase and w for the wetting phase) we denote by $M_{m}^\alpha (s^\alpha )$ (resp. $M_{f}^\alpha (s^\alpha )$), the matrix (resp. fracture network) phase mobility, and by $P_{c,m}(s^{nw})$ (resp. $P_{c,f} (s^{nw})$), the matrix (resp. fracture network) capillary pressure function. The inverse of the monotone graph extension of the matrix (resp. fracture network) capillary pressure is denoted by $S_m^{nw}(p)$ (resp. $S_f^{nw}(p)$). We will also denote by $\rho ^\alpha$ the phase density which for the sake of simplicity is assumed constant for both phases $\alpha \in \{nw,w\}$.

Let $\alpha \in \{nw,w\}$, we denote by $u_m^\alpha$ (resp. $u_f^\alpha$) the phase pressure and by $s^{\alpha }_m$ (resp. $s^{\alpha }_f$) the phase saturation in the matrix (resp. the fracture network) domain. The Darcy velocity of phase $\alpha \in \{nw,w\}$ in the matrix domain is defined by

$$ \mathbf{q}_m^{\alpha } = - M_{m}^{\alpha }(s_{m}^{\alpha }) \Lambda _m( \nabla u_m^{\alpha } - \rho ^{\alpha }\mathbf{g}), $$

where $\mathbf{g}= -g \nabla z$ stands for the gravity vector with g the gravitational acceleration constant. The flow in the matrix domain is described by the volume balance equation

$$\begin{aligned} \phi _m \partial _t s_m^{\alpha } + \hbox { div}(\mathbf{q}_m^{\alpha }) = 0, \end{aligned}$$

(3.1)

for $\alpha \in \{nw,w\}$, and the closure laws defined by the macroscopic capillary pressure law together with the sum to one of the phase saturations

$$\begin{aligned} s^{nw}_m = S^{nw}_m( p_{c,m}), \quad p_{c,m}= u^{nw}_m - u^w_m, \quad s^{w}_m = 1 - s^{nw}_m. \end{aligned}$$

(3.2)

On the fracture network $\Gamma$, we denote by $\nabla _{\tau }$ the tangential gradient and by $\hbox { div}_{\tau }$ the tangential divergence. In addition, we can define the two sides ± of the fracture network $\Gamma$ in $\Omega \setminus \overline{\Gamma }$ and the corresponding unit normal vectors $\mathbf{n}^{\pm }$ at $\Gamma$ inward to the sides ±. Let $\gamma _{\mathbf{n}^{\pm }}$ (resp. $\gamma ^\pm$) formally denote the normal trace (resp. trace) operators at both sides of the fracture network $\Gamma$ for vector fields in $H_\mathrm{div}(\Omega \setminus \overline{\Gamma })$ (resp. scalar fields in $H^1(\Omega \setminus \overline{\Gamma })$. The Darcy tangential velocity of phase $\alpha \in \{nw,w\}$ in the fracture network ${\Gamma }$ integrated over the width of the fracture is defined by

$$ \mathbf{q}_{f}^{\alpha } = - d_f M_{f}^{\alpha }( s_{f}^{\alpha }) \Lambda _f (\nabla _{\tau } u_f^\alpha - \rho ^{\alpha } \mathbf{g}_{\tau }), $$

with $\mathbf{g}_{\tau } = \mathbf{g}- (\mathbf{g}\cdot \mathbf{n}^{+})\mathbf{n}^{+}$. The flow in the fracture network ${\Gamma }$ is described, for each phase $\alpha \in \{nw,w\}$, by the volume balance equation

$$\begin{aligned} d_f \phi _f \partial _t s_f^{\alpha } + \hbox { div}_{\tau }(\mathbf{q}_{f}^{\alpha }) + \gamma _{\mathbf{n}^+}\mathbf{q}^{\alpha }_m + \gamma _{\mathbf{n}^-}\mathbf{q}^{\alpha }_m = 0, \end{aligned}$$

(3.3)

and by the closure laws

$$\begin{aligned} s_f^{nw} = S_f^{nw}( p_{c,f}), \quad p_{c,f}= u^{nw}_f - u^w_f, \quad s_f^{w} = 1 - s_f^{nw}. \end{aligned}$$

(3.4)

3.2.1 Two-Phase DFM Discontinuous Pressure Model

We consider the transmission conditions introduced in [16]. They are based on a two-point approximation of each phase normal flux within the fracture combined with a phase potential upwinding of the phase mobility taking into account the phase saturation jump at the mf interface. Let us first define, for both phases $\alpha \in \{nw,w\}$, the “single” phase normal flux in the fracture network

$$\begin{aligned} V^{\alpha ,\pm }_{f,n} = \lambda _{f,n} \left( \frac{\gamma ^\pm u_m^\alpha - u_f^\alpha }{d_f / 2} - \rho ^\alpha \mathbf{g}\cdot \mathbf{n}^\pm \right) , \end{aligned}$$

(3.5)

which does not include the phase mobility. For any $a\in \mathbb {R}$, let us set $a^+ = \max \{0,a\}$ and $a^- = \min \{0,a\}$. The conditions coupling the matrix and fracture unknowns then read, for $\alpha \in \{nw,w\}$ (see the right Fig. 3.2):

$$\begin{aligned} \gamma _{\mathbf{n}^{\pm }} \mathbf{q}_m^{\alpha } = \mathbf{q}_{f,\mathbf{n}^\pm }^{\alpha }, \quad \mathbf{q}_{f,\mathbf{n}^\pm }^{\alpha } = M_f^\alpha (S_f^\alpha (\gamma ^\pm p_{c,m})) (V^{\alpha ,\pm }_{f,n})^+ + M_f^\alpha (s_f^\alpha ) (V^{\alpha ,\pm }_{f,n})^-. \end{aligned}$$

(3.6)

The hybrid dimensional two-phase flow discontinuous pressure model looks for $u^\alpha _m, u^\alpha _f,s^\alpha _m, s^\alpha _f$, $\alpha \in \{nw,w\}$, satisfying (3.1)–(3.2) and (3.3)–(3.4) together with the transmission conditions (3.6).

Fig. 3.2

(Left): example of a 2D DFM discontinuous pressure model with the normal vectors $\mathbf{n}^{\pm }$ at both sides of a fracture, the matrix phase pressure and saturation $u_m^\alpha$, $s^\alpha _m$, the fracture phase pressure and saturation $u_f^\alpha$, $s^\alpha _f$, the matrix Darcy phase velocity $\mathbf{q}^\alpha _m$ and the fracture network tangential Darcy phase velocity $\mathbf{q}^\alpha _f$. (Right): illustration of the coupling condition $\mathbf{q}_{f,\mathbf{n}^+}^\alpha = \gamma _{\mathbf{n}^+} \mathbf{q}_m^\alpha$ for the hybrid-dimensional discontinuous pressure model

3.2.2 Two-Phase DFM Continuous Pressure Model

In the case of pervious fractures, for which the ratio of the transversal permeability of the fracture to the width of the fracture is large compared with the ratio of the permeability of the matrix to the size of the domain, it is classical to assume that the phase pressures are continuous at the interfaces between the fractures and the matrix domain. Let us also mention that in the context of two-phase flows the continuous pressure DFM models have to be used with caution. It has been shown in [1, 16] that even highly pervious fractures may still act as barriers. This is due to the potential degeneracy of the mobilities in the transmission condition (3.6) and to the saturation jumps resulting from the high contrast of the capillary pressure curves across mf interface. Typically a fracture filled with the non-wetting phase would act as a barrier for the wetting phase, and therefore would induce a discontinuity of the wetting phase’s pressure. We refer to [1, 16] for a detailed comparison of continuous and discontinuous pressure models in case of very pervious fractures.

The continuous pressure model replaces the transmission condition (3.6) by the following phase pressure continuity conditions at mf interfaces:

$$\begin{aligned} \gamma ^+ u^{\alpha }_m = \gamma ^-u^\alpha _m = u_f^\alpha \text { on } {\Gamma }, \, \alpha \in \{nw,w\}. \end{aligned}$$

(3.7)

It results that we can denote by $u^\alpha$ the matrix pressure of phase $\alpha \in \{nw,w\}$ and by $\gamma u^\alpha$ the fracture pressure of phase $\alpha \in \{nw,w\}$, where $\gamma$ is the trace operator on ${\Gamma }$ for functions in $H^1(\Omega )$ (Fig. 3.3).

The hybrid dimensional two-phase flow continuous pressure model looks for $s^{\alpha }_m$, $s^{\alpha }_f$, and $u^\alpha$, $\alpha = nw,w$ satisfying (3.1)–(3.2) and (3.3)–(3.4).

Fig. 3.3

Example of a 2D DFM continuous pressure model with the normal vectors $\mathbf{n}^{\pm }$ at both sides of a fracture, the phase pressure $u^\alpha$ and its trace $\gamma u^\alpha$ on the fracture network $\Gamma$, the matrix phase saturation $s^\alpha _m$, the fracture phase saturation $s^\alpha _f$, the matrix Darcy phase velocity $\mathbf{q}^\alpha _m$ and the fracture network tangential Darcy phase velocity $\mathbf{q}^\alpha _f$

For both continuous and discontinuous pressure models, a no-flux boundary conditions is prescribed at the tips of the immersed fractures, that is to say on $\partial {\Gamma }\setminus \partial \Omega$, and the volume conservation and pressure continuity conditions are imposed at the fracture intersections. We refer to [13, 16] for more details on those conditions.

Finally, one should provide some appropriate initial and boundary data. To fix ideas, we consider in a non homogeneous Dirichlet boundary conditions on the matrix boundary $\partial \Omega _\mathrm{Dir}\subset \partial \Omega$ and on the fracture boundary $\Sigma _\mathrm{Dir} \subset \partial \Gamma \cap \partial \Omega$. Homogeneous Neumann boundary conditions are set on $\partial \Omega _N = \partial \Omega \setminus \overline{\partial \Omega }_\mathrm{Dir}$ and on $\Sigma _N = (\partial \Gamma \cap \partial \Omega )\setminus \overline{\Sigma }_\mathrm{Dir}$.

3.3 Vertex Approximate Gradient (VAG) Discretization of Two-Phase DFM Continuous Pressure Models

The VAG discretization of hybrid dimensional two-phase Darcy flows introduced in [13] considers generalised polyhedral meshes of $\Omega$ in the spirit of [29]. Let us briefly recall some notations related to the space discretization. We denote by $\mathcal {M}$ the set of disjoint open polyhedral cells, by $\mathcal {F}$ the set of faces and by $\mathcal {V}$ the set of nodes of the mesh. For each cell $K\in \mathcal {M}$ we denote by $\mathcal {F}_K \subset \mathcal {F}$ the set of its faces and by $\mathcal {V}_K$ the set of its nodes. Similarly, we will denote by $\mathcal {V}_\sigma$ the set of nodes of $\sigma \in \mathcal {F}$. The set $\mathcal {M}_\sigma$ denotes the two cells sharing an interior face $\sigma$ or the single cell to which the boundary face $\sigma$ belongs. The set $\mathcal {M}_\mathbf{s}$ (resp. $\mathcal {F}_\mathbf{s}$) is the subset of cells (resp. faces) sharing the node $\mathbf{s}\in \mathcal {V}$.

Let $\mathcal {E}_\sigma$ denote the set of edges of the face $\sigma \in \mathcal {F}$. It is then assumed that for each face $\sigma \in \mathcal {F}$, there exists a so-called “centre” of the face ${\mathbf{x}}_\sigma \in {\sigma }\setminus \bigcup _{e\in \mathcal {E}_\sigma } e$ such that ${\mathbf{x}}_\sigma = \sum _{\mathbf{s}\in \mathcal {V}_\sigma } \beta _{\sigma ,\mathbf{s}}~\mathbf{x}_\mathbf{s}, \text { with } \sum _{\mathbf{s}\in \mathcal {V}_\sigma } \beta _{\sigma ,\mathbf{s}}=1,$ and $\beta _{\sigma ,\mathbf{s}}\ge 0$ for all $\mathbf{s}\in \mathcal {V}_\sigma$. The face $\sigma$ is not necessarily planar, hence the term generalised polyhedral mesh. More precisely, each face $\sigma$ is assumed to be defined by the union of the triangles $T_{\sigma ,e}$ defined by the face centre ${\mathbf{x}}_\sigma$ and each edge $e\in \mathcal {E}_\sigma$.

The mesh is supposed to be conforming w.r.t. the fracture network ${\Gamma }$ in the sense that there exists a subset $\mathcal {F}_{{\Gamma }}$ of $\mathcal {F}$ such that $\overline{{\Gamma }}= \bigcup _{\sigma \in \mathcal {F}_{{\Gamma }}} \overline{\sigma }.$ We set

$$ \mathcal {V}_{\Gamma }= \bigcup _{\sigma \in \mathcal {F}_{\Gamma }} \mathcal {V}_\sigma , $$

and, for $\mathbf{s}\in \mathcal {V}_{\Gamma }$, we define $\mathcal {F}_{{\Gamma },\mathbf{s}} = \mathcal {F}_\mathbf{s}\cap \mathcal {F}_{\Gamma }$ as the subset of faces in $\mathcal {F}_{\Gamma }$ sharing the node $\mathbf{s}$.

The VAG discretization proposed in [13] is based upon the following set of degrees of freedom (d.o.f.)

$$ \mathcal {D}= \mathcal {M}\cup \mathcal {V}\cup \mathcal {F}_{\Gamma }$$

and the corresponding vector space:

$$ X_{\mathcal {D}} =\{v_\nu \in \mathbb {R}, \, \nu \in \mathcal {D}\}. $$

The d.o.f. are exhibited in Fig. 3.4 for a given cell K with one fracture face $\sigma$ in bold. Let us denote by

$$ \mathcal {V}_\mathrm{Dir}= \{\mathbf{s}\in \mathcal {V}\,|\, \mathbf{x}_\mathbf{s}\in \overline{\partial \Omega }_\mathrm{Dir} \cup \overline{\Sigma }_\mathrm{Dir}\}, $$

the subset of Dirichlet nodes.

A finite element discretization is built from the vector space of d.o.f. $X_{\mathcal {D}}$ using a tetrahedral sub-mesh of $\mathcal {M}$ and a second order interpolation at the face centres $\mathbf{x}_\sigma$, $\sigma \in \mathcal {F}\setminus \mathcal {F}_{\Gamma }$ defined by the operator $I_\sigma : X_{\mathcal {D}}\rightarrow \mathbb {R}$ such that

$$ I_\sigma (v) = \sum _{\mathbf{s}\in \mathcal {V}_\sigma } \beta _{\sigma ,\mathbf{s}} v_\mathbf{s}. $$

The tetrahedral sub-mesh is defined by

$$\begin{aligned} \mathcal { T} = \{T_{K,\sigma ,e}, e\in \mathcal {E}_\sigma , \sigma \in \mathcal {F}_K, K\in \mathcal {M}\}, \end{aligned}$$

(3.8)

where $T_{K,\sigma ,e}$ is the tetrahedron joining the cell centre ${\mathbf{x}}_K$ to the triangle $T_{\sigma ,e}$. For a given $v_{\mathcal {D}}\in X_{\mathcal {D}}$, we define the function $\pi _\mathcal { T}v_{\mathcal {D}}$ as the continuous piecewise affine function on each tetrahedron of $\mathcal { T}$ such that $\pi _\mathcal { T}v_{\mathcal {D}}({\mathbf{x}}_K) = v_K$, $\pi _\mathcal { T}v_{\mathcal {D}}(\mathbf{x}_\mathbf{s}) = v_\mathbf{s}$, $\pi _\mathcal { T}v_{\mathcal {D}}({\mathbf{x}}_\sigma ) = v_\sigma$, and $\pi _\mathcal { T}v_{\mathcal {D}}({\mathbf{x}}_{\sigma '}) = I_{\sigma '}(v)$ for all $K\in \mathcal {M}$, $\mathbf{s}\in \mathcal {V}$, $\sigma \in \mathcal {F}_{\Gamma }$, and $\sigma '\in \mathcal {F}\setminus \mathcal {F}_{\Gamma }$. The nodal basis of this finite element discretization will be denoted by $\eta _K$, $\eta _\mathbf{s}$, $\eta _\sigma$, for $K\in \mathcal {M}$, $\mathbf{s}\in \mathcal {V}$, $\sigma \in \mathcal {F}_{\Gamma }$.

Fig. 3.4

For a cell K and a fracture face $\sigma$ (in bold), examples of VAG d.o.f. $u_K$, $u_\mathbf{s}$, $u_\sigma$, $u_{\mathbf{s}'}$ and VAG fluxes $F_{K,\sigma }$, $F_{K,\mathbf{s}}$, $F_{K,\mathbf{s}'}$, $F_{\sigma ,\mathbf{s}}$

The VAG scheme is a control volume scheme in the sense that it results, for each d.o.f. not located at the Dirichlet boundary and each phase, in a volume balance equation. The two main ingredients are therefore the conservative fluxes and the porous volumes. The VAG matrix and fracture fluxes are exhibited in Fig. 3.4. They are derived from the variational formulation on the finite element subspace. For $u_{\mathcal {D}}\in X_{\mathcal {D}}$, the matrix fluxes $F_{K,\nu }(u_{\mathcal {D}})$ connect the cell $K\in \mathcal {M}$ to all the d.o.f. located at the boundary of K, namely $\nu \in \Xi _K = \mathcal {V}_K \cup (\mathcal {F}_K \cap \mathcal {F}_{\Gamma })$. They are defined by

$$ F_{K,\nu }(u_{\mathcal {D}}) = \int _K -\Lambda _m(\mathbf{x}) \nabla \pi _\mathcal { T}u_{\mathcal {D}}(\mathbf{x}) \cdot \nabla \eta _\nu (\mathbf{x}) d\mathbf{x}= \sum _{\nu '\in \Xi _K}\mathbb {T}_{K}^{\nu ,\nu '}(u_K-u_{\nu '}), $$

with the cell transmissibilities

$$ \mathbb {T}_K^{\nu ,\nu '} = \int _K \Lambda _m(\mathbf{x}) \nabla \eta _{\nu '}(\mathbf{x}) \cdot \nabla \eta _\nu (\mathbf{x}) d\mathbf{x}. $$

The fracture fluxes $F_{\sigma ,\mathbf{s}}(u_{\mathcal {D}})$ connect each fracture face $\sigma \in \mathcal {F}_{\Gamma }$ to its nodes $\mathbf{s}\in \mathcal {V}_\sigma$ and are defined by

$$ F_{\sigma ,\mathbf{s}}(u_{\mathcal {D}}) = \int _\sigma -d_f \Lambda _f \nabla _\tau \gamma \pi _\mathcal { T}u_{\mathcal {D}}(\mathbf{x}) \cdot \nabla _\tau \gamma \eta _\mathbf{s}(\mathbf{x}) d\sigma (\mathbf{x}) = \sum _{\mathbf{s}'\in \mathcal { V}_\sigma }\mathbb {T}_{\sigma }^{\mathbf{s},\mathbf{s}'}(u_\sigma -u_{\mathbf{s}'}), $$

with the fracture face transmissibilities

$$ \mathbb {T}^{\mathbf{s},\mathbf{s}'}_\sigma = \int _\sigma d_f(\mathbf{x}) \Lambda _f(\mathbf{x}) \nabla _\tau \gamma \eta _{\mathbf{s}'}(\mathbf{x}) \cdot \nabla _\tau \gamma \eta _\mathbf{s}(\mathbf{x}) d\sigma (\mathbf{x}), $$

where $d\sigma (\mathbf{x})$ denotes the Lebesgue $d-1$ dimensional measure on ${\Gamma }$.

The porous volumes are obtained by distributing the porous volumes of each cell $K\in \mathcal {M}$ and fracture face $\sigma \in \mathcal {F}_\Gamma$ to the d.o.f. located on their respective boundaries. For each $K\in \mathcal {M}$ we define a set of non-negative volume fractions $\left( \alpha _{K,\nu }\right) _{\nu \in \Xi _K\setminus \mathcal {V}_\mathrm{Dir} }$ satisfying $\displaystyle \sum \limits _{\nu \in \Xi _K\setminus \mathcal {V}_\mathrm{Dir} } \alpha _{K,\nu } \le 1$, and we set

$$ \phi _{K,\nu } = \alpha _{K,\nu }\int _K \phi _m(\mathbf{x}) d\mathbf{x}. $$

Similarly, for all $\sigma \in \mathcal {F}_\Gamma$ we set

$$ \phi _{\sigma ,\mathbf{s}} = \alpha _{\sigma ,\mathbf{s}}\int _\sigma \phi _f(\mathbf{x}) d_f(\mathbf{x}) d\sigma (\mathbf{x}), $$

with the non-negative volume fractions $\left( \alpha _{\sigma ,\mathbf{s}}\right) _{\mathbf{s}\in \mathcal {V}_\sigma \setminus \mathcal {V}_\mathrm{Dir}}$ satisfying $\displaystyle \sum \limits _{\mathbf{s}\in \mathcal {V}_\sigma \setminus \mathcal {V}_\mathrm{Dir}}\alpha _{\sigma ,\mathbf{s}} \le 1$. Then, we set for all $K\in \mathcal {M}$ and $\sigma \in \mathcal {F}_{\Gamma }$:

$$ \phi _K= \int _K \phi _m(\mathbf{x}) d\mathbf{x}-\sum _{\nu \in \Xi _K\setminus \mathcal {V}_\mathrm{Dir}} \phi _{K,\nu }, $$

$$ \phi _\sigma = \int _\sigma \phi _f(\mathbf{x}) d_f(\mathbf{x}) d\sigma (\mathbf{x}) -\sum _{\mathbf{s}\in \mathcal {V}_\sigma \setminus \mathcal {V}_\mathrm{Dir}}\phi _{\sigma ,\mathbf{s}}. $$

On practical meshes with cell sizes at mf interfaces much larger than the fracture width, the flexibility in the choice of the weights $\alpha _{K,s}$ and $\alpha _{\sigma ,s}$ is shown in [13] (see also [30]) to be a crucial asset compared with usual CVFE approaches, allowing to improve significantly the accuracy of the scheme. As exhibited in Fig. 3.5, and in contrast with the usual CVFE approaches, the fracture porous volumes can be defined with no contribution of the matrix porous volume, thus avoiding to enlarge artificially the flow path in the fractures and to slow down the front speed. This is achieved by choosing the volume fractions such that

$$ \begin{array}{llll} &{}\alpha _{K,\sigma } &{}= 0 \,\,\text { for all } &{}\,\,\sigma \in \mathcal {F}_{\Gamma }, \, K\in \mathcal {M}_\sigma ,\\ &{}\alpha _{K,\mathbf{s}} &{}= 0 \,\,\text { for all } &{}\,\, \mathbf{s}\in \mathcal {V}_{\Gamma }, \,K \in \mathcal {M}_\mathbf{s}. \end{array} $$

Fig. 3.5

Example of control volumes at cells, fracture face, and nodes, in the case of two cells K and L splitted by one fracture face $\sigma$ (the width of the fracture has been enlarged in this Figure). (left): VAG choice of the porous volumes avoiding mixing between fracture and matrix porous volumes. (right): CVFE like choice of the porous volumes mixing fracture and matrix porous volumes leading to a considerable enlargement of the fracture drain on practical meshes

3.3.1 VAG Phase Potential Two-Point (TP) Upwind Formulation

We consider in the following of Sect. 3.3, the usual approach (termed f-upwind model) for which a single rock type is assigned to each d.o.f. Quite naturally, the fracture rock type is associated with d.o.f. located on ${\Gamma }$, while the matrix rock type is associated to the remaining d.o.f., that is we set

$$ P_{c,\nu }(s) = \left\{ \begin{array}{rc} P_{c,m}(s) &{} \text {if } \nu \not \in (\mathcal {V}_{\Gamma }\cup \mathcal {F}_{\Gamma }),\\ P_{c,f}(s) &{} \text {if } \nu \in (\mathcal {V}_{\Gamma }\cup \mathcal {F}_{\Gamma }), \end{array}\right. $$

and

$$ M_{\nu }^\alpha (s) = \left\{ \begin{array}{rc} M^\alpha _{m}(s) &{} \text {if } \nu \not \in (\mathcal {V}_{\Gamma }\cup \mathcal {F}_{\Gamma }),\\ M^\alpha _{f}(s) &{} \text {if } \nu \in (\mathcal {V}_{\Gamma }\cup \mathcal {F}_{\Gamma }), \end{array}\right. \alpha \in \{nw,w\}. $$

The set of discrete unknowns is defined by the set of phase pressure $u^\alpha _{\mathcal {D}}\in X_{\mathcal {D}}$ and phase saturation $s^\alpha _{\mathcal {D}}\in X_{\mathcal {D}}$ for each phase $\alpha \in \{nw,w\}$.

The “single” phase VAG Darcy fluxes, not including the phase mobility, are defined, for each phase $\alpha \in \{nw,w\}$, by

$$ F^\alpha _{K,\nu }(u^\alpha _{\mathcal {D}}) = F_{K,\nu }(u^\alpha _{\mathcal {D}}) + \rho ^\alpha g F_{K,\nu }(z_{\mathcal {D}}), $$

$$ F^\alpha _{\sigma ,\mathbf{s}}(u^\alpha _{\mathcal {D}}) = F_{\sigma ,\mathbf{s}}(u^\alpha _{\mathcal {D}}) + \rho ^\alpha g F_{\sigma ,\mathbf{s}}(z_{\mathcal {D}}), $$

with $z_{\mathcal {D}} = (\mathbf{x}_\nu )_{\nu \in \mathcal {D}}$, and for $K\in \mathcal {M}$, $\sigma \in \mathcal {F}_{\Gamma }$, $\nu \in \Xi _K$, $\mathbf{s}\in \mathcal {V}_\sigma$. They are combined with the usual Two-Point (TP) phase potential upwinding of the mobilities [8, 23], leading to the following two-phase Darcy VAG fluxes

$$ q^\alpha _{K,\nu } = M_K^\alpha (s_K^\alpha ) (F^\alpha _{K,\nu }(u^\alpha _{\mathcal {D}}))^+ + M_\nu ^\alpha (s_\nu ^\alpha ) (F^\alpha _{K,\nu }(u^\alpha _{\mathcal {D}}))^-, $$

$$ q^\alpha _{\sigma ,\mathbf{s}} = M_\sigma ^\alpha (s_\sigma ^\alpha ) (F^\alpha _{\sigma ,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^+ + M_\mathbf{s}^\alpha (s_\mathbf{s}^\alpha ) (F^\alpha _{\sigma ,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^-. $$

Let us define the accumulation terms by

$$ \left\{ \begin{array}{llll} &{} \mathcal {A}^\alpha _K &{} = \phi _K s^\alpha _K, &{} K\in \mathcal {M},\\ &{} \mathcal {A}^\alpha _\sigma &{} = \displaystyle \bigr ( \phi _\sigma + \sum _{K\in \mathcal {M}_\sigma } \phi _{K,\sigma } \bigr ) s^\alpha _\sigma , &{} \sigma \in \mathcal {F}_{\Gamma },\\ &{} \mathcal {A}^\alpha _\mathbf{s}&{} = \displaystyle \bigr ( \sum _{K\in \mathcal {M}_\mathbf{s}} \phi _{K,\mathbf{s}} + \sum _{\sigma \in \mathcal {F}_{{\Gamma },\mathbf{s}}} \phi _{\sigma ,\mathbf{s}} \bigr ) s^\alpha _{\mathbf{s}}, &{} \mathbf{s}\in \mathcal {V}\setminus \mathcal {V}_\mathrm{Dir}. \end{array}\right. $$

Note that neither the accumulation terms $\mathcal {A}^\alpha _\sigma$ and $\mathcal {A}^\alpha _\mathbf{s}$ nor the mf fluxes take into account the discontinuity of the saturations across mf interface. In other terms, the discrete problem does not involve quantities such as $P_{c,m}(s_f)$. An alternative approach is described in Sect. 3.3.5.

For $N\in \mathbb {N}^*$, let us consider the time discretization $t^0= 0< t^1<\cdots< t^{n-1}< t^n \cdots < t^N = T$ of the time interval [0, T]. We denote the time steps by $\Delta t^n = t^{n}-t^{n-1}$ for all $n=1,\cdots ,N$. The superscript n will be used to denote the unknowns at time $t^n$. To reduce the amount of notation, only the previous time step superscript $n-1$ will be specified in the following, while the superscript n will not be specified by default.

The set of discrete equations couples the volume balance equations at each d.o.f. excluding the Dirichlet nodes

$$\begin{aligned} \left\{ \begin{array}{rl} \displaystyle {\mathcal {A}^\alpha _K - \mathcal {A}_K^{\alpha ,n-1} \over \Delta t^n} + \displaystyle \sum _{\nu \in \Xi _K} q^\alpha _{K,\nu } = 0, &{} K\in \mathcal {M}, \, \alpha =nw,w,\\ \displaystyle {\mathcal {A}^\alpha _\sigma - \mathcal {A}_\sigma ^{\alpha ,n-1} \over \Delta t^n} + \displaystyle \sum _{\mathbf{s}\in \mathcal { V}_\sigma } q^\alpha _{\sigma ,\mathbf{s}} - \sum _{K\in \mathcal {M}_\sigma } q^\alpha _{K,\sigma }= 0, &{} \sigma \in \mathcal {F}_\Gamma , \, \alpha =nw,w,\\ \displaystyle {\mathcal {A}^\alpha _\mathbf{s}- \mathcal {A}_\mathbf{s}^{\alpha ,n-1} \over \Delta t^n} + \displaystyle \sum _{K\in \mathcal {M}_\mathbf{s}} - q^\alpha _{K,\mathbf{s}} + \sum _{\sigma \in \mathcal {F}_{\Gamma ,\mathbf{s}}} - q^\alpha _{\sigma ,\mathbf{s}} = 0, &{} \mathbf{s}\in \mathcal {V}\setminus \mathcal {V}_\mathrm{Dir}, \, \alpha =nw,w, \end{array}\right. \end{aligned}$$

(3.9)

combined with the closure laws

$$\begin{aligned} \left\{ \begin{array}{rc} s^{nw}_\nu + s^{w}_\nu = 1, &{} \nu \in \mathcal {D},\\ u^{nw}_\nu - u^{w}_\nu = P_{c,\nu }(s^{nw}_\nu ), &{} \nu \in \mathcal {D}, \end{array}\right. \end{aligned}$$

(3.10)

and the Dirichlet boundary conditions

$$\begin{aligned} s^{nw}_s = s^{nw}_{\mathrm{Dir},\mathbf{s}} \quad u^{nw}_s = u^{nw}_{\mathrm{Dir},\mathbf{s}}, \quad \mathbf{s}\in \mathcal {V}_\mathrm{Dir}, \end{aligned}$$

(3.11)

for given $s^{nw}_{\mathrm{Dir},\mathbf{s}} \in [0,1]$, $u^{nw}_{\mathrm{Dir},\mathbf{s}}$, $s\in \mathcal {V}_\mathrm{Dir}$.

To solve the discrete nonlinear system (3.9), one first uses the closure equations (3.10) to eliminate the unknowns $s^{w}_\nu$ and $u^{w}_\nu$ for $\nu \in \mathcal {D}$ reducing the system to the primary unknowns $u^{nw}_\nu , s^{nw}_\nu$, $\nu \in \mathcal {D}$ coupled by the set of equations (3.9) and the Dirichlet boundary conditions (3.11). A Newton’s method is used to solve this nonlinear system at each time step of the simulation. At each Newton step, the Jacobian matrix is assembled and the cell unknowns $u^{nw}_K, s^{nw}_K$, $K\in \mathcal {M}$ are eliminated without any fill-in using the linearized cell volume balance equations reducing the system to the node and fracture face primary unknowns only. This elimination results in a huge gain in terms of system size in particular for tetrahedral meshes. The reduced linear system is solved using a Krylov subspace solver preconditioned by a CPR-AMG preconditioner. This preconditioner combines multiplicatively an AMG preconditioner on a pressure block (elliptic part of the system) with a zero fill-in incomplete factorization of the full system. Let us refer to [42, 47] for its detailed description. In the following numerical experiments, the pressure block is simply obtain as the sum over both phases of the volume balance equations on each fracture face and non Dirichlet node.

3.3.2 What Is Wrong with Two-Point Upwinding at mf Interfaces

In this Section, we discuss one particular difficulty that the nodal discretizations have in regard of the discrete fluxes reconstruction. As shown below, due to the dual control volumes at mf interfaces, nodal schemes may result in fluxes having an opposite sign compared to the fluxes computed at the physical mf interfaces. Using Two-Point upwinding, this results in an artificial diffusion of the saturation toward an upstream direction. To avoid this drawback we propose below an alternative Multi-Point upwinding technique.

For a given constant velocity $\mathbf{q}$, let us choose $u_{\mathcal {D}} \in X_{\mathcal {D}}$ such that $u_\nu = -\Lambda _m^{-1}\mathbf{q}\cdot \mathbf{x}_\nu$ for all $\nu \in \mathcal {D}$. From $-\Lambda _m \nabla \pi _\mathcal { T} u_{\mathcal {D}} = \mathbf{q}$, we obtain

$$ F_{K,\mathbf{s}}(u_{\mathcal {D}}) = \mathbf{q}\cdot \int _K \nabla \eta _\mathbf{s}(\mathbf{x}) d\mathbf{x}, $$

at a given fracture node $s\in \mathcal {V}_{\Gamma }$, and cell $K\in \mathcal {M}_\mathbf{s}$.

Fig. 3.6

Example of a 2D mesh with three isosceles triangular cells at the interface with a fracture in bold. It is assumed that the unit normal vectors are such that $\mathbf{n}_2 = -\mathbf{n}$, $\mathbf{n}_1= -\mathbf{n}_3$ and that $\mathbf{n}_1\cdot \mathbf{n}=0$. The cell centers are chosen as the isobarycenters of their 3 nodes

For the sake of simplicity, let us assume the geometrical configuration illustrated in Fig. 3.6. It results that

$$ \begin{array}{rcl} F_{K,\mathbf{s}}(u_{\mathcal {D}}) &{}=&{} - {1\over 2} |\mathbf{s}_2 \sigma _1| \mathbf{q}\cdot \mathbf{n}_1,\\ F_{J,\mathbf{s}}(u_{\mathcal {D}}) &{}=&{} - {1\over 2} |\mathbf{s}_3 \sigma _2| \mathbf{q}\cdot \mathbf{n}_3 = -F_{K,\mathbf{s}}(u_{\mathcal {D}}),\\ F_{I,\mathbf{s}}(u_{\mathcal {D}}) &{}=&{} + {1\over 2} |\mathbf{s}_2 \mathbf{s}_3| \mathbf{q}\cdot \mathbf{n},\\ F_{K,\sigma _1}(u_{\mathcal {D}}) &{}=&{} + {1\over 2} |\mathbf{s}\mathbf{s}_1| \mathbf{q}\cdot \mathbf{n},\\ F_{J,\sigma _2}(u_{\mathcal {D}}) &{}=&{} + {1\over 2} |\mathbf{s}\mathbf{s}_4| \mathbf{q}\cdot \mathbf{n}= F_{I,\sigma _1}(u_{\mathcal {D}}). \end{array} $$

We remark that, whatever the velocity $\mathbf{q}$, either the flux $F_{K,\mathbf{s}}(u_{\mathcal {D}})$ or the flux $F_{J,\mathbf{s}}(u_{\mathcal {D}})$ have the opposite sign as the one of $\mathbf{q}\cdot \mathbf{n}$. Assuming, to fix ideas that $\mathbf{q}\cdot \mathbf{n}>0$, it results from the Two-Point upwinding used for the transport scheme of a given phase with Darcy velocity $\mathbf{q}$, that the phase propagates from the fracture either to the upstream cell K or the upstream cell J.

On the other hand, let us remark that the ill-orientated discrete fluxes cancel out when summing over the cells connected to the node $\mathbf{s}$ and located on the same side with respect to the planar fracture, that is we have

$$\begin{aligned} F_{K,\mathbf{s}}(u_{\mathcal {D}}) + F_{I,\mathbf{s}}(u_{\mathcal {D}})+F_{J,\mathbf{s}}(u_{\mathcal {D}}) = {1\over 2} |\sigma _1 \sigma _2| \mathbf{q}\cdot \mathbf{n}. \end{aligned}$$

(3.12)

This property actually holds for an arbitrary number of polygonal cells sharing the node $\mathbf{s}$ and whatever the choice of the cell centers. In the three-dimensional case, this property also holds for tetrahedral meshes.

In the following Subsection, this property on the sum of the fluxes is exploited to avoid the artificial diffusion of the phase toward an upstream direction.

3.3.3 Multi-Point (MP) Upwind Fluxes at mf Interfaces

We first define an equivalence relation on each subset $\mathcal {M}_s$ of cells, for any fixed node $\mathbf{s}\in \mathcal {V}$, by

$$ \begin{array}{rc} K\equiv _{\mathcal {M}_s} L\quad \Longleftrightarrow \quad &{}\text { there exists }n\in \mathbb {N}\text { and a sequence }(\sigma _i)_{i=1,\dots ,n}\text { in } \mathcal {F}_s\backslash \mathcal {F}_{\Gamma },\\ &{}\text { such that }K\in \mathcal {M}_{\sigma _1},L\in \mathcal {M}_{\sigma _n}\text { and }\mathcal {M}_{\sigma _{i+1}}\cap \mathcal {M}_{\sigma _i} \ne \emptyset \\ &{}\text { for }i=1,\dots ,n-1. \end{array} $$

Let us then denote by $\overline{\mathcal {M}}_s$ the set of all classes of equivalence of $\mathcal {M}_s$ and by $\overline{K}_s$ the element of $\overline{\mathcal {M}}_s$ containing $K\in \mathcal {M}$. Obviously $\overline{\mathcal {M}}_s$ might have more than one element only if $s\in \mathcal {V}_{\Gamma }$. Note that $\overline{K}_s$ is both considered as a subset of cells of $\mathcal {M}_s$ as well as an additional d.o.f. located at the same point than the node $\mathbf{s}$ i.e. we set $\mathbf{x}_{\overline{K}_\mathbf{s}} = \mathbf{x}_\mathbf{s}$ (Fig. 3.7).

Fig. 3.7

(left) 2D mesh with 3 fracture faces in bold and the 3 d.o.f. in $\overline{\mathcal {M}}_\mathbf{s}$ at the node $\mathbf{s}\in \mathcal {V}_{\Gamma }$, (right) Darcy fluxes joining each cell $L\in {\overline{K}_\mathbf{s}}$ to the new d.o.f. ${\overline{K}_\mathbf{s}}$, and joining the new d.o.f. ${\overline{K}_\mathbf{s}}$ to the node $\mathbf{s}$ (the node $\mathbf{s}$ and ${\overline{K}_\mathbf{s}}$ are located at the same point $\mathbf{s}$ but they have been separated for the sake of clarity of the Figure)

Let us define the phase mobilities

$$\begin{aligned} M^\alpha _{\overline{K}_\mathbf{s}}, \,\mathbf{s}\in \mathcal {V}_{\Gamma }, \,\overline{K}_\mathbf{s}\in \overline{\mathcal {M}}_\mathbf{s}, \, \alpha \in \{nw,w\}, \end{aligned}$$

(3.13)

as matrix fracture additional unknowns. Then, using phase potential upwinding of the mobilities, let us define for all $L\in \overline{K}_\mathbf{s}$ the half Darcy fluxes between L and $\overline{K}_\mathbf{s}$ by

$$ q^\alpha _{L,\overline{K}_\mathbf{s}} = M_L^\alpha (s_L^\alpha ) (F^\alpha _{L,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^+ + M^\alpha _{\overline{K}_\mathbf{s}} (F^\alpha _{L,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^-, $$

as well as the half Darcy flux between $\overline{K}_\mathbf{s}$ and $\mathbf{s}$ by

$$ q^\alpha _{\overline{K}_\mathbf{s},\mathbf{s}} = M_\mathbf{s}^\alpha (s^\alpha _\mathbf{s})(F_{\overline{K}_\mathbf{s},\mathbf{s}}^\alpha )^- + M^\alpha _{\overline{K}_\mathbf{s}} (F_{\overline{K}_\mathbf{s},\mathbf{s}}^\alpha )^+, $$

where we set by flux conservation

$$ F_{\overline{K}_\mathbf{s},\mathbf{s}}^\alpha = \sum _{L\in \overline{K}_\mathbf{s}} F^\alpha _{L,\mathbf{s}}(u^\alpha _{\mathcal {D}}). $$

The flux continuity equation

$$\begin{aligned} q^\alpha _{\overline{K}_\mathbf{s},\mathbf{s}} = \sum _{L\in \overline{K}_\mathbf{s}} q^\alpha _{L,\overline{K}_\mathbf{s}}, \end{aligned}$$

(3.14)

is used to eliminate the mobility unknown $M^\alpha _{\overline{K}_\mathbf{s}}$ leading to the following convex linear combination of the cells $L\in \overline{K}_\mathbf{s}$ and node $\mathbf{s}$ mobilities:

$$\begin{aligned} \displaystyle M^\alpha _{\overline{K}_\mathbf{s}} = { \displaystyle \sum \limits _{L \in \overline{K}_\mathbf{s}} (F^\alpha _{L,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^+ M_L^\alpha (s_L^\alpha ) - M_\mathbf{s}^\alpha (s^\alpha _\mathbf{s}) (\sum \limits _{L\in \overline{K}_\mathbf{s}} F^\alpha _{L,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^- \over \displaystyle \sum \limits _{L \in \overline{K}_\mathbf{s}} (F^\alpha _{L,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^+ - (\sum \limits _{L\in \overline{K}_\mathbf{s}} F^\alpha _{L,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^- }. \end{aligned}$$

(3.15)

We deduce the definition of the new Multi-Point upwind flux

$$ q^\alpha _{K,\mathbf{s}} = q^\alpha _{K,\overline{K}_\mathbf{s}} = M_K^\alpha (s_K^\alpha ) (F^\alpha _{K,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^+ + M^\alpha _{\overline{K}_\mathbf{s}} (F^\alpha _{K,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^-, $$

denoted by VAG MP in the following and to be used in the conservation equations (3.9). Compared with the Two-Point upwind flux

$$ q^\alpha _{K,\mathbf{s}} = M_K^\alpha (s_K^\alpha ) (F^\alpha _{K,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^+ + M_\mathbf{s}^\alpha (s_\mathbf{s}^\alpha ) (F^\alpha _{K,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^-, $$

denoted by VAG TP, the VAG MP flux uses the fracture node saturation $s_\mathbf{s}^\alpha$ only if $\sum _{L\in \overline{K}_\mathbf{s}} F^\alpha _{L,\mathbf{s}}(u^\alpha _{\mathcal {D}}) <0$, which, in view of (3.12), ensures that the phase will not go out from the fracture on the wrong side in the case of a linear phase pressure field.

Note also that, if $\overline{K}_\mathbf{s}$ contains only one cell, both the VAG TP and VAG MP fluxes match, this is why the fluxes $q^\alpha _{K,\sigma }$, $\sigma \in \mathcal {F}_K\cap \mathcal {F}_{\Gamma }$ do not need to be modified.

The matrix fracture mobility unknowns (3.13) and flux continuity equations (3.14) can be kept in the nonlinear system and solve simultaneously with the other unknowns and equations. Let us recall that the CPR-AMG preconditioner combines multiplicatively an AMG preconditioner on a pressure block (elliptic part of the system) with a zero fill-in incomplete factorization of the full system. The matrix fracture mobility unknowns $M^\alpha _{\overline{K}_\mathbf{s}}$ and the flux continuity equations (3.14), $\mathbf{s}\in \mathcal {V}_{\Gamma }$, $\overline{K}_\mathbf{s}\in \overline{\mathcal {M}}_\mathbf{s}$, are not included in the definition of the pressure block due to their hyperbolic nature. It results that the pressure block has the same number of unknowns and sparsity pattern as the one of the usual VAG TP scheme. Since the AMG step is the most expensive part of the CPR-AMG two stage preconditioner, this explains why keeping the matrix fracture mobility unknowns is quite efficient.

On the other hand, the elimination of the matrix fracture mobility unknowns together with the flux continuity equations in (3.15) leads to a rather large fill-in of the Jacobian (depending on the density of the fracture network) and also prevents the elimination of the cell unknowns connected to the fractures. The following numerical experiments confirm that it is much more efficient in terms of CPU time to keep the matrix fracture mobility unknowns in the linear system.

3.3.4 Numerical Experiments

The Objectives of this Subsection is to compare the solutions obtained with the following schemes:

• the CVFE like VAG scheme with rock type mixture and Two-Point upwinding of the mobilities at mf interfaces (VAG CVFE),

• the VAG scheme with no rock type mixture and Two-Point upwinding of the mobilities at mf interfaces (VAG TP),

• the VAG scheme with no rock type mixture and Multi-Point upwinding of the mobilities at mf interfaces (VAG MP). The VAG MP scheme is implemented either with elimination of the interface mobility unknowns (VAG MP) or without elimination of these unknowns (VAG MP no elim).

• the Hybrid Finite Volume (HFV) scheme with cell, face and fracture edge unknowns as described in [37] (HFV).

All these schemes are implemented in the same code using the Fortran 90 programming language combined with the gfortran compiler. The linear systems are solved using the Slatec library [48] for the GMRes iterative solver and the ILU0 preconditioner as well as the AMG1R5 library for the Algebraic MultiGrid preconditioner [45].

Tables 3.1 and 3.2 exhibit the following entries:

• mesh: number of cells,

• dof: number of degrees of freedom of each scheme (with 2 physical primary unknowns per d.o.f.),

• $dof_{lin}$: number of degrees of freedom in the linear system after reduction. Let us recall that the cell unknowns are eliminated for VAG CVFE, VAG TP, HFV, and VAG MP no elim, while the interface mobilities together with the cell unknowns not connected to the fractures are eliminated for VAG MP,

• $N_z$: number of nonzero elements in the reduced Jacobian (with $2\times 2$ matrix elements).

Note that for the VAG MP no elim implementation, the pressure block is stored seperately after reduction with a lower number of d.o.f. and nonzero elements than the remaining part of the Jacobian. This is a key point to lower the CPU time when the CPR-AMG preconditioner is used. Then, the first $dof_{lin}$ (resp. $N_z$) entry corresponds to the pressure block, and the second entry to the remaining part.

These tables also include the following entries:

• $N_{\Delta t}$: number of successful time steps,

• $N_{chop}$: number of time step chops,

• $N_{Newton}$: average number of Newton iterations per successful time step,

• $N_{GMRes}$: average number of GMRes iteration per Newton step,

• CPU (s): CPU time in seconds.

The CPU time takes into account the full time loop including the outputs in ensight format files at each time step but excluding the preprocessing computations (mesh reading, mesh connectivity, VAG transmissibilities, CSR format of the Jacobian) which are negligeable in terms of CPU time compared with the time loop.

3.3.4.1 Tracer DFM Model with a Single Fracture

Let us denote by (x, y) the Cartesian coordinates of $\mathbf{x}$ and let us set $\Omega = (0,1 \text { m})^2$, $\mathbf{x}_1 = (0,{\frac{1}{4}})$, $\mathbf{x}_2 = (1,0.875)$. We consider a single fracture defined by $\Gamma = (\mathbf{x}_1,\mathbf{x}_2)$ with tangential permeability $\Lambda _f = 200$ m$^2$ and width $d_f = 10^{-3}$ m. The matrix permeability is isotropic and set to $\Lambda _m = 1$ m$^2$. The matrix and fracture porosities are set to $\phi _m=\phi _f=1$. Let us set

$$ \mathbf{t} = \left( \begin{array}{c} 1 \\ 0.625 \end{array}\right) , \quad \mathbf{q}= \left( \begin{array}{c} 1 \\ {1 \over 3} \end{array}\right) . $$

We consider the hybrid-dimensional tracer model obtained from the two-phase DFM model by setting $M_m^\alpha (s) = M_f^\alpha (s) = s$ for $\alpha \in \{nw,w\}$, $P_{c,m}(s) = P_{c,f}(s) = 0$, $g=0$. The pressure analytical solution is defined for $\alpha \in \{nw,w\}$ by

$$ u^\alpha (\mathbf{x},t) = 1 - \Lambda _m^{-1} \mathbf{x}\cdot \mathbf{q}, $$

leading to the matrix Darcy velocity

$$ \mathbf{q}^\alpha _m = \mathbf{q}, $$

and the tangential fracture velocity integrated over the width

$$ \mathbf{q}_f^\alpha = d_f \Lambda _{f} { (\mathbf{t}\cdot \Lambda _m^{-1} \mathbf{q}) \over | \mathbf{t}|^2 } \mathbf{t}, $$

This pressure solution is exactly solved by the VAG scheme using Dirichlet condition at the boundary of the domain. An input Dirichlet boundary condition is imposed for the non-wetting phase saturation (tracer) with zero value at the matrix boundary and a value of 1 at the fracture boundary $\mathbf{x}_1$. The initial condition is defined by a zero non-wetting phase saturation both in the fracture and matrix domains. Figure 3.8 illustrates that the tracer VAG TP solution goes out on the wrong side of the fracture on a few layers of cells, while it is not the case for the HFV and VAG MP solutions as expected. The VAG CVFE stationary tracer solution is not plotted since it is the same than the VAG TP stationary tracer solution. Figure 3.9 exhibits the stationary solutions along the fracture showing that the HFV and VAG MP solutions match on both meshes while the VAG TP solution is not fully converged even on the fine mesh. Figure 3.10 exhibits the tracer volume in the fracture as a function of time. Again, the HFV and VAG MP solutions match on both meshes, while the tracer front in the fracture is clearly slown down for the VAG TP solution on both meshes. This is much worse for the VAG CVFE solution due to the fracture enlargement resulting from the rock type mixture at mf interfaces.

Fig. 3.8

Stationary solution for the non-wetting phase saturation (tracer) in the matrix and in the fracture obtained by, from left to right, the HVF, VAG MP and VAG TP schemes, and, from top to bottom, on the $16\times 16$ and $128\times 128$ topologically Cartesian meshes

Fig. 3.9

Stationary non-wetting phase saturation along the fracture as a function of x obtained by the HVF, VAG MP, VAG TP schemes on the $16\times 16$ and $128\times 128$ topologically Cartesian meshes

Fig. 3.10

Volume of the non-wetting phase in the fracture as a function of time for the HVF, VAG MP, VAG TP, VAG CVFE scheme solutions on the $16\times 16$ and $128\times 128$ topologically Cartesian meshes

3.3.4.2 Large 2D DFM Model

This test case considers the DFM model with the matrix domain $\Omega = (0,100 \, \mathrm {m})\times (0,186.5 \, \mathrm {m})$ and a fracture network including 581 connected components both exhibited in Fig. 3.11. The fracture width is $d_f = 1$ cm and the fracture network is homogeneous and isotropic with $\Lambda _f = 10^{-11}$ m$^2$, $\phi _f = 0.2$. The matrix is homogeneous and isotropic with $\Lambda _m = 10^{-14}$ m$^2$, $\phi _m = 0.4$.

The relative permeabilities are given by $k_{r,f}^\alpha (s^\alpha ) = s^\alpha$ and $k_{r,m}^\alpha (s^\alpha ) = (s^\alpha )^2$, $\alpha \in \{nw,w\}$ and the capillary pressure is fixed to $P_{c,m}(s^{nw}) = - 10^4 \ln (1-s^{nw})$ Pa in the matrix and to $P_{c,f}(s^{nw}) = 0$ Pa in the fracture network. The fluid properties are defined by their dynamic viscosities $\mu ^{nw} = 5. ~10^{-3}$, $\mu ^w = 10^{-3}$ Pa s and their mass densities $\rho ^w = 1000$ and $\rho ^{nw} = 700$ kg m$^{-3}$.

The reservoir is initially saturated with the wetting phase. Dirichlet boundary conditions are imposed at the top boundary with a wetting phase pressure of 1 MPa and $s^{w}_m = 1$, as well as at the bottom boundary with $s^{nw}_m = 0.9$ and $u^w = 4 \,\mathrm {MPa}$. The remaining boundaries are assumed impervious and the final simulation time is fixed to $t_f= 1800$ days.

The time stepping is defined by $\Delta t^1 = \Delta t_{init} = 10$ days, and for all $n\ge 1$ by

$$\begin{aligned} \Delta t^{n+1} = \max (\Delta t_{max},1.2 \Delta t^{n}) \text { with } \Delta t_{max} = 10\, \text {days}, \end{aligned}$$

(3.16)

in case of a successful time step $\Delta t^n$, and $\Delta t^{n+1} = {\Delta t^{n} \over 2}$, in case of non convergence of the Newton algorithm in ${Newton}_\mathrm{max} = 30$ iterations. This last value is chosen not to small to avoid too many time step failures even on the finest mesh but also not to large to avoid increased CPU time in case of time step failures induced by residual oscillations.

The criterion of convergence for the Newton algorithm is based on a relative residual in $l_1$ norm smaller than $Res_\mathrm{max}$ or on a Newton step in $l_\infty$ norm (scaled by $10^{-6}$ for the primary pressure unknown and by 1 for the other primary unknown) smaller than $dx_\mathrm{max}$ with

$$\begin{aligned} Res_\mathrm{max} = 10^{-5}, \quad dx_\mathrm{max} = 10^{-4}. \end{aligned}$$

(3.17)

Note also that the Newton step is relaxed such that its $l_\infty$ norm (scaled by $10^{-6}$ for the primary pressure unknown and by 1 for the other primary unknown) is smaller than $dx_\mathrm{obj}$ with

$$\begin{aligned} dx_\mathrm{obj} = 1. \end{aligned}$$

(3.18)

Fig. 3.11

Triangular mesh of the DFM model with 32340 (32k) cells and 5344 fracture faces (Courtesy of M. Karimi-Fard, Stanford, and A. Lapène, Total). This mesh is refined uniformly to obtain the 129k and 517k cells meshes

Fig. 3.12

Non-wetting phase saturation in the matrix and fracture network at time $t_f=1800$ days for the HVF, VAG MP, VAG TP, VAG CVFE schemes from left to right, and the 32k, 129k, 517k cells meshes from top to bottom

Fig. 3.13

Non-wetting phase volume in the fracture network as a function of time for the VAG MP, HFV, VAG TP and VAG CFVE schemes on the 3 meshes of sizes 32k, 129k and 517k cells

The non-wetting phase saturation is exhibited at final simulation time in Fig. 3.12 in the matrix and in the fracture network, and the volume of the non-wetting phase as a function of time is presented in Fig. 3.13. We clearly see in Figs. 3.12 and 3.13 that the VAG CVFE discretization considerably slows down the non-wetting phase front in the fracture network due to the drain enlargement induced by the mixing of matrix and fracture porous volumes at mf interfaces. The VAG TP discretization does a better job but still underestimates the front speed in the fracture network. As clearly exhibited by Fig. 3.12, this is due to the fact that the VAG TP scheme propagates the non-wetting phase on the wrong side of the fractures as explained in Sect. 3.3.2. From Fig. 3.13, the VAG TP solution gets very close to the VAG MP solution after two level of refinement of the coarse mesh, while the VAG CVFE solution has not yet converged on the finest mesh. The comparison between the VAG MP and HFV solutions shows that they are in good agreement for all meshes. It appears in Fig. 3.13 that the HFV scheme converges more slowly then the VAG MP scheme.

The numerical behavior of the four schemes is reported in Table 3.1 with CPU time is in seconds on Intel E5-2670 2.6 GHz. We remark that the average number of Newton iterations is in all cases quite smaller than ${Newton}_\mathrm{max}$ due to significant variations in the number of Newton iterations during the simulation. This can be explained typically by a higher number of Newton iterations when the non-wetting phase reaches the tips of the fracture network.

For this large 2D network, the VAG MP implementation with elimination of the matrix fracture mobilities leads to a twice large CPU time than the VAG MP implementation with no elimination. Regarding the comparison between VAG MP and VAG TP, we notice a twice larger CPU time, which is a rather good result for such a large network. The comparison between HFV and VAG MP shows for this 2D test case that HFV is competitive on the coarse mesh due to the additional matrix fracture unknowns for VAG MP, but becomes more expensive on the two refined meshes. We will see in the next test case that the situation is much more in favor of the VAG schemes on tetrahedral 3D meshes.

Table 3.1 Numerical behavior of the simulation for the 2D DFM test case on the 3 meshes and for the HFV, VAG CVFE, VAG TP and VAG MP schemes. The VAG MP scheme is implemented either with elimination (VAG MP) or without elimination (VAG MP no elim) of the mf interface mobility unknowns. We refer to the beginning of Sect. 3.3.4 for the description of the entries

3.3.4.3 3D DFM Model

The DFM model of matrix domain $\Omega =(0,100\,\text {m})^3$ and its coarsest tetrahedral mesh conforming to the fracture network are illustrated in Fig. 3.14. The fracture network is assumed to be of constant aperture $d_f = 1$ cm. The matrix and fracture porosities, permeabilities, relative permeabilities and capillary pressures are the same as in the previous test case. The fluid properties are also the same than in the previous test case.

Fig. 3.14

Geometry of the domain $\Omega = 100$ m $\times 100$ m $\times 100$ m with the fracture network in red (left), coarsest tetrahedral mesh with 47670 cells (right)

At initial time, the reservoir is fully saturated with the wetting phase. Then, non-wetting phase is injected from below, which is managed by imposing Dirichlet conditions at the bottom and at the top of the reservoir. We impose at the bottom boundary either an overpressure $\Delta p=2$ MPa or no overpressure $\Delta p=0$ MPa w.r.t. the hydrostatic distribution of the water pressure. The remaining boundaries are assumed impervious and the final simulation time is fixed to $t_f= 360$ days for $\Delta p=2$ MPa and to $t_f= 3600$ days for $\Delta p=0$ MPa. The time stepping is defined as in (3.16) using $\Delta t_{init} = 0.1$ days, ${Newton}_\mathrm{max} = 30$, and either $\Delta t_{\max } = 10$ days for $\Delta p=2$ MPa or $\Delta t_{\max } = 100$ days for $\Delta p=0$ MPa. The criterion of convergence for the Newton algorithm is defined as in (3.17) with $Res_\mathrm{max} = 10^{-6}$ and $dx_\mathrm{max} = 10^{-5}$, and the relaxation of the Newton step is controlled as in (3.18) by the parameter $dx_{obj} = 1$.

Fig. 3.15

Non-wetting phase saturation solutions obtained with the HVF, VAG MP, VAG TP, VAG CVFE schemes from left to right, at time $t_f =360$ days (top), and at time $t=100$ days (bottom), with overpressure $\Delta p = 2$ MPa, and the mesh of size 450k cells. The threshold in the matrix is $S_m^{nw} > 0.1$ (bottom)

From Figs. 3.15 and 3.16, we observe that the VAG TP and VAG CVFE schemes are far from convergence even on the finest mesh with 450k cells while the solution provided by the VAG MP scheme is quite close to the one of the HFV scheme. The discrepancy between, on the one hand, the VAG TP and VAG CVFE, and, on the other hand, the VAG MP and HFV schemes is even more striking on the coarse mesh for the no-overpressure gravity dominant test case exhibited in Figs. 3.17 and 3.18. In terms of CPU time, as exhibited in Table 3.2, the VAG MP scheme implemented with no elimination of the matrix fracture mobility unknowns is competitive compared with the VAG TP scheme. It is also much cheaper than the HFV scheme which leads to a much larger number of d.o.f. and requires both more Newton and GMRes iterations than the VAG schemes. Note that the HFV scheme cannot be run in a reasonable CPU time for the finest mesh of size 1600k cells.

Fig. 3.16

Non-wetting phase volume in the fracture network as a function of time for the 3D DFM test case with the overpressure $\Delta p = 2$ MPa using the VAG MP, HFV, VAG TP and VAG CFVE schemes on the 2 meshes of sizes 47k and 450k cells

Fig. 3.17

Non-wetting phase saturation solutions obtained with the HVF, VAG MP, VAG TP, VAG CVFE schemes from left to right, at time $t_f =3600$ days with no overpressure $\Delta p = 0$ MPa, and the mesh of size 47k cells. The threshold in the matrix is $S_m^{nw} > 0.1$ (bottom)

Fig. 3.18

Non-wetting phase volume in the fracture network as a function of time for the 3D DFM test case with no overpressure $\Delta p = 0$ MPa using the VAG MP, HFV, VAG TP and VAG CFVE schemes on the 47k cells mesh

3.3.5 Capturing the Saturation Jumps at mf Interfaces

Given cellwise and fracture facewise constant rock types, the idea introduced in [20, 43, 44] for CVFE methods and in [14, 17, 31] for the VAG scheme is to define as many saturations as rock types shared at a given node or fracture face. This allows to capture the saturation jumps at rock type interfaces resulting from the continuity of the capillary pressure in the graphical sense [18, 21, 22, 27, 28].

Table 3.2 Numerical behavior of the simulation for the 3D DFM test case with the overpressure $\Delta p = 2$ MPa on the three meshes of sizes 47k, 450k and 1600k cells. The VAG MP scheme is implemented either with elimination (VAG MP) or without elimination (VAG MP no elim) of the mf interface mobility unknowns. We refer to the beginning of Sect. 3.3.4 for the description of the entries

The choice of the primary unknowns may greatly affect the convergence of Newton’s method used to solve the nonlinear system at each time step of the simulation. For the cells and the nodal d.o.f. associated with a single rock the choice of the primary unknowns does not change compared to Sect. 3.3.1. That is we use the non-wetting phase’s pressure and saturation as pair of primary unknowns. In contrast the d.o.f. located at rock type interfaces require a special treatment. For such d.o.f. $\nu \in \mathcal {V}_\Gamma \cup \mathcal {F}_\Gamma$ we set again the pressure of the non-wetting phase as the first primary unknown, while the second primary unknown is chosen based on the variable switching strategy introduced in [14]. For a given rock type $\mathrm{rt} \in \mathcal {RT}=\{m,f\}$ let $\widetilde{P}_{c,\mathrm{rt}}$ denote the monotone graph extension of $P_{c,\mathrm{rt}}$ as introduced in [21, 22]. For each subset $\chi \in \{\{m\}, \{m,f\}\}$ of $\mathcal {RT}$, non-decreasing continuous functions

$$\begin{aligned} \left\{ \begin{array}{ll} &{} P_{c,\chi }(\tau ),\\ &{} S^{nw}_{\chi ,\mathrm{rt}}(\tau ), \text { for all } \mathrm{rt}\in \chi , \end{array}\right. \end{aligned}$$

(3.19)

are built such that

$$ P_{c,\chi }(\tau ) \in \widetilde{P}_{c,\mathrm{rt}}(S^{nw}_{\chi ,\mathrm{rt}}(\tau )), \text { for all } \tau \text { and } \mathrm{rt}\in \chi , $$

and such that $P_{c,\chi }(\tau ) + \sum _{\mathrm{rt}\in \chi } S^{nw}_{\chi ,\mathrm{rt}}(\tau )$ is strictly increasing. Then, we set

$$ S^{w}_{\chi ,\mathrm{rt}}(\tau ) = 1 -S^{nw}_{\chi ,\mathrm{rt}}(\tau ). $$

The variable $\tau$ is going to be used as the second primary unknown.

The main advantage of this framework, which applies to an arbitrary number of rock types, is to incorporate in the construction of the functions (3.19) the saturation jump condition at different rock type interfaces and to apply to general capillary pressure functions. In practice, we use $\tau = s^{nw}$ for $\chi =\{m\}$ and the parametrization defined in [14] for $\chi =\{m,f\}$. This parametrization is based on a generalization of variable switch approaches (see also [43]) between $s_f^{nw}, s_m^{nw}, p_c$ and applies to general, including non invertible, capillary functions (see numerical section for an example and Fig. 3.20).

Let us set

$$ \left\{ \begin{array}{lll} &{} \mathrm{rt}_K = m, &{}\,K\in \mathcal {M},\\ &{} \mathrm{rt}_\sigma = f,&{} \,\sigma \in \mathcal {F}_{\Gamma }, \end{array}\right. \quad \left\{ \begin{array}{ll} \chi _\nu =\{m\}, &{}\,\nu \in \mathcal {M}\cup (\mathcal {V}\setminus \mathcal {V}_{\Gamma }), \\ \chi _\nu =\{m,f\}, &{}\,\nu \in \mathcal {V}_{\Gamma }\cup \mathcal {F}_{\Gamma }. \end{array}\right. $$

Using the above framework, given the primary unknowns $u^{nw}_{\mathcal {D}} = (u^{nw}_\nu )_{\nu \in \mathcal {D}}$ and $\tau _{\mathcal {D}} = (\tau _\nu )_{\nu \in \mathcal {D}}$, we set $u^{w}_{\mathcal {D}} = (u^{w}_\nu )_{\nu \in \mathcal {D}}$ with $u^w_\nu = u^{nw}_\nu - P_{c,\chi _\nu }(\tau _\nu )$ for all d.o.f. $\nu \in \mathcal {D}$, and we define the discrete values of the saturation as follows. For all cells $K\in \mathcal {M}$ and the nodes $\mathbf{s}\in \mathcal {V}\setminus \mathcal {V}_\Gamma$ associated with the single matrix rock type, we set

$$ \begin{array}{lllll} &{} s^\alpha _K &{}= S^{\alpha }_{\chi _K,\mathrm{rt}_K}(\tau _K) &{}= S^{\alpha }_{\{m\},m}(\tau _K) = \tau _K\\ &{} s^\alpha _{K,\mathbf{s}} &{}= S^{\alpha }_{\chi _\mathbf{s},\mathrm{rt}_K}(\tau _\mathbf{s}) &{}=S^{\alpha }_{\{m\},m}(\tau _\mathbf{s}) =\tau _\mathbf{s}, &{} \,K\in \mathcal {M}_\mathbf{s}. \end{array} $$

For the fracture faces $\sigma \in \mathcal {F}_\Gamma$, we set

$$ \begin{array}{lllll} &{} s^\alpha _\sigma &{}= S^{\alpha }_{\chi _\sigma ,\mathrm{rt}_\sigma }(\tau _\sigma ) &{}= S^{\alpha }_{\{m,f\},f}(\tau _\sigma )\\ &{} s^\alpha _{K,\sigma } &{}= S^{\alpha }_{\chi _\sigma ,\mathrm{rt}_K}(\tau _\sigma ) &{}=S^{\alpha }_{\{m, f\},m}(\tau _\sigma ), &{} \,K\in \mathcal {M}_\sigma . \end{array} $$

For the nodes $\mathbf{s}\in \mathcal {V}_\Gamma$, located at the mf interface, we set

$$ \left\{ \begin{array}{lllll} &{} s^\alpha _{K,\mathbf{s}} &{}= S^{\alpha }_{\chi _\mathbf{s},\mathrm{rt}_K}(\tau _\mathbf{s}) &{}=S^{\alpha }_{\{m,f\},m}(\tau _\mathbf{s}),\\ &{} s^\alpha _{\sigma ,\mathbf{s}} &{}= S^{\alpha }_{\chi _\mathbf{s},\mathrm{rt}_\sigma }(\tau _\mathbf{s}) &{}= S^{\alpha }_{\{m,f\},f}(\tau _\mathbf{s}), &{} \,\sigma \in \mathcal {F}_{{\Gamma },\mathbf{s}}. \end{array}\right. $$

As exhibited in Fig. 3.19, the above definition of the saturations at the mf interfaces takes into account the jump of the saturations induced by the different rock types.

Fig. 3.19

Saturations inside the cells K and L, the fracture face $\sigma$ and at the mf interfaces taking into account the saturation jumps induced by the different rock types

Let us remark that, in our specific example, since the matrix domain is homogeneous in terms of capillary pressure-saturation relation, the variables $s^\alpha _{K,\mathbf{s}}, {K\in \mathcal {M}_\mathbf{s}}$ (resp. $s^\alpha _{K,\sigma }, {K\in \mathcal {M}_\sigma }$) refer to the same nodal (resp. facial) saturation values. Similarly, the values $s^\alpha _{\sigma ,\mathbf{s}}, \sigma \in \mathcal {F}_{\Gamma ,\mathbf{s}}$ are identical. This is however not true for general heterogeneous matrix and fracture domains.

We define the accumulation terms by

$$ \left\{ \begin{array}{llll} &{} \mathcal {A}^\alpha _K &{} = \phi _K s^\alpha _K, &{} K\in \mathcal {M},\\ &{} \mathcal {A}^\alpha _\sigma &{} = \displaystyle \phi _\sigma s^\alpha _\sigma + \sum _{K\in \mathcal {M}_\sigma } \phi _{K,\sigma } s^\alpha _{K,\sigma }, &{} \sigma \in \mathcal {F}_{\Gamma },\\ &{} \mathcal {A}^\alpha _\mathbf{s}&{} = \displaystyle \sum _{K\in \mathcal {M}_\mathbf{s}} \phi _{K,\mathbf{s}} s^\alpha _{K,\mathbf{s}} + \sum _{\sigma \in \mathcal {F}_{{\Gamma },\mathbf{s}}} \phi _{\sigma ,\mathbf{s}} s^\alpha _{\sigma ,\mathbf{s}}, &{} \mathbf{s}\in \mathcal {V}\setminus \mathcal {V}_\mathrm{Dir}, \end{array}\right. $$

and the VAG fluxes with TP phase potential upwinding of the mobilities by

$$ q^\alpha _{K,\nu } = M_{\mathrm{rt}_K}^\alpha (s_{K}^\alpha ) (F^\alpha _{K,\nu }(u^\alpha _{\mathcal {D}}))^+ + M_{\mathrm{rt}_K}^\alpha (s_{K,\nu }^\alpha ) (F^\alpha _{K,\nu }(u^\alpha _{\mathcal {D}}))^-, $$

$$ q^\alpha _{\sigma ,\mathbf{s}} = M_{\mathrm{rt}_\sigma }^\alpha (s_\sigma ^\alpha ) (F^\alpha _{\sigma ,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^+ + M_{\mathrm{rt}_\sigma }^\alpha (s_{\sigma ,\mathbf{s}}^\alpha ) (F^\alpha _{\sigma ,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^-, $$

for all $\alpha \in \{nw,w\}$ and $K\in \mathcal {M}$, $\sigma \in \mathcal {F}_{\Gamma }$, $\nu \in \Xi _K$, $\mathbf{s}\in \mathcal {V}_\sigma$.

The VAG TP discretization capturing the saturation jumps at rock type interfaces looks for $u^{nw}_{\mathcal {D}}$ and $\tau _{\mathcal {D}}$ satisfying the conservation equations (3.9) together with the Dirichlet boundary conditions

$$\begin{aligned} \tau _\mathbf{s}= \tau _{\mathrm{Dir},\mathbf{s}} \quad u^{nw}_\mathbf{s}= u^{nw}_{\mathrm{Dir},\mathbf{s}}, \quad \mathbf{s}\in \mathcal {V}_\mathrm{Dir}. \end{aligned}$$

(3.20)

It will be termed VAG TP m-upwind discretization in the following. The VAG MP m-upwind discretization can also be defined as previously using the MP upwind flux

$$ q^\alpha _{K,\mathbf{s}} = q^\alpha _{K,\overline{K}_\mathbf{s}} = M_{\mathrm{rt}_K}^\alpha (s_K^\alpha ) (F^\alpha _{K,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^+ + M^\alpha _{\overline{K}_\mathbf{s}} (F^\alpha _{K,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^-, $$

for $\mathbf{s}\in \mathcal {V}_{\Gamma }$ with the interface mobility

$$ \displaystyle M^\alpha _{\overline{K}_\mathbf{s}} = { \displaystyle \sum \limits _{L \in \overline{K}_\mathbf{s}} (F^\alpha _{L,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^+ M_{\mathrm{rt}_L}^\alpha (s_L^\alpha ) - M_{\mathrm{rt}_K}^\alpha (s^\alpha _{K,\mathbf{s}}) (\sum \limits _{L\in \overline{K}_\mathbf{s}} F^\alpha _{L,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^- \over \displaystyle \sum \limits _{L \in \overline{K}_\mathbf{s}} (F^\alpha _{L,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^+ - (\sum \limits _{L\in \overline{K}_\mathbf{s}} F^\alpha _{L,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^- }, $$

assuming that $\mathrm{rt}_L = \mathrm{rt}_K$ for all $L\in \overline{K}_\mathbf{s}$. This assumption can always be verified by setting new interface face(s) between the different rock types in $\overline{K}_\mathbf{s}$. This discretization will be termed VAG MP m-upwind discretization in the following.

A comparison of the f-upwind and m-upwind models with reference equi-dimensional solutions can be found in [1, 16]. Basically, it concludes that, thanks to the saturation jump capturing at mf interfaces, the m-upwind model provides a better approximation than the f-upwind model as long as the fractures are not fully filled with the non-wetting phase. When the fractures are filled, the m-upwind model overestimates the fracture capillary pressure and underestimates the capillary barrier effect. In that case the f-upwind model provides a better approximation.

In the following numerical section, the VAG TP and MP m-upwind discretizations are compared both in terms of solutions and CPU times.

Fig. 3.20

(Top): capillary pressure as a function of the non-wetting phase saturation for both the fracture (f) and matrix (m) rock types with $b_m=10^4$ and $b_f=10^3$ Pa. (Bottom): capillary pressure and fracture and matrix non-wetting phase saturations as functions of the parameter $\tau \in [0,\tau _2)$

3.3.5.1 Numerical Experiments

In this subsection, we compare the m-upwind version of the VAG TP and VAG MP schemes using the same code implementation as described in the beginning of Sect. 3.3.4. The test case considers the large DFM model exhibited in Fig. 3.21 with domain $\Omega = (0,85)\times (0,60)\times (0,140)$ m kindly provided by the authors of the Benchmark [11, 12].

The fracture width is $d_f = 1$ cm and the fracture network is homogeneous and isotropic with $\Lambda _f = 10^{-11}$ m$^2$, $\phi _f = 0.2$. The matrix is homogeneous and isotropic with $\Lambda _m = 10^{-14}$ m$^2$, $\phi _m = 0.4$.

The relative permeabilities are given by $k_{r,f}^\alpha (s^\alpha _f) = s^\alpha _f$ and $k_{r,m}^\alpha (s^\alpha _m) = (s^\alpha _m)^2$, $\alpha \in \{nw,w\}$ and the capillary pressure is fixed to $P_{c,m}(s^{nw}_m) = - b_m \ln (1-s^{nw}_m)$ Pa in the matrix and to $P_{c,f}(s^{nw}_f) = - b_f \ln (1-s^{nw}_f)$ Pa in the fracture network, with $b_f = 10^3$ Pa, and $b_m = 10^4$ Pa. The fluid properties are defined by their dynamic viscosities $\mu ^{nw} = 5. ~10^{-3}$, $\mu ^w = 10^{-3}$ Pa s and their mass densities $\rho ^w = 1000$ and $\rho ^{nw} = 700$ kg m$^{-3}$.

Fig. 3.21

Large DFM model with its mesh of size 495233 tetrahedral cells and 66908 fracture faces provided by the authors of the Benchmark [11]

The parametrization $\tau$ at mf interfaces introduced in [14] is recalled below and illustrated in Fig. 3.20 for the convenience of the reader.

$$\begin{aligned} S_{{\{m,f\},f}}^{nw}(\tau ) = \left\{ \begin{array}{ll} \tau , &{} \tau \in [0, \tau _1),\\ 1 - (\tau _1+(1-\tau _1)^{b_f\over b_m}-\tau )^{b_m\over b_f}, &{} \tau \in [\tau _1, \tau _2), \end{array} \right. \end{aligned}$$

(3.21)

$$\begin{aligned} S_{{\{m,f\},m}}^{nw}(\tau ) = \left\{ \begin{array}{ll} 1 - (1-\tau )^{b_f\over b_m}, &{} \tau \in [0, \tau _1), \\ \tau - \tau _1 + 1 - (1-\tau _1)^{b_f\over b_m}, &{} \tau \in [\tau _1, \tau _2), \end{array} \right. \end{aligned}$$

(3.22)

and

$$\begin{aligned} P_{c,\{m,f\}}(\tau ) = \left\{ \begin{array}{ll} -b_f \ln (1-\tau ), &{}\tau \in [0, \tau _1),\\ -b_m \ln \Bigl (\tau _1+(1-\tau _1)^{b_f\over b_m} -\tau \Bigr ), &{} \tau \in [\tau _1, \tau _2), \end{array} \right. \end{aligned}$$

(3.23)

where $\tau _1 = 1 - ({b_f\over {b_m}})^{b_m\over {b_m-b_f}}$ and $\tau _2 = \tau _1+ (1-\tau _1)^{b_f \over b_m}$.

The reservoir is initially saturated with the wetting phase. Output Dirichlet boundary conditions are imposed at the boundary $\{0,85\}\times (0,20)\times (110,140)$ with a wetting phase pressure of 1 MPa and $s^{w}_m = 1$, and input Dirichlet boundary conditions are set at the boundary $\{0\}\times (40,60)\times (0,30)\cup (0,30)\times (40,85)\times \{0\}$ with $s^{nw}_m = 0.9$ and $u^w = 4 \, \mathrm {MPa}$. The remaining boundaries are assumed impervious and the final simulation time is fixed to $t_f= 3600$ days. The time stepping is defined as in (3.16) using $\Delta t_{init} = 0.01$ days, $\Delta t_\mathrm{max} = 100$ days and $Newton_\mathrm{max}=25$. The criterion of convergence for the Newton algorithm is defined as in (3.17) with $Res_\mathrm{max} = 10^{-5}$ and $dx_\mathrm{max} = 10^{-4}$, and the relaxation of the Newton step is controlled as in (3.18) by the parameter $dx_{obj} = 1$.

Fig. 3.22

Non-wetting phase saturation volumes in the matrix (left) and in the fracture network (right) as a function of time obtained for the VAG TP and the VAG MP m-upwind schemes

Fig. 3.23

Non-wetting phase saturation in the matrix (top) and in the fracture network (bottom) obtained for the VAG TP (left) and VAG MP (right) m-upwind schemes at time $t=350$ days

The same issue at mf interfaces as for the VAG TP f-upwind approximation can be noticed in Fig. 3.23 for the VAG TP m-upwind discretization in the sense that the non-wetting phase can go out from the fractures on the wrong side for the VAG TP approximation. Nevertheless, thanks to the rather large saturation jump captured by the m-upwind model in this test case, it involves small amounts of the non-wetting phase and does not have visible effects on overall quantities (see Fig. 3.22) nor on the non-wetting phase saturation front (see Fig. 3.23). In terms of CPU time, as exhibited in Table 3.3, a factor of roughly 1.7 is observed in favor of the TP discretization due to the additional mf interface unknowns on this rather large fracture network and to the slightly larger number of Newton iterations for the MP scheme.

Let us refer to [13] for a numerical comparison between the m-upwind VAG TP scheme and the m-upwind VAG CVFE scheme (i.e. without adaptive distribution of the porous volumes at mf interfaces). It shows that the m-upwind VAG CVFE scheme still slows down the transport in the fractures in particular for a high matrix fracture permeability ratio.

Table 3.3 Numerical behavior of the simulation field test case for the VAG TP and MP m-upwind schemes. We refer to the beginning of Sect. 3.3.4 for the description of the entries

3.4 Vertex Approximate Gradient (VAG) Discretization of Two-Phase DFM Discontinuous Pressure Models

Discontinuous pressure models are required to account for fractures acting as barriers. Such barriers are usually induced by a low fracture normal permeability combined with a capillary barrier effect. Note that even in the case of a high normal fracture permeability, a barrier behavior can still be observed for a given phase due to the degeneracy of the phase mobility when the fracture is filled by the other phase (see [1, 16]). Compared to the single phase flow models the possibility of such capillary barriers constitutes an additional motivation for the use of discontinuous pressure models.

Fig. 3.24

Single phase VAG discretization of the discontinuous pressure hybrid-dimensional model: example of discrete unknowns in 2D with 3 fracture faces intersecting at node $\mathbf{s}$ (left), and VAG fluxes (matrix fluxes in red, fracture fluxes in black and matrix fracture fluxes in dark red) in a 3D cell K with a fracture face $\sigma$ in bold (right)

VAG discrete unknowns: as exhibited in Fig. 3.24, the discrete unknowns are defined by the matrix d.o.f.

$$ \mathcal {D}_m = \mathcal {M}\cup \{ {{\overline{K}}_\mathbf{s}} \,|\, {\overline{K}}_\mathbf{s}\in \overline{\mathcal {M}}_\mathbf{s}, \mathbf{s}\in \mathcal {V}\setminus \mathcal {V}_{\Gamma }\} \cup \mathcal {D}_{mf} $$

and by the fracture d.o.f.

$$ \mathcal {D}_f = \mathcal {F}_{\Gamma }\cup \mathcal {V}_{\Gamma }, $$

where $\mathcal {D}_{mf}\subset \mathcal {D}_m$ are the mf interface d.o.f.

$$ \mathcal {D}_{mf} = \overline{\mathcal {M}}_{\Gamma }\cup \overline{\mathcal {F}}_{\Gamma }, $$

with

$$ \overline{\mathcal {M}}_{\Gamma }= \{{{\overline{K}}_\mathbf{s}} \,|\, {\overline{K}}_\mathbf{s}\in \overline{\mathcal {M}}_\mathbf{s}, \mathbf{s}\in \mathcal {V}_{\Gamma }\},\quad \quad \overline{\mathcal {F}}_{\Gamma }= \{ K_\sigma \,|\,K\in \mathcal {M}_\sigma , \sigma \in \mathcal {F}_{\Gamma }\}. $$

Let us set $\mathcal {D}= \mathcal {D}_m\cup \mathcal {D}_f$ and let us remark that for $\mathbf{s}\in \mathcal {V}\setminus \mathcal {V}_{\Gamma }$, $\overline{\mathcal {M}}_\mathbf{s}$ is reduced to the set of cells around $\mathbf{s}$ and the d.o.f. $\overline{K}_\mathbf{s}\in \overline{\mathcal {M}}_\mathbf{s}$ is considered to match with the node $\mathbf{s}$.

For each cell $K\in \mathcal {M}$, let us also define the following subset of d.o.f. located at the boundary of the cell:

$$ \Xi _K = \{ {\overline{K}}_\mathbf{s}, \mathbf{s}\in \mathcal {V}_K, \,K_\sigma ,\sigma \in \mathcal {F}_{\Gamma }\cap \mathcal {F}_K\}. $$

The subset of Dirichlet d.o.f. is denoted by $\mathcal {D}_\mathrm{Dir}\subset \mathcal {D}$.

As in Sect. 3.3.5, the definition of the primary and secondary unknowns at the d.o.f. located at the rock type interfaces is based on the parametrization of the capillary pressure graphs (3.19). To fix ideas, we assume the presence of 3 rock types $\mathcal {RT}=\{m,f_d, f_b\}$ where $f_d$ is a fracture drain rock type and $f_b$ is a fracture barrier rock type while m denote again the matrix rock type Let the fracture network $\Gamma$ be partitioned into the networks ${\Gamma }_d$ of fractures acting as drains and the network ${\Gamma }_b$ of fractures acting as barriers. In order to simplify the presentation of the numerical scheme, we will assume that $\overline{\Gamma }_d\cap \overline{\Gamma }_b=\emptyset$. Then, the collection $\chi$ of rock types associated with any given d.o.f. take values in

$$ \{\{m\},\{f_d\},\{f_b\},\{m,f_d\}, \{m,f_b\}\}. $$

corresponding to assume no intersections between fractures acting as drain and barrier. In practice, we use the parametrization $\tau = s^{nw}$ for $\chi =\{m\}, \{f_d\}, \{f_b\}$ and the parametrizations defined in [14] for $\chi =\{m,f_d\}$ or $\{m,f_b\}$. More precisely, let us set for $\star = b,d$

$$ \left\{ \begin{array}{lll} &{} \mathrm{rt}_K = m, &{}\,K\in \mathcal {M},\\ &{} \mathrm{rt}_\sigma = f_\star ,&{} \,\{\sigma \in \mathcal {F}_{\Gamma }\,|\, \mathbf{x}_\sigma \in {\Gamma }_\star \}, \end{array}\right. \left\{ \begin{array}{ll} \chi _\nu =\{m\}, &{}\,\nu \in \mathcal {D}_m\setminus \mathcal {D}_{mf}, \\ \chi _\nu =\{f_\star \}, &{}\,\{\nu \in \mathcal {D}_f \,|\, \mathbf{x}_\nu \in \overline{{\Gamma }}_\star \} := \mathcal {D}_f^\star , \\ \chi _\nu =\{m,f_\star \}, &{}\,\{\nu \in \mathcal {D}_{mf} \,|\, \mathbf{x}_\nu \in \overline{{\Gamma }}_\star \} := \mathcal {D}_{mf}^\star ,\\ \end{array}\right. $$

Using the above framework, given the primary unknowns $u^{nw}_{\mathcal {D}} = (u^{nw}_\nu )_{\nu \in \mathcal {D}}$ and $\tau _{\mathcal {D}} = (\tau _\nu )_{\nu \in \mathcal {D}}$, we set $u^{w}_{\mathcal {D}} = (u^{w}_\nu )_{\nu \in \mathcal {D}}$ with $u^w_\nu = u^{nw}_\nu - P_{c,\chi _\nu }(\tau _\nu )$ for all d.o.f. $\nu \in \mathcal {D}$, and we define the discrete values of the saturation as follows. For all d.o.f. associated with a single rock type, that is $K \in \mathcal {M}$ and $\sigma \in \mathcal {F}_\Gamma$ we set

$$ s^\alpha _K = S^{\alpha }_{\chi _K,\mathrm{rt}_K}(\tau _K) = \tau _K, \quad s^\alpha _\sigma = S^{\alpha }_{\chi _\sigma ,\mathrm{rt}_\sigma }(\tau _\sigma ) = \tau _K, $$

for all $\nu \in \Xi _K\cap \mathcal {D}_{m}\setminus \mathcal {D}_{mf}, \,K\in \mathcal {M}$, we set

$$ s^\alpha _{K,\nu } = S^{\alpha }_{\chi _\nu ,\mathrm{rt}_K}(\tau _\nu )= S^{\alpha }_{\{m\},m}(\tau _\nu ) = \tau _\nu , $$

for all $\mathbf{s}\in \mathcal {V}_\mathbf{s}$, $\sigma \in \mathcal {F}_{\Gamma }$, we set

$$ s^\alpha _{\sigma ,\mathbf{s}} = S^{\alpha }_{\chi _\mathbf{s},\mathrm{rt}_\sigma }(\tau _\mathbf{s}) =\tau _\mathbf{s}, $$

while for all mf interface d.o.f. from $\mathcal {D}_{mf}$, and with $\star = b,d$, we impose

$$ \left\{ \begin{array}{lllll} &{} s^\alpha _{K,\nu } &{}= S^{\alpha }_{\chi _\nu ,\mathrm{rt}_K}(\tau _\nu )&{}= S^{\alpha }_{\{m,f_\star \},m}(\tau _\nu ), &{}\nu \in \Xi _K\cap \mathcal {D}_{mf}^\star , \,K\in \mathcal {M},\\ &{} s^\alpha _{\sigma ,K_\sigma } &{}= S^{\alpha }_{\chi _{K_\sigma },\mathrm{rt}_\sigma }(\tau _{K_\sigma })&{}= S^{\alpha }_{\{m,f_\star \},f_d}(\tau _{K_\sigma }), &{} K_\sigma \in \overline{\mathcal {F}}_{\Gamma }\cap \mathcal {D}_{mf}^\star ,\\ &{} s^\alpha _{\sigma , \overline{K}_\mathbf{s}} &{} = S^\alpha _{\chi _{\overline{K}_\mathbf{s}, \mathrm{rt}_\sigma }}(\tau _{\overline{K}_\mathbf{s}})&{} = S^\alpha _{\chi _{\{m,f_\star \}, f_d}}(\tau _{\overline{K}_\mathbf{s}}), &{} \overline{K}_\mathbf{s}\in \overline{\mathcal {M}}_{\Gamma }\cap \mathcal {D}_{mf}^\star , \sigma \in \mathcal {F}_{{\Gamma },\overline{K}_\mathbf{s}},\\ \end{array}\right. $$

where $\mathcal {F}_{{\Gamma },\overline{K}_\mathbf{s}} = \mathcal {F}_{{\Gamma },\mathbf{s}}\cap (\bigcup _{K\in \overline{K}_\mathbf{s}}\mathcal {F}_K)$.

Discrete fluxes: the VAG fluxes connect each cell K (resp. each fracture face $\sigma$) to its boundary d.o.f. $\nu \in \Xi _K$ (resp. $\mathbf{s}\in \mathcal {V}_\sigma$) using the same transmissibility coefficients as for the continuous pressure model

$$ F_{K,\nu }(u_{\mathcal {D}_m}) = \sum _{\nu '\in \Xi _K}\mathbb {T}_{K}^{\nu ,\nu '}(u_K-u_{\nu '}), \quad F_{\sigma ,\mathbf{s}}(u_{\mathcal {D}_f}) = \sum _{\mathbf{s}'\in \mathcal { V}_\sigma }\mathbb {T}_{\sigma }^{\mathbf{s},\mathbf{s}'}(u_\sigma -u_{\mathbf{s}'}). $$

Additionally, two-point matrix fracture fluxes are defined by

$$ F_{\overline{K}_\mathbf{s}, \mathbf{s}}(u_{\overline{K}_\mathbf{s}}, u_\mathbf{s}) = T_{\overline{K}_\mathbf{s}, \mathbf{s}}(u_{\overline{K}_\mathbf{s}} - u_\mathbf{s}),\quad F_{K_\sigma , \sigma }(u_{K_\sigma }, u_\sigma ) = T_{K_\sigma , \sigma }(u_{K_\sigma } - u_\sigma ), $$

for $\mathbf{s}\in \mathcal {V}_{\Gamma }$, $\overline{K}_\mathbf{s}\in \overline{\mathcal {M}}_\mathbf{s}$ and $\sigma \in \mathcal {F}_{\Gamma }$, $K\in \mathcal {M}_\sigma$, with

$$ T_{\overline{K}_\mathbf{s}, \mathbf{s}} = {1\over 3} \sum _{T\in \Delta \,|\, \mathbf{s}\in \overline{T}}\int _T {2\lambda _{f,n} \over d_f} d\sigma (\mathbf{x}),\quad T_{K_\sigma , \sigma } = \int _\sigma {2\lambda _{f,n} \over d_f} d\sigma (\mathbf{x}), $$

where $\Delta$ is the triangular submesh of ${\Gamma }$ defined as the trace on $\Gamma$ of the tetrahedral submesh $\mathcal {T}$ introduced in (3.8) (see [15]) for details).

Setting $z_{\mathcal {D}_m} = (z_\nu )_{\nu \in \mathcal {D}_m}$ and $z_{\mathcal {D}_f} = (z_\nu )_{\nu \in \mathcal {D}_f}$, the two-phase VAG fluxes combine the VAG single phase Darcy fluxes including gravity

$$ F^\alpha _{K,\nu }(u^\alpha _{\mathcal {D}_m}) = F_{K,\nu }(u^\alpha _{\mathcal {D}_m}) + \rho ^\alpha g F_{K,\nu }(z_{\mathcal {D}_m}), \quad F^\alpha _{\sigma ,\mathbf{s}}(u^\alpha _{\mathcal {D}_f}) = F_{\sigma ,\mathbf{s}}(u^\alpha _{\mathcal {D}_f}) + \rho ^\alpha g F_{\sigma ,\mathbf{s}}(z_{\mathcal {D}_f}), $$

$$ F^\alpha _{\overline{K}_\mathbf{s}, \mathbf{s}}(u^\alpha _{\overline{K}_\mathbf{s}}, u^\alpha _\mathbf{s}) = F_{\overline{K}_\mathbf{s}, \mathbf{s}}(u^\alpha _{\overline{K}_\mathbf{s}}, u^\alpha _\mathbf{s}) - {1\over 3} \rho ^\alpha \sum _{T\in \Delta \,|\, \mathbf{s}\in \overline{T}}\int _T \lambda _{f,n} \mathbf{g}\cdot \mathbf{n}_{\overline{K}_\mathbf{s},T} d\sigma (\mathbf{x}), $$

$$ F^\alpha _{K_\sigma , \sigma }(u^\alpha _{K_\sigma }, u^\alpha _\sigma ) = F_{K_\sigma , \sigma }(u^\alpha _{K_\sigma }, u^\alpha _\sigma ) - \rho ^\alpha \int _\sigma \lambda _{f,n} \mathbf{g}\cdot \mathbf{n}_{K,\sigma } d\sigma (\mathbf{x}), $$

with the usual Two-Point phase potential upwinding of the mobilities, leading to define

$$ q^\alpha _{K,\nu } = M_{\mathrm{rt}_K}^\alpha (s_{K}^\alpha ) (F^\alpha _{K,\nu }(u^\alpha _{\mathcal {D}}))^+ + M_{\mathrm{rt}_K}^\alpha (s_{K,\nu }^\alpha ) (F^\alpha _{K,\nu }(u^\alpha _{\mathcal {D}}))^-, $$

for all $K\in \mathcal {M}$, $\nu \in \Xi _K$,

$$ q^\alpha _{\sigma ,\mathbf{s}} = M_{\mathrm{rt}_\sigma }^\alpha (s_\sigma ^\alpha ) (F^\alpha _{\sigma ,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^+ + M_{\mathrm{rt}_\sigma }^\alpha (s_{\sigma ,\mathbf{s}}^\alpha ) (F^\alpha _{\sigma ,\mathbf{s}}(u^\alpha _{\mathcal {D}}))^-, $$

for all $\sigma \in \mathcal {F}_{\Gamma }$, $\mathbf{s}\in \mathcal {V}_\sigma$,

$$ \begin{array}{rlll} q^\alpha _{\overline{K}_\mathbf{s},\mathbf{s}} &{}=&{} \displaystyle {1\over \mathrm{Card}(\mathcal {F}_{{\Gamma },\overline{K}_\mathbf{s}}) }\sum _{\sigma \in \mathcal {F}_{{\Gamma },\overline{K}_\mathbf{s}}} \Bigl ( &{} M_{\mathrm{rt}_\sigma }^\alpha (s_{\sigma ,\overline{K}_\mathbf{s}}^\alpha ) (F^\alpha _{\overline{K}_\mathbf{s}, \mathbf{s}}(u^\alpha _{\overline{K}_\mathbf{s}}, u^\alpha _\mathbf{s}))^+ \\ &{}&{} &{}+ M_{\mathrm{rt}_\sigma }^\alpha (s_{\sigma ,\mathbf{s}}^\alpha ) (F^\alpha _{\overline{K}_\mathbf{s}, \mathbf{s}}(u^\alpha _{\overline{K}_\mathbf{s}}, u^\alpha _\mathbf{s}))^- \Bigr ) \end{array} $$

for all $\mathbf{s}\in \mathcal {V}_{\Gamma }$, $\overline{K}_\mathbf{s}\in \overline{\mathcal {M}}_\mathbf{s}$, and

$$ q^\alpha _{K_\sigma ,\sigma } = M_{\mathrm{rt}_\sigma }^\alpha (s_{\sigma ,K_\sigma }^\alpha ) (F^\alpha _{K_\sigma , \sigma }(u^\alpha _{K_\sigma }, u^\alpha _\sigma ))^+ + M_{\mathrm{rt}_\sigma }^\alpha (s_{\sigma }^\alpha ) (F^\alpha _{K_\sigma , \sigma }(u^\alpha _{K_\sigma }, u^\alpha _\sigma ))^- $$

for all $\sigma \in \mathcal {F}_{\Gamma }$, $K\in \mathcal {M}_\sigma$.

Control volumes and accumulation terms: as for the continuous pressure model, porous volumes $\phi _{K,\nu }, \nu \in \Xi _K\setminus \mathcal {D}_\mathrm{Dir}$ (resp. $\phi _{\sigma ,\mathbf{s}}, \mathbf{s}\in \mathcal {V}_\sigma \setminus \mathcal {D}_\mathrm{Dir}$) are obtained by distribution of the cell $K\in \mathcal {M}$ (resp. fracture face $\sigma \in \mathcal {F}_{\Gamma }$) porous volume. A porous volume $\phi _{\sigma ,\overline{K}_\mathbf{s}}$ (resp. $\phi _{\sigma ,K_\sigma }$) is also distributed from the fracture face $\sigma$ to the interface d.o.f. $\overline{K}_\mathbf{s}$ (resp. $K_\sigma$) for $\sigma \in \mathcal {F}_{{\Gamma },\overline{K}_\mathbf{s}}$, $\overline{K}_\mathbf{s}\in \overline{\mathcal {M}}_{\Gamma }$ (resp. for $K_\sigma \in \overline{\mathcal {F}}_{\Gamma }$). These interface porous volumes are required to avoid the singularity of the linear systems obtained after Newton linearization. Their influence on the solution is small provided that they are chosen small enough (see [25]). Then we set

$$ \left\{ \begin{array}{lll} &{} \phi _K = \displaystyle \int _K \phi _m(\mathbf{x}) d\mathbf{x}- \sum _{\nu \in \Xi _K\setminus \mathcal {D}_\mathrm{Dir}} \phi _{K,\nu }, &{} K\in \mathcal {M},\\ &{} \begin{array}{lll} &{}\displaystyle \phi _\sigma = \int _\sigma d_f(\mathbf{x}) \phi _f(\mathbf{x}) d\mathbf{x}&{}- \displaystyle \sum _{\mathbf{s}\in \mathcal {V}_\sigma \setminus \mathcal {D}_\mathrm{Dir}} \phi _{\sigma ,\mathbf{s}} - \sum _{K\in \mathcal {M}_\sigma } \phi _{\sigma , K_\sigma }\\ &{}&{}- \displaystyle \sum _{\overline{K}_\mathbf{s}\in \overline{\mathcal {M}}_{{\Gamma }} \setminus \mathcal {D}_\mathrm{Dir}\,|\, \sigma \in \mathcal {F}_{{\Gamma },\overline{K}_\mathbf{s}}} \phi _{\sigma ,\overline{K}_\mathbf{s}}, \end{array}&\sigma \in \mathcal {F}_{\Gamma }, \end{array}\right. $$

and we define the accumulations terms by

$$ \left\{ \begin{array}{llll} &{} \mathcal {A}^\alpha _K &{} = \phi _K s^\alpha _K, &{} K\in \mathcal {M},\\ &{} \mathcal {A}^\alpha _{\overline{K}_\mathbf{s}} &{} = \displaystyle \sum _{K\in \mathcal {M}_\mathbf{s}} \phi _{K,\overline{K}_\mathbf{s}} s^\alpha _{K,\overline{K}_\mathbf{s}}, &{} \mathbf{s}\in \mathcal {V}\setminus (\mathcal {D}_\mathrm{Dir}\cup \mathcal {V}_{\Gamma }),\\ &{} \mathcal {A}^\alpha _\sigma &{} = \displaystyle \phi _\sigma s^\alpha _\sigma , &{} \sigma \in \mathcal {F}_{\Gamma },\\ &{} \mathcal {A}^\alpha _{\mathbf{s}} &{} = \displaystyle \sum _{\sigma \in \mathcal {F}_{{\Gamma },\mathbf{s}}} \phi _{\sigma ,\mathbf{s}} s^\alpha _{\sigma ,\mathbf{s}}, &{} \mathbf{s}\in \mathcal {V}_\Gamma \setminus \mathcal {D}_\mathrm{Dir},\\ &{} \mathcal {A}^\alpha _{K_\sigma } &{} = \displaystyle \phi _{\sigma , K_\sigma } s^\alpha _{\sigma ,K_\sigma } + \phi _{K,K_\sigma } s^\alpha _{K,K_\sigma }, &{} K_\sigma \in \overline{\mathcal {F}}_{\Gamma },\\ &{} \mathcal {A}^\alpha _{\overline{K}_\mathbf{s}} &{} = \displaystyle \sum _{K\in \overline{K}_\mathbf{s}} \phi _{K,\overline{K}_\mathbf{s}} s^\alpha _{K,\overline{K}_\mathbf{s}} + \sum _{\sigma \in \mathcal {F}_{{\Gamma },\overline{K}_\mathbf{s}}} \phi _{\sigma ,\overline{K}_\mathbf{s}} s^\alpha _{\sigma ,\overline{K}_\mathbf{s}}, &{} \overline{K}_\mathbf{s}\in \overline{\mathcal {M}}_{\Gamma }\setminus \mathcal {D}_\mathrm{Dir},\\ \end{array}\right. $$

Conservation equations: the VAG discretization of the discontinuous pressure model solves for $u^{nw}_{\mathcal {D}}$ and $\tau _{\mathcal {D}}$ such that

$$\begin{aligned} \left\{ \begin{array}{lllll} &{}\displaystyle {\mathcal {A}^\alpha _K - \mathcal {A}_K^{\alpha ,n-1} \over \Delta t^n} &{}+ \displaystyle \sum _{\nu \in \Xi _K} q^\alpha _{K,\nu } &{}= 0, &{} K\in \mathcal {M},\\ &{}\displaystyle {\mathcal {A}^\alpha _{\overline{K}_\mathbf{s}} - \mathcal {A}_{\overline{K}_\mathbf{s}}^{\alpha ,n-1} \over \Delta t^n} &{}- \displaystyle \sum _{K\in \mathcal {M}_\mathbf{s}} q^\alpha _{K,\overline{K}_\mathbf{s}} &{}= 0, &{} \mathbf{s}\in \mathcal {V}\setminus (\mathcal {V}_{\Gamma }\cup \mathcal {D}_\mathrm{Dir}),\\ &{}\displaystyle {\mathcal {A}^\alpha _\sigma - \mathcal {A}_\sigma ^{\alpha ,n-1} \over \Delta t^n} &{}+ \displaystyle \sum _{\mathbf{s}\in \mathcal { V}_\sigma } q^\alpha _{\sigma ,\mathbf{s}} - \sum _{K\in \mathcal {M}_\sigma } q^\alpha _{K_\sigma ,\sigma } &{}= 0, &{} \sigma \in \mathcal {F}_\Gamma , \\ &{}\displaystyle {\mathcal {A}^\alpha _\mathbf{s}- \mathcal {A}_\mathbf{s}^{\alpha ,n-1} \over \Delta t^n} &{}\displaystyle - \sum _{\sigma \in \mathcal {F}_{\Gamma ,\mathbf{s}}} q^\alpha _{\sigma ,\mathbf{s}} - \displaystyle \sum _{\overline{K}_\mathbf{s}\in \overline{\mathcal {M}}_\mathbf{s}} q^\alpha _{\overline{K}_\mathbf{s},\mathbf{s}} &{}= 0, &{} \mathbf{s}\in \mathcal {V}_{\Gamma }\setminus \mathcal {D}_\mathrm{Dir}, \\ &{}\displaystyle {\mathcal {A}^\alpha _{K_\sigma } - \mathcal {A}_{K_\sigma }^{\alpha ,n-1} \over \Delta t^n} &{}- \displaystyle \,\,q^\alpha _{K,K_\sigma } + q^\alpha _{K_\sigma ,\sigma } &{}= 0, &{} K_\sigma \in \overline{\mathcal {F}}_{\Gamma },\\ &{}\displaystyle {\mathcal {A}^\alpha _{\overline{K}_\mathbf{s}} - \mathcal {A}_{\overline{K}_\mathbf{s}}^{\alpha ,n-1} \over \Delta t^n} &{}- \displaystyle \sum _{K\in \overline{K}_\mathbf{s}} q^\alpha _{K,\overline{K}_\mathbf{s}} + q^\alpha _{\overline{K}_\mathbf{s},\mathbf{s}} &{}= 0, &{} \overline{K}_\mathbf{s}\in \overline{\mathcal {M}}_{\Gamma }\setminus \mathcal {D}_\mathrm{Dir},\\ &{}\tau _\nu = \tau _{\mathrm{Dir},\nu }, &{} u^{nw}_\nu = u^{nw}_{\mathrm{Dir},\nu }, &{}&{} \nu \in \mathcal {D}_\mathrm{Dir}. \end{array}\right. \end{aligned}$$

(3.24)

f and m-upwind discontinuous pressure models: the above discontinuous pressure model, termed mf nonlinear model in the following, leads to difficulties to solve the nonlinear system (3.24) due to the combination of highly contrasted matrix and fracture rock types and to the small pore volumes at mf interface d.o.f. One possibility to solve this issue, still preserving the ability to take into account fractures acting as drains or barriers, is to linearize the matrix fracture transmission conditions w.r.t. the mf interface unknowns and to apply a f or m-upwind approximation of the mobilities. This idea, developed in [16] for the VAG discretization and in [1] for the TPFA discretization, replaces the primary unknowns $u^{nw}_\nu , \tau _\nu$ at matrix fracture d.o.f. $\nu \in \mathcal {D}_{mf}$ by both phase pressures $u^{nw}_\nu , u^w_\nu$, $\nu \in \mathcal {D}_{mf}$, and the conservation equations at matrix fracture d.o.f. by

$$ F^\alpha _{\overline{K}_\mathbf{s}, \mathbf{s}}(u^\alpha _{\overline{K}_\mathbf{s}}, u^\alpha _\mathbf{s}) - \sum _{K\in \overline{K}_\mathbf{s}} F^\alpha _{K,\overline{K}_\mathbf{s}}(u^\alpha _{\mathcal {D}_m}) = 0, \quad F^\alpha _{K_\sigma , \sigma }(u^\alpha _{K_\sigma }, u^\alpha _\sigma ) - F^\alpha _{K,K_\sigma }(u^\alpha _{\mathcal {D}_m}) = 0, $$

for $\overline{K}_\mathbf{s}\in \overline{\mathcal {M}}_{\Gamma }$ and $K_\sigma \in \overline{\mathcal {F}}_{\Gamma }$. Note that the pore volumes $\phi _{\sigma ,\overline{K}_\mathbf{s}}$ and $\phi _{\sigma ,K_\sigma }$ are set to zero. Since phase saturations are no longer defined at matrix fracture d.o.f., one need to modify the upwind mobilities in the definition of the fluxes $q^\alpha _{K,\overline{K}_\mathbf{s}}$, $\overline{K}_\mathbf{s}\in \overline{\mathcal {M}}_{\Gamma }$ now connecting directly the cell K and the fracture d.o.f. $\mathbf{s}$, and in the definition of $q^\alpha _{K,K_\sigma }$, $K_\sigma \in \overline{\mathcal {F}}_{\Gamma }$ now connecting the cell K and the fracture d.o.f. $\sigma$. These new connectivities modify the fracture conservations equations for $\sigma \in \mathcal {F}_{\Gamma }$ and $\mathbf{s}\in \mathcal {V}_{\Gamma }\setminus \mathcal {D}_\mathrm{Dir}$ as follows:

$$\begin{aligned} \left\{ \begin{array}{llll} &{}\displaystyle {\mathcal {A}^\alpha _\sigma - \mathcal {A}_\sigma ^{\alpha ,n-1} \over \Delta t^n} + \displaystyle \sum _{\mathbf{s}\in \mathcal { V}_\sigma } q^\alpha _{\sigma ,\mathbf{s}} - \sum _{K\in \mathcal {M}_\sigma } q^\alpha _{K,K_\sigma } &{}= 0, &{} \sigma \in \mathcal {F}_\Gamma , \\ &{}\displaystyle {\mathcal {A}^\alpha _\mathbf{s}- \mathcal {A}_\mathbf{s}^{\alpha ,n-1} \over \Delta t^n} - \sum _{\sigma \in \mathcal {F}_{\Gamma ,\mathbf{s}}} q^\alpha _{\sigma ,\mathbf{s}} - \displaystyle \sum _{\overline{K}_\mathbf{s}\in \overline{\mathcal {M}}_\mathbf{s}} q^\alpha _{K,\overline{K}_\mathbf{s}} &{}= 0, &{} \mathbf{s}\in \mathcal {V}_{\Gamma }\setminus \mathcal {D}_\mathrm{Dir}, \\ \end{array}\right. \end{aligned}$$

(3.25)

The modified fluxes are defined by

$$\begin{aligned} \left\{ \begin{array}{ll} q^\alpha _{K,\overline{K}_\mathbf{s}} &{}= M_{\mathrm{rt}_K}^\alpha (s_{K}^\alpha ) (F^\alpha _{K,\overline{K}_\mathbf{s}}(u^\alpha _{\mathcal {D}}))^+ + M_{\mathrm{rt}_K}^\alpha (S^\alpha _{\chi _{\overline{K}_\mathbf{s}}, \mathrm{rt}_K}(\tau _\mathbf{s})) (F^\alpha _{K,\overline{K}_\mathbf{s}}(u^\alpha _{\mathcal {D}}))^-,\\ \\ q^\alpha _{K,K_\sigma } &{}= M_{\mathrm{rt}_K}^\alpha (s_{K}^\alpha ) (F^\alpha _{K,K_\sigma }(u^\alpha _{\mathcal {D}}))^+ + M_{\mathrm{rt}_K}^\alpha (S^\alpha _{\chi _{K_\sigma }, \mathrm{rt}_K}(\tau _\sigma )) (F^\alpha _{K,K_\sigma }(u^\alpha _{\mathcal {D}}))^-, \end{array}\right. \end{aligned}$$

(3.26)

for the m-upwind discontinuous pressure model, and by

$$\begin{aligned} \left\{ \begin{array}{ll} q^\alpha _{K,\overline{K}_\mathbf{s}} = M_{\mathrm{rt}_K}^\alpha (s_{K}^\alpha ) (F^\alpha _{K,\overline{K}_\mathbf{s}}(u^\alpha _{\mathcal {D}}))^+ + M_{\mathrm{rt}_\mathbf{s}}^\alpha (S_{\chi _{\mathbf{s}}, \mathrm{rt}_\mathbf{s}}(\tau _\mathbf{s})) (F^\alpha _{K,\overline{K}_\mathbf{s}}(u^\alpha _{\mathcal {D}}))^-,\\ \\ q^\alpha _{K,K_\sigma } = M_{\mathrm{rt}_K}^\alpha (s_{K}^\alpha ) (F^\alpha _{K,K_\sigma }(u^\alpha _{\mathcal {D}}))^+ + M_{\mathrm{rt}_\sigma }^\alpha (S_{\chi _{\sigma }, \mathrm{rt}_\sigma }(\tau _\sigma )) (F^\alpha _{K,K_\sigma }(u^\alpha _{\mathcal {D}}))^-, \end{array}\right. \end{aligned}$$

(3.27)

for the f-upwind discontinuous pressure model, where a fracture rock type $\mathrm{rt}_\mathbf{s}$ has been assigned to the node $\mathbf{s}$. As for the continuous pressure model, a Multi-Point upwinding can also be introduced for these fluxes using the additional mobility unknowns $M_{\overline{K}_\mathbf{s}}^\alpha$, and $M_{K_\sigma }^\alpha$, $\alpha \in \{nw,w\}$. Note that, for fracture acting as drains, these f and m-upwind discontinuous pressure models provide basically the same solutions than respectively the f and m-upwind continuous pressure models. As already mentioned, this is not the case of the mf nonlinear discontinuous pressure model (3.24) due to the possible degeneracy of the phase mobilities appearing in the matrix fracture transmission conditions.

3.4.1 Numerical Experiments

In this subsection, we compare on the following test case, the mf nonlinear, the m-upwind and the f-upwind models using a reference solution obtained by the equi-dimensional model. The code implementation is the same for all models and described in the beginning of Sect. 3.3.4. The m-upwind and f-upwind models would require the design of specific preconditioners due to the two independent elliptic pressure unknowns at mf interfaces combined with a single independent elliptic unknown at cells and fracture faces. This explains the use for these two models of the direct linear solver SuperLU from the library [49]. The GMRes iterative solver combined with the CPR-AMG preconditioner is still used for the mf nonlinear and equi-dimensional models. It results that the overall numbers of Newton iterations $N_{Newton}N_{\Delta t}$ are more relevant for performance comparison than the CPU times which are not reported for this test case.

Fig. 3.25

Coarse mesh over the domain under consideration, which contains two intersecting fractures with high permeability and low capillarity and one upper fracture with low permeability and high capillarity. The size of the domain is $4\,\mathrm {m}\times 8\,\mathrm {m}$ and the fractures have an aperture of 4 cm

We consider a fractured domain as defined in Fig. 3.25. The matrix permeability is isotropic of 0.1 Darcy and matrix porosity is 0.2. The two lower fractures are drains (f$_d$) of isotropic permeability 100.0 Darcy and porosity 0.4. In the upper fracture, acting as a barrier (f$_b$), the permeability is isotropic of 0.001 Darcy and the porosity is 0.2. The capillary pressures are the same than in Sect. 3.3.5.1 with the Corey parameters $b_m = 1$ bar in the matrix, $b_{f_b} = 10$ bar in the barrier fracture and $b_{f_d} = 0.1$ bar in the drain fractures. Initially, the reservoir is saturated with water (density $1000\, \mathrm {kg} / \mathrm {m}^3$, viscosity 0.001 Pa s) and oil (density $700\, \mathrm {kg}/\mathrm {m}^3$, viscosity 0.005 Pa s) is injected in the bottom fracture, which is managed by imposing non-homogeneous Neumann conditions at the injection location. The oil then rises by gravity, thanks to it’s lower density compared to water and by the overpressure induced by the imposed injection rate. Also, Dirichlet boundary conditions are imposed at the upper boundary of the domain. Elsewhere, we have homogeneous Neumann conditions.

The tests are driven on triangular meshes, extended to 3D prismatic meshes by adding a second layer of nodes as a translation of the original nodes in normal direction to the plane of the original 2D domain (cf. Fig. 3.25). The equi-dimensional mesh contains two layers of cells in the fractures. In order to focus on modelling errors, the meshes are chosen to be fine with cell sizes of the same order as the fracture aperture. The final simulation time is fixed to $t_f= 54$ days. The time stepping is defined as in (3.16) using $\Delta t_{init} = 0.01$ days and $\Delta t_{\max } = 0.1$ days for the equi-dimensional and hybrid dimensional mf nonlinear models, and $\Delta t_{init} = 0.002$ days and $\Delta t_{\max } = 0.27$ days for the hybrid-dimensional m-upwind and f-upwind models. The maximum number of Newton iterations per time step is fixed as ${Newton}_\mathrm{max} = 35$. The criterion of convergence for the Newton algorithm is defined as in (3.17) with $Res_\mathrm{max} = 10^{-6}$ and $dx_\mathrm{max} = 10^{-4}$, and the relaxation of the Newton step is controlled as in (3.18) by the parameter $dx_{obj} = 0.5$.

The hybrid dimensional mf nonlinear and m-upwind models make use of the parametrization (3.21)–(3.23) at the mf interfaces.

Fig. 3.26

Comparison of the equi-dimensional model and of the mf nonlinear, m-upwind and f-upwind discontinuous pressure DFM models (from left to right) numerical solutions for non-wetting phase saturation at final time $t=54$ days

In this test case, we study the presence of a fracture, which acts as a barrier, both by its low permeability and by its high capillarity compared to the rock matrix. As a result of the higher capillarity, the sign of the matrix-fracture non-wetting phase saturation jump $S^{nw}_m(\gamma ^\pm p_{c,m})-S^{nw}_f(\gamma ^\pm p_{c,m})$ at the mf interfaces is non negative.

Figures  3.26, 3.27 and 3.28 compare the above mf nonlinear, m-upwind and f-upwind discontinuous pressure models to a reference equi-dimensional model. For the f-upwind and m-upwind models, mass transfer of the non-wetting phase from the matrix to the barrier is overestimated, since in this direction, saturation jumps are not accounted for. The assumption of constant saturation across the fracture for these models consequently leads to an overestimation of the non-wetting phase leaving the barrier. This overestimation is most severe for the m-upwind model, which takes into account saturation jumps for fluxes directed from the fracture to the matrix. Again, the mf nonlinear model does not suffer from the difficulties described above, since it provides mass transport that passes by the mf interfaces and takes into account the saturation jumps. Table 3.4 compares the numerical behavior of the different models on this test case.

Fig. 3.27

Comparison of the equi-dimensional model and of the mf nonlinear, m-upwind and f-upwind discontinuous pressure DFM models (from left to right) numerical solutions for water overpressure at final time $t=54$ days

Fig. 3.28

Matrix and fracture volumes occupied by the non-wetting phase as a function of time for the equi-dimensional model and for the mf nonlinear, m-upwind and f-upwind discontinuous pressure DFM models

Table 3.4 Numerical behavior of the simulation obtained by the VAG scheme for the equi-dimensional model and for the mf nonlinear, m-upwind and f-upwind discontinuous pressure DFM models, as presented in Sect. 3.4. We refer to the beginning of Sect. 3.3.4 for the description of the entries with $dof_{lin}$ and $N_z$ accounting for the elimination of the cell unknowns in the linear systems

3.5 Conclusions and Perspectives

This article reviews the nodal VAG discretization of DFM two-phase Darcy flow models. For linear transmission conditions, the adaptation of the control volumes combined with a Multi-Point upwind approximation of the mobilities for f-upwind models or taking into account the saturation jump for m-upwind models, allows to obtain a similar accuracy as face based discretizations with a much lower CPU time on tetrahedral meshes. Nonlinear mf transmission conditions provide a more accurate DFM model than linear transmission conditions. As discussed in [1, 16], they can account for a large range of physical processes at mf interfaces which cannot be captured by linear mf transmission conditions even in the case of fractures acting as drains. It is typically the case for fractures acting as capillary barriers, or for highly permeable fractures filled with a given phase acting as a barrier for the other phase. The VAG discretization of DFM models with nonlinear mf transmission conditions still raises the issue of numerical efficiency regarding the nonlinear convergence due to the combination of highly nonlinear transmission conditions with tiny volumes at mf interfaces. Improving the numerical efficiency for this type of DFM models is the object of ongoing researches in two directions. The first is to go back to face based discretizations allowing the elimination of the mf interface unknowns with a local nonlinear interface solver as in [1] using TPFA discretization on orthogonal meshes and in [2] using an HFV discretization. The second perspective is to use the more robust Hybrid Upwinding approximation of the mobilities to define the two-phase Darcy fluxes at mf interfaces as proposed in [6] for TPFA schemes and in [19] for the VAG discretization.