Abstract
We present a new model for two phase Darcy flows in fractured media, in which fractures are modelled as submanifolds of codimension one with respect to the surrounding domain (matrix). Fractures can act as drains or as barriers, since pressure discontinuities at the matrix-fracture interfaces are permitted. Additionally, a layer of damaged rock at the matrix-fracture interfaces is accounted for. The numerical analysis is carried out in the general framework of the Gradient Discretisation Method. Compactness techniques are used to establish convergence results for a wide range of possible numerical schemes; the existence of a solution for the two phase flow model is obtained as a byproduct of the convergence analysis. A series of numerical experiments conclude the paper, with a study of the influence of the damaged layer on the numerical solution.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Flow and transport in fractured porous media are of paramount importance for many applications such as petroleum exploration and production, geological storage of carbon dioxide, hydrogeology, or geothermal energy. Two classes of models, dual continuum and discrete fracture matrix models, are typically employed and possibly coupled to simulate flow and transport in fractured porous media. Dual continuum models assume that the fracture network is well connected and can be homogenised as a continuum coupled to the matrix continuum using transfer functions. On the other hand, discrete fracture matrix models (DFM), on which this paper focuses, represent explicitly the fractures as co-dimension one surfaces immersed in the surrounding matrix domain. The use of lower dimensional rather than equi-dimensional entities to represent the fractures has been introduced in [4, 8, 31, 36, 37] to facilitate the grid generation and to reduce the number of degrees of freedom of the discretised model. The reduction of dimension in the fracture network is obtained from the equi-dimensional model by integration and averaging along the width of each fracture. The resulting so called hybrid-dimensional model couple the 3D model in the matrix with a 2D model in the fracture network taking into account the jump of the normal fluxes as well as additional transmission conditions at the matrix-fracture interfaces. These transmission conditions depend on the mathematical nature of the equi-dimensional model and on additional physical assumptions. They are typically derived for a single phase Darcy flow for which they specify either the continuity of the pressure in the case of fractures acting as drains [4, 9] or Robin type conditions in order to take into account the discontinuity of the pressure for fractures acting either as drains or barriers [5, 11, 31, 37].
Fewer works deal with the extension of hybrid-dimensional models to two-phase Darcy flows. Most of them build directly the model at the discrete level as in [8, 34, 40] or are limited to the case of continuous pressures at the matrix-fracture interfaces as in [8, 10, 40]. In [35], an hybrid-dimensional two-phase flow model with discontinuous pressures at the matrix-fracture interfaces is proposed using a global pressure formulation. However, the transmission conditions at the interface do not take into account correctly the transport from the matrix to the fracture.
In this paper, a new hybrid-dimensional two-phase Darcy flow model is proposed accounting for complex networks of fractures acting either as drains or barriers. The model takes into account discontinuous capillary pressure curves at the matrix-fracture interfaces. It also includes a layer of damaged rock at the matrix-fracture interface with its own mobility and capillary pressure functions. This additional layer is not only a modelling tool. It also plays a major role in the convergence analysis of the model by giving time estimates on the approximate interfacial saturations, which yield their compactness (see Remark 4.7) and enables the identification of their limit. Moreover, when solving the discrete equations with a Newton-Raphson method, a non-zero distribution of volume at the interfacial unknowns is in general required for the Jacobian not to be degenerate. The sensitivity of the discrete solution as well as of the computational performance on interfacial parameters is studied in the test case section. The results suggest that the model converges with vanishing interfacial volume. However, this is still an open question.
The discretisation of hybrid-dimensional Darcy flow models has been the object of many works using cell-centred Finite Volume schemes with either Two Point or Multi Point Flux Approximations (TPFA and MPFA) [2, 3, 5, 33, 36, 41, 43], Mixed or Mixed Hybrid Finite Element methods (MFE and MHFE) [4, 34, 37], Hybrid Mimetic Mixed Methods (HMM, which contains Mixed/Hybrid Finite Volume and Mimetic Finite Difference schemes [22]) [6, 9, 11, 30], Control Volume Finite Element Methods (CVFE) [8, 33, 38,39,40], and the Vertex Approximate Gradient (VAG) scheme [9,10,11, 44, 45]. Let us also mention that non-matching discretisations of the fracture and matrix meshes are studied for single phase Darcy flows in [7, 14, 32, 42]. The convergence analysis for single-phase flow models with a single fracture is established in [4, 37] for MFE methods, in [14] for non matching MFE discretisations, and in [5] for TPFA discretisations. The case of single-phase flows with complex fracture networks is studied in the general framework of the gradient discretisation method in [9] for continuous pressure models and in [11] for discontinuous pressure models. For hybrid-dimensional two-phase flow models, the only convergence analysis is to our knowledge done in [10] for the VAG discretisation of the continuous pressure model with fractures acting only as drains. Let us recall that the gradient discretisation method (GDM) enables convergence analysis of both conforming and non conforming discretisations for linear and non-linear second order elliptic and parabolic problems. It accounts for various discretisations such as conforming Finite Element methods, MFE and MHFE methods, some TPFA and symmetric MPFA schemes, and the VAG and HHM schemes [24]. The main advantage of this framework is to provide, for a given model, a convergence proof for all schemes satisfying some abstract conditions, at the reduced cost of a single convergence analysis; see e.g. [19, 20, 23, 28, 29]. We refer to the monograph [21] for a detailed presentation of the GDM.
The main purpose of this paper is to propose an extension of the gradient discretisation method to our hybrid-dimensional two-phase Darcy flow model. This provides, in an abstract framework, the convergence of the approximate solution to a weak solution of the model; as a by-product, this proves the existence of a solution to this continuous model. The numerical analysis is partially based on the previous work [29] dealing with the gradient discretisation method for single medium two-phase Darcy flows. The main new difficulty addressed in this work compared with the analysis of [29] and [10] comes from the transmission conditions at the matrix-fracture interfaces; these conditions involve an upwinding between the fracture phase pressures and the traces of the matrix phase pressures. Note that, as in [29] and [10], the convergence analysis assumes that the phase mobilities do not vanish.
The outline of this paper is as follows. Section 2 introduces the geometry of the fracture network, the function spaces, the strong and weak formulations of the model as well as the assumptions on the data. Section 3 details the gradient discretisation method, including the definition of the abstract reconstruction operators, of the discrete variational formulation (gradient scheme), and of the coercivity, consistency, limit conformity and compactness properties. Section 4 proves the main result of this paper which is the convergence of the gradient scheme solution to a weak solution of the model. This convergence is established using compactness arguments, and requires us to establish various compactness results on the approximation solutions: averaged in time and space, uniform-in-time and weak-in-space, etc. The Minty monotonicity trick is used to identify the limit of the non-linear term resulting from the the upwinding between the fracture and matrix phase pressures. Section 5 studies on a 2D numerical example the influence of the additional layer of damaged rock at the matrix-fracture interface on the solution of the model. The discretisation used in this test case is based on the VAG scheme which can be shown from [11] to satisfy the assumptions of our gradient discretisation method. Note that numerical comparisons of our model with the equi-dimensional model as well as with the continuous pressure model of [10] can be found in [1, 12] without the accumulation term in the interfacial layer, which plays a minor role in the numerical tests when this layer is thin with respect to the fracture (see Sect. 5). It is shown that the discontinuous pressure model analysed in this paper is more accurate than the continuous pressure model of [10] even in the case of fractures acting only as drains; this improved accuracy is due to more accurate transmission conditions at the matrix-fracture interfaces.
2 Notation and model
2.1 Geometry
Let \(\Omega \) denote a bounded domain of \({\mathbb {R}}^d\) (\(d=2,3\)), polyhedral for \(d=3\) and polygonal for \(d=2\). To fix ideas the dimension will be fixed to \(d=3\) when it needs to be specified, for instance in the naming of the geometrical objects or for the space discretisation in the next section. The adaptations to the case \(d=2\) are straightforward.
Let \( \overline{\Gamma }= \bigcup _{i\in I} \overline{\Gamma }_i \) and its interior \(\Gamma = \overline{\Gamma }{\setminus } \partial \overline{\Gamma }\) denote the network of fractures \(\Gamma _i\subset \Omega \), \(i\in I\). Each \(\Gamma _i\) is a planar polygonal simply connected open domain included in a plane \({\mathcal {P}}_i\) of \({\mathbb {R}}^d\). It is assumed that the angles of \(\Gamma _i\) are strictly smaller than \(2\pi \), and that \(\Gamma _i\cap \overline{\Gamma }_j=\emptyset \) for all \(i\ne j\). For all \(i\in I\), let us set \(\Sigma _i = \partial \Gamma _i\), with \(\mathbf n _{\Sigma _i}\) as unit vector in \({\mathcal {P}}_i\), normal to \(\Sigma _i\) and outward to \({\Gamma _{}}_i\). Further \(\Sigma _{i,j}= \Sigma _i\cap \Sigma _j\) for \(i\not =j\), \(\Sigma _{i,0} = \Sigma _i\cap \partial \Omega \), \(\Sigma _{i,N} = \Sigma _i{\setminus }(\bigcup _{j\in I\setminus \{i\}}\Sigma _{i,j}\cup \Sigma _{i,0})\), \(\Sigma = \bigcup _{(i,j)\in I\times I, i\ne j} ( \Sigma _{i,j}{\setminus }\Sigma _{i,0} )\) and \(\Sigma _0 = \bigcup _{i\in I} \Sigma _{i,0}\). It is assumed that \(\Sigma _{i,0} = \overline{\Gamma }_i\cap \partial \Omega \).
We define the two unit normal vectors \(\mathbf n _{{\mathfrak {a}}^{\pm (i)}}\) at each planar fracture \({\Gamma _{}}_i\), such that \(\mathbf n _{{\mathfrak {a}}^+(i)} + \mathbf n _{{\mathfrak {a}}^-(i)} = 0\) and oriented outward to the matrix side \({\mathfrak {a}}^\pm (i)\) (cf. Fig. 1). We define the set of indices \(\chi = \{{\mathfrak {a}}^+(i), {\mathfrak {a}}^-(i)\mid i\in I\}\), such that \(\#\chi = 2\# I\). For ease of notation, we use the convention \({\Gamma _{}}_{{\mathfrak {a}}^+(i)} = {\Gamma _{}}_{{\mathfrak {a}}^-(i)} = {\Gamma _{}}_i\).
For \(\AA = {\mathfrak {a}}^\pm (i)\in \chi \), we denote by \(\gamma _{{\mathfrak {a}}}\) the one-sided trace operator on \({\Gamma _{}}_{\mathfrak {a}}\). It satisfies the condition  , where
, where  .
.
On the fracture network \({\Gamma _{}}\), the tangential gradient is denoted by \(\nabla _\tau \), and is such that
where, for each \(i\in I\), the tangential gradient \(\nabla _{\tau _i}\) is defined by fixing a reference Cartesian coordinate system of the plane \({\mathcal {P}}_i\) containing \({\Gamma _{}}_i\). In the same manner, we denote by \( \mathrm{div}_{\tau } \mathbf q = (\mathrm{div}_{\tau _i} \mathbf q _i )_{i\in I} \) the tangential divergence operator.
2.2 Continuous model and hypotheses
We describe here the continuous model and assumptions that are implicitly made throughout the paper. In the matrix domain \(\Omega {\setminus }\overline{{\Gamma _{}}}\), let us denote by \(\Lambda _m\in L^{\infty }(\Omega )^{d\times d}\) the symmetric permeability tensor, chosen such that there exist \(\overline{\lambda }_m\ge \underline{\lambda }_m > 0\) with
Analogously, in the fracture network \({\Gamma _{}}\), we denote by \(\Lambda _f\in L^{\infty }(\Gamma )^{(d-1)\times (d-1)}\) the symmetric tangential permeability tensor, and assume that there exist \(\overline{\lambda }_f\ge \underline{\lambda }_f > 0\), such that
On the fracture network \({\Gamma _{}}\), we introduce an orthonormal system \((\varvec{\tau }_1(\mathbf x ),\varvec{\tau }_2(\mathbf x ),\mathbf n (\mathbf x ))\), defined a.e. on \({\Gamma _{}}\). Inside the fractures, the normal direction is assumed to be a permeability principal direction. The normal permeability \(\lambda _{f,\mathbf n } \in L^{\infty }(\Gamma )\) is such that \(\underline{\lambda }_{f,\mathbf n } \le \lambda _{f,\mathbf n }(\mathbf x ) \le \overline{\lambda }_{f,\mathbf n }\) for a.e. \(\mathbf x \in \Gamma \) with \(0 < \underline{\lambda }_{f,\mathbf n } \le \overline{\lambda }_{f,\mathbf n }\). We also denote by \(d_f \in L^\infty ({\Gamma _{}})\) the width of the fractures, assumed to be such that there exist \({\overline{d}}_f\ge {\underline{d}}_f > 0\) with \( {\underline{d}}_f \le d_f(\mathbf x ) \le {\overline{d}}_f \) for a.e. \(\mathbf x \in \Gamma \). The half normal transmissibility in the fracture network is denoted by
Furthermore, \(\phi _m\) and \(\phi _f\) are the matrix and fracture porosities, respectively, \(\rho ^\alpha \in {\mathbb {R}}^+\) denotes the density of phase \(\alpha \) (with \(\alpha =1\) the non-wetting and \(\alpha =2\) the wetting phase) and \(\mathbf g \in {\mathbb {R}}^d\) is the gravitational vector field. We assume that \(\underline{\phi }_{m,f}\le \phi _{m,f}\le \overline{\phi }_{m,f}\), for some \(\underline{\phi }_{m,f},\overline{\phi }_{m,f}> 0\). \((k_m^\alpha ,k_f^\alpha )\) and \((S_m^\alpha ,S_f^\alpha )\) are the matrix and fracture phase mobilities and saturations, respectively. Hypothesis on these functions are stated below.
The PDEs model writes: find phase pressures  and velocities
and velocities  (\(\alpha = 1,2\)), such that
(\(\alpha = 1,2\)), such that

The matrix-fracture coupling condition on \((0,T)\times {\Gamma _{}}_{\mathfrak {a}}\) (for all \({\mathfrak {a}}\in \chi \)) are

where  , with
, with  representing the interfacial width and
representing the interfacial width and  the interfacial porosity (cf. Fig. 2). We assume that each of these parameters is uniformly bounded below. In these equations, we have
the interfacial porosity (cf. Fig. 2). We assume that each of these parameters is uniformly bounded below. In these equations, we have

In the above, we used the shorthand notations

as well as, for \({{\mu \in \{m,f\}}\cup \chi }\),  and a.e. \((t,\mathbf x )\in (0,T)\times {M_\mu }\),
and a.e. \((t,\mathbf x )\in (0,T)\times {M_\mu }\),

Here and in the following, \({M_\mu }\) is defined by
The various boundary conditions imposed on the domain are: homogeneous Dirichlet conditions at the boundary of the domain, pressure continuity and flux conservation at the fracture-fracture intersections, and zero normal flux at the immersed fracture tips. In other words,

Let us define \(L^2(\Gamma ) = \{v = (v_i)_{i\in I}, v_i\in L^2(\Gamma _i), i\in I\}\). The assumptions under which the model is considered are:
-
 and
and  ,
, -
For \({\mu \in \{m,f\}}\) and \(\alpha =1,2\),
 ,
, -
For \({{\mu \in \{m,f\}}\cup \chi }\):
 is a Caratheodory function; for a.e. \(\mathbf x \in {M_\mu }\),
is a Caratheodory function; for a.e. \(\mathbf x \in {M_\mu }\),  is a non-decreasing Lipschitz continuous function on \({\mathbb {R}}\); for all \(q\in {\mathbb {R}}\),
is a non-decreasing Lipschitz continuous function on \({\mathbb {R}}\); for all \(q\in {\mathbb {R}}\),  is piecewise constant on a finite partition
is piecewise constant on a finite partition  of polytopal subsets of \({M_\mu }\).
of polytopal subsets of \({M_\mu }\). -
For \(\alpha =1,2\) and \({{\mu \in \{m,f\}}\cup \chi }\): there exist constants
 , such that
, such that  is a Caratheodory function.
is a Caratheodory function.
Recall that a Caratheodory function is measurable w.r.t. its first argument and continuous w.r.t. its second argument.
2.3 Weak formulation
The subspace \(H^1(\Gamma )\) of \(L^2(\Gamma )\) consists in functions \(v = (v_i)_{i\in I}\) such that \(v_i\in H^1(\Gamma _i)\) for all \(i\in I\), with continuous traces at the fracture intersections \(\Sigma _{i,j}\) for all \(i\not =j\). Its subspace of functions with vanishing traces on \(\Sigma _0\) is denoted by \(H^1_{\Sigma _0}(\Gamma )\).
Let us now define the hybrid-dimensional function spaces that are used as variational spaces for the Darcy flow model. Starting from
consider the subspace
where (with  the trace operator on \(\partial {\Omega }\))
the trace operator on \(\partial {\Omega }\))

The weak formulation of (1) amounts to finding  satisfying the following variational equalities, for any \(\alpha = 1,2\) and any
satisfying the following variational equalities, for any \(\alpha = 1,2\) and any  :
:

Here,

with \(\mathrm{d}\tau ({x})\) the \(d-1\) dimensional Lebesgue measure on \(\Gamma \).
3 The gradient discretisation method
The gradient discretisation method consists in selecting a set (called a gradient discretisation) of a finite-dimensional space and reconstruction operators on this space, and in substituting them for their continuous counterpart in the weak formulation of the model. The scheme thus obtained is called a gradient scheme. Let us first define the set of discrete elements that make up a gradient discretisation.
Definition 3.1
(Gradient discretisation (GD)) A spatial gradient discretisation for a discrete fracture matrix model is  , where
, where
-
 is a finite-dimensional space of degrees of freedom (DOFs),
is a finite-dimensional space of degrees of freedom (DOFs), -
For
 ,
,  reconstructs a function on \({{M_\mu }}\) from the DOFs,
reconstructs a function on \({{M_\mu }}\) from the DOFs, -
For
 ,
,  reconstructs a gradient on \({{M_\mu }}\) from the DOFs,
reconstructs a gradient on \({{M_\mu }}\) from the DOFs, -
For \({\mathfrak {a}}\in \chi \),
 reconstructs, from the DOFs, a jump on \({{\Gamma _{{\mathfrak {a}}}}}\) between the matrix and fracture,
reconstructs, from the DOFs, a jump on \({{\Gamma _{{\mathfrak {a}}}}}\) between the matrix and fracture, -
For \({{\mathfrak {a}}\in \chi }\),
 reconstructs, from the DOFs, a trace on \({{\Gamma _{{\mathfrak {a}}}}}\) from the matrix.
reconstructs, from the DOFs, a trace on \({{\Gamma _{{\mathfrak {a}}}}}\) from the matrix.
These operators must be chosen such that the following expression defines a norm on  :
:

The spatial gradient discretisation \({\mathcal {D}_S}\) is extended to a space-time gradient discretisation by setting  with
with
-
 a discretisation of the time interval [0, T],
a discretisation of the time interval [0, T], -
 an operator designed to interpolate the initial condition.
an operator designed to interpolate the initial condition.
The space-time operators act on a family  the following way: for all \({n = 0,\dots ,N-1}\) and all
the following way: for all \({n = 0,\dots ,N-1}\) and all  ,
,

We extend these functions at \({t=0}\) by considering the corresponding spatial operators on  .
.
If  is a family in
is a family in  , the discrete time derivatives
, the discrete time derivatives  are defined such that, for all \({n = 0,\dots ,N-1}\) and all
are defined such that, for all \({n = 0,\dots ,N-1}\) and all  , with
, with  ,
,

Let  be a basis of
be a basis of  . If
. If  , we write
, we write  . Then, for \({g\in C({\mathbb {R}})}\), we define
. Then, for \({g\in C({\mathbb {R}})}\), we define  by
by  . In other words, g(w) is defined by applying g to each degree of freedom of w. Although this definition depends on the choice of basis
. In other words, g(w) is defined by applying g to each degree of freedom of w. Although this definition depends on the choice of basis  , we do not explicitly indicate this dependency. This definition of g(w) is particularly meaningful in the context of piecewise constant reconstructions, see Remark 3.3 below.
, we do not explicitly indicate this dependency. This definition of g(w) is particularly meaningful in the context of piecewise constant reconstructions, see Remark 3.3 below.
The gradient scheme for (1) consists in writing the weak formulation (2) with continuous spaces and operators replaced by their discrete counterparts, after a formal integration-by-parts in time. In other words, the gradient scheme is: find  such that, with
such that, with  ,
,

and, for any \({\alpha = 1,2}\) and  ,
,

3.1 Properties of gradient discretisations
The convergence analysis of the GDM is based on a few properties that sequences of GDs must satisfy.
Definition 3.2
(Piecewise constant reconstruction operator) Let  be the basis of
be the basis of  chosen in Sect. 3. For
chosen in Sect. 3. For  , an operator
, an operator  is called piecewise constant if it has the representation
is called piecewise constant if it has the representation

where  is a partition of \({{M_\mu }}\) up to a set of zero measure, and \({{\mathbb {1}}_{\omega _\nu ^\mu }}\) is the characteristic function of \({\omega _\nu ^\mu }\).
is a partition of \({{M_\mu }}\) up to a set of zero measure, and \({{\mathbb {1}}_{\omega _\nu ^\mu }}\) is the characteristic function of \({\omega _\nu ^\mu }\).
In the following, all considered function reconstruction operators  and
and  are assumed to be piecewise constant.
are assumed to be piecewise constant.
Remark 3.3
Recall that, if \({g\in C^0({\mathbb {R}})}\) and  , then
, then  is defined by the degrees of freedom
is defined by the degrees of freedom  . Then, any piecewise constant reconstruction operator \({\Pi }\) commutes with g in the sense that
. Then, any piecewise constant reconstruction operator \({\Pi }\) commutes with g in the sense that  .
.
The coercivity property enables us to control the functions and trace reconstruction by the norm on  . This is a combination of a discrete Poincaré inequality and a discrete trace inequality.
. This is a combination of a discrete Poincaré inequality and a discrete trace inequality.
Definition 3.4
(Coercivity of spatial GD) Let

A sequence \({(\mathcal {D}_S^l)_{l\in {\mathbb {N}}}}\) of gradient discretisations is coercive if there exists \({\mathcal {C}_P > 0}\) such that

This consists in choosing a family
The consistency ensures that a certain interpolation error goes to zero along sequences of GDs.
Definition 3.5
(Consistency of spatial GD) For  and
and  , define
, define

and  . A sequence
. A sequence  of gradient discretisations is GD-consistent (or consistent for short) if, for all
of gradient discretisations is GD-consistent (or consistent for short) if, for all  ,
,

To define the notion of limit-conformity, we need the following two spaces:

where \({C_b^\infty ({\Omega }\setminus \overline{{\Gamma _{}}})\subset C^\infty ({\Omega }\setminus \overline{{\Gamma _{}}})}\) is the set of functions \({\varphi }\), such that for all \(\mathbf{x \in {\Omega }}\) there exists \({r > 0}\), such that for all connected components \({\omega }\) of  one has \({\varphi \in C^\infty (\overline{\omega })}\), and such that all derivatives of \({\varphi }\) are bounded. The limit-conformity imposes that, in the limit, the discrete gradient and function reconstructions satisfy a natural integration-by-part formula (Stokes’ theorem).
one has \({\varphi \in C^\infty (\overline{\omega })}\), and such that all derivatives of \({\varphi }\) are bounded. The limit-conformity imposes that, in the limit, the discrete gradient and function reconstructions satisfy a natural integration-by-part formula (Stokes’ theorem).
Definition 3.6
(Limit-conformity of spatial GD) For all  ,
,  and
and  , define
, define

and  . A sequence \({(\mathcal {D}_S^l)_{l\in {\mathbb {N}}}}\) of gradient discretisations is limit-conforming if, for all
. A sequence \({(\mathcal {D}_S^l)_{l\in {\mathbb {N}}}}\) of gradient discretisations is limit-conforming if, for all  and all
and all  ,
,

Remark 3.7
(Domain of  ) Usually, the measure
) Usually, the measure  of limit-conformity is defined on spaces in which the Darcy velocities of solutions to the model are expected to be, not smooth spaces as \(\mathbf{C ^\infty _{\Omega }\times \mathbf C ^\infty _{\Gamma }}\) [21, Definition 2.6]. However, if we do not aim at obtaining error estimates (which is the case here, given that such estimates would require unrealistic regularity assumptions on the data and the solution),
of limit-conformity is defined on spaces in which the Darcy velocities of solutions to the model are expected to be, not smooth spaces as \(\mathbf{C ^\infty _{\Omega }\times \mathbf C ^\infty _{\Gamma }}\) [21, Definition 2.6]. However, if we do not aim at obtaining error estimates (which is the case here, given that such estimates would require unrealistic regularity assumptions on the data and the solution),  only needs to be defined and to converge to 0 on spaces of smooth functions—see Lemma A.2.
only needs to be defined and to converge to 0 on spaces of smooth functions—see Lemma A.2.
For any space-dependent function f, define  . Likewise, for any time-dependent function g, let
. Likewise, for any time-dependent function g, let  . The compactness property ensures a sort of discrete Rellich theorem (compact embedding of \({H^1_0}\) into \({L^2}\)). By the Kolmogorov theorem, this compactness is equivalent to a uniform control of the translates of the functions.
. The compactness property ensures a sort of discrete Rellich theorem (compact embedding of \({H^1_0}\) into \({L^2}\)). By the Kolmogorov theorem, this compactness is equivalent to a uniform control of the translates of the functions.
Definition 3.8
(Compactness of spatial GD) For all  and
and  , with
, with  and
and  , where \({\tau ({\mathcal {P}}_i)}\) is the (constant) tangent space of \({{\mathcal {P}}_i}\), define
, where \({\tau ({\mathcal {P}}_i)}\) is the (constant) tangent space of \({{\mathcal {P}}_i}\), define

where all the functions on \({{\Omega }}\) (resp. \({{\Gamma _{}}_i}\)) have been extended to \({{\mathbb {R}}^d}\) (resp. \({{\mathcal {P}}_i}\)) by 0 outside their initial domain. Let  . A sequence \({(\mathcal {D}_S^l)_{l\in {\mathbb {N}}}}\) of gradient discretisations is compact if
. A sequence \({(\mathcal {D}_S^l)_{l\in {\mathbb {N}}}}\) of gradient discretisations is compact if

All these properties for spatial GDs naturally extend to space–time GDs with, for the consistency, additional requirements on the time steps and on the interpolants of the initial conditions.
Definition 3.9
(Properties of space-time gradient discretisations) A sequence of space-time gradient discretisations \({(\mathcal {D}^l)_{l\in {\mathbb {N}}}}\) is
-
1.
Coercive if \({(\mathcal {D}_S^l)_{l\in {\mathbb {N}}}}\) is coercive.
-
2.
Consistent if
-
(i)
\({(\mathcal {D}_S^l)_{l\in {\mathbb {N}}}}\) is consistent,
-
(ii)
 as \({l\rightarrow \infty }\), and
as \({l\rightarrow \infty }\), and -
(iii)
For all
 , letting
, letting  we have, as \({l\rightarrow \infty }\),
we have, as \({l\rightarrow \infty }\), 
-
(i)
-
3.
Limit-conforming if \({(\mathcal {D}_S^l)_{l\in {\mathbb {N}}}}\) is limit-conforming.
-
4.
Compact if \({(\mathcal {D}_S^l)_{l\in {\mathbb {N}}}}\) is compact.
Elements of  are identified with functions
are identified with functions  by setting, for
by setting, for  with
with  ,
,

This definition is compatible with the choices of space-time operators made in Definition 3.1, in the sense that, for any \({t\in (0,T]}\),  (and similarly for the other reconstruction operators). With the identification (10), the norm on
(and similarly for the other reconstruction operators). With the identification (10), the norm on  is
is

4 Convergence analysis
In the rest of this paper, when the phase parameter \({\alpha }\) is absent this implicitly means that it is equal to 1. For example, we write  for
for  . The main convergence result is the following.
. The main convergence result is the following.
Theorem 4.1
(Convergence Theorem) Let \({(\mathcal {D}^l)_{l\in {\mathbb {N}}}}\) be a coercive, consistent, limit-conforming and compact sequence of space-time gradient discretisations, with piecewise constant reconstructions. Then for any \({l\in {\mathbb {N}}}\) there is a solution  of (5) with \({\mathcal {D}=\mathcal {D}^l}\).
of (5) with \({\mathcal {D}=\mathcal {D}^l}\).
Moreover, there exists  solution of (2) such that, up to a subsequence as \({l\rightarrow \infty }\),
solution of (2) such that, up to a subsequence as \({l\rightarrow \infty }\),
-
1.
The following weak convergences hold, for
 ,
,  (11)
(11) -
2.
The following strong convergences hold, with
 and
and  :
:  (12)
(12)
Remark 4.2
(Uniform-in-time strong-in-space convergence) It is additionally proved in [26] that the saturations converge uniformly-in-time strongly in \({L^2}\) (that is, in \({L^\infty (0,T;L^2({\Omega }))}\)).
Remark 4.3
(Discretisation spaces varying with the time step) As mentioned in [13, Remark 3.5] for a different model, it is also possible to consider gradient schemes in which the gradient discretisation changes at each time step. This consists in choosing a family\({\widetilde{\mathcal {D}}_{S}=(\mathcal {D}_{S,n})_{n=0,\ldots ,N_l}}\) of spatial gradient discretisations \({\mathcal {D}_{S,n}}\) (as in Definition 3.1), in considering unknowns  and in defining the space-time operators (3) with
and in defining the space-time operators (3) with  ,
,  ,
,  and
and  respectively replaced by
respectively replaced by  ,
,  ,
,  and
and  . The gradient scheme is then written as in (5). For a sequence \({(\widetilde{\mathcal {D}}^l_{S})_{l\in {\mathbb {N}}}}\) of such families of spatial GDs, the notions coercivity, consistency, limit-conformity and compactness are defined by writing the bound and convergences in (6), (7), (8) and (9) with
. The gradient scheme is then written as in (5). For a sequence \({(\widetilde{\mathcal {D}}^l_{S})_{l\in {\mathbb {N}}}}\) of such families of spatial GDs, the notions coercivity, consistency, limit-conformity and compactness are defined by writing the bound and convergences in (6), (7), (8) and (9) with  ,
,  ,
,  and
and  replaced by
replaced by

With these notions, Theorem 4.1 still holds.
By using spatial GDs that change at each time step, one can represent in the GDM framework numerical methods with moving or dynamically refined meshes, or whose gradient reconstruction involves time-dependent parameters (as in \({\mathbb {RT}_k}\) Mixed Finite Elements with a diffusion tensor that depends on some unknown of the system; see [13, Section 4.1]).
Before delving into the proof of the theorem, let us give an overview of the strategy. The convergence of the solutions to the gradient schemes (5) is established by a compactness technique, as briefly described in [18, Section 1.2]: (i) prove a priori estimates on the solutions to the scheme, (ii) using discrete compactness theorems, deduce from these estimates that the (reconstructions of the) approximate solutions are compact in appropriate spaces, (iii) prove that any limit, in these spaces, of the approximate solutions is a solution to the continuous model (2).
-
(i)
A priori estimates. The first a priori estimates are classically obtained by using the approximate solution
 itself as a test function in the scheme (5). After summing the two equations corresponding to each phase, the diffusion terms then directly yield an estimate on
itself as a test function in the scheme (5). After summing the two equations corresponding to each phase, the diffusion terms then directly yield an estimate on  . The time derivative term form the discrete counterpart of
. The time derivative term form the discrete counterpart of  which, after integration in time, would yield an estimate on
which, after integration in time, would yield an estimate on  with
with  . To make explicit that this estimate is actually an estimate on the saturation, we re-write
. To make explicit that this estimate is actually an estimate on the saturation, we re-write  as
as  for a well-chosen \({B_\mu }\). These a priori estimates are stated in Lemma 4.4. These initial estimates only concern spatial derivatives of the approximate solution (they are a discrete equivalent of \({L ^2(0,T;H^1_0)}\) estimates). Since this solution depends on both time and space, estimates are also required on its (discrete) time derivative to establish the compactness in an appropriate space. These time derivative estimates are the purpose of Lemma 4.6 and, classically for parabolic PDEs, they are obtained in a weak spatial norm (a sort of discrete \({H^{-1}}\) norm). They are obtained on
for a well-chosen \({B_\mu }\). These a priori estimates are stated in Lemma 4.4. These initial estimates only concern spatial derivatives of the approximate solution (they are a discrete equivalent of \({L ^2(0,T;H^1_0)}\) estimates). Since this solution depends on both time and space, estimates are also required on its (discrete) time derivative to establish the compactness in an appropriate space. These time derivative estimates are the purpose of Lemma 4.6 and, classically for parabolic PDEs, they are obtained in a weak spatial norm (a sort of discrete \({H^{-1}}\) norm). They are obtained on  and, thanks to the modelling of the damaged rock type at the matrix-fracture interface (term
and, thanks to the modelling of the damaged rock type at the matrix-fracture interface (term  in (1b)), also on
in (1b)), also on  . These estimates are instrumental to obtain the compactness in time and space of all the saturations in the model.
. These estimates are instrumental to obtain the compactness in time and space of all the saturations in the model. -
(ii)
Compactness. The estimates on the discrete spatial and temporal derivatives, together with the compactness property of the gradient discretisations, yield estimates on the spatial and temporal translates of the saturations (Lemmas 4.8 and 4.9). A use of the Kolmogorov theorem and of the consistency of the gradient discretisations (to identify, through Lemma A.2, weak limits of reconstructed gradients and traces as the gradient and trace of the limit of the approximate solutions) then give the convergences (11) and (12); this is stated in Theorem 4.11. A discontinuous Ascoli-Arzela theorem (Theorem A.1) is then applied in Theorem 4.13 to obtain the convergence of the saturations uniformly-in-time and weakly in \({L^2(\Omega )}\). This uniform-in-time convergence is essential to pass to the limit, in (iii) below, in the energy estimate (16) (which involves pointwise-in-time values of the saturations).
-
(iii)
The limit is a solution of the model. The conclusion, presented in Sect. 4.3, consists in proving that the limit of the approximate solutions is a solution to the continuous model. As we do not have strong convergence of the phase pressures
 , the main challenge in analysing this limit arises from the non-linear upwinding terms
, the main challenge in analysing this limit arises from the non-linear upwinding terms  . The limit of this term is obtained by using the monotony properties of this upwinding, a Minty trick, and the discrete energy estimate (16).
. The limit of this term is obtained by using the monotony properties of this upwinding, a Minty trick, and the discrete energy estimate (16).
4.1 Preliminary estimates
Let us introduce some useful auxiliary functions. These functions are the same as in [19, 25], with adjustments to account for the fact that the saturations depends on \(\mathbf{x }\) and might not vanish at \({p=0}\). For \({{{\mu \in \{m,f\}}\cup \chi }}\), let \({R_{S_\mu (\mathbf x ,\cdot )}}\) be the range of \({S_\mu (\mathbf x ,\cdot )}\). The pseudo-inverse of \({S_\mu (\mathbf x ,\cdot )}\) is the mapping \({[S_\mu (\mathbf x ,\cdot )]^i:R_{S_\mu (\mathbf x ,\cdot )}\rightarrow {\mathbb {R}}}\) defined by

That is, \({[S_\mu (\mathbf x ,\cdot )]^i(q)}\) is the point z in \({R_{S_\mu (\mathbf x ,\cdot )}}\) that is the closest to \({S_\mu (\mathbf x ,0)}\) and such that \({S_\mu (\mathbf x ,z)=q}\). The function \({B_\mu (\mathbf x ,\cdot ):{\mathbb {R}}\rightarrow [0,\infty ]}\) is given by

\({B_\mu (\mathbf x ,\cdot )}\) is convex lower semi-continuous (l.s.c.) and satisfies the following properties [25]
and, for some \({K_0}\), \({K_1}\) and \({K_2}\) not depending on \(\mathbf{x }\) or r,
In the following, we write \({A\lesssim B}\) for “\({A\le MB}\) for a constant M depending only on an upper bound of  and on the data in the assumptions of Sect. 2.2”.
and on the data in the assumptions of Sect. 2.2”.
Lemma 4.4
(Energy estimates) Under the assumptions of Sect. 2.2, let \({\mathcal {D}}\) be a gradient discretisation with piecewise constant reconstructions  ,
,  . Let
. Let  be a solution of the gradient scheme of (5). Take \({T_0\in (0,T]}\) and \({k\in \{0,\ldots ,N-1\}}\) such that \({T_0\in (t_k,t_{k+1}]}\). Then
be a solution of the gradient scheme of (5). Take \({T_0\in (0,T]}\) and \({k\in \{0,\ldots ,N-1\}}\) such that \({T_0\in (t_k,t_{k+1}]}\). Then

As a consequence,

Proof
We remove the spatial coordinate \(\mathbf{x }\) in the arguments, when not needed. Reasoning as in [19, Lemma 4.1], Property (14) gives

where we have used, by definition,  . Similarly,
. Similarly,

Equation (16) is then obtained by taking  (for \({\alpha =1,2}\)) in the gradient scheme (5), by summing the resulting equations over \({\alpha =1,2}\), by using (18) and (19), and by reducing the time integrals in the left-hand side from \({[0,t_{k+1}]}\) to \({[0,T_0]}\), due to the non-negativity of the integrands.
(for \({\alpha =1,2}\)) in the gradient scheme (5), by summing the resulting equations over \({\alpha =1,2}\), by using (18) and (19), and by reducing the time integrals in the left-hand side from \({[0,t_{k+1}]}\) to \({[0,T_0]}\), due to the non-negativity of the integrands.
The inequality (17) is the consequence of a few simple estimates on the terms of (16) with \({T_0=T}\). For the symmetric diffusion terms (for \({\alpha =1,2}\) and  ), we write
), we write

where  if \({\mu =m}\). The matrix–fracture coupling terms are handled by noticing that, for any
if \({\mu =m}\). The matrix–fracture coupling terms are handled by noticing that, for any  ,
,  and
and  , so that for
, so that for  and
and  ,
,

Here, we have used  ,
,  and \({|s|^2=(s^+)^2+(s^-)^2}\). Plugging estimates (15), (20) and (21) in (16) (with \({T_0=T}\)) and invoking Cauchy–Schwarz inequalities leads to
and \({|s|^2=(s^+)^2+(s^-)^2}\). Plugging estimates (15), (20) and (21) in (16) (with \({T_0=T}\)) and invoking Cauchy–Schwarz inequalities leads to

The proof of (17) is complete by noticing that the left-hand side is equal to  , and by using Young’s inequality and the definition of
, and by using Young’s inequality and the definition of  in the right-hand side. \(\square \)
in the right-hand side. \(\square \)
The existence of a solution to the gradient scheme follows by a standard fixed point argument based on the Leray–Schauder topological degree, see e.g. [10, proof of Lemma 3.2] or [23, Step 1 in the proof of Theorem 3.1].
Corollary 4.5
Under the assumptions of Lemma 4.4, there exists a solution to the gradient scheme (5).
We now want to obtain estimates on the discrete time derivatives. Let the dual norm of  be defined by
be defined by

Lemma 4.6
(Weak estimate on time derivatives) Under the assumptions of Sect. 2.2, let \({\mathcal {D}}\) be a gradient discretisation with piecewise constant reconstructions  ,
,  . Let
. Let  be a solution of the gradient scheme of (5). Then,
be a solution of the gradient scheme of (5). Then,

Remark 4.7
(Damaged rock modelling) The modelling of the damaged rock type (term  in (1b)) is essential to obtain the estimate on
in (1b)) is essential to obtain the estimate on  above. These estimates are required to obtain the compactness of this discrete saturation (see Theorems 4.11 and 4.13).
above. These estimates are required to obtain the compactness of this discrete saturation (see Theorems 4.11 and 4.13).
Proof
Take  and apply (5) with \({\alpha =1}\) to the test function
and apply (5) with \({\alpha =1}\) to the test function  , where
, where  is at an arbitrary position n. This shows that, for all
is at an arbitrary position n. This shows that, for all  and
and 

where we have used the definition of  in the last step. Taking the supremum over all
in the last step. Taking the supremum over all  such that
such that  shows that
shows that

Take the square of this relation, use \({(a+b)^2\le 2a^2+2b^2}\), and apply Jensen’s inequality to introduce the square inside the time integral. Multiply then by  and sum over n to conclude. \(\square \)
and sum over n to conclude. \(\square \)
Lemma 4.8
(Estimate on time translates) Under the assumptions of Sect. 2.2, let \({\mathcal {D}}\) be a gradient discretisation with piecewise constant reconstructions  ,
,  . For any \({h>0}\) and any solution
. For any \({h>0}\) and any solution  of (5),
of (5),

where we recall that  and
and  , and where all functions of time have been extended by 0 outside (0, T).
, and where all functions of time have been extended by 0 outside (0, T).
Proof
Let us start by assuming that \({h\in (0,T)}\), and let us consider integrals over \({(0,T-h)}\) (we therefore do not use extensions outside (0, T) yet). By the Lipschitz continuity and monotonicity of the saturations  we have
we have  . Thus, setting
. Thus, setting  for all \({s\in {\mathbb {R}}}\),
for all \({s\in {\mathbb {R}}}\),

In the last line, we simply wrote  as the sum of the jumps if
as the sum of the jumps if  between s and \({s+h}\) (likewise for
between s and \({s+h}\) (likewise for  ).
).
For a fixed s, define  by
by

With this choice,

We keep s fixed and concentrate on the integrand of the outer integral in the right-hand side of (25). Estimate (23), the definition (22) of  , and Young’s inequality yield
, and Young’s inequality yield

Returning to (25), integrate the previous estimate over \({s\in (0,T-h)}\). In this step, it is crucial to realise that

Hence, recalling the definition of v,

Since  , this proves (24) with \({L^2(0,T-h)}\) norms in the left-hand side, instead of \({L^2(0,T)}\) norms. The complete form of (24) follows by recalling that
, this proves (24) with \({L^2(0,T-h)}\) norms in the left-hand side, instead of \({L^2(0,T)}\) norms. The complete form of (24) follows by recalling that  , so that
, so that  (and similarly for other saturation terms). \(\square \)
(and similarly for other saturation terms). \(\square \)
Lemma 4.9
(Estimate on space translates) Under the assumptions of Sect. 2.2, let \({\mathcal {D}}\) be a gradient discretisation with piecewise constant reconstructions  ,
,  . Let
. Let  be a solution of (5), and let
be a solution of (5), and let  , with
, with  and
and  , where \({\tau ({\mathcal {P}}_i)}\) is the (const.) tangent space of \({{\mathcal {P}}_i}\). Then, extending the functions
, where \({\tau ({\mathcal {P}}_i)}\) is the (const.) tangent space of \({{\mathcal {P}}_i}\). Then, extending the functions  and
and  by 0 outside \({{M_\mu }}\),
by 0 outside \({{M_\mu }}\),

where we recall that  , and
, and  is given in Definition 3.8.
is given in Definition 3.8.
Proof
Let us focus on the matrix \({{\Omega }}\), and remember that, as a function of \(\mathbf{x }\),  is piecewise constant on a polytopal partition
is piecewise constant on a polytopal partition  . Write
. Write

Let  be the set of points \(\mathbf{x }\) that do not belong to the same element \({\Omega _j}\) as their translate
be the set of points \(\mathbf{x }\) that do not belong to the same element \({\Omega _j}\) as their translate  . By assumption on
. By assumption on  ,
,

Moreover, since each \({{\Omega }_j}\) is polytopal,  . Hence,
. Hence,

On the other hand, by definition of \({{\mathcal {T}}_{D_S}}\) and the Lipschitz continuity of  ,
,

Plugging (28) and (29) into (27) and reasoning similarly for \(\iff S\) and  concludes the proof. \(\square \)
concludes the proof. \(\square \)
Remark 4.10
This proof is the only place where the assumption that each  is polytopal is used; this is to ensure that
is polytopal is used; this is to ensure that  (and likewise for fracture and interfacial terms). Obviously, this asssumption on the sets
(and likewise for fracture and interfacial terms). Obviously, this asssumption on the sets  could be relaxed (e.g., into “each
could be relaxed (e.g., into “each  has a Lipschitz-continuous boundary”), but assuming that these sets are polytopal is not restrictive for practical applications.
has a Lipschitz-continuous boundary”), but assuming that these sets are polytopal is not restrictive for practical applications.
4.2 Initial convergences
We can now state our initial convergence theorem for sequences of solutions to gradient schemes. This theorem does not yet identify the weak limits of such sequences.
Theorem 4.11
(Averaged-in-time convergence of approximate solutions) Let \({(\mathcal {D}^l)_{l\in {\mathbb {N}}}}\) be a coercive, consistent, limit-conforming and compact sequence of space-time gradient discretisations, with piecewise constant reconstructions. Let  be such that
be such that  is a solution of (5) with \({\mathcal {D}=\mathcal {D}^l}\). Then, there exists
is a solution of (5) with \({\mathcal {D}=\mathcal {D}^l}\). Then, there exists  such that, up to a subsequence as \({l\rightarrow \infty }\), the convergences (11) and (12) hold.
such that, up to a subsequence as \({l\rightarrow \infty }\), the convergences (11) and (12) hold.
Proof
Combining Lemmata 4.4 and A.2 immediately gives (11) up to a subsequence. By assumption,  and therefore, by Lemmata 4.8 and 4.9 and the Kolmogorov compactness theorem, there exists a subsequence of
and therefore, by Lemmata 4.8 and 4.9 and the Kolmogorov compactness theorem, there exists a subsequence of  that strongly converges in
that strongly converges in  and a subsequence of
and a subsequence of  that strongly converges in
that strongly converges in  . Also, by assumption,
. Also, by assumption,  are non-decreasing functions, which allows us to identify the limits in (12) by applying Corollary A.3. \(\square \)
are non-decreasing functions, which allows us to identify the limits in (12) by applying Corollary A.3. \(\square \)
Let  be the subspace of functions in
be the subspace of functions in  vanishing on a neighbourhood of the boundary \(\partial \Omega \). Define also
vanishing on a neighbourhood of the boundary \(\partial \Omega \). Define also  as the image of \({C_0^\infty ({\Omega })}\) through the trace operator
as the image of \({C_0^\infty ({\Omega })}\) through the trace operator  .
.
The following lemma and theorem add a uniform-in-time weak \(L^2\) convergence property to the convergences established in Theorem 4.11.
Lemma 4.12
(Uniform-in-time, weak-in-space translate estimates) Under the assumptions of Sect. 2.2, let \({\mathcal {D}}\) be a gradient discretisation with piecewise constant reconstructions  ,
,  . Let
. Let  be a solution of the gradient scheme (5), and
be a solution of the gradient scheme (5), and  . Then, for all
. Then, for all  and all \({s,t\in [0,T]}\),
and all \({s,t\in [0,T]}\),

where \({C_\varphi }\) only depends on \({\varphi }\), \({\iff d}\) is the width of the fractures, and  .
.
Proof
Let us introduce an interpolant  such that, for all
such that, for all  ,
,  . As in the proof of Lemma 4.8, let
. As in the proof of Lemma 4.8, let  for all \({r\in [0,T]}\). Denote by L the left-hand side of (30) and introduce
for all \({r\in [0,T]}\). Denote by L the left-hand side of (30) and introduce  in the first sum and
in the first sum and  in the second sum to write
in the second sum to write



Here, the terms (31) and (32) have been estimated by using  and the definition of
and the definition of  . Let \({L_1}\) be the second addend in (33). Assuming that \({t<s}\), and hence \({n(t)\le n(s)}\), write
. Let \({L_1}\) be the second addend in (33). Assuming that \({t<s}\), and hence \({n(t)\le n(s)}\), write  and
and  as the sum of their jumps, and recall the definition (22) of
as the sum of their jumps, and recall the definition (22) of  to obtain
to obtain

Use now Lemmata 4.6 and the Cauchy–Schwarz inequality to infer

By the triangle inequality,

Plugging this into (34) and the resulting inequality into (33) concludes the proof. \(\square \)
Theorem 4.13
(Uniform-in-time, weak-in-space convergence) Under the assumptions of Theorem 4.11, for all  and
and  ,
,  and
and  are continuous for the weak topologies of \({L^2({M_\mu })}\) and \({L^2({\Gamma _{}}_{{\mathfrak {a}}})}\), respectively, and
are continuous for the weak topologies of \({L^2({M_\mu })}\) and \({L^2({\Gamma _{}}_{{\mathfrak {a}}})}\), respectively, and

where the definition of the uniform-in-time weak \(L^2\) convergence is recalled in “Appendix A.1”.
Proof
The proof hinges on the discontinuous Arzelà-Ascoli theorem (Theorem A.1 in the appendix). Consider first the matrix saturation. The space  is dense in \(L^2({\Omega })\). Apply (30) to
is dense in \(L^2({\Omega })\). Apply (30) to  . Since
. Since  , only the term involving
, only the term involving  remains in the left-hand side. The resulting estimate and the property
remains in the left-hand side. The resulting estimate and the property  show that the sequence of functions
show that the sequence of functions  satisfies the assumptions of Theorem A.1 with
satisfies the assumptions of Theorem A.1 with  . Hence,
. Hence,  has a subsequence that converges uniformly on [0, T] weakly in \(L^2({\Omega })\). Given (12), the weak limit of this sequence must be
has a subsequence that converges uniformly on [0, T] weakly in \(L^2({\Omega })\). Given (12), the weak limit of this sequence must be  .
.
A similar reasoning, based on the space  —which is dense in \(L^2(\Gamma )\)—and using \(\varphi =(0,\iff \varphi )\) in (30), gives the uniform-in-time weak \(L^2(\Gamma )\) convergence of
—which is dense in \(L^2(\Gamma )\)—and using \(\varphi =(0,\iff \varphi )\) in (30), gives the uniform-in-time weak \(L^2(\Gamma )\) convergence of  towards
towards  .
.
Let us now turn to the convergence of the trace saturations. Take  such that the support of
such that the support of  is non empty for exactly one \({\mathfrak {a}}\in \chi \). Considering
is non empty for exactly one \({\mathfrak {a}}\in \chi \). Considering  in (30) leads to
in (30) leads to

Since it was established that  converges uniformly-in-time weakly in \(L^2({\Omega })\), the sequence
converges uniformly-in-time weakly in \(L^2({\Omega })\), the sequence  is equi-continuous and the last term in (36) therefore tends to 0 uniformly in l as \({s-t\rightarrow 0}\). Hence, (36) enables the usage of Theorem A.1, by noticing that
is equi-continuous and the last term in (36) therefore tends to 0 uniformly in l as \({s-t\rightarrow 0}\). Hence, (36) enables the usage of Theorem A.1, by noticing that  is dense in \({{L^2({\Gamma _{}}_{{\mathfrak {a}}})}}\), and gives the uniform-in-time weak \({{L^2({\Gamma _{}}_{{\mathfrak {a}}})}}\) convergence of
is dense in \({{L^2({\Gamma _{}}_{{\mathfrak {a}}})}}\), and gives the uniform-in-time weak \({{L^2({\Gamma _{}}_{{\mathfrak {a}}})}}\) convergence of  . \(\square \)
. \(\square \)
4.3 Proof of Theorem 4.1
The proof of the main convergence theorem can now be given.
First step: passing to the limit in the gradient scheme.
Let us introduce the family of functions  :
:

and their continuous counterparts  :
:

The following properties are easy to check. Firstly, since \(\iff T\),  and
and  are positive and \(s\mapsto s^+\) and \(s\mapsto -s^-\) are non-decreasing,
are positive and \(s\mapsto s^+\) and \(s\mapsto -s^-\) are non-decreasing,

Secondly, by the convergences (12), for \({(\beta _l)_{l\in {\mathbb {N}}}\subset {L^2({\Gamma _{}}_{{\mathfrak {a}}})}}\) and \({\beta \in {L^2({\Gamma _{}}_{{\mathfrak {a}}})}}\),

Thirdly, by Lemma 4.4, the sequences  (
( , \(\alpha =1,2\)) are bounded in
, \(\alpha =1,2\)) are bounded in  and there exists thus
and there exists thus  such that, up to a subsequence,
such that, up to a subsequence,

Consider  , where
, where  and
and  . Take
. Take  as “test function” in (5). Here,
as “test function” in (5). Here,  is defined as in the proof of Lemma 4.12. Apply the discrete integration-by-parts of [21, Section D.1.7] on the accumulation terms in (5), let
is defined as in the proof of Lemma 4.12. Apply the discrete integration-by-parts of [21, Section D.1.7] on the accumulation terms in (5), let  and use standard convergence arguments [19, 21] based on Theorem 4.11 to see that
and use standard convergence arguments [19, 21] based on Theorem 4.11 to see that

Note that Equation (40) also holds for any smooth  , by density of tensorial functions in smooth functions [17, Appendix D]. Recalling the weak formulation (2), proving Theorem 4.1 is now all about showing that
, by density of tensorial functions in smooth functions [17, Appendix D]. Recalling the weak formulation (2), proving Theorem 4.1 is now all about showing that

This is achieved by using Minty’s trick.
Second step: proof that

Having in mind to employ the energy inequality (16) with \(T_0=T\), we first establish, for  and
and  , the following convergences as \({l\rightarrow \infty }\):
, the following convergences as \({l\rightarrow \infty }\):



The convergence (43) is obvious by Theorem 4.11. From the choice (4) of the scheme’s initial conditions, together with the consistency of the interpolation operator  ,
,  in \({{L^2({M_\mu })}}\) and
in \({{L^2({M_\mu })}}\) and  in \({{L^2({\Gamma _{}}_{{\mathfrak {a}}})}}\), as \({l\rightarrow \infty }\). Then, (15) and [27, Lemma A.1] yield (44) and (45).
in \({{L^2({\Gamma _{}}_{{\mathfrak {a}}})}}\), as \({l\rightarrow \infty }\). Then, (15) and [27, Lemma A.1] yield (44) and (45).
We further show that



By the uniform-in-time weak \(L^2\) convergences of Theorem 4.13,  in \({{L^2({M_\mu })}}\) and
in \({{L^2({M_\mu })}}\) and  in \({{L^2({\Gamma _{}}_{{\mathfrak {a}}})}}\), as \({l\rightarrow \infty }\). Note also that, since (by assumption)
in \({{L^2({\Gamma _{}}_{{\mathfrak {a}}})}}\), as \({l\rightarrow \infty }\). Note also that, since (by assumption)  and
and  are not explicitly space-dependent on each open set of the formerly introduced partitions of \({{M_\mu }}\) and \({{\Gamma _{{\mathfrak {a}}}}}\), respectively, so are
are not explicitly space-dependent on each open set of the formerly introduced partitions of \({{M_\mu }}\) and \({{\Gamma _{{\mathfrak {a}}}}}\), respectively, so are  and
and  . On these partitions,
. On these partitions,  and
and  are convex l.s.c. and an easy adaptation of [25, Lemma 4.6] (which essentially states the \(L^2\)-weak l.s.c. of strongly l.s.c. convex functions on \(L^2\)), to account for the terms
are convex l.s.c. and an easy adaptation of [25, Lemma 4.6] (which essentially states the \(L^2\)-weak l.s.c. of strongly l.s.c. convex functions on \(L^2\)), to account for the terms  and \(\eta \), thus shows that (46) and (47) hold. To prove (48), apply the Cauchy-Schwarz inequality to write
and \(\eta \), thus shows that (46) and (47) hold. To prove (48), apply the Cauchy-Schwarz inequality to write

and take the inferior limit as \({l\rightarrow \infty }\), using the strong convergence of  and weak convergence of
and weak convergence of  to pass to the limit in the left-hand side and the first term in the right-hand side.
to pass to the limit in the left-hand side and the first term in the right-hand side.
Let us now come back to the proof of (42). Plugging the convergences (43)–(48) into (16) with \(T_0=T\) yields

Recall that \({C_0^\infty ([0, T ))\otimes [C_{\Omega }^\infty \times C_{{\Gamma _{}}}^\infty ]}\) is dense in  . Owing to “Appendix A.3”, we infer from (40) that
. Owing to “Appendix A.3”, we infer from (40) that  , that
, that  (where
(where  is the adjoint of
is the adjoint of  ), and that, for any
), and that, for any  ,
,

Note that the duality product between  and
and  is taken respective to the measure
is taken respective to the measure  , and remember the abuse of notation (57). Apply this to
, and remember the abuse of notation (57). Apply this to  . Recalling that
. Recalling that  , we have
, we have  and thus
and thus

[19, Lemma 3.6] establishes a temporal integration-by-parts property by using arguments purely based on the time variable, and that can easily be adapted to our context, even considering the “combined” time derivatives  and the heterogeneities of the media treated here—i.e. the presence of
and the heterogeneities of the media treated here—i.e. the presence of  , see assumptions in Sect. 2.2. This adaptation yields
, see assumptions in Sect. 2.2. This adaptation yields

and

Plugging these relations into (50) and using (49) concludes the proof of (42).
Third step: conclusion.
As in the first step, take  and set
and set  . Developing the monotonicity property (37) of
. Developing the monotonicity property (37) of  , integrating over \({(0,T)\times {\Gamma _{{\mathfrak {a}}}}}\) and summing over
, integrating over \({(0,T)\times {\Gamma _{{\mathfrak {a}}}}}\) and summing over  yields
yields

Use (38), (39) and (11) to pass to the limit in the second and third integral terms:

Use (42) and the density of the tensorial function spaces \({C_0^\infty ([0, T ))\otimes [C_{\Omega }^\infty \times C_{{\Gamma _{}}}^\infty ]}\) in  (cf. [11, proposition 2.3]) to obtain
(cf. [11, proposition 2.3]) to obtain

for all  . The conclusion is now standard in the Minty trick (see e.g. [21, Proof of Theorem 3.34]): for any smooth
. The conclusion is now standard in the Minty trick (see e.g. [21, Proof of Theorem 3.34]): for any smooth  , choose
, choose  and let \({\epsilon \rightarrow 0}\) to derive (41) and conclude the proof. \(\square \)
and let \({\epsilon \rightarrow 0}\) to derive (41) and conclude the proof. \(\square \)
5 Two-phase flow test cases
We present in this section a series of test cases for two-phase flow through a fractured 2 dimensional reservoir of geometry as shown in Fig. 3. The domain \({\Omega }\) is of extension \((0,10)\mathrm {m}\times (0,20)\mathrm {m}\) and the fracture width \(d_f\) is assumed constant equal to \(1\,{\mathrm {cm}}\). We consider isotropic permeability in the matrix and in the fracture. The following geological configuration is considered: the matrix and fracture permeabilities are  Darcy and \(\iff \lambda = 100\) Darcy, respectively; the matrix and fracture porosities are
Darcy and \(\iff \lambda = 100\) Darcy, respectively; the matrix and fracture porosities are  and \(\iff \phi = 0.4\), respectively.
and \(\iff \phi = 0.4\), respectively.
Initially, the reservoir is saturated with water (density \(\rho ^2 = 1000\ {\mathrm {kg}}/\mathrm {m}^3\), viscosity \(\kappa ^2 = 0.001\,{\mathrm {Pa.s}}\)) and oil (density \(\rho ^1 = 700\ {\mathrm {kg}}/\mathrm {m}^3\), viscosity \(\kappa ^1 = 0.005\,{\mathrm {Pa.s}}\)) is injected from below. Also, hydrostatic distribution of pressure is assumed. The oil then rises by gravity, thanks to its lower density compared to water. At the lower boundary of the domain, we impose constant capillary pressure of 0.1 bar and water pressure of 3 bar; at the upper boundary, the capillary pressure is constant equal to 0 bar and the water pressure is 1 bar. Elsewhere, homogeneous Neumann conditions are imposed.
We use the VAG scheme to obtain solutions for the DFM. We refer to [11] for a presentation of the scheme as a gradient scheme, and for proofs that, under standard regularity assumptions on the meshes, the corresponding sequences of gradient discretisations are coercive, GD-consistent, limit-conforming and compact. The tests are driven on a triangular mesh extended to a 3D mesh with one layer of prisms (we use a 3D implementation of the VAG scheme). The resulting numbers of cells and degrees of freedom are exhibited in Table 1. The mesh size is of order \(10 d_f\).
The non-linear system of equations occurring at each time step is solved via a Newton algorithm with relaxation. To solve the linear system obtained at each step of the Newton iteration, we use the sequential version of the SuperLU direct sparse solver [15, 16]. The stopping criterion on the \(L^1\) relative residual is \({\mathrm{crit}}_{\mathrm{Newton}}^{\mathrm{rel}}\). To ensure well defined values for the capillary pressure, after each Newton iteration, we project the (oil) saturation on the interval \([0,1-10^{-14}]\). The time stepping is progressive, i.e. after each iteration, the upcoming time step is deduced by multiplying the previous one by 2, while imposing a maximal time step \(\Delta t_{max}\). If at a given time iteration the Newton algorithm does not converge after 35 iterations, then the actual time step is divided by 4 and the time iteration is repeated. The number of time step failures at the end of a simulation is indicated by \(\mathbf N _{\mathrm{Chop}}\).
Inside the matrix domain the capillary pressure function is given by Corey’s law \(p_m = -a_m\log (1-S_m)\) with \(a_m = 1\) bar. Inside the fracture network, we suppose \(p_f = -a_f\log (1-S_f)\) with \(a_f = 0.02\) bar. The matrix and fracture relative permeabilities of each phase \(\alpha \) are given by Corey’s laws  and
and  , and the phase mobilities are defined by
, and the phase mobilities are defined by  ,
,  (see Fig. 4). The phase saturations at the interfacial layers are defined by the interpolation
(see Fig. 4). The phase saturations at the interfacial layers are defined by the interpolation

with parameter \({\theta \in [0,1]}\). The mapping  is a diffeomorphism so the choice
is a diffeomorphism so the choice

is valid, since this function can be written as  with
with  . Finally, the interfacial porosity
. Finally, the interfacial porosity  is set to 0.2 and
is set to 0.2 and

with parameter \(\varepsilon >0\). The parameter \(\eta \) is then defined by 
Let us start with some remarks. From the capillary pressure functions (cf. Fig. 4), it is obvious that for given p, the one-sided jump of the oil saturation is negative, i.e.

To account for the interfacial zone properly, the mobilities have to be adjusted by choosing the model parameter \(\theta \) depending on the rock type characteristics of the layer. Obviously, \(\theta = 0\) refers to a fracture rock type and \(\theta = 1\) to a matrix rock type.
On the other hand, with larger \(\eta \), the volume of the interfacial layers gets augmented and the interfacial accumulation terms play a more important role. The availability of the supplementary volume has a direct impact on the phase front speed inside the fracture during its filling: (51)–(52) show that the volume of oil in the interfacial layers is strictly decreasing as a function of \(\theta \), given a distribution of capillary pressures. This indicates that, from the accumulation point of view, the fracture front speed should grow with growing \(\theta \), and this effect should be enhanced by a larger \(\eta \).
Figure 5a indicates that, for a fixed \(\theta = 0, 0.5, 1\), the solutions are not sensitive to small variations of \(\varepsilon \). Quantitatively, we see that the solution for \(\varepsilon =0.1\) is close to the solution for \(\varepsilon = 10^{-6}\). With respect to the computational performance exposed in Table 2, we thus see that choosing \(\varepsilon =0.1\) is a good compromise between accuracy and cost. This point is presented in more detail for the intermediate rock type, i.e. \(\theta =0.5\), in Fig. 6. Figure 5b confirms the aforementioned feature of extended (large \(\varepsilon \)) interfacial layers to delay the propagation of the oil in the drain. As suggested, this effect is even more important, with decreasing \(\theta \). In Fig. 5c, we study the impact of the choice of the interfacial mobility for parameters \(\theta = 0, 0.5, 1\) on the solution. Here, the interfacial accumulation is negligible due to an \(\varepsilon \) close to zero. Let us remark that in the limit of a vanishing interfacial layer, i.e. \(\eta =0\), we aim at recovering the fracture mobilities for the mass exchange fluxes between the matrix-fracture interface and the fracture. Hence, in this case, the right choice of \(\theta \) would be 0. We observe that changing the mobilities does not much influence the solution, due to the fact that fluxes are mostly oriented from the fracture towards the interfacial layers. The regions where a difference is observed in the fracture oil front for the different models are those with a small positive oil saturation. There, the relative permeabilities for \(\theta = 0\) and \(\theta = 0.5\) are very close and the difference to \(\theta = 1\) is at its peak; this explains the behaviour of the fracture front for the three models.
Table 2 shows that the computational cost increases with decreasing \(\varepsilon \) and that, in the case of \(\varepsilon =0\), the Jacobian becomes singular. Furthermore, the efficiency severely deteriorates for \(\theta = 1\). In this case, \(S_{\mathfrak {a}}'(p)\) is (significantly) smaller during the filling of the fracture (for capillary pressures p below a characteristic  ), since \(S_m'(p)\ll S_f'(p)\). When oil fluxes oriented from the fracture to the interface are present, the Jacobian is thus ill-conditioned.
), since \(S_m'(p)\ll S_f'(p)\). When oil fluxes oriented from the fracture to the interface are present, the Jacobian is thus ill-conditioned.
6 Conclusion
We introduced a new discrete fracture matrix model for two phase Darcy flow, permitting pressure discontinuity at the matrix-fracture interfaces. It respects the heterogeneities of the media and between the matrix and the fractures, since it takes into account saturation jumps due to different capillary pressure curves in the respective domains. It also considers damaged layers located at the matrix-fracture interfaces. Another feature of the model are upwind fluxes between these interfacial layers and the fractures. The upwinding is needed for transport dominated flow in normal direction to the fractures. The extension to gravity is straightforward (cf. [12]).
We developed the numerical analysis of the model in the framework of the gradient discretisation method, which contains for example the VAG and HMM schemes. Based on compactness arguments, we showed in Theorem 4.1 the strong \(L^2\) convergence of the saturations and the weak \(L^2\) and \(H^1\) convergences for the pressures to a solution of Model (1). In Theorem 4.13, we established uniform-in-time, weak \(L^2\) in space convergence for the saturations, a result that is extended to uniform-in-time, strong \(L^2\) in space convergence in [26].
Finally, we presented a series of test cases, with the objective to study the impact of the interfacial layer on the solution. The observed behaviour of the solutions for the different situations corresponds to the expectations. It exhibits significant differences, during the filling of the fracture, for large interfacial layers and small differences for small layers. In terms of computational cost, we saw that the presence of a damaged zone at the matrix-fracture interface is needed in order to solve the linear system of the discrete problem, occurring at each time step. We also observed that for a large contrast between the drain’s and the interfacial layer’s capillary pressures, the simulation becomes expensive. Therefore, we see that, in order to cope with both, fractures acting as drains or as barriers, the possibility to deal with mixed rock types for the damaged zone is essential.
References
Aghili, J., Brenner, K., Hennicker, J., Masson, R., Trenty, L.: Two-phase discrete fracture matrix models with nonlinear transmission conditions (2018). https://hal.archives-ouvertes.fr/hal-01764432. Accessed 3 May 2018
Ahmed, R., Edwards, M., Lamine, S., Huisman, B., Pal, M.: Control-volume distributed multi-point flux approximation coupled with a lower-dimensional fracture model. J. Comput. Phys. 284, 462–489 (2015)
Ahmed, R., Edwards, M.G., Lamine, S., Huisman, B.A., Pal, M.: Three-dimensional control-volume distributed multi-point flux approximation coupled with a lower-dimensional surface fracture model. J. Comput. Phys. 303, 470–497 (2015)
Alboin, C., Jaffré, J., Roberts, J., Serres, C.: Modeling fractures as interfaces for flow and transport in porous media. SIAM J. Sci. Comput. 295, 13–24 (2002)
Angot, P., Boyer, F., Hubert, F.: Asymptotic and numerical modelling of flows in fractured porous media. ESAIM. Math. Model. Numer. Anal. 43(2), 239–275 (2009)
Antonietti, P.F., Formaggia, L., Scotti, A., Verani, M., Verzott, N.: Mimetic finite difference approximation of flows in fractured porous media. ESAIM M2AN 50, 809–832 (2016)
Berrone, S., Pieraccini, S., Scialò, S.: An optimization approach for large scale simulations of discrete fracture network flows. J. Comput. Phys. 256, 838–853 (2014)
Bogdanov, I.I., Mourzenko, V.V., Thovert, J.-F., Adler, P.M.: Two-phase flow through fractured porous media. Phys. Rev. E 68(2), 026703 (2003)
Brenner, K., Groza, M., Guichard, C., Lebeau, G., Masson, R.: Gradient discretization of hybrid-dimensional Darcy flows in fractured porous media. Numer. Math. 134(3), 569–609 (2016)
Brenner, K., Groza, M., Guichard, C., Masson, R.: Vertex approximate gradient scheme for hybrid-dimensional two-phase Darcy flows in fractured porous media. ESAIM. Math. Model. Numer. Anal. 2(49), 303–330 (2015)
Brenner, K., Hennicker, J., Masson, R., Samier, P.: Gradient discretization of hybrid-dimensional Darcy flow in fractured porous media with discontinuous pressures at matrix-fracture interfaces. IMA J. Numer. Anal. 37(3), 1551–1585 (2017)
Brenner, K., Hennicker, J., Masson, R., Samier, P.: Hybrid dimensional modelling of two-phase flow through fractured porous media with enhanced matrix fracture transmission conditions. J. Comput. Phys. 357, 100–124 (2018)
Cheng, H.M., Droniou, J., Le, K.-N.: Convergence analysis of a family of ELLAM schemes for a fully coupled model of miscible displacement in porous media, pp. 1–38 (2017)
D’Angelo, C., Scotti, A.: A mixed finite element method for Darcy flow in fractured porous media with non-matching grids. ESAIM. Math. Model. Numer. Anal. 46(2), 465–489 (2012)
Demmel, J., Eisenstat, S., Gilbert, J., Li, X., Liu, J.: A supernodal approach to sparse partial pivoting. SIAM J. Matrix Anal. Appl. 20(3), 720–750 (1999)
Demmel, J., Gilbert, J., Grigori, L., Li, X., Shao, M., Yamazaki, I.: Technical Report LBNL-44289, Lawrence Berkeley National Laboratory, SuperLU Users’ Guide, September (1999). http://crd.lbl.gov/~xiaoye/SuperLU
Droniou, J.: Intégration et espaces de sobolev à valeurs vectorielles. Polycopiés de l’Ecole Doctorale de Maths-Info de Marseille (2001). https://hal.archives-ouvertes.fr/hal-01382368. Accessed 19 Dec 2016
Droniou, J.: Finite volume schemes for diffusion equations: introduction to and review of modern methods. Math. Models Methods Appl. Sci. 24(8), 1575–1619 (2014)
Droniou, J., Eymard, R.: Uniform-in-time convergence of numerical methods for non-linear degenerate parabolic equations. Numer. Math. 132(4), 721–766 (2016)
Droniou, J., Eymard, R., Feron, P.: Gradient Schemes for Stokes problem. IMA J. Numer. Anal. 36(4), 1636–1669 (2016)
Droniou, J., Eymard, R., Gallouët, T., Guichard, C., Herbin, R.: The Gradient Discretisation Method. Mathematics and Applications. Springer, Heidelberg (2018). (To appear)
Droniou, J., Eymard, R., Gallouët, T., Herbin, R.: A unified approach to mimetic finite difference, hybrid finite volume and mixed finite volume methods. Math. Models Methods Appl. Sci. 20(2), 265–295 (2010)
Droniou, J., Eymard, R., Gallouët, T., Herbin, R.: Gradient schemes: a generic framework for the discretisation of linear, nonlinear and nonlocal elliptic and parabolic equations. Math. Models Methods Appl. Sci. 13(23), 2395–2432 (2013)
Droniou, J., Eymard, R., Herbin, R.: Gradient schemes: generic tools for the numerical analysis of diffusion equations. M2AN Math. Model. Numer. Anal. 50(3), 749–781 (2016). (Special issue—Polyhedral discretization for PDE)
Droniou, J., Eymard, R., Talbot, K.S.: Convergence in \(C([0;T];L^2(\Omega ))\) of weak solutions to perturbed doubly degenerate parabolic equations. J. Differ. Equ. 260(11), 7821–7860 (2016)
Droniou, J., Hennicker, J., Masson, R.: Uniform-in-time convergence of numerical schemes for a two-phase discrete fracture model, vol. 199, pp. 275–283 (2017)
Droniou, J., Talbot, K.S.: On a miscible displacement model in porous media flow with measure data. SIAM J. Math. Anal. 46(5), 3158–3175 (2014)
Eymard, R., Guichard, C., Herbin, R.: Small-stencil 3D schemes for diffusive flows in porous media. ESAIM. Math. Model. Numer. Anal. 46(2), 265–290 (2012)
Eymard, R., Guichard, C., Herbin, R., Masson, R.: Gradient schemes for two-phase flow in heterogeneous porous media and Richards equation. ZAMM Z. Angew. Math. Mech. 94(7–8), 560–585 (2014)
Faille, I., Fumagalli, A., Jaffré, J., Roberts, J.E.: Model reduction and discretization using hybrid finite volumes of flow in porous media containing faults. Comput. Geosci. 20, 317–339 (2016)
Flauraud, E., Nataf, F., Faille, I., Masson, R.: Domain decomposition for an asymptotic geological fault modeling. C. R. Mec. 331(12), 849–855 (2003)
Fumagalli, A., Scotti, A.: A reduced model for flow and transport in fractured porous media with non-matching grids. In: Cangiani, A., Davidchack, R., Georgoulis, E., Gorban, A., Levesley, J., Tretyakov, M. (eds) Numerical Mathematics and Advanced Applications 2011. Springer, Berlin, Heidelberg (2013). https://doi.org/10.1007/978-3-642-33134-3_53
Haegland, H., Assteerawatt, A., Dahle, H., Eigestad, G., Helmig, R.: Comparison of cell- and vertex-centered discretization methods for flow in a two-dimensional discrete-fracture-matrix system. Adv. Water Resour. 32, 1740–1755 (2009)
Hoteit, H., Firoozabadi, A.: An efficient numerical model for incompressible two-phase flow in fractured media. Adv. Water Resour. 31(6), 891–905 (2008)
Jaffré, J., Mnejja, M., Roberts, J.: A discrete fracture model for two-phase flow with matrix-fracture interaction. Procedia Comput. Sci. 4, 967–973 (2011)
Karimi-Fard, M., Durlofsky, L., Aziz, K.: An efficient discrete-fracture model applicable for general-purpose reservoir simulators. SPE J. 9(02), 227–236 (2004)
Martin, V., Jaffré, J., Roberts, J.E.: Modeling fractures and barriers as interfaces for flow in porous media. SIAM J. Sci. Comput. 26(5), 1667–1691 (2005)
Matthai, S.K., Mezentsev, A.A., Belayneh, M.: Finite element—node-centered finite-volume two-phase-flow experiments with fractured rock represented by unstructured hybrid-element meshes. SPE Reserv. Eval. Eng. 10(06), 740–756 (2007)
Monteagudo, J.E., Firoozabadi, A.: Control-volume model for simulation of water injection in fractured media: incorporating matrix heterogeneity and reservoir wettability effects. SPE J. 12(03), 355–366 (2007)
Reichenberger, V., Jakobs, H., Bastian, P., Helmig, R.: A mixed-dimensional finite volume method for two-phase flow in fractured porous media. Adv. Water Resour. 29(7), 1020–1036 (2006)
Sandve, T., Berre, I., Nordbotten, J.: An efficient multi-point flux approximation method for discrete fracture-matrix simulations. J. Comput. Phys. 231(9), 3784–3800 (2012)
Schwenck, N., Flemisch, B., Helmig, R., Wohlmuth, B.: Dimensionally reduced flow models in fractured porous media: crossings and boundaries. Comput. Geosci. 19, 1219–1230 (2015)
Tunc, X., Faille, I., Gallouët, T., Cacas, M.C., Havé, P.: A model for conductive faults with non-matching grids. Comput. Geosci. 16(2), 277–296 (2012)
Xing, F., Masson, R., Lopez, S.: Parallel vertex approximate gradient discretization of hybrid-dimensional Darcy flow and transport in discrete fracture networks. Comput. Geosci. 21, 595–617 (2017)
Xing, F., Masson, R., Lopez, S.: Parallel numerical modelling of hybrid-dimensional compositional non-isothermal Darcy flows in fractured porous media. J. Comput. Phys. 345, 637–664 (2018)
Acknowledgements
The authors would like to thank Total S.A. and the Australian Research Council’s Discovery Projects funding scheme (Project Number DP170100605) for supporting this work.
Author information
Authors and Affiliations
Corresponding author
A Appendix
A Appendix
1.1 A.1 Uniform-in-time weak \(L^2\) convergence
Let A be a subset of \({{\mathbb {R}}^n}\), endowed with the standard Lebesgue measure, and \(\{\varphi _\ell \,:\,\ell \in {\mathbb {N}}\}\) be a dense countable set in \(L^2(A)\). On any bounded ball of \(L^2(A)\), the weak topology can be defined by the following distance:

A sequence \({(v_m)_{m\in {\mathbb {N}}}}\) of bounded functions \([0,T]\rightarrow L^2(A)\) converges uniformly on [0, T] weakly in \({L^2(A)}\) to some v if it converges uniformly for the weak topology of \({L^2(A)}\), meaning that, for all \({\phi \in L^2(A)}\), \({\langle v_m(\cdot ),\phi \rangle _{L^2(A)} \rightarrow \langle v(\cdot ),\phi \rangle _{L^2(A)}}\) uniformly on [0, T] as \({m\rightarrow \infty }\).
With this introductory material, the following result is a consequence of [21, Theorem 4.26] or [19, Theorem 6.2] (see also the reasoning at the end of [19, Proof of Theorem 3.1]).
Theorem A.1
(Discontinuous weak \({L^2}\) Ascoli–Arzela theorem) Let \({\mathcal {R}}\) be a dense subset of \({L^2(A)}\) and \((v_m)_{m\in {\mathbb {N}}}\) be a sequence of functions \({[0,T]\rightarrow L^2(A)}\) such that
-
\(\sup _{m\in {\mathbb {N}}}\sup _{t\in [0,T]}\Vert v_m(t)\Vert _{L^2(A)}<+\infty \),
-
for all \(\varphi \in \mathcal {R}\), there exist \(\omega _\varphi :[0,T]^2\rightarrow [0,\infty )\) and \((\delta _m(\varphi ))_{m\in {\mathbb {N}}}\subset [0,\infty )\) satisfying
$$\begin{aligned}&\omega _\varphi (s,t)\rightarrow 0 \text{ as } s-t\rightarrow 0\,,\;\delta _m(\varphi )\rightarrow 0 \text{ as } m\rightarrow \infty \,, \text{ and } \\&\forall (s,t)\in [0,T]^2\,,\;\forall m\in {\mathbb {N}}\,,\; |\langle v_m(s)-v_m(t),\varphi \rangle _{L^2(A)}|\le \delta _m(\varphi )+\omega _\varphi (s,t). \end{aligned}$$
Then, there exists a function \(v:[0,T]\rightarrow L^2(A)\) such that, up to a subsequence as \(m\rightarrow \infty \), \(v_m\rightarrow v\) uniformly on [0, T] weakly in \({L^2(A)}\). Moreover, v is continuous on [0, T] for the weak topology of \({L^2(A)}\).
1.2 A.2 Generic results on gradient discretisations
The following lemma is a classical result in the context of the standard gradient discretisation method, see e.g. [21, Lemma 4.7]. We give a sketch of its proof for gradient discretisations adapted to discrete fracture matrix model.
Lemma A.2
(Regularity of the limit) Let \({(\mathcal {D}^l)_{l\in {\mathbb {N}}}}\) be a coercive and limit-conforming sequence of gradient discretisations, and let  be such that
be such that  , where \(N_l\) is the number of time steps of \(\mathcal {D}^l\). We assume that
, where \(N_l\) is the number of time steps of \(\mathcal {D}^l\). We assume that  is bounded. Then, there exists
is bounded. Then, there exists  such that, up to a subsequence, the following weak convergences hold:
such that, up to a subsequence, the following weak convergences hold:

Proof
By coercivity and since  is bounded, all the sequences in (53) are bounded in their respective spaces. Up to a subsequence, we can therefore assume that there exists
is bounded, all the sequences in (53) are bounded in their respective spaces. Up to a subsequence, we can therefore assume that there exists  ,
,  ,
,  and
and  such that
such that  ,
,  ,
,  and
and  weakly in their respective \(L^2\) spaces as \(l\rightarrow \infty \).
weakly in their respective \(L^2\) spaces as \(l\rightarrow \infty \).
Take  ,
,  and \(\rho \in C^\infty _0(0,T)\). For F a function of \(\mathbf x \), set \((\rho \otimes F)(t,\mathbf x )=\rho (t)F(\mathbf x )\). The definition of
and \(\rho \in C^\infty _0(0,T)\). For F a function of \(\mathbf x \), set \((\rho \otimes F)(t,\mathbf x )=\rho (t)F(\mathbf x )\). The definition of  (see Definition 3.6) yields
(see Definition 3.6) yields

The limit-conformity shows that the right-hand side of this inequality tends to 0. Hence,

Applying this to  with
with  , and using the density of tensorial functions
, and using the density of tensorial functions  in
in  (see [17, Appendix D]) shows that
(see [17, Appendix D]) shows that  . With
. With  where
where  , we obtain
, we obtain  . Considering now
. Considering now  with
with  and applying the divergence theorem gives
and applying the divergence theorem gives  . Finally, taking
. Finally, taking  with a general
with a general  yields
yields  . \(\square \)
. \(\square \)
With [29, Lemma 3.6], we can state the following.
Corollary A.3
Under the assumptions of Lemma A.2, if  and
and  are continuous, non-decreasing functions and if
are continuous, non-decreasing functions and if  strongly converges in \({{L^2((0,T)\times {M_\mu })}}\) and
strongly converges in \({{L^2((0,T)\times {M_\mu })}}\) and  strongly converges in
strongly converges in  , then
, then

1.3 A.3 Identification of time derivatives
We discuss here how weak formulations, with derivatives on test functions, enable us to recover some regularity properties on time derivatives of quantities of interest.
Let us start with a classical situation, similar to [19, Remark 1.1]. Let \({(M,\nu )}\) be a measured space and E be a Banach space densely embedded in \({L^2(M)}\), so that \({E\hookrightarrow L^2(M)\hookrightarrow E'}\). Assume also that \({E'}\) is separable. Let \({{\mathcal {L}}:L^2(0,T;E)\rightarrow {\mathbb {R}}}\) be a continuous linear form and let \({{\mathcal {E}}\subset C^1_0([0,T);E)}\) be such that \({\mathcal {E}}_0=\{\Phi \in {\mathcal {E}}\,:\, \Phi (0,\cdot )=0\}\) is dense in \({L^2(0,T;E)}\). Suppose that \({U\in L^2(0,T;E)}\) and \({U_0\in L^2(M)}\) satisfy, for all \({\Phi \in {\mathcal {E}}}\),
This relation shows that
is linear (equal to \({\mathcal {L}}\)) on \({\mathcal {E}}_0\), and continuous for the topology of \({L^2(0,T;E)}\). By density of \({{\mathcal {E}}_0}\) in this space, \({\Xi }\) can be extended into an element of \({(L^2(0,T;E))'=L^2(0,T;E')}\) (see [17, Theorem 1.4.1]). We denote this element by \({\partial _t U}\), as it clearly corresponds to the distributional derivative of U [17, Section 2.1.2]. By [17, Section 2.5.2] this shows that \({U:[0,T]\rightarrow L^2(M)}\) is continuous and, using [17, Proposition 2.5.2] to integrate by parts in (54), that \({U(0)=U_0}\) and
By density of \({{\mathcal {E}}}\) in \({L^2(0,T;E)}\), this relation actually holds for any \({\Phi \in L^2(0,T;E)}\).
We now consider the setting in the proof of Theorem 4.1 (see Section 4.3). Fixing \({M=M_f}\), \({\mathrm{d}\nu =\mathrm{d}\tau _f}\), \({E=V_f^0}\), \({{\mathcal {E}}=C^1([0,T];C^\infty _\Gamma )}\) and

and using (40) with  and
and  , for \({\alpha ,\beta =1,2}\) with \({\alpha \ne \beta }\), this identifies
, for \({\alpha ,\beta =1,2}\) with \({\alpha \ne \beta }\), this identifies  as an element of
as an element of  .
.
Let us now deal with a slightly more complicated case, in which the time derivatives of two functions need to be combined to exhibit a certain regularity. With the same M and E as above, take \({(N,\lambda )}\) a measured space and \({\gamma :E\rightarrow L^2(N)}\) a continuous linear mapping. Assume that \({U\in L^2(0,T;E)}\), \({V\in L^2(0,T;L^2(N))}\), \({U_0\in L^2(M)}\) and \({V_0\in L^2(N)}\), satisfy, for all \({\phi \in {\mathcal {E}}}\),
The same reasoning as above shows that
can be extended into a linear continuous form on \({L^2(0,T;E)}\). Letting \({\gamma ^*: L^2(N)\rightarrow E'}\) be the adjoint of \({\gamma }\) (that is, \({\langle g,\gamma (\Phi )\rangle _{L^2(N)}=\langle \gamma ^*g,\Phi \rangle _{E',E}}\) for all \({g\in L^2(N)}\) and \({\Phi \in E}\)), the form \({\widetilde{\Xi }}\) is naturally denoted by \({\partial _t U + \gamma ^* \partial _t V}\). Note that, in this sum, the two terms cannot be separated and it cannot, for example, be asserted that \({\partial _t U\in L^2(0,T;E')}\) and \({\gamma ^*\partial _t V\in L^2(0,T;E')}\). Then, a reasoning similar to the one in [17] shows that \({U+\gamma ^* V:[0,T]\rightarrow L^2(M)}\) is continuous with value \({U_0+\gamma ^*V_0}\) at \({t=0}\), and that, for all \({\Phi \in L^2(0,T;E)}\),
To write more natural equations, in the paper we sometimes make an abuse of notation and separate the two derivatives. We then write
where, in the right-hand side, the duality brackets do not have indices, to avoid claiming that \({\partial _t U\in L^2(0,T;E')}\) or \({\gamma ^*\partial _t V\in L^2(0,T;E')}\), and to remember that these two terms must be understood together.
Used in (40) with \({\gamma =\gamma _{\mathfrak {a}}}\) for all \({{\mathfrak {a}}\in \chi }\), the above reasoning and notations enable us to identify the (combined) time derivatives of  and
and  as an element of
as an element of  .
.
Rights and permissions
About this article
Cite this article
Droniou, J., Hennicker, J. & Masson, R. Numerical analysis of a two-phase flow discrete fracture matrix model. Numer. Math. 141, 21–62 (2019). https://doi.org/10.1007/s00211-018-0994-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-018-0994-y


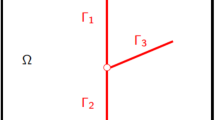

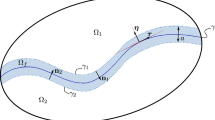


 . The upwinding takes into account the damaged rock type at the matrix-fracture interfaces. The arrows show the positive orientation of the normal fluxes
. The upwinding takes into account the damaged rock type at the matrix-fracture interfaces. The arrows show the positive orientation of the normal fluxes  and
and 
 and
and  ,
, ,
, is a Caratheodory function; for a.e.
is a Caratheodory function; for a.e.  is a non-decreasing Lipschitz continuous function on
is a non-decreasing Lipschitz continuous function on  is piecewise constant on a finite partition
is piecewise constant on a finite partition  of polytopal subsets of
of polytopal subsets of  , such that
, such that  is a Caratheodory function.
is a Caratheodory function. is a finite-dimensional space of degrees of freedom (DOFs),
is a finite-dimensional space of degrees of freedom (DOFs), ,
,  reconstructs a function on
reconstructs a function on  ,
,  reconstructs a gradient on
reconstructs a gradient on  reconstructs, from the DOFs, a jump on
reconstructs, from the DOFs, a jump on  reconstructs, from the DOFs, a trace on
reconstructs, from the DOFs, a trace on  a discretisation of the time interval [0, T],
a discretisation of the time interval [0, T], an operator designed to interpolate the initial condition.
an operator designed to interpolate the initial condition. as
as  , letting
, letting  we have, as
we have, as 
 ,
, 
 and
and  :
: 
 itself as a test function in the scheme (
itself as a test function in the scheme ( . The time derivative term form the discrete counterpart of
. The time derivative term form the discrete counterpart of  which, after integration in time, would yield an estimate on
which, after integration in time, would yield an estimate on  with
with  . To make explicit that this estimate is actually an estimate on the saturation, we re-write
. To make explicit that this estimate is actually an estimate on the saturation, we re-write  as
as  for a well-chosen
for a well-chosen  and, thanks to the modelling of the damaged rock type at the matrix-fracture interface (term
and, thanks to the modelling of the damaged rock type at the matrix-fracture interface (term  in (
in ( . These estimates are instrumental to obtain the compactness in time and space of all the saturations in the model.
. These estimates are instrumental to obtain the compactness in time and space of all the saturations in the model. , the main challenge in analysing this limit arises from the non-linear upwinding terms
, the main challenge in analysing this limit arises from the non-linear upwinding terms  . The limit of this term is obtained by using the monotony properties of this upwinding, a Minty trick, and the discrete energy estimate (
. The limit of this term is obtained by using the monotony properties of this upwinding, a Minty trick, and the discrete energy estimate (


