Public Transportation

Abstract

This chapter focuses on network design methodologies applied to problems arising at the strategic and tactical planning of public transportation systems, including both urban and intercity services. The main problems discussed are the design of bus, rail and metro networks, which involve making decisions over links or groups of links from a given underlying network. In general terms, the resulting network should take into account the interests of different stakeholders, namely, the ones who perceive the cost of traveling across the network and those who perceive the cost of building the infrastructure and operating the services over it. We present several mathematical formulations, including aspects like passenger behavior, multiple objectives and multiple levels of decisions. Then, we present an overview of solution approaches covering both exact and heuristic methods and considering several sub-problems like route generation, route selection and route set generation and improvement. Finally, bibliographical notes and conclusions are provided.

1 Introduction

Public Transportation (PT) refers to shared transportation services (Teodorovic and Janic 2016) which operate using infrastructure like roads or rails, and vehicles like buses or trains. Usually, it includes urban public transit and intercity public transportation, both characterized by fixed routes and schedules which are available for use by all persons who pay the established fare (Vuchic 2007). PT has been gaining importance since sustainability is increasingly identified as one of the primary goals of the society. When compared against other motorized transport modes, PT exhibits higher efficiency rates in terms of energy consumption, greenhouse emissions, noise pollution and usage of public space. However, both setting and operating of PT systems involve very large expenditures. Moreover, the performance of these systems from the viewpoint of the users is a key aspect in order to offer a successful service, which reveals the need for effective planning methodologies.

The planning of PT systems offers various opportunities for optimization. The whole process can be decomposed into several planning stages which define a sequence of hierarchical decisions, namely, network design, frequency and timetable determination, and fleet and crew scheduling (Ceder and Wilson 1986; Goosens et al. 2004). According to this approach, network design plays a very relevant role within the overall planning process since it impacts in every subsequent stage, and therefore in every component cost of the system. In that context, the meaning of the term public transport network depends on the specific mode. For systems based on buses which share the street with regular vehicles (i.e., cars) there is no cost of infrastructure building, or it can be negligible. On the other hand, rapid transit, rail and metro systems involve large investments due to building of exclusive corridors, railways and tunnels; we refer to these elements as the physical network. In addition, in PT systems there is a second network level which is defined by the services that operate over the street network for classical bus systems and over the physical network for rapid transit, rail and metro systems: the routes followed by the vehicles. This level is referred as the route network. The operation of these routes determines a relevant component of the operating cost of the system, in the form of vehicle and personnel cost per distance and time unit respectively. Also, both topological structure and frequency (vehicles passing per time unit) of the routes determine largely the level of service offered to the users in terms of overall travel time, which includes time spent walking (from origin and to destination stops or stations), waiting, and on-board the vehicle.

When approached as a network design problem, models of both physical and route networks represent stops and stations as network nodes, and street and rail sections as network links. Usually, the nodes are fixed and decisions are related to inclusion or exclusion of the links in the solution. In the most general case, each link has attributes like building cost, travel time and capacity. A first approach for PT network design is the general fixed charge network design model described in Chap. 2, where each commodity represents a specific group of people traveling from some origin node to another destination node. However, there are distinctive characteristics of PT systems which add particular difficulties. When modeling the design of routes, decisions are not related to single links, instead they refer to a sequence of links. Moreover, the system is composed by several routes which may overlap, i.e., they can share common links. Also, the performance evaluation of the system from the viewpoint of the users entails modeling their behavior with respect to the set of enabled links or routes. This is a very particular characteristic of PT network design models, since users behave by themselves and their interests can be conflicting with the interests of the operator, which entails considering special features in the corresponding network design models.

This chapter presents concepts, models and solution methods for PT network design. In order to precise the scope, we consider only models that include topological variables (Farahani et al. 2013), i.e., variables which represent decisions about nodes and links. However, we also consider models that include non-topological variables like frequency or vehicle size, when they represent decisions which are taken simultaneously with topological ones. These non-topological variables have great influence on PT network design, although they do not define directly its structure.

Regarding chapter organization, Sect. 2 states the main concepts and notation whereas Sect. 3 presents several models for PT network design including several problem aspects. Section 4 presents relevant solution methods, both for the models presented at Sect. 3 as for other models whose solution approaches exhibit key algorithmic concepts. Section 5 presents a compilation of the main bibliography in chronological order, whereas Sect. 6 offers perspectives for future research in the topic.

2 Background

2.1 Basic Concepts and Notation

The physical structure of PT systems suggests a direct network representation. The elements of the network have attributes which represent parameters of the users (people who use the services), the operators (companies or agencies which offer the services) and the whole society (typically related to infrastructure building).

Let $\mathcal {G}$ be a directed graph with corresponding set of nodes $\mathcal {N}$ which represents junctions, stops or stations and set of arcs $\mathcal {A}$ which represents sections of streets or rails between nodes. There are several ways to build the graph model $\mathcal {G}$ from real data; the international community has not agreed in a single standard one (Heyken Soares et al. 2019). Given that in many cases PT systems exhibit a symmetric pattern of services, we also consider an undirected variant of $\mathcal {G}$ with corresponding sets of vertices $\mathcal {V}$ and edges $\mathcal {E}$. An arc $a \in \mathcal {A}$ (edge $e \in \mathcal {E}$) can be identified by its corresponding ordered (unordered) pair of endpoint nodes (i, j) (vertices [i, j]). Also, for each arc $a \in \mathcal {A}$ we define user cost $c^u_a \geq 0$ which represents the cost (usually travel time) experienced by the user when traversing a, and operator cost $c^o_a \geq 0$ which represents the cost incurred by the operator due to offering a service which traverses a (usually travel time or distance). Undirected versions of both user and operator cost are defined for edges $e \in \mathcal {E}$, namely, $c^u_e$ and $c^o_e$ respectively. In general terms, each arc a ∈ A has capacity u _a ≥ 0 which states the maximum flow that can traverse a per time unit. The entities which flow over arcs can be either persons (mostly referred as users or passengers) or vehicles (buses, trains), depending on the specific context. Thus, if an arc represents a physical element (street or rail section), the flow is measured in terms of vehicles and its magnitude is directly proportional to the frequencies of the services which operate over the arc. On the other hand, if an arc represents a route section, the flow is measured in terms of passengers and its magnitude is directly proportional to the demand attracted by the route, i.e., the passengers traveling on-board the vehicles operating the route. The passenger demand for PT is modeled as a set of commodities $\mathcal {K}$. Each element $k \in \mathcal {K}$ has origin and destination nodes O(k) and D(k), respectively, and demand (passengers per time unit in a given time horizon) d _k > 0 between ${O(k)}\in \mathcal {N}$ and ${D(k)}\in \mathcal {N}$. In the context of PT systems, $\mathcal {K}$ defines an origin-destination (OD) matrix and each element $k \in \mathcal {K}$ is called OD pair. These commodities share the same network, therefore, when applicable, they are collectively constrained by arc capacities. The demand corresponding to OD pair $k \in \mathcal {K}$ is said to be covered if O(k) and D(k) are connected by the PT network, independent on its capacity. Moreover, if the network capacity allows flowing the whole amount d _k, the demand is also said to be satisfied.

A PT route is defined as a sequence of adjacent nodes or vertices in $\mathcal {G}$ and it has a cyclic pattern. When defined in terms of undirected edges, it is assumed that it operates in both directions. On the other hand, directed routes should be defined as cycles in $\mathcal {G}$. Let $\mathcal {R}$ be the set of all routes in $\mathcal {G}$ according to this definition. In the most general case, a route stops at every node where it passes. Therefore, passengers can access the corresponding service (either to board or to alight) in all those nodes. Each route $r \in \mathcal {R}$ has frequency f _r ≥ 0 which expresses the number of vehicles per time unit operating the route. The special case f _r = 0 is sometimes used to state that route r is disabled. A route with its frequency is sometimes referred as a line.

The operation cost of routes depends on both distance and time. Assuming a constant average speed, the distance component of the variable cost of a route $r \in \mathcal {R}$ is proportional to its cycle time $\sum _{a \in r} c^o_a$. Moreover, the time component is proportional to its frequency f _r. A combined measure of the variable cost can be defined as $f_r \sum _{a \in r} c^o_a$, which stands for the number of vehicles that operate simultaneously in r. In the most general case, this measure is taken as a proxy for operation cost.

Regarding user cost, the PT network determines one of its main attributes: travel time. For OD pair $k \in \mathcal {K}$, it is assumed without loss of generality that users travel along the shortest path defined by the enabled arcs, which can be formulated as

$$\displaystyle \begin{aligned} \mbox{Minimize} \ \ \sum_{a \in \mathcal{A}} c_a^u {x_{a}} \end{aligned} $$

(17.1)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mbox{Subject to} \ \ & \sum_{a \in \mathcal{A}^+_n} {x_{a}} - \sum_{a \in \mathcal{A}^-_n} {x_{a}} = w_{nk}, &\displaystyle \ \forall \, n \in \mathcal{N}, {} \end{array} \end{aligned} $$

(17.2)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & 0 \leq {x_{a}} \leq {u_{a}} , &\displaystyle \ \forall \, a \in \mathcal{A} , {} \end{array} \end{aligned} $$

(17.3)

where sets $\mathcal {A}^+_n \subseteq \mathcal {A}$ and $\mathcal {A}^-_n \subseteq \mathcal {A}$ denote outgoing and incoming arcs respectively of node $n \in \mathcal {N}$ and w _nk is equal to d _k if n = O(k), − d _k if n = D(k) and 0 otherwise.

Formulation (17.1)–(17.3) denotes a minimum cost flow problem (Ahuja et al. 1993), where decision variable x _a represents the flow of passengers over arc a. Moreover, the value u _a defines a capacity constraint for arc $a \in \mathcal {A}$. Thus, if a is enabled because its corresponding physical link is built and there is a line which operates over it, a sufficiently large value of u _a will allow the entire demand d _k to flow over a. This is the case in which all passengers follow the same (shortest) path from O(k) to D(k). But if u _a values are not large enough, some passengers are forced to take other paths with larger cost due to insufficient capacity in the shortest path, which gives rise to a capacitated user equilibrium with constant arc cost (Correa et al. 2004). This is a variation of the classical equilibrium in private car networks where the cost of each arc depends on its flow, therefore all different paths followed by the demand corresponding to the same OD pair have the same cost (Sheffi 1985). Typically, arc capacities in PT networks are defined by the capacity of the infrastructure (allowable speed, number of lanes) and the services (route frequency and vehicle capacity). In PT network design models, these elements can be either fixed parameters as well as decision variables. In any case, let $P_k \in \mathcal {A}$ ($\mathcal {E}$ in the undirected version) denote the set of arcs (edges) with flow greater than zero in the optimal solution of (17.1)–(17.3). If capacities allow the whole demand d _k to flow over the same path, then P _k denotes the shortest path between O(k) and D(k). Otherwise, it denotes the set of arcs corresponding to all the paths followed by the demand. Any of these paths can represent either direct trips (using a single line) or trips with transfers (using two or more lines), depending on the modeling of the network and the hypothesis assumed regarding passenger behavior.

So far, formulation (17.1)–(17.3) represents reasonably the passenger behavior taking into account only the on-board travel time. Walking time can also be modeled using this formulation, by including specific nodes that represent trip origins and destinations (e.g., nodes representing geographical zones) and walking arcs connecting these nodes with the stops and stations. However, in some cases the waiting time should also be considered, either as an attribute for shortest path calculations or as a parameter for evaluating system performance. The waiting time at the stop is non-linearly related to the frequency of the line or set of lines which lead to destination. This phenomenon entails more complex formulations. Moreover, the effect of capacity over the waiting time and the flow distribution on lines leads to even more complex formulations with respect to passenger behavior.

2.2 Problem Nomenclature, General Formulation and Solution Approach for Public Transportation Network Design

Public transportation network design involves managing several levels of networks. In this context, we denote as PND (Physical Network Design) the problem of designing the physical network, i.e., decisions related to building dedicated bus lanes, rail or metro lines. Moreover, we denote as RND (Route Network Design) the problem of designing the routes over an existing physical network. This may comprise the design of a single route with a particular goal or the design of a complete set of routes to satisfy the whole demand of a given scenario.

In order to formulate a general optimization model for public transportation network design, firstly we can identify topological and non-topological decision variables (Farahani et al. 2013), namely, X ^t and X ⁿ respectively. In the first group there are decisions related to nodes and arcs of $\mathcal {G}$, e.g., station location, rail building or route structure. Relevant non-topological decision variables include route frequency and vehicle capacity. Moreover, in PT network design models we need variables that represent the behavior of passengers, namely, X ^b. These variables are not controlled directly by the planner, however, they depend on his decisions regarding infrastructure building and service provision. For that reason, usually they are modeled explicitly since they determine a relevant component of system performance.

The objective function expresses the goal of the planner, which may take several forms. It can be either a direct formulation of the interests of both users and operators, or it can represent a more general system goal. Very often, the planner is forced to manage opposite interests. For instance, a high number of routes with high frequencies contribute to increase the level of service from the viewpoint of the user, but it causes high operation costs as well, which might not be sustainable in the economic sense. This leads to consider multiobjective formulations (Ehrgott 2005).

The modeling of passenger behavior entails considering a hierarchical process where the planner makes a decision (e.g., regarding routes) and the passengers choose their routing over those services, producing flow values which are necessary for the planner in order to fully compute its measure of system performance. Despite the fact that this hierarchical process in some cases can be modeled properly as a standard optimization problem, its most general formulation entails a multiple-level (more specifically, two-level or bilevel) formulation (Bard 1998).

Finally, the constraints can be of several types, ranging from criteria of the planners (which may include performance indicators of users, operators and the overall system) to physical constraints regarding route structure, infrastructure and vehicle capacity. Budgetary constraints imposed over infrastructure building and service operation are often included as well.

A generic formulation for the public transportation network design problem can be defined as (17.4)–(17.7). For m > 1 the objective function is a vector which represents several goals which should be taken into account simultaneously. Constraint (17.5) may take standard forms like equalities or inequalities. Constraint (17.6) states that passenger behavior variables X ^b should take the optimal value of an additional optimization problem, where $\bar {X}^b$ are decision variables and H states the criterion of the users for traveling over the network set by the planner through fixed values X ^t and X ⁿ, constrained by function Z. An example of this second level optimization problem is the shortest path routing stated by (17.1)–(17.3).

$$\displaystyle \begin{aligned} \mbox{Minimize} \ \ [F_1(X^t,X^n,X^b), \ldots F_m(X^t,X^n,X^b)] \end{aligned} $$

(17.4)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mbox{Subject to} \ \ & G(X^t,X^n,X^b) \leq 0, {} \end{array} \end{aligned} $$

(17.5)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & X^b = \mbox{argmin} \ \ H(X^t,X^n,\bar{X}^b), {} \end{array} \end{aligned} $$

(17.6)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & \mbox{Subject to} \ \ Z(X^t,X^n,\bar{X}^b) \leq 0. {} \end{array} \end{aligned} $$

(17.7)

Both PND and RND addressed as optimization problems, exhibit several sources of complexity. The underlying network design problem already has a combinatorial structure which entails high computational complexity (Johnson et al. 1978). The feasible space of topological variables of RND is huge, given the size of the set $\mathcal {R}$ of all possible routes. Passenger behavior sub-models usually included as the second level problem in (17.4)–(17.7) add complexity to the overall formulation, especially when the more complex variants of (17.1)–(17.3) are considered. The multiobjective and multilevel structure poses the need for specific resolution methods, which can be either exact or heuristic. In general terms, exact methods always rely over an explicit mathematical programming formulation. Conversely, these formulations are often used to implement heuristic methods instead of exact ones. The RND problem is approached by two different strategies in order to determine the values of topological variables X ^t: (1) generating a pool of many good candidate routes (which we call route generation) and then selecting the optimal subset (route selection) and (2) generating a set of routes which constitutes a feasible solution, which may be improved in a further stage (route set generation and improvement). Moreover, heuristic and metaheuristic methods for RND often decouple the sub-problems of determining the optimal values for non-topological variables X ⁿ and passenger behavior variables X ^b. The resolution of these sub-problems are coded into specific sub-routines which are called appropriately during the overall optimization process.

3 Models for Public Transportation Network Optimization

In this section we present several models for both PND and RND problems. The passenger behavior appears explicitly on RND, since a full characterization of the public transportation services (lines) is modeled. For that reason Sects. 3.1–3.4 focus on RND, assuming a physical network already established. The models presented apply to different PT modes, which share common elements in the context of strategic and tactical planning, namely, networks, lines, passengers, vehicles, capacities and budgetary constraints. Differences among the general hypotheses assumed in the models presented, are mainly due to the specific transport mode under discussion. Thus, in models for intercity railway line planning (Sect. 3.1), the underlying network is sparse and the passengers are assumed to schedule their arrival to the station according to the timetable. In models for bus line planning (Sect. 3.2) the underlying network (streets) is assumed to be dense. In bus based systems including services with different characteristics regarding frequency and regularity, the modeling of waiting time is relevant (Sect. 3.3). Whenever line capacity comes into play (Sect. 3.4), the services should be designed taking into account the reaction of the users. The issue of transfers between lines appears in almost every medium to large sized scenario. Transfers have a great impact on both users (perceived level of service) and operators (number of lines, which influences operations cost), and its modeling is not straightforward.

Table 17.1 provides a list of main symbols used in this section. Moreover, the nonnegative real variable x is used to denote flow, either over arcs a, routes r and paths p, also indexed by commodity k. Similarly, the binary variable y is used to denote the decision of including a route r or line l into the solution.

Table 17.1 Definitions of main symbols

3.1 User and Operator Oriented Models with Fixed Passenger Behavior

In railway systems it is reasonable to assume that services will be provided along shortest paths from passenger viewpoint over the physical network. This allows introducing the system-split hypothesis, which states that passengers always travel along shortest paths in $\mathcal {G}$ (with respect to cost $c_a^u$) independently of the routes. Consequently, the passenger behavior can be fixed, thus simplifying the models by solving a priori problem (17.1)–(17.3) for each commodity $k \in \mathcal {K}$ and loading the corresponding flows over the network links.

Model (17.8)–(17.13) selects an optimal subset of routes with their corresponding frequencies, from a given pool $\mathcal {R}_0 \subseteq \mathcal {R}$ of routes defined over the physical network (Bussieck et al. 1997). The model adopts the undirected versions of both $\mathcal {G}$ and $\mathcal {R}$, and takes into account demand data given as an OD matrix. The system performance is represented by the amount of direct demand satisfied, denoted by x _rk for route $r \in \mathcal {R}_0$ and OD pair $k \in \mathcal {K}$.

Constraint (17.9) bounds the passenger flow (thus preventing infinite values) by the demand of each OD pair, while constraint (17.10) links passenger flow with the capacity of each route r, which is defined as the product of the train capacity C and the route frequency f _r. Finally, constraint (17.11) states that the sum of the frequencies of all routes passing by edge e must be equal to the load of that edge (t _e, resulting from the fixed system-split flows computed a priori) divided by the train capacity. This last constraint prevents unnecessary high frequencies by setting values which ensure route capacity. The routes included in the solution are those r such that f _r > 0.

$$\displaystyle \begin{aligned} \mbox{Maximize} \ \ \sum_{r \in \mathcal{R}_0} \sum_{k \in \mathcal{K} , P_k \subseteq r} x_{rk} \end{aligned} $$

(17.8)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mbox{Subject to} \ \ & \sum_{r \in \mathcal{R}_0, P_k \subseteq r} x_{rk} \leq d_k, &\displaystyle \ \forall \, k \in \mathcal{K}, {} \end{array} \end{aligned} $$

(17.9)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & \sum_{k \in \mathcal{K}, e \in P_k \subseteq r} x_{rk} \leq C f_r, &\displaystyle \ \forall \, e \in \mathcal{E}, \, r \in \mathcal{R}_0, {} \end{array} \end{aligned} $$

(17.10)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & \sum_{r \in \mathcal{R}_0, e \in r} f_r = \ulcorner t_e / C \urcorner, &\displaystyle \ \forall \, e \in \mathcal{E}, {} \end{array} \end{aligned} $$

(17.11)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & x_{rk} \geq 0, &\displaystyle \ \forall \, r \in \mathcal{R}_0, \, k \in \mathcal{K}, {} \end{array} \end{aligned} $$

(17.12)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & f_r \in \mathbb{Z}_+, &\displaystyle \ \forall \, r \in \mathcal{R}_0. {} \end{array} \end{aligned} $$

(17.13)

Note that depending on the routes included in the pool $\mathcal {R}_0$, the whole demand $d_k, \forall k \in \mathcal {K}$ will be satisfied (either directly or indirectly) or not. If for each $k \in \mathcal {K}$, the pool $\mathcal {R}_0$ includes at least one route comprising both O(k) and D(k), the whole demand is likely to be satisfied directly. This kind of solution does not take into account explicitly the interest of the operator, since there is not an explicit upper bound on the number of lines. For this reason, formulation (17.8)–(17.13) is referred as user oriented.

On the other hand, operator oriented models usually seek to minimize operation costs (Goosens et al. 2004). We use the concept of line to define set $\hat {\mathcal {R}}_0 = \mathcal {R}_0 \times \mathcal {F} \times \mathcal {S}$, where $\mathcal {F} \subset \mathbb {Z}_+$ denotes possible values of frequencies and $\mathcal {S} \subset \mathbb {Z}_+$ denotes possible values for number of carriages, both corresponding to each route $r \in \mathcal {R}_0$. Each element $l \in \hat {\mathcal {R}}_0$ has route r _l, frequency f _l and number of carriages s _l. Model (17.14)–(17.18) also assumes an a priori system-split loading of OD flows to each edge e of the network, which determines the required frequency f _e and number of carriages s _e. Parameter k _l states the line cost (including fixed and variable components per train and carriage), while y _l is a binary decision variable which states whether or not to include line $l \in \hat {\mathcal {R}}_0$ in the solution.

$$\displaystyle \begin{aligned} \mbox{Minimize} \ \ \sum_{l \in \hat{\mathcal{R}}_0} k_l y_l \end{aligned} $$

(17.14)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mbox{Subject to} \ \ & \sum_{l \in \hat{\mathcal{R}}_0(e)} f_l y_l \geq f_e, &\displaystyle \ \forall \, e \in \mathcal{E}, {} \end{array} \end{aligned} $$

(17.15)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & \sum_{l \in \hat{\mathcal{R}}_0(e)} f_l s_l y_l \geq c_e, &\displaystyle \ \forall \, e \in \mathcal{E}, {} \end{array} \end{aligned} $$

(17.16)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & \sum_{l \in \mathcal{R}_0, r_l=r} y_l \leq 1, &\displaystyle \ \forall \, r \in \mathcal{R}_0, {} \end{array} \end{aligned} $$

(17.17)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & y_l \in \{0,1\}, &\displaystyle \ \forall \, l \in \hat{\mathcal{R}}_0. {} \end{array} \end{aligned} $$

(17.18)

Constraints (17.15) and (17.16) ensure capacity fulfillment by setting appropriate values of frequency and number of carriages, where $\hat {\mathcal {R}}_0(e) = \{l \in \hat {\mathcal {R}}_0 / e \in r_l\}$. Constraint (17.17) ensures that for each route $r \in \mathcal {R}_0$, at most one line from $\hat {\mathcal {R}}_0$ is selected.

Note that formulation (17.14)–(17.18) minimizes operation costs, while passengers’ interest is taken into account by the system-split hypothesis and the constraints which ensure sufficient capacities in the selected lines.

3.2 Explicit Modeling of Passenger Behavior

If the physical network is dense, there are many possibilities for defining routes. This is the case of bus based systems, where the physical network is defined in terms of the streets. In this scenario, the system-split approach is not a reasonable assumption. Therefore, since the demand flows cannot be fixed a priori, the passenger behavior is represented explicitly by means of specific decision variables (Borndörfer et al. 2007). For route $r \in \mathcal {R}$, let y _r be a binary (topological) variable which states whether or not r is included in the solution and let f _r be a real (non-topological) variable which represents its frequency. While routes are defined over the undirected version of $\mathcal {G}$, passenger paths are defined over its directed counterpart. Let $\mathcal {P}$ be the set of all directed passenger paths in $\mathcal {G}$ and let $\mathcal {P}(k) \subseteq \mathcal {P}$ be the set of paths from O(k) to D(k). The path-based formulation is defined by (17.19)–(17.25), where the behavioral variable x _p stands for the amount of flow over path p.

$$\displaystyle \begin{aligned} \mbox{Minimize} \ \ \sum_{p \in \mathcal{P}} \sum_{a \in p} c_a^u x_{p} + \sum_{r \in \mathcal{R}} \left( k_r^f y_r + k_r^v f_r \right) \end{aligned} $$

(17.19)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mbox{Subject to} \ \ & \sum_{p \in \mathcal{P}(k)} x_{p} = d_k, &\displaystyle \ \forall \, k \in \mathcal{K}, {} \end{array} \end{aligned} $$

(17.20)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & \sum_{p \in \mathcal{P}/a \in p} x_{p} \leq \sum_{r \in \mathcal{R}/a \in r} C_r^p f_r, &\displaystyle \ \forall \, a \in \mathcal{A}, {} \end{array} \end{aligned} $$

(17.21)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & \sum_{r \in \mathcal{R}(e)} f_r \leq C_e^v, &\displaystyle \ \forall \, e \in \mathcal{E}, {} \end{array} \end{aligned} $$

(17.22)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & f_r \leq F y_r, &\displaystyle \ \forall \, r \in \mathcal{R}, {} \end{array} \end{aligned} $$

(17.23)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & y_r \in \{0,1\}, f_r \geq 0, &\displaystyle \ \forall \, r \in \mathcal{R}, {} \end{array} \end{aligned} $$

(17.24)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & x_{p} \geq 0, &\displaystyle \ \forall \, p \in \mathcal{P}.{} \end{array} \end{aligned} $$

(17.25)

Unlike the models presented in Sect. 3.1, objective function (17.19) represents simultaneously the interest of both users and operators. The first term accounts for total travel time of users while the second one groups both fixed and variable operator cost, using parameters $k_r^f$ and $k_r^v$ respectively for route $r \in \mathcal {R}$. Constraint (17.20) imposes flow conservation for passenger demand over paths. Line capacity is ensured by constraint (17.21), where parameter $C_r^p$ stands for the number of places in vehicles performing route r. Similarly, constraint (17.22) ensures that lines passing by edge e (street section) do not surpass collectively its capacity (measured in terms of vehicles per time unit), stated by parameter $C_e^v$. Finally, constraint (17.23) states that the frequency of route r can be greater than zero only if r is part of the solution, where F is a parameter whose value should be sufficiently high.

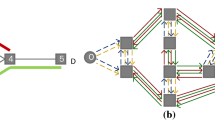
Formulation (17.19)–(17.25) denotes a multicommodity flow problem with capacities imposed to both route frequencies and passenger flows. The first term of the objective function ensures that passengers follow the shortest path over the network resulting from the enabled routes. Moreover, two issues are worth to be mentioned. First, due to constraint (17.21), the flow of a given OD pair $k \in \mathcal {K}$ may be split into several paths with different cost due to insufficient capacity on the shortest path (capacitated user equilibrium). Second, transfers between lines are ignored, since the flow over a specific path is enabled by constraint (17.21) if each of its arcs belongs to at least one route enabled by constraint (17.23). This means that in the optimal solution, passengers may be forced to perform an arbitrary number of transfers between routes. The first issue is further discussed in Sect. 3.4 while the second one may be approached by using the expanded network $\hat {\mathcal {G}}(\mathcal {R}_0)$ shown in Fig. 17.1, where each node of $\mathcal {G}$ is replicated for each $r \in \mathcal {R}_0 \subseteq \mathcal {R}$. Each arc is also replicated for each route, which allows to model different costs for different lines passing by the same arc. Transfer arcs are added to connect nodes which represent the same stop or station for different lines. Finally, boarding and alighting arcs are added to connect origins and destinations with stops or stations. By using this expanded network, transfers between routes can be weighted and counted in the optimization models.

Fig. 17.1

Expanded network comprising two routes passing by two common stations

3.3 Including Waiting Time

In public transportation systems, waiting time is recognized as one of the most onerous components of the user total travel time. In some cases, ignoring waiting time in the modeling may be justified reasonably. For instance, users of intercity services with low frequency can schedule their arrivals to the stop or station, assuming that timetable information is available and reliable. Moreover, users of metro or rapid transit systems may experience low waiting time due to availability of high frequency services. However, in other systems like most of bus based ones, modeling of waiting time is relevant in order to state a realistic scenario.

To do that, an expanded network as shown in Fig. 17.1 (without transfer arcs) is used (Cancela et al. 2015), where $\mathcal {A}^b \subset \mathcal {A}$ denotes the set of boarding arcs.

Over this network, we can formulate the problem of selecting the optimal subset of routes from a provided pool $\mathcal {R}_0$ and setting the frequency for each selected route, taken from a discrete set of values $\mathcal {F}=\{F_1,\ldots F_m\}$ indexed by q. This discretization of frequencies is introduced to obtain a linear formulation. Each element of $\mathcal {F}$ (therefore, each possible value of frequency) has its own boarding arc in the network. Let y _r be a binary topological variable which expresses whether route $r \in \mathcal {R}_0$ is selected and f _rq be a non-topological binary variable which states that frequency F _q is assigned to route r. Moreover, let x _ak be the amount of demand corresponding to OD pair k which flows over arc a and let z _nk be the waiting time multiplied by the flow of OD pair k at node n (both x and z are behavioral variables). The maximum number of available vehicles is denoted by parameter B.

$$\displaystyle \begin{aligned} \mbox{Minimize} \ \ \sum_{k \in \mathcal{K}} \left( \sum_{a \in \mathcal{A}} c_a^u x_{ak} + \sum_{n \in \mathcal{N}} z_{nk} \right) \end{aligned} $$

(17.26)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mbox{Subject to} \ \ & \sum_{r \in \mathcal{R}_0} 2 \sum_{q \in \mathcal{F}} F_q f_{rq} \sum_{e \in r} c^o_e \leq B, &\displaystyle \ \forall \, k \in \mathcal{K}, {} \end{array} \end{aligned} $$

(17.27)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & \sum_{a \in \mathcal{A}^+_n} x_{ak} - \sum_{a \in \mathcal{A}^-_n} x_{ak} = w_{nk}, &\displaystyle \ \forall \, n \in \mathcal{N}, \, k \in \mathcal{K}, {} \end{array} \end{aligned} $$

(17.28)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & x_{ak} \leq \mathcal{F}(a) z_{nk}, &\displaystyle \ \forall \, a \in \mathcal{A}^{b+}, \, n \in \mathcal{N}, \, k \in \mathcal{K}, {}\qquad \qquad \end{array} \end{aligned} $$

(17.29)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & x_{ak} \leq d_k y_{\mathcal{R}_0(a)}, &\displaystyle \ \forall \, a \in \mathcal{A}, \, k \in \mathcal{K}, {} \end{array} \end{aligned} $$

(17.30)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & x_{ak} \leq d_k f_{\mathcal{R}_0(a)\mathcal{F}(a)}, &\displaystyle \ \forall \, a \in \mathcal{A}^b, \, k \in \mathcal{K}, {} \end{array} \end{aligned} $$

(17.31)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & \sum_{q \in \mathcal{F}} f_{rq} = y_r &\displaystyle \ \forall \, r \in \mathcal{R}_0, {} \end{array} \end{aligned} $$

(17.32)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & x_{ak} \geq 0, &\displaystyle \ \forall \, a \in \mathcal{A}, \, k \in \mathcal{K}, {} \end{array} \end{aligned} $$

(17.33)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & z_{nk} \geq 0, &\displaystyle \ \forall \, n \in \mathcal{N}, \, k \in \mathcal{K}, {} \end{array} \end{aligned} $$

(17.34)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & y_r \in \{0,1\}, &\displaystyle \ \forall \, r \in \mathcal{R}_0, {} \end{array} \end{aligned} $$

(17.35)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & f_{rq} \in \{0,1\}, &\displaystyle \ \forall \, r \in \mathcal{R}_0, \, q \in \mathcal{F}.{} \end{array} \end{aligned} $$

(17.36)

Formulation (17.26)–(17.36) minimizes user total travel time, including on-board and waiting components. Constraint (17.27) imposes a limit on the number of vehicles used, thus representing the interest of the operator, while constraint (17.28) is a typical flow conservation condition. Activation constraint (17.30) states that demand can flow only over arcs of enabled routes, while a similar activation constraint (17.31) states that demand can flow only over arcs corresponding to the frequency assigned to each route. In these expressions, $\mathcal {R}_0(a)$ and $\mathcal {F}(a)$ denote the route from $\mathcal {R}_0$ and the frequency of $\mathcal {F}$ respectively, corresponding to arc $a \in \mathcal {A}$. Constraint (17.32) states that only one value of frequency from $\mathcal {F}$ can be assigned to each route. Finally, constraint (17.29) models the fact that passengers corresponding to OD pair k waiting at node n are distributed among the set of most convenient lines (in the sense of overall expected travel time) that lead to their destination. For fixed values of variables y and f, the result corresponds to the optimal strategies passenger behavior model (Spiess and Florian 1989). That model assumes that: (1) users seek to minimize the expected total travel time along the network, (2) the waiting time is inversely proportional to the sum of the frequencies of lines which lead to destination, and (3) the distribution of demand among these lines is proportional to their frequencies. A direct formulation of these assumptions followed by a series of algebraic transformations (Spiess and Florian 1989) allow to observe that the formulation of this passenger behavior model corresponds to a variation of the shortest path problem (17.1)–(17.3), where the waiting time term is added in the objective function and the flow-splitting constraint (17.29) distributes the demand flow among different routes passing by the same stop.

3.4 Multiple Objectives and Levels of Decisions

The models presented in previous sections consider decisions of different stakeholders within a single formulation having a standard structure. In some cases this can be a reasonable modeling approach, however, there are situations where a more structured formulation is needed in order to model properly particular characteristics of the problem, namely:

• Different stakeholders may have conflicting objectives, therefore it is impossible to arrive to the best solution from a single point of view. In public transportation systems we can observe this interplay between users and operators, which reveals the multiobjective nature of the problem (Ehrgott 2005). The models presented in Sect. 3.1 are biased by definition towards some of these specific objectives. The models of Sects. 3.2 and 3.3 formulate implicitly multiobjective problems and allow for exploring different compromise solutions by weighting and constraining objectives.

• Some stakeholders may require to know the reaction of subordinate ones, in order to fully determine their decisions. Since most public transportation network design models are conceived to support decisions of the planners, the way in which passengers use the routes should be modeled in order to know its consequence over the system performance. This modeling requires considering different levels of decisions, where there is a leader (the planner) who restrains decisions of a follower (the passengers), in order to arrive to an optimal solution for the whole system. This characteristic of many passenger transportation problems entails formulating a two-level (bilevel) optimization problem (Bard 1998). The models presented in Sects. 3.2 and 3.3 include variables which represent decisions of the planner (y and f) and the passengers (x and z), which are pushed jointly towards the same direction by the objective functions and constraints.

Model (17.37)–(17.43) optimizes simultaneously the objectives of users and operators while ensuring sufficient capacity in the lines that passengers decide to use (Goerigk and Schmidt 2017). Lines are taken from a provided set $\mathcal {R}_0$. Let $C^o_r$ be the operation cost (e.g., length) of route $r \in \mathcal {R}_0$ and $C \in \mathbb {N}$ be the capacity of vehicles, expressed in number of passengers. The remaining symbols are defined as in previous sections.

The existence of two objective functions implies that the optimal solution is the set of all efficient (or Pareto optimal) solutions, instead of a single optimal solution. That set represents the whole range of optimal trade-off levels (in terms of routes and frequencies) between both objectives of vector (17.37). The lower-level problem (17.40)–(17.43) states that passengers move along the shortest path defined by the routes enabled by the upper-level, i.e., those with f _r > 0. Equation (17.40) states that variable x _ak of the upper-level must take optimal values from its lower-level counterpart $\bar {x}_{ak}$. Constraint (17.38) determines frequencies in order to allow passengers moving along shortest paths with sufficient capacity. This means that passengers perceive unlimited capacity in routes, therefore, for each OD pair $k \in \mathcal {K}$ the demand d _k is not split. Note that by eliminating objective (17.40) and moving constraints (17.41)–(17.43) to the upper-level, we would obtain a (single level) relaxation of the original problem where the routing of passengers follows a capacitated user equilibrium.

$$\displaystyle \begin{aligned} \mbox{Minimize} \ \ [\sum_{k \in \mathcal{K}} \sum_{a \in \mathcal{A}} c_a^u x_{ak}, \sum_{r \in \mathcal{R}_0} f_r C^o_r] \end{aligned} $$

(17.37)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mbox{Subject to} \ \ & \sum_{k \in \mathcal{K}} x_{ak} \leq f_{\mathcal{R}_0(a)} C, &\displaystyle \ \forall \, a \in \mathcal{A}, {} \end{array} \end{aligned} $$

(17.38)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & f_r \in \mathbb{N}, &\displaystyle \ \forall \, r \in \mathcal{R}_0, {} \end{array} \end{aligned} $$

(17.39)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & x_{ak} \in \mbox{argmin} \ \ \sum_{a \in \mathcal{A}} c_a^u \bar{x}_{ak}, {} \end{array} \end{aligned} $$

(17.40)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & \mbox{Subject to} \ \ \sum_{a \in \mathcal{A}^+_n} \bar{x}_{ak} - \sum_{a \in \mathcal{A}^-_n} \bar{x}_{ak} = w_{nk}, &\displaystyle \ \forall \, n \in \mathcal{N}, \, k \in \mathcal{K}, {} \end{array} \end{aligned} $$

(17.41)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & \bar{x}_{ak} \leq d_k f_{\mathcal{R}_0(a)}, &\displaystyle \ \forall \, a \in \mathcal{A}, \, k \in \mathcal{K}, {} \end{array} \end{aligned} $$

(17.42)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & \bar{x}_{ak} \in \mathbb{N}, &\displaystyle \ \forall \, a \in \mathcal{A}, \, k \in \mathcal{K}. {} \end{array} \end{aligned} $$

(17.43)

3.5 Other Relevant Models

The problem of route design in bus rapid transit systems exhibits particular characteristics. First, routes are defined over predefined corridors with linear structure, unlike the mesh-like structure of the street network used by regular bus based systems. Moreover, for a given corridor comprising n stations or stops, the number of possible routes is 2ⁿ since limited-stop services are under consideration in order to reduce travel time. Thus, several parallel routes can be defined over the same corridor, each of them having a different set of stops. To model this feature, an expanded network similar to the one shown in Fig. 17.1 can be used, where each station is replicated for each route (Walteros et al. 2015). Both on-board (travel) and walking arcs are considered, including arcs which model access to the stations, walking inside the stations and changing of routes at the same station. Whenever a route skips a station, the travel time between its previous and next stations must fulfil the triangular inequality, thus modeling the fact that there is no delay due to skipping intermediate stations. The domain of topological variables is defined by all possible routes over all corridors. Typical constraints include arc capacity given by the capacity of the stations and the lines. Also, frequencies can be included as decision variables, which are bounded by a total number of available vehicles (Schmid 2014).

The PND problem involves decisions regarding infrastructure building of metro and rapid transit systems, namely, the construction of stations and tracks or corridors. Even though decisions regarding routes is not a primary concern in the context of this problem, they are taken into account due to their relevance regarding system performance. A typical way of addressing this problem is to choose a small number of routes, maximizing the coverage of a given demand between a set of fixed points, subject to a maximum available construction budget (Laporte et al. 2007). The binary variables s _rv and y _re state whether route r uses station $v \in \mathcal {V}$ and edge $e \in \mathcal {E}$ respectively. The passenger behavior is modeled with binary variables z _k and x _ek which state whether OD pair $k \in \mathcal {K}$ uses the public transportation network and whether it employs edge $e \in \mathcal {E}$ from that network, respectively. The formulation aims at the maximization of trips attracted to the public network, where the demand is split according to parameters which express the user cost of traversing each edge by using the public mode or the private one (typically, the car mode). An extension to this model considers the incremental building of the network across a set $\mathcal {T}$ of given periods (Marín and Jaramillo 2008). In this context, some problem data depend on the specific period $t \in \mathcal {T}$, namely, the OD matrix, construction costs, available budget and user cost within the public network. Clearly, in order to support multistage long-term planning, the dimensionality of the model is increased.

A different modeling approach for incremental building of the physical network proposes the design of single routes, which can be used as building block for obtaining a complete system made by different routes (Dufourd et al. 1996). In this case, decisions are the location of a single route, while maximizing population coverage under constraints of number of stations and inter-station spacing. A route is defined as a sequence of potential stations $s \in \mathcal {S}$ taken from a grid which represents a discretization of the study region. Each potential station s has coordinates in the Euclidean space, which are used to estimate its population catchment based in concentric geometrical shapes and the distance between the station and squares of the grid which intersect with the shape. This is a variation of covering-path like problems, which results in a non-linear integer mathematical program. Moreover, variations of this model consider the coverage of origin-destination trips instead of the maximization of population catchment (Laporte et al. 2005). This is done by replacing the original objective function by an expression which relates coverage areas of pairs of stations. Furthermore, this value is multiplied by a logit factor in order to determine the share of demand that is attracted by the public network, which is assumed to compete against a private mode. Construction costs are represented in these models by constraints on maximum route length and number of stations.

4 Solution Approaches

In this section, we present an overview of solution methods for public transportation network design problems, either related to models of Sect. 3 or to other ones which exhibit relevant algorithmic ideas. In a first level, methods are classified into mathematical programming and heuristic based ones, depending on whether they are based on an explicit mathematical formulation.

4.1 Mathematical Programming Based Methods

Several problems related to PT network design are formulated as mathematical programs, usually mixed integer linear ones (MILP). In most cases, small problem instances can be solved by using commercial MILP software developed by third parties. However, for larger instances some solution methods involve specific algorithmic developments. These methods are strongly determined by the mathematical formulation, since they exploit its properties. They can be classified into branch-and-bound-and-cut and decomposition methods.

4.1.1 Branch-and-Bound-and-Cut Methods

Problem (17.8)–(17.13) is solved by using branch and bound with three problem specific improvements: a relaxation obtained by aggregating variables x _rk across all routes $r \in \mathcal {R}_0$, cutting planes induced by constraints (17.10) and (17.11) in the relaxed problem, and upper and lower bounds derived by using the relaxed problem. It is worth noting that solutions of the relaxed problem ensure demand satisfaction by all lines collectively but they disregard the capacities of individual lines, therefore they cannot be easily transformed into feasible solutions of the original problem.

Moreover, problem (17.14)–(17.18) is solved firstly by applying a formulation strengthening through preprocessing, which involves coefficient reduction, variable reduction linked to the coefficient reduction and constraint reduction using dominance rules. Next, the branch and bound is enriched with cutting planes derived from constraints (17.15) and (17.16), several branching rules and a primal heuristic which builds a solution based in the resolution of the linear relaxation.

In order to find the set of efficient solutions for the multiobjective problem (17.37)–(17.43) the 𝜖-constraint method is applied with respect to the second objective. This means that the second component of vector (17.37) is transformed into a constraint, which enables to find efficient solutions by varying its right-hand side. Moreover, the bilevel structure of the problem is eliminated by substitution of the lower-problem (17.40)–(17.43) by its optimality conditions. This can be done by combining duality, specific properties of the shortest-path problem and linearization techniques.

4.1.2 Decomposition Methods

Problem (17.19)–(17.25) is solved by a column generation approach, given the super-polynomial number of variables. In a first step, the linear relaxation is solved by iteratively pricing passenger and line path variables until no improvement is found. The pricing of passenger variables is a polynomial-time solvable shortest path problem. On the other hand, the pricing of line variables is a NP-hard maximum weighted path problem. In a second step, the algorithm builds an integer solution from the set of routes having nonzero frequencies in the optimal solution of the linear relaxation. This is done by a greedy procedure which deletes routes as long as all OD pairs are covered and the objective value decreases.

The PND problem of choosing a small number of routes while maximizing demand coverage can be solved by applying the Benders decomposition (Marín and Jaramillo 2009). The problem is partitioned into the master (which involves variables related to infrastructure building) and the sub-problem (which deals with passenger behavior). At each iteration of the algorithm, dual variables of the sub-problem define optimality or feasibility cuts which are added to the constraints of the master problem. Moreover, several extensions are introduced in order to improve the performance of the method, namely, separation of the sub-problem by OD pair, elimination of inactive cuts and specific shortest path algorithms to solve the sub-problem. These improvements allow for solving realistic size instances of the problem.

4.2 Heuristic Based Methods

We refer as heuristic methods for PT network design to those which are not driven by an explicit mathematical programming formulation. The algorithms presented apply to variants of models presented in Sect. 3. The objectives to be optimized can be, among others: user benefit maximization, operator cost minimization or total welfare maximization (Kepaptsoglou and Karlaftis 2009). Moreover, the heuristic methods for RND are classified into: (1) route generation and route selection, and (2) route set generation and improvement. The first approach considers the generation of single routes (route generation), which also can be used to compose a pool of candidate routes from which an optimal subset will be then selected (route selection). The second approach generates a complete solution in a first stage (route set generation), which can be then improved (route set improvement).

4.2.1 Route Generation and Selection

In the context of RND, the route generation and selection approach entails generating firstly a pool of many good candidate routes, from which the optimal (or best possible) subset is selected in a second stage. When generating the pool, usually the following criteria are taken into consideration: (1) the candidate routes should be good, both for users and operators, (2) each element of the pool has to fulfil some constraints which can be verified at route level individually, e.g., route length, duration and circuity, overlapping with existing routes, (3) a compromise between a small pool concentrated in few routes and a larger pool which provides more diversity should be managed. The usual way for generating candidate routes is based on shortest paths between node pairs of $\mathcal {G}$, which can include origins and destinations of OD pairs given by set $\mathcal {K}$ or all possible node pairs taken from $\mathcal {N} \times \mathcal {N}$. These routes are expected to provide a good level of service in terms of travel time from the users viewpoint. But since this pool could be very restrictive, additional routes are usually generated. To do this, different ideas can be applied: (1) taking a route generated from a shortest path P and generating additional similar routes by successively eliminating each edge from P and recomputing the shortest path, (2) generating k-shortest paths for every node pair of $\mathcal {G}$ (as we increase the value of k, a larger and more diverse pool can be obtained). Since routes generated from shortest paths could be biased towards the interest of users, alternative ways of generating routes biased towards operator’s interest are taken into consideration, for instance, including in the pool routes generated by analyzing the concentration of demand flow in the arcs of $\mathcal {G}$ (Cipriani et al. 2012). To do that, a system-split like procedure is first run, which produces the aggregated flow from all OD pairs $k \in \mathcal {K}$ over each arc $a \in \mathcal {A}$. Then, routes are generated by selecting highly loaded arcs and adding links until specific termination criteria involving route constraints are met. So far, the candidate routes generated by these methods do not collectively ensure the fulfilment of global constraints at the route selection level, like demand coverage (in the topological sense) and demand satisfaction (in terms of capacity). This issue can be addressed by a model based pool generation (over minimal spanning trees) which ensures capacity fulfilment (Gattermann et al. 2016).

Heuristics based on route generation and selection involve a second phase where the best possible subset of routes is selected from the pool of candidate routes. This entails solving a set covering like problem, with a large number of variables. We identify two approaches to solve this problem heuristically for RND: (1) genetic algorithms based search, and (2) neighborhood based search. In the first group, usually the route identifiers are coded into a chromosome which can be of either fixed or variable length, thus allowing solutions with different number of routes. The individuals (sets of routes, i.e., solutions to RND) are then evolved using classical genetic operators like one point or two point crossover, and mutation. Note that crossing two individuals entails exchanging routes between solutions. Regarding neighborhood based search, a set of neighbors of a given solution to RND can be defined by replacing each route by one of its contiguous (similar) elements in the pool. Note that the structure of the routes defined during the pool generation does not change due to the search process. Moreover, since the pool does not necessary guarantee demand coverage of all demand OD pairs, the unsatisfied demand can be included in the objective function to penalize this fact.

4.2.2 Route Set Generation and Improvement

The route set generation approach produces a complete solution for RND. Usually, feasibility at both route and solution level is ensured. Most algorithms perform an incremental construction, which can be either biased or unbiased. In the first group, the main idea is to build some skeleton routes which are then enlarged by inserting nodes until the whole demand given by set $\mathcal {K}$ is covered. Skeletons are built by connecting high demand OD pairs, either enumerating and selecting the best sequence of intermediate nodes or computing shortest paths. Then, additional demand is covered by inserting nodes into the initial skeletons. However, the node insertion should discard cases where the resulting route becomes too large, circuitous or overloaded. The solutions generated by these methods are expected to be good by construction, however, they can be improved in a further stage. On the other hand, the unbiased approach aims at generating initial solutions which need to be improved in a second stage. In this case, the route set generation method should ensure diversity, while the route set improvement should ensure a comprehensive exploration of the search space. Usually, the construction is performed by selecting randomly an initial node and then adding randomly additional nodes. The solution should guarantee minimal levels of demand coverage and connectivity. To do that, usually all nodes of $\mathcal {G}$ should be reached by routes, and a reasonable number of route intersections (which enable transfers) should be ensured.

The route set improvement entails either modifying existing routes or generating new ones. We again identify two different approaches depending on the adoption of genetic or neighborhood search. In the first group, problem specific genetic operators can be applied to the initial solution, namely, add/delete arc, route merge, route break, route sprout and route crossover. Regarding neighborhood search, a typical approach applies simple arc add/delete operators to each route of the solution. A more complex neighborhood structure involves exploring alternative deviating paths from an initial one, which can be modified at given points (Zhao and Zeng 2008). It is worth noting that whatever the neighborhood structure is adopted, any method for escaping from local optima can be used, e.g., simulated annealing or tabu search.

A related methodology which falls within this category is the generation and improvement of a single route in the context of PND. This is done by considering the grid-based set of potential nodes and constructing either a random walk along one of the two diagonals of the square grid (Dufourd et al. 1996) or a greedy biased initial solution (Bruno et al. 2002). Then, local search is applied, where the neighborhood of the solution is obtained by moving one of its stations to a contiguous position in the grid.

4.2.3 Handling Specific Problem Features

Heuristic methods for PT network design often have to deal with two distinctive problem characteristics: (1) the multiobjective structure due to existence of conflicting objectives, and (2) the bilevel structure resulting from the passenger behavior model.

The treatment of multiple objectives is sometimes performed implicitly, where algorithms are conceived to balance the different objectives during solution construction (Baaj and Mahmassani 1995; Mauttone and Urquhart 2009a). In this case, the output is a single solution but, by changing appropriately some parameters, different trade-off solutions can be obtained. A different approach consists of solving heuristically a model which weights the different objectives into a single function (Pattnaik et al. 1998). By changing the weights, different trade-off solutions can be obtained. Finally, some other algorithms produce in a single run, an entire set of trade-off solutions (Israeli and Ceder 1995; Mauttone and Urquhart 2009b; Oliveira and Barbieri 2015). This is attained by means of specific operators and parameter settings.

In the context of heuristics, whenever a solution is changed due to local move or genetic operator, usually the passenger behavior model should be run in order to evaluate the system performance under the new conditions. This entails solving variants of the shortest path problem (17.1)–(17.3). In absence of capacity constraints, the computation is equivalent to solving $|\mathcal {K}|$ independent shortest path problems. But, if passengers are restrained by vehicle capacity, the resulting multicommodity flow problem is more difficult to solve. In this case, specific accelerating techniques can help to reduce computation time (Walteros et al. 2015). Although more complex and detailed passenger behavior models exist in the literature (Desaulniers and Hickman 2007), their complexity in PT network optimization models and algorithms must be kept bounded, given the strategic and tactical characteristics of the problems involved. In any case, the computational effort spent by calling the passenger behavior model is significant with respect to the overall execution time of PT network design algorithms.

5 Bibliographical Notes

Some relevant surveys are worth to be mentioned before discussing the specific literature on public transportation network design. In Schöbel (2012), the RND problem is discussed from a mathematical programming perspective, providing formalization for several concepts including the notion of user and operator oriented models. Kepaptsoglou and Karlaftis (2009) review models and algorithms for RND, proposing the classification of solution approaches into (1) candidate route generation and route configuration and (2) route construction and improvement. Laporte and Mesa (2015) review methodologies for PND, including the location of stations, design of a single route and of the entire network. In Farahani et al. (2013), an overview of methodologies for several urban transportation network design problems is provided, including both private and public modes. The study focuses in models and algorithms dealing with topological variables, presents a general bilevel formulation for the problems and identifies problem instances reported in the literature up to the year of publication. More recently, Iliopoulou et al. (2019) review metaheuristic approaches to RND, identifying relevant algorithmic aspects like route representation, repair and recombination.

Early work in public transportation network optimization consists of heuristics and it can be traced from Lampkin and Saalmans (1967), where the heuristic for route set construction based in skeletons and further node insertion is proposed. This method was later extended by Silman et al. (1974), who include a route deletion procedure and consider transfers between routes when computing demand coverage and travel time. Dubois et al. (1979) tackle both PND and RND problems for bus systems. Actually, the PND does not entail infrastructure building, instead it refers to selecting the set of streets which will be used by the bus routes, which reduces the size of the underlying network used as input in the RND problem. Unlike the methods mentioned above, which allow for generating a route set from an empty solution, the concept of route set improvement is developed by Mandl (1980). That author proposes a method that applies insertion and deletion of nodes in routes and interchange of parts between routes of an already existing solution. The route set construction based on skeletons is resumed by Baaj and Mahmassani (1995), who enrich the procedure for node selection and insertion. Also, these authors propose the idea of building skeletons based on k-shortest paths instead of the shortest one, in order to diversify the search during construction. Mauttone and Urquhart (2009a) modify the node insertion procedure by proposing a pair insertion which seeks to cover high demand OD pairs directly. More recently, Islam et al. (2019) propose a greedy algorithm inspired by the work of Baaj and Mahmassani (1995), which builds routes between high demand OD pairs by appending shortest route segments that consider both travel cost and demand coverage.

The first studies which apply metaheuristics to RND consist of genetic algorithms. Pattnaik et al. (1998) solve the route selection problem by encoding the identifiers of routes taken from a predefined pool, into a chromosome which can be of either fixed or variable length. Further developments propose extensions to include frequency encoding (Tom and Mohan 2003) and parallel implementations (Agrawal and Tom 2004). Another relevant application of metaheuristics to route selection in the context of RND is due to Fan and Machemehl (2006), who apply simulated annealing to select the best subset of routes from a predefined pool of candidates. Fan and Mumford (2010) apply simulated annealing for searching on the space of route structure. A different application of genetic algorithms to RND is proposed by Ngamchai and Lovell (2003) for the route set improvement problem, implementing several problem specific operators which modify the structure of the routes of the initial solution. More recent applications of metaheuristics involve the use of ant and bee colony optimization (Nikolic and Teodorovic 2014; Szeto and Jiang 2014; Yu et al. 2012) and particle swarm optimization (Kechagiopoulos and Beligiannis 2014), either for construction or for improvement of solutions.

Mathematical programming approaches are more recent and they were firstly applied to passenger rail transportation. Regarding RND, Bussieck et al. (1997) proposed the user oriented model and the corresponding solution method based in relaxations, cutting planes and bounds. The operator oriented model is due to Claessens et al. (1998), who also present complexity results and a solution method based in reformulation and lower bounding. Their work is resumed by Goosens et al. (2004), who propose a solution method based on formulation strengthening and branch and cut. Goosens et al. (2006) extend the model to allow lines with different stopping patterns. While the studies mentioned above consider fixed passenger behavior, Borndörfer et al. (2007) introduce a path-based model which generates the routes. They also present complexity results and a solution method based on column generation. Other formulations which include explicit modeling of passenger behavior have been proposed by Guan et al. (2006) and Cancela et al. (2015). Finally, other relevant work include the study of Schöbel and Scholl (2006), who proposed the expanded network to account for transfers, previously adopted by Spiess and Florian (1989) and later improved by Goerigk and Schmidt (2017). Regarding PND problems, Laporte et al. (2007) propose a base formulation, which is then extended by Marín and Jaramillo (2008). The single route location problem is due to Dufourd et al. (1996), then extended by Laporte et al. (2005). Latest developments in this line are due to Gutiérrez-Jarpa et al. (2017).

We should mention several studies which are relevant due to the treatment of particular aspects of public transportation network design problems. Lee and Vuchic (2005) model elastic demand by allowing a variable share of public transportation demand from a given fixed overall demand and they study the influence of several parameters over the resulting networks. Szeto and Jiang (2014) use information from the mathematical formulation to reduce the number of calls to the passenger behavior model in the context of a metaheuristic solving method. Bagloee and Ceder (2011) handle large size networks comprising up to 13,487 nodes, 52,742 arcs and 142,041 OD pairs. Mumford (2013) makes an effort to establish a set of benchmark instances for public transportation network optimization.

Finally, it is worth noting the existence of a complementary stream of publications dealing with public transportation network design from a structural point of view. Laporte et al. (2000) identify several network structures (star, cartwheel, triangle and grid) and evaluate their effectiveness according to indexes that represent the interest of passengers. In this line, more recently Fielbaum et al. (2018) apply some of the models discussed in this chapter to cities with different structures (monocentric, polycentric and dispersed) paying attention to the role of transfers, thus, filling the gap between the different streams of research on the same topic.

6 Conclusions and Perspectives

Public transportation network design problems have been studied since more than five decades ago. Several problem aspects are well explained by the existing models. Moreover, several solution methods have been tested and documented, constituting a rich basis for developing new ones. In the following, we identify current challenges and future perspectives of this area of research.

Mathematical programming approaches face the challenge of solving huge mixed integer linear problems (MILP). The small city used as test case for RND in (Borndörfer et al. 2007) seems to establish the limit on the size of solvable instances using this approach. Newer MILP solvers should be evaluated regarding exact resolution, even considering formulations which incorporate additional problem features like transfers (Schöbel and Scholl 2006), waiting time (Cancela et al. 2015) and capacities (Goerigk and Schmidt 2017).

Metaheuristics have shown to be the most effective methods for solving medium and large-sized problem instances. Nevertheless, they face the main challenge of minimizing the calls to the passenger behavior model, which is the most critical algorithmic component of the overall solution methods. Techniques like the one proposed by Szeto and Jiang (2014), which attempts to discard unnecessary solution evaluations should be explored. Regarding experimental evaluation of accuracy of metaheuristics, the lack of a well established set of benchmark instances with reference values is a weakness of the field. This situation needs to be addressed, a remarkable contribution in this sense is the work of Mumford (2013). Recent works have shown progress on the field (Iliopoulou et al. 2019), mainly in the computational aspect of the methods that tackle the combinatorial complexity of the problem, where more elaborated experiments are conducted regarding parameter tuning, benchmark and reproducibility.

The modeling of passenger behavior under vehicle capacity constraints is a very relevant aspect of public transportation network design models. The capacitated user equilibrium modeled in Borndörfer et al. (2007) assumes that some users are willing to choose longer paths with respect to other users traveling from the same origin to the same destination. This could be questionable in the context of real systems. A different approach is adopted in the bilevel model of Goerigk and Schmidt (2017), which ensures sufficient capacity for all users. However, this entails taking into account two other issues: (1) solving the more complex bilevel formulation, and (2) discussing whether real systems are able to implement these solutions, mainly due to high frequency requirements. While the design of uncongested public transportation systems can be a reasonable goal, sometimes it is necessary to recognize that congestion plays a role in network design due to limitations on the available resources. The effect of congestion over passengers (especially over waiting time and route choice) leads to complex models (Gendreau 1984) which have been successfully addressed at the descriptive level (Cepeda et al. 2006), i.e., models that represent passenger behavior given a fixed set of routes. However, normative models for congested public transportation network design are much more difficult to solve, since they turn into mathematical programs with equilibrium constraints (Colson et al. 2007).

Finally, other aspects of public transportation network design like stochastic demand (An and Lo 2016) and integration of stages (Canca et al. 2017) also deserve attention, due to their relevance at the practical level as for the challenge they pose at both modeling and algorithmic levels. In fact, these issues have been recently approached by the research community, as part of the effort to build models which are able to better represent real life systems.