Transit network design with pollution minimization

Abstract

A critical step in the design of urban transport networks is the determination of the routes and the frequencies of buses. This situation entails a highly combinatorial optimization problem with a complex computational solution, even for small instances. Several studies have addressed such a situation, minimizing travel times as the main objective. However, the growing trend toward the development of sustainable transport operations requires that the design of the network also considers the emissions of toxic gases that result from combustion, which leads to a new variant of this type of problem, called the pollution transit network design problem. In this paper, the problem is formulated as a biobjective mathematical programming model. Complex problem instances are proposed for this problem, and by using a multi-objective genetic algorithm, we approach the unimodal and bimodal version of the problem by taking into account the elastic demand between buses and cars. By using the proposed mathematical programming model and the genetic algorithm for small and large problem instances, respectively, we show that the generated pollutant emissions are drastically reduced without increasing travel times or costs.

1 Introduction

The design of transit systems has a strong impact on the quality of life for inhabitants of modern cities. This impact involves travel time, noise, congestion, accidents, and pollution. Designing these systems is particularly difficult because of the multiple objectives and constraints that must be taken into consideration (Ceder 2015; Vuchic 2005). This has led to the transit network design problem (TNDP), which has multiple definitions, the most common of which consists of determining the frequencies and the set of routes that make up a transit network operated by buses to minimize the total travel time for all passengers (Farahani et al. 2013; Guihaire and Hao 2008; Kepaptsoglou and Karlaftis 2009). The transit network is designed over an infrastructure network that represents streets and potential bus stops, and a fixed matrix demand between the stops or between separated centroids. Once the routes have been determined, the allocation of a heterogeneous bus fleet that considers different technologies should be optimized (Jiménez and Román 2016). The TNDP has been formulated as a mathematical model considering integer and real variables. However, today, transport systems must be designed to offer users service with low levels of congestion and taking into account environmental considerations.

The mathematical models that represent the TNDP are complex; therefore, the search for an optimal solution for large problem instances is a challenging task (Magnanti and Wong 1984). These characteristics make it difficult to formulate a problem that considers all variables from the real world (Newell 1979). Some recent studies have formulated the TNDP as linear integer programming models that minimize the total travel time in unimodal networks, considering only buses and solving the problem with exact methods (Cancela et al. 2015; Wan and Lo 2003). In a study by Zhang et al. (2014), a non-linear model that maximizes the profit in a multimodal network (buses and cars) is formulated and solved using an active-set algorithm. Both linear and non-linear programming models tested simplified small and medium non-congested networks. To increase the quality of the solutions, column generation methods have also been proposed (Borndörfer et al. 2007; Schöbel and Scholl 2006); however, the required computation time remains high.

To find a solution for the TNDP, most researchers address the problem using metaheuristics. Because of the NP-hardness of the problem (Magnanti and Wong 1984), traditional methods have difficulties finding optimal solutions. Mathematical models typically include integer variables, non-linear equations, and logical constraints; thus, if a model can be proposed for a specific real situation, it is hard to solve it to optimality. Metaheuristics, such as genetic algorithms, handle such characteristics in a better way (Chakroborty 2003). In fact, several studies propose genetic algorithms or hybrid evolutionary algorithms to address the mono-objective TNDP, minimizing the cost of passengers or a weighted cost between the cost of passengers and the cost of operators. These approaches consider specific mutations and crossover operators to take advantage of the characteristics of the problem (Wang and Lin 2010; Zhao et al. 2015). Other studies consider several objectives and propose metaheuristics to find efficient Pareto solutions that minimize passenger travel time and operator costs. Thus, Mumford (2013) and John et al. (2014) propose evolutionary algorithms for the TNDP that consider only the definition of routes, using specific operators and heuristic techniques that support the process. Also, a multi-objective metaheuristic has been developed to determine the definition of both routes and frequencies, approaching a more complex problem (Arbex and da Cunha 2015; Mauttone and Urquhart 2010). Nikolić and Teodorović (2014) address the multi-objective problem by developing a bee colony algorithm to optimize three objectives using a prioritization method and a lexicographic order, obtaining only one solution. All these metaheuristic approaches proved to be efficient in finding quality solutions to larger instances compared to exact methods; however, such studies considered only one mode of transportation (buses) and did not include environmental considerations.

Although the impact that transit systems have on the pollution in cities is known, the inclusion of this aspect into the models has gained relevance only in recent years. In fact, transit systems are considered an important tool to reduce CO₂ emissions, which are one of the most significant components in Greenhouse Gases (GHG). Furthermore, the transportation sector is one of the largest contributors to global GHG emissions; therefore, the reduction of pollution is an important aspect to consider when designing transportation systems (US EPA 2014). Many studies have regarded this issue with freight transportation, and the minimization of GHG emissions has led to the green vehicle routing problem, which includes environmental considerations in the classic vehicle routing problem (which differs from the TNDP) (Pradenas et al. 2013; Demir et al. 2014; Lin et al. 2014; Toth and Vigo 2014; Sanchez et al. 2016; Bravo et al. 2019). Also, other studies in the field of green logistics have attracted much interest from governments and companies trying to reduce their impact on the environment (Sbihi and Eglese 2010). However, the reduction of CO₂ emissions has received less attention in the design of public transportation systems. To the best of our knowledge, the study by Pternea et al. (2015) is the only related work that estimates the GHG emissions of buses in an objective function that maximizes the general welfare. Pternea et al. (2015) proposed a heuristic method to solve the problem of maximizing the general welfare in a network that does not consider traffic congestion. Also, a multi-criteria approach has been proposed for the decision making in an urban transport network design that includes environmental considerations; however, the approach is not intended to design a complete transit network (Pérez et al. 2015).

The consideration of various modes of transportation leads to a variation of the TNDP that represents more realistic situations. The research by Gallo et al. (2011) proposed a scatter search algorithm to optimize the frequency of a subway line with elastic demand distributed between metros, buses, and cars in a real-sized network. Although the algorithm does not design a complete network, it proposes an assignment method of passengers into the different modes. Additionally, Miandoabchi et al. (2012) proposed a multi-objective evolutionary algorithm to design a network that considers cars and buses. The solution to the problem allows for defining the number of tracks, the direction of new or existing streets, and the bus routes, without considering frequencies. An approach for the design of rapid railway networks that considers the elastic demand between competing modes (Cadarso and Marín 2017; Canca et al. 2016) and multimodal models that allow the design of a transit network composed of traditional buses, electric buses, and cars (Beltran et al. 2009) have also been proposed. The different transport modes considered have different levels of CO₂ emissions and, consequently, when included in the design of the system, generate different non-dominated solutions. Also, the design of a biobjective system instead of a mono-objective system generates better compromise solutions, resulting in greater flexibility for the system’s operational management.

Here, we present a biobjective approach to finding solutions in the Pareto frontier according to the design of a multimodal transit system on a congested network and considering the minimization of CO₂ emissions. This problem is called the pollution transit network design problem (P-TNDP) and consists of determining the routes and frequencies of a public transport network operated by buses, considering congestion and minimizing both total travel time and emissions. Evaluating only one mode of transport, omitting the capacity of buses, and treating speed and frequency as discrete variables, we obtain a particular problem that we call P-TNDPa, for which a mathematical programming model is proposed. To evaluate the simplifications adopted in this mathematical model, a second problem, P-TNDPb, is considered, which also evaluates one mode of transport but considers bus capacity and continuity in speed and frequency variables. The bimodal situation is studied by the problem P-TNDPc, which is an extension of the P-TNDPb and includes buses and cars. Because the mathematical model obtains solutions only for small P-TNDPa instances, a multi-objective genetic algorithm (MGA) is designed to find solutions for the P-TNDPb and P-TNDPc.

2 Biobjective mathematical programming model for the P-TNDPa

The proposed model achieves the minimization of both the total travel time and CO₂ emissions in a space of constraints defined by the fleet size and road congestion. The model also includes a user cost function and the set of constraints associated with the allocation problem.

The mathematical formulation is based on the network $G = (V,E)$ that represents a physical infrastructure network. Each node $v \in V$ represents a bus stop connected by edges that represent bidirectional streets. Each edge $e = (i,j) \in E$ is associated with a distance $l_{e}$ and a practical capacity $\kappa_{e}$ that indicates the number of buses that can run on a street per time unit without experiencing congestion. There is a set of possible routes denoted by $r \in R$, where $E_{r} \subseteq E$ is the set of edges that conform the route r and $R_{e} \subseteq R$ is the set of routes that pass through the edge $e$. The travel demand is considered to be inelastic and is given by an origin–destination (OD) matrix $D = \{ d_{ij} \}$, where i and j represent the stop nodes, and the value $d_{ij}$ indicates the number of passengers to be transported from vertex i to vertex j per time unit. In addition, the demand is also represented by a vector K, where each OD pair is associated with a $k \in K$, defining $\delta_{k} = d_{ij}$ and identifying the vertices of the origin and destination as $O_{k} = i$ and $D_{k} = j$, respectively. For the physical network, routes or lines are defined as sequences of adjacent nodes given that they circulate in both directions. A parameter B, which represents the maximum number of buses that can be used in the network, is also considered.

A classical assignment model of optimal strategies is used (Spiess and Florian 1989). To formulate this model, a trajectory network $G^{T} = (N,A)$ is constructed. For every route $r \in R$ that passes through a vertex $v \in V$, a node $n_{rv} \in N$ is generated. In addition, for every OD pair, its respective origin and destination nodes are created. Additionally, the arcs $a \in A$ are divided into three exclusive groups as follows: travel arcs $A^{V}$, which model the movement of the passengers inside the buses; waiting arcs $A^{W}$, which model the passengers who are waiting and transferring between different routes in a particular node; and destination arcs $A^{D}$, which represent the end of a trip, such that $A = A^{V} \cup A^{W} \cup A^{D}$. For a particular node $n,$ the sets $A_{n}^{ + } ,A_{n}^{ - } \subset A$ are defined with the outgoing and incoming arcs from (to) that node, and the set $A_{n}^{W + } \subset A^{W}$ is defined with the outgoing waiting arcs from that node. In addition, we define the parameter $b_{nk}$, which assumes the value $\delta_{k}$ for the source node, $- \delta_{k}$ for the destination node and 0 for the intermediate nodes. As an example, Fig. 1a shows a physical network with five vertices and six edges on which three routes are defined. Figure 1b shows the network of trajectories corresponding to an OD pair.

Fig. 1

Example of physical network (a) and trajectory network (b)

To obtain a linear model, the frequencies and speeds of buses are discretized. In the case of the frequencies, a set of parameters $\varTheta = \{ \theta_{f} \}$, indexed by $f \in F,$ is assigned and indicates the possible values of frequencies to be assigned to the routes. This change requires adding parallel waiting arcs in the trajectory network. Note that each waiting arc $a \in A^{W}$ is associated with a unique frequency f denoted by $f(a)$. Similarly, for the speeds, a set of parameters $\varPhi = \{ \varphi_{u} \}$, indexed by $u \in U$ and containing the possible values of the average speed, must be generated in decreasing order. A set of utilization factors of arcs $\varPi = \{ \pi_{u} \}$ is generated in increasing order where $\pi_{1} = 1$. It is assumed that the speed is constrained by the capacity of the arcs. Therefore, each edge has a practical capacity $\kappa_{e}$ indicating that the bus lines can operate at an optimum speed $\varphi_{1}$. If the flow of buses increases over the practical capacity by a factor of $\pi_{u}$, then the speed of all routes in that edge will decrease to the respective $\varphi_{u}$ value. This change requires the addition of parallel travel arcs for each of the possible speed values, making the cost of each arc equal to $c_{a} = \frac{{l_{e(a)} }}{{\varphi_{u(a)} }}$. Note that each travel arc $a \in A^{V}$ is associated with a unique route $r$, edge $e$ of the physical network and speed level $u$, denoted by $r(a)$, $e(a)$ and $u(a),$ respectively.

Considering a G^T = (N, A), a P-TNDPa is formulated with functions (1)–(20). The first objective and a subset of constraints are based on the model proposed by Cancela et al. (2015). We additionally consider CO₂ emissions and traffic congestion. The model is formulated according to the following decision variables:

• $x_{r}$ = 1 if the route r is part of the solution, otherwise, $x_{r} = 0.$

• $y_{rf }$ = 1 if the frequency $\theta_{f}$ is assigned to the route r, otherwise, $y_{rf } = 0$.

• $z_{eu}$ = 1 if the edge e operates in a speed interval u, otherwise, $z_{eu } = 0$.

• $q_{refu}$ = 1 if the frequency $\theta_{f}$ is assigned to the route r and if the edge e is operating in the interval u, otherwise, $q_{refu } = 0$.

• $v_{ak}$ = is the number of passengers who travel through arc a [pas/h] corresponding to the k-th OD pair.

• $w_{nk}$ = is the waiting time multiplied by the demand in node n corresponding to the k-th OD pair.

Additionally, we consider x_r(a) as the variable associated with the route that generates arc a. In the same way, z_e(a)u(a) refers to the vertex and speed interval that generates arc a, whereas y_r(a)f(a) refers to the path and frequency of arc a.

$$ Min_{x,y,z,q,w,u} \quad Z_{1} = \mathop \sum \limits_{k \in K} \left( {\mathop \sum \limits_{a \in A} c_{a} v_{ak} + \mathop \sum \limits_{n \in N} w_{nk} } \right) $$

(1)

$$ Min_{x,y,z,q,w,u} \quad Z_{2} = 2\mathop \sum \limits_{e \in E} \mathop \sum \limits_{u \in U} \mathop \sum \limits_{{r \in R_{e} }} \mathop \sum \limits_{f \in F} EM_{u} \frac{{l_{e} }}{{\varphi_{u} }}\theta_{f} q_{refu} $$

(2)

$$ \begin{aligned} & Subject\; to{:} \\ & \quad 2\mathop \sum \limits_{{f \in {\text{F}}}} \theta_{f} \mathop \sum \limits_{{a \in A^{V} }} \frac{{l_{e(a)} }}{{\varphi_{u(a)} }}q_{r(a)e(a)fu(a)} \le B \\ \end{aligned} $$

(3)

$$ \mathop \sum \limits_{{a \in A_{n}^{ + } }} v_{ak} - \mathop \sum \limits_{{a \in A_{n}^{ - } }} v_{ak} = b_{nk} \quad \forall n \in N,k \in K $$

(4)

$$ v_{ak} \le \theta_{f(a)} w_{nk} \quad a \in A_{n}^{w + } ,n \in N,k \in K $$

(5)

$$ v_{ak} \le \delta_{k} x_{r(a)} \quad \forall a \in A,k \in K $$

(6)

$$ v_{ak} \le \delta_{k} z_{e(a)u(a)} \quad \forall a \in A^{V} ,k \in K $$

(7)

$$ v_{ak} \le \delta_{k} y_{r(a)f(a)} \quad \forall a \in A^{w} ,k \in K $$

(8)

$$ \mathop \sum \limits_{{r \in R_{e} }} \mathop \sum \limits_{{f \in {\text{F}}}} \theta_{f} y_{rf} \le \kappa_{e} \mathop \sum \limits_{u \in U} \pi_{u} z_{eu} \quad \forall e \in E $$

(9)

$$ \mathop \sum \limits_{{f \in {\text{F}}}} y_{rf} = x_{r} \quad \forall r \in R $$

(10)

$$ \mathop \sum \limits_{u \in U} q_{refu} = y_{rf} \quad \forall r \in R;\; f \in F;\; e \in E_{r} $$

(11)

$$ \mathop \sum \limits_{{f \in {\text{F}}}} q_{refu} \le z_{eu} \quad \forall e \in E;\; u \in U;\; r \in R_{e} $$

(12)

$$ \mathop \sum \limits_{u \in U} z_{eu} \le \mathop \sum \limits_{{r \in R_{e} }} x_{r} \quad \forall e \in E $$

(13)

$$ \mathop \sum \limits_{u \in U} z_{eu} \le 1\quad \forall e \in E $$

(14)

$$ v_{ak} \ge 0\quad \forall a \in A,k \in K $$

(15)

$$ w_{nk} \ge 0\quad \forall n \in N,k \in K $$

(16)

$$ x_{r} \in \{ 0,1\} \quad \forall r \in R $$

(17)

$$ y_{rf} \in \{ 0,1\} \quad \forall r \in R,f \in F $$

(18)

$$ z_{eu} \in \{ 0,1\} \quad \forall e \in E,u \in U $$

(19)

$$ q_{refu} \in \{ 0,1\} \quad \forall r \in R, e \in E,f \in F, u \in U. $$

(20)

The proposed formulation has two objectives: objective function (1) represents the minimization of the total travel time, considering vehicle travel time, waiting time and penalization for transfers (cost of waiting arcs); objective function (2) represents the minimization of the CO₂ emission rate of the system, where $EM_{u}$ is the emission rate (kg of CO₂/h) generated by buses operating at interval speed u.

Constraint (3) establishes a maximum for the size of the bus fleet required to operate the system. Constraints (4) and (5) correspond to the assignment model and divide the passenger routes among the possible routes and determine the waiting times. The former corresponds to the passenger flow balance at the nodes, while the latter relates the waiting time at each node to the frequency of the routes. Constraints (6)–(8) ensure that passengers use only the routes selected in the solution according to respective speeds and frequencies. Constraints (9) correspond to the utilization of the capacity of the arcs, which varies according to the speed range selected for each arc, thus representing congestion in the streets. Constraints (10) indicate that for each selected route, a frequency should be assigned. Constraints (11)–(14) ensure the coherence of the values of the variables $q_{refu}$ and $z_{eu}$. Finally, constraints (15)–(20) indicate the values that each of the variables can take.

3 A multi-objective genetic algorithm for the P-TNDPb and the P-TNDPc

To determine the Pareto solutions of large P-TNDPb and P-TNDPc instances, we propose a multi-objective genetic algorithm (MGA) that operates in genotype–phenotype mode. The genotype of a solution is a binary string that represents its characteristics, whereas the phenotype is the feasible solution. Specifically, the genotype is a string in which each element has value 1 if the route is included in the solution or 0, otherwise. As the phenotype, an algorithmic module is responsible for performing the elementary operations on the genotype and another independent module is involved with the construction and evaluation of a feasible solution. The evaluation of the solutions is performed with measures of quality and diversity using the dominance depth ranking and crowding distance operators (Talbi 2009). Dominance depth ranking divides the population into subsets of solutions that are ordered and ranked according to the dominance between sets. Crowding distance operators measure the diversity in the Euclidean space of both objective functions as the area of the rectangle defined by the left and right neighboring solutions of the current solution, so that a high value implicitly represents a high diversity of the solution. The evolutionary process is repeated for a fixed number of generations.

The genotype algorithmic module performs selection, variation and replacement operations. The tournament selection method is used, which consists of randomly selecting a small set of solutions to choose the best one in the set. To that end, the method first selects by the quality measure and then, in case of a tie, by the diversity measure. After selection, three crossover operators and two mutation operators are considered. The first uniform crossover operator swaps each gene between the parent solutions with a certain probability. Second, the one-point crossover operator selects a random point of the solution vector, and the segments beyond this point are swapped between both parents’ solutions. The third operator is the two-points crossover that consists of selecting two points of the parent solution and swapping the segment of the gene that results from both parents. The proposed algorithm includes three crossover operators, which are selected randomly in each case to increment the variability of the search process. Additionally, two mutation operators are considered. When a solution is selected to be mutated, the operator to be used is randomly determined. The first operator is the bit flip mutation, where each gene of the vector solution has a probability to change from 0 to 1 and vice versa. The second operator is the one bit mutation for which exactly one gene of the vector solution is randomly selected to change from 0 to 1 or vice versa. The replacement of the population occurs using the environmental replacement operator. From a population constructed with the union of the current population and their descendants, the individuals of the new population are selected according to the measures of quality and diversity.

3.1 Unimodal fitness evaluation for the P-TNDPb

The fitness evaluation consists of solving an assignment subproblem to determine the total travel time and the resulting emission rate; then, the indicators of quality and diversity of the generated solutions can be evaluated. The assignment method is based on the iterative algorithm by Nikolić and Teodorović (2014) and is modified to include traffic congestion. This method assigns passengers to paths with a maximum of one transfer. Consequently, if an OD pair is not connected by at least one transfer, the resulting solution is considered infeasible. In addition, if the procedure does not converge, the solution is also considered infeasible. The process assigns passengers with and without transfers into the different possible paths depending on the frequency of each route, prioritizing the paths without transfers. Thus, based on the flows of passengers assigned to each route, the frequencies and speeds are updated. Specifically, for each OD pair, the number of passengers is distributed on the routes with zero or one transfer. From this result, the number of buses in each route, the travel time and the average bus speed in each arc are calculated. The procedure iterates until the speeds and frequency values stabilize. The frequency of route $r$ is determined so that the number of buses is sufficient to transport all assigned passengers, and it is given by $f_{r} = \frac{{Q_{r,max} }}{{\alpha_{max} \times Cb_{r} }}$, where $Q_{r,max}$ is the maximum volume of passengers along the route, $\alpha_{max}$ is the coefficient of maximum utilization, and $Cb_{r}$ is the bus capacity of buses operating on route r.

The number of buses required to operate route $r$ is given by $N_{r} = \frac{{f_{r} \times T_{r} }}{60}$, where T_r is the total travel time on route r. The number of buses that circulate through arc e in one direction is given by adding the frequencies of the routes, i.e., $F_{e} = \sum\nolimits_{{r \in R_{e} }} {f_{r} }$, where $R_{e}$ is the set of routes that pass through arc e. ${\text{Let }}\kappa_{e}$ be the practical capacity of arc e and $T_{e,0}$ be the free flow time of arc e given by $T_{e,0} = \frac{{60 \times l_{e} }}{{1000 \times v_{max} }}$, where $l_{e}$ is the length of the arc e and $v_{max}$ is the maximum speed. Then, considering the congestion of the arcs, the travel time $T_{e}$ is computed by Eq. (21) and $v_{e} = \frac{{60 \times l_{e} }}{{1000 \times T_{e} }}$. This function is selected to model traffic congestion due to its simplicity and low computational cost, which facilitates the MGA’s performance estimation (Patriksson 2015). Other approaches can be used by simply replacing the traffic congestion evaluation module in the phenotype.

$$ T_{e} = \left\{ {\begin{array}{*{20}l} {T_{e,0} , } &\quad { if \; F_{e} \le \kappa_{e} } \\ {T_{e,0} *exp\left( {\frac{{F_{e} }}{{\kappa_{e} }} - 1} \right),} &\quad {if\; F_{e} > \kappa_{e} } \\ \end{array} } \right.. $$

(21)

The evaluation of the first objective function in Eq. (1), which corresponds to the total travel time of the passengers, is calculated by adding the waiting time, bus travel time and an estimated fixed transfer time between lines. The waiting time of a passenger $W_{t}$ depends on the frequency of the possible routes to be used for the passenger and corresponds to half of the time waited between the arrivals of two buses at the stop, i.e., $W_{t} = \frac{30}{{\mathop \sum \nolimits_{{r \in R_{AB,t} }} f_{r} }}$. The vehicle travel time is the sum of the travel times in each arc included in the journey. To evaluate the objective in Eq. (2), emissions generated in an arc are obtained by multiplying the emission factor corresponding to the average speed of an arc by the flow of buses that circulate on it. The emissions of the whole system are the sum of the emissions of each of the arcs multiplied by 2 because all routes and arcs are bidirectional. Then, the emissions on an arc ($E_{a}$) are given by $E_{a} = 2 \times \sum\nolimits_{e \in E}^{{}} {E_{{(v_{e} )}} F_{e} }$, where $E_{{(v_{e} )}}$ is the emission factor corresponding to the speed v_e and E is the set of arcs that form the network.

3.2 Bimodal fitness evaluation for the P-TNDPc

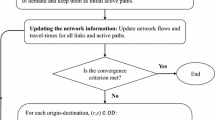
To evaluate the fitness for the P-TNDPc, which considers two transportation modes, private cars and public buses, two travel assignment processes are performed, one for each mode of transportation. The procedure presented in Fig. 2 first determines the minimum travel time for each OD pair considering an arbitrary distribution of the demand for both modes of transportation. Then, based on the times obtained, the distribution of the demand is updated using a logit binomial model. Finally, the travel assignment is performed with the new demands and both objective functions are evaluated.

Fig. 2

Bimodal assignment procedure

The assignment is performed sequentially, first by assigning the travel of cars considering that the bus routes operate with a certain initial frequency and then by assigning the passengers by the unimodal procedure described in Sect. 3.1. If any OD pair is not connected by paths with one or without transfers, all the demand is assigned to private cars. Unlike the unimodal method, the bus travel time $T_{e}^{b}$ in arc e depends on the flow of both buses and cars and is obtained by Eq. (22), where $\kappa_{e}$ is the practical capacity of arc e, $F_{e}^{b}$ and $F_{e}^{c}$ are the flow of buses and cars through arc e and $T_{e,0}^{b}$ is the time of free flow for buses in arc e given by $T_{e,0}^{b} = \frac{{60 \times l_{e} }}{{1000 \times v_{max}^{b} }},$ where $l_{e}$ is the length of arc e and $v_{max}^{b}$ is the maximum operating speed of the buses.

$$ T_{e}^{b} = \left\{ {\begin{array}{*{20}l} {T_{e,0}^{b} , } & { \quad if\; F_{e}^{b} + F_{e}^{c} \le \kappa_{e} } \\ {T_{e,0}^{b} \times exp\left( {\frac{{F_{e}^{b} + F_{e}^{c} }}{{\kappa_{e} }} - 1} \right), } & { \quad if \; F_{e}^{b} + F_{e}^{c} > \kappa_{e} } \\ \end{array} } \right.. $$

(22)

Car assignment is performed by means of an incremental assignment heuristic. The process consists of a fixed number of I iterations, and in each of them, part of the demand is assigned to the shortest path between each OD pair of nodes, updating the speeds in each iteration according to the congestion. Thus, the demand corresponding to a pair can be distributed among different paths. This heuristic requires low computational cost and, although the convergence to an equilibrium solution is not ensured, the resulting flow is good enough for practical purposes (Patriksson 2015; Sheffi 1985). Because more than one person can travel by car, the proposed model considers an average number of passengers per car ($u_{c}$), and the demand of cars in an OD pair is equal to the demand of travel by car divided by $u_{c}$. The car travel times are computed similarly to buses.

After the initial travel assignment, the minimum travel time between each OD pair in each mode of transportation is determined. In addition, for public transportation, the average waiting time in the path corresponding to the minimum time is computed, and the case that corresponds to the penalty for transfer is determined. Next, the demand of every OD pair is divided by a binomial logit method between buses and cars, such as in Khan (2007). Thus, the utility of traveling by car is defined as a linear combination of the minimum travel time for the trip and a cost, which is considered constant. In turn, the utility of traveling by bus is a combination of in-vehicle travel time, estimated waiting time, cost of travel and access time to the stop. The last two elements are considered as constant.

To evaluate both objective functions, the total travel time is obtained by adding the car travel times to the bus travel times, the waiting times, and the transfer times. Car emissions are computed by the arcs, multiplying the flow by the factor corresponding to the average speed of the cars in the arc and the total car emissions are added to the bus emissions.

4 Experimental design

The performances of the mathematical programming model and the genetic algorithm are evaluated in the test instances generated from the networks used in state-of-the-art studies and modified to include traffic congestion in the arcs. The networks considered in this paper come from studies by Cancela et al. (2015) with 5 OD pairs; Wan and Lo (2003) with 9 OD pairs; and Mandl (1980) with 172 OD pairs. In these studies, the cost of each arc corresponds to the travel time between two nodes, but since the speed is variable in the P-TNDP, the cost must correspond to the distance. This distance is calculated by the speed equation, considering the maximum speed and assuming the time is equal to the cost value in the original instance. Additionally, for each arc, the practical capacity is arbitrarily determined, which is different for the unimodal and bimodal cases. Figure 3 shows the three networks with the attributes of distance (d), unimodal practical capacity (UC) and bimodal practical capacity (BC) in each arc.

Seven test instances were generated for the P-TNDPa from the three networks presented in Fig. 3. Since the frequencies and speeds are discrete variables in the P-TNDPa, different instances were generated from the same network considering different values for each variable. The parameters used in these instances are presented in Table 1, where the columns correspond to the instance name, type of network, possible values for frequencies (θ_f), possible values for speeds (φ_u), factors of capacity utilization ($\pi_{u}$), emission factors for each speed (EM_u), limit of buses to operate the network (B) and penalty time for transfers (p).

Fig. 3

Networks used: a Cancela et al. (2015), b Wan and Lo (2003) and c Mandl (1980)

Table 1 Test instances for the P-TNDPa

Five test instances were generated for the P-TNDPb and P-TNDPc. The difference between the instances is in the considered practical capacity (UC or BC). Additional parameters related to cars are required for the P-TNDPc. Details are presented in Table 2, where the columns correspond to the instance name, type of network, problem approached, bus capacity ($Cb$), average number of passengers per car ($u_{c}$), penalty for transfers (p), tolerance of convergence for frequency and speed ($c_{f}$ and $c_{v}$, respectively), initial speed ($f_{0}$), and maximum speed of cars ($v_{max}^{c}$) and buses ($v_{max}^{b}$). Cells marked with “–” indicate that the parameter is not required in the P-TNDPb. In addition, there are other parameters that have the same value in all instances: the maximum utilization of the bus capacity ($\alpha_{max}$) is set to 1, the tolerance for path consideration ($c_{t}$) is set to 1.5, the minimum frequency of the routes ($f_{min}$) is set to 2 buses/h, and the maximum frequency ($f_{max}$) is set to 900 buses/h.

Table 2 Test instances for the P-TNDPb and P-TNDPc

The proposed methods require generating a set of initial feasible routes (Farahani et al. 2013; Kepaptsoglou and Karlaftis 2009). Because the total number of possible routes increases exponentially with the size of the network, a heuristic method is proposed based on the fact that the most attractive routes are those that directly join the origin-destination pairs, i.e., routes without transfers. The algorithm by Yen (1971) that provides the m shortest routes between the pairs of nodes that concentrate most of the demand is used.

All the results were performed on an Intel^® Core i7 computer equipped with a processor of 3.2 GHz and 8 GB of installed RAM memory. The mathematical programming model was implemented in GAMS and solved in CPLEX 12.6.1 (GAMS Development Corporation, 2014) using the ε-constraint method. The evolutionary algorithms were implemented in the C++ language using the ParadisEO software (Cahon et al. 2004). The MGA was run 15 times per instance and obtained a set of 15 solutions per run that were non-dominated. Since it is a biobjective problem, the comparison between the non-dominated solutions set found in the different runs of the algorithms was performed by means of the hypervolume indicator, which includes the considerations for the quality and diversity of each set.

5 Results

The complex process of assigning parameters to the MGA was executed with ParamILS, a procedure that, through an iterated local search, determines the set of parameters that generate the best performance of the algorithm (Hutter et al., 2009). Using this process, we determined a set of 13 values (Table 3). The algorithm selects the values among a set of alternatives for each parameter, which were defined based on values commonly used in the literature.

Table 3 Control parameters of evolutionary algorithms

The CO₂ emissions generated by a designed transit system can be reduced significantly with a small increase in the total travel time. A transit network designed according to the proposed models produces significantly fewer emissions with a small increase in the total travel time compared to a solution for the TNDP. Figure 4a shows the sets of efficient solutions determined for the P-TNDPa and P-TNDPb on the same network using the mathematical programming model (instances I1–I4) and the MGA (instance J1). We found that reductions of approximately 40% can be obtained by increasing the total travel time by less than 5% compared to the solution that minimizes only the travel time, which corresponds to the upper point in each curve and represents the solution for the TNDP. Figure 4b shows the solutions obtained for the second network considered using the mathematical programming model (instances I5–I6) and the MGA (instance J2). In this case, it is possible to reduce emissions by 15% with a 1% increase in travel time, which is repeated in the bimodal instance. This demonstrates the importance and convenience of considering the second objective function: by only minimizing the total travel time, which is what most of the previous studies have done, the solutions obtained can still be improved with regards to CO₂ emissions without significantly increasing passenger travel time.

Fig. 4

Results with mathematical programming model and MGA of Cancela et al. (2015) network (a) and Wan and Lo (2003) network (b)

The comparison between the different approaches proposed shows that the MGA provides better solutions for the P-TNDPb than the exact methods for the P-TNDPa, although the P-TNDPb is more restrictive than the P-TNDPa. This is because the frequency and speed are discrete variables in the P-TNDPa, whereas they are continuous variables in the P-TNDPb, providing greater flexibility and resulting in better use of the resources in the solutions. In Fig. 4a, the solutions found for the different instances of the P-TNDPa are depicted, suggesting that the increasing number of frequencies and possible speeds also increase the quality of the solutions obtained.

The MGA obtains similar results with respect to previous approaches proposed in the literature. Table 4 shows the results obtained in three studies that use the Mandl network (Bagloee and Ceder 2011; Cancela et al. 2015; Nikolić and Teodorović 2014). The comparison between the methods is not direct because each work approaches the problem with particular conditions. However, using the methods proposed in Sect. 2, it is possible to recalculate the objective function from the sets of routes selected in each study. The three above-mentioned studies do not consider traffic congestion or the minimization of emissions. Also, the assignment method used in these studies is different since the first two permit more than one transfer. For the comparison, among the results obtained by Nikolić and Teodorović (2014), the solution that minimizes travel time was considered. The evaluation for each problem instance was performed under free-flow conditions (instances denoted by without cap in Table 4) and congestion (instances denoted by with cap in Table 4), with the conditions considered in the optimization process of the previous studies in the first case and those of the MGA in the second the case. Although the results obtained are not the same as those reported in the studies, the values are close to the original values and correspond to an indicator for the MGA performance. The following aspects are indicated for each solution: the total travel time, the total emissions rate of the system, the number of routes selected, the number of buses required to operate the network, the proportion of passengers that travel directly (q₀), and the proportion of passengers who travel with one or more transfers (q₁). The solutions of the MGA correspond to the extreme points of the best Pareto frontier found, that is, the solutions that minimize the total travel time and the emissions rate. The results of the problem instances that consider no congestion indicate that the solutions obtained in this study are competitive with respect to the other methods regarding the total travel time, as seen in the second column of the first group of solutions in Table 4, where the difference between the best travel time found in the literature and the worst of the Pareto set obtained by the MGA is less than 5%. However, these were not the conditions considered by the algorithm for the optimization. Also, the percentage of passengers who travel without any transfer is the same as that of previous studies, approximately 10%. Furthermore, when traffic congestion was considered, the obtained solutions are better with respect to both the travel time and the rate of emissions, as seen in the second group of solutions in Table 4. The resulting solutions, although presenting a larger number of routes, require fewer buses to operate the network, implying an economic improvement in the obtained solutions. This is because, in the algorithm proposed, the number of selected routes is unlimited, in contrast to the previous studies.

Table 4 Comparison of results of MGA and previous approaches applied in the P-TNDPb

The solutions determined for the P-TNDPc by the MGA present shorter travel times and higher rates of emissions with respect to the solutions found for the P-TNDPb. This is because the demand is covered by cars, which circulate at higher speeds but with higher rates of emissions per passenger. Table 5 shows the solutions corresponding to the set of efficient solutions of greater hypervolume found with the MGA for instance J5. For each solution, the total travel time (TT) and the division between the time corresponding to travel by cars (TT_c) and buses (TT_b) are expressed in minutes. Similarly, the rates of total emissions of the system (ET) and the division between emissions produced by cars (ET_c) and buses (ET_b) are presented in kg of CO₂/h. Moreover, the following aspects are also indicated: the number of selected routes, number of buses required to operate the network, proportion of passengers that travel directly (q₀), proportion of passengers who travel with one or more transfers (q₁), and the proportion of passengers who travel by car (q_c). It can be seen that although the cars satisfy, on average, 37% of the demand, they represent just 27% of the total travel time but 66% of the total emissions. Therefore, it can be inferred that the passengers who travel by car travel faster but with a higher emission rate per passenger.

Table 5 Set of efficient solutions found with MGA in J5

In the three problems considered, the solutions that minimize CO₂ emissions also have smaller numbers of buses in circulation, implying that emissions can be reduced without increasing the operational cost of the system. This situation, which is repeated in the sets of non-dominated solutions found for both the unimodal and bimodal problem, can be observed in the 9th column of Table 5. Moreover, the 10th and 11th columns show that for the P-TNDPc, the solutions that minimize bus emissions satisfy a greater proportion of the demand with respect to those solutions that minimize the travel time and increase the number of trips that include transfers. This is because, in the solutions in which travel times are minimized, more routes are selected and with greater frequencies to reduce waiting and transfer times. However, the used capacity of the buses in circulation is lower compared to that of the solutions that minimize emissions. Furthermore, it is observed that the variation in the distribution of the demand between buses and cars is not highly significant, with variations of less than 10%. Therefore, most of the variations in time and emissions are produced by traveling with public transportation. This is mainly due to the distribution model selected and the coefficients assigned to the model, which have been extracted from a state-of-the-art study. However, in the case of being applied to an actual instance, the coefficients must be estimated on the basis of the specific circumstances of an instance to achieve a true representation of the local reality.

The MGA provided better solutions in less time than the exact method. Table 6 shows the average running time required for the exact method (largest of the corresponding instances) and for the MGA. Notes that the running time required for the exact method corresponds to the generation of only one solution while the MGA generates a set of solutions in only one run. Moreover, the exact method was stopped after a predetermined running time. For the largest instance of the P-TNDPa in Cancela’s network (instance I4), each solution required more than 1000 s; a gap of approximately 10% was recorded between the found and feasible solutions. In turn, running the MGA on the same network (instance J1) provided a set of solutions within an average of 140 s. In the case of Mandl’s network, the mathematical programming model (instance I7) did not find any feasible solution within a 12-h period, whereas the MGA provided a set of efficient solutions after an average of 190 s for the same network (instance J4).

Table 6 Running time

6 Conclusions

In this study, we present mathematical models to design a multimodal transit system considering congestion and CO₂ pollution simultaneously. Such situations are embedded in three instances of the P-TNDP: P-TNDPa P-TNDPb and P-TNDPc. A mathematical programming model and a multi-objective genetic algorithm are proposed, considering the minimization of the total travel time and total emissions of the system subject to budgetary constraints. Although the TNDP has been extensively studied in the literature, incorporating environmental objectives and the study of bimodal networks and congested networks have received less attention, and to the best of our knowledge, there have been no prior studies that include all these aspects in a single model. The proposed mathematical model and the evolutionary algorithms are solved with several test instances, which are constructed based on three physical networks used in the literature and adapted to include the capacity of the arcs, which is a necessary aspect of estimating emissions in relation to the congestion in the arcs.

To find efficient Pareto frontier solutions, the ε-constraint method is applied to solve the mathematical programming model, whereas the MGA, which includes measures of quality and diversity, provides a set of solutions in a single run. The results show that for the studied instances, it is possible to achieve significant reductions of approximately 15% in the emissions of the public transportation systems by increasing the total travel time of the passengers by less than 2% relative to the solutions obtained with a single objective. This implies that solutions found in other studies could be improved by considering environmental objectives. Also, it is observed that the reductions in the emissions imply a reduction in the size of the fleet, which can imply a reduction in the operational cost of the system. By comparing the different solution methods, it is observed that the evolutionary algorithm provides better results than the mathematical programming model due to its greater flexibility.

The running times necessary to solve the mathematical programming model are high, even for small instances. Therefore, the proposed mathematical model is not suitable for the design of actual transit networks. In contrast, the evolutionary algorithm provides good solutions in significantly shorter times than the exact method. Therefore, this method is suitable for applications to real instances. Furthermore, by using approximate methods, aspects of greater complexity can be easily included.

As for the future work, the MGA may be modified in several ways to get better and more meaningful results. A more sophisticated emission model may be applied that, for example, considers the acceleration process during the stops of the buses instead of only the average speed. Furthermore, other pollutants may be considered besides CO₂, such as NO_x, PM or VOC, which have impacts not only on the environment but also on human health. Regarding the solution technique, the MGA could be adapted to incorporate a problem-specific solution representation and variation operators, which take advantage of the characteristics of the problem to generate better solutions. Also, the MGA may be tested in larger instances to fully determine its potential to be applied in real life problems.