A Comparison of Word2Vec, HMM2Vec, and PCA2Vec for Malware Classification

Abstract

Word embeddings are often used in natural language processing as a means to quantify relationships between words. More generally, these same word embedding techniques can be used to quantify relationships between features. In this paper, we first consider multiple different word embedding techniques within the context of malware classification. We use hidden Markov models to obtain embedding vectors in an approach that we refer to as HMM2Vec, and we generate vector embeddings based on principal component analysis. We also consider the popular neural network-based word embedding technique known as Word2Vec. In each case, we derive feature embeddings based on opcode sequences for malware samples from a variety of different families. We show that we can obtain better classification accuracy based on these feature embeddings, as compared to HMM experiments that directly use the opcode sequences, and serve to establish a baseline. These results show that word embeddings can be a useful feature engineering step in the field of malware analysis.

1 Introduction

Malware detection and analysis are critical aspects of information security. The 2019 Internet Threat Security Report [46] claims an increase of 25% in 1 year in the number of attack groups using malware to disrupt businesses and organizations. According to the 2016 California Data Breach Report [13], malware contributed to 54% of all breaches and 90% of total records breached, with a staggering 44 million records breached due to malware in the years 2012–2016. Statistics such as these imply that malware is an increasing threat.

In this paper, we apply machine learning classification techniques to engineered features that are derived from malware samples. This feature engineering involves machine learning techniques. In effect, we apply machine learning to higher level features, where these features are themselves obtained using machine learning models. The motivation is that machine learning can serve to distill useful information from training samples, and hence the classification techniques may perform better on such data. In this research, we consider the effectiveness of using these derived features in the context of malware classification.

Specifically, we use word embeddings based on opcodes to derive features for subsequent classification. We consider three distinct word embedding techniques. First, we derive word embeddings from trained hidden Markov models (HMM). We refer to this technique as HMM2Vec. We then consider an analogous technique based on principal component analysis (PCA), which we refer to as PCA2Vec. And, as a third approach, we experiment with the popular neural network-based word embedding technique known as Word2Vec. In each case, we generate word embeddings for a significant number of samples from a variety of malware families. We then use several classification techniques to determine how well we can classify these samples using word embeddings as features.

The remainder of this paper is organized as follows. We provide a selective survey of relevant related work in Sect. 2. Section 3 contains an extensive and wide-ranging discussion of machine learning topics that play a role in this research. In Sect. 4, we provide details on the word embedding techniques that form the basis of our experiments. Section 5 gives our experiments and results, while Sect. 6 provides our conclusion and some paths for future work.

2 Related Work

Malware analysis and detection are challenging problems due to a variety of factors, including the large volume of malware and obfuscation techniques [10]. Every day, thousands of new malware are generated—manual analysis techniques cannot keep pace. Obfuscation is widely used by malware developers to make it difficult to analyze their malicious code.

Signature-based malware detection methods rely on pattern matching with known signatures [47]. Signature detection is relatively fast, and it is effective against “traditional” malware. However, extracting signatures is a labor-intensive process, and obfuscation techniques can defeat signature scanning.

Anomaly-based techniques are based on “unusual” or “virus-like” behavior or characteristics. An example of anomaly detection is behavior-based analysis, which can be used to analyze a sample when executed or under emulation [47]. When an executable file performs any action that does not fit its expected behavior, an alarm can be triggered. Such a method can detect obfuscated and zero-day malware, but it is slow, and generally subject to excessive false positives.

Recently, machine learning techniques have proven extremely useful for malware detection. The effectiveness of machine learning algorithms depends on the characteristics of the features used by such models. In malware detection and classification, a sample can be represented by a wide variety of features, including mnemonic opcodes, raw bytes, API calls, permissions, header information, etc. Opcodes are a popular feature that form the basis of the analysis considered in this paper.

In [7], the author experiments with opcodes and determines that such features can be successfully used to detect malware. The paper [11] achieves good results using API calls as a feature. Such features can be somewhat more difficult for malware writers to obfuscate, since API calls relate to the essential activity of software. However, extracting API calls from an executable is more costly than extracting opcodes.

Another example of malware research involving opcodes can be found in [33]. This paper features opcode n-grams, with a Markov blanket used to select from the large set of available n-gram. Classification is based on hidden Markov models, and experiments are based on five malware families.

In [3], malware opcodes are treated as a language, with Word2Vec used to quantify contextual information. Classification relies on k-nearest neighbors (${k}-NN$). The research in [34] also uses Word2Vec to generate feature vectors based on opcode sequences, with a deep neural network employed for malware classification. In this latter research, the number of opcodes is in the range of 50–200, and the length of the Word2Vec embeddings range from 250 to 750.

Word2Vec embeddings are used as features to train bi-directional LSTMs in [20]. The experiments achieve good accuracy for malware detection, but training is costly. In [14], the author proposed a word embedding method based on opcode graphs—the graph is projected into vector space, which yields word embeddings. This technique is also computationally expensive.

In comparison to previous research, we consider additional vector embedding techniques, we experiment with a variety of classification algorithms, we use a smaller number of opcodes, and we generate short embedding vectors. Since we use a relatively small number of opcodes and short embedding vectors, our techniques are all highly efficient and practical. In addition, our experiments are based on a recently collected and challenging malware dataset.

3 Background

In this section, we present background information on the various learning techniques that are used in the experiments discussed in Sect. 5. Specifically, we introduce neural networks, beginning with some historical background and moving on to a modern context. We also introduce HMMs and PCA, which form the basis for the word embedding techniques that we refer to as HMM2Vec and PCS2Vec, respectively. Finally, we introduce four classification techniques, which are used in our experiments.

In Sect. 4, we discuss HMM2Vec, PCA2Vec, and the neural network-based word embedding technique, Word2Vec, in detail. For our experiments in Sect. 5, we use these three word embedding techniques to generate features to classify malware samples.

Fig. 1

Artificial neuron

3.1 Neural Networks

The concept of an artificial neuron [12, 49] is not new, as the idea was first proposed by McCulloch and Pitts in the 1940s [22]. However, modern computational neural networks begins with the perceptron, as introduced by Rosenblatt in the late 1950s [37].

3.1.1 McCulloch–Pitts Artificial Neuron

An artificial neuron with three inputs is illustrated in Fig. 1. In the original McCulloch–Pitts formulation, the inputs $X_i\in \{0,1\}$, the weights $w_i\in \{+1,-1\}$, and the output $Y\in \{0,1\}$. The output Y is 0 (inactive) or 1 (active), based on whether or not the linear function $\sum w_i X_i$ exceeds the specified threshold T. This form of an artificial neuron was modeled on neurons in the brain, which either fire or it do not (thus $Y\in \{0,1\}$), and have input that comes from other neurons (thus each $X_i\in \{0,1\}$). The weights $w_i$ specify whether an input is excitatory (increasing the chance of the neuron firing) or inhibitory (decreasing the chance of the neuron firing). Whenever $\sum w_i X_i > T$, the excitatory response wins, and the neuron fires—otherwise the inhibitory response wins and the neuron does not fire.

3.1.2 Perceptron

A perceptron is less restrictive than a McCulloch–Pitts artificial neuron. With a perceptron, both the inputs $X_i$ and the weights $w_i$ can be real valued, as opposed to the binary restrictions of McCulloch–Pitts. As with the McCulloch–Pitts formulation, the output Y of a perceptron is generally taken to be binary.

Given a real-valued input vector $X=(X_0,X_1,\ldots ,X_{n-1})$, a perceptron can be viewed as an instantiation of a function of the form

$$ f(X) = \sum _{i=0}^{n-1} w_i X_i + b , $$

that is, a perceptron computes a weighted sum of the input components. Based on a threshold, a single perceptron can define a binary classifier. That is, we can classify a sample X as “type 1” provided that $f(X) > T$, for some specified threshold T, and otherwise we classify X as “type 0.”

In the case of two-dimensional input, the decision boundary of a is of the form

$$\begin{aligned} f(x,y) = w_0 x + w_1 y + b \end{aligned}$$

(1)

which is the equation of a line. In general, the decision boundary of a perceptron is a hyperplane. Hence, a perceptron can only provide ideal separation in cases where the data itself is linearly separable.

As the name suggests, a multilayer perceptron (MLP) is an ANN that includes multiple (hidden) layers in the form of perceptrons. An example of an MLP with two hidden layers is given in Fig. 2, where each edge represent a weight that is to be determined via training. Unlike a single layer perceptron, MLPs are not restricted to linear decision boundaries, and hence an MLP can accurately model more complex functions. For example, the XOR function—which cannot be modeled by a single layer perceptron—can be modeled by an MLP.

To train a single layer perceptron, simple heuristics will suffice, assuming that the data is actually linearly separable. From a high-level perspective, training a single layer perceptron is somewhat analogous to training a linear support vector machine (SVM), except that for a perceptron, we do not require that the margin (i.e., minimum separation between the classes) be maximized. But training an MLP is clearly far more challenging, since we have hidden layers between the input and output, and it is not obvious how changes to the weights in these hidden layers will affect each other or the output.

Fig. 2

MLP with two hidden layers

As an aside, it is interesting to note that for SVMs, we deal with data that is not linearly separable by use of the “kernel trick,” where the input data is mapped to a higher dimensional “feature space” via a (nonlinear) kernel function. In contrast, perceptrons (in the form of MLPs) overcome the limitation of linear separability by the use of multiple layers. With an MLP, it is as if a nonlinear kernel function has been embedded directly into the model itself through the use of hidden layers, as opposed to a user-specified explicit kernel function, which is the case for an SVM.

We can view the relationship between ANNs and deep learning as being somewhat akin to that of Markov chains and hidden Markov models (HMM). That is, ANNs serve as a basic technology that can be used to build powerful machine learning techniques, analogous to the way that an HMM is built on the foundation of an elementary Markov chain.

3.2 Hidden Markov Models

A generic hidden Markov model is illustrated in Fig. 3, where the $X_i$ represent the hidden states and all other notations are shown in Table 1. The state of the Markov process, which we can be viewed as being hidden behind a “curtain” (the dashed line in Fig. 3), is determined by the current state and the A matrix. We are only able to observe the observations ${\mathscr {O}}_i$, which are related to the (hidden) states of the Markov process by the matrix B.

Fig. 3

Hidden Markov model

3.2.1 Notation and Basics

The notation used in an HMM is summarized in Table 1. Note that the observations are assumed to come from the set $\{0,1,\ldots ,M-1\}$, which simplifies the notation with no loss of generality. That is, we simply associate each of the M distinct observations with one of the elements $0,1,\ldots ,M-1$, so that we have ${\mathscr {O}}_i\in V=\{0,1,\ldots ,M-1\}$ for $i=0,1,\ldots ,T-1$.

Table 1 HMM notation

The matrix $A=\{a_{ij}\}$ is $N\times N$ with

$$ a_{ij} = P(\text{state } q_j \text{ at } t+1\,|\, \text{ state } q_i \text{ at } t) . $$

The matrix A is row stochastic, that is, each row satisfies the properties of a discrete probability distribution. Also, the probabilities $a_{ij}$ are independent of t, and hence the A matrix does not vary with t. The matrix $B=\{b_j(k)\}$ is of size $N\times M$, with

$$ b_j(k) = P(\text{observation } k \text{ at } t\,|\, \text{ state } q_j \text{ at } t) . $$

As with the A matrix, B is row stochastic, and the probabilities $b_j(k)$ are independent of t. The somewhat unusual notation $b_j(k)$ is convenient when specifying the HMM algorithms.

An HMM is defined by A, B, and $\pi$ (and, implicitly, by the dimensions N and M). Thus, we denote an HMM as $\lambda = (A,B,\pi )$.

Suppose that we are given an observation sequence of length four, that is,

$$ {\mathscr {O}}= \bigl ( {\mathscr {O}}_0,{\mathscr {O}}_1,{\mathscr {O}}_2,{\mathscr {O}}_3 \bigr ) . $$

Then the corresponding (hidden) state sequence is denoted as

$$ X = \bigl ( X_0,X_1,X_2,X_3 \bigr ) . $$

We let  denote the probability of starting in state $X_0$, and  denotes the probability of initially observing ${\mathscr {O}}_0$, while  is the probability of transiting from state $X_0$ to state $X_1$. Continuing, we see that the probability of a given state sequence X of length four is

(2)

Note that in this expression, the $X_i$ represent indices in the A and B matrices, not the names of the corresponding states.

To find the optimal state sequence in the dynamic programming (DP) sense, we simply choose the sequence (of length four, in this case) with the highest probability. In contrast, to find the optimal state sequence in the HMM sense, we choose the most probable symbol at each position. The optimal DP sequence and the optimal HMM sequence can differ.

3.2.2 The Three Problems

There are three fundamental problems that we can solve using HMMs. Here, we briefly describe each of these problems.  

Problem 1:

Given the model $\lambda = (A,B,\pi )$ and a sequence of observations ${\mathscr {O}}$, determine $P({\mathscr {O}}\,|\,\lambda )$. That is, we want to compute a score for the observed sequence ${\mathscr {O}}$ with respect to the given model $\lambda$.

Problem 2:

Given $\lambda = (A,B,\pi )$ and an observation sequence ${\mathscr {O}}$, find an optimal state sequence for the underlying Markov process. In other words, we want to uncover the hidden part of the hidden Markov model.

Problem 3:

Given an observation sequence ${\mathscr {O}}$ and the parameter N, determine a model $\lambda = (A,B,\pi )$ that maximizes the probability of ${\mathscr {O}}$. This can be viewed as training a model to best fit the observed data. This problem is generally solved using Baum–Welch re-estimation [35, 43], which is a discrete hill climb on the parameter space represented by A, B, and $\pi$. There is also an alternative gradient ascent technique for HMM training [4, 45].

 

Since the technique we use to train an HMM (Problem 3) is a hill climb, in general, we obtain a local maximum. Training with different initial conditions can result in different local maxima, and hence it is often beneficial to train multiple HMMs with different initial conditions, and select the highest scoring model.

3.2.3 Example

Consider, for example, the problem of speech recognition which, not coincidentally, is one of the earliest and best-known successes of HMMs. In speech problems, the hidden states can be viewed as corresponding to movements of the vocal cords, which are not directly observed. Instead, we observe the sounds that are produced, and extract training features from these sounds. In this scenario, we can use the solution to HMM Problem 3 to train an HMM $\lambda$ to, for example, recognize the spoken word “yes.” Then, given an unknown spoken word, we can use the solution to Problem 1 to score the word against the trained model $\lambda$ and determine the likelihood that the word is “yes.” In this case, we do not need to solve Problem 2, but it is possible that such a solution (i.e., uncovering the hidden states) might provide additional insight into the underlying speech model.

English text analysis is another classic application of HMMs, which appears to have been first considered by Cave and Neuwirth [9]. This application nicely illustrates the strength of HMMs and it requires no background in any specialized field, such as speech processing or information security.

Given a length of English text, we remove all punctuation, numbers, etc., and converts all letters to lower case. This leaves 26 distinct letters and word-space, for a total of 27 symbols. We assume that there is an underlying Markov process (of order one) with two hidden states. For each of these two hidden states, we assume that the 27 symbols are observed according to fixed probability distributions.

This defines an HMM with $N=2$ and $M=27$, where the state transition probabilities of the A matrix and the observation probabilities of the B matrix are unknown, while the observations ${\mathscr {O}}_t$ consist of the series of characters we have extracted from the given text. To determine the A and B matrices, we must solve HMM Problem 3, as discussed above.

We have trained such an HMM, using the first $T=50{,}000$ observations from the Brown Corpus,¹ which is available at [8]. We initialized each element of $\pi$ and A randomly to approximately 1/2, taking care to sure that the matrices are row stochastic. For one specific iteration of this experiment, the precise values used were

and

$$ A = \left( \begin{array}{cc} 0.47468 &{} 0.52532\\ 0.51656 &{} 0.48344 \end{array}\right) \! . $$

Each element of B was initialized to approximately 1/27, again, under the constraint that B must be row stochastic. The values in the initial B matrix (more precisely, the transpose of B) appear in the second and third columns of Table 2.

Table 2 Initial and final $B^T$

After the initial iteration, we find $\text{ log }\bigl (P({\mathscr {O}}\,|\lambda )\bigr ) = -165097.29$ and after 100 iterations, we have $\text{ log }\bigl (P({\mathscr {O}}\,|\,\lambda )\bigr ) = -137305.28 .$ These model scores indicate that training has improved the model significantly over the 100 iterations.

In this particular experiment, after 100 iterations, the model $\lambda =(A,B,\pi )$ has converged to

with the converged $B^T$ appearing in the last two columns of Table 2.

The most interesting part of an HMM is generally the B matrix. Without having made any assumption about the two hidden states, the B matrix in Table 2 shows us that one hidden state consists of vowels while the other hidden state consists of consonants. Curiously, from this perspective, word-space acts more like a vowel, while y is not even sometimes a vowel.

Of course, anyone familiar with English would not be surprised that there is a significant distinction between vowels and consonants. But, the crucial point here is that the HMM has automatically extracted this statistically important distinction for us—it has “learned” to distinguish between consonants and vowels. And, thanks to HMMs, this feature of English text could be easily discovered by someone who previously had no knowledge whatsoever of the language.

Cave and Neuwirth [9] obtain additional results when considering HMMs with more than two hidden states. In fact, they are able to sensibly interpret the results for models with up to $N=12$ hidden states.

For more information on HMMs, see [43], which includes detailed algorithms including scaling or Rabiner’s classic paper [35].

3.3 Principal Component Analysis

Principal component analysis (PCA) is a linear algebraic technique that provides a powerful tool for dimensionality reduction. Here, we provide a very brief introduction to the topic; for more details, Shlens’ tutorial is highly recommended [40], while a good source for the math behind PCA is [39]. The discussion at [42] provides a brief, intuitive, and fun introduction to the subject.

Geometrically, PCA aligns a basis with the (orthogonal) directions having the largest variances. These directions are defined to be the principal components. A simple illustration of such a change of basis appears in Fig. 4.

Fig. 4

A better basis

Intuitively, larger variances correspond to more informative data—if the variance is small, the training data is clumped tightly around the mean and we have limited ability to distinguish between samples. In contrast, if the variance is large, there is a much better chance of separating the samples based on the characteristic (or characteristics) under consideration. Consequently, once we have aligned the basis with the variances, we can ignore those directions that correspond to small variances without losing significant information. In fact, small variances often contribute only noise, in which cases we can actually improve our results by neglecting those directions that correspond to small variances.

The linear algebra behind PCA training (i.e., deriving a new-and-improved basis) is fairly deep, involving eigenvalue analysis. Yet, the scoring phase is simplicity itself, requiring little more than the computation of a few dot products, which makes scoring extremely efficient and practical.

Note that we treat singular value decomposition (SVD) as a special case of PCA, in the sense that SVD provides a method for determining the principal components. It is possible to take the opposite perspective, where PCA is viewed as a special case of the general change of basis technique provided by SVD. In any case, for our purposes, PCA and SVD can be considered as essentially synonymous.

3.4 Classifiers

In the research presented in this paper, we consider four different classifiers, namely, k-nearest neighbors (${k}-NN$), multilayer perceptron (MLP), random forest (RF), and support vector machine (SVM). We have already discussed MLPs above, so in this section, we give a brief overview of ${k}-NN$, RF, and SVM.

3.4.1 k-Nearest Neighbors

Perhaps the simplest possible machine learning algorithm is k-nearest neighbors (${k}-NN$). In the scoring phase, ${k}-NN$ consists of classifying based on the k-nearest samples in the training set, typically using a simple majority vote. Since all computation is deferred to the scoring phase, ${k}-NN$ is considered to be a “lazy learner.”

Fig. 5

Examples of ${k}-NN$ classification [44]

Figure 5 shows examples of ${k}-NN$, where the training data consists of two classes, represented by the open blue squares and the solid red circles, with the green diamond (the point labeled X) being a point that we want to classify. Figure 5a shows that if we use the 1-nearest neighbor, we would classify the green diamond as being of same type as the open blue squares, whereas Fig. 5b shows that X would be classified as the solid red circle type if using the 3-nearest neighbors.

3.4.2 Random Forest

A random forest (RF) generalizes a simple decision tree algorithm. A decision tree is constructed by building a tree, based on features from the training data. It is easy to construct such trees, and trivial to classify samples once a tree has been constructed. However, decision trees tend to overfit the input data.

An RF combines multiple decision trees to generalize the training data. To do so, RFs use different subsets of the training data as well as different subsets of features, a process known as bagging [44]. A simple majority vote of the decision trees comprising the RF is typically used for classification [18].

3.4.3 Support Vector Machine

Support vector machines (SVM) are a class of supervised learning methods that are based on four major ideas, namely, a separating hyperplane, maximizing the “margin” (i.e., separation between classes), working in a higher dimensional space, and the so-called kernel trick. The goal in SVM is to use a hyperplane to separate labeled data into two classes. If it exists, such a hyperplane is chosen to maximize the margin [44].

An example of a trained SVM is illustrated in Fig. 6. Note that the points that actually minimize the distance to the separating hyperplane correspond to support vectors. In general, the number of support vectors will be small relative to the number of training data points, and this is the key to the efficiency of SVM in the classification phase.

Fig. 6

Support vectors in SVM [44]

Of course, there is no assurance that the training data will be linearly separable. In such cases, a nonlinear kernel function can be embedded into the SVM process in such a way that the input data is, in effect, transformed to a higher dimensional “feature space.” In this higher dimensional space, it is far more likely that the transformed data will be linearly separable. This is the essence of the kernel trick—an example of which is illustrated in Fig. 7. That we can transform our training data in such a manner is not surprising, but the fact that we can do so without paying any significant penalty in terms of computational efficiency makes the kernel trick a very powerful “trick” indeed. However, the kernel function must be specified by the user, and selecting an (near) optimal kernel can be challenging.

Fig. 7

A function $\phi$ illustrating the kernel trick [44]

3.4.4 Last Word on Classification Techniques

We note in passing that MLP and SVM are related techniques, as both of these approaches generate nonlinear decision boundaries (assuming a nonlinear kernel). For SVM, the nonlinear boundary is based on a user-specified kernel function, whereas the equivalent aspect of an MLP is learned as part of the training process—in effect, the “kernel” is learned when training an MLP. This suggests that MLPs have an advantage, since there are limitations on SVM kernels, and selecting an optimal kernel is more art than science. However, the trade-off is that more data and more computation will generally be required to train a comparable MLP, since the MLP has more to learn, in comparison to an SVM.

It is also the case that ${k}-NN$ and RF are closely related. In fact, both are neighborhood-based algorithms, but with neighborhood structures that are somewhat different [19].

Thus, we generally expect that the results obtained using SVM and MLP will be qualitatively similar, and the same is true when comparing results obtained using ${k}-NN$ and RF. By using these four classifiers, we obtain a “sanity check” on the results. If, for example, our SVM and MLP results differ dramatically, this would indicate that we should investigate further. On the other hand, if, say, our MLP and RF results differ significantly, this would not raise the same level of concern.

4 Word Embedding Techniques

Word embeddings are often used in natural language processing as they provide a way to quantify relationships between words. Here, we use word embeddings to generate higher level features for malware classification.

In this section, we discuss three distinct word embedding techniques. First, we consider word embeddings derived from trained HMMs, which we refer to as HMM2Vec. Then we consider a word embedding technique based on PCA, which we refer to as PCA2Vec. Finally, we discuss the popular neural network-based technique known as Word2Vec.

4.1 HMM2Vec

Before discussing the basic ideas behind Word2Vec, we consider a somewhat analogous approach to generating vector representations based on hidden Markov models. To begin with we consider individual letters, as opposed to words—we call this simpler version Letter2Vec.

Recall that an HMM is defined by the three matrices A, B, and $\pi$, and is denoted as $\lambda =(A,B,\pi )$. The $\pi$ matrix contains the initial state probabilities, A contains the hidden state transition probabilities, and B consists of the observation probability distributions corresponding to the hidden states. Each of these matrices is row stochastic, that is, each row satisfies the requirements of a discrete probability distribution. Notation-wise, N is the number of hidden states, M is the number of distinct observation symbols, and T is the length of the observation (i.e., training) sequence. Note that M and T are determined by the training data, while N is a user-defined parameter.

Suppose that we train an HMM on a sequence of letters extracted from English text, where we convert all uppercase letters to lowercase and discard any character that is not an alphabetic letter or word-space. Then $M=27$, and we select $N=2$ hidden states, and we use $T=50{,}000$ observations for training. Note that each observation is one of the $M=27$ symbols (letters plus word-space). For the example discussed below, the sequence of $T=50{,}000$ observations was obtained from the Brown corpus of English [8]. Of course, any source of English text could be used.

In one specific case, an HMM trained with the parameters listed in the previous paragraph yields the B matrix in Table 2. Observe that this B matrix gives us two probability distributions over the observation symbols—one for each of the hidden states. We observe that one hidden state essentially corresponds to vowels, while the other corresponds to consonants. This simple example nicely illustrates the concept of machine learning, as no assumption was made a priori concerning consonants and vowels, and the only parameter we selected was the number of hidden states N. Thanks to this training process, the model has learned a crucial aspect of English directly from the data.

Suppose that for a given letter $\ell$, we define its Letter2Vec representation $V(\ell )$ to be the corresponding row of the converged matrix $B^T$ in the last two columns of Table 2. Then, for example,

(3)

Next, we consider the distance between these Letter2Vec embeddings. However, instead of using Euclidean distance, we measure distance based on cosine similarity.

The cosine similarity of vectors X and Y is the cosine of the angle between the two vectors. Let $X=(X_0,X_1,\ldots ,X_{n-1})$ and $Y=(Y_0,Y_1,\ldots ,Y_{n-1})$. Then the cosine similarity is given by

$$ \cos _{\theta }(X,Y) = \frac{\displaystyle \sum _{i=0}^{n-1} X_i Y_i}{ \sqrt{\displaystyle \sum _{i=0}^{n-1} X_i^2}\sqrt{\displaystyle \sum _{i=0}^{n-1} Y_i^2}}. $$

In general, $-1\le \cos _{\theta }(X,Y)\le 1$, but since our Letter2Vec encoding vectors consist of probabilities—and hence are non-negative—we have $0\le \cos _{\theta }(X,Y)\le 1$ for the X and Y under consideration.

For the vector encodings in (3), we find that for the vowels “a” and “e,” the cosine similarity is $\cos _{\theta }(V({{\,\mathrm{a}\,}}),V({{\,\mathrm{e}\,}}))=0.9999$. In contrast, the cosine similarity between the vowel “a” and the consonant “t” is $\cos _{\theta }(V({{\,\mathrm{a}\,}}),V({{\,\mathrm{t}\,}}))=0.0817$. These results indicate that these Letter2Vec embeddings—which are derived from a trained HMM—provide useful information on the similarity (or not) of pairs of letters.

Analogous to our Letter2Vec embeddings, we could train an HMM on words (or other features) and then use the columns of the resulting B matrix (equivalently, the rows of $B^T$) to define word (feature) embeddings.

The state of the art for Word2Vec based on words from English text is trained on a dataset corresponding to $M=10{,}000$, $N=300$ and $T=10^9$. Training an HMM with such parameters would be decidedly non-trivial, as the work factor for Baum–Welch re-estimation is on the order of $N^2 T$.

While the word embedding technique discussed in the previous paragraph—we call it HMM2Vec—is plausible, it has some potential limitations. Perhaps the biggest issue with HMM2Vec is that we typically train an HMM based on a Markov model of order one. That is, the current state only depends on the immediately preceding state. By basing our word embeddings on such a model, the resulting vectors would likely provide only a very limited sense of context. While we can train HMMs using models of higher order, the work factor would be prohibitive.

4.2 PCA2Vec

Another option for generating embedding vectors is to apply PCA to a matrix of pointwise mutual information (PMI). To construct a PMI matrix, based on a specified window size W, we compute $P(w_i,w_j)$ for all pairs of words $(w_i,w_j)$ that occur within a window W of each other within our dataset, and we also compute $P(w_i)$ for each individual word $w_i$. Then we define the PMI matrix as

$$ X = \{x_{ij}\} = \text{ log }\frac{P(w_j,w_i)}{P(w_i)P(w_j)}. $$

We treat column i of X, denoted $X_i$, as the feature vector for word $w_i$. Next, we perform PCA (using a singular value decomposition) based on these $X_i$ feature vectors, and we project the feature vectors $X_i$ onto the resulting eigenspace. Finally, by choosing the N dominant eigenvalues for this projection, we obtain embedding vectors of length N.

It is shown in [32] that these embedding vectors have many similar properties as Word2Vec embeddings, with the author providing examples analogous to those we give in the next section. Interestingly, it may be beneficial in certain applications to omit some of the dominant eigenvectors when determining the PCA2Vec embedding vectors [17].

For more details on using PCA to generate word embeddings, see [17]. The aforecited blog [32] gives an intuitive introduction to the topic.

4.3 Word2Vec

Word2Vec is a technique for embedding “words”—or more generally, any features—into a high-dimensional space. In Word2Vec, the embeddings are obtained by training a shallow neural network. After the training process, words that are more similar in context will tend to be closer together in the Word2Vec space.

Perhaps surprisingly, certain algebraic properties also hold for Word2Vec embeddings. For example, according to [30], if we let

and we define $V(w_i)$ to be the Word2Vec embedding of $w_i$, then $V(w_3)$ is the vector that is closest to

$$ V(w_0) - V(w_1) + V(w_2), $$

where “closest” is in terms of cosine similarity. Results such as this indicate that Word2Vec embeddings capture meaningful aspects of the semantics of the language.

Word2Vec uses a similar approach as the HMM2Vec concept outlined above. But, instead of using an HMM, Word2Vec embeddings are obtained from shallow (one hidden layer) neural network. Analogous to HMM2Vec, in Word2Vec, we are not interested in the resulting model itself, but instead we make use the learning that is represented by the trained model to define word embeddings. Next, we consider the basic ideas behind Word2Vec. Our approach is similar to that found in the excellent tutorial [21]. Here, we describe the process in terms of words, but these “words” can be general features.

Suppose that we have a vocabulary of size M. We encode each word as a “one-hot” vector of length M. For example, suppose that our vocabulary consists of the set of $M=8$ words

Then we encode “for” and “man” as

respectively.

Now, suppose that our training data consists of the phrase

(4)

To obtain our training samples, we specify a window size W, and for each offset we consider pairs of words within the specified window. For this example, we select $W=2$, so that we consider words at a distance of one or two, in either direction. For the sentence in (4), a window size of two gives us the training pairs in Table 3.

Table 3 Training data

Consider the pair “(for,man)” from the fourth row in Table 3. As one-hot vectors, this training pair corresponds to the input vector 10000000 and output vector 00010000.

A neural network similar to that illustrated in Fig. 8 is used to generate Word2Vec embeddings. The input is a one-hot vector of length M representing the first element of a training pair, such as those in Table 3. The network is trained to output the second element of each ordered pair which, again, is represented as a one-hot vector. The hidden layer consists of N linear neurons and the output layer uses a softmax function to generate M probabilities, where $p_i$ is the probability of the output vector corresponding to $w_i$ for the given input.

Fig. 8

Neural network for Word2Vec embeddings

Observe that the Word2Vec network in Fig. 8 has NM weights that are to be determined via training, and these weights are represented by the blue lines from the hidden layer to the output layer. For each output node $\omega _i$, there are N edges (i.e., weights) from the hidden layer. The N weights that connect to output node $\omega _i$ form the Word2Vec embedding $V(w_i)$ of the word $w_i$.

The state of the art in Word2Vec for English text is trained on a vocabulary of some $M=10{,}000$ words, and embedding vectors of length $N=300$, training on about $10^9$ samples. Clearly, training a model of this magnitude is an extremely challenging computational task, as there are $3\times 10^6$ weights to be determined, not to mention a huge number of training samples to deal with. Most of the complexity of Word2Vec comes from tricks that are used to make it feasible to train such a large network with such a massive amount of data.

One trick that is used to speed training in Word2Vec is “subsampling” of frequent words. Common words such as “a” and “the” contribute little to the model, so these words can appear in training pairs at a much lower rate than they are present in the training text.

Another key trick that is used in Word2Vec is “negative sampling.” When training a neural network, each training sample potentially affects all of the weights of the model. Instead of adjusting all of the weights, in Word2Vec, only a small number of “negative” samples have their weights modified per training sample. For example, suppose that the output vector of a training pair corresponds to word $w_0$. Then the “positive” weights are those connected to the output node $\omega _0$, and these weights are modified. In addition, a small subset of the $M-1$ “negative” words (i.e., every word in the dataset except $w_0$) are selected and their corresponding weights are adjusted. The distribution used to select negative cases is biased toward more frequent words.

A general discussion of Word2Vec can be found in [5], while an intuitive—yet reasonably detailed—introduction is given in [21]. The original paper describing Word2Vec is [30] and an immediate follow-up paper discusses a variety of improvements that mostly serve to make training practical for large datasets [31].

5 Experiments and Results

In this section, we summarize our experimental results. These results are based on HMM2Vec, PCA2Vec, and Word2Vec experiments. But, first we discuss the dataset that we have used for all of the experiments reported in this section.

5.1 Dataset

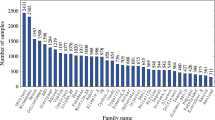
The experimental results discussed in this section are based on the families in Table 4, with the number of available samples listed. In order to keep the test set balanced, from each of these families, we randomly selected 1000 samples, for a total of 7000 samples in our classification experiments. These families have been used in many recent studies, including [6, 48], for example.

Table 4 Malware families and the number of samples

The malware families in Table 4 are of a wide variety of different types. Next, we briefly discuss each of these families.

 

BHO:

can perform a wide variety of malicious actions, as specified by an attacker [25].

CeeInject:

is designed to conceal itself from detection, and hence various families use it as a shield to prevent detection. For example, CeeInject can obfuscate a bitcoin mining client, which might have been installed on a system without the user’s knowledge or consent [24].

FakeRean:

pretends to scan the system, notifies the user of nonexistent issues, and asks the user to pay to clean the system [29].

OnLineGames:

steals login information of online games and tracks user keystroke activity [26].

Renos:

will claim that the system has spyware and ask for a payment to remove the supposed spyware [23].

Vobfus:

is a family that downloads other malware onto a user’s computer and makes changes to the device configuration that cannot be restored by simply removing the downloaded malware [27].

Winwebsec:

is a trojan that presents itself as antivirus software—it displays misleading messages stating that the device has been infected and attempts to persuade the user to pay a fee to free the system of malware [28].

 

In the remainder of this section, we present our experimental results. First, we discuss the selection of parameters for the various classifiers. Then we give results from a series of experiments for malware classification, based on each of the three word embedding techniques discussed in Sect. 4, namely, HMM2Vec, PCA2Vec, and Word2Vec. Note that all of our experiments were performed using scikit-learn [38].

Table 5 Classifier hyperparameters tested

Table 6 Classifier hyperparameters selected

5.2 Classifier Parameters

For each of our word embedding classification experiments, we test the three classifiers discussed in Sect. 3.4, namely, k-nearest neighbors (${k}-NN$), random forest (RF), and support vector machine (SVM), along with the multilayer perceptron (MLP), which is discussed in Sect. 3.1.2. The features considered are the word embeddings from HMM2Vec, PCA2Vec, and Word2Vec. Note that this gives us a total of 12 distinct experiments.

For each case, we performed a grid search over a set of hyperparameters using GridSearchCV [41] in scikit-learn. GridSearchCV performs fivefold cross validation to determine the best parameters for each embedding technique. The parameters tested are listed in Table 5. Observe that for each of the three different word embedding techniques, we tested 36 combinations of parameters for MLP, we tested 12 combinations for SVM, we tested 16 combinations for ${k}-NN$, and we tested 400 RF combinations. Overall, we conducted

$$ 3\cdot (36+12+16+400) = 1392 $$

experiments to determine the parameters for the remaining experiments.

The optimal parameters selected for each classifier and for each embedding technique are listed in Table 6. We note that overall there is considerable agreement between the parameters for the different word embedding techniques, but in two cases ( and ), a different parameter is selected for each of the three embedding techniques.

5.3 Baseline Results

First, we consider experiments based on opcode sequences and HMMs. These results serve as a baseline for comparison with the vector embedding techniques that are the primary focus of this research. We choose these HMM-based experiments for the baseline, as HMM trained on opcode features have proven popular and highly successful in the field of malware analysis [1, 2, 16, 36, 50].

Specifically, we train an HMM for each of the seven families in our dataset, using $N=2$ hidden states in each case. For classification, we score a sample against all seven of these HMMs, and the resulting score vector (of length seven) serves as our feature vector. We use the same classification algorithms as in our word embedding experiments, namely, ${k}-NN$, MLP, RF, and SVM.

Note that we use the same opcode sequences here as in our vector embedding experiments. Specifically, the top 20 most frequent opcodes are used, with all remaining opcodes deleted.

The confusion matrices for these baseline HMM experiments are given in Fig. 9. The accuracies obtained for ${k}-NN$, MLP, RF, and SVM are 0.92, 0.44, 0.91, and 0.78, respectively. We see that MLP and SVM both perform poorly, whereas the neighborhood-based techniques, namely, ${k}-NN$ and RF, are both strong, considering that we have seven classes. In addition, ${k}-NN$ and RF give very similar results.

Fig. 9

Confusion matrices for baseline HMM experiments

5.4 HMM2Vec Results

For these experiments, we train an HMM on each sample in our dataset. Recall that our dataset consists of 1000 samples from each of the seven families listed in Table 4. We train each of these 7000 models with $N=2$ hidden states, using the $M=20$ most frequent opcodes over all malware samples. Opcodes outside the top 20 are ignored.

As mentioned in Sect. 3.2.2, we often train multiple HMMs with different initial conditions, and select the best scoring model. This becomes more important as the length of the observation sequence decreases. Hence, when training our HMMs, we perform multiple random restarts—the number of restarts is determined by the length of the training sequence, as indicated in Table 7.

Table 7 Number of random restarts

Each B matrix is $2\times 20$, where each row corresponds to one of the hidden states of the model. From each of these matrices, we construct a vector of length 40 by appending the two rows. Since the order of the hidden states can vary between models, we select the order of the rows so as to obtain a consistency with respect to the most common opcode. That is, the row corresponding to the state that accumulates the highest probability for MOV is the first half of the feature vector, with the other row of the B matrix becoming the last 20 elements of the feature vector. This accounts for any cases where the hidden states differ.

Based on the resulting feature vectors, we use the parameters in the HMM2Vec column of Table 6 to classify the samples using ${k}-NN$, MLP, RF, and SVM. The confusion matrices for each of these cases is give in Fig. 10.

Fig. 10

Confusion matrices for HMM2Vec experiments

The accuracies obtained for ${k}-NN$, MLP, RF, and SVM based on HMM2Vec features are 0.93, 0.91, 0.93, and 0.89, respectively. From the confusion matrices in Fig. 10, we see that the greatest source of misclassifications is between FakeRean and Winwebsec families. In most—but not all—of our subsequent experiments, these two families will prove to be the most challenging to distinguish.

5.5 PCA2Vec Results

For our PCA2Vec experiments, we generate embedding vectors for each of the 7000 samples in our training set, as discussed in Sect. 4.2. We then train and classify the 7000 malware samples using these PCA2Vec feature vectors. The confusion matrices for these experiments are summarized in Fig. 11.

Fig. 11

Confusion matrices for PCA2Vec experiments

As above, each model is based on the 20 most frequent opcodes, which gives us a $20\times 20$ PMI matrix. For consistency with the HMM2Vec experiments discussed above, we consider the two most dominant eigenvectors, and for consistency with the Word2Vec models discussed below, we use a window size of $W=10$ when constructing the PMI matrix. The resulting projection into the eigenspace is $2\times 20$, which we vectorize to obtain a feature vector of length 40.

The accuracies obtained for ${k}-NN$, MLP, RF, and SVM based on PCA2Vec features are 0.84, 0.78, 0.88, and 0.76, respectively. From these numbers, we see that PCA2Vec performed poorly for each of the classifiers considered, as compared to HMM2Vec.

5.6 Word2Vec Results

Analogous to the HMM2Vec and PCA2Vec experiments above, we classify the samples using the same four classifiers but with Word2Vec embeddings as features. The confusion matrices for these experiments are given in Fig. 12.

Fig. 12

Confusion matrices for Word2Vec experiments

As with the PCA2Vec experiments above, to generate our Word2Vec models, we use a window size of $W=10$. And, to be consistent with both the HMM2Vec and PCA2Vec models discussed above, we use a vector length of two, giving us feature vectors of length 40. We use the so-called continuous-bag-of-words (CBOW) model, which is the model that we described in Sect. 4.3.

The accuracies obtained for ${k}-NN$, MLP, RF, and SVM based on Word2Vec features are 0.93, 0.91, 0.93, and 0.89, respectively. These results match those obtained using HMM2Vec.

In Sect. 5.8, we compare the accuracies obtained in our baseline HMM, HMM2Vec, PCA2Vec, and Word2Vec experiments. But first we discuss possible overfitting issues with respect to the ${k}-NN$ and RF classifiers discussed above.

5.7 Overfitting

As discussed above in Sect. 3.4.4, both ${k}-NN$ and random forest are neighborhood-based classification algorithms, but with different neighborhood structure. Thus, we expect that these two classification algorithms will generally perform in a somewhat similar manner, at least in a qualitative sense.

For ${k}-NN$, small values of k tend to result in overfitting. To avoid overfitting, the rule of thumb is that we should choose $k\approx \sqrt{N}$, where N is the number of samples in the training set [15]. Since we use an 80-20 split for training-testing and we have 7000 samples, for our ${k}-NN$ experiments, this rule of thumb gives us $k=\sqrt{5600}\approx 75$. However, for each feature set considered, our grid search yielded an optimal value of $k\le 3$.

In Fig. 13, we graph the accuracy of ${k}-NN$ as a function of k for the baseline HMM, HMM2Vec, and Word2Vec feature sets. We see that all of these techniques perform more poorly as k increases. In particular, for $k\approx 75$, the performance of each is poor in comparison to $k\le 3$, and this effect is particularly pronounced in the case of the baseline HMM. This provides strong evidence that small values of k in ${k}-NN$ result in overfitting for each feature set, and the overfitting is especially pronounced for the baseline HMM.

Fig. 13

${k}-NN$ results as a function of k

For a random forest, the overfitting that is inherent in decision trees is mitigated by using more trees. In contrast, if the depth of the trees in the random forest is too large, the effect is analogous to choosing k too small in ${k}-NN$, and overfitting is likely to occur.

To explore overfitting in our RF experiments, in Fig. 14, we give the misclassification results for the baseline HMM, HMM2Vec, and Word2Vec features, as a function of the maximum depth of the trees. In this case, Word2Vec performs best for smaller (maximum) depths, which indicates that the baseline HMM and HMM2Vec features are more prone to overfitting.

Fig. 14

Random forest results as a function of tree depth

Fig. 15

Random forest maximum depth vs number of trees

In Fig. 15a and b, we give misclassification results as a function of both the maximum depth and the number of trees for the baseline HMM and for HMM2Vec features, respectively. From these results, we see that the baseline HMM performs similarly as a function of the maximum depth, regardless of the number of trees. In contrast, the HMM2Vec features yield consistently better results than the baseline HMM (as a function of the maximum depth), except when the number of trees is very small. This indicates that, with respect to the maximum depth, overfitting is significantly worse for the baseline HMM, since the overfitting cannot be overcome by increasing the number of trees.

From the discussion in this section, we see that all of our ${k}-NN$ experimental results suffer from some degree of overfitting, with this effect being most significant in the case of the baseline HMM. For our RF results, overfitting is a relatively minor issue for the HMM2Vec- and Word2Vec-engineered features but, as with ${k}-NN$, it is a significant problem for the baseline HMM. Consequently, both the ${k}-NN$ and RF results we have reported for the baseline HMM are overly optimistic, as these represent cases where significant overfitting has occurred.

5.8 Discussion

Figure 16 gives the overall accuracy for each of our multiclass experiments using ${k}-NN$, MLP, RF, and SVM classifiers, for our baseline HMM opcode experiments, and for each of the HMM2Vec-, PCA2Vec-, and Word2Vec-engineered feature experiments. In general, we expect RF and ${k}-NN$ to perform somewhat similarly, since both are neighborhood-based algorithms. We also expect that in most cases, SVM and MLP will perform in a qualitatively similar manner to each other, since these techniques are closely related. We find that these expectations are generally met in our experiments, which can be viewed as a confirmation of the validity of the results.

Fig. 16

Accuracies for combinations of features and classifiers

From our 16 distinct experiments, we see that HMM2Vec and Word2Vec perform best, with PCA2Vec lagging far behind. The baseline HMM does well with respect to the neighborhood-based classifiers, namely, RF and ${k}-NN$. However, as discussed in the previous section, these neighborhood-based techniques overfit the training data in the baseline HMM experiments. Neglecting these overfit results, we see that using the HMM2Vec- and Word2Vec-engineered features with SVM and MLP classifiers, give us the best results. Furthermore, these HMM2Vec and Word2Vec results are substantially better than either of the reliable results obtained for the baseline HMM, that is, the baseline HMM results using SVM and MLP classifiers.

6 Conclusion and Future Work

In this paper, we have presented results for a number of experiments involving word embedding techniques in malware classification. We have applied machine learning techniques to raw features to generate engineered features that are used for classification. Such a concept is not entirely unprecedented as, for example, PCA is often used to reduce the dimensionality of data before applying other machine learning techniques. However, the authors are not aware of previous work involving the use word embedding techniques in the same manner considered in this paper.

Our results show that word embedding techniques can be used to generate features that are more informative than the original data. This process of distilling useful information from the data before classifying samples is potentially useful, not only in the field of malware analysis, but also in other fields where learning plays a prominent role.

For future work, it would be interesting to consider other families and other types of malware. It would also be worthwhile to consider more complex and higher dimensional data—as with dimensionality-reduction techniques, such data would tend to offer more scope for improvement using the word embedding strategies considered in this paper.