Hidden Markov models for malware classification

Abstract

Previous research has shown that hidden Markov model (HMM) analysis is useful for detecting certain challenging classes of malware. In this research, we consider the related problem of malware classification based on HMMs. We train multiple HMMs on a variety of compilers and malware generators. More than 8,000 malware samples are then scored against these models and separated into clusters based on the resulting scores. We observe that the clustering results could be used to classify the malware samples into their appropriate families with good accuracy. Since none of the malware families in the test set were used to generate the HMMs, these results indicate that our approach can effective classify previously unknown malware, at least in some cases. Thus, such a clustering strategy could serve as a useful tool in malware analysis and classification.

1 Introduction

Automatically classifying malware is a challenging task. In this research, we apply hidden Markov models and cluster analysis to this problem. The use of hidden Markov models was inspired by previous research in metamorphic detection [3, 36].

We train HMMs for several metamorphic generators and several different compilers. The rationale is that, as in [3], we can view the metamorphic generators, broadly speaking, as a type of “compiler”. Then we use the resulting models to score each of more than 8,000 malware samples. Based on these scores, the malware samples are separated into clusters using the $k$-means algorithm [18, 21]. We analyze the resulting clusters and show that they correspond to certain characteristics of the malware. Since none of the malware families in our test set were used to generate the HMMs, our results indicate that HMM-based analysis can be an effective tool for automatically classifying new malware strains.

This paper is organized as follows. In Sect. 2, we give an overview of previous work on malware classification. Section 3 provides background information on hidden Markov models and their role in malware research. Section 4 covers the $k$-means clustering algorithm and other related approaches, while Sect. 5 discusses our implementation of $k$-means clustering in more detail. Experimental results are presented and analyzed in Sect. 6. Finally, Sect. 7 contains our conclusion and suggestions for future work.

2 Related work

A considerable amount of previous work has been done on malware classification. In this section, we discuss a few representative sample of malware classification techniques that have appeared in the literature.

2.1 Structured control flow

Control flow information can be used to analyze programs. Such information is typically analyzed in the form of a call graph. In [7], the authors propose a malware classification system based on approximate matching of control flow graphs. Control flow information is shown to be relatively invariant among polymorphic and metamorphic malware.

2.2 Behavioral analysis

Classification systems can be based on static analysis and/or behavioral analysis. Static-based techniques relies on features extracted from static files, while dynamic-based analysis relies on features that are extracted during code execution (or emulation). Static-based approaches are generally more efficient, but also more limited in their ability to extract behavior-based information. Static approaches sometimes use low-level features such as calls to external libraries, strings, and byte sequences for classification [13]. Other static approaches extract higher-level information from binaries, such as sequences of API calls [7] or opcode information [36].

Although variants in a malware family may have very different static signatures, they almost certainly share characteristic behavioral patterns. In [6], an automatic classification system is analyzed. This system can be trained to accurately identify new variants within known malware families, using observed similarities in behavioral features. Examples of behavioral features analyzed include resource usage and the frequency of calls to specific kernel functions. The results presented in [6] indicate that their behavioral classifier can accurately identify new variants within certain malware families.

2.3 Data mining methods

In [13], the authors extract the byte sequences from executables and analyze the resulting $n$-grams. They consider several classifiers including instance-based learning, Naïve Bayes, decision trees, support vector machines (SVM), and boosting. The best results in [13] are obtained using boosted decision trees.

2.4 VILO

Malware classification schemes can be binary or familial. In the binary malware classification problem, an unknown executable is classified as either being malicious or benign, while in the familial malware classification problem, a malicious executable is classified as belonging to a particular group of malware. Familial malware classification is considered in [16], where the authors develop a system referred to as VILO. The VILO system makes use of three elements, namely, opcode mnemonic permutation features (which the authors refer to as $N$-perm feature vectors), TFIDF weighting of features [12], and the nearest-neighbor algorithm. The $N$-perms are obtained by sliding a window of size $n$ overlapping opcodes. Such $n$-grams are somewhat more robust against certain elementary code obfuscations such as instruction reordering [36].

VILO implements a nearest neighbor algorithm with similarities computed over TFIDF-weighted $N$-perms. The results in [16] showed that VILO is a fast and effective learner of real-world malware. TFIDF weighting ensures that features that are common across many types of executables are not overly emphasized [16].

3 Hidden Markov models

In this section, we provide an overview of hidden Markov models (HMMs). We then briefly discuss previous malware-related research involving HMMs.

Hidden Markov models (HMMs) have proven to be a useful tool for statistical pattern analysis in a wide variety of applications, including speech recognition [24], biological sequence analysis [14], software piracy detection [15], and—most relevant to the work presented here—malware detection [36]. This section gives a brief overview of training and scoring using HMMs.

A statistical model that has states and known, fixed probabilities for the state transitions is called a Markov process or model [30]. In such a Markov model, the states are visible to the observer. In contrast, a hidden Markov model (HMM) has states that are not directly observable [24]. HMMs can be viewed as a machine learning technique, in the sense that the training process automatically extracts the relevant statistical information from the training data. An HMM also acts as a state machine, where every state is associated with a probability distribution that relates the hidden state to the set of observation symbols. As in any Markov process, the transitions between states have fixed probabilities.

We can train an HMM on a given observation sequences [30]. We can also score an observation sequence against a trained HMM to determine the probability of observing such a sequence under the constraints of the specified model. The more closely that the scored sequence matches the training data, the higher the score.

Note that the training and scoring process as it is generally applied is in stark contrast to clustering. The goal of clustering is to extract relevant structure—which may or may not actually exist—from a given dataset, without the aid of a training set to determine thresholds. In other words, we apply clustering when in a data exploration mode, while training requires a dataset of some known type or types.

Before providing additional details on the training and scoring algorithms, we must define some notation. The notation in Table 1 is fairly standard [30].

Table 1 HMM notation

A hidden Markov model is defined by the matrices $A, B$ and $\pi$. Consequently, we denote an HMM as $\lambda = (A, B, \pi )$.

Fig. 1

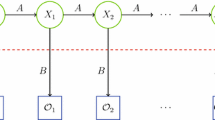
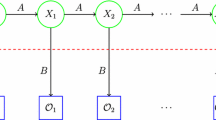
A hidden Markov model [30]

Figure 1 gives a generic view of a hidden Markov model. Note that the region above the dashed line is the “hidden” part of the model, that is, we cannot directly observe the state transitions. However, we can indirectly obtain information about the hidden states via the observations $\mathcal{O}$ and the probability distributions in the $B$ matrix.

The utility of HMMs derives primarily from the fact that there are efficient algorithms to solve each of the following three problems [30].

Problem 1

Given a model $\lambda = (A, B, \pi )$ and an observation sequence $\mathcal{O}$, we can determine the probability $P(\mathcal{O}\,|\,\lambda )$. That is, an observation sequence can be scored to see how well it fits a given model.

Problem 2

Given a model $\lambda = (A, B, \pi )$ and an observation sequence $\mathcal{O}$, we can determine an optimal state sequence for the Markov model. Here, “optimal” is in the sense of maximizing the expected number of correct states. This is in contrast to dynamic programming, where “optimal” is defined as the highest scoring overall path.

Problem 3

Given an observation sequence $\mathcal{O}$ and the parameter $N$ (the number of hidden states) we can determine a model $\lambda$ that maximizes probability of $\mathcal{O}$. That is, we can train a model to best fit an observation sequence.

For the research presented in this paper, the algorithms for Problems 1 and 3 are used. First we train HMMs for a variety of compilers and malware generators. When training a model, we use the algorithm that solves Problem 3. The resulting HMMs are then used to score a large collection of malware samples. For this step, we are using the algorithm that solves Problem 1.

Next, we discuss the HMM algorithms in some detail. The presentation here follows that in [30].

The so-called forward algorithm and backward algorithm are used when training the model, and the forward algorithm is also used for scoring. In these algorithms, we calculate the probability of being in a state $q_{i}$ at time $t$, relative to a given observation sequence $\mathcal{O}$. When scoring a sequence, the forward algorithm is used to determines $P(\mathcal{O}\,|\,\lambda )$.

Define

$$\begin{aligned} \alpha _{t}(i) = P(\mathcal{O}_{0}, \mathcal{O}_{1},\ldots ,\mathcal{O}_{t},x_{t}=q_{i}\,|\,\lambda ) \end{aligned}$$

(1)

for $t = 0,1,\ldots ,T-1$ and $i = 0, 1,\ldots , N-1$. Note that $\alpha _{t}(i)$ is the probability of the partial observation sequence up to time $t$, where the underlying Markov process is in state $q_i$ at time $t$. A direct calculation of the $\alpha _{t}(i)$ requires $2TN^T$ multiplications [30]. Fortunately, there is an efficient recursive calculation, which is known as the forward algorithm (or $\alpha$ pass). The forward algorithm proceeds as follows.

• 1. Let $\alpha _{0}(i) = \pi _{i}b_{i}(\mathcal{O}_{0})$, for $i = 0, 1, \ldots , N-1$

• 2. For $t = 1, 2, \ldots , T - 1$ and $i = 0, 1, \ldots , N - 1$ compute

  $$\begin{aligned} \alpha _{t}(i) = \sum _{j=1}^{N-1} \alpha _{t-1}(j)a_{ji} b_{i}(\mathcal{O}_{t}) \end{aligned}$$

The forward algorithm only requires about $N^2T$ multiplications. Also, from the definition in (1), it is clear that $P(\mathcal{O}\,|\,\lambda ) = \sum _{i=0}^{N-1} \alpha _{T-1}(i)$. Therefore, the forward algorithm provides an efficient method for scoring an observation sequence $\mathcal{O}$ against a given model $\lambda$. Below, we will see that the forward algorithm also plays a pivotal role when training an HMM.

There is an analogous backward algorithm (or $\beta$ pass) where we compute the partial sums from back-to-front. Define

$$\begin{aligned} \beta _{t}(i) = P(\mathcal{O}_{t+1}, \mathcal{O}_{t+2},\ldots , \mathcal{O}_{T-1},x_{t}=q_{i},\lambda ) \end{aligned}$$

for $t = 0,1,\ldots ,T-1$ and $i= 0, 1,\ldots ,N-1$. The $\beta _{t}(i)$ can be calculated efficiently as follows.

• 1. Let $\beta _{T-1}(i) =1$, for $i=0,1,\ldots ,N-1$

• 2. For $t=T-2, T-3,\ldots ,0$ and $i=0,1,\ldots ,N-1$, compute

  $$\begin{aligned} \beta _{t}(i) = \sum _{j=0}^{N-1} a_{ij}b_{j}(\mathcal{O}_{t+1})\beta _{t+1}(j) \end{aligned}$$

Next, define

$$\begin{aligned} \gamma _{t}(i) = P(x_{t}=q_{i}\,|\,\mathcal{O},\lambda ) \end{aligned}$$

for $t=0,1,\ldots ,T-2$ and $i=0,1,\ldots ,N-1$. Since $\alpha _t(i)$ measures the relevant probability up to time $t$ and $\beta _t(i)$ measures the relevant probability after time $t$, we have

$$\begin{aligned} \gamma _{t}(i) = {\frac{\alpha _t(i)\beta _t(i)}{P(\mathcal{O}\,|\,\lambda )}} \end{aligned}$$

The most likely (hidden) state at time $t$ is the state for which $\gamma _{t}(i)$ is maximized. Thus, we now have the tools to efficiently solve Problem 1 (using the forward algorithm) and Problem 2 (based on the $\gamma _t(i)$). Next, we turn our attention to solving Problem 3, that is, training an HMM.

The Baum–Welch algorithm enables us to iteratively re-estimate the parameters of the model $\lambda =(A,B,\pi )$. Recall that $N$ is the number of hidden states and $M$ is the number of unique observation symbols, and these are given. Therefore, the model parameters that we want to determine consist of the elements of the matrices $A, B$, and $\pi$, where $A$ is $N\times N, B$ is $N\times M$ and $\pi$ is $1\times N$. Each of these matrices is row-stochastic.¹

Let

$$\begin{aligned} \gamma _t(i,j) = P(x_t=q_i,x_{t+1}=q_j\, | \,\mathcal{O},\lambda ) . \end{aligned}$$

for $t=0,1,\ldots ,T-2$ and $i,j\in \{0,1,\ldots ,N-1\}$. Note that $\gamma _t(i,j)$ is the probability of being in state $q_i$ at time $t$ and transiting to state $q_j$ at time $t+1$. From the definitions of $\alpha$, $\beta$, $A$ and $B$, it follows that

$$\begin{aligned} \gamma _t(i,j) = \frac{\alpha _t(i)a_{ij}b_j(\mathcal{O}_{t+1})\beta _{t+1}(j)}{ P(\mathcal{O}\,|\,\lambda )} . \end{aligned}$$

Also, it is easily verified that

$$\begin{aligned} \gamma _t(i) = \sum _{j=0}^{N-1}\gamma _t(i,j) . \end{aligned}$$

Now, given the $\gamma _t(i)$ and the $\gamma _t(i,j)$, the model $\lambda =(A,B,\pi )$ can be re-estimated as follows [30].

• 1. For $i=0,1,\ldots ,N-1$, let

  $$\begin{aligned} \pi _i = \gamma _0(i) \end{aligned}$$

  (2)

• 2. For $i=0,1,\ldots ,N-1$ and $j=0,1,\ldots ,N-1$, compute

  $$\begin{aligned} a_{ij} = \sum _{t=0}^{T-2}\gamma _t(i,j) \bigg / \sum _{t=0}^{T-2}\gamma _t(i). \end{aligned}$$

  (3)

• 3. For $j=0,1,\ldots ,N-1$ and $k=0,1,\ldots ,M-1$, compute

  $$\begin{aligned} b_j(k) = \mathop {\mathop {\sum }\limits _{{t\in \{0,1,\ldots ,T-2\}}}}\limits _{\mathcal{O}_{t=k}} \gamma _t(j)\bigg / \, \sum _{t=0}^{T-2}\gamma _t(j) . \end{aligned}$$

  (4)

The numerator in (3) gives the expected number of transitions from state $q_i$ to state $q_j$, while the denominator is the expected number of transitions from $q_i$ to any state. Consequently, the ratio is the probability of transiting from state $q_i$ to state $q_j$ which, based on the values of the $\gamma _t(i)$ and $\gamma _t(i,j)$, is our current best estimate of $a_{ij}$.

The numerator of (4) is the expected number of times we are in state $q_j$ with observation $k$, while the denominator is the expected number of times we are in state $q_j$. The ratio is the probability of observing symbol $k$, given that the model is in state $q_j$. Again, given the current values of $\gamma _t(i)$, this is is our best estimate of $b_j(k)$.

The re-estimation process is iterative. First, we initialize $\lambda =(A,B,\pi )$ by choosing random values such that $\pi _i\approx 1/N$ and $a_{ij}\approx 1/N$ and $b_j(k)\approx 1/M$. Note that it is necessary that $A, B$ and $\pi$ are randomized, since precisely uniform values will result in a local maximum, from which the model cannot climb to an improved solution [30]. In addition, $\pi , A$ and $B$ must be row stochastic.

To summarize, the solution to Problem 3 proceeds as follows.

• 1. Initialize, $\lambda =(A,B,\pi )$.

• 2. Compute $\alpha _t(i), \beta _t(i), \gamma _t(i,j)$ and $\gamma _t(i)$.

• 3. Re-estimate the model $\lambda =(A,B,\pi )$.

• 4. Repeat steps 2 and 3 until a suitable stopping criteria is met.

For the HMMs considered in this paper, we determined experimentally that a threshold of 800 iterations is more than sufficient for convergence. Hence, we use this number of iterations as our stopping criteria.

Previous research has shown that an HMM trained on opcode sequences can effectively distinguish highly metamorphic malware families from benign code [36]. In subsequent research [2–4, 25, 29], these HMM results have served as a benchmark for comparing the effectiveness of various proposed detection techniques. While some of this research has improved on HMM analysis in certain challenging cases, the HMM results remain competitive in nearly all cases. In addition, in [3], HMMs are shown to be effective for identifying code generated by different compilers. Consequently it is reasonable to consider the effectiveness of HMMs as a tool for automatic malware classification.

4 Clustering

Cluster analysis is the process of grouping objects into subsets that have meaning in the context of a particular problem. In this section, we first discuss clustering in general terms. Then we focus our attention on $k$-means clustering, which is the technique employ in this paper.

There are several different ways to categorize clustering algorithms, which we now consider. Except where otherwise noted, the discussion here is primarily derived from [10].

• Exclusive versus non-exclusive: An exclusive classification is a partition of the set of objects, that is, each object belongs to exactly one subset, or cluster. Non-exclusive classification allows for overlapping classification, in which objects can be assigned to more than one cluster.

• Intrinsic versus extrinsic: Intrinsic classification relies on unsupervised learning, that is, no predetermined labels are applied to the objects. In contrast, extrinsic classification requires category labels on the objects and is therefore a form of supervised learning.

• Agglomerative versus divisive: In an agglomerative approach, each point is initially considered as a cluster in itself. The two “nearest” clusters are combined into one cluster repeatedly until all clusters are merged into a single cluster. Consequently, agglomerative clustering can be viewed as a “bottom up” approach. In contrast, divisive is a “top down” approach where all observations start in one cluster, and splits are performed recursively as the clustering algorithm proceeds.

• Hierarchical versus partitional: As the name implies, hierarchical clustering algorithms break up the data into a hierarchy of clusters. In contrast, partitional algorithms divide the data set into mutually disjoint partitions. Hierarchical clustering algorithms produce a hierarchy of clusters called a dendogram, either by merging smaller clusters into larger ones or dividing larger clusters to smaller ones [9]. One of the most popular partitional clustering algorithms is the $k$-means clustering algorithm, which we now discuss in more detail.

4.1 $k$-Means clustering algorithm

In this research, we have applied the $k$-means clustering algorithm to malware classification. This procedure classifies the dataset into $k$ clusters, where the number $k$ is specified in advance. Finding globally optimal clusters in $k$-means is an NP-hard problem, but there is a simple and fast heuristic that will converge to “locally” optimal clusters.

The $k$-means (heuristic) algorithm is one of the simplest unsupervised learning algorithms for the clustering problem [17]. Initially, we specify $k$ and a centroid for each of the $k$ clusters. These initial centroids can be chosen at random, or they can be selected to satisfy some property, such as being spaced uniformly throughout the data. Once the initial centroids have been selected, each data point is associated with its nearest centroid and placed in the corresponding cluster. The centroids are then recalculated based on the current placement of data points. The process of computing centroids and regrouping the data points is repeated until the distance between the previous and newly-computed centroids is negligible. In practice, it is usually desirable to repeat the entire clustering process with multiple sets of initial centroids, since the solution may depend heavily on the initial placement of centroids.

Suppose we have a set of $N$ malware samples, denoted $m_1, m_2,\ldots ,m_N$. Then for the malware classification results presented in Sect. 6, the $k$-means clustering algorithm proceeds as follows.

• 1. Specify the number of clusters $k$.

• 2. Initialize the $k$ centroids. Denote these centroids as $\mathcal{C}_{1},\mathcal{C}_{2}, \ldots ,\mathcal{C}_{k}$.

• 3. Determine the Euclidean distance of each malware sample from each centroid $\mathcal{C}_i$, that is, compute $d(m_i,\mathcal{C}_j)$ for $i=1,2,\ldots ,N$ and $j=1,2,\ldots ,k$.

• 4. Each malware file is associated with its nearest centroid, that is, $m_i$ is assigned to the cluster $j$ for which $d(m_i,\mathcal{C}_j)$ is minimized.

• 5. Recalculate the centroids for each cluster.

• 6. Repeat steps 3 through 5 until there is minimal change in cluster centroids.

We provide more implementation-specific details in Sect. 5.4. Note that in our experiments, we tested several values of $k$, and for each $k$, several different initial clusters were considered.

The $k$-means clustering algorithm is generally computationally faster than comparable hierarchical clustering algorithms. In addition, $k$-means tends to produce tighter clusters than hierarchical clustering. However, a possible disadvantage of $k$-means clustering is that the value of $k$ must be specified in advance, and we may have no good estimate for the optimal number of clusters. Another possible concern is that different initial values for the centroids may produce different clusters. In an attempt to minimize these issues, various measures are available to quantify the “quality” of a set of clusters. Next, we briefly discuss two such measures.

4.2 Cluster quality

Intuitively, it seems clear that we should prefer results where individual clusters are tightly packed and the distance between clusters is relatively large. These properties, referred to as cohesion and separation, respectively, can be combined into a single number known as the silhouette coefficient [11].

For an element $x$, we compute its silhouette coefficient as follows. Suppose we have a set of $k$ clusters, denoted $C_1,C_2,\ldots ,C_k$, where $x$ belongs to cluster $C_{\ell }$. Let $a$ be the average distance between $x$ and all of the other points in its cluster $C_{\ell }$. For each $j$, such that $j\ne \ell$, let $b_j$ be the average distance between $x$ and all of the points in cluster $C_j$. Let $b$ be the minimum of these $b_j$. Then the silhouette coefficient of $x$ is given by

$$\begin{aligned} S(x) = \frac{b-a}{\max \{a,b\}} . \end{aligned}$$

(5)

A silhouette coefficient calculation is illustrated in Fig. 2.

Fig. 2

Silhouette coefficient example

Note that $a$ in Eq. (5) is dependent on the cohesiveness of the cluster that $x$ belongs to while, in a sense, $b$ measures the distance from $x$ to the nearest other cluster. Also, typically, $b>a$ in which case $S(x) = 1 - a/b$. Intuitively, if $x$ is “well-clustered” then $a$ would be relatively small and $b$ relatively large, resulting in $S(x)$ near 1. Conversely, if $a$ is nearly as large as $b$, then $S(x)$ is close to 0 and we have considerably less confidence that $x$ is properly clustered. The average of $S(x)$ over all points $x$ can be viewed as a topological measure of the quality of a given clustering. We employ the silhouette coefficient when analyzing our experimental results in Sect. 6.

An even simpler measure of cluster quality is “purity,” in the sense of cluster uniformity [11]. Let $m_{ij}$ be the number of elements of type $i$ in cluster $C_j$ and $m_j$ the total number of elements in $C_j$. Also, let $m=\sum m_j$, that is, $m$ is the total number of elements. Then we compute $p_{ij}=m_{ij}/m_j$ and

$$\begin{aligned} U_j = \max _i\{p_{ij}\}. \end{aligned}$$

(6)

Note that $U_j$ is in the range 0–1, and $U_j=1$ implies that $C_j$ contains only one type of element, in which case the cluster has the maximum possible purity. The overall purity for the clustering is computed as the weighted sum

$$\begin{aligned} U = \sum _{j=1}^k \frac{m_j}{m}\, U_j . \end{aligned}$$

We also use this concept of purity in Sect. 6.

5 Implementation

This section provides implementation details for the experiments we performed. First, we give information related to training the HMMs. Then we provide a brief overview of the dataset and how it is processed, and how the scores are computed. Finally, we discuss our use of the $k$-means clustering algorithm.

5.1 Training HMMs

As in [3], hidden Markov models were trained for each of four different compilers, namely, GCC, MinGW, TurboC, and Clang. Another HMM was trained on hand-written assembly code, which we refer to as the TASM model. In addition, we generated models for two metamorphic malware generators, namely, the Next Generation Virus Construction Kit (NGVCK) [35] and the experimental metamorphic worm (MWOR) developed and analyzed in [29].

For each model, we used 800 iterations of the Baum–Welch re-estimation algorithm. We experimented with the number of hidden states ranging from $N=2$ to $N=6$. Since the number of hidden states had little impact, in Sect. 6, we only provide results for $N=2$ hidden states. The number of assembly code files used for training each model is given in Table 2.

Table 2 Number of files to train HMMs

5.2 Dataset

For this research, we obtained the dataset available from the Malicia project website [22]. This dataset contains more than 11,000 malware binaries collected from more than 500 drive-by download servers over a period of 11 months [22]. Each malware sample is available in the form of a binary. In addition, a database is provided that contains metadata on each sample, including when the malware was collected, where it was collected, and the malware family type. However, the malware type was unspecified or listed as “unknown” for a significant percentage of the files. Type information was necessary for the analysis of the clusters we obtained (as discussed in Sect. 6) and hence only the samples with a specified type were included in our research. We found 8,119 of these malware samples had a specified family type and hence these files were used in our malware classification experiments. Since our classification is based on opcode sequences, each of the corresponding 8,119 executable (exe or dll) files was disassembled using objdump. After disassembly, the opcode sequences were extracted and scored against each of the HMMs discussed in Sect. 5.1.

5.3 Scoring

After successful training, an HMM should assign higher scores to files that are more similar to the training dataset and lower scores to files that are less similar. The HMM score is computed in the form of a log likelihood. Since this score is length dependent, as in [36] and elsewhere, we normalize by the length to obtain a log likelihood per opcode (LLPO) score. Consequently, we can directly compare scores regardless of the length of the files.

5.4 Clustering

Each malware sample $m_i$ is first scored against each of the seven HMMs as discussed above. The resulting 7-tuple of scores is used for clustering. We experimented with the number of clusters ranging from $k=2$ to $k=15$. For each $k$, we select the initial centroids so they are “uniformly” spaced throughout the data. That is, we first compute $a_{\min } = \min _i\{a_i\}$ and $a_{\max } = \max _i\{a_i\}$, and similarly for $b$ through $g$. Next, let

$$\begin{aligned} \tilde{a} = \frac{a_{\max } - a_{\min }}{k+1} \end{aligned}$$

with $\tilde{b},\tilde{c},\ldots ,\tilde{g}$ defined similarly. Then the initial centroids are given by

$$\begin{aligned} \mathcal{C}_{\ell } = ( a_{\min } + \ell \cdot \tilde{a},\, b_{\min } + \ell \cdot \tilde{b},\, \ldots , g_{\min } + \ell \cdot \tilde{g}) \end{aligned}$$

for $\ell =1,2,\ldots ,k$. Note that for each dimension, we are simply dividing the range of values into $k+1$ equal-sized segments, and for $\mathcal{C}_{\ell }$ we select the edge of segment $\ell$.

The process of recomputing the centroids is also straightforward. Suppose cluster $\ell$, with centroid $\mathcal{C}_{\ell }$, contains the $n$ malware samples, $m_1,m_2,\ldots ,m_n$. Then the relevant scores for these samples are given in Table 3. We calculate the mean in each dimension. For example, the mean of scores in the “$a$” dimension for the data in Table 3 is computed as

$$\begin{aligned} a_{{{\mathrm{mean}}}} = {\frac{(a_{1}+a_{2}+\cdots +a_{n})}{n}} . \end{aligned}$$

The resulting means form a seven-tuple which is our new $\ell {{{\mathrm{th}}}}$ centroid, that is, we let

$$\begin{aligned} \mathcal{C}_{\ell } = (a_{{{\mathrm{mean}}}},b_{{{\mathrm{mean}}}}, c_{{{\mathrm{mean}}}},d_{{{\mathrm{mean}}}}, e_{{{\mathrm{mean}}}},f_{{{\mathrm{mean}}}},g_{{{\mathrm{mean}}}}) \end{aligned}$$

Each of the $k$ centroids is updated similarly.

Table 3 Malware scores

Once the new centroids have been computed, the malware samples are regrouped by placing each sample in the cluster corresponding to the nearest of the $k$ centroids. This process of recomputing centroids and regrouping the data points continues until the Euclidean distance between the previous centroids and the new centroids is negligible, or until the regrouping has no effect.

6 Experiments and results

This section provides information on our experimental results. First, we summarize the hardware and software used in the experiments. Then we present and discuss our main results.

6.1 Setup

Since we are dealing with live malware, for recovery purposes we used a virtual machine container. The specifications of the host machine and guest virtual machine are as follows.

Host Sony Vaio T15, Intel Corei5-3337U (1.80 GHz), 4.00 GB RAM, Windows 8

Guest Oracle VirtualBox 4.2.18 VM (1 GB memory), Linux Ubuntu 12.04.3 LTS

The malware samples were scored on the guest machine. All processing that did not directly involve malware files (HMM training, $k$-means clustering, and so on) was performed on the host machine.

6.2 Results

As mentioned in Sect. 5, in addition to the malware binaries, we also have metadata available. This metadata includes information on the malware family type. We use this malware family type to gauge the success of our classification technique. After filtering out some samples that lacked family information, we had a dataset containing 8,119 malware samples suitable for our experiments.

6.2.1 Classification and clustering

We performed clustering using $k$-means as discussed perviously. We tested each $k$ from 2 to 15. Here, we only present selected cases; for additional results see [1].

As can be seen from Table 4, among the samples in our dataset, there are three dominant families, namely, Winwebsec, Zbot, and Zeroaccess. Next, we briefly discuss these three dominant malware families.

Table 4 Dataset malware distribution

Winwebsec is a category of Windows malware that falsely claims to be anti-virus softwares. The software offers to remove non-existent threats for a fee [34].

Zbot is a family of Trojans that steals information. It usually targets system information, online credentials, and banking details, but it can be customized to gather other information [32].

Zeroaccess is a family of Trojans that installs an advanced rootkit. It can also create a hidden file system, download more malware, and open a back door on the compromised computer, among several other features [33].

In Fig. 3, we present our clustering results in the form of a stacked column charts, grouped by cluster, for various numbers of clusters. We see that the Winwebsec family dominates the largest cluster, while Zbot and Zeroaccess tend to be grouped together until we have a larger number of clusters (and even then, there is significant overlap between these two sets). Also, for larger values of $k$, many of the minor clusters tend to be highly uniform. Figure 4 contains the same results as in Fig. 3, but grouped by family.

Fig. 3

Stacked column charts (grouped by cluster)

Fig. 4

Stacked column charts (grouped by family)

As discussed in Sect. 4.2, the average silhouette coefficient provides a measure of the quality of a given clustering. For our experiments with $k=2$ to $k=15$ clusters, the average silhouette coefficient is given in Table 5.

Table 5 Average silhouette coefficient

Next, we consider a score based on these clusterings, and plot Receiver Operating Characteristic (ROC) curves for each. To construct an ROC curve, the true positive rate is plotted against the false positive rate as a threshold varies through the range of data values. The area under the ROC curve (AUC) provides a convenient measure of the quality of a binary classifier. An AUC of 1.0 indicates ideal separation (i.e., there exists a threshold for which no detection errors occur), while an AUC of 0.5 indicates that the classifier is no more successful than flipping a coin.

The basis for our score is the silhouette coefficient, as discussed in Sect. 4.2. We are given a set of clusters, where $x$ is an element of one, say, cluster $C_j$. To compute a score for $x$, we first calculate $S(x)$, the silhouette coefficient of $x$. Recall that $S(x)$ is a measure of the quality of the clustering of $x$, that is, it provides a measure of the confidence we have that $x$ is properly clustered. Next, as in Eq. (6), we let $p_{ij}=m_{ij}/m_j$, where $m_{ij}$ is the number of elements of family $i$ in cluster $C_j$, and $m_j$ is the number of elements in cluster $C_j$. Finally, we define the scoring functions

$$\begin{aligned} \hbox {score}_i(x) = p_{ij}\, S(x) \end{aligned}$$

(7)

where $\hbox {score}_i(x)$ is the score of $x$ with respect to family $i$.

The motivation for the score in Eq. (7) is that the silhouette coefficient $S(x)$ quantifies the confidence we have that $x$ is in the correct cluster, while $p_{ij}$ gives us the relative probability that a member of family $i$ is in cluster $C_j$. Both of these factors are relevant when considering the likelihood of a match. However, there are many other possible scores that could be considered and we do not claim that this is an optimal score. The results here are only intended to provide a reasonable lower bound on classification success based on the available clusters.

Here, we only consider the three dominant families in our dataset, where

$$\begin{aligned} \hbox {score}_0(x)&= \hbox {Winwebsec score of file }x \\ \hbox {score}_1(x)&= \hbox {Zbot score of file }x \\ \hbox {score}_2(x)&= \hbox {Zeroaccess score of file }x . \end{aligned}$$

Also, note that we are only using information gleaned directly from the clusters to determine the score. Computing the score does not require any knowledge of the actual family type of the file $x$ and hence could easily be applied to files of unknown type that were not part of the original clustering process. In addition, none of the samples in the clusters were used to train the HMMs that generate the vector of scores used for clustering. Consequently, when we score files from the clusters, we are not scoring any files from the training set. We emphasize these points because the process used here is somewhat different than the training and scoring process, as it is usually applied to binary classification problems. Here, we compute and analyze scores merely as a means to (roughly) quantify the success and potential utility of our clustering technique, not to make strong claims about detection rates.

Again, the HMMs that form the basis for clustering (and hence scoring) were intentionally not trained on the actual families under consideration. The goal here is to see how well these models can be adapted to the classification of the families under consideration. It is also important to realize that the non-family files being scored consist entirely of other malware, that is, no benign files are used. Intuitively, we expect that, in general, malware is more like other malware than it is like benign files. Consequently, these results can be viewed as something of a worst-case scenario, with respect to classification rates.

Using the scoring function in Eq. (7), we scored all of the elements for each of our clustered sets for $k=2,3,\ldots ,15$, for each of the families Winwebsec, Zbot, and Zeroaccess, i.e., using $\hbox {score}_0, \hbox {score}_1$, and $\hbox {score}_2$, respectively. Figure 5 contains scatterplots for the $k=9$ case. Also, ROC curves are given for each of these three families for $k=3$ and $k=9$ in Figs. 6 and 7, respectively. The AUC values for $k=2,3,\ldots ,15$ (and all three families) appear in Table 6. Note that the AUC can be interpreted as the probability that a randomly chosen positive instance will score higher than a randomly chosen negative instance [5].

Fig. 5

Score scatterplots for $k=9$ clusters

Fig. 6

ROC curves for $k=3$

Fig. 7

ROC curves for $k=9$

Table 6 Area under the ROC curve

Lastly, we performed experiments testing every possible score combination from the 7 HMMs listed in Table 2. Our goal is to determine whether a proper subset of these scores might yield better results than using the all of the scores. These experiments were conducted for $k=2,3,\ldots ,15$ clusters. To measure the quality of the resulting clusterings, we rely on the concept of purity, as defined in Sect. 4.2.

Suppose we have a set of clusters and a we are given a new file to classify. We would score the file using the HMMs, and assign the new file to a cluster based on the nearest centroid. We could then simply classify the file according to the dominant family in its assigned cluster. Under this scenario, the ideal case occurs when each cluster consists entirely of members of one family. Therefore, we define a purity-based score where, for simplicity, we restrict our attention to the three dominant families in our dataset, namely, Winwebsec, Zbot, and Zeroaccess.

Suppose that $C_1,C_2,\ldots ,C_k$ are the clusters obtained from the $k$-means algorithm. Let

$$\begin{aligned} x_i&= \hbox {number of Winwebsec files in cluster } C_i\\ y_i&= \hbox {number of Zbot files in cluster } C_i\\ z_i&= \hbox {number of Zeroaccess files in cluster } C_i \end{aligned}$$

and let $M_i = \max \{x_i,y_i,z_i\}$. Then we define a score for this particular set of clusters as

$$\begin{aligned} \hbox {score} = \frac{M_1 + M_2 + \cdots + M_k}{T} \end{aligned}$$

where $T$ is the total of all Winwebsec, Zbot, and Zeroaccess files. In the ideal case, each cluster is a solid color (neglecting the files not in the three major families), and we have $\hbox {score} = 1$. In general, $0 \le \hbox {score} < 1$, and the smaller the score, the further we are from the ideal case.

Our score results appear in Fig. 8 in the form of a heat map. In the left-hand column, the score combination is represented by the given binary vector, where the bit order corresponds to

$$\begin{aligned} \hbox {GCC}, \hbox {MinGW}, \hbox {TurboC}, \hbox {Clang}, \hbox {TASM}, \hbox {MWOR}, \hbox {NGVCK} . \end{aligned}$$

For example, the number 127 in the left-hand column of Fig. 8 indicated that scores in that row used all seven HMMs, while 63 implies that all scores other than the model for GCC were use, 124 means that all scores except MWOR and NGVCK were used, etc. Also, note that in each of these experiments, we used $N=2$ hidden states for all HMMs, and uniform initial placement of centroids.

Fig. 8

Heat map of HMM score combinations versus $k$ http://cs.sjsu.edu/faculty/stamp/heatmap/heatmapsBig.pdf

From Fig. 8, we see that six or more clusters are needed to obtain the best results, and that there are various score combinations that yield near-optimal results. Also, since the best results exceed 0.82, we could properly classify malware from these three families at such a rate, by simply choosing the dominant family in each cluster.

Interestingly, comparing the AUC values in Table 6 to the top row in Fig. 8, we see that a score based on the silhouette coefficient can do somewhat better than the purity-based calculation used to construct the heatmap. It is also worth noting that a strategy of simply guessing the category based on relative frequencies would, according to Table 4, have a probability of success of only

$$\begin{aligned} \left( \frac{4{,}361}{7{,}803}\right) ^2 + \left( \frac{2{,}136}{7{,}803}\right) ^2 + \left( \frac{1{,}306}{7{,}803}\right) ^2 \approx 0.4150. \end{aligned}$$

Consequently, the HMM clustering technique considered here can provide a significant improvement over the random case.

6.2.2 Discussion

Since the HMMs we used were not specific to the malware under consideration, the results in this section show that it is possible to automatically classify some classes of previously unseen malware in an effective way using this HMM analysis. There are several potential benefits to such clustering. For example, rapid clustering of malware could enable faster response to new threats—if new malware samples fit into an existing cluster, it is likely that they are similar to those that predominate in that cluster. Hence, this new malware might be analyzed more quickly, and possibly handled with previously developed detection and/or removal strategies. In addition, malware clustering could serve as a useful tool in the categorization of malware. In spite of previous attempts to develop malware classification and naming schemes [20, 27, 31], each anti-virus vendor seems to have its own classification system, and these appear to have little or no logical connection to malware structure or function. A rapid and automated method, such as that considered here, could serve to bring some order to this classification chaos.

7 Conclusion and future work

In this paper, we provided experimental results for malware clustering based on hidden Markov model scores. Our dataset contained more than 8,000 malware samples, with three large, distinct families making up the bulk of the data. We scored the malware samples using HMMs based on a variety of compilers and metamorphic generators, as well as hand-written assembly code. Here, we provided experimental results for $k = 2,3,4,\ldots ,15$ clusters; see [1] for some additional details.

The primary insight here is that a relatively straightforward HMM-based scoring system is able to automatically discriminate between malware classes with reasonable accuracy—in spite of the fact that no training occurred relative to the specific families in the dataset. While our results are not sufficiently sensitive for malware detection, this relatively simple test could be used to stratify samples into broad categories, which could serve as an aid in malware analysis and classification.

There are several enhancements to—and extensions of—this work that could prove interesting. For example, variations on the $k$-means algorithm could be tested, including $k$-medians, $k$-medoids, and fuzzy c-means. In addition, different approaches to clustering such as the EM algorithm [8] could prove useful.

In this paper, we only considered scores based on hidden Markov models, and of the seven scores considered, five are based on standard compilers. It is highly likely that more malware-specific HMMs would yield significantly stronger results. It is also likely that the inclusion of some additional scoring methods would add strength to the results. In particular, scoring techniques that are not based on statistical analysis of opcodes would likely complement the strengths of the HMM technique used here. Examples of such scores include the eigenvector-based score developed in [26] the structural entropy score in [4, 28], and call graph based strategies, such as those in [19, 23].