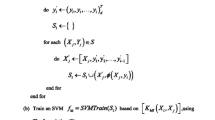Discriminative Multi-label Model Reuse for Multi-label Learning

Abstract

Traditional Chinese Medicine (TCM) with diagnosis scales is a holistic way for diagnosing Parkinson’s Disease, where symptoms can be represented as multiple labels. To solve this problem, multi-label learning provides a framework for handling such task and has exhibited excellent performance. Besides, it is a challenging issue of how to effectively utilize label correlations in multi-label learning. In this paper, we propose a novel algorithm named Discriminative Multi-label Model Reuse (DMLMR) for multi-label learning, which exploits label correlations with model reuse, instance distribution adaptation and label distribution adaptation. Experiments on real-world dataset of Parkinson’s disease demonstrate the superiority of DMLMR for diagnosing PD. To prove the effectiveness of the proposed DMLMR, extensive experiments on four benchmark multi-label datasets show that DMLMR significantly outperforms other state-of-the-art multi-label learning algorithms.

1 Introduction

Tradition Chinese Medicine (TCM) is a new way for PD [13]. For one thing, TCM scales includes tongue phase as well as four traditional methods of diagnosis: observation, listening, interrogation and pulse-taking. For another, syndrome types of PD in TCM can be divided into following 5 categories: (1) stirring wind due to phlegma-heat, (2) stirring wind due to blood heat, (3) deficiency of both qi and blood, (4) insufficiency of the liver and kidney, (5) deficiency of both yin and yang. Moreover, each TCM syndrome type can be subdivided into primary and secondary syndrome types.

TCM scholars are supposed to collect disease information of patients, and categorize a patient into one or more syndrome types based on TCM theory and rich experience. This diagnostic process requires doctors equipped with extensive experience of Syndrome Differentiation at the time of treatment. Due to the essential characteristic of TCM, TCM scales appear to be overwhelmingly dependent on personal experience of doctors. The problems of diagnosing PD in TCM lie in two aspects: specialists of PD are in short supply and diagnostic levels of doctors are inconsistent. Consequently, the diagnosis of PD might be subjective, which violates the original intention of effectiveness. Therefore, it is desired to design a semi-automatic mechanism for diagnosing PD in TCM.

In this paper, we formalize the problem of diagnosing Parkinson’s disease in TCM into a multi-label learning problem, where we treat TCM scales as features and treat syndrome types as multiple labels. In multi-label learning [21], each instance can be represented by multiple labels simultaneously. For example, an image may be annotated with both sea and beach. The task of multi-label learning is to learn a classification model which can predict all the relevant labels for unseen instances. Nowadays, multi-label learning has been applied to various application scenarios, such as text classification [9], image annotation [11], video annotation [14], social networks [17], music emotion categorization [18]. In addition, the exploration of label correlations has been accepted as a key component of effective multi-label learning approaches [6, 23].

The main contributions of this paper include:

• Real-world Parkinson’s disease diagnosis in Traditional Chines Medicine is investigated and assessed.

• We formalize the problem of diagnosing PD in TCM as a multi-label learning problem, by treating TCM scales as features while treating syndrome types as multiple labels. Meanwhile, we apply multi-label classification technology to diagnose PD in TCM.

• We propose a novel Discriminative Multi-label Model Reuse (DMLMR) algorithm to deal with multi-label learning problem, which perform excellently in handling diagnosis of Parkinson’s disease in TCM. Extensive experiments on four benchmark multi-label datasets show that DMLMR algorithm significantly outperforms the state-of-the-art multi-label learning algorithms.

The remainder of the paper is organized as follows. Section 2 briefly reviews some related work of multi-label learning. Section 3 presents formulation of the problem and our proposed DMLMR algorithm. Section 4 reports the experimental results, followed by the conclusion in Sect. 5.

2 Related Work

Generally, multi-label learning algorithms can be categorized into following three strategies based on the order of label correlations considered by the system.

First-order strategy copes with multi-label learning problem in a label-by-label manner. Binary Relevance (BR) [1] takes each label independently and decomposes it into multiple binary classification tasks. However, BR neglects the relationship among labels.

Second-order strategy introduces pairwise relations among multiple labels, such as the ranking between the relevant and irrelevant labels [5]. Calibrated Label Ranking (CLR) [4] firstly transforms the multi-label learning problem into label ranking problem by introducing the pairwise comparison. Recently, LLSF [7] performs joint label-specific feature selection and take the label correlation matrix as prior knowledge.

High-order strategy builds more complex relations among labels for multi-label learning. Classifier Chain (CC) [15] transforms the multi-label classification problem into a chain of binary classification problems, where the quality is dependent on the label order in the chain. Ensemble Classifier Chains (ECC) [16] constructs multiple CCs by using different random label orders. Multi-modal Classifier Chains (MCC) [22] release the reliance of label order by combining predicted labels as a new modality. Multi-label k-nearest neighbour (MLkNN) [20] builds a Bayesian model by using the k-nearest neighbour method to obtain the prior and likelihood. In addition, there are also some high-order approaches that exploit label correlations on the hypothesis space. For example, a boosting approach Multi-label Hypothesis Reuse (MLHR) [8] is proposed to exploit label correlations with a hypothesis reuse mechanism. Latent Semantic Aware Multi-view Multi-label Learning (LSA-MML) [19] implicitly encodes the label correlations by the common representation based on the uncovering latent semantic bases and the relations among them. Considering the potential association between paired labels, Dual-Set Multi-Label Learning (DSML) [10] exploits pairwise inter-set label relationships for assisting multi-label learning. Most of the existing approaches take label correlations as prior knowledge, which may not correctly characterize the real relationships among labels. And then, Collaboration based Multi-Label Learning (CAMEL) [3] is proposed to learn the label correlations via sparse reconstruction in the label space.

3 Methodology

This section mainly gives the detail description of Discriminative Multi-label Model Reuse (DMLMR) algorithm after a preliminary notation explanation.

3.1 Preliminaries and Problem Formulation

Before describing the problem formulation, we begin with some notations and preliminaries.

Let $\mathcal {X} = \mathbb {R}^{d}$ denote the d dimensional feature space, and $\mathcal {Y} = \{-1, 1\}^{L}$ denote the label space with L labels.

Given the training dataset $\mathcal {D} = \{(\varvec{x}_{i}, \varvec{y}_{i})\}_{i=1}^{N}$ with N instances, the task of multi-label learning is to learn a mapping function $\varvec{H}: \mathcal {X}\rightarrow \mathcal {Y}$, which maps from feature space to label space. The i-th instance $(\varvec{x}_{i}, \varvec{y}_{i})$ contains a feature vector $\varvec{x}_{i}=[x_{1}, x_{2}, \dots , x_{d}] \in \mathcal {X}$ and a label vector $\varvec{y}_{i}=[y^{1}, y^{2}, \cdots , y^{L}] \in \mathcal {Y}$, where $y^{k}=1$ indicating $\varvec{x}_{i}$ is associated with the k-th label, $y^{k}=-1$ otherwise. $\mathcal {T} = \{(\varvec{x}_{i}, \varvec{y}_{i})\}_{i=1}^{M}$ denotes testing dataset. In addition, $\varvec{H}(\cdot ) = [H^{1}(\cdot ), H^{2}(\cdot ), \dots , H^{L}(\cdot )]$ can be used to predict labels for unseen instances in $\mathcal {T}$, where $H^{k}(\cdot )$ denotes the classifier of the k-th label.

For simplicity, we denote $\varvec{X} = [\varvec{x}_{1}, \varvec{x}_{2}, \cdots , \varvec{x}_{N}]^{T} \in \mathbb {R}^{N\times d}$ as the instance matrix, and $\varvec{Y} = [\varvec{y}_{1}, \varvec{y}_{2}, \cdots , \varvec{y}_{N}]^{T} \in \mathbb {R}^{N\times L}$ as the label matrix. The original training dataset can be alternatively represented by $\mathcal {D} = \{(\varvec{X}, \varvec{Y})\}$.

With analysis in Sect. 1, the problem of diagnosing Parkinson’s disease can be modeled as multi-label learning problem.

Fig. 1.

The overall flowchart of DMLMR algorithm. Cylinder shadowed with orange denotes label distribution, while cylinder shadowed with blue denotes instance distribution.

3.2 Discriminative Multi-label Model Reuse

In this subsection, we introduce Discriminative Multi-label Model Reuse (DMLMR) algorithm in detail. The pseudo code of DMLMR is presented in Algorithm 1.

At first, we train on the original dataset $\mathcal {D}$ with a base multi-label algorithm (here we adopt CC algorithm) and get $\varvec{F}(\cdot ) = [F^{1}(\cdot ), \cdots , F^{k}(\cdot ), \cdots , F^{L}(\cdot )]$, where $F^{k}(\cdot )$ represents the original classifier for the k-th label. $\varvec{\tau }= [\tau _{1}, \cdots , \tau _{T}]$ denotes chain of selected labels, where T denotes number of boosting round. DMLMR maintains one label distribution $\varvec{WL}_{t}=[WL_{t}^{1}, \cdots , WL_{t}^{k}, \cdots , WL_{t}^{L}]$, where $WL_{t}^{k}$ is the weight of the k-th label at t-th boosting round. Initially, $\varvec{\tau }= \emptyset$ and $WL_{1}^{k}=\frac{1}{L}$, which means $\varvec{WL}_{1} = [\frac{1}{L}, \cdots , \frac{1}{L}]$.

Figure 1 illustrates an overview of our proposed DMLMR algorithm. At t-th boosting round, there are following 5 steps.

Label Sampling. We sample one label a according to the label distribution $\varvec{WL}_{t}$, where $a\in \{1, 2, \cdots , L\}$. And then we update $\varvec{\tau }$ by concatenating $\varvec{\tau }$ and a, i.e., $\varvec{\tau }= [\varvec{\tau }, a]$.

Instance Distribution Adaptation. After getting one sampled label a, we transform the original dataset $\mathcal {D}$ into two dataset $\mathcal {D}_{a}=\{(\varvec{X}, \varvec{Y}_{a})\}$ and $\varvec{D}_{-a}=\{(\varvec{X}, \varvec{Y}_{-a})\}$.

Fig. 2.

Illustration of label vector $\varvec{Y}_{a}$ and $\varvec{Y}_{-a}$ in $\varvec{Y}$. In the left part, matrix shadowed with orange represents $\varvec{Y}_{a}$. In the right part, matrix shadowed with orange represents $\varvec{Y}_{-a}$.

Here $\varvec{Y}_{a}$ and $\varvec{Y}_{-a}$ are label vectors associated with instance matrix $\varvec{X}$, which is shown in Fig. 2. More specifically, $\varvec{Y}_{a} \in \mathbb {R}^{N}$ denotes the a-th column vector of the matrix $\varvec{Y}$ (versus $\varvec{y}_{i} \in \mathbb {R}^{L}$ for the i-th row vector of $\varvec{Y}$), and $\varvec{Y}_{-a} = [\varvec{Y}_{1}, \cdots , \varvec{Y}_{a-1}, \varvec{Y}_{a+1}, \cdots , \varvec{Y}_{L}] \in \mathbb {R}^{N\times (L-1)}$ represents the matrix that excludes the a-th column vector of the matrix $\varvec{Y}$.

And then we get $\varvec{F}_{a}(\cdot )$ and $\varvec{F}_{-a}(\cdot )$, where $\varvec{F}_{a}(\cdot ) = F^{a}(\cdot )$ denotes the original classifier of $\mathcal {Y}_{a}$ and $\varvec{F}_{-a} = [F^{1}(\cdot ), \cdots , F^{a-1}(\cdot ), F^{a+1}(\cdot ), \cdots , F^{L}(\cdot )]$ denotes the original classifiers of $\mathcal {Y}_{-a}$, where $\mathcal {Y}_{a} = \{-1, 1\}$ denotes label space of the a-th label and $\mathcal {Y}_{-a} = \{-1, 1\}^{L-1}$ denotes label space of all the labels exclude the a-th label.

In order to exploit label correlations, we maintain two instance distributions $\varvec{WD}_{1}$ and $\varvec{WD}_{2}$ adapted by Eq. 1, where $WD_{1}^{i}$ and $WD_{2}^{i}$ are the weight for the i-th instance with respect to $\mathcal {Y}_{a}$ and $\mathcal {Y}_{-a}$, respectively.

$$\begin{aligned} \begin{aligned} WD_{1}^{i}= \frac{1}{N}\cdot \lambda _{intra}^{\mathbb {I}(F_{a}(\varvec{x}_{i})\ne \varvec{y}_{i,a})}\cdot \lambda _{inter}^{\mathbb {I}(F_{-a}(\varvec{x}_{i})\ne \varvec{y}_{i,-a})} \\ WD_{2}^{i} = \frac{1}{N}\cdot \lambda _{intra}^{\mathbb {I}(F_{-a}(\varvec{x}_{i})\ne \varvec{y}_{i,-a})}\cdot \lambda _{inter}^{\mathbb {I}(F_{a}(\varvec{x}_{i})\ne \varvec{y}_{i,a})}\end{aligned} \end{aligned}$$

(1)

where $\mathbb {I}(\cdot )$ denotes the indicator function which outputs 1 if $\cdot$ is true, 0 otherwise. Additionally, $\varvec{y}_{i,a}$ denotes ground truth of a-th label associated with $\varvec{x}_{i}$ and $\varvec{y}_{i,-a}$ denotes ground truth of all the labels excludes a-th label associated with $\varvec{x}_{i}$. $\lambda _{intra}$ is the intra-set reweight parameter and $\lambda _{inter}$ is the inter-set reweight parameter. Take $WD_{1}^{i}$ as an example, item $\lambda _{intra}^{\mathbb {I}(F_{a}(\varvec{x}_{i})\ne \varvec{y}_{i,a})}$ considers the mistake made by label in $\mathcal {Y}_{a}$, i.e, a model that has made mistake will be emphasized by assigning a higher weight. Item $\lambda _{inter}^{\mathbb {I}(F_{-a}(\varvec{x}_{i})\ne \varvec{y}_{i,-a})}$ considers inter-set relationship between $\mathcal {Y}_{a}$ and $\mathcal {Y}_{-a}$, i.e., the weight of an instance on $\mathcal {Y}_{a}$ will be increased when misclassified on $\mathcal {Y}_{-a}$. Meaning of items in $WD_{2}^{i}$ is similar to that in $WD_{1}^{i}$.

At the end of the training process, we normalize $\varvec{WD}_{1}$ and $\varvec{WD}_{2}$ to form a valid distribution.

Instance Sampling. We decompose the original problem into two dependent sub-problems.

And then we sample two datasets $\mathcal {D}_{1}= \{(\varvec{X}_{1}, \varvec{Y}_{a})\}$ and $\mathcal {D}_{2} = \{(\varvec{X}_{2}, \varvec{Y}_{-a})\}$ i.i.d. according to instance distributions $\varvec{WD}_{1}$ and $\varvec{WD}_{2}$ respectively, where $\varvec{X}_{1} \in \mathbb {R}^{N\times d}$, $\varvec{Y}_{a} \in \mathbb {R}^{N\times 1}$, $\varvec{X}_{2} \in \mathbb {R}^{N\times d}$, $\varvec{Y}_{-a} \in \mathbb {R}^{N\times (L-1)}$.

Bipartite Model Reuse We train on two datasets $\mathcal {D}_{1}$ and $\mathcal {D}_{2}$ with model reuse and get 3 models $\varvec{G}_{1}$, $\varvec{G}_{2}$ and $\varvec{G}_{3}$.

• Firstly, we train on the dataset $\mathcal {D}_{2}$ with basic multi-label learning algorithm (here we adopt CC algorithm), and then we get model $\varvec{G}_{1}: \mathcal {X} \rightarrow \mathcal {Y}_{-a}$.

• Secondly, we reuse model $\varvec{G}_{1}$ on $\mathcal {D}_{1}$ and get predicted label vector $\varvec{G}_{1}(\varvec{x}_{i})$. And then, we concatenate feature vector with predicted label vector, i.e, $[\varvec{x}_{i}, \varvec{G}_{1}(\varvec{x}_{i})]$. Training on dataset $\mathcal {D}_{1}$, we get model $\varvec{G}_{2}: \mathcal {X} + \mathcal {Y}_{-a} \rightarrow \mathcal {Y}_{a}$.

• Thirdly, we reuse model $\varvec{G}_{2}$ on $\mathcal {D}_{2}$ and get predicted label vector $\varvec{G}_{2}(\varvec{x}_{i})$. And then, we concatenate $\varvec{x}_{i}$ with predicted label vector, i.e, $[\varvec{x}_{i}, \varvec{G}_{2}([\varvec{x}_{i}, \varvec{G}_{1}(\varvec{x}_{i})])]$. Training on dataset $\mathcal {D}_{2}$, we get model $\varvec{G}_{3}: \mathcal {X} + \mathcal {Y}_{a} \rightarrow \mathcal {Y}_{-a}$.

It is notable that $\varvec{G}_{2}$ reuses model $\varvec{G}_{1}$, so $\varvec{G}_{3}$ reuses two models $\varvec{G}_{1}$ and $\varvec{G}_{2}$. Model trained on one dataset is reused on the other dataset, which provides additional help for the final classification. Furthermore, we provide theoretical analysis for bipartite model reuse. $\varvec{h}_{a}(\cdot )=\varvec{G}_{2}(\cdot )$ and $\varvec{h}_{-a}(\cdot )=\varvec{G}_{3}(\cdot )$ in the following analysis.

Definition 1

Generalization error of hypothesis $\varvec{h}(\cdot )$ mapping from $\mathcal {X}$ to $\mathcal {Y}$ based on HammingLoss:

$$\begin{aligned} \begin{aligned} R(\varvec{h})=\mathop {\mathbb {E}}_{(\varvec{x}, \varvec{y}) \sim \mathcal {D}}\Big [\frac{1}{L} \sum _{k=1}^{L} \mathbb {I}(\varvec{h}(\varvec{x}) \ne \varvec{y}^{k})\Big ] \\ \end{aligned} \end{aligned}$$

(2)

where $\varvec{y}^{k}$ is the ground-truth of the k-th label.

Definition 2

Empirical error of hypothesis $\varvec{h}(\cdot )$:

$$\begin{aligned} \begin{aligned} \hat{R}(\varvec{h})=\frac{1}{m} \sum _{i=1}^{m}\Big (\frac{1}{L}\sum _{k=1}^{L} \mathbb {I}(\varvec{h}(\varvec{x}) \ne \varvec{y}^{k})\Big ) \\ \end{aligned} \end{aligned}$$

(3)

Lemma 1

$R(\varvec{h})\le max\{R(\varvec{h}_{a}), R(\varvec{h}_{-a})\}$, where $\varvec{h}(\cdot )$ is composed of $\varvec{h}_{a}(\cdot )$ and $\varvec{h}_{-a}(\cdot )$.

Proof

$$\begin{aligned} \begin{aligned} R(\varvec{h})&= \mathop {\mathbb {E}}\limits _{(\varvec{x}, \varvec{y}) \sim \mathcal {D}}\Big [\frac{1}{L} \sum \limits _{k=1}^{L} \mathbb {I}(\varvec{h}(\varvec{x}) \ne \varvec{y}^{k})\Big ] \\&=\frac{1}{L} \mathop {\mathbb {E}}\limits _{(\varvec{x}, \varvec{y}) \sim \mathcal {D}}\Big [\mathbb {I}(\varvec{h}_{a}(\varvec{x}) \ne \varvec{y}^{a})\Big ] \\&\quad + \frac{1}{L} \mathop {\mathbb {E}}_{(\varvec{x}, \varvec{y}) \sim \mathcal {D}}\Big [\sum \limits _{k=1, k\ne a}^{L} \mathbb {I}(\varvec{h}_{-a}(\varvec{x}) \ne \varvec{y}^{k})\Big ] \\&= \frac{1}{L} \big (R(\varvec{h}_{a}) + (L-1)R(\varvec{h}_{-a})\big ) \\&\quad \le \frac{1}{\,}L max\{R(\varvec{h}_{a}), R(\varvec{h}_{-a})\}(1+L-1)\} \\&= max\{R(\varvec{h}_{a}), R(\varvec{h}_{-a})\} \end{aligned} \end{aligned}$$

   $\square$

Lemma 2

$R(\varvec{h}_{-a})\le max\{R(h^{k})\}_{k=1, k\ne a}^{L}$

Proof

$$\begin{aligned} \begin{aligned} R(\varvec{h}_{-a})&= \mathop {\mathbb {E}}\limits _{(\varvec{x}, \varvec{y}) \sim \mathcal {D}}\Big [\frac{1}{L-1} \sum \limits _{k=1, k\ne a}^{L} \mathbb {I}(h^{k}(\varvec{x}) \ne \varvec{y}^{k})\Big ] \\&= \frac{1}{L-1} \mathop {\mathbb {E}}_{(\varvec{x}, \varvec{y}) \sim \mathcal {D}}\Big [\sum _{k=1, k\ne a}^{L} \mathbb {I}(h^{k}(\varvec{x}) \ne \varvec{y}^{k})\Big ] \\&= \frac{1}{L-1} \mathop {\mathbb {E}}_{(\varvec{x}, \varvec{y}) \sim \mathcal {D}}\Big [\sum _{k=1, k\ne a}^{L} R(h^{k})\Big ] \\&\le \frac{1}{L-1}(L-1) max\{R(h^{k})\}_{k=1, k\ne a}^{L} =R(\varvec{h}_{m})\\ \end{aligned} \end{aligned}$$

   $\square$

where $\varvec{h}_{-a}(\cdot )=[h^{1}(\cdot ), \cdots , h^{a-1}(\cdot ), h^{a+1}(\cdot ), \cdots , h^{L}(\cdot )]$, and for simplicity, we denote $max\{R(h^{k})\}_{k=1, k\ne a}^{L}$ as $R(\varvec{h}_{m})$.

Theorem 31

In mono-label case, let $H\subset \mathbb {R}^{\mathcal {X}\times \mathcal {Y}}$ be a hypothesis set. Fix $\rho >0$. Assume there exists $r > 0$ such that $k(\varvec{x}, \varvec{x})\le r^{2}$ for all $\varvec{x} \in \mathcal {X}$. For any $\delta >0$, with probability at least $1-\delta$, the following holds for all $h \in H$. [12]

$$\begin{aligned} R(h)\le \hat{R}_{\rho }(h)+2\sqrt{\frac{r^{2}\wedge ^{2}/\rho ^{2}}{m}}+3\sqrt{\frac{log(2/\delta )}{m}} \end{aligned}$$

(4)

Combine Lemma 1, Lemma 2 and Theorem 31, we have:

Proof

$$\begin{aligned} \begin{aligned} R(\varvec{h})&\le max\{R(\varvec{h}_{a}), R(\varvec{h}_{-a}) \\&\le max\Big \{\hat{R}_{\rho }(\varvec{h}_{a})+2\sqrt{\frac{r^{2}\wedge ^{2}/\rho ^{2}}{m}}+3\sqrt{\frac{log(2/\delta )}{m}},\\&\qquad \qquad \hat{R}_{\rho }(\varvec{h}_{m})+2\sqrt{\frac{r^{2}\wedge ^{2}/\rho ^{2}}{m}}+3\sqrt{\frac{log(2/\delta )}{m}}\Big \} \\&\le max \{\hat{R}_{\rho }(\varvec{h}_{a}), \hat{R}_{\rho }(\varvec{h}_{m})\}+ 2\sqrt{\frac{r^{2}\wedge ^{2}/\rho ^{2}}{m}} + 3\sqrt{\frac{log(2/\delta )}{m}} \end{aligned} \end{aligned}$$

   $\square$

The convergence rate of generalization error is standard as $O(\frac{1}{\sqrt{m}})$, which validates the effect of bipartite model reuse.

Label Distribution Adaptation. In order to select most discriminative label for bipartite model reuse, we are supposed to adapt label distribution according to the models trained by bipartite model reuse. We get prediction $\varvec{f}_{t}(\cdot )=\varvec{G}_{3}(\cdot )$, and $\varvec{f}_{t}(\cdot )=[f_{t}^{1}(\cdot ), \cdots , f_{t}^{a-1}(\cdot ), f_{t}^{a+1}(\cdot ), \cdots , f_{t}^{L}(\cdot )]$ where $f_{t}^{k}(\cdot )$ denotes the classifier of the k-th label. And then we test on dataset $\mathcal {T}$ with $\varvec{f}_{t}(\cdot )$ and $\varvec{F}_{-a}(\cdot )$ respectively. We get importance rate of the a-th label for other labels as follows:

$$\begin{aligned} \alpha _{t} = \frac{SubAcc(\varvec{f}_{t})}{SubAcc(\varvec{F}_{-a})} \end{aligned}$$

(5)

where $SubsetAcc_{t}(\varvec{f}_{t}) = \frac{1}{M}\sum _{i=1}^{{M}}\mathbb {I}\big (\varvec{f}_{t}(\varvec{x}_{i})=\varvec{y}_{i, -a}\big )$ and $SubsetAcc_{t}(\varvec{F}_{-a}) = \frac{1}{M}\sum _{i=1}^{{M}}\mathbb {I}\big (\varvec{F}_{-a}(\varvec{x}_{i})=\varvec{y}_{i, -a}\big )$.

On the other hand, we will increase the weight of the a-th label if $\alpha _{t}>1$, i.e, the a-th label has a positive effect to other labels with bipartite model reuse. The weight of other labels exclude the a-th label remain unchanged. And then we adapt label distribution $\varvec{WL}_{t+1} = [WL_{t+1}^{1}, \cdots , WL_{t+1}^{k}, \cdots , WL_{t+1}^{L}]$ for next boosting round.

$$\begin{aligned} WL_{t+1}^{k}= WL_{t}^{k} \cdot \alpha _{t}^{\mathbb {I}(k=a)} \end{aligned}$$

(6)

where $\mathbb {I}(\cdot )$ is an indicator function and $k=\{1,\cdots , L\}$. Similar to $\varvec{WD}_{1}$ and $\varvec{WD}_{2}$, we then normalize $\varvec{WL}_{t+1}$.

Above all, Overall Model Reuse is adopted. As is shown in Fig. 1, we get $\varvec{f}_{1}(\cdot ), \varvec{f}_{2}(\cdot ), \cdots , \varvec{f}_{T}(\cdot )$ after T number of boosting round. Finally we integrate all models together and get $\varvec{H}(\cdot )=[H^{1}(\cdot ), \cdots , H^{k}(\cdot ), \cdots , H^{L}(\cdot )]$, where $H^{k}(\cdot )$ denotes final classifier of the k-th label. In the testing phase, labels are predicted for instance $\varvec{x}$ according to:

$$\begin{aligned} H^{k}(\varvec{x}) = \mathop {argmax} \limits _{l} \sum _{t=1, k\ne \tau _{t}}^{T} \alpha _{t}\cdot \mathbb {I} (f_{t}^{k}(\varvec{x})=l) \end{aligned}$$

(7)

where $l\in \{-1, 1\}$, $k = \{1, \cdots , L\}$.

4 Experiments

In this section, we validate the effectiveness of our proposed DMLMR algorithm on real-world dataset of Parkinson’s disease and various benchmark multi-label datasets.

4.1 Dataset Description

Firstly, we manually collect real-world dataset of Parkinson’s disease in Traditional Chinese Medicine (TCM). Furthermore, we will briefly present the feature and label generation procedure for Parkinson’s disease diagnosis.

Both Parkinson-P and Parkinson have 91 TCM scales as features. However, Parkinson-P has 5 primary symptoms. Parkinson has 10 syndrome types: 5 primary syndrome types and 5 secondary syndrome types. More details with regard to syndrome types can be found in Sect. 1.

It is notable that DMLMR is designed for diagnosing Parkinson’s disease, it is also a general multi-label learning algorithm. For comprehensive performance evaluation, we collect 4 benchmark multi-label datasets.

• ML2000: is an image dataset from [20], including 2000 images from 5 categories.

• Scene: has 2407 images and 6 possible labels [1].

• Emotions: is a set of 593 songs with 6 clusters of music emotions [16].

• Genbase: consists of 662 proteins with known structure families that belong in 27 labels [2].

Table 1 summarizes the detailed characteristics of all datasets, Given a multi-label dataset $\mathcal {D} =\{(\varvec{X}, \varvec{Y})\}$, we use $|\mathcal {D}|$, $dim(\mathcal {D})$, $L(\mathcal {D})$, $LCard(\mathcal {D})$, $LDen(\mathcal {D})$ and $F(\mathcal {D})$ to represent number of instances, feature dimension, number of possible labels, label cardinality, label density and feature type, respectively.

• $LCard(\mathcal {D})=\frac{1}{N}\sum _{i=1}^{N}|\varvec{y}_{i}|$ measures the average number of labels per instance.

• $LDen(\mathcal {D})=\frac{LCard(\mathcal {D})}{L(\mathcal {D})}$ normalizes $LCard(\mathcal {D})$ by the number of possible labels.

Table 1. Characteristics of datasets.

4.2 Evaluation Metrics

To have a fair comparison, we employ five widely-used evaluation metrics, including: HammingLoss, SubsetAcc, $MacroF_{1}$, $MicroF_{1}$, $ExampleF_{1}$ [21].

4.3 Comparing Algorithms

We compare our proposed DMLMR algorithm with six state-of-the-art multi-label algorithms, listed as follows:

• BR [1]: first-order algorithm which transforms the multi-label learning task into multiple binary classification tasks

• CC [15]: a novel chaining method that considers the relativity between labels

• ECC [15]: state-of-the-art supervised ensemble multi-label learning method

• MLKNN [20]: is a kNN style multi-label classification algorithm, and outperforms some existing algorithms

• LLSF [7]: second-order algorithm which exploits different feature sets for the discrimination of different labels

• CAMEL [3]: a novel method to learn the label correlations via sparse reconstruction in the label space.

Table 2. Performance comparison on Parkinson-P and Parkinson dataset. $\uparrow /\downarrow$ indicates that the larger/smaller the better of a criterion. The best results are in bold.

Table 3. Performance comparison on four benchmark multi-label datasets. $\uparrow /\downarrow$ indicates that the larger/smaller the better of a criterion. The best results are in bold.

4.4 Experimental Results

For all these algorithms, we report the best results of the optimal parameters in terms of classification performance. 10-fold cross validation (CV) is performed on each dataset. To better characterize the comparison, we take the mean metric value as well as the standard deviation of each algorithm. Note that for all the employed multi-label evaluation metrics, their values vary within the interval [0,1]. The larger the value of them, the better the performance of the classifier for all of these evaluation metrics except HammingLoss.

Experimental results of our proposed DMLMR and other comparing algorithms on real-world dataset of Parkinson’s disease and four benchmark multi-label datasets are listed in Table 2 and Table 3 respectively. From the results, it is obvious that DMLMR algorithm can achieve best or at least comparable performance on all datasets with different evaluation metrics, which reveals that DMLMR algorithm is a high-competitive multi-label learning algorithm.

4.5 Influence of Parameters

More experiments are conducted on one real-world Parkinson-P dataset and one benchmark multi-label Scene dataset to explore parameter sensitivity.

Inter-set Reweight Parameter. $\varvec{\lambda _{inter}}$ is used for exploring the inter-set relationship between $\mathcal {Y}_{a}$ and $\mathcal {Y}_{-a}$. For Parkinson-P dataset, we fix $\lambda _{intra}=1.5$, $T=3$, and then we set $\lambda _{inter}$ between 1.0 and 1.5 with an interval of 0.1. For Scene dataset, we fix $\lambda _{intra}=2$, $T=3$, and then we set $\lambda _{inter}$ between 1.0 and 1.5 with an interval of 0.1.

As shown in Table 4, the performance of $\lambda _{inter} > 1.0$ is better than others when $\lambda _{inter}=1.0$ in most cases, which validates the effectiveness of exploiting inter-set label relationship. In addition, we get optimal performance when $\lambda _{inter}=1.7$ on Parkinson-P dataset and $\lambda _{inter}=1.3$ on Scene dataset.

Intra-set Reweight Parameter. $\varvec{\lambda _{intra}}$ is used for exploring the intra-set relationship on $\mathcal {Y}_{a}$ (or $\mathcal {Y}_{-a}$). Based on the above discussion of inter-set reweight parameter $\lambda _{inter}$, for Parkinson-P dataset, we fix $\lambda _{intra}=1.7$, $T=3$, and then we set $\lambda _{inter}$ between 1.0 and 3 with an interval of 0.5. For Scene dataset, we fix $\lambda _{intra}=1.3$, $T=3$, and then we set $\lambda _{inter}$ between 1.0 and 3 with an interval of 0.5. In Table 5, we find that $\lambda _{intra}=1.25$ or $\lambda _{intra}=1.5$ for Parkinson-P dataset may be a relatively proper setting, while $\lambda _{intra}=2.0$ or $\lambda _{intra}=2.5$ for Scene dataset.

Fig. 3.

Performance of changes made by the number of boosting rounds T on Parkinson-P and Scene dataset, with $\lambda _{inter}$ and $\lambda _{intra}$ fixed.

Table 4. Performance comparison on Parkinson-P and Scene dataset when $\lambda _{inter}$ increases with $\lambda _{intra}$ and T fixed. $\uparrow /\downarrow$ indicates that the larger/smaller the better of a criterion. The best results are in bold.

Table 5. Performance comparison on Parkinson-P and Scene dataset when $\lambda _{intra}$ increases from 1.0 to 3.0 with $\lambda _{inter}$ and T fixed. $\uparrow /\downarrow$ indicates that the larger/smaller the better of a criterion. The best results are in bold.

Boosting Round $\varvec{T}$. We fix $\lambda _{inter}=1.7$, $\lambda _{intra}=1.25$ for Parkinson-P dataset and fix $\lambda _{inter}=1.3$, $\lambda _{intra}=2.0$ for Scene dataset. With $\lambda _{inter}$ and $\lambda _{intra}$ fixed, we get the optimal results when $T=8$ on Parkinson-P dataset. Similarly, we get the optimal results when $T=7$ on Scene dataset.

For one thing, increasing number of boosting rounds will make classifier overly complex and may lead to overfitting. We can see from Fig. 3(a) that when boosting round $T=10$, all evaluation metrics decline slightly, which accords with our intuition since DMLMR is an approach with a boosting framework.

For another, classifier should have low training error and a small number of boosting rounds in order to achieve good performance. As is shown in Fig. 3, with $\lambda _{inter}$ and $\lambda _{intra}$ fixed, the performance of DMLMR is unstable in the initial increasing phase of T. After that, DMLMR improves remarkably. Eventually, as the number of boosting round T increases, all curves tend to be smoother, which show convergence when $T>6$ for Parkinson-P and $T>7$ for Scene dataset.

5 Conclusion

Traditional Chinese Medicine (TCM) is a new way for diagnosing Parkinson’s disease (PD). In this paper, we apply multi-label classification technology to diagnose PD in TCM, where we treat TCM scales as features and treat syndrome types as multiple labels. Furthermore, we propose a novel Discriminative Multi-label Model Reuse (DMLMR) algorithm to advance diagnosing PD in TCM. DMLMR exploits label correlations by selecting discriminative label with label distribution adaptation, and then trains with model reuse. An assessment on the real-world dataset of PD shows that DMLMR obtains remarkable results in terms of various evaluation metrics, and DMLMR validates its ability of diagnosing PD in TCM. Extensive experiments on multi-label benchmark datasets show that DMLMR outperforms the state-of-the-art counterparts. In the future, how to extend to scenario with partial labels is a very interesting work.