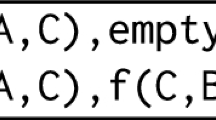CONNER: A Concurrent ILP Learner in Description Logic

Abstract

Machine Learning (ML) approaches can achieve impressive results, but many lack transparency or have difficulties handling data of high structural complexity. The class of ML known as Inductive Logic Programming (ILP) draws on the expressivity and rigour of subsets of First Order Logic to represent both data and models. When Description Logics (DL) are used, the approach can be applied directly to knowledge represented as ontologies. ILP output is a prime candidate for explainable artificial intelligence; the expense being computational complexity. We have recently demonstrated how a critical component of ILP learners in DL, namely, cover set testing, can be speeded up through the use of concurrent processing. Here we describe the first prototype of an ILP learner in DL that benefits from this use of concurrency. The result is a fast, scalable tool that can be applied directly to large ontologies.

1 Introduction

Graphic processing units (GPU) can be used with benefits for general purpose computation. GPU-based data parallelism has proven very efficient in a number of application areas [1]. We have recently proposed a GPU-accelerated approach to the computation of the cover set for a given hypothesis expressed in $\mathcal {ALC}$ description logic, which results in a speed up of two orders of magnitude when compared with a single-threaded CPU implementation [2]. The present article combines this approach with an implementation of a well-studied refinement operator and a search strategy for the exploration of the hypothesis space. The result is the first version of a GPU-accelerated inductive learner, further on referred to as CONNER$\,1.0$ (CONcurrent learNER).

In more detail, here we present the first complete description of the way binary predicates (or roles in description logic parlance) are handled by our cover set procedure, which is now extended beyond $\mathcal {ALC}$ to make use of cardinality restrictions (e.g. $\textit{OffpeakTrain} \sqsubseteq \,\, \le 6 \,\, hasCar{.}{} \textit{Car}$) and data properties (e.g. $\textit{Bike} \sqsubseteq \,\, \textit{numberOfWheels} =2)$. We test the speed and accuracy of our learner on a combination of synthetic and real world data sets. To emphasise the low cost of adoption of this algorithm, we have run the tests on a commodity GPU, Nvidia GeForce GTX 1070.

The rest of this paper is structured as follows: Sect. 2 covers relevant work, Sect. 3 completes the previously published description of how the hypothesis cover set is computed [2] with the algorithms handling value restriction and existential restriction, and tests the speed of their execution. Section 4 extends the list of operators with the algorithms for handling the cardinality restriction and data property operators. Section 5 describes a complete GPU-accelerated ILP learner in DL, CONNER, and evaluates its performance, while Sect. 6 draws conclusions and outlines future work.

2 Background

CONNER lays at the intersection of ILP, parallel computation, and description logics (Fig. 1). In this section, we review the notable overlaps between these three areas. Algathani and Kazakov [2] can be further consulted for a suitable overview of the basics of GPU architecture.

Fig. 1.

Intersection of ILP, parallel computation and DL [3, 5, 8,9,10, 16,17,18,19,20,21,22,23,24].

Arguably, the implementation of an ILP algorithm can be defined by the ways it approaches hypothesis cover set testing, the application of its refinement operator, and the search algorithm used to explore the hypothesis space. While all three are amenable to parallelisation, here we focus our efforts in this direction on the first component, and with a description logic as a hypothesis language.

Description Logics (DL) is a family of subsets of first order logic that are used to represent knowledge in the form of ontologies. $\mathcal{ALC}$ (Attributive Language with Complement) is a commonly used subset of DL, which makes use of propositional operators, as well as two binary operators, existential restriction and value restriction. As ontologies continue to gain popularity, e.g. in the form of linked open data, this strengthens the case for learners that can work directly with this type of data. A few notable examples of ILP learners in DL follow.

DL-FOIL [3] is an adaptation of the classical ILP algorithm FOIL [4] to DL as data and hypothesis language. It still uses a top-down refinement operator with search guided by information gain, but the latter is modified to accommodate the use of the Open World Assumption (OWA).

The DL-Learner [5] is a framework for learning in DL. The framework allows the user to select from different reasoners to handle inference. It is also possible to choose from four learning algorithms: OWL Class Expression Learner (OCEL), Class Expression Learning for Ontology Engineering (CELOE), EL Tree Learner (ELTL), and Inductive Statistical Learning of Expressions (ISLE). One can also choose from different refinement operators. The framework provides facilities to handle large datasets by the use of sampling.

APARELL [6] is an ILP algorithm for the learning of ordinal relations (e.g. better_than [7]) in DL. The algorithm borrows ideas from the Progol/Aleph pair of algorithms about the way hypothesis search operates. APARELL processes DL data directly from OWL ontologies, and can read any format which is supported by the OWL API.

There have been several attempts to implement reasoners in DL using parallel computation [8, 9]. The most relevant effort here is Chantrapornchai and Choksuchat’s [10] recently proposed GPU-accelerated framework for RDF query processing, TripleID-Q. The framework maintains a separate hash table for each of the three arguments (subject, predicate, object) of the RDF triples. Each triple is represented through the three hash keys (all integers) and stored in the shared memory of the GPU. RDF queries are mapped onto that representation and the data is split among multiple GPU threads to retrieve the matching triples in parallel. In this context, the work of Martínez-Angeles et al. on the use of GPU to speed up cover set computation for first-order logic ILP systems, such as Aleph, should also be noted [11].

3 Concurrent, GPU-Accelerated Cover Set Computation

A GPU can manipulate matrices very efficiently. Here we complete the description of the GPU-powered approach first presented by Algahtani and Kazakov [2], which aims at speeding up the calculation of the cover set of hypotheses expressed in $\mathcal {ALC}$ description logic. We also present experimental results on the performance of this algorithm.

DL allows one to describe concepts $C_i$ defined over a universe of individuals $I_i$, and to define roles relating individuals to each other. Concept membership can be represented as a Boolean matrix M of size $|C| \times |I|$ (see Fig. 2). Using this representation, it is possible to employ data parallelism for the application of logic operations to concepts. We have already shown how the three propositional operators $\{ \sqcap$, $\sqcup$, $\lnot \}$ can be implemented, and tested the speed with which they are computed [2]. Here we describe the concurrent implementation of the value restriction operator ($\forall r{.}C$) and the existential restriction operator ($\exists r{.}C$).

Either restriction operator takes a role and a concept as input, and makes use of the concept matrix M and another matrix, R, storing all role assertions (see Fig. 2). The matrix is sorted by the role. As a consequence, all assertions of a given role are stored in a contiguous range of rows. This facilitates a more efficient GPU memory access pattern (namely, coalesced memory access). For each role, the start and end row indices corresponding to its range of rows are stored in a hash table, H, and can be retrieved efficiently using the role name as key.

Algorithm 1 shows the implementation of the existential operator. Its first step is to allocate memory for the output array and set all values to 0 (representing ). This is done in a concurrent, multi-threaded fashion. The range of rows in R storing all assertions of Role is then looked up in H (in $\mathcal{O}(1)$ time). After that, the role assertions in R within the role range are divided among a number of threads, and for each such assertion, a check in matrix M is made whether belongs to Concept (i.e. the concept in the existential restriction). The result of this step is combined through OR with the current value in row of the output array and stored back there.

This implementation avoids the use of conditional statement, which could slow down the process. At the same time, it is important that an atomic OR is used to avoid a race-condition situation between the individual threads.¹

Fig. 2.

Main data structures in the GPU memory

The implementation of the value restriction operator $\forall \textit{Role}.\textit{Concept}$ is analogous to the existential restriction, with the only difference being that all initial values in the result array are set to 1 (i.e. ), and an atomic AND operator is applied instead of OR.²

Table 1. Execution times for computing the cover sets of $\exists has\_car$.Long and $\forall has\_car$.Long (average of 10).

Fig. 3.

Computing existential ($\exists$) and value ($\forall$) role restrictions

To evaluate the execution times of the two restriction operators, we use a dataset consisting of multiple copies of Michalski’s eastbound/westbound trains dataset [12], here in its DL representation [5]. The dataset consists of 12 concepts (unary predicates), and 5 roles (binary predicates); these predicates describe 10 trains (5 eastbound and 5 westbound) and their respective cars. The results are shown in Table 1 and plotted in Fig. 3. It should be noted that only the number of assertions for the given role has an impact on the execution times when matrix R is traversed: while matrix M grows with the number of individuals, access time to each row remains the same as, internally, an individual is represented directly with its row index in M. Also, the actual content of the assertions for the role in question makes no difference, which is why this dataset is appropriate here. The results show that the execution times remain virtually constant up to a point, possibly until the full potential for parallel computation in the GPU is harnessed, and then grow more slowly than $\mathcal{O}(n)$ for the range of dataset sizes studied.

4 Extending the Hypothesis Language

This section describes how the hypothesis language has now been extended to include cardinality and data property (also known as concrete role) restrictions. The result is a type of description logic referred to as $\mathcal {ALCQ^{(D)}}$.

4.1 Cardinality Restriction Support

The cardinality operator restricts for a given role the allowed number of assertions per individual. A cardinality restriction can be qualified (Q), or unqualified (N), where N is a special case of Q. In Q, any concept can be used in the restriction. While in N, only the Top Concept is used. There are three kinds of cardinality restrictions: the minimum ($\ge$), maximum ($\le$), and the exactly (==) restriction. Algorithm 2 implements the first of these three.

It first clears the result array (just as in the existential restriction). It then uses the CUDA atomic addition to increment the counter of the corresponding for every assertion matching the role and concept. The values in the are then compared with the cardinality condition, and the counter for each individual is replaced with 1 or 0 (representing True/False) according to whether the condition in question has been met. The condition in this last loop determines the type of cardinality restriction: min ($\ge$), max ($\le$), or exactly (==).

4.2 Data Property Restriction Support

Data properties (or concrete roles) map individuals on to simple values. In this implementation, we (currently) limit the range of values to numerical ones: integer, float and Boolean; supporting other types like Strings, is considered for future work. In order to handle such properties in the GPU, the individuals and their data properties are mapped on to a matrix, D (see Fig. 2), in a way similar to matrix M. Each cell in the new 2D matrix, is of float datatype, as it is inclusive to integers and Booleans. As with the cardinality restrictions, there are three kinds of data property restrictions: min, max, and exactly. Algorithm 3 shows how the minimum data property restriction is implemented, with the other two requiring only a trivial variation.

In Algorithm 3, a parallel for loop will iterate through all individuals, and the array will be set to 1 for all individuals matching the condition or to 0 otherwise. For the maximum and exactly restriction types, the condition will be changed to $\le$ (for maximum), and == (for exactly).

5 CONNER: All Together Now

The work described in this section was motivated by the desire to incorporate our approach to computing the DL hypothesis cover set in a learner in order to gauge the benefits this approach can offer.

5.1 TBox Processing

Every ontology consists of two parts, the so called ABox and TBox. Both of these need to be processed to establish correctly the membership of individuals to concepts. It is possible to employ off-the-shelf reasoners for this purpose. Indeed, this is the approach employed by DL-Learner. While it is expected that CONNER will make the same provision in the next iteration of its development, we have decided to use our own implementation here in order to have full control over how the planned tests are run. The implementation described below is somewhat limited, but sufficient for the test data sets used.

The ABox explicitly lists individuals belonging to a given concept or relation. These are easily processed and matrices M and R updated accordingly. The TBox provides intensional definitions of concepts ($C \equiv \dots$) and their hierarchy (e.g. $C_1 \subset C_2$). Here we only handle subsumption between single concepts. This information is processed by a dedicated multi-pass algorithm which updates matrix M, and is repeated until no further changes in concept definitions occur. Cyclic references are also detected and flagged up as an error. For instance, if the membership of the concept is defined extensively, through the ABox, and the TBox contains the statement $\subset$ , the individuals in will also be marked in matrix M as belonging to the concept after the TBox is processed (Fig. 4). The TBox needs only be processed once, when the ontology is imported, and represents no overhead on any subsequent computations. The hierarchy of concepts derived from the TBox statements is then used by the refinement operator to generate candidate hypotheses.

Fig. 4.

Example of processing the TBox

5.2 Refinement Operator and Search Algorithm

CONNER borrows the top-down refinement operators used in DL-Learner. The operator used with $\mathcal{ALC}$ is complete, albeit improper ([13], pp. 69–70). Figure 5 shows a sample $\mathcal{ALC}$ refinement path produced by this operator for a data set discussed in this section. When the hypothesis language is extended to $\mathcal {ALCQ^{(D)}}$, i.e., to include cardinality restrictions and data properties, the corresponding operator is no longer complete ([13], pp. 72–73).

The original operator is capable of producing a hypothesis consisting of a single clause (making use of the disjunction operator, when needed). A refinement step of the type $\top \rightarrow C \sqcup C \sqcup \dots \sqcup C$ is used to produce a disjunction of concepts that are all subsumed by C, e.g. moving from $Car \sqcup Car$ to $Petrol \sqcup Electric$ (potentially excluding Diesel). Here the number of copies of C appears to be part of the user input reminiscent of, say, the limit on the maximum length of the target clause used in Progol. We have experimented with alternatives, such as cautious learning where the above step is omitted from the refinement operator, and the disjunction of all consistent clauses found is used in the final hypothesis.

The refinement operator can be used under the closed world assumption (CWA), where test examples not covered by the hypothesis are labelled as negative examples. An example of such use was employed when the DL-Learner was tested by its author on Michalski’s trains ([13], pp. 143–146). We have done the same to replicate the results, but we also implement the open world assumption (OWA), which is more commonly used with DL. In this case, two hypotheses H$^+$ and H$^-$ are learned for the target class and its complement (by swapping the positive and negative examples). Test data is labelled as a positive, resp. negative example when either hypothesis is true, and an “I don’t know” label is produced when neither or both hypotheses are true.

The learner uses informed search with a scoring function derived from the one used in the OCEL algorithm of the DL-Learner [13]:

$$\begin{aligned} ocel\_score(N) = accuracy(N) + 0.5 {.} acc\_gain(N) -0.02 {.}n \end{aligned}$$

(1)

Here $acc\_gain(N)$ is the increase in accuracy w.r.t. the parent of N, where N is the candidate hypothesis (e.g. conjunction of concepts and/or restrictions), and n is an upper bound on the length of child concepts, which we set to be equal to the number of concepts in the ontology. We extend this function to take into account the length of a hypothesis (i.e. #concepts + #operators) and its depth which represents (here) the refinement steps taken to reach the current hypothesis, not necessarily its depth in the search tree. Thus the scoring function in CONNER is:

$$\begin{aligned} conner\_score(N) = 10 * ocel\_score(N) - length(N) - depth(N) \end{aligned}$$

(2)

The parser currently used to parse the hypotheses tested is Dijkstra’s shunting-yard algorithm. The effect of its use here is equivalent to using a binary parse tree, so all conjunctions and disjunctions of three and more concepts are handled as series of applications of the given operator to a pair of concepts. This simplifies the parsing task, but results in a significant drop in performance when compared to simultaneously computing conjunctions or disjunctions of K concepts in the given hypothesis (cf. [2]). A more sophisticated parser or the use of lazy evaluation [2] can be employed with potential benefits, but are not discussed here for reasons of space. We do use memoization [14] in the evaluation of each hypothesis, where partial computations are stored and reused.

Fig. 5.

A sample $\mathcal {ALC}$ refinement path to a solution: Michalski’s trains

5.3 Evaluation

The overall run time of the learner is first tested under the CWA on data consisting of multiple copies of the Michalski train set (in its DL version distributed with DL-Learner’s examples). While the task results in a relatively limited hypothesis space, this artificial data strains the cover set algorithm exactly as much as any real world data set with the same number of instances and assertions. The results are shown in Table 2 and Fig. 6. All experiments are deterministic and the results of multiple runs on the same data are remarkably consistent, so presenting results of single runs was deemed sufficient. Figure 5 shows the search path to the solution found. The solution itself is listed again in Table 3.

Table 2. Learning time vs size of data set (multiple copies of Michalski’s trains)

Fig. 6.

Plot of results in Table 2: learning time vs size of data set

To confirm that all components of the learner have been correctly implemented, and to further test its speed, another artificial data set in the style of Michalski’s trains (here with four cars each) has been generated and used in a second set of experiments.³ There are 21,156 unique trains (5,184 eastbound and 15,972 westbound) in the data set, which are represented through 105,780 individuals and 148,092 role assertions. Table 4 shows the average run times of the learner for data sets of varying size using 10-fold cross-validation. Under CWA, out-of-sample accuracy of 100% was achieved for all reported samples except for one of the samples of the lowest reported size. The hypothesis found in most cases is . The rule is found by the DL-Learner as its first solution when applied to all data. The two hypotheses are functionally equivalent.

Table 3. Solution to Michalski’s trains task in DL and FOL

Table 4. Learning time vs sample size (21,156 unique trains, 10-fold cross-validation)

We have also tested CONNER on the well-known mutagenesis ILP dataset [15] in its DL representation, using 10-fold cross-validation, with the following results:

6 Conclusion and Future Work

This article completes the implementation of the first working prototype of the CONNER algorithm. The results suggest that this GPU-powered ILP learner in DL has a lot of potential to scale up learning from ontologies. We have demonstrated how GPGPU can be used to accelerate the computation of the cover set of a hypothesis expressed in $\mathcal{ALC}$ and $\mathcal {ALCQ^{(D)}}$ description logics. The results add to our previous findings (cf. [2]) that even the use of a commodity GPU can provide the ability to process data sets of size well beyond what can be expected from a CPU-based sequential algorithm of the same type, and within a time that makes the evaluation of hypotheses on a data set with $10^7$–$10^8$ training examples a viable proposition.

Future work should consider provisions for the use of external, off-the-shelf reasoners. However, extending the in-house facilities in this aspect is expected to play an important role when the use of concurrency in the search, and its possible integration with cover set computation are considered. Finally, it should be said that the use of DL as hypothesis language simplifies the task of parallelising the cover set computation when compared to a Horn clause-based hypothesis language. It is clear that some of the problems traditionally tackled through learning in first-order logic can be effectively modelled in DL, and a broader evaluation of the trade-off between expressive power and potential speed up that this choice offers would certainly also provide useful insights.