Recent Updates of the Residual Stress Decomposition Method for Shakedown Analysis

Abstract

Almost every structure or mechanical component is exposed to repeated loading conditions. As a result, materials exceed the elastic regime and plastic strains develop. The outcome of these loadings may be estimated either using a time-consuming step by step analysis or adopting modern Direct Methods which are capable to predict final cyclic states, like the elastic shakedown (safe state), the alternating plasticity, or the ratcheting (unsafe states). Towards this direction, the Residual Stress Decomposition Method (RSDM) was developed. The RSDM estimates the asymptotic cyclic state of a structure exposed to a given cyclic loading. The RSDM-S is based on the same theoretical background as RSDM and was developed in order to estimate the shakedown domain of a structure. Both methods have been tested for cyclic thermal and mechanical loads. In the present work, the RSDM-S is updated towards faster convergence by avoiding some unnecessary calculations and extended to account also for cyclic imposed displacements. Computational implementation was performed in an open source research oriented finite element analysis program. Three-dimensional brick elements are used to deal model complex geometries. The material adopted is elastic perfectly plastic von Mises type of law. Examples of application are given, proving the versatility of the approach.

1 Introduction

Most structures and mechanical components are subjected to variable repeated loads and applied displacements. Typical variable loadings, like traffic loads, are applied to bridges, pavements, railway structures. Other structures, like buildings, bridges, pipelines, during their lifetime, undergo different earthquake actions, which may be considered as variable imposed displacements to their base. Mechanical engineering parts may also be subjected to variable mechanical and/or thermal loads. All these structures are usually designed to operate in the elastic regime, even if this leads to cost-ineffective solutions. However, the high level of variable loading or excessive applied displacements may force structural or mechanical members to develop plastic strains that eventually will end up to an asymptotic limit state such as ratcheting, low cycle fatigue or shakedown [1]. It may happen that, up to a specific limit of imposed displacement or load, inside the plastic regime, the plastic strains are stabilized and the structure responds elastically again. This safe state is known as shakedown, which has an effect to extend the life cycle of a structure.

When the exact load history is known one may estimate whether a structure will shakedown, using time-consuming step-by-step procedures. Thus, there is a need for faster procedures. Direct methods offer this possibility, as they attempt to find the stabilized state without tracing the whole load path. Also, when the exact loading history is not known, but only its variation intervals, they offer the only way to determine the shakedown limits. Most of these approaches are connected to the extremum theorems of structural plasticity and use optimization algorithms. Recent applications include railway structures [2] and pavements [3]. Direct methods, not related to mathematical programming, have also been proposed like the Simplified Theory of Plastic Zones (STPZ) method [4] or the Linear Matching Method (LMM) which has been recently extended to include limited kinematic hardening [5].

Another direct method, that does not use optimization algorithms, called Residual Stress Decomposition Method for Shakedown (RSDM-S) has been developed for the evaluation of shakedown domains [6, 7]. Its roots are in RSDM [8, 9], a direct method that may estimate the asymptotic cyclic state of a structure under a given cyclic loading. The basic idea behind both approaches is the decomposition of the expected in this state cyclic residual stresses in Fourier series, whose coefficients are estimated in an iterative way. The two procedures may be easily attached to any existing finite element program.

In the present work RSDM-S is slightly reformulated to avoid unnecessary calculations. Also, the initial parameters of the method are revisited towards the minimum number of iterations needed for a smooth and robust convergence. In the previous versions of the RSDM-S the loading was considered to be mechanical and/or thermal. However, boundary displacements varying within prescribed limits, are also possible [10]. The RSDM-S is herein extended to account for cyclic imposed displacements. Additionally, the portability of the method is demonstrated, while it is embedded in an open source finite element research-oriented computer code FEAP [11]. Brick elements have been used so that difficult geometries may be handled in either two or three dimensions. Examples of application are also presented.

2 Theoretical Considerations

The RSDM-S was developed in previous years [6, 7] and refers to structures made of elastic-perfectly plastic von Mises type of material, subjected to cyclic thermo-mechanical loadings varying inside a prescribed field. These loads may have a cyclic variation between a specified maximum and a minimum value.

2.1 The Case of Imposed Displacements

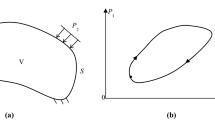
In Fig. 1 one may see a structure of volume V and surface S, which is partially rigidly supported ($S_{u}$) and partially subjected to cyclically imposed displacements ($S_{pr}$). The rest of its surface is free. There are no surface tractions or body forces applied on the structure.

Fig. 1

Body subjected to time dependent imposed displacement

Let us suppose that the displacements are applied periodically with period T, i.e. ${{\bar{\mathbf{u}}}}(t) = {{\bar{\mathbf{u}}}}(t + T)$. One and two-dimensional displacement domains are considered herein.

Without loss of generality, we assume that the minimum values of the two prescribed displacements are zero with the starred quantities representing their maximum values. The corresponding cyclic program of the imposed displacements, is $(0 \to \bar{u}_{1}^{*} \to ({\bar{\text{u}}}_{1}^{*} ,{\bar{\text{u}}}_{2}^{*} ) \to \bar{u}_{2}^{*} \to 0)$ (Fig. 2). These variations are shown [6] in either the time domain (a), or the applied displacement domain, which, in the sequel, will be called loading domain (b).

Fig. 2

Independent cyclic imposed displacement variation over one time period a time domain, b loading (applied displacement) domain

It has been proved in [1] that, for stable materials, if a structure shakes down under a cyclic loading program containing the vertices of the loading domain then it will shake down for any loading path contained in this domain. This domain may be isotropically varied if multiplied with a load factor γ. Thus, the idea behind RSDM-S is to find the largest loading domain for which shakedown occurs.

In response to the cyclic loading program, the stresses in the structure at a cycle point τ = t/T are decomposed into an elastic part ${\varvec{\sigma}}_{pr}^{el}$, in response to the applied external cyclic displacement, assuming a completely elastic behavior, and a residual stress part ${\varvec{\rho}}$. In the search for the shakedown factor γ, the elastic stresses are themselves multiplied by this factor. Thus, the total stress vector can now be written:

$${\varvec{\sigma}} = \gamma {\varvec{\sigma}}_{pr}^{el} + {\varvec{\rho}}$$

(1)

The elastic problem is solved first. Using the principle of virtual displacements (PVD), one may write:

$$\int\limits_{V} {\left(\delta {\varvec{\varepsilon}}_{pr}^{el} \right)^{T} {\varvec{\sigma}}_{pr}^{el} } \,dV = \int_{{S_{pr} }} {\left(\delta {\mathbf{u}}_{pr}^{el} \right)^{T} {\mathbf{f}}_{pr} } \,dS = 0$$

(2)

Since due to the fact that ${\mathbf{u}}_{pr}^{el} = {{\bar{\mathbf{u}}}}$, $\delta {\mathbf{u}}_{pr}^{el} = {\mathbf{0}}$ on $S_{pr}$.

We partition the nodes of the finite element (FE) mesh into those over the volume, the free boundary, the rigid boundary and the nodes on the prescribed displacement boundary. Denoting their corresponding displacements by ${\mathbf{r}}_{pr}^{el}$ and ${\bar{\text{r}}}^{el}$ one may connect them to the strains through two different FE compatibility matrices B and ${\mathbf{B}}^{{\prime }}$:

$${\varvec{\varepsilon}}_{pr}^{el} = {\mathbf{Br}}_{pr}^{el} + {\mathbf{B}}^{{\prime }} {{\bar{\mathbf{r}}}}^{el}$$

(3)

Because of (3) the virtual strain increment is:

$$\delta {\varvec{\varepsilon}}_{pr}^{el} = {\mathbf{B}}\left(\delta {\mathbf{r}}_{pr}^{el} \right)$$

(4)

The stresses are related to the elastic strains through the material matrix D

$${\varvec{\upsigma}}_{pr}^{el} = {{\mathbf{D}\varvec{\varepsilon}}}_{pr}^{el}$$

(5)

Substituting Eqs. (3)–(5) to (2) and doing the algebraic manipulation one may get:

$${\mathbf{Kr}}_{pr}^{el} = - \left(\int\limits_{V} {{\mathbf{B}}^{T} {\mathbf{DB}}^{{\prime }} \,dV} \right){{\bar{\mathbf{r}}}}^{el}$$

(6)

where ${\mathbf{K}} = \int\nolimits_{V} {{\mathbf{B}}^{T} {\mathbf{DB}}} \,{\kern 1pt} dV$ is the stiffness matrix of the structure.

With the displacements ${{\bar{\mathbf{r}}}}^{el}$ known, the Eq. (6) may be solved to obtain ${\mathbf{r}}_{pr}^{el}$ and therefore ${\varvec{\varepsilon}}_{pr}^{el}$ and ${\varvec{\upsigma}}_{pr}^{el}$ may be obtained.

The total strain rate may be decomposed into three terms:

$${{\dot{\varvec{\varepsilon}}}} = {{\dot{\varvec{\varepsilon}}}}_{pr}^{el} {{ + \dot{\varvec{\varepsilon}}}}_{{\mathbf{r}}}^{el} {{ + \dot{\varvec{\varepsilon}}}}^{pl}$$

(7)

Note that the terms ${{\dot{\varvec{\varepsilon}}}}$ and ${{\dot{\varvec{\varepsilon}}}}^{{{{el}}}}$ in (7) are kinematically admissible. Thus, the sum:

$${{\dot{\varvec{\varepsilon}}}}_{r} = {{\dot{\varvec{\varepsilon}}}}_{{\mathbf{r}}}^{el} + {{\dot{\varvec{\varepsilon}}}}^{pl}$$

(8)

is also kinematically admissible. This may be expressed as ${{\dot{\varvec{\varepsilon}}}}_{r} = {{\mathbf{B}\dot{\mathbf{r}}}}_{r}$, where ${\text{r}}_{r}$ are the FE displacements of the sought solution of the boundary value problem to account for the residual stresses.

The elastic term ${{\dot{\varvec{\varepsilon}}}}_{{\mathbf{r}}}^{el}$ is related to the residual stress via the material matrix D. Thus, one may write:

$${{\dot{\varvec{\varepsilon}}}}_{r} = {\mathbf{D}}^{ - 1} {{\dot{\varvec{\rho}}}} + {{\dot{\varvec{\varepsilon}}}}^{pl} \to {{\dot{\varvec{\rho}}}} = {{\mathbf{D}\dot{\varvec{\varepsilon}}}}_{r} - {{\mathbf{D}\dot{\varvec{\varepsilon}}}}^{pl}$$

(9)

Equilibrium of the residual stresses with zero loads may be manifested through the PVD:

$$\begin{aligned} \int {\left( {\delta \dot{\boldsymbol\varepsilon}_{r} } \right)^{\rm T} \dot{\boldsymbol\rho }dV} = 0 \to \left( {\int {\left( {\mathbf B^{T} \mathbf D\mathbf B} \right)} dV} \right)\dot{\mathbf r}_{r} & = \int {\mathbf B^{T} \mathbf D\dot{\boldsymbol\varepsilon }^{pl} dV} \\ \to \mathbf K\dot{\mathbf r}_{r} = \int {\mathbf B^{T} \mathbf D\dot{\boldsymbol \varepsilon }^{pl} dV} \\ \end{aligned}$$

(10)

The above formulation avoids the additional evaluation of the derivatives of the elastic stresses in contrast to the original RSDM-S [6,7,8] and thus shortens the amount of calculations.

The rhs of (10) is determined in a simple radial return type of algorithm as was proposed in [6]. Solving (10) one may evaluate through (9) the residual stress rate ${{\dot{\varvec{\rho}}}}$ at a cycle point τ.

The expected cyclic nature of the residual stresses at the asymptotic cycle allows one to evaluate the residual stresses themselves. This may be done by their decomposition into Fourier series [6]:

$${\varvec{\uprho}}(\tau ) = \frac{1}{2}{\mathbf{a}}_{0} + \sum\limits_{k = 1}^{\infty } {\left\{ {\cos \left(2k\pi \tau \right) \cdot {\mathbf{a}}_{k} + \sin \left(2k\pi \tau \right) \cdot {\mathbf{b}}_{k} } \right\}}$$

(11)

The Fourier coefficients are evaluated by numerical time integration of the computed ${{\dot{\varvec{\rho}}}}$ vectors at each cycle point τ [6].

Equations (9)–(11) together with Eq. (1) are continuously updated [6,7,8] through an iterative sequence of lowering the load factor, which starts from a high initial value. Iterations stop when the only remaining term in (11) is the constant term ${\mathbf{a}}_{0}$ which is the condition that the structure has shaken down [12, 13]. Thus, the shakedown factor $\gamma_{sh}$ may be evaluated and the shakedown domain may be established.

Note: The RSDM-S was published in 2014. A method, called SCM, that does not employ Fourier series, was published in 2019 [14]. However, it is virtually the same with RSDM-S, as features and methodology are the same. The residual stresses’ derivatives are evaluated in the same way and integration is also carried out over time points inside a period. SCM uses just the vertices of the loading domain, as time points, and thus it is wrongly stated [14] that, because of the Fourier series, the RSDM-S is slow, as it must utilize many time points inside the cycle to represent the applied loading. Unfortunately, it is not realized that the number of the time points used, is a direct consequence of a proper description of the cyclic loading program, either in the time domain or in the loading domain ([6], Fig. 2) and has nothing to do with the Fourier series. For example, if the loading domain (see Fig. 2b) is employed, RSDM-S, uses also only the vertices, as time points. At the same time only three coefficients of the Fourier series have proved sufficient, with the convergence being continuously descending and smooth [6], something which does not appear with SCM.

Moreover the criterion of convergence of the SCM is a direct result of the convergence criterion of the RSDM-S.

2.2 Numerical Modifications on the RSDM-S

Except for the theoretical modification discussed above, some numerical interventions to the original RSDM-S are presented herein. Although necessary to be introduced for the applied displacement loading case, they are also applicable to the cases of thermomechanical loading domains.

In the previous work [6], the “ω” factor has been introduced in order to prevent overshooting of the shakedown load. However, in case of imposed displacement, the use of “ω” could lead to a continuous halving of itself, being finally ineffective. To account for such cases, the following calibration procedure is proposed. In order to follow the path towards the shakedown factor γ_sh, in each convergence step, the sum of norms ${\upvarphi }(\upgamma) = \sum\nolimits_{k = 1}^{\infty } {\left\| {{\mathbf{a}}_{k} } \right\|} + \sum\nolimits_{k = 1}^{\infty } {\left\| {{\mathbf{b}}_{k} } \right\|}$ is used to contract the loading domain [6,7,8]. The contraction factor should always be positive. However, this is not always the case, as the magnitude of φ depends on the initial elastic stresses used to start the iterations. It has been observed that a good ratio of the maximum initial elastic stress over the yield stress should be lower than 10⁻⁴. So, a recalculation of the initial elastic stress vector is proposed, by multiplying it with this initial stress multiplication factor of the value of 10⁻⁴. If this ratio is greater than 10⁻⁴, for example 10⁻³, the method may not converge, because the shakedown factor could be overshot. On the other hand, if the ratio was lower, namely 10⁻⁵, the convergence was slowing down. The proposed remedy appears to be general as it works for all the considered examples, either past or present.

The updates and modifications of the RSDM-S were programmed inside the source code of FEAP. FEAP is a research oriented finite element analysis software developed in Berkeley [10]. Thus RSDM-S is fully functional in FEAP for the case of structures, modelled by brick elements and subjected to cyclic thermomechanical loadings with or without imposed displacements.

3 Application Examples

Several examples of application have been tested using the updated RSDM-S. The first example considers cyclic mechanical loading and the next two, of increasing complexity, are examples with applied cyclic displacements.

3.1 The Simple Frame

The first example is the simple frame of Fig. 3a, considered also in [6, 15, 16]. Two distributed loads (P₁ and P₂) act independently, varying from the value “0” to the maximum values $P_{1}^{*}$ and $P_{2}^{*}$, as shown in Fig. 3b. The ratio $P_{1}^{*}$ over $P_{2}^{*}$ is equal to 3. The mechanical properties were E = 20,000 kN/cm², ν = 0.3, σ_y = 10 kN/cm². The updated RSDM-S was run considering five time points of the loading cycle (that coincide with the vertices of the loading domain) and three Fourier coefficients. 350 brick elements were used for the discretization (Fig. 4). The saving in the computing time, as compared with the original RSDM-S is about 30%.

Fig. 3

a Geometry and loads, b loading cycle

Fig. 4

2D view and 3D view of the frame using 350 brick elements

Three different cases were considered, accounting for different initial setups of the method:

• Case A: Three Fourier coefficients were used and the initial stress multiplication factor was 10⁻⁶. Although starting from a very high initial loading factor, a smooth convergence (Fig. 5) towards the shakedown factor was observed which was found 2.8; however, the rate was slow since it required almost 20,000 iterations. The reason is the small initial stress multiplication factor. As a result, the rate of decrease of φ is quite small.

  Fig. 5

  

  Convergence of the loading factor when the initial elastic stresses multiplication factor is equal to 10⁻⁶

• Case B: Three Fourier Coefficients were used and the initial stress multiplication factor was 10⁻². The shakedown factor is equal to 2.59 and the convergence is smooth as presented in Fig. 6. It coincides with [6], whereas other results reported in the literature, are 2.473 [15] and 2.487 [16], using different meshes of plane triangular elements.

  Fig. 6

  

  Convergence of the loading factor considering 3 Fourier coefficients when the initial elastic stress multiplication factor is equal to 10⁻²

  The method needed 1637 iterations to calculate the shakedown factor. Note that, in case A, even if the starting loading factor was 32, as the one used in the present case, still almost 15,000 iteration would be necessary to converge.

• Case C: Eighty Fourier Coefficients were used and the initial stress multiplication factor was 10⁻². The shakedown factor is equal to 2.58 and the convergence is smooth as presented in Fig. 7.

  Fig. 7

  

  Convergence of the loading factor considering 80 Fourier coefficients

The method needed 1875 iterations to calculate the shakedown factor.

If someone compares the cases B and C, it is obvious that the use of three Fourier coefficients is enough to achieve a fast and accurate estimation of the shakedown factor. The comparison of the two cases is presented in Fig. 8.

Fig. 8

Comparison of case B and case C

3.2 The Slab with the Hole

The benchmark problem of the square plate having a circular hole in its center, is the next example considered. The plate is subjected to imposed displacements along its edges. Due to symmetry, only one quarter of the plate is discretized (Fig. 9). Let D be the diameter of the circle, L the length of the slab and d the thickness, then $D/L = 0.2$, $d/L = 0.05$. In the present work, L is equal to 10 m. The boundary conditions along the X-axis and the Y-axis are considered rolled. Results for one and two cyclic displacements $\bar{u}_{1}$ and $\bar{u}_{2}$ varying proportionally from 0 to $\bar{u}_{1}^{*}$ and $\bar{u}_{2}^{*}$ (Fig. 10) will be investigated. The material properties are E = 180 GPa, v = 0.3 and σ_y = 200 MPa. The model consists of 220 brick elements. The shakedown limit was estimated, using the RSDM-S for the following cases:

Fig. 9

Geometry, loading and discretization of the slab

Fig. 10

Proportionally imposed displacements

• Case A: Only the displacement $\bar{u}_{1}$ is applied.

• Case B: Both displacements $\bar{u}_{1}$ and $\bar{u}_{2}$ are applied

It is pointed out that the results of case A were validated performing step-by-step analyses using the Abaqus software.

In case A the shakedown displacement is equal to 0.15 mm and the convergence appears smooth (Fig. 11). It is pointed out that, the shakedown factor starts from a high value, namely 6000, and quite fast converges to the shakedown limit.

Fig. 11

Convergence of the loading factor

In order to check the validity of the results, step-by-step analyses were performed. The first simulation considered cyclic imposed displacements with magnitude varying from 0 to 0.14 mm. The analysis ran over 100 cycles and the structure finally shaked down and the plastic strain stabilized. Contour plotting of the equivalent plastic strain at the last step is shown in Fig. 12.

Fig. 12

Contour plot of equivalent plastic strain at the end of the step by step analysis when the magnitude of the imposed displacement is equal to 0.14 mm

The Fig. 13 depicts the evolution of the plastic strain at the critical point A of Fig. 12.

Fig. 13

Equivalent plastic strain of point A in case of 0.14 mm

In the second simulation with Abaqus, the magnitude of the imposed displacement varied from 0 to 0.20 mm. The plastic strains developed inside the grey-zone (Fig. 14) were continuously increasing, revealing a ratchet mechanism. Figure 15 depicts the equivalent plastic strain at the critical point A.

Fig. 14

Contour plot of equivalent plastic strain in the end of step by step analysis when the magnitude of the displacement is equal 0.2 mm

Fig. 15

Equivalent plastic strain of point A in case of the maximum cyclic displacement of 0.2 mm

In the case B, the displacements $\bar{u}_{1}$ and $\bar{u}_{2}$ act, proportionally, along the free sides of the slab. Having performed shakedown analyses with the RSDM-S, for different ratios of $\bar{u}_{1}^{*} /\bar{u}_{2}^{*}$, the results are depicted in Fig. 16.

Fig. 16

Shakedown domain in case of two imposed displacements. The yield displacement corresponds to the yielding due to both actions

It is pointed out that, in the case of the two imposed displacements, the Abaqus step-by-step analyses could not converge. Thus, the results could not be validated.

3.3 The Tee-Junction

This example discusses the shakedown domain for a common tee junction in the case of cyclic imposed displacement. Tee-junctions are widely used for the connection of different piping elements. Being parts of pipelines, these components usually undergo severe repeated earthquake loading.

The junction of Fig. 17 consists of a main pipe, with 8-inch outer diameter, connected to a secondary pipe with a smaller 6-inch diameter. The secondary pipe is also called “branch”. In the present example, the main pipe is considered fixed at the ends and the imposed displacements are applied to the free end of the branch.

Fig. 17

Mesh of the tee junction

The model consists of 9936 brick elements. The following load cases were examined

• Case A: The displacement is applied along the X-axis

• Case B: The displacement is applied along the Y-axis

In case A the yield displacement is equal to 1.43 mm and the shakedown displacement was estimated, by the RSDM-S, as 2.6 mm. The convergence of the applied displacement towards shakedown is smooth and is presented in the Fig. 18.

Fig. 18

Convergence of the displacement towards its shakedown value

The result was validated with step-by-step inelastic analyses, using the Abaqus software. Two different analyses were performed, one below and one above the estimated shakedown value. Thus, the first case run was of a maximum cyclic applied displacement of 2.4 mm, and the second, of 3.2 mm. It turned out that, in the 2.4 mm case the structure shakes down. Figure 19 depicts the spread of the equivalent plastic strain at the last time-step of the analysis. Also, the equivalent plastic strain evolution, in the most stressed point A, is presented in Fig. 20. After the first cycles, the plastic strain does not increase, thus the structure responds elastically.

Fig. 19

Contour of the plastic strain in the shakedown state

Fig. 20

Equivalent plastic strain evolution for the critical Gauss point for maximum cyclic imposed displacement equal to 2.4 mm

In the second analysis, the magnitude of the maximum applied displacement was set equal to 3.2 mm. As a result, ratcheting appeared. The Fig. 21 shows the evolution of the equivalent plastic strain for this case, at the same point A.

Fig. 21

Equivalent plastic strain evolution for the critical Gauss point for cyclic imposed displacement equal to 3.2 mm

Similar results came up for the case B, where the displacement is applied along the Y-axis. The yield displacement is equal to 1.89 mm and the shakedown displacement evaluated by RSDM-S is equal to 3.2 mm. The convergence of the applied displacement towards shakedown is smooth, as presented in Fig. 22.

Fig. 22

Convergence of the loading factor in case B

Once again for the validation of the results, the problem was imported to Abaqus and was solved twice, using step-by-step analyses. The maximum value of the cyclic displacement was considered equal to 3 mm and 5 mm respectively.

Figure 23 depicts the distribution of the equivalent plastic strain at the last step of the analysis for the 3 mm.

Fig. 23

Distribution of equivalent plastic strain

As expected, the structure shakes down, and one may see that the corresponding equivalent plastic strain, for the point A, after a few cycles, does stabilize (Fig. 24).

Fig. 24

Equivalent plastic strain evolution for the critical Gauss point for cyclic imposed displacement equal to 3.0 mm (Case B)

In the case of greater maximum imposed displacement (5 mm) the structure is shown to have exceeded the shakedown limit and the point A lies on a ratcheting area (Fig. 25).

Fig. 25

Plastic strain evolution for the critical Gauss point for cyclic imposed displacement equal to 5.0 mm (Case B)

4 Concluding Remarks

The present work presents an evolution of the Residual Stress Decomposition Method for Shakedown of elastoplastic structures (RSDM-S) towards better efficiency and robustness. It has also been modified to account for cyclically imposed displacements. A convergence factor, which in the previous versions has been used to overcome overshooting, appears not to be working properly for the case of applied displacements. A different factor that was called initial stress multiplication factor was used instead. This factor multiplies the elastic stresses, which for the case of applied displacements could be quite high. It appears to be efficient in all the cases of loading either mechanical or applied displacements. The updated method was used successfully to evaluate the shakedown load and domains of a holed slab and a tee junction, which were subjected to cyclic displacements. As in the previous version of the RSDM-S the use of no more than three Fourier terms together with the least amount of time points to describe the cyclic loading program proved to be enough for an approach that is numerically stable and with a smooth and fast convergence.