Modeling of Shape Memory Behavior of Semi-crystalline Polymer Considering Both Amorphous and Crystalline Phases

Abstract

Shape memory polymers easily form different temporary shapes and recover their permanent shape even after undergoing large deformation. In this work, shape memory behavior of a typical semi-crystalline polymer is modeled and the constitutive equations for the original amorphous and the semi-crystalline phases are derived. The amorphous and crystalline phases were characterized by an Ogden and a neo-Hookean response, respectively. The model was used to simulate a typical uniaxial cycle of deformation. The results demonstrated very good agreement between simulation and experimental data.

1 Introduction

Shape memory materials represent an important class of smart materials with the ability to return from a temporary shape to the permanent one. Such a property, known as shape memory recovery, is generally induced by an external stimulus such as heat, electricity or magnetism and allows the shape memory materials, use in a wide range of applications [1]. The mechanism responsible for the shape memory of the polymer is the fact that the polymer has a semi-crystalline state. In this case, melting temperature, Tm, is the recovery temperature, T_r, and such polymers are called semi-crystalline shape memory polymers [2]. In their later work, Barot et al. [2] extended the model to fit a full thermodynamic framework and derived constitutive equations that were invariant in their description of mechanical stress and strain. Their model is fully three-dimensional and fulfills general physical requirements such as frame invariance and the second law of thermodynamics [3]. They assumed both amorphous and crystalline phases as a neoHookean solid. In some cases, the model is not in a good agreement with experimental data. In this work, different hyperelastic functions are considered for amorphous and crystalline phases due to different behavior of polymer chains in each phase. The model was used to simulate a typical uniaxial cycle of deformation.

2 Theoretical

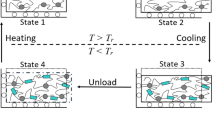
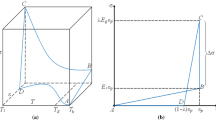
The modeling of semi-crystalline shape memory polymers could delineate into four parts; namely the rubbery phase (at a temperature beyond T_r), the semi-crystalline phase (at a temperature beneath T_r), the crystallization process (on cooling to below T_r) and the melting process (on heating back above T_r). Each of these parts should address separately.

Above the recovery temperature, the semi-crystalline shape memory polymer behaves like an isotropic rubber and models as an incompressible isotropic hyperelastic material. Crystallization is a time-dependent process and takes place in a gradual manner. To model the shape memory behavior of semi-crystalline polymer, beyond the recovery temperature, we have to make constitutive assumptions for this mixed region. The newly formed crystalline phase is assumed to be an elastic solid. For such a case, the equation of total stress for a semi-crystalline shape memory polymer is:

$$ \varvec{T} = - pI + (1 - \alpha )2\rho \varvec{F}_{a} \frac{{\partial \psi_{a} }}{{\partial \varvec{C}_{a} }}\varvec{F}_{a}^{T} + \int_{{t_{1} }}^{{t_{2} }} {2\rho \varvec{F}_{c} \frac{{\partial \psi_{c} }}{{\partial \varvec{C}_{c} }}\varvec{F}_{c}^{T} \frac{d\alpha }{d\tau }d\tau } $$

(1)

Where, p is the Lagrange multiplier due to the constraint of incompressibility, α is the amount of crystalline phase, F_a and F_c are the deformation gradient in amorphous and crystalline phases, ψ_a and ψ_c are the Helmholtz potential of amorphous and crystalline phases and C_a and C_c are the right Cauchy-Green tensor for amorphous and crystalline phases, respectively. The first part of the equation represents the amorphous phase and the integration part indicates the transition of the amorphous phase to the crystalline one, by passing through the T_m. The amorphous and crystalline phases could characterize by an Ogden and a neo-Hookean response, respectively.

In a uniaxial extension, the shape memory polymer stretches beyond the transition temperature (step 1) and cools down while keeping the length fixed (step 2). During the cooling process, crystallization takes place. By completing the crystallization process, the polymer unloads (step 3), then reheats. The crystals melt and the crystalline shape memory polymer reverts back to the original amorphous phase (step 4). According to the Eq. (1), in a uniaxial extension, the stress for each step (1 to 4) in a cycle is as follow (Eqs. (2) to (5)):

$$ N_{11} \left( t \right) = \frac{{2\mu_{1} }}{{\alpha_{1} }}\left( {\Lambda \left( t \right)^{{\alpha_{1} - 1}} - \left( {\frac{1}{{\sqrt {\Lambda \left( t \right)} }}} \right)^{{\alpha_{1} + 2}} } \right) $$

(2)

$$ N_{11} \left( t \right) = 2\left( {1 - \alpha } \right)\frac{{\mu_{1} }}{{\alpha_{1} }}\left( {\Lambda \left( t \right)^{{\alpha_{1} - 1}} - \left( {\frac{1}{{\sqrt {\Lambda \left( t \right)} }}} \right)^{{\alpha_{1} + 2}} } \right) $$

(3)

$$ \begin{aligned} & N_{11} \left( t \right) = 2\left( {1 - \alpha_{0} } \right)\frac{{\mu_{1} }}{{\alpha_{1} }}\left( {\Lambda \left( t \right)^{{\alpha_{1} - 1}} - \left( {\frac{1}{{\sqrt {\Lambda \left( t \right)} }}} \right)^{{\alpha_{1} + 2}} } \right) \\ & \quad \quad \quad + \mu_{c}\Lambda \left( t \right)L_{1} - \mu_{c} \left( {\frac{1}{{\left( {\Lambda \left( t \right)} \right)^{2} }}} \right)L_{2} + \mu_{c1} \left( {\Lambda \left( t \right)} \right)^{3} L_{3} - \mu_{c1}\Lambda \left( t \right)L_{1} \\ \end{aligned} $$

(4)

$$ \begin{aligned} & N_{11} \left( t \right) = 0 = 2\left( {1 - \alpha \left( t \right)} \right)\frac{{\mu_{1} }}{{\alpha_{1} }}\left( {\varLambda \left( t \right)^{{\alpha_{1} - 1}} - \left( {\frac{1}{{\sqrt {\varLambda \left( t \right)} }}} \right)^{{\alpha_{1} + 2}} } \right) \\ & \quad \quad \quad + \mu_{c} \varLambda \left( t \right)L_{1} - \mu_{c} \left( {\frac{1}{{\left( {\varLambda \left( t \right)} \right)^{2} }}} \right)L_{2} + \mu_{c1} \left( {\varLambda \left( t \right)} \right)^{3} L_{3} - \mu_{c1} \varLambda \left( t \right)L_{1} \\ \end{aligned} $$

(5)

Where, N₁₁ is the nominal stress, $\Lambda$ is the stretch ratio, α₁ and μ₁ are constants for Ogden model. μ_c and μ_c1 are the shear modulus of crystalline phase. L₁; L₂ and L₃ are integrals that are defined through:

$$ \begin{aligned} & L_{1} = \int_{{t_{s} }}^{{t^{ * } }} {\frac{1}{{\left( {\Lambda \left( \tau \right)} \right)^{2} }}\frac{d\alpha }{d\tau }d\tau } \\ & L_{2} = \int_{{t_{s} }}^{{t^{ * } }} {\Lambda \left( \tau \right)\frac{d\alpha }{d\tau }d\tau } \\ & L_{3} = \int_{{t_{s} }}^{{t^{ * } }} {\frac{1}{{\left( {\Lambda \left( \tau \right)} \right)^{4} }}\frac{d\alpha }{d\tau }d\tau } \\ \end{aligned} $$

(6)

3 Results and Discussion

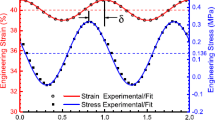
Figure 1 shows the stress versus strain for a uniaxial extension, illustrating the thermomechanical behavior of a semi-crystalline shape memory polymer in a full cycle. In this Fig. the experimental data (Barikani et al. [4]) are compared with two models (Barot et al. [2] and our proposed model).

Fig. 1.

Plot of nominal stress versus strain for a uniaxial extension. Crystallization process takes place at constant strain. O indicates experimental data (Barikani et al.). Solid line demonstrates Barot et al. model and dash line shows our proposed model

As observed, on loading beyond T_m (step 1) the stress and strain go up. In this step, the experimental data predicted with our model show better result than those obtained by Barot et al. model. In step 2, by cooling to beneath T_m at a fixed strain, the stress goes down as the crystalline phase is born in a stressed state. On unloading (step 3), the stress decreases to zero. On reheating beyond T_m (step 4), the shape memory polymer recovers its original shape. The experimental data are in good agreement with Barot et al. and our models. In steps 2 to 4, the crystalline phase is dominant in the polymer, so, in both models, the crystalline phase has to consider by neo-Hookean model.

Therefore, our proposed model can reasonably predict the shape memory behavior of a typical semi-crystalline polymer.

4 Conclusion

In this work, we formulated constitutive equations to predict the thermomechanical behavior of a typical semi-crystalline shape memory polymer. The amorphous and crystalline phases had different behaviors, thus the amorphous phase and crystalline phase were characterized by an Ogden and a neo-Hookean response, respectively. The proposed model exhibited good agreement with experimental data.