1 Introduction

Shape memory polymers (SMPs) are smart polymeric materials that have an ability to retain a temporary shape and return to their original shape when triggered by an external stimulus [1]. The external stimuli can be temperature [2], light [3, 4] or chemical environment [5]. Compared to shape memory alloys, SMPs possess many advantageous features, such as modest cost, high durability and easy to manufacture [6]. In addition, SMPs can be made biodegradable and biocompatible by tuning them chemically [7]. Based on these advantageous features, SMPs are finding a wide range of applications in various fields, such as actuators and sensors in microelectromechanical system (MEMS) [8], as arterial stents in the biomedical field [9], and in additive manufacturing [10], to name a few.

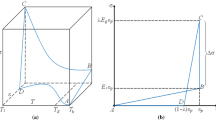
Crystallizable shape memory polymers (CSMPs) are a significant subclass of thermally activated SMPs in which the temporary shape is fixed by a crystalline phase while recovery to original shape is due to the melting of this crystal phase [11]. The schematic illustration of the shape memory cycles of CSMPs is shown in Fig. 1. State 1 denotes the original undeformed shape. Above the recovery temperature T r the polymers exhibit a rubber-like behavior due to the presence of chemical cross-links. On deforming above T r , the polymer molecules between the cross-links stretch (State 2). If the polymer is now cooled down to a temperature below T r , crystallization takes place and the crystals are formed in this deformed shape. The onset of crystallization is accompanied by a sharp drop in the stress (from State 2 to State 3). After unloading (State 3 to State 4) the polymer remains in a deformed shape (temporary shape) with a small amount of recovery. This recovery is due to the presence of two components (amorphous and crystalline) each with their stress-free states. The amorphous part has a tendency to retract to its original shape while the crystalline part prefers the deformed shape. As the crystalline part is a lot stiffer, the recovery strain is small. When the polymer is heated back to a temperature above T r the crystallites melt returning to their original amorphous state, the polymer retracts to its original shape.

Fig. 1
figure 1

Schematic illustration of crystallizable shape memory polymers

Full size image

The significant efforts in the constitutive modeling of CSMPs have been published in the literature (e.g. [12–15]). However, in most cases, the CSMPs in their rubbery-state (above recovery temperature T r ) are modeled as a hyperelastic material. Though most of the CSMPs exhibit hyperelastic behavior above their recovery temperature, severe viscoelastic behavior has been observed in a certain class of CSMPs [16]. The mechanical behavior of CSMPs will be much more complicated with viscoelastic behavior since the loading and unloading process would be rate dependent. In addition, the effects of phase transition and temperature on relaxation time during the shape memory cycles have to be taken into consideration. Therefore, to model the mechanical behavior of CSMPs we need to characterize their behavior both above and below the recovery temperature as well as the process of crystallization and melting. Above the recovery temperature, the polymers behave like viscoelastic materials and a rate type model is required to simulate their mechanical behavior. Besides, the effect of temperature and crystallization on the relaxation time of the material has to been incorporated into the rate type model. When cooled down to below their recovery temperature, the crystallizable part of the polymer will crystallize. Crystallization does not all take places at an instant but generally takes place in a gradual manner. In order to model this, we have to make constitutive assumptions for the mixed region. This mixture of the crystalline and amorphous phases is treated as a constrained mixture. We allow co-occupancy of the phases in an averaged sense as is done in tradition mixture theory [17]. In addition, it is assumed that the amorphous and crystalline components are constrained to move together, which for polymers is a reasonable assumption as the same molecule traverses both the amorphous and crystalline phase and the presence of cross-links and crystallites prevents the diffusion of individual polymer molecules. Moreover, the orientation of the crystals depends on the deformation of the polymer during the crystallization process, and in turn the orientation of the crystals is a key element that determines the mechanical properties of this semi-crystalline polymer. Lastly, we note that after crystallization the material is a mixture of various phases with different stress-free states. For this reason, the model for crystallization used in this work has been developed within the frame-work of multiple natural configurations [18]. The material responses of materials belonging to many different classes have been modeled using this framework, some of them are: multi-network polymers [19], metal plasticity [20], viscoelastic materials [21, 22], crystallization in polymers [23], crystallizable SMPs [12], and light-activated SMPs [24]. Classical elasticity and linear viscous fluids arise as simple cases within this theory.

In this paper, we extend our earlier work on CSMPs with a focus on studying the mechanical behavior of the materials when viscoelasticity is taken into consideration. The model developed is used to solve a specific boundary value problem, namely uniaxial extension. The rest of the paper is arranged in the following order. Section 2 introduces the finite deformation constitutive model. In Sect. 3 we apply our model to uniaxial extension boundary value problems. The results of model predictions are presented in Sect. 4. We draw a conclusion in Sect. 5.

2 Constitutive model

As we discussed above, in order to model the mechanical behavior of the crystallizable SMPs, we have to characterize the original viscoelastic amorphous network and the subsequently formed semi-crystalline network due to crystallization. In addition, the kinetics of crystallization and associated time–temperature history have to be studied. The original amorphous network is modeled as finite strain temperature-dependent viscoelastic material with a multi-branch model. Here, we assume that the material only has one relaxation mechanism, but with the tacit understanding that our model can be easily extended to model specific viscoelastic materials by adding multiple relaxation mechanisms. The 1-D rheological model is shown in Fig. 2. For the original amorphous networks, we have one equilibrium branch to simulate the hyperelastic behavior and one non-equilibrium branch, associated with one relaxation mechanism, to simulate the viscoelastic behavior. Based on the theory of multiple “natural configurations”, the crystalline phases are energy elastic materials that are formed in the different stress-free states (natural configurations). Thus, for the crystalline networks we use a series of equilibrium branches with thermal switches in parallel to simulate their mechanical behavior.

Fig. 2
figure 2

1D rheological model of crystallizable shape memory polymers

Full size image

2.1 Original amorphous network

In Fig. 2, an equilibrium branch and one non-equilibrium branch are arranged in parallel. Thus the total Cauchy stress of amorphous network is given as:

$$ {\mathbf{T}}_{a} = - p{\mathbf{I}} + {\mathbf{T}}^{eq} + {\mathbf{T}}^{neq} $$
(1)

2.1.1 Hyperelastic behavior of the equilibrium branch

The incompressible Neo-Hookean model is used for the hyperelastic behavior. The Cauchy stress tensor for the incompressible Neo-Hookean material is given by:

$$ {\mathbf{T}}^{eq} =- p{\mathbf{I}} + \mu {\mathbf{B}} $$
(2)

where μ is the shear modulus of equilibrium branch and \( {\mathbf{B}} \) is the left Cauchy–Green tensor.

2.1.2 Viscoelastic behavior of the non-equilibrium branch

For the viscoelastic behavior of the non-equilibrium branches, the deformation gradient can be further decomposed into an elastic part and a viscous part, shown in Fig. 3:

$$ {\mathbf{F}} = {\mathbf{F}}_{{\kappa_{p} }} {\mathbf{F}}_{{\kappa_{R} }} $$
(3)

where \( {\mathbf{F}}_{{\kappa_{R} }} \) is a relaxed configuration obtained by elastic unloading by \( {\mathbf{F}}_{{\kappa_{p} }} \). The Cauchy stress of non-equilibrium branch \( {\mathbf{T}}^{neq} \) is given by:

$$ {\mathbf{T}}^{neq} = - p{\mathbf{I}} + \mu_{1} {\mathbf{B}}_{{\kappa_{p} }} $$
(4)

\( {\mathbf{B}}_{{\kappa_{p} }} \) is the left Cauchy–Green tensor and can be solved from the evolution equation given by:

$$ {\dot{\mathbf{B}}}_{{\kappa_{p} }} - {\mathbf{LB}}_{{\kappa_{p} }} - {\mathbf{B}}_{{\kappa_{p} }} {\mathbf{L}}^{T} = \frac{{\mu_{1} }}{{\eta_{1} }}\left( {\frac{3}{{tr\left( {{\mathbf{B}}_{{\kappa_{p} }}^{ - 1} } \right)}}{\mathbf{I}} - {\mathbf{B}}_{{\kappa_{p} }} } \right) $$
(5)

where \( {\mathbf{L}} \) is the velocity gradient from the original configuration κ R to the current configuration κ c(t), μ 1 and η 1 are the shear modulus and viscosity of the non-equilibrium branch, respectively. The viscosity η 1 is a function of temperature and crystallinity. It will be discussed later in Sects. 2.1.3 and 2.3. The details about the derivation of Eq. (5) are referred to Rajagopal and Srinivasa [25] and Rao and Rajagopal [26].

Fig. 3
figure 3

Natural configurations associated with a single viscoelastic non-equilibrium branch

Full size image

2.1.3 Temperature dependent relaxation time

The relaxation time of the non-equilibrium branch is temperature dependent, for polymer melts it is commonly described through the following relationship [23]:

$$ \eta_{1} = \bar{\eta }_{1} *\exp \left( {L_{\theta } \left( {\frac{1}{\theta } - \frac{1}{{\theta_{R} }}} \right)} \right) $$
(6)

In the above equation, θ is the thermodynamic temperature of the material, \( \bar{\eta }_{1} \) is the viscosity at a given reference temperature θ R , and L θ is a constant.

2.2 Crystallization rate

Typically, to model the crystallization process in a full thermodynamics framework we would have to prescribe an activation criterion that depends on various thermodynamic variables. After the activation criterion is met the polymer begins to crystallize and the rate of crystallization comes out of the thermodynamics associated with the problem [13]. In this paper, however, we directly prescribe a crystallization rate equation, as the main purpose of this paper is to understand the mechanical behavior of the CSMPs.

2.3 Semi-crystalline network

The crystallization does not all take places at an instant but generally takes place in a gradual manner. In order to model this, we make following constitutive assumptions. First, we assume a homogenous crystallization process and this can be realized through cooling the polymer in an isothermal experimental environment. Besides, we assume that the crystallized material is born in a stress-free state and the newly formed crystallites behave like an elastic solid. There is a fair amount of previous research publications supporting this assumption for polymers undergoing crystallization [17]. In addition, it is assumed that the amorphous and crystalline phases are constrained to move together, which is a reasonable assumption for polymers. Last, we assume that the Cauchy Stress contributed by the different networks is additive. Based on the above assumptions, the Cauchy Stress of the mixture is given by:

$$ \begin{aligned} {\mathbf{T}} & = - p{\mathbf{I}} + {\mathbf{T}}_{a} + {\mathbf{T}}_{c} \\ & = - p{\mathbf{I}} + \left( {1 - \alpha } \right)\left( {\mu {\mathbf{B}} + \mu_{1} {\mathbf{B}}_{{\kappa_{p} }} } \right) \\ & \quad + 2\rho \int_{{t_{1} }}^{{t_{2} }} {{\mathbf{F}}_{{\kappa_{c(\tau )} }} \frac{{\partial \psi_{c(\tau )} }}{{\partial {\mathbf{C}}_{{\kappa_{c(\tau )} }} }}{\mathbf{F}}_{{\kappa_{c(\tau )} }}^{T} \frac{d\alpha }{d\tau }} d\tau \\ \end{aligned} $$
(7)

where ψ c(τ) is the Helmholtz potential of the crystalline phase, \( {\mathbf{C}}_{{\kappa_{c(\tau )} }} \) is the right Cauchy Green tensor from the original configuration to the configuration that the crystalline phases were formed in (“natural configuration”) and α is the crystallinity. The integral is introduced to capture the evolution of the “natural configurations” if crystallization takes place while the polymers are being deformed. For a more detailed discussion of the Helmholtz potential of crystalline phases and the derivation of the stress tensor, please see Rao and Rajagopal [27, 28]. Now we assume a specific form of Helmholtz potential function for crystalline phases. It is given as:

$$ \psi_{c(\tau )} = c_{11} (I_{1} - 3) + c_{12} (J_{1} - 1)^{2} + c_{13} (K_{1} - 1)^{2} $$
(8)

where c 11, c 12, c 13 are material constants and I 1 is the first invariant of Cauchy–Green tensor. The invariants J 1 and K 1 are given by:

$$ J_{1} = \;{\mathbf{n}}_{{\kappa_{c(\tau )} }} \cdot {\mathbf{C}}_{{\kappa_{c(\tau )} }} {\mathbf{n}}_{{\kappa_{c(\tau )} }} \;{\text{and}}\;\;K_{1} = {\mathbf{m}}_{{\kappa_{c(\tau )} }} \cdot {\mathbf{C}}_{{\kappa_{c(\tau )} }} {\mathbf{m}}_{{\kappa_{c(\tau )} }} $$
(9)

where \( {\mathbf{n}}_{{\kappa_{c(\tau )} }} \) and \( {\mathbf{m}}_{{\kappa_{c(\tau )} }} \) are eigenvectors of \( {\mathbf{C}}_{{\kappa_{c(\tau )} }} \). Then we substitute Eqs. (8) and (9) into Eq. (7), the stress of the semi-crystalline network can be then given as:

$$ \begin{aligned} {\mathbf{T}} & = - p{\mathbf{I}} + {\mathbf{T}}_{a} + {\mathbf{T}}_{c} \\ & = - p{\mathbf{I}} + (1 - \alpha )\left( {\mu {\mathbf{B}} + \mu_{1} {\mathbf{B}}_{{\kappa_{p} }} } \right) \\ & \quad + 4\rho \int_{{t_{1} }}^{{t_{2} }} {c_{11} {\mathbf{B}}_{{\kappa_{c(\tau )} }} \frac{d\alpha }{d\tau }} d\tau \\ & \quad + 4\rho \int_{{t_{1} }}^{{t_{2} }} {{\mathbf{F}}_{{\kappa_{c(\tau )} }} [c_{12} (J_{1} - 1){\mathbf{n}}_{{\kappa_{c(\tau )} }} \otimes {\mathbf{n}}_{{\kappa_{c(\tau )} }} + c_{13} (K_{1} - 1){\mathbf{m}}_{{\kappa_{c(\tau )} }} \otimes {\mathbf{m}}_{{\kappa_{c(\tau )} }} ]{\mathbf{F}}_{{\kappa_{c(\tau )} }}^{T} \frac{d\alpha }{d\tau }} d\tau \\ \end{aligned} $$
(10)

Finally, we note that the crystallinity will pin down the viscoelastic behavior of the amorphous networks. After crystallization, the relaxation mechanism will be given as:

$$ \eta_{1} = \bar{\eta }_{1} *\exp \left( {L_{\theta } \left( {\frac{1}{\theta } - \frac{1}{{\theta_{R} }}} \right)} \right)*\exp \left( {L_{\alpha } \alpha } \right) $$
(11)

where L α is a constant and α is the crystallinity.

2.4 Melting rate

After the onset of melting, the crystallites melt and the polymer transforms back to the amorphous network. As more and more of the crystallites melt the behavior of the polymer is increasingly rubber-like as more of the polymer is released from the crystalline phase. As with the crystallization rate, it is possible to derive this equation from thermodynamic considerations, similar to the methodology used to derive the crystallization rate equation in Rao and Rajagopal [23, 26]. Since for this paper that is not the primary thrust, we will prescribe a rate equation for melting that mimics the general melting behavior.

3 Application to uniaxial extension

In this section, we apply our model to study the mechanical behavior of CSMPs subjected to uniaxial extension. In the deformation cycle, the polymer is deformed to an intermediate shape, and while the strain is kept constant the temperature is reduced. Once the temperature is below the recovery temperature T r , the crystallization is initiated. After the crystallization, due to the existence of the crystalline phases, the polymer will remain in its temporary shape when the external load is removed. The polymer can return to its original shape through melting the crystalline phase by heating or an increase in the temperature. For the uniaxial extension problems, the left Cauchy-Green tensor \( {\mathbf{B}} \) is given by:

$$ {\mathbf{B}} = diag\left( {\begin{array}{*{20}c} {\varLambda \left( t \right)^{2} } & {\frac{1}{\varLambda \left( t \right)}} & {\frac{1}{\varLambda \left( t \right)}} \\ \end{array} } \right) $$
(12)

The velocity gradient \( {\mathbf{L}} \) then can be calculated as:

$$ {\mathbf{L}} = {\dot{\mathbf{F}}\mathbf{F}}^{{{\mathbf{ - 1}}}} = diag\left( {\begin{array}{*{20}c} {\frac{K}{1 + Kt}} & { - \frac{K}{{2\left( {1 + Kt} \right)}}} & { - \frac{K}{{2\left( {1 + Kt} \right)}}} \\ \end{array} } \right) $$
(13)

where K is the stretch rate and Λ(t) = 1 + Kt. The left Cauchy-Green tensor of crystalline phases \( {\mathbf{B}}_{{\kappa_{c(\tau )} }} \) is given by:

$$ {\mathbf{B}}_{{\kappa_{c\left( \tau \right)} }} = \left( {\begin{array}{*{20}c} {\frac{{\varLambda \left( t \right)^{2} }}{{\varLambda \left( \tau \right)^{2} }}} & {\frac{\varLambda \left( \tau \right)}{\varLambda \left( t \right)}} & {\frac{\varLambda \left( \tau \right)}{\varLambda \left( t \right)}} \\ \end{array} } \right) $$
(14)

where Λ(τ) is the stretch in the stress-free state (“natural configuration”) that that crystalline phase is formed. Also we already know the invariants I 1, J 1 and K 1 can be solved from \( {\mathbf{B}}_{{\kappa_{c\left( \tau \right)} }} \). Substituting Eqs. (8), (12), (13) and (14) into Eqs. (5) and (10), and with the proper boundary conditions and time–temperature history, the problem can be solved. The Cauchy stress in the direction of extension is given as:

$$ \begin{aligned} T_{11} & = (1 - \alpha )\left[ {\mu \left( {\varLambda \left( t \right)^{2} - \frac{1}{\varLambda \left( t \right)}} \right) + \mu_{1} \left( {B_{{\kappa_{p} }}^{11} - B_{{\kappa_{p} }}^{22} } \right)} \right] \\ & \quad + \mu_{c1} \int_{{t_{c1} }}^{t} {\left[ {\frac{{\varLambda \left( t \right)^{2} }}{{\varLambda \left( \tau \right)^{2} }} - \frac{\varLambda \left( \tau \right)}{\varLambda \left( t \right)}} \right]} \frac{d\alpha }{d\tau }d\tau + \mu_{c2} \int_{{t_{c1} }}^{t} {\left[ {\frac{{\varLambda \left( t \right)^{2} }}{{\varLambda \left( \tau \right)^{2} }} - 1} \right]} \left[ {\frac{\varLambda \left( t \right)}{\varLambda \left( \tau \right)}} \right]^{2} \frac{d\alpha }{d\tau }d\tau \\ \end{aligned} $$
(15)

where μ c1 = 2ρc 1 and μ c2 = 4ρc 2. Next we will derive equations for each stage of the shape memory deformation cycle for uniaxial extension.

3.1 Loading

During the loading process, the material is above the transition temperature and totally amorphous. Hence, from Eq. (15) in the absence of crystallinity the stress reduces to:

$$ T_{11} = \mu \left( {\varLambda \left( t \right)^{2} - \frac{1}{\varLambda \left( t \right)}} \right) + \mu_{1} \left( {B_{{\kappa_{p} }}^{11} - B_{{\kappa_{p} }}^{22} } \right) $$
(16)

For the case when the final stretch is known, by prescribing the stretch as a function of time, the progression of stress is readily known from Eq. (16) by solving Eq. (5).

3.2 Crystallization under constant strain

In this article, we consider the case when the crystallization takes place while the strain is kept constant. When crystallization is done under constant strain, there is no change in the stretch:

$$ \varLambda \left( \tau \right) = \varLambda \left( {t_{c1} } \right)\quad t_{c1} < \tau < t < t_{c2} $$
(17)

where, t c1 is the time when crystallization is initiated, t is the current time, τ is some intermediate time and t c2 is the time at which crystallization ends. Using, Eq. (15) in Eq. (17) and noting that the crystalline phase is formed in a stress-free state and hence the contribution to the stress from the crystalline phase, while the stretch is kept constant, is zero results in the following equation for the stress:

$$ T_{11} = \left( {1 - \alpha \left( t \right)} \right)\left[ {\mu \left( {\varLambda \left( t \right)^{2} - \frac{1}{\varLambda \left( t \right)}} \right) + \mu_{1} \left( {B_{{\kappa_{p} }}^{11} - B_{{\kappa_{p} }}^{22} } \right)} \right] $$
(18)

We have to note here when strain is kept constant, the stress will be relaxed due to viscoelasticity and it can be solved from the evolution equation. As we discussed above, we assume that the rate at which crystallization takes place is given by a crystallization rate equation, with the tacit understanding that such an equation can be derived from a firm basis in thermodynamics. The specific equation chosen to mimic the rate of crystallization is given through a differential equation for the mass fraction of the crystalline phase and is given by:

$$ \begin{aligned} & \alpha \left( t \right) = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{for}}\;0 < t < t_{c1} \hfill \\ & \frac{d\alpha }{dt} = G\left( {t - t_{c1} } \right)\left( {\alpha_{0} - \alpha } \right)\;\;\;\;\;\;\;\;\;\;\;{\text{for}}\;t_{c1} < t < t_{c2} \hfill \\ \end{aligned} $$
(19)

where, in the above equation G is a constant, α 0 is the maximum crystallinity possible in the material and t c1 is the time at which crystallization is initiated. The above equation is solved numerically using a standard numerical scheme for ordinary differential equations.

3.3 Unloading

It is important to note that during unloading, the material is a mixture of two different phases, the crystalline and amorphous phases with each having different stress-free states. Hence both phases will not unload to a stress-free state though the mixture will be stress-free. The equation for the stress during unloading is given as:

$$ \begin{aligned} T_{11} & = (1 - \alpha )\left[ {\mu \left( {\varLambda \left( t \right)^{2} - \frac{1}{\varLambda \left( t \right)}} \right) + \mu_{1} \left( {B_{{\kappa_{p} }}^{11} - B_{{\kappa_{p} }}^{22} } \right)} \right] \\ & \quad + \mu_{c1} \int_{{t_{c1} }}^{{t_{c2} }} {\left[ {\frac{{\varLambda \left( t \right)^{2} }}{{\varLambda \left( \tau \right)^{2} }} - \frac{\varLambda \left( \tau \right)}{\varLambda \left( t \right)}} \right]} \frac{d\alpha }{d\tau }d\tau \\ & \quad + \mu_{c2} \int_{{t_{c1} }}^{{t_{c2} }} {\left[ {\frac{{\varLambda \left( t \right)^{2} }}{{\varLambda \left( \tau \right)^{2} }} - 1} \right]} \left[ {\frac{\varLambda \left( t \right)}{\varLambda \left( \tau \right)}} \right]^{2} \frac{d\alpha }{d\tau }d\tau \\ \end{aligned} $$
(20)

In the above equation the limit of the integral is now t c2, i.e. the time at which crystallization ended and α 0 is the final crystallinity. Here, we rewrite the Eq. (20) as:

$$ \begin{aligned} T_{11} & = (1 - \alpha )\left[ {\mu \left( {\varLambda \left( t \right)^{2} - \frac{1}{\varLambda \left( t \right)}} \right) + \mu_{1} \left( {B_{{\kappa_{p} }}^{11} - B_{{\kappa_{p} }}^{22} } \right)} \right] \hfill \\ & \quad + \mu_{c1} \varLambda \left( t \right)^{2} L_{1} - \mu_{c1} \left( {\frac{1}{\varLambda \left( t \right)}} \right)L_{2} + \mu_{c2} \varLambda \left( t \right)^{4} L_{3} - \mu_{c2} \varLambda \left( t \right)^{2} L_{1} \hfill \\ \end{aligned} $$
(21)

where L 1, L 2 and L 3 are integrals that are defined through:

$$ \begin{aligned} L_{1} & = \int_{{t_{c1} }}^{{t_{c2} }} {\frac{1}{{\varLambda \left( \tau \right)^{2} }}\frac{d\alpha }{d\tau }} d\tau \hfill \\ L_{2} & = \int_{{t_{c1} }}^{{t_{c2} }} {\varLambda \left( \tau \right)\frac{d\alpha }{d\tau }} d\tau \hfill \\ L_{3} & = \int_{{t_{c1} }}^{{t_{c2} }} {\frac{1}{{\varLambda \left( \tau \right)^{4} }}\frac{d\alpha }{d\tau }} d\tau \hfill \\ \end{aligned} $$
(22)

The values of these integrals are estimated numerically and remain unchanged during the unloading process as their integrands only depend on the stretches and crystallization rates during crystallization.

3.4 Melting

After unloading, the polymer is in its temporary shape. Return to the original shape is accomplished by melting the crystalline phase. This is done by heating the polymer to above the melting temperature of the crystalline phase. The Cauchy stress can be solved with Eq. (21) as well while the incremental values of crystallinity are obtained from the prescribed melting equation for crystallinity, which is given by:

$$ \frac{d\alpha }{dt} = G\left( {t - t_{m1} } \right)\left( {0 - \alpha } \right)\quad {\text{for}}\;t_{m1} < t < t_{m2} $$
(23)

where in above equation t m1 is the time at which melting is initiated and t m2 is the time at which melting ceases.

4 Results and discussion

In this section, we present the results of the model predictions for the shape memory cycles subjected to uniaxial extensions. Due to the lack of experiment data, here we prescribe the time–temperature history shown in Fig. 4. Segment ‘a’ to ‘b’ is above the recovery temperature and the polymer is loaded to an intermediate shape at this temperature. At the point ‘b’, we start to cool down the polymer and the crystallization is initiated at t c1 and ceases at t c2. Segment ‘c’ to ‘d’ is the unloading process at the room temperature. During segment ‘d’ to ‘e’, the material is heated up and the melting starts at t m1 and ends at t m2. During both the cooling and heating processes, we assume a linear rate of temperature change. Figure 5 shows the history of crystallization and melting solved through Eq. (19) and Eq. (23) based on the prescribed time–temperature history. In addition, the material parameters used in the calculation are shown in Table 1.

Fig. 4
figure 4

Prescribed time–temperature history

Full size image
Fig. 5
figure 5

Plot of time versus crystallinity with various final crystallinities

Full size image
Table 1 List of material parameters
Full size table

Figure 6 shows the time versus the Cauchy stress of the CSMP under a uniaxial extension with a deformation rate of 0.005/s. Here, we can see that during the cooling process (before crystallization) since we keep the strain constant the stress will decrease due to the viscoelastic nature of the material. After the onset of crystallization, the stress relaxed much faster. This is because the crystalline phase formed in stress-free state and released the energy of the material. Figure 7 shows the engineering strain versus Cauchy stress in the same cycle. We find that the new material is significantly stiffer as compared to the original amorphous material and retains the temporary shape after removal the external load.

Fig. 6
figure 6

Plot of time versus Cauchy stress with 0.005/s deformation rate and 30% final crystallinity

Full size image
Fig. 7
figure 7

Plot of engineering strain versus Cauchy stress with 0.005/s deformation rate and 30% final crystallinity

Full size image

Figure 8 shows the time versus the Cauchy stress of the material under a uniaxial extension with a deformation rate of 0.005/s. Results of different final crystallinity are taken into consideration. We note that the drop in the stress observed during crystallization increased for larger final crystallinity. Figure 9 shows the engineering strain versus the Cauchy stress of the material for the same cycle. Also, the material with more crystallinity is stiffer than the material with less crystallinity, this can be discerned by looking at the slope during unloading.

Fig. 8
figure 8

Plot of time versus Cauchy stress with 0.005/s deformation rate and various final crystallinities

Full size image
Fig. 9
figure 9

Plot of engineering strain versus Cauchy stress with 0.005/s deformation rate and various final crystallinities

Full size image

Figure 10 shows the time versus Cauchy stress with 30% final crystallinity but at different deformation rates. We can observe that with viscoelastic behavior the loading process is rate dependent. The unloading process shows hyperelastic behavior due to the existence of stiffer elastic crystalline phases.

Fig. 10
figure 10

Plot of time versus Cauchy stress with 30% final crystallinity and various deformation rates

Full size image

5 Conclusion

In this work, we extend our earlier work on CSMPs to incorporate the temperature-dependent viscoelasticity into the developed constitutive model. The viscoelastic behavior of CSMPs is simulated through a rate type model developed by Rajagopal and Srinivasa [25]. The model of the semi-crystalline polymer network is developed based on the mixture theory and the theory of “multiple natural configurations”. In addition, we apply our developed framework to study the uniaxial extension boundary value problems. Our analytical results are consistent with experimental observations.