Abstracted Visualization of Halo Topologies in Dark Matter Simulations

Abstract

This work focuses on particle-based ΛCDM (cold dark matter) simulations. The features of interest are clusters of dark matter particles, called halos. Halos are governed by the laws of motion and gravitation, and they may, consequently, merge over time. In this paper, we present visualization methods for the topology of the resulting tree-like accumulation history of the halos, as well as for the underlying halo data. We combine direct visualization methods of merger trees, in which trajectories over time are depicted in 3D space, with novel visual topological abstracts that are obtained by mapping time to one spatial axis while projecting halo positions on the remaining two axes. The user can explore and analyze both halos and merger trees through our unified visualization interface, which uses linked views complementing each other. All of our methods pay special attention to the periodic boundary conditions that are typically used during the underlying physical simulation.

1 Introduction

In cosmology, large-scale particle-based ΛCDM (cold dark matter) simulations are a popular way to gain knowledge about the structure formation in the early universe. The simulated dark matter movements allow the scientists to understand the formation of galaxies and other major stellar structures [31]. To deduce galaxy formation models from these simulations, it is necessary to comprehend how the simulated dark matter particles attract each other and form clusters, called halos. These halos, again, exert gravitational forces on each other and merge to even larger structures. Using the history of these merging processes it is possible to build so-called merger trees that describe the mass assembly of the halos in a topological manner [10].

Visualization of the halos and their assembly histories can be a useful tool for understanding the simulated phenomena. To this end, visualizing merger trees and the accompanying halos were the subject of the IEEE SciVis Contest in 2015 [8]. The data published for the contest originate from the Dark Sky simulations [27], which are a series of some of the largest cosmological N-body simulations ever performed.

Contributions

We present visualization methods both for dark matter halos as well as merger trees. In particular, we present a direct visualization of the halo positions in the merger trees. This visualization highlights each halo’s trajectory and the individual merge events. To better understand the history of the halo trajectories in the merger tree, we furthermore present a novel method to generate visual topological abstracts. Inspired by the clarity of two-dimensional graph drawings, the topological abstracts map the time axis to one of the three spatial dimensions. In contrast to 2D drawings, however, our method is able to communicate the spatial relationship between a primary halo trajectory and secondary trajectories that merge with the primary. This is achieved by projecting the 3D halo positions onto the remaining two coordinate axes in a consistent fashion. Using the data provided for the aforementioned contest, we demonstrate that our visual topological abstracts highlight the mutual gravitational interactions between halo trajectories effectively. By rendering the resulting structures as colored tubes, our method further allows us to communicate the virial radius of halos as well as one additional attribute, for example velocity dispersion, spin, mass, etc. All of our methods specifically resolve periodic boundary conditions. Such boundary conditions are common for ΛCDM simulations and, if unaccounted for, will result in visual artifacts as halo trajectories leave through one face of the domain and re-enter at the opposite side.

2 Related Work

Large N-body simulations have become more and more popular over the last years. Reasons are the ever increasing computational power of the supercomputers used to run the simulation, coupled with algorithmic advances. As a result, the data output has grown tremendously in size and fidelity. In 2005, the Millennium Run simulated about ten billion particles [28], whereas the Dark Sky simulations of 2014 comprise around one trillion particles in the largest run [27]. This amounts to an increase of two orders of magnitude in less than 9 years.

The resulting data can be visualized showing the raw particles [7, 11, 23]. Rendering large point-based data sets is a well-known problem in scientific visualization and has been addressed many times, for example by Hopf and Ertl [9] or Rizzi et al. [22]. More related to this specific area, Ahrens et al. [1] presented an approach for comparative visualizations of cosmological data sets, where the results of different simulations can be compared. For more information on visualizing data from physical sciences, we would like to refer to the survey by Lipşa et al. [13].

Alternatively or to support the visualization of the raw particles, halos and other structures can be extracted from the data to gain insight into the data’s underlying topology. To this end, a wide variety of halo identification tools have been proposed (e.g., Knebe et al. [12] or Onions et al. [18]). Most of these tools try to apply the density profile proposed by Navarro et al. [17] to the particle data sets to detect the halos. In the context of the Dark Sky simulations, halos have been extracted using a modified version of the Rockstar algorithm [3] running in largely distributed processing environments. The modification allowed the direct generation of merger trees, which are normally computed separately using other algorithms [10, 31]. Especially the so-called major mergers, which are merge events of halos of similar size, are of interest to the community [4].

While the visualization of raw particles is rather common, visualizations of halo data or their merger trees are rare [29, 30], although the assembly history of dark matter halos is of keen interest, as stated by Wechsler et al. [33], for example. These may have been the main motivations for the task of the 2015 IEEE SciVis Contest [8], which actively requested the visualization of the merger trees. Scherzinger et al. [24], who won the contest, addressed this topic with a direct graph drawing of the merger tree graph. Merger trees of the accumulation topology can also be understood as a special case of contour trees, which themselves are special cases of Reeb graphs [20]. In contrast to merger trees, the construction [5] and visualization [19, 32] of contour trees is well-studied. Unlike contour trees, however, merger trees typically allow joining of nodes only, as splitting would indicate erroneous cluster assignment of a given halo.

3 Visualization Methods

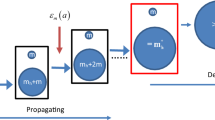
Our data was released during the 2015 IEEE SciVis Contest. It comprises 89 time steps of raw dark matter particles (128³), halos (∼550,000), and spatio-temporal halo merger trees (∼7500). In this work, we deliberately ignore the raw particle data and focus on the halos. Each halo comprises a wide variety of physical quantities, including position, radius, angular momentum, and other, more specialized variables. As depicted in Fig. 1, merger trees are constructed bottom-up, starting with the oldest halos. A halo is assigned a new ID for each time step, and old halos store the ID of the younger halo they evolve into. If halos merge, each of the older halos stores the ID of the younger, merged halo. Furthermore, halos store their virial radius and, additionally, eccentricity. The virial radius R _vir of a halo is the radius where the dark matter density inside the described sphere exceeds a certain threshold that depends on the chosen properties of the simulated universe (analogously, M _vir is the mass of dark matter inside the sphere).

Fig. 1

(a) Possible merger tree in two-dimensional representation, with the youngest halo as root node at the top. (b) Merger tree with halo positions, colored according to merging relationships. Direct temporal predecessors of the selected halo (red) are green, temporal successors are blue

The spatial locations of the halos and their size can be directly visualized in the 3D view (see Fig. 2a) of our application, which combines different linked views on the halo data. In this view, the user can also select a halo for inspecting its history (see Fig. 1b). This adds the predecessors and successors of the selected halo, showing the merger tree while preserving spatial positions and sizes of the halos. Furthermore, a line representation of the merger trees (see Fig. 3) can be selected to counter occlusion caused by large halos. However, halos can have thousands of predecessors, which still results in a very complex visual representation of limited utility. We therefore propose an additional view showing a topological abstract of the merger tree, which enables the user to explore the development of the selected halo over time while preserving the virial radii of the halos involved as well as limited information about the spatial relations between them.

Fig. 2

Halos rendered as spheres (a–b) or ellipsoids (c). (a) and (b) Colored according to velocity dispersion (blue=low, red=high). Cutouts in (b) allow exploring sub-halos. In (c), depth darkening depicts a large distance between the shadowing and the shadowed object

Fig. 3

Tree visualization behavior at bounding box borders. Positions of early time steps are green, positions of late time steps are red. In (a), the periodic boundary condition hints are depicted in magenta. In (b), the missing part (desaturated) is shown directly at the side of the available part. The desaturation is best visible with dark backgrounds (c)

3.1 Direct Halo Visualization

Our direct visualisation of the halo data is based on ellipsoids, which are tessellated and scaled on the GPU from an icosahedron created for each halo. Using geometry instead of impostors allows for displaying sub-halos by cutting out occluding geometry in a shader program (see Fig. 2b). Sub-halos are halos which are already bound by gravitation to a bigger host halo, but which have not yet merged. As a consequence, sub-halos typically lie inside their corresponding host halo. In addition to Blinn-Phong shading, we also use depth darkening by Luft et al. [15] to add an ambient occlusion-like shadow effect behind every object. The effect increases with the distance between the front objects and objects behind them (see Fig. 2c). The resulting additional depth cue eases depth perception of overlapping halos, while maintaining the overall appearance of non-occluded objects in the background.

The ellipsoidal representation of the halos can be used to construct a spatial representation of a merger tree by just showing the predecessors and successors of a selected halo (see Fig. 1b). Using color coding, we can, on the one hand, show the temporal relation of the elements in the tree to the selected halo. On the other hand, the user may also choose any of the halo properties from the simulation and map them to the color of both, merger tree and halos.

Besides preserving important 3D spatial relationships, this representation also allows for showing the virial radius in a natural way, namely as size of the ellipsoids. However, as can be seen in Fig. 1b, halos with a large virial radius may hide merge events when using solid ellipsoids. Sacrificing the size as attribute for mapping data, a line representation can solve this issue. It can be used to obtain an image containing the trajectories of all halos of the entire simulation run. To improve the perception of line orientation, we applied the line lighting technique by Mallo et al. [16] (see also Fig. 3).

This line representation nevertheless suffers from artifacts induced by periodic boundary conditions, which are common in cosmological simulations. The periodic boundary conditions result in one half of a tree appearing on one side of the bounding box of the simulation domain, while the other half appears on the opposite side. We provide two ways to remedy this situation. First, the user can enable a visual cue of where straight edges leaving or entering the bounding box appear also on the other side (see Fig. 3). This allows for a quick diagnosis of boundary effects. Second, to fully eliminate this kind of distraction, we also offer the option to duplicate the part of the tree that crosses the boundary. The duplicated part of the tree is shifted such that the merger tree is rendered as a whole. This shifted part of the tree, which is outside the simulation bounding box, is rendered with desaturated colors to indicate the duplication. Consequently, this allows the user to explore the tree as a whole, that is, as if there was no boundary between the two halves. The rendering of the duplicated version of the trees is performed in a geometry shader. For each tree that has to be duplicated, a second instance of each rendered line is spawned on the other side of the bounding box.

While rendering merger trees directly as depicted in Fig. 1 conveys the spatial geometry of each trajectory well, it is not free of problems. Firstly, since this is essentially a projection along the time axis, the history of each trajectory is hard to grasp. Secondly, additional visual clutter may be produced by instancing a primitive per halo and per time step, given that some merger trees comprise more than 4000 halos. While the first issue can be resolved by color-coding time, this solution may be inadequate if additional attributes are to be visualized on top of the geometry.

3.2 Topological Abstracts of Merger Trees

For the aforementioned reasons, we also propose visual topological abstracts of merger trees. The key idea of these visual abstracts is similar to the tx transform video technique popularized by Reinhart [21]. In essence, we map time to one of the spatial axes while projecting 3D positions to the remaining two spatial axes.

Given a primary trajectory P consisting of samples p _i in space-time ${\mathbb {R}}^3\times {\mathbb {R}}^+_0$,

$$\displaystyle \begin{aligned} \mathbf{P} &= \left\{{\mathbf{p}}_i\right\}_{i=1}^{N},\; {\mathbf{p}}_i \in {\mathbb{R}}^3\times{\mathbb{R}}^+_0,\; N\in {\mathbb{N}}, \end{aligned} $$

(1)

we would like to project samples of a second trajectory

$$\displaystyle \begin{aligned} \mathbf{S} &= \left\{{\mathbf{s}}_i\right\}_{i=1}^{M},\; {\mathbf{s}}_i \in {\mathbb{R}}^3\times{\mathbb{R}}^+_0,\; M\in {\mathbb{N}} \end{aligned} $$

(2)

onto the XY plane. For this, we postulate the following goals:

• (1) Convey the 3D distance $\left \|{\mathbf {s}}_i-{\mathbf {p}}_j\right \|{ }_2$, where p _j is the sample on P closest in time to s _i.

• (2) Preserve the altitudinal angle between s _i and the primary trajectory P.

• (3) Show both the virial radius of the halo at samples s _i, p _j and one additional, user-selectable attribute.

In addition, we want to straighten P such that we can map time onto the remaining Z axis. Goal (1) ensures that the user can judge the relative distance between P and S, while goal (2) provides visual information on the relative orientation of S with respect to P. Finally, goal (3) provides the user with a sense of the relative scale of each halo and conveys additional attributes like velocity dispersion, spin, mass, etc.

To achieve these goals, we begin by computing the orthonormal Frenet-Serret frame using only the three spatial components of each point p _i:

$$\displaystyle \begin{aligned} \begin{array}{llllllllllll} &{\mathbf{T}}_i &&= \left.\frac{\partial}{\partial t}\mathbf{P}\right|{}_{{\mathbf{p}}_i},\quad \quad &&{\mathbf{N}}_i &&= {\mathbf{T}}_i^\perp\left( \left.\frac{\partial^2}{\partial t^2}\mathbf{P}\right|{}_{{\mathbf{p}}_i}\right),\quad \quad &&{\mathbf{B}}_i &&= {\mathbf{T}}_i\otimes{\mathbf{N}}_i, \end{array} \end{aligned}$$

followed by normalization,

$$\displaystyle \begin{aligned} \begin{array}{llllllllllll} {} &{\mathbf{T}}_i &&\leftarrow \frac{{\mathbf{T}}_i}{\left\|{{\mathbf{T}}_i}\right\|{}_2},\quad \quad &&{\mathbf{N}}_i &&\leftarrow \frac{{\mathbf{N}}_i}{\left\|{{\mathbf{N}}_i}\right\|{}_2},\quad \quad &&{\mathbf{B}}_i &&\leftarrow \frac{{\mathbf{B}}_i}{\left\|{{\mathbf{B}}_i}\right\|{}_2}. \end{array} \end{aligned} $$

(3)

Here, ${\mathbf {T}}_i^\perp$ denotes projection into the orthogonal complement of T _i and ⊗ denotes the cross-product. T _i, N _i, B _i denote, respectively, tangent, normal, and binormal at sample p _i of the trajectory P with respect to time t (also see Fig. 4, left).

Fig. 4

Quantities arising in the projection of samples s _i onto the primary halo trajectory. Left: Frenet-Serret frame along a trajectory, parametrized by time. Right: Projecting a sample s _i onto s″, on the NB plane through position p ^′ of the primary trajectory (blue quantities on the NB plane)

We then proceed by projecting the samples of the secondary trajectory. For each sample s _i, we first find two samples p _j, p _j+1 such that the time of p _j is smaller and the time of p _j+1 is greater or equal to the time of s _i. Using linear interpolation, we then compute the point p ^′ on P that is closest in time to s _i. We also use linear interpolation followed by re-orthonormalization to compute a Frenet-Serret frame T, N, B at p ^′. Using this fame, we project the spatial part of s _i along T onto the NB plane. To simplify the following exposition, we again consider only the three spatial components of the involved vectors (refer also to Fig. 4, right).

$$\displaystyle \begin{aligned} {\mathbf{s}}^\prime &:= {\mathbf{p}}^\prime + {\mathbf{T}}^{\perp} \left({\mathbf{s}}_i - {\mathbf{p}}^\prime\right), \end{aligned} $$

(4)

where T ^⊥ again denotes projection into the orthogonal complement of T. While this ensures that goal (2) is achieved, a re-normalization establishes goal (1):

$$\displaystyle \begin{aligned} \mathbf{s}'' &:= {\mathbf{p}}^\prime + \frac{{\mathbf{s}}^\prime-{\mathbf{p}}^\prime}{\left\|{\mathbf{s}}^\prime-{\mathbf{p}}^\prime\right\|{}_2}\left\|{\mathbf{s}}_i-{\mathbf{p}}^\prime\right\|{}_2. \end{aligned} $$

(5)

This allows us to express s″ solely in terms of N and B. Straightening the trajectories P, S after this projection thus becomes a simple matter of mapping the local coordinate axes: B↦X, N↦Y and T↦Z. For samples of the primary and secondary trajectories, 3D positions are thus obtained as

$$\displaystyle \begin{aligned} {\mathbf{p}}_j \mapsto \begin{bmatrix} 0 \\ 0 \\ \mathrm{time}\left({\mathbf{p}}_j\right)\end{bmatrix},\quad {\mathbf{s}}_i \mapsto \begin{bmatrix} \langle \mathbf{s}'',\mathbf{B}\rangle\\ \langle \mathbf{s}'',\mathbf{N}\rangle\\ \mathrm{time}\left({\mathbf{s}}_i\right)\end{bmatrix}. \end{aligned} $$

(6)

Finally, to achieve goal (3), we extrude the trajectories obtained by the above embedding using a logarithmic mapping of the virial radius. The logarithmic mapping is necessary in order to cope with the high dynamic range of this attribute. We first assign radii to samples using a homeomorphic mapping,

$$\displaystyle \begin{aligned} r &= \alpha\frac{\log\left(1+R_{\mathrm{vir}}\right)}{\log\left(1+\mathrm{max}~R_{\mathrm{vir}}\right)}, \end{aligned} $$

(7)

which results in $r \in \left [0,\alpha \right ]$. R _vir is the so-called virial radius of a halo, whereas $\alpha \in {\mathbb {R}}^+$ is a user-defined parameter to control the overall thickness. To compute the final geometry, we use a transfinite generalization of the Power Diagram [2]. Power Diagrams are a generalization of Voronoi diagrams, in which the Euclidean distance is replaced with the power of a point with respect to a sphere. Given a point p and a sphere with center c and radius r, the power is defined as $\left \|\mathbf {p}-\mathbf {c}\right \|{ }_2^2 - r^2$. The power vanishes if p is on the sphere, it is positive for p outside the sphere and negative for p inside the sphere. Assigning to each sample on P and S a radius allows us to compute the minimum power value on a regular 3D grid. The 0-isocontour, which can be obtained by contouring algorithms such as Marching Cubes [14], is then the desired surface fulfilling all of our goals. In our case, the generalization to the transfinite case is achieved by considering linear interpolations between two circles. Figure 5 depicts selected iso-contours of a single segment in 2D.

Fig. 5

Power isocontours of two circles C ₁ at (0, 0) with radius 0.5, and C ₂ at (5, 0) with radius 1. We plot isocontours at − 0.5, −0.25, 0, 1, 2, 3. Blue hues correspond to positive values, whereas red hues correspond to negative values

In addition to the actual scalar power field, we also keep track of the nearest site on the trajectories for each 3D grid position. This allows us to propagate attributes from the trajectory to the actual surface. Since time and virial radius are already encoded in the geometry, an additional attribute can then be mapped to a color to satisfy the second half of goal (3) as depicted in Fig. 6.

Fig. 6

A topological abstract with six selected, color-coded attributes (units in brackets). (a) Virial density (M _sun∕h). (b) Virial mass (M _sun∕h). (c) Spin. (d) Scale radius (kpc∕h). (e) Angular momentum magnitude ((M _sun ⋅ Mpc ⋅km)∕(h² ⋅s)). (f) Velocity magnitude (km/s)

3.3 Implementation Details

To ensure that the Frenet-Serret frame is smooth, we first compute T _i using central differences, followed by a smoothing step and then re-normalization prior to computing N _i, B _i as described in Eq. (3). In order to obtain smooth trajectories, we subdivide segments p _i, p _i+1 and s _i, s _i+1. Due to the scaling of Eq. (5), which preserves 3D distances, simple linear interpolation between the end-points of line segments results in curved arcs in the final surface.

We implemented the Power Diagram using a variation of a parallel vector propagation [25, 26]. However, instead of storing the vector to the closest point as in the aforementioned references, we store the ID of the site and compute the power of a point with respect to the line segment analytically. We compute the Power Diagrams on a 1 024³ regular grid and we set the maximum radius α to about 15 voxel lengths.

In order to obtain consistent topological abstracts, we resolve periodic boundary conditions as follows: We choose the first sample of the primary trajectory as anchor point. For every remaining sample of the primary trajectory, we consider the Euclidean distance between the previous sample and the current sample. Of the six wrap-around cases, we choose the one resulting in the minimum distance. The periodicity is resolved analogously for the secondary trajectories, except for the first sample of each trajectory where we minimize the distance to the anchor point.

4 Discussion

The visualization methods described in Sect. 3 are combined in an interactive, unified visualization framework (see also Fig. 7). Our framework uses linked views in which selections are propagated across all different visualization methods. This allows users to quickly move between halo and merger tree visualizations. In the halo view, the user has the option to select any of the visualizations depicted in Fig. 2. In particular, cutouts of tessellated host halo clusters allows to explore the interior of halos (Fig. 2b). Cutouts were chosen over transparency since they do not require depth sorting, which can quickly become prohibitive for large simulation data. Furthermore, depth darkening provides the user with additional depth cues (Fig. 2c). Unlike using fogging to provide depth cues, depth darkening does not change the appearance of non-occluded objects.

Fig. 7

Overview of our unified visualization framework. Left: Halo view with slider to select timestep. The user can pick a halo to display the corresponding merger tree’s topology in the linked views to the right. Right, top: Topological abstract. Right, bottom: Direct merger tree visualization using spheres (left) and lines (right). Periodic boundary conditions are fully resolved. All topology visualizations show the color-coded velocity magnitude. The color-encoded value range is: 6.59 km∕s _ __ __ __ __ __ __ __ __ 2009.36 km∕s

For visualizing halo trees, we provide two visualization approaches. The first approach is the direct visualization of halos and merger trees, explained in Sect. 3.1. To provide users with intuitive illustrations, special attention has been paid to the periodic boundary conditions commonly used in ΛCDM simulations. In our framework, edges of the trajectory crossing boundaries can either be highlighted (Fig. 3a) or be desaturated (Fig. 3c) to aid the user in understanding the domain extent. Alternatively, they can be fully resolved to help in understanding the underlying spatial structure (Fig. 3b). Our direct visualization approach provides a good spatial overview, but it may be difficult to assess a single halo trajectory’s history. To address this issue, we provide as second visualization approach, namely our novel visual topological abstracts explained detailed in Sect. 3.2. While our topological abstracts maintain some spatial information (distance and altitudinal angle), they do not match the spatial clarity of the direct method. In contrast to the direct method, our topological abstracts provide the user with clear cues about the history of each trajectory, mutual gravitational interactions, and geometric deformations of the halos. This is illustrated in Fig. 8, which shows three different visual topological abstracts generated with our method. The straight line in the center represents the primary halo trajectory with multiple secondary trajectories projected into the primary’s Frenet-Serret space. As can be seen, merging secondary halos enter the first halo’s gravitational field. The mutual gravitational pull coupled with the inertia of the involved halos frequently results in oscillations prior to halos merging that can be clearly seen in the visualization. Furthermore, as halos are absorbed in the primary halo, their virial radius commonly expands, which is also obvious from our visual abstract. For these reasons, our visualization framework combines complementing visualization methods using linked views. While the camera is freely movable in the halo visualization (Fig. 7 left), the two direct merger tree views (Fig. 7 bottom right) allow a linked rotation around the center. The rendering of the topological abstract (Fig. 7 top right) can be rotated around the main axis, that is, around the straightened primary halo trajectory. Panning and zooming is supported by all views.

Fig. 8

Topological abstracts of three merger trees. Top: A halo merger tree comprising a total of 4175 halo samples. The primary halo trajectory (green arrow) is aligned in the center, with time increasing from left to right and mapped to the following color scale: min __ __ __ __ __ __ __ __ __ __ __ max. Mutual gravitational pull between primary and secondary trajectories coupled with the inertia of the halos result in clearly visible oscillations in the altitudinal angle (blue arrow). As secondary halos merge with the primary halo, their radius increases (red arrow) as a result of the gravitational pull of the primary trajectory. This can also be seen in the inset showing the velocity dispersion in this area, using the same coloring scheme in the value range [0.0, 1069.9] km∕s. The part of the halo closer to the future host halo is accelerated faster than the part further away, resulting in an increase of the dispersion. Middle: The primary halo (green arrow) is the result of two large secondary halos merging (blue arrow). Bottom: Multiple secondary halos approach the primary halo trajectory (green arrow) and start oscillating (blue arrow) until they finally merge (red arrow)

5 Conclusion and Future Work

We presented a unified interactive visualization framework for rendering merger trees and their accompanying halo data. Our framework uses linked views with complementing visualization methods to comprehensively communicate the complex topology arising in merger trees effectively and efficiently.

The richness of cosmological data sets leaves plenty of tasks for the future: We would like to incorporate our halo topology visualization into existing visualization frameworks geared towards the visual exploration of large particle simulations, e.g., [22, 23]. Our direct visualization method could be improved further by the use of methods specialized to the rendering of dense line ensembles, such as the method of Everts et al. [6]. Furthermore, we also want to incorporate non-spatial visualizations of merger trees similar to the tracking graphs of Widanagamaachchi et al. [34].

While our framework is geared towards the understanding of the topology arising in merger trees, we would further like to grow our visualization into a semi-automated analysis tool. In collaboration with domain scientists, we would like to provide users with automatically extracted and scientifically significant statistics in regions of interest around the halos. In particular, we believe that our topological abstracts are helpful in visually classifying different types of halo formation, as depicted in Fig. 9. However, a comparative study of such classes is left for future work.

Fig. 9

Representative examples for visually identified topological classes, with direct rendering of the merger tree as inset. Shown value: Max. velocity (39.09 km∕s _ __ __ __ __ __ __ __ __ 1164.39 km∕s) Top row: Complex interactions of multiple secondary trajectories swirling around a primary halo forming early in time. Middle row: Smaller halo merger trees result in significantly less complex structures. Bottom row: If the primary halo forms later in time, secondary trajectories are straightened prior to the start of the primary trajectory