Hierarchical Analysis of Halo Center in Cosmology

Abstract

Ever-increasing data size raises many challenges for scientific data analysis. Particularly in cosmological N-body simulation, finding the center of a dark matter halo suffers heavily from the large computational cost associated with the large number of particles (up to 20 million). In this work, we exploit the latent structure embed in a halo, and we propose a hierarchical approach to approximate the exact gravitational potential calculation for each particle in order to more efficiently find the halo center. Tests of our method on data from N-body simulations show that in many cases the hierarchical algorithm performs significantly faster than existing methods with a desirable accuracy.

1 Introduction

Cosmological N-body simulation [2, 4] is essential for identifying dark matter halos and studying the formation of large-scale structure such as galaxies and clusters of galaxies. For example, the halos in a simulation provide the information needed to analyze structure formation and the galaxy distribution of the universe, which is useful to predict specific models to be compared with observations and therefore understand the physics of gravitational collapse in an expanding universe [17]. One way of identifying halo is through the friends-of-friends (FOF) algorithm [8, 9]. Alternatively, one can identify a halo by adopting a certain definition for the halo center and grows spheres around it until given criteria is satisfied [21].

However, one key limitation of these N-body simulations is its rapid increase in computational load with the number of particles, even given the computing power of today’s advanced supercomputers. In particular, the calculation of the bounded potential (BP), i.e., the gravitational force, is the most time consuming task in N-body simulations [4]: in modern cosmological simulations, large halos can comprise tens of millions of particles [13]. Therefore, any improvement for this online analysis is vital.

A number of existing algorithms have been developed to run such large calculations. The most straightforward way to calculate the force is to carry out a direct pairwise summation over all particles, which is a brute-force algorithm and requires $O(N_p^2)$ operations [1, 16]. A large halo in a modern simulation may have up to 20 million particles, and thus such a global operation comes with considerable expense and quickly becomes impractical. Alternatively, given the fact that the particles close to each other share common properties, one can group particles that lie close together and treat them as if they are a single source, hence, the force of a distant group of particles is approximated by pseudo particle located at the center of mass of the group. Such methods include the tree method where the particles are arranged in a tree structure [5, 14], and the fast multipole method (FMM) [7]. FMM improves the tree method by including higher moments of mass distribution within a group.

Fig. 1.

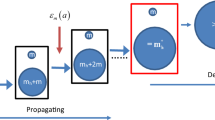
Illustration of MBP and MCP of two halos with different shapes [19]. Notice that when the halo is approximately spherical, MBP and MCP coincide. Otherwise, they can be far away from each other.

In this work, we focus on the calculation of the halo center, which is a natural byproduct of the BP calculation, and is commonly defined as the “most bounded particle” (MBP). MBP is the particle within a halo with the lowest BP. Another type of halo center is the “most connected particle” (MCP), which is the particle within a halo with the most “friends.” Figure 1 [19] demonstrates MCP and MBP separately for two different halos and suggests that, given a halo, its MBP and MCP may or may not coincide. Finding the MCP is relatively simple: one sweeps through the virtual edges connecting two particles provided by FOF-based halo finding. However, finding the MBP is much more computationally expensive directly due to the calculation of BP. Some efforts have been made to estimate the exact MBP. The most intuitive and common way is to approximate the MBP location by MCP. However, this approach can provide a reliable estimation only when the halo is roughly spherical, which unfortunately is not always the case. Other recent developments include using a $A^{*}$ search algorithm to approximate the BPs [10], which is proved eight times faster than the brute-force algorithm. Another approach is to utilize a binning algorithm to rule out the particles that cannot be the MBP, in order to reach a complexity of $O(mN_p)$; however, for most of the time, m can be still very large. High-performance computing also has been used to accelerate the calculation [19]. One common feature of these approaches is that the BP is exactly calculated, meaning that the summation is over every other particle in the halo.

Inspired by the tree-based methods, we propose to further exploit the latent or intrinsic structure within the data, grouping the data into corresponding clusters and then performing operations on the respective groups. We notice that, given the definition of BP (defined below in Sect. 2), the farther the particle is away from another, the less the impact of this particle on the other’s BP. This realization can be illustrated by the BP map of a halo. Given a 3D dark matter halo from an N-body simulation with 89,887 particles, we show its 2D projection for better visualization in Fig. 2 on the left side. The right side shows that the BP map is smooth in the sense of small value change around a local neighborhood. Therefore, in this work, instead of exactly calculating every BP to find the MBP, we exploit the local smoothness of the BP map and propose a hierarchical approach to approximate the BP by its so-called local BP, which is defined only on a local neighborhood.

Different from existing methods, our approach provides following benefits:

• It provides a more flexible framework to incorporate domain knowledge, such as different properties of halo in terms of linkage length. Therefore, the accuracy and computational cost can be optimally balanced.

• It is able to recover the local minimum which also contains important physical information for the scientific discovery.

• We provides the theoretical error bounds and complexity analysis of our proposed framework.

• Systematic experiments reveals that our proposed method is significantly faster and yet accurate as the number of particles are increasing, which is critical for halo center finding.

Fig. 2.

Left: 2D projection of a 3D halo with 89,887 particles. We can see three major dense areas that can yield at least three local minima of problem (2.2); right: its global BP map calculated by Eq. (2.1). We can see a smooth change of the BP value around a local neighborhood.

We organize our presentation as follows. In Sect. 2, we introduce our hierarchical framework based on several key components, including construction of the tree structure and an algorithm for finding local extremes. In Sect. 3, we analyze the error bounds and complexity of our proposed hierarchical framework. In Sect. 4, we compare our proposed framework with a brute-force algorithm (as to provide gold standards for accuracy) and FMM on many synthetic halos with different configurations. In Sect. 5, we present our conclusions and discuss ideas for future development.

2 Method

Given a collection of $N_p$ distinct particles $\mathbf{X}=\{X_i : i=1,\dots ,N_p\}$ in a halo, we denote a MBP by $X_p$. The BP of a given particle $X_i$ is computed as the sum over all other particles of the negative of mass divided by the distance,

$$\begin{aligned} \displaystyle P(X_i)= \sum _{\begin{array}{c} j\ne i \\ j\in [1,\dots ,N_p] \end{array}}\frac{-m_j}{d(X_i,X_j)}, \, \qquad i=1,\dots ,N_p, \end{aligned}$$

(2.1)

where $X_i\in \mathbb {R}^3$ is the ith particle represented by its position coordinates, $m_i$ is its corresponding mass, and $d(X_i,X_j)$ is the Euclidean distance between particles $X_i$ and $X_j$. Then, we have the following optimization problem,

(2.2)

We notice that the BP map from every particle is relatively smooth in its local region. Therefore, our approach is, starting from the whole domain, to approximate the BP map by a few sampled (seed) particles that are sufficiently far away from each other. By comparing the local BP of the sample particles, we gradually narrow the search region to a smaller area where the MBP can be. In other words, at each hierarchical level (as described in Algorithm 1), we approximate the BP map of the corresponding search region by the local BPs of a few sample particles.

Three critical questions need attention. First, how many sample particles should be enough to approximate the whole domain? Second, how far do the sample particles have to be away from each other to guarantee a sufficient coverage? Third, how can one determine the threshold used to calculate the local BP? Intuitively, the deeper the hierarchical level is, the smaller the search region is; therefore, larger thresholds can approximate the BP better. Thus, an essential step is to perform a range search to allocate the neighboring particles given a threshold. Our approach is to use a kd-tree to first construct the neighborhood among particles. A kd-tree is a data structure that partitions the space through alternative dimensions for organizing points in a k-dimensional space [6]. Since kd-trees divide the range of a domain in half at an alternative dimension at each level of the tree, they are efficient for performing range searches. This structure is constructed only once, in the beginning. Throughout the process, the preconstructed tree structure is used to search for ranges at a given distance threshold. For example, if a tree is storing values corresponding to distance, then a range search looks for all members of the tree in the distance that are smaller than the given threshold. Throughout the paper, we employ the range search algorithm presented in [15].

Once the kd-tree is constructed, on the first level we uniformly sample a few particles from $\mathbf{X}$ and approximate their local BPs (denoted as $\tilde{P}$) by the range search at a given distance threshold $\varepsilon _1>0$ as follows:

$$\begin{aligned} \displaystyle \tilde{P}(X_i)= \sum _{\begin{array}{c} j\ne i\\ X_j\in B(X_i,\varepsilon _1) \end{array}}\frac{-m_j}{d(X_i,X_j)},\qquad i=1,\dots ,N_p, \end{aligned}$$

(2.3)

where $B(X_i,\varepsilon _1)$ is the ball with center $X_i$ and radius $\varepsilon _1$. Accordingly, we have a particle with minimum local BP as

(2.4)

where $X_{\tilde{p}}$ is the approximation to a global MBP $X_p$. The next step is to interpolate the coarse BP map for every particle in the halo and use a peak-finding algorithm to locate the particles having the first few smallest BPs while their pairwise distance is bigger than another distance threshold denoted by $\varepsilon >0$. These particles are then used as the next-level sample particles. We mark the particle with the smallest local BP as a temporary $X_{\tilde{p}}$. Then we start a range search on each newly selected sample particle. From the second level, instead of calculating only local BPs for the sample particles, we calculate local BPs for every particle in the ranges and repeat the steps of interpolating, peak finding, and locating the temporary $X_{\tilde{p}}$ until the current temporary $X_{\tilde{p}}$ coincides with the previous temporary $X_{\tilde{p}}$. We fix the number of sample particles at each level as $N_s$ and denote the collection of the current samples as Seeds. The full procedure is described in Algorithm 1, and the step of locating peaks in the BP map is described in Algorithm 2.

We now discuss in detail how we choose the distance thresholds. First, to determine $\varepsilon _1$ that defines the neighborhood, we need to analyze the sensitivity of $\varepsilon _1$ for preserving the pattern of the true BP map. Given the same halo as shown in Fig. 2, we first compare the local $X_{\tilde{p}}$ provided by Eq. 2.4 and the global $X_p$ provided by Eq. 2.2. Given 100 different $\varepsilon _1$ that are equally spaced in the region [0, 1], we generate their corresponding $X_{\tilde{p}}$ as a function of $\varepsilon _1$ and calculate its error compared with $X_p$, respectively, as $|X_{\tilde{p}}(\varepsilon _1)-X_p|$. The result is shown in Fig. 3a. We can see that as $\varepsilon _1$ increases, $X_{\tilde{p}}$ has a better chance to match $X_p$. In particular, as $\varepsilon _1>0.1$, the difference between $X_{\tilde{p}}$ and $X_p$ is negligible given the sufficient physical distance threshold used to distinguish two particles as $10^{-3}$.

Furthermore, we fix $\varepsilon _1=0.3$ to calculate the corresponding local BPs and compare them with its global BP, as shown in Fig. 3b. Notice that $\varepsilon _1=0.3$ is considered very small given the mean of all pairwise distances as 2.1. The x-axis arranges the particle indices to monotonically increase the global BPs. As we can see, although there is almost a constant offset between the local- and global-potential profiles, the local BP map preserves the shape of the global BP, which suggests that the minimizer of the local BPs can closely approximate the minimizer of the global BPs.

Fig. 3.

Left: we compare the relative error between $X_p$ and $X_{\tilde{p}}$ generated by different $\varepsilon _1$ from Eq. (2.4). As $\varepsilon _1$ increases, the local $X_{\tilde{p}}$ has a better chance to coincide with the global $X_p$; Right: Given $\varepsilon _1=0.3$ as the choice for the rest of the tests, the local BP map has a pattern similar to that of the global BP map, which makes them share the same minimizer.

These numerical tests suggest a reasonable choice of $\varepsilon _1=0.3$ on the first level, so that the local BP map agrees well with the global BP map. Because of the common features (e.g., mean of the pairwise distances between particles, linkage length) shared by different dark matter halos, we keep $\varepsilon _1=0.3$ for different halos from the same simulation system. Accordingly, the choice of $\varepsilon _1$ suggests that $\varepsilon$, which is the distance threshold to avoid seed particles being too close to each other, should be at least as big as $\varepsilon _1$ in order to guarantee a good coverage of the domain of interest.

3 Error Bounds and Complexity Analysis

In this section, we first provide a preliminary error estimate of the proposed method. Again, since the BP function is a function of inverse Euclidean distance, distance greater than $\epsilon _1$ can be negligible to some extent. Together with the local smooth property of BP function, the error $P(X_i)- \tilde{P}(X_i)$ can be analyzed analogous to the cumulative distribution function error between Gaussian distribution and truncated Gaussian distribution. We assume each term in function $P(X_i)$ follows a Gaussian distribution with respect to $d(X_i,X_j)$, where its mean is 0 and standard deviation is $\sigma$, then we have

$$\begin{aligned} \begin{array}{lll} \Vert P(X_i)-\tilde{P}(X_i)\Vert &{}= &{}\displaystyle 1-\frac{1}{2}\left[ {\text {erf}}\left( \frac{\epsilon _1}{\sqrt{2}\sigma }\right) -{\text {erf}}\left( \frac{-\epsilon _1}{\sqrt{2}\sigma }\right) \right] \\ &{} = &{}\displaystyle 1-{\text {erf}}\left( \frac{\epsilon _1}{\sqrt{2}\sigma }\right) ,\\ \end{array} \end{aligned}$$

(3.5)

where $\displaystyle {\text {erf}} x={\frac{2}{\sqrt{\pi }}}\int _{0}^{x}e^{-t^{2}}\,dt$ is the error function. As shown in Fig. 4, we can see that as $\epsilon _1$ gets larger, the estimation error of local BP is getting smaller and approaching 0.

Fig. 4.

The estimation error provided by Eq. (3.5). As $\epsilon _1$ gets larger, the estimation error gets smaller and approaches 0.

Next, we estimate the complexity of our proposed hierarchical algorithm. Each level involves the following computations:

• Conduct a range search for each Seed: $O(N_p N_s)$.

• After level 1, approximate the local BP for each particle in the neighborhood of the seed particles: $O(n^2 N_s)$, where $n\ll N_p$ is roughly the number of particles in each neighborhood. Figure 5 shows the relationship between n and $N_p$ empirically for various of halos.

• Find the peak: the dominant calculation is sorting, which takes $O(N_s n\log n)$.

On average, three levels are needed in order to converge, and the complexity of a one-time kd-tree construction is $O(N_p \log N_p)$. By summing up these components, the total complexity is

$$\begin{aligned} \displaystyle O(N_p \log N_p+n^2). \end{aligned}$$

Fig. 5.

Given various halos with different numbers of particles, we report the corresponding mean value of n resulting from the proposed Algorithm 1. It suggests that compared with $N_p$, n is significantly smaller.

4 Numerical Results

We now illustrate the performance of the proposed algorithm on a set of halos from catalogs created by the in situ halo finder [18] of the Hybrid Accelerated Cosmology Code (HACC) [12]. All the numerical experiments are implemented in MATLAB and performed on a platform with 32 GB of RAM and two Intel E5430 Xeon CPUs. We first demonstrate the proposed approach on the 2D projection of the 3D halo shown in Fig. 2 where we uniformly downsample only 4,933 particles for a better visualization. This halo is a relatively challenging example since it contains approximately three locally dense areas, which results in three local minima for problem (2.2). We demonstrate the recursive process in Fig. 6, where Fig. 6a shows where the seed particles are on the first level with its corresponding local BP map and Fig. 6b shows similar information for the second level. Figure 7 shows the result where the recursively calculated local $X_{\tilde{p}}$ agrees with the global $X_p$.

Fig. 6.

Demonstration of the hierarchical process. Figure 6a illustrates the performance of the first level. The left side shows where the seed particles (denoted as $+$) are located along with the color-coded global BP map. The right side shows the local BP map provided by the previously chosen seed particles; The second level is shown similarly in Fig. 6b. We can see that the local BP map resembles well the global BP map of the corresponding region.

Fig. 7.

Result of the recursive process shown in Fig. 6: the approximated local MBP agrees with the global MBP in terms of both location and potential value. Its centroid is labeled to show multiple dense areas in this particular 2D halo.

4.1 2D Result

First, we benchmark the performance of the proposed method on 455 2D halos which are projected from the corresponding 3D dark matter halos simulated by HACC. In Fig. 8, we compare the performance of three different methods for finding the MBP: brute force where we explicitly calculate every point-wise distance between particles, the proposed recursive method with $N_s=10$ and fixed $\varepsilon$, and the FMM using an optimized MATLAB implementation [20]. We can see from the time plot, as the number of particles increases, the proposed recursive approach is outperforming FMM and brute force, while the accuracy in terms of potential error of the returned MBP from our recursive approach is better than FMM in average. Notice here that in order to easily visualize the value, we sort the potential error as shown in y-axis.

Fig. 8.

Performance comparison of finding MBP for various 2D halos using three different algorithms: brute force, our proposed hierarchical method with $N_s=10$ and fixed $\varepsilon _1$, and FMM. Left: time elapsed; Right: error of potential between the MBP located by proposed method and FMM, respectively.

4.2 3D Result

Next, we run our algorithm on 455 simulated 3D dark matter halos, using different algorithm configurations. However, due to the difficulty of having optimally implemented MATLAB-based 3D FMM code, in this section, we only compare the performance of our proposed approach against brute force using different parameter settings. For the first test we fix $N_s=10$, $\varepsilon _1=0.3$, and $\varepsilon =\varepsilon _1$ for each level. On the left of Fig. 9, we can see that as the number of particles increases from different halos, our hierarchical method is 100 times faster than the brute-force method. The middle panel shows the location accuracy of our hierarchical method compared with that of the brute-force method. We note that in reality, if two particles are separated by a distance less than $10^{-3}$, we do not distinguish these two particles. As a result, 90% of the halos in this test achieve location error smaller than $10^{-3}$, which is a desirable accuracy. We also report the relative potential error on the right panel, which is given as $\displaystyle \frac{\left| P(X_{\tilde{p}})-P(X_p) \right| }{\left| P(X_p)\right| }$.

Fig. 9.

3D halo result with fixed $\varepsilon _1$. Left: time elapsed for the hierarchical approach and the brute-force approach. Middle: location accuracy of the MBP approximation for different halos with different structures and numbers of particles. Right: Potential error between the approximated MBP and the global MBP.

We also examine our algorithm by gradually reducing the neighborhood radius $\varepsilon _1$ by half along each level. Accordingly, $\varepsilon$ is scaled by half as well along each level. Figures 10 and  11 show the effect of having $N_s=100$ and $N_s=10$ seed particles, respectively, where the initial $\varepsilon _1=0.3$ and scaled by half along each level. We can see that the computational time saved is slightly better than without scaling $\varepsilon _1$. We also note that the accuracy has kept relatively similar to the case where $\varepsilon _1$ is fixed in terms of finding the $X_p$. Furthermore, if we examine the relative error between the potential values $P(X_p)$ and $P(X_{\tilde{p}})$, we obtain a mean of these errors to be $10^{-3}$. This suggests that our hierarchical algorithm can find the local minimum if not the global minimum. This capability is also useful since the local minimum of the MBP optimization problem also obtains important features [11]. We note that the oscillatory behavior of the time elapsed and the MBP error on halos with relatively small number of particles are due to the different hierarchical levels required for different structures (such as number of local minima).

Fig. 10.

Result of applying the hierarchical method for the same set of halos with $N_s=100$, and $\varepsilon _1$ scaled by half along each level.

Fig. 11.

Result of applying the hierarchical method for the same set of halos with $N_s=10$, and $\varepsilon _1$ scaled by half along each level.

5 Conclusion and Future Work

We propose a hierarchical framework to accelerate the performance of finding a halo center, in particular, the MBP. Instead of using an exact calculation to find the global MBP, which is extremely expensive because of the large number of particles in a typical halo, we explore the smooth property and the hierarchical structure of the BP map and approximate the global BP only by the local information. The preliminary numerical results suggest that our method is comparable to fast multipole method (even slightly better) in terms of both speed and accuracy, and show dramatic speedup compared with the most common brute-force approach. On the other hand, comparing to existing methods, our approach provides a more flexible framework to incorporate domain knowledge, such as linkage length used to define a halo, to optimally choose the hyper parameters $\epsilon$ and $\epsilon _1$ used in the Algorithm 1.

Therefore, opportunities remain to further accelerate the performance. First, one can explore different ways of performing tree data structure, such as R-tree [3], to better exploit the geographical correlations among particles. Furthermore, one can explore ways to shrink the range search parameter along each level guided by the density of the local region. For example, if the density is high, the search parameter $\varepsilon _1$ should not decrease. Another key area of investigation is the initial sampling strategy. We believe the algorithm presented in this work can be generalized to other applications that share the same feature as halo center finding, such as approximation of the pairwise distance matrix.