13.1 Introduction

The spin-1/2 Heisenberg chain was the first quantum many-body Hamiltonian to be solved exactly by H. Bethe in 1931 [6]. This pioneer work led to the development of the Bethe ansatz for integrable one-dimensional models, of which the spin-1/2 Heisenberg model and its anisotropic extension, the XXZ chain, are notable examples [20]. In addition to the Bethe ansatz solution, analytical field theory methods [1] and sophisticated numerical techniques [38] have been successfully applied over several decades to reveal some remarkable properties of the antiferromagnetic Heisenberg chain. For instance, it is known that the exact ground state for a chain with an even number of spins is a singlet, i.e. a nondegenerate state invariant under global SU(2) spin rotations. While this behavior is familiar from the ground state of the two-spin problem with antiferromagnetic exchange interaction, it contrasts starkly with the classical picture of Néel order later proposed to describe the ground state of antiferromagnets in two- or three-dimensional bipartite lattices [26]. Moreover, the excitation spectrum on top of this ground state is organized in terms of elementary excitations that carry spin-1/2, as opposed to the spin 1 of a magnon in ordered magnets [10]. Selection rules then imply that these excitations, nowadays called spinons, must be created in pairs. Such fractionalization of the spin quantum number in spin chain materials has been confirmed experimentally through the observation of a two-spinon continuum in the spectrum probed by inelastic neutron scattering [24].

Inspired by the physics of the antiferromagnetic spin-1/2 chain and by Pauling’s idea of valence bonds as a theory for unconventional metals, in 1973 P. Anderson proposed the concept of a quantum spin liquid [3]. While a precise definition is still lacking [31], the term has been used to refer to phases of interacting spin systems which evade long-range magnetic order even at zero temperature, due to the strong quantum fluctuations in the ground state. Hallmarks of quantum spin liquids are a high degree of many-body entanglement and an excitation spectrum characterized by deconfined fractional excitations analogous to the spinons in the Heisenberg spin chain. In contrast with the exact methods available in one dimension, to describe fractionalization in two and three dimensions one usually resorts to approximate solutions of effective theories where the elementary excitations are slave fermions or bosons (generically called partons) coupled to emergent gauge fields. Essentially, a spin liquid phase arises when the fluctuations of the gauge field are harmless enough to allow for parton deconfinement. In this case, mean-field approximations manage to capture the essential features of Anderson’s resonating valence bond state [36]. Beyond the mean-field level, there are a few examples of spin models, such as Kitaev’s honeycomb model [19], which are exactly solved by parton representations involving Majorana fermions and static Z\(_2\) gauge fields.

Kalmeyer and Laughlin put forward one of the earliest proposals of wave functions that can describe a quantum spin liquid ground state [16]. Starting from a Holstein-Primakoff representation for spin operators, they argued that the antiferromagnetic Heisenberg model on the triangular lattice was equivalent to a model of strongly interacting bosons in the presence of a fictitious magnetic field at filling factor \(\nu =1/2\). This observation motivated the proposal of a gapped ground state corresponding to a fractional quantum Hall effect of bosonic spin excitations. As a result, the Kalmeyer–Laughlin state shares some properties with the electronic fractional quantum Hall effect, such as topological order, anyonic quasiparticles and gapless chiral edge states. A crucial difference is that the quasiparticles can carry spin and energy, but no electric charge. Furthermore, rather than an external magnetic field, the mechanism for breaking time reversal and mirror symmetries in the Kalmeyer–Laughlin state is a nonzero expectation value of the scalar spin chirality operator \(\hat{\chi }_{ijk}=\mathbf{S}_i\cdot (\mathbf{S}_j\times \mathbf{S}_k)\), where i, j, k are any three sites that form a triangular plaquette on the lattice [4, 37]. In fact, a finite value of \(\langle \hat{\chi }_{ijk} \rangle \) in the absence of long-range magnetic order is the defining property of a chiral spin liquid. A direct way to drive the system into a chiral spin liquid phase is to add to the Hamiltonian the three-spin interaction \(J_\chi \hat{\chi }_{ijk}\), which favors either sign of the chirality for each triangle depending on the sign of the coupling constant \(J_\chi \). Such term breaks time reversal symmetry explicitly while preserving the spin SU(2) symmetry. This route was used to stabilize the Kalmeyer–Laughlin state on the kagome lattice with uniform three-spin interactions [5]. Other examples of gapped chiral spin liquids include non-Abelian phases in spin-1 systems [13] and in the Kitaev model in a magnetic field [19]. On the experimental side, perhaps the best evidence for a chiral spin liquid state comes from a recent measurement of quantized thermal Hall conductance associated with a Majorana edge state in a Mott insulating material with strong spin-orbit coupling [18].

Fig. 13.1
figure 1

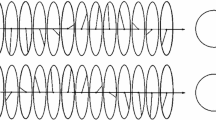
Schematic representation of a coupled-wire construction of the integer quantum hall effect. a Dispersion relation for tunnel-coupled wires, showing the avoided level crossings at the Fermi level \(E_F\). b In real space, the gapped bulk states correspond to pairs of right and left movers living in different adjacent wires, while the edge harbors gapless chiral states

Full size image

As examples of strongly correlated topological phases, chiral spin liquids present a challenge for analytical approaches which do not rely on mean-field approximations. The question then is: can we go back to the beginning and use our knowledge about the Heisenberg spin chain to construct and analyze chiral spin liquid states? In principle, all we need to do is to couple spin chains in such a way that the spinons living in each chain are set free to propagate in two dimensions. This is more easily said than done, because interchain exchange interactions usually give rise to magnetically ordered or dimerized phases [33]. On the other hand, a precedent for how to obtain microscopic Hamiltonians for topological phases starting from one-dimensional critical systems is the so-called coupled-wire approach [17, 32, 35]. Figure 13.1 illustrates the idea for the simple example of an integer quantum Hall phase [32]. Consider an array of noninteracting quantum wires contained in the xy plane which is threaded by an external magnetic field \(\mathbf{B}=B\hat{\mathbf{z}}\). If we work in the Landau gauge \(\mathbf{A}=-By\hat{\mathbf{x}}\), where \(\hat{\mathbf{x}}\) is the direction parallel to the wires, the dispersion relations associated with different wires are shifted in momentum space as shown in Fig. 13.1a. Turning on a finite tunnelling amplitude between neighboring wires gaps out the crossing points in the spectrum. If the Fermi level lies exactly at the energy of the crossing points, in the low-energy limit we are left with a single pair of gapless chiral fermionic modes: a left-moving mode associated with the upper wire and a right-moving one associated with the lower wire; see Fig. 13.1b. This describes an incompressible phase with chiral edge states which is adiabatically connected with the integer quantum Hall effect (in this example, \(\nu =1\)) in a spatially isotropic two-dimensional system. The advantage of the coupled-wire approach is that we can adapt it to include electron-electron interactions nonperturbatively in the wires by treating them as Luttinger liquids. The result is a coupled-wire construction of fractional quantum Hall states [17]. More generally, the idea is to start with a set of critical one-dimensional systems described by the appropriate conformal field theory, and gap out pairs of modes with right and left movers that live in different wires, until the total central charge is reduced to that of a particular chiral edge state [35].

The purpose of this chapter is to review the coupled-chain construction of chiral spin liquids that use Heisenberg chains as building blocks [12, 23, 29]. The key step is to couple the chains with suitable time-reversal-symmetry-breaking perturbations that involve three-spin interactions on triangular geometries. We start in Sect. 13.2 by discussing the low-energy effective field theory for a single Heisenberg chain. In Sect. 13.3, we explain the coupled-chain construction of the Kalmeyer–Laughlin chiral spin liquid using arrays of parallel spin chains. Section 13.4 deals with the construction of a gapless chiral spin liquid on a lattice constructed from weakly-coupled crossing chains. Finally, in Sect. 13.5 we present some concluding remarks and discuss some open questions.

13.2 Effective Field Theory for the Spin-1/2 Heisenberg Chain

The Heisenberg chain is described by the Hamiltonian

$$\begin{aligned} H_{1D}=J\sum _{j=1}^N\mathbf{S}_j\cdot \mathbf{S}_{j+1}, \end{aligned}$$
(13.1)

where \(\mathbf{S}_j\) are spin-1/2 operators acting the local Hilbert space at site j, \(J>0\) is the antiferromagnetic exchange coupling, and N is the number of sites with periodic boundary conditions. The low-energy physics of the spin-1/2 chain is described by the SU(2)\(_1\) Wess-Zumino-Novikov-Witten model, which is a conformal field theory with central charge \(c=1\) [2]. To derive bosonization formulas for the local operators in the theory, one can start from the one-dimensional Hubbard model at half-filling and gap out the charge degrees of freedom in the Mott insulating phase. The spin operator is represented in the continuum limit by

$$\begin{aligned} \mathbf{S}_j\mapsto \mathbf{S}(x)\sim \mathbf{J}_{L}(x)+ \mathbf{J}_{R}(x)+(-1)^j\mathbf{n}(x), \end{aligned}$$
(13.2)

where \(\mathbf{J}_{\nu }\), with \(\nu =R,L=\pm \), are chiral SU(2) currents associated with right- or left-moving modes, respectively, and \(\mathbf{n}\) is the staggered magnetization field. The components of the chiral currents can be written in terms of chiral bosons in the form

$$\begin{aligned} J^z_\nu (x)=\frac{\nu }{\sqrt{4 \pi }} \partial _x \varphi _{\nu }(x) , \qquad J^\pm _\nu (x) =\frac{1}{2 \pi } \,e^{\pm i \sqrt{4 \pi } \varphi _{\nu }(x)}. \end{aligned}$$
(13.3)

where the bosonic fields obey the algebra \([\varphi _{\nu }(x),\partial _{x'} \varphi _{\nu '}(x') ] =i \nu \delta _{\nu \nu '} \delta (x-x') \). The components of the staggered magnetization are

$$\begin{aligned} n^{\pm }(x)=\mathscr {A}e^{\pm i\sqrt{\pi }\left( \varphi _{L}+\varphi _{R}\right) },\qquad \quad n^{z}(x)=\mathscr {A}\sin \left[ \sqrt{\pi }\left( \varphi _{L}-\varphi _{R}\right) \right] , \end{aligned}$$
(13.4)

where \(\mathscr {A}\) is a non-universal constant of order 1. Another local operator in the theory is the dimerization operator \(\varepsilon (x)\), which appears in the expansion of the scalar \({\mathbf{S}_j\cdot \mathbf{S}_{j+1}}\sim (-1)^j\varepsilon (x)\) in the continuum limit. Its bosonized form reads

$$\begin{aligned} \varepsilon (x) =\mathscr {A}'\cos \left[ \sqrt{\pi }\left( \varphi _{L}-\varphi _{R}\right) \right] , \end{aligned}$$
(13.5)

where \(\mathscr {A}'\) is another non-universal constant.

The symmetry properties of the local operators are important to analyze the perturbations of the conformal field theory. Under translation by one site, \(x\mapsto x+1\), the fields transform in the form

$$\begin{aligned} \mathscr {L}:\, \mathbf{J}_{\nu }\mapsto \mathbf{J}_{\nu },\quad \mathbf{n}\mapsto -\mathbf{n},\quad \varepsilon \mapsto -\varepsilon . \end{aligned}$$
(13.6)

Time reversal \(\mathscr {T}\) involves complex conjugation and acts on the fields as follows:

$$\begin{aligned} \mathscr {T}:\,\mathbf{J}_{R}\leftrightarrow -\mathbf{J}_{L},\quad \mathbf{n}\mapsto -\mathbf{n},\quad \varepsilon _l\mapsto \varepsilon _l. \end{aligned}$$
(13.7)

Site parity, defined as the reflection \(\mathscr {P}_s\) about an axis passing through a given site, takes \(x\rightarrow -x\) and

$$\begin{aligned} \mathscr {P}_s:&\mathbf{J}_{R}\leftrightarrow \mathbf{J}_{L},\quad \mathbf{n}\mapsto \mathbf{n}, \quad \varepsilon \mapsto -\varepsilon . \end{aligned}$$
(13.8)

Site parity, defined as the reflection \(\mathscr {P}_l\) about an axis passing through the middle of link between two sites, takes \(x\rightarrow -x\) and

$$\begin{aligned} \mathscr {P}_l:&\mathbf{J}_{R}\leftrightarrow \mathbf{J}_{L},\quad \mathbf{n}\mapsto -\mathbf{n}, \quad \varepsilon \mapsto \varepsilon . \end{aligned}$$
(13.9)

The low-energy effective Hamiltonian for a single Heisenberg chain is written in terms of the chiral currents as

$$\begin{aligned} H_{1D}\sim \int \mathrm{{d}}x\, \left[ \frac{2\pi v}{3}\left( \mathbf{J}_R^2+\mathbf{J}_L^2\right) +2\pi v g_{bs}\mathbf{J}_L\cdot \mathbf{J}_R\right] . \end{aligned}$$
(13.10)

Here \(v\propto J\) is the spin velocity and \(g_{bs}<0\) is the dimensionless coupling constant for the marginally irrelevant backscattering operator [1]. As the effective \(g_{bs}\) vanishes (logarithmically) in the low-energy limit, the theory becomes equivalent to free bosons and the asymptotic decay of correlation functions can be calculated exactly.

13.3 Coupling Parallel Chains: The Kalmeyer–Laughlin State

Let us now couple spin-1/2 chains to build towards the two-dimensional limit. We start with two parallel chains with a zigzag geometry as illustrated in Fig. 13.2 [12]. We consider the interchain exchange coupling \(J'\) together with a three-spin interaction \(J_\chi \),

$$\begin{aligned} H=\sum _{j}\left[ J\sum _{l=1,2}\mathbf{S}_{j,l}\cdot \mathbf{S}_{j+1,l}+J'\mathbf{S}_{j,1}\cdot (\mathbf{S}_{j,2}+\mathbf{S}_{j+1,2})\right] +J_\chi \sum _{ijk\in \triangle }\hat{\chi }_{ijk}, \end{aligned}$$
(13.11)

in the regime \(|J'|,|J_\chi |\ll J\). The ordering of the spins i, j, k in the triple product \(\hat{\chi }_{ijk}\) is set to correspond to a configuration with uniform chirality, as indicated by all the arrows in Fig. 13.2 pointing either clockwise or counterclockwise. Note that the operator \(\hat{\chi }_{ijk}\) is odd under time reversal, which takes \(\mathbf{S}_i\mapsto -\mathbf{S}_i\), and under a reflection that exchanges two of the three sites, \(\hat{\chi }_{ijk}=-\hat{\chi }_{jik}=-\hat{\chi }_{ikj}\).

Fig. 13.2
figure 2

Two parallel Heisenberg chains coupled by exchange and three-spin interactions in a zigzag geometry

Full size image

The unperturbed effective Hamiltonian for \(J'=J_\chi =0\) is given by two copies of the chain Hamiltonian in (13.10), with operators in each chain labeled by the index \(l=1,2\). For small \(J'\) and \(J_\chi \), the leading interchain couplings in the effective field theory are all marginal operators. There is a twist operator [27] that depends on the staggered magnetization fields,

$$\begin{aligned} \delta H_{tw}=2\pi v g_{tw}\int \mathrm{{d}}x\,\mathbf{n}_1\cdot \partial _x \mathbf {n}_2, \end{aligned}$$
(13.12)

and two operators that couple the chiral currents in different chains

$$\begin{aligned} \delta H_{RL}=2 \pi v \int \mathrm{{d}}x\, ( g_+ \mathbf {J}_{1,R} \cdot \mathbf {J}_{2,L} +g_-\mathbf {J}_{1,L} \cdot \mathbf {J}_{2,R} ), \end{aligned}$$
(13.13)

where \(g_{\pm }= g\pm g_\chi \) with \(g\propto J'\) and \(g_\chi \propto J_\chi \) to first order. For \(J'>0\) and \(J_\chi =0\), this problem reduces to the familiar zigzag chain, whose ground state in the regime \(J/J'\gtrsim 0.241\) is fully gapped and breaks translational invariance due to dimerization \(\langle \varepsilon (x)\rangle \ne 0\) (as in the Majumdar–Ghosh model [22]). Within the effective field theory, the dimerized phase is understood as the regime where both \(g_+\) and \(g_-\) flow to strong coupling under the renormalization group, eventually pinning the bosonic fields to the minima of a sine-Gordon potential [14]. The new interesting possibility that appears when we add the time-reversal-symmetry-breaking interaction \(J_\chi \) is that \(g_+\) and \(g_-\) can have opposite signs if \(J_\chi \) is large enough, in the regime \(|g_\chi |>|g|\). In this case, one of them flows to strong coupling while the other flows to zero. As a result, we obtain a gapless quasi-one-dimensional phase with one pair of gapless chiral modes, either \(J_{1,R}\) and \(J_{2,L}\) for \(J_\chi >0\), or \(J_{1,L}\) and \(J_{2,R}\) for \(J_\chi <0\). Such phase of the two-leg system can actually be verified exactly for a special value of \(J_\chi \) where the model is integrable [12].

The next step is to generalize this approach to an array of \(N_c\) spin chains with the same coupling between neighboring chains, forming an anisotropic triangular lattice. From the effective field theory perspective, we have to write down all the possible local interchain interactions allowed by symmetry. Here it is important to analyze how the local operators of the SU(2)\(_1\) Wess-Zumino-Novikov-Witten model transform under the various symmetry operations. Particularly important are the roles of time reversal \(\mathscr {T}\) and the reflection \(\mathscr {P}\) that acts as site parity for chains labeled by odd values of l and as link parity for chains with even values of l. While both \(\mathscr {P}\) and \(\mathscr {T}\) are broken by the three-spin interaction, the Hamiltonian and the chiral spin liquid ground state we are looking for preserve the product \(\mathscr {PT}\). The symmetries of the lattice model are enough to rule out relevant operators in the effective field theory for two chains, but not for \(N_c>2\). In fact, if we allow for coupling between next-nearest-neighbor chains, the effective Hamiltonian for the two-dimensional array contains two relevant operators which involve the staggered magnetization and the dimerization fields:

$$\begin{aligned} \delta H_\mathrm{{rel}}=v\varLambda \sum _l \int \mathrm{{d}}x \left( g_n \mathbf {n}_l \cdot \mathbf {n}_{l+2}+ g_\varepsilon \varepsilon _l\varepsilon _{l+2}\right) , \end{aligned}$$
(13.14)

where \(\varLambda \) is an ultraviolet cutoff with units of momentum and \(g_n\) and \(g_\varepsilon \) are dimensionless coupling constants. The \(g_n\) interaction favors a transition to a collinear antiferromagnetic phase in which the \(\mathbf{n}_l(x)\) fields are pinned, while \(g_\varepsilon \) favors a dimerized or valence bond crystal phase where \(\varepsilon _l(x)\) acquires a nonzero expectation value [33]. Note, however, that these interactions couple next-nearest-neighbor chains. If we start from a lattice model that contains only weak couplings \(J'\) and \(J_\chi \) between nearest-neighbor chains, the couplings \(g_n\) and \(g_\varepsilon \) can only be generated at second order in \(J'\) or \(J_\chi \), or even be pushed to higher order if we consider other lattices than the triangular one [12]. As a result, even if the marginal current-current interactions (13.13) are less relevant than the interactions in (13.14), either \(g_+\) or \(g_-\) can reach strong coupling before the other perturbations depending on the initial conditions of the renormalization group flow. When this happens, the low-energy physics is governed by the interaction that gaps out pairs of chiral modes in different chains, leaving gapless modes on the edge of the two-dimensional array. There is no magnetic order at such fixed point since the spin operators have zero expectation value. The picture is analogous to Fig. 13.1b if we replace the wires by Heisenberg chains and, instead of a chiral fermion, the edge state correspond to a chiral SU(2)\(_1\) Wess-Zumino-Novikov-Witten model. This is precisely the edge state of the Kalmeyer–Laughlin chiral spin liquid [16].

We can use the coupled-chain construction to verify other properties of the Kalmeyer–Laughlin chiral spin liquid. For instance, the fractional spin of the bulk quasiparticles follow from a semiclassical analysis of the dominant sine-Gordon potential in the strong coupling limit. Bosonizing the transverse part of the current-current interaction (13.13) generalized for N chains, we find

$$\begin{aligned} \delta H_{RL}\sim g_+\sum _l \int \mathrm{{d}}x\,\cos [\sqrt{4 \pi }(\varphi _{l,L} -\varphi _{ l+1,R} )]. \end{aligned}$$
(13.15)

In the gapped phase, the bosonic fields are pinned to the minima of the potential, given by \(\sqrt{4 \pi }(\varphi _{l,L} -\varphi _{l+1,R} ) = 2 \pi n + \pi , n \in \mathbb {N}\). A quasiparticle localized in the bulk corresponds to an excitation in which the value of the fields jumps by \(\pm 2\pi \) over some finite region in space. The change in the total spin associated with this kink is

$$\begin{aligned} \varDelta S^z= & {} \sum _l \int \mathrm{{d}}x\, (J^z_{l,L}+J^z_{l,R})\nonumber \\= & {} \frac{1}{\sqrt{4 \pi }} \sum _l \int \mathrm{{d}}x\, \partial _x (\varphi _{l,L} - \varphi _{l+1,R} )\nonumber \\= & {} \pm \frac{1}{2}, \end{aligned}$$
(13.16)

as expected for spinons. Similarly, we can demonstrate the spinon’s anyonic statistics by constructing operators that transport quasiparticles around one another. We can also consider the operators that transport quasiparticles around the entire system in the noncontractible directions of a torus (on a system with periodic boundary conditions), given by [12]

$$\begin{aligned} U_x= & {} e^{i \sqrt{ \pi } \int dx \partial _x \varphi _{l_0,L}(x) },\qquad U_y=\prod _l e^{i\sqrt{\pi }[\varphi _{l,L}(x_0)-\varphi _{l,R}(x_0)]}, \end{aligned}$$
(13.17)

where \(l_0\) labels an arbitrary fixed chain and \(x_0\) is an arbitrary point along the chains. It is easy to verify that these operators obey the algebra \(U_xU_y=e^{i2\theta }U_yU_x\) with \(\theta =\pi /2\), which can be identified with the statistical phase of semions [30].

The coupled-chain construction has been generalized to obtain non-Abelian chiral spin liquids [21, 23] and even a time-reversal-invariant \(\mathbb Z_2\) spin liquid [28].

13.4 Coupling Crossed Chains with Staggered Chirality: Gapless Chiral Spin Liquid

The coupled-chain construction described in the previous section leads to gapped chiral spin liquids, where gapless chiral modes are confined to the edges of an array with open boundary conditions. We will now discuss an alternative construction of a gapless chiral spin liquid [8], which can be viewed as sliding Luttinger liquid phase [25] with gapless chiral modes in the bulk. This construction is inspired by the proposal of a gapless chiral spin in kapellasite, a material described by an extended Heisenberg model on the kagome lattice [8].

Fig. 13.3
figure 3

Crossed spin chains that serve as the starting point for the construction of a gapless chiral spin liquid. There are three sets of parallel chains labeled by \(q=1,2,3\) (colored in blue, green, and red, respectively). Pairs of chains are coupled at their crossing by three-spin interactions at the triangles where two sites belong to one chain and the third site to the other chain

Full size image

As our starting point, we consider three sets of decoupled parallel chains as shown in Fig. 13.3. Each set is labeled by an index \(q=1,2,3\), such that a chain in set \(q\pm 1\) forms an angle of \(\pm 2\pi /3\) measured from a chain in set q. It is convenient to use a coordinate system where, for fixed q, the different parallel chains are distinguished by an index \(l\in \mathbb Z\) that increases in the direction set by \(q+1\) chains [11]. The spin operator at site j of the lth chain along the q direction is denoted by \(\mathbf{S}_{q}(j,l)\). In the low-energy limit, the effective Hamiltonian for decoupled chains is given by the sum of (13.10) for each chain, with chiral currents denoted as \(\mathbf{J}_{q\nu }(x,l)\).

We can then couple pairs of spin chains with local interactions at their crossings. Most natural is a Heisenberg exchange coupling between spins on sites closest to the crossing point. In the geometry of Fig. 13.3, this corresponds to nearest-neighbor exchange \(J_1\) on the underlying kagome lattice. For comparison, the dominant exchange coupling J along the chain directions lies on the diagonals of the hexagons of this kagome lattice [8]. In order to stabilize a chiral spin liquid phase, we also add to the model the three-spin interaction given by

$$\begin{aligned} \delta H_\chi= & {} J_\chi \sum _{q, j,l} [{\mathbf{S}}_q(-j-1, l) \times {\mathbf{S}}_q(-j, l)] \cdot [{\mathbf{S}}_{q+1}(j+l,j) + {\mathbf{S}}_{q+1}(j+l-1,j)\nonumber \\&\qquad +{\mathbf{S}}_{q+2}(-l-1,-j-l) + {\mathbf{S}}_{q+2}(-l,-j-l) ]\,. \end{aligned}$$
(13.18)

This interaction is defined on triangles where two spins belong to the same chain, labeled by q, l, whereas the third spin belongs to another chain that crosses the link between the first two sites; see Fig. 13.3. The sign the coupling for each triangle is chosen so as to preserve a C\(_3\) rotational symmetry as well as a reflection symmetry with respect to chain directions. This reflection symmetry is such that the chirality is staggered between two triangles that share two sites on the same chain. This symmetry, absent in the Kalmeyer–Laughlin state, plays an important role in the projective symmetry group classification of chiral spin liquids on the triangular and kagome lattices [7].

When taking the continuum limit in the interchain couplings, it becomes important to pay special attention to the transverse coordinate l in the spin operators \(\mathbf{S}_{q}(j,l)\). First, chains with even or odd values of l transform differently, either as site parity or link parity, under reflections by the planes perpendicular to the chain directions (which is not a symmetry of the model with finite \(J_\chi \), but can be combined with time reversal to yield an actual symmetry). Thus, we must include in the mode expansion of the low-energy fields both a uniform and a staggered component for the dependence on the transverse coordinate l. Second, we must take into account that, over a finite length \(\varDelta x\) much larger than the lattice spacing, each spin chain crosses a number of chains proportional to \(\varDelta x\). For this reason, the continuum limit in the longitudinal direction also entails a coarse-graining of the chain index in the transverse direction. The one-dimensionality of the system in the weak coupling regime is preserved by imposing the usual power-law decay of correlation functions along the chain direction, but short-range correlations in the transverse direction with a length scale set by the ultraviolet cutoff of the theory.

Within this field theory approach, we can analyze the effects of the perturbations allowed by symmetry. The leading perturbations to the decoupled-chain fixed point are relevant operators that involve the staggered magnetization and the dimerization fields:

$$\begin{aligned} \delta H_{rel}= & {} v\varLambda \sum _q\int \mathrm{{d}}x \mathrm{{d}}y\, \left[ \kappa _n \mathbf{n}_{qo}(-x,y) \cdot \mathbf{n}_{q+1,e}(x+y,x)\right. \nonumber \\&\left. +\kappa _\varepsilon \varepsilon _{qo}(-x,y)\, \varepsilon _{q+1,e}(x+y,x)\right] , \end{aligned}$$
(13.19)

where \(\kappa _n\) and \(\kappa _\varepsilon \) are dimensionless coupling constants. The lower indices e, o refer to the uniform and staggered parts of the fields with respect to the transverse coordinate, respectively, which are even or odd under translation by one chain spacing in the transverse direction. As in the coupled-chain construction of the Kalmeyer–Laughlin state, the coupling constants of the relevant operators are generated at second order in the bare couplings of the original lattice model. When \(\kappa _n\) reaches strong coupling before all other perturbations, the two-dimensional system orders magnetically in one of the so-called cuboc phases [11]. When \(\kappa _\varepsilon \) prevails, it gives rise to a valence bond crystal. These are the two phases expected in the model of crossed chains weakly coupled by time-reversal-invariant exchange interactions [11]. However,the three-spin interaction in (13.18) generates in the continuum limit various marginal current-current couplings, such as

$$\begin{aligned} \delta H_{RR}={2\pi v\lambda }\sum _q\int \mathrm{{d}}x\mathrm{{d}}y\, \mathbf{J}_{qRe}(-x,y)\cdot \mathbf{J}_{q+1,Re}(x+y,x). \end{aligned}$$
(13.20)

There is a similar term that couples left-moving currents, but similarly to the case of \(g_+\) and \(g_-\) in (13.13), the asymmetry between the corresponding couplings is of first order in \(J_\chi \). As a result, an interesting regime becomes possible where the chiral interaction favors strong coupling between right-moving spin currents in all chains, while the left-moving currents remain essentially free. A renormalization group analysis [29] shows that such a regime can be reached for sufficiently large bare values of \(J_\chi \), such that \(\lambda \) in (13.20) reaches strong coupling before the relevant operators (13.19).

The simple picture for the ground state in this regime is a chiral spin liquid where each chain harbors only one chiral mode, moving either to the “right” or to the “left”, where the directions of “right” and “left” depend on the orientation of the chain and varies with q as illustrated in Fig. 13.3. Note that, due to the C\(_3\) rotational symmetry, which imposes the angles of \(\pm 2\pi /3\) between chains with different q values, there is no preferred direction for the propagation of excitations in the bulk. Despite being gapless, the corresponding Hamiltonian for this chiral spin liquid is a stable fixed point of the renormalization group. In fact, gapping out one chiral sector of the theory (say, the right-moving bosons \(\varphi _{qR}(x,y)\)) implies that all excitations involving the staggered magnetization or the dimerization are gapped, since these fields couple to both chiral sectors; cf. (13.4) and (13.5). Thus, the relevant perturbations (13.19) are ruled out from the low-energy theory and a sliding Luttinger liquid phase becomes stable.

We can calculate physical properties of the gapless chiral spin liquid using the operators in the coupled-chain construction [29]. For instance, the large-distance decay of the spin-spin correlation is dominated by the gapless chiral modes propagating along the chain directions:

$$\begin{aligned} \langle \mathbf{S}_q(j,l)\cdot \mathbf{S}_{q'}(j',l')\rangle \sim \langle \mathbf{J}_{qL}(x,y) \cdot \mathbf{J}_{q'L}(x',y')\rangle \sim - \frac{\varDelta (y-y', \alpha ^*)}{(x-x')^{2}}\, \delta _{qq'}\,, \end{aligned}$$
(13.21)

where \(\varDelta (y, \alpha ^*)\) is a non-universal function that describes short-range correlations in the transverse direction with characteristic length scale \(\alpha ^*\). The latter is set by the scale where the marginally relevant operator (13.20) reaches strong coupling and is related to the gap in the right-moving chiral sector. Note that the correlation does not oscillate as a function of the distance in the chain direction and decays with a universal exponent governed by the scaling dimension of the chiral currents in the one-dimensional theory. By contrast, correlation functions for the staggered magnetization and dimerization operators must decay exponentially.

Fig. 13.4
figure 4

Bipartition of the two-dimensional spin system. The entanglement entropy between the finite subsystem A with characteristic length L with the rest of the system B is calculated by counting the number of chiral one-dimensional modes that cross the boundary of A

Full size image

While the gapless chiral spin liquid is not topologically ordered in the same sense of the Kalmeyer–Laughlin state (namely, nontrivial ground state degeneracy on the torus), it can be described as a highly entangled phase of matter. Consider a finite subsystem A with characteristic length L contained within the two-dimensional system. The von Neumann entanglement entropy S of A with the rest of the system can be estimated by

$$\begin{aligned} S\sim N_{\text {chains}}\times S_{\text {chain}}\sim \frac{c_L}{6}L \ln L, \end{aligned}$$
(13.22)

where \(N_{\text {chains}}\) is the number of chains that cross the boundary of A and \( S_{\text {chain}}\sim \frac{c_L}{6}\ln L\) is the entanglement entropy associated with each chiral mode with chiral central charge \(c_L\). Therefore, the gapless chiral spin liquid is highly entangled in the sense that it exhibits a logarithmic violation to the area law, a behavior also observed for free fermions with a Fermi surface and strongly correlated systems whose spectrum can be mapped to a large number of one-dimensional modes [34].

It is also interesting to note that this gapless chiral spin liquid is stable against weak disorder [29]. Intuitively, due to the energy gap in one chiral sector, backscattering is suppressed and only forward scattering processes (where “forward” may mean scattering a right mover in a q chain to a right mover in a different \(q\pm 1\) direction) are allowed at low energies (Fig. 13.4).

13.5 Conclusion

Coupled-wire constructions have proven a useful tool to study topological phases of matter. The work discussed in this chapter shows that chiral spin liquids can also be approached this way. For instance, we have constructed the Kalmeyer–Laughlin chiral spin liquid using an array of parallel spin chains coupled by three-spin interactions that explicitly break time reversal and reflection symmetries. This is a gapped topological phase equivalent to a fractional quantum Hall effect of bosons at filling factor \(\nu =1/2\), and its topological properties can be verified within the coupled-chain construction without resorting to Chern–Simons gauge fields.

We have also discussed a construction of a gapless chiral spin liquid that starts from weakly coupled crossed chains. In this case, the low-energy picture that emerges corresponds to gapping out one chiral sector of each chain while the other sector remains gapless. This gapless chiral spin liquid also exhibits some exotic physical properties, such as spatially anisotropic power-law-decaying correlation functions and a logarithmic violation of the entanglement area law.

Some interesting open questions pertain to explicitly deriving a relation between the operators in the coupled-chain construction, which stem from the conformal field theory describing the one-dimensional modes, and the matter and gauge field operators in the usual parton construction of quantum spin liquids. Particularly in the case of the gapless chiral spin liquid, a possible duality between the chiral one-dimensional modes and a spinon Fermi surface state with a line Fermi surface protected by the reflection symmetry has been suggested in [29]. Another interesting route to pursue is an alternative construction of chiral spin liquids based on networks of Y junctions of spin chains tuned to a chiral boundary fixed point [9].