1 Introduction

Low-dimensional magnets have attracted the attention of the scientific community in the last years (see Diep 2005 and the references therein). Among them, edge-sharing chains of cuprates provide a natural example of frustrated lattice systems, the frustration resulting from the competition between ferromagnetic (F) nearest-neighbor (NN) and antiferromagnetic (AF) next-nearest-neighbor (NNN) interactions. In this paper, we study some of the multiple scale properties of these systems, focusing on a classical spin model at zero temperature as a first step toward the understanding of its quantum analogue (see Dmitriev and Krivnov 2011 for a discussion about the relation between classical and quantum models in chains of cuprates) as well as of its behavior for small temperature, while a general analysis of the system for finite temperature would require different techniques.

We consider a minimal energy model describing the magnetic properties of one-dimensional frustrated magnetic systems: the so-called F–AF spin chain model. On the one-dimensional torus \([0,1]\), the state of the system is described by the values of a vectorial spin variable parameterized over the points of the set \(\mathbb {Z}_{n}=\{i \in \mathbb {Z}:\ \lambda _{n} i \in [0,1]\}\) where \(\lambda _{n}\) is a small parameter \(\lambda _{n}\rightarrow 0\) as \(n\rightarrow \infty \). The energy of a given state of the system \(u:i\in \mathbb {Z}_{n}\mapsto u^{i}\in S^{1}\) is

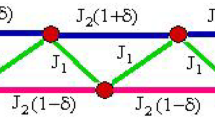
$$\begin{aligned} E_{n}(u)=-J_{1}\sum _{i\in \mathbb {Z}_{n}}\lambda _{n}(u^{i},u^{i+1})+J_{2}\sum _{i\in \mathbb {Z}_{n}}\lambda _{n}(u^{i},u^{i+2}), \end{aligned}$$
(1.1)

where \(J_{1},J_{2}>0\) are the NN and the NNN interaction parameters, respectively, and \((\cdot ,\cdot )\) denotes the scalar product between vectors in \({\mathbb {R}}^{2}\). While the first term of the energy is ferromagnetic and favors the alignment of neighboring spins, the second, being antiferromagnetic, frustrates it as it favors antipodal next-to-nearest neighboring spins. As a result, the frustration of the system depends on the relative strength of the ferromagnetic/antiferromagnetic constants. A more refined analysis shows that the frustration can be actually measured in terms of \(\alpha =J_{1}/J_{2}\). More specifically (see Proposition 3.2 and Remark 3.3), for \(\alpha \ge 4\) the ground state of the system is ferromagnetic, while for \(0<\alpha \le 4\) it is helimagnetic (see Fig. 1). The description of the ground states of the F–AF system for a choice of the parameters such that \(\alpha \simeq 4\) is the main aim of our analysis. In this case, the system is said to be close to the ferromagnet/helimagnet transition point [examples of edge-sharing cuprates in the vicinity of the ferromagnetic/helimagnetic transition point can be found in Drechsler et al. (2007), while an analysis of the thermodynamic properties of such spin chains can be found in Dmitriev and Krivnov (2011), Harada and Mikeska (1988) and Harada (1984)].

Fig. 1
figure 1

Ground states of the spin system for \(0<\alpha <4\) for clockwise and counterclockwise chirality

Full size image

In order to study F–AF chains close to the ferromagnet/helimagnet transition point, we need to perform a multiple scale analysis of the energy in (1.1). We start by first scaling the functional in (1.1) by a small parameter \(\lambda _{n}\) (\(\lambda _{n}\rightarrow 0\) as \(n\rightarrow \infty \)). Further dividing by \(J_{2}\) (so that the frustration parameter is now \(\alpha =J_{1}/J_{2}\)) and \(\mathbb {Z}_{n}=\{i \in \mathbb {Z}:\ \lambda _{n} i \in [0,1]\}\), we define \(E_{n}:\{u:\mathbb {Z}_{n}\mapsto u^{i}\in S^{1}\}\rightarrow {\mathbb {R}}\) as

$$\begin{aligned} E_{n}(u)=-\alpha \sum _{i\in \mathbb {Z}_{n}}\lambda _{n}(u^{i},u^{i+1})+\sum _{i\in \mathbb {Z}_{n}}\lambda _{n}(u^{i},u^{i+2}). \end{aligned}$$
(1.2)

It turns out that the ground states of \(E_{n}\) can be completely characterized (see Proposition 3.2 and Remark 3.3). Neighboring spins are aligned if \(\alpha \ge 4\) (ferromagnetic order), while they form a constant angle \(\varphi =\pm \arccos (\alpha /4)\) if \(0<\alpha <4\) (helimagnetic order). In this last case, the two possible choices for \(\varphi \) correspond to either clockwise or counterclockwise spin rotations, or in other words to a positive or a negative chirality (see Fig. 1). Such a degeneracy is known in literature as chirality symmetry. The energy necessary to break this symmetry is, to the best of our knowledge, an open problem. In this paper, we provide a solution to this problem in the case of a system close to the ferromagnet/helimagnet transition point, that is, to say that we are able to find the correct scaling to detect the symmetry breaking and to compute the asymptotic behavior of the scaled energy describing this phenomenon as \(\alpha \) is close to \(4\). Before coming to the description of our analysis, it is worth noticing that if instead of a vector spin parameter with continuous symmetry we consider a scalar one, i.e., \(u\in \{\pm 1\}\), then the helicity symmetry translates into the periodicity of the ground states. In this case, in Braides and Cicalese (forthcoming) it has been proved that the asymptotic analysis of these systems can be performed without any restriction on the values of \(\alpha \).

To set up our problem, we let the ferromagnetic interaction parameter \(\alpha \) depend on \(n\) and be close to \(4\) from below, that is, in (1.2) we substitute \(\alpha \) by \(\alpha _{n}=4(1-\delta _{n})\) for some vanishing sequence \(\delta _{n}>0\). For such energies in Theorem 2.1, we prove that, as a consequence of an abstract result proven in Alicandro et al. (2008), their \(\Gamma \)-limit (with respect to the weak-\(\star \) convergence in \(L^{\infty }\)) as \(n\rightarrow \infty \) is a constant functional whose value can be approached by weakly vanishing sequences \(u_{n}\) that may mix on a mesoscopic scale configurations having opposite chirality. Such a poor description suggests that, in order to get further information on the ground states of the system, we need to consider higher order \(\Gamma \)-limits (see Anzellotti and Baldo 1993; Anzellotti et al. 1994; Braides 2002 and Braides and Truskinovsky 2008 for more details as well as for the general theory of development by \(\Gamma \)-convergence). Note that the choice of the right energy scaling which may capture the phenomena we are interested in is not straightforward. On one hand, we look for a limit energy accounting for \(0\)-dimensional (surface-type) discontinuities of some appropriate order parameter related to the chirality. On the other hand, the continuous symmetry of the order parameter \(u\in S^{1}\) adds a new difficulty: It allows for very slow variations in the angle between neighboring spins. As a consequence, the correct scaling is not the \(\lambda _{n}\) scaling (‘surface’-type scaling) as it is in the case of \(u\in \{\pm 1\}\) as shown in Alicandro et al. (2006) (see also Braides and Cicalese forthcoming). Similar problems regarding the continuos symmetry of the order parameter arise already in Cicalese et al. (2009) in the context of strain-alignment-coupled systems (also analyzed in Cesana and DeSimone (2009) and Cesana and DeSimone (2011)) and in Alicandro and Cicalese (2009) for NN systems in the context of XY spin models (see also Alicandro et al. 2011, 2013; Alicandro and Ponsiglione 2014 and Braides et al. 2013 for related Ginzburg–Landau-type models). In (Alicandro and Cicalese (2009), Example 1), it is explicitly proved that the system does not undergo any phase separation that may be detected by a surface scaling. Such an example can be straightforwardly exported in the context of frustrated spin chains, and as a consequence, we are led to renormalize the energy of the system and study the asymptotic behavior of a new functional \(H_{n}\) defined as

$$\begin{aligned} H_{n}(u)=\frac{E_{n}(u)-\min E_{n}}{\mu _{n}\lambda _{n}} \end{aligned}$$
(1.3)

for some \(\mu _{n}\rightarrow 0\) to be found. In terms of \(H_{n}\), finding the energy the system spends in a transition between two states with different chirality translates into the following problem: depending on the scale \(\delta _{n}\)

  1. (i)

    find a scaling \(\mu _{n}\) and an order parameter \(z_{n}\) such that if \(\sup _{n}H_{n}(u_{n})\le C\), then as \(n\rightarrow \infty \), \(z_{n}\) converges to some \(z\) describing a system whose chirality may have at most a finite number of discontinuities,

  2. (ii)

    for such a choice of \(\mu _{n}\), compute the \(\Gamma \)-limit of \(H_{n}\) (with respect to the convergence \(z_n\rightarrow z\) in the previous step) and interpret the limit functional as the energy the system spends on the scale \(\lambda _{n}\mu _{n}\) for a finite number of chirality transitions.

The main result of this paper is contained in Theorem 4.2 that states that the right scale to consider in order to keep track of energy concentration is \(\lambda _{n}\delta _{n}^{3/2}\) (corresponding to the choice \(\mu _{n}=\delta _{n}^{3/2}\)). We prove that, within this scaling, several regimes are possible. Roughly speaking, for \(n\) large enough, we show that the spin system has a chirality transition on a scale of order \(\lambda _{n}/\sqrt{\delta _{n}}\). As a result, depending on the value of \(\lim _{n}\lambda _{n}/\sqrt{\delta _{n}}:=l\in [0,+\infty ]\) different scenarios are possible (see Fig. 2 for a schematic picture of the transition). If \(l=+\infty \), chirality transitions are forbidden (equivalently we find that the energy for a transition is infinite). If \(l>0\), the spin system may have diffuse and regular macroscopic (on an order one scale) chirality transitions whose limit energy is finite on \(W^{1,2}(I)\) (provided some boundary conditions are taken into account). When \(l=0\), transitions on a mesoscopic scale are allowed. In this case, the continuum limit energy is finite on \(BV(I)\) and counts the number of jumps of the chirality of the system.

Fig. 2
figure 2

Optimal configuration of the spins of the F–AF chain in a chirality transition (above). The transition in terms of a scalar parameter related to the chirality of the system (see section for more details)

Full size image

The heuristics to the estimates contained in the proof of Theorem 4.2, leading to the correct scaling factor, are shown in the following formal computation. After explicitly calculating \(\min E_{n}\), the functional \(H_{n}\) in (1.4) takes the form (see (4.2))

$$\begin{aligned} H_{n}(u)=\frac{1}{2}\sum _{i}\lambda _{n}\left| \lambda _{n}^{2}\left( \frac{u^{i+2}-2u^{i+1}+u^{i}}{\lambda ^{2}_{n}}\right) +2\delta _{n}u^{i+1}\right| ^{2} \end{aligned}$$

For a small enough \(\lambda _{n}\), we may use the approximation \((u^{i+2}-2u^{i+1}+u^{i})/\lambda _{n}^{2}\simeq u''(\lambda _{n}(i+1))\) so that expanding the squares and substituting sums with integrals we get

$$\begin{aligned} H_{n}(u)=\frac{1}{2}\int \left( \lambda _{n}^{4}|u''(x)|^{2}+4\delta _{n}^{2}+4\delta _{n}\lambda _{n}^{2}u(x)\cdot u''(x)\right) \, {\mathrm{d}}x \end{aligned}$$
(1.4)

(in passing we note that the case \(J_{1}=4J_{2}\), that is, \(\delta _{n}=0\), would lead to a straightforward scaling and to a simple continuum limit). Further integrating by parts in (1.4), we can write

$$\begin{aligned} H_{n}(u)=\frac{1}{2}\int \left( \lambda _{n}^{4}|u''(x)|^{2}+4\delta _{n}^{2}-4\delta _{n}\lambda _{n}^{2}|u'(x)|^{2}\right) \, {\mathrm{d}}x. \end{aligned}$$

Taking \(u=(\cos (\varphi ),\sin (\varphi ))\) and introducing the angular velocity \(\theta =\varphi '\), we have \(|u'|^{2}=\theta ^{2}\) and \(|u''|^{2}=\theta ^{4}+(\theta ')^{2}\) so that the functional \(H_{n}\) can be rewritten in terms of \(\theta \) as

$$\begin{aligned} H_{n}(\theta )&= \frac{1}{2}\displaystyle \int \left( \lambda _{n}^{4}\theta '(x)^{2}+\lambda _{n}^{4}\theta (x)^{4}+4\delta _{n}^{2}-4\delta _{n}\lambda _{n}^{2}\theta (x)^{2}\right) \, {\mathrm{d}}x\\&= \frac{1}{2}\displaystyle \int \left( \lambda _{n}^{4}\theta '(x)^{2}+\left( \lambda _{n}^{2}\theta (x)^{2}-2\delta _{n}\right) ^{2}\right) \, {\mathrm{d}}x \end{aligned}$$

In terms of the scaled angular velocity \(z=\frac{\lambda _{n}}{\sqrt{2\delta _{n}}}\theta \), we have

$$\begin{aligned} H_{n}(z)=\displaystyle \int \left( \lambda _{n}^{2}\delta _{n}z'(x)^{2}+2\delta _{n}^{2}\left( z^{2}-1 \right) ^{2}\right) \, {\mathrm{d}}x \end{aligned}$$

The scaling \(\sqrt{2}\lambda _{n}\delta _{n}^{3/2}\) turns the above functional into a Modica-Mortola-type one with parameter \(\varepsilon _{n}:=\lambda _{n}/\sqrt{2\delta _{n}}\), namely

$$\begin{aligned} \frac{H_{n}(z)}{\sqrt{2}\lambda _{n}\delta _{n}^{3/2}}=\displaystyle \int \left( \varepsilon _{n}z'(x)^{2}+\frac{1}{\varepsilon _{n}}\left( z^{2}-1 \right) ^{2}\right) \, {\mathrm{d}}x, \end{aligned}$$

modeling, for \(\varepsilon _{n}\ll 1\), phase transitions in the scaled angular velocity which correspond to chirality transitions.

We think it is worth noticing that, to the best of our knowledge, this paper shows for the first time the presence of multiple scale regimes in a chirality transition. It is our opinion that this phenomenon is quite general and suggests that the analysis of frustrated discrete systems should take advantage from a rigorous variational method any time the parameters describing frustration and scaling may compete. As a final technical remark, we would like to point out that, although our analysis is presently confined to the one-dimensional case, it constitutes the building block of a similar analysis of more general \(n\)-dimensional systems as the celebrated frustrated \(XY\)-model proposed by Villain (1977). Indeed, in such a case the \(\Gamma \)-limit of the energy can be obtained by estimating the energy of proper one-dimensional subsets. The detailed analysis of these and other issues is deferred to a forthcoming paper (Cicalese et al. in preparation).

2 Notation and Preliminaries

Denoting by \(I=(0,1)\) and by \(\lambda _{n}\) a vanishing sequence of positive numbers, we define \(\mathbb {Z}_n(I)\) as the set of those points \(i \in \mathbb {Z}\) such that \(\lambda _{n} i \in {\overline{I}}\). Given \(x\in {\mathbb {R}}\), we denote by \([x]\) the integer part of \(x\). The symbol \(S^{1}\) stands as usual for the unit sphere of \({\mathbb {R}}^2\). Given a vector \(v\in {\mathbb {R}}^{2}\) of components \(v_{1}\) and \(v_{2}\) with respect to the canonical basis, we will use the notation \(v=(v_{1}|v_{2})\). Given two vectors \(a,b\in {\mathbb {R}}^{2}\), we will denote by \((a,b)\) their scalar product. We will denote by \({{\mathcal {U}}}_{n}(I)\) the space of functions \(u:i\in \mathbb {Z}_{n}(I)\mapsto u^{i}\in S^{1}\) and by \(\overline{{\mathcal U}}_{n}(I)\) the subspace of those \(u\) such that

$$\begin{aligned} (u^{1},u^{0})=(u^{[1/\lambda _{n}]},u^{[1/\lambda _{n}]-1}). \end{aligned}$$
(2.1)

Given \(K\in {\mathbb {R}}^{m}\), we denote by \(co(K)\) the convex hull of \(K\). We set \(Q_{h}=\left( 0,h\right) \). Given \(v=(v_{1},v_{2}),w=(w_{1},w_{2})\in S^{1}\), we define the function \(\chi [v,w]:S^{1}\times S^{1}\rightarrow {\pm 1}\) as

$$\begin{aligned} \chi [v,w]=\mathrm{sign}(v_{1}w_{2}-v_{2}w_{1}), \end{aligned}$$

with the convention that \(\mathrm{sign}(0)=-1\).

We recall some preliminary results concerning the general theory of spin-type discrete systems in the bulk scaling. The following theorem has been proved in Alicandro et al. (2008). We state it here in a version which best fits our setting. Let \(K\subset {\mathbb {R}}^{m}\) be a bounded set. For all \(\xi \in \mathbb {Z}\), let \(f^\xi :{\mathbb {R}}^{2m}\rightarrow {\mathbb {R}}\) be a function such that

  1. (H1)

    \(f^\xi (u,v)=f^{-\xi }(v,u)\),

  2. (H2)

    for all \(\xi \), \(\displaystyle {f^\xi (u,v)=+\infty }\) if \((u,v)\not \in K^2\),

  3. (H3)

    for all \(\xi \), there exists \(C^\xi \ge 0\) such that \(\displaystyle {|f^\xi (u,v)|\le C^\xi }\) for all \((u,v)\in K^2\), and \(\sum _\xi C^\xi <\infty \).

Let us define the set of functions

$$\begin{aligned} D_{n}(I,{\mathbb {R}}^m)= \{u:{\mathbb {R}}\rightarrow {\mathbb {R}}^m\,:\,u \ \mathrm{constant \ on }\ \lambda _{n}(i+[0,1))\ \mathrm{for \ any }\ i\in \mathbb {Z}_n(I)\} \end{aligned}$$

and the family of functionals \(F_n:L^\infty (I,{\mathbb {R}}^m)\rightarrow (-\infty ,+\infty ]\)

$$\begin{aligned} F_n(u)={\left\{ \begin{array}{ll}\displaystyle \sum \limits _{\xi \in \mathbb {Z}}\sum \limits _{ i \in R_n^\xi (I)}\lambda _{n}f^\xi (u^{i},u^{i+\xi }) &{} \text {if}\,u\in D_{n}(I,{\mathbb {R}}^m)\\ +\infty &{} \text {otherwise},\end{array}\right. } \end{aligned}$$
(2.2)

where \(R_{n}^\xi (I):=\{i\in \mathbb {Z}_n(I):\ i+\xi \in \mathbb {Z}_n(I)\}\). Given \(v:\mathbb {Z}\rightarrow {\mathbb {R}}^{m}\) and \(A\subset {\mathbb {R}}\) open and bounded, we define the discrete average of \(v\) in \(A\) as

$$\begin{aligned} \langle v \rangle _{1,A}=\frac{1}{\#(\mathbb {Z}\cap A)}\displaystyle {\sum _{i \in {\mathbb {Z}}\cap A}v^{i}}. \end{aligned}$$

Theorem 2.1

(see Alicandro et al. 2008) Let \(\{f^\xi \}_{\xi }\) satisfy hypotheses (H1)–(H3). Then \(F_n\) \(\Gamma (w*-L^{\infty })\)-converges to

$$\begin{aligned} F(u)=\int _{I} f_\mathrm{hom}(u(x))\mathrm{d}x \end{aligned}$$

for all \(u\in L^{\infty }(I,co(K))\), where \(f_\mathrm{hom}\) is given by the following homogenization formula

(2.3)

where \(R_{1}^\xi (I):=\{i\in \mathbb {Z}\cap I:\ i+\xi \in \mathbb {Z}\cap I\}\).

We now state (with minor variations) a result proved in Braides and Yip (2012) regarding the discrete approximations of Modica-Mortola type energies. We say that a function \(W:{\mathbb {R}}\rightarrow [0,+\infty )\) is a double-well potential if it is locally Lipschitz and satisfies the following properties:

  1. (1)

    \(W(z)=0\) if and only if \(z\in \{\pm 1\}\),

  2. (2)

    \(\lim _{{z\rightarrow \pm \infty }}W(z)=+\infty \),

  3. (3)

    there exists \(C_{0}>0\) such that \(\{z:\, W(z)\le C_{0}\}=I_{1}\cup I_{2}\) with \(I_{1},I_{2}\) intervals on which \(W\) is convex.

Let \(\epsilon _{n},\eta _{n}\) be two sequences of positive numbers such that \(\lim _{n}\epsilon _{n}=0\), \(\lim _{n}\epsilon _{n}/\eta _{n}=1\) and \(\lim _{n}\lambda _{n}/\epsilon _{n}=0\) and let \(G_{n}:L^{1}(I)\rightarrow [0,+\infty ]\) be defined as

$$\begin{aligned} G_{n}(u)={\left\{ \begin{array}{ll}\displaystyle \epsilon _{n}\sum _{i}\lambda _{n}\left( \frac{u^{i+1}-u^{i}}{\lambda _{n}}\right) ^{2}+\frac{1}{\eta _{n}}\sum _{i}\lambda _{n}W(u^{i}) &{} \text {if}\, u\in D_{n}(I,{\mathbb {R}})\\ +\infty &{} \text {otherwise},\end{array}\right. } \end{aligned}$$
(2.4)

with \(W\) a double-well potential. The following \(\Gamma \)-convergence result holds.

Theorem 2.2

Let \(G_{n}:L^{1}(I)\rightarrow [0,+\infty ]\) be as in (2.4), then, with respect to the \(L^{1}(I)\) convergence,

$$\begin{aligned} \Gamma \hbox {-}\lim _{n}G_{n}(u)={\left\{ \begin{array}{ll} C_{W}\#(S(u)\cap I) &{} \text {if}\,u\in BV(I,\{\pm 1\})\\ +\infty &{} \text {otherwise in}\,L^{1}(I),\end{array}\right. } \end{aligned}$$
(2.5)

where \(C_{W}:=2\int _{-1}^{+1}\sqrt{W(s)}\ \mathrm{d}s\).

Proof

The proof follows by Theorem \(2.1\) in Braides and Yip (2012) once we observe that for all \(u_{n}\) such that \(\sup _{n}G_{n}(u_{n})\le C\) we have

$$\begin{aligned} \left| \frac{1}{\eta _{n}}-\frac{1}{\epsilon _{n}}\right| \sum _{i}\lambda _{n}W(u^{i})\le C\ \frac{|\eta _{n}-\epsilon _{n}|}{\epsilon _{n}}, \end{aligned}$$

so that

$$\begin{aligned} G_{n}(u_{n})=\displaystyle \epsilon _{n}\sum _{i}\lambda _{n}\left( \frac{u^{i+1}-u^{i}}{\lambda _{n}}\right) ^{2}+\frac{1}{\epsilon _{n}}\sum _{i}\lambda _{n}W(u^{i})+o(1). \end{aligned}$$

\(\square \)

Remark 2.3

In the explicit case, \(W(s)=(1-s^{2})^{2}\) the constant \(c_{W}=\frac{8}{3}\).

3 The Energy Model: The Bulk Scaling

In this section, we introduce the F–AF model of a frustrated ferromagnetic spin chain and prove a first result concerning the \(\Gamma \)-limit of its bulk scaling.

Let \(I=(0,1)\) and let us consider a pairwise-interacting discrete system on the lattice \(\mathbb {Z}_n(I)\) whose state variable is denoted by \(u:\mathbb {Z}_n(I)\rightarrow S^{1}\). Such a system is driven by an energy \(E_n:{\mathcal U}_{n}(I)\rightarrow (-\infty ,+\infty )\) given by

$$\begin{aligned} E_n(u)=-J_{1}\sum _{i=0}^{\left[ 1/\lambda _{n}\right] -2}\lambda _{n}(u^{i},u^{i+1})+J_{2}\sum _{i=0}^{{\left[ 1/\lambda _{n}\right] -2}}\lambda _{n}(u^{i},u^{i+2}), \end{aligned}$$

for some nonnegative constants \(J_{1},J_{2}\). In what follows, without loss of generality, with a slight abuse of notation we refer to \(E_{n}\) as to \(E_{n}/J_{2}\). As a result, setting \(\alpha =J_{1}/J_{2}\), we consider the family of energies

$$\begin{aligned} E_n(u)=-\alpha \sum _{i=0}^{\left[ 1/\lambda _{n}\right] -2}\lambda _{n}(u^{i},u^{i+1})+\sum _{i=0}^{{\left[ 1/\lambda _{n}\right] -2}}\lambda _{n}(u^{i},u^{i+2}). \end{aligned}$$
(3.1)

Moreover, we will consider the case \(\alpha \in (0,4]\); the case \(\alpha >4\) will be shortly discussed in Remark 3.3.

Since we are not interested to the possible formation of boundary layers, we fix periodic boundary conditions on the system as in (2.1), that is, we take \(u\in \overline{{\mathcal U}}_{n}(I)\).

Remark 3.1

The periodic boundary conditions in (2.1) are an alternative to the computation of the \(\Gamma \)-limit of \(E_{n}\) with respect to a local convergence.

As usual in the analysis of discrete systems, we may embed the family of functionals on a common functional space, extending \(E_{n}\) to some Lebesgue space. To this end, we associate to any \(u\in \overline{{\mathcal U}}_{n}(I)\) a piecewise-constant interpolation belonging to the class

$$\begin{aligned} C_n(I,S^{1}):=\{u\in \overline{{\mathcal U}}_{n}(I): u(x)=u(\lambda _{n}i)\,\,\hbox { if } x \in \lambda _{n}(i+[0,1)),\,i \in \mathbb {Z}_n(I)\}. \end{aligned}$$
(3.2)

As a consequence, we may see the family of energies \(E_n\) as defined on a subset of \(L^\infty (I,S^{1})\) and consider their extension on \(L^\infty (I,S^{1})\). With an abuse of notation, we do not introduce a new symbol for these functionals and set \(E_n:L^\infty (I,S^{1})\rightarrow (-\infty ,+\infty ]\) as

(3.3)

We now define the functional \(H_{n}:L^\infty (I,S^{1})\rightarrow (-\infty ,+\infty ]\) as

(3.4)

Since \(|u^{i}|=1\) for all \(i\in \mathbb {Z}_{n}\), thanks to (2.1), the energy in (3.3) can be rewritten, in terms of \(H_{n}\) as

$$\begin{aligned} E_n(u)=H_{n}(u)-\left( 1+\frac{\alpha ^{2}}{8}\right) (1-c_{n}\lambda _{n}), \end{aligned}$$
(3.5)

for \(c_{n}=\frac{1}{\lambda _{n}}-\left[ \frac{1}{\lambda _{n}}\right] +1\in [1,2)\), so that

$$\begin{aligned} \sum _{i=0}^{{[1/\lambda _{n}]-2}}\lambda _{n}=(1-c_{n}\lambda _{n}). \end{aligned}$$
(3.6)

Equality (3.5) suggests that in order to study the asymptotic properties of \(E_{n}\) we can equivalently study the nonnegative functional \(H_{n}\).

3.1 Ground States of \(H_{n}\)

In this section, we characterize the global minimizers of \(E_{n}\) and we give upper and lower bounds on its \(\Gamma \)-limit as \(n\rightarrow \infty \) for different values of \(\alpha \). As a corollary we show that in the case \(\alpha =4\), the continuum limit is indeed trivial.

Proposition 3.2

Let \(E_{n}:L^\infty (I,S^{1})\rightarrow (-\infty ,+\infty ]\) be the functional in (3.1) and \(0\le J_1 \le 4\). Then

$$\begin{aligned} \min _{u\in L^\infty (I,S^{1})} E_{n}(u)=-\left( 1+\frac{\alpha ^{2}}{8}\right) (1-c_{n}\lambda _{n}). \end{aligned}$$
(3.7)

Furthermore, a minimizer \(u_n\) of \(E_n\) over \(L^\infty (I,S^{1})\) satisfies

$$\begin{aligned} (u_n^{i},u_n^{i+1})=\frac{\alpha }{4}\quad \hbox {and}\quad (u_n^{i},u_n^{i+2})=\frac{\alpha ^{2}}{8}-1 \end{aligned}$$
(3.8)

for all \(i=0,\ldots , \left[ 1/\lambda _{n}\right] -2\).

Proof

Let \(H_n\) be defined as in (3.4). Since \(H_n \ge 0\), by (3.5) we deduce \(E_n(u)\ge -\left( 1+\frac{\alpha ^{2}}{8}\right) (1-c_{n}\lambda _{n})\) for all \(u \in L^\infty (I,S^{1})\). Now, fix \(\varphi \in [-\frac{\pi }{2}, \frac{\pi }{2}]\) so that \(\cos (\varphi )=\frac{\alpha }{4}\). Then, we construct \(u_n \in C_n(I,S^{1})\) by setting, for all \(i=0,\ldots , \left[ 1/\lambda _{n}\right] \),

$$\begin{aligned} u^i_n=(\cos (\varphi i)|\sin (\varphi i)). \end{aligned}$$

By the trigonometric identities, we get

$$\begin{aligned} u^i_n+u^{i+2}_n= 2 \cos (\varphi ) u^{i+1}_n= \frac{\alpha }{2}u^{i+1}_n \end{aligned}$$

for all \(i=0,\ldots , \left[ 1/\lambda _{n}\right] -2\). This implies \(H_n(u_n)=0\) and thus \(E_n(u_n)=-\left( 1+\frac{\alpha ^{2}}{8}\right) (1-c_{n}\lambda _{n})\) and (3.7) follows.

Consider now a minimizer \(u_n\) of \(E_n\) over \(L^\infty (I,S^{1})\). By definition of \(E_{n}\), we have that \(u_{n}\in C_n(I,S^{1})\). By (3.7), it must be \(H_n(u_n)=0\), which in turn implies

$$\begin{aligned} u^{i+1}_n=\frac{2}{\alpha }(u^{i}_n+u^{i+2}_n) \end{aligned}$$
(3.9)

for all \(i=0,\ldots , \left[ 1/\lambda _{n}\right] -2\). Since \(u_n\) takes values on the unit sphere, by taking the modulus squared in (3.9) we further get that

$$\begin{aligned} 1=\frac{4}{\alpha ^{2}}|u^{i}_n+u^{i+2}_n|^{2}=\frac{8}{\alpha ^{2}}(1+ (u^{i}_n,u^{i+2}_n)), \end{aligned}$$

so that

$$\begin{aligned} (u^{i}_n,u^{i+2}_n)=\frac{\alpha ^{2}}{8}-1. \end{aligned}$$

By this and (3.9), we also get

$$\begin{aligned} (u^{i}_n,u^{i+1}_n)=\frac{2}{\alpha }(u^{i}_n,u^{i}_n+u^{i+2}_n)=\frac{2}{\alpha }(1+(u^{i}_n,u^{i+2}_n))=\frac{\alpha }{4}, \end{aligned}$$

as required.\(\square \)

Remark 3.3

Note that the case \(\alpha >4\) is trivial. In fact, the ground states are all ferromagnetic, that is, \(u_{n}^{i}=\bar{u}\) for all \(i=0,\ldots ,[1/\lambda _{n}]\) and for some \(\bar{u}\in S^{1}\). Indeed in this case, set \(E_{n}^{(\alpha =4)}\) the energy in (3.3) for \(\alpha =4\), we have that, for all \(u\in \overline{{\mathcal U}}_{n}(I)\)

$$\begin{aligned} E_n(u)&= -\alpha \sum _{i=0}^{\left[ 1/\lambda _{n}\right] -2}\lambda _{n}(u^{i},u^{i+1})+\sum _{i=0}^{{\left[ 1/\lambda _{n}\right] -2}}\lambda _{n}(u^{i},u^{i+2})\end{aligned}$$
(3.10)
$$\begin{aligned}&= E_{n}^{(\alpha =4)}(u)-(\alpha -4)\sum _{i=0}^{\left[ 1/\lambda _{n}\right] -2}\lambda _{n}(u^{i},u^{i+1}). \end{aligned}$$
(3.11)

By the previous proposition, \(E_{n}^{(\alpha =4)}\) is minimized on uniform states, which trivially also holds true for the second term in the above sum. In particular, the minimal value can be straightforwardly computed:

$$\begin{aligned} \min E_{n}(u)=-\left( \alpha -1\right) (1-c_{n}\lambda _{n}). \end{aligned}$$

3.2 Zero Order Estimates

The following theorem is the main result of this section.

Theorem 3.4

Let \(E_{n}:L^\infty (I,S^{1})\rightarrow (-\infty ,+\infty ]\) be the functional in (3.1). Then \(\Gamma \hbox {-}\lim _{n}E_{n}(u)\) with respect to the weak-\(*\) convergence in \(L^{\infty }(I)\) is given by

$$\begin{aligned} E(u):={\left\{ \begin{array}{ll} \int _{I}f_\mathrm{hom}(u(x))\ \mathrm{d}x&{}\mathrm{if} \, |u|\le 1,\\ +\infty &{}\mathrm{otherwise}\,in \, L^{\infty }(I,{\mathbb {R}}^{2}), \end{array}\right. } \end{aligned}$$
(3.12)

where the convex function \(f_\mathrm{hom}:B_{1}\rightarrow {\mathbb {R}}\) is given by the following asymptotic homogenization formula:

$$\begin{aligned} f_\mathrm{hom}(z)\!:=\!\lim _{\rho \rightarrow 0}\lim _{k\rightarrow \infty }\frac{1}{k}\inf \left\{ -\alpha \sum _{i=0}^{k-2}(v^{i},v^{i+1})\!+\!\sum _{i=0}^{k-2}(v^{i},v^{i+2}),\ \langle u \rangle _{1,(0,k)}\in {\overline{B}(z,\rho )}\right\} .\nonumber \\ \end{aligned}$$
(3.13)

Furthermore

  1. (i)

    if \(\alpha \ge 4\), then \(f_\mathrm{hom}(z)=-(\alpha -1)\),

  2. (ii)

    if \(0<\alpha \le 4\), then the following estimate holds:

    $$\begin{aligned} \frac{(\alpha -4)^{2}}{8}|z|^{2}\le f_\mathrm{hom}(z)+\left( 1+\frac{\alpha ^{2}}{8}\right) \le \frac{(\alpha -4)^{2}}{8}|z|. \end{aligned}$$
    (3.14)

    Moreover, there exists \(h:[0,1]\rightarrow {\mathbb {R}}\) convex and monotone non-decreasing such that \(f_\mathrm{hom}(z)=h(|z|)\).

  3. (iii)

    if \(0<\alpha \le 4\), we have that \(\min E(u)=E(0)=-(1-\frac{\alpha ^{2}}{8})\).

Proof

The formula in (3.13) follows applying Theorem 2.1 in the special case

$$\begin{aligned} f^{\xi }(u,v)={\left\{ \begin{array}{ll} -\frac{\alpha }{2}(u,v) &{}\text{ if } |\xi |=1,\\ \frac{1}{2}(u,v) &{}\text{ if } |\xi |=2,\\ 0 &{}\text {otherwise}\\ \end{array}\right. } \end{aligned}$$
(3.15)

and \(K=S^{1}\). To prove (i), we notice that, as observed in Remark 3.3, \(E_{n}\) is minimized by constant \(S^{1}\)-valued functions and its minimum is \(-(\alpha -1)(1-c_{n}\lambda _{n})\). Since \(E_{n}\) \(\Gamma \)-converges to \(E\) given by (3.12), we have that

$$\begin{aligned} f_\mathrm{hom}(z)&\ge -(\alpha -1), \quad \forall z\in B^{1},\end{aligned}$$
(3.16)
$$\begin{aligned} f_\mathrm{hom}(z)&= -(\alpha -1), \quad \forall z\in S^{1}. \end{aligned}$$
(3.17)

By the convexity of \(f_\mathrm{hom}\), (i) follows.

We divide the proof of (ii) into the lower bound and the upper bound estimates.

Lower bound: Let \(u_{n}\in C_{n}(I,S^{1})\) be such that \(u_{n}\mathrel {\mathop {\rightharpoonup }\limits ^*}u\) in \(L^{\infty }(I,{\mathbb {R}}^{2})\), by (3.5) it is left to prove that

$$\begin{aligned} \liminf _{n}H_{n}(u_{n})\ge \frac{(\alpha -4)^{2}}{8}\int _{I}|u(x)|^{2}\ \mathrm{d}x. \end{aligned}$$
(3.18)

We define the functions \(w_{n}\) to be piecewise constant on the cells of the lattice and such that

$$\begin{aligned} w_{n}^{i}={\left\{ \begin{array}{ll}\frac{u_{n}^{i}+u_{n}^{i+2}}{2}&{}\mathrm{if}\, i=0,\ldots ,[1/\lambda _{n}]-2,\\ 0&{}\mathrm{if}\,i=[1/\lambda _{n}]-1. \end{array}\right. } \end{aligned}$$
(3.19)

Let us show that \(w_{n}\mathrel {\mathop {\rightharpoonup }\limits ^*}u\) in \(L^{\infty }(I,{\mathbb {R}}^{2})\). Since \(\sup _{n}\Vert w_{n}\Vert _{\infty }\le 1\) and \(u_{n}\mathrel {\mathop {\rightharpoonup }\limits ^*}u\) in \(L^{\infty }(I,{\mathbb {R}}^{2})\), it suffices to show that, for all \((a,b)\subset \subset I\), it holds

$$\begin{aligned} \int _{a}^{b}(u_{n}(x)-w_{n}(x))\ \mathrm{d}x\rightarrow 0. \end{aligned}$$
(3.20)

The above limit follows on observing that

$$\begin{aligned} \left| \int _{a}^{b}(u_{n}(x)-w_{n}(x))\ \mathrm{d}x\right|&\le \left| \sum _{i=[a/\lambda _{n}]}^{[b/\lambda _{n}]}\lambda _{n}(u^{i}_{n}-w^{i}_{n})\right| +o(1)\\&= \frac{1}{2}\left| \sum _{i=[a/\lambda _{n}]}^{[b/\lambda _{n}]}\lambda _{n}(u^{i}_{n}-u^{i+2}_{n})\right| \\&+\,o(1) \le 4\Vert u_{n}\Vert _{\infty }\lambda _{n}+o(1)\rightarrow 0. \end{aligned}$$

We also need to define the functions \(\hat{u}_{n}\) piecewise constant on the cell of the lattice and such that \(\hat{u}_{n}^{i}:=u_{n}^{i+1}\). An analogous computation as the one above shows that \(\hat{u}_{n}\mathrel {\mathop {\rightharpoonup }\limits ^*}u\) in \(L^{\infty }(I,{\mathbb {R}}^{2})\). We now may write that

$$\begin{aligned} H_{n}(u_{n})=2\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\left| \frac{u_{n}^{i}+u_{n}^{i+2}}{2}-\frac{\alpha }{4}u_{n}^{i+1}\right| ^{2}\ge 2\int _{I}|w_{n}(x)-\tfrac{\alpha }{4}\hat{u}_{n}(x)|^{2}\ \mathrm{d}x+o(1). \end{aligned}$$
(3.21)

By the weak lower semicontinuity of the \(L^{2}\) norm, we deduce (3.18).

Upper bound: We first prove that \(f_\mathrm{hom}(0)=-(1-\frac{\alpha ^{2}}{8})\). Using the already proved lower bound in \((ii)\), it is left to show that \(f_{\hom }(0)\le -(1-\frac{\alpha ^{2}}{8})\). To this end, we construct the sequence of piecewise-constant functions \(u_{n}\) on the cells of the lattice such that \(u_{n}^{i}=(\cos \varphi i,\sin \varphi i)\). It holds that \(u_{n}\mathrel {\mathop {\rightharpoonup }\limits ^*}0\) and, moreover, as shown in Proposition 3.2 \(E_{n}(u_{n})=(1-c_{n}\lambda _{n})(-1-\frac{\alpha ^{2}}{8})\). As a result

$$\begin{aligned} f_\mathrm{hom}(0)=\int _{I}f_\mathrm{hom}(0)\ \mathrm{d}x\le \liminf _{n} E_{n}(u_{n})=-1-\frac{\alpha ^{2}}{8}. \end{aligned}$$
(3.22)

We now prove the upper bound for \(z\in S^{1}\). Let us consider a constant sequence \(u_{n}=z\). Using formula (3.3) and (3.5), we have that

$$\begin{aligned} E_{n}(u_{n})=(1-c_{n}\lambda _{n})\left( -1-\frac{\alpha ^{2}}{8}+\frac{(\alpha -4)^{2}}{8}\right) . \end{aligned}$$

Arguing as before, it follows that, for all \(z\in S^{1}\), \(f_\mathrm{hom}(z)+(1+\frac{\alpha ^{2}}{8})\le \frac{(\alpha -4)^{2}}{8}\).

Now for all \(z\in B^{1}\) the upper bound follows by the convexity of \(f_\mathrm{hom}\).

Finally, by the definition of \(f_\mathrm{hom}\) it follows that for all \(z\in B^{1}\) \(f_\mathrm{hom}(Rz)=f_\mathrm{hom}(z)\) for all \(R\in SO(2)\). As a consequence of this and (Rockafellar (1970), Corollary 12.3.1 and Example below), we also get that \(f_\mathrm{hom}(z)=h(|z|)\) for some \(h:[0,1]\rightarrow {\mathbb {R}}\) convex and monotone non-decreasing. Eventually (iii) follows by (ii).\(\square \)

Remark 3.5

We notice that \(0\) is the unique minimizer of \(f_\mathrm{hom}\), in all the cases when the \(\Gamma \)-limit is non-trivial, that is, for \(0<\alpha <4\).

4 Renormalization of the Energy Close to the Ferromagnetic State and Chirality Transitions

In this section, motivated by the study of spin systems close to the helimagnet/ferromagnet transition point, we let the ferromagnetic interaction parameter \(\alpha \) be scale dependent and approach the transition value \(4\) from below. Namely we set \(\alpha =\alpha _{n}=4(1-\delta _{n})\) for some \(\delta _{n}>0\), \(\delta _{n}\rightarrow 0\). We then perform a renormalization of the energy \(E_{n}\) and introduce a new functional whose asymptotic behavior will better describe the ground states of the system. More precisely we define \(E_{n}^{hf}:L^{\infty }(I,{\mathbb {R}}^{2})\rightarrow (-\infty ,+\infty ]\) and \(H_{n}^{hf}:L^{\infty }(I,{\mathbb {R}}^{2})\rightarrow [0,+\infty ]\)as:

$$\begin{aligned} E^{hf}_{n}(u)&:= {\left\{ \begin{array}{ll} \displaystyle -4(1-\delta _{n})\sum \nolimits _{i=0}^{\left[ 1/\lambda _{n}\right] -2}\lambda _{n}(u^{i},u^{i+1})+\sum \nolimits _{i=0}^{{\left[ 1/\lambda _{n}\right] -2}}\lambda _{n}(u^{i},u^{i+2})&{}\mathrm{if}\,u\in C_n(I,S^{1})\\ +\infty &{}\mathrm{otherwise}. \end{array}\right. }\qquad \quad \end{aligned}$$
(4.1)
$$\begin{aligned} H^{hf}_{n}(u)&:= {\left\{ \begin{array}{ll} \frac{1}{2}\sum \nolimits _{i}\lambda _{n}\left| u^{i+2}-2(1-\delta _{n})u^{i+1}+u^{i}\right| ^{2}&{}\mathrm{if} \,u\in C_n(I,S^{1})\\ +\infty &{}\mathrm{otherwise}. \end{array}\right. } \end{aligned}$$
(4.2)

Note that by Theorem 3.4 it holds

$$\begin{aligned} H^{hf}_{n}(u)=E^{hf}_{n}(u)-\min E_{n}^{hf}=E^{hf}_{n}(u)+(3-4\delta _{n}+2\delta _{n}^{2})(1-c_{n}\lambda _{n}) \end{aligned}$$
(4.3)

Proposition 4.1

Let \(E_{n}^{hf}:L^\infty (I,S^{1})\rightarrow (-\infty ,+\infty ]\) be the functional in (4.1). Then \(\Gamma \hbox {-}\lim _{n}E_{n}(u)\) with respect to the weak-\(*\) convergence in \(L^{\infty }\) is given by

$$\begin{aligned} E(u):={\left\{ \begin{array}{ll} -3&{}\mathrm{if}\, |u|\le 1,\\ +\infty &{}\mathrm{otherwise}\,in\, L^{\infty }(I,{\mathbb {R}}^{2}). \end{array}\right. } \end{aligned}$$

Proof

Observing that for all \(u\in C_{n}(I,S^{1})\) it holds that

$$\begin{aligned} |E^{hf}_{n}(u)-E^{{\alpha =4}}_{n}|\le 4\delta _{n}, \end{aligned}$$
(4.4)

the result immediately follows by Theorem 3.4 (i).\(\square \)

In what follows, we will define a convenient order parameter such that the \(\Gamma \)-limit of a scaled version \(H_{n}^{hf}\) is given by a functional penalizing the helimagnetic transition around the ferromagnetic state.

We first introduce the order parameter. Given \(u_{n}\in C_{n}(I,S^{1})\), for \(i=0,1,\ldots ,[1/\lambda _{n}]-1\) we associate to each \(u_{n}^{i},u_{n}^{i+1}\) the corresponding oriented central angle \(\theta _{n}^{i}\in [-\pi ,\pi )\) given by

$$\begin{aligned} \theta _{n}^{i}:=\chi [u_{n}^{i},u_{n}^{i+1}]\arccos ((u_{n}^{i},u_{n}^{i+1})). \end{aligned}$$
(4.5)

We now set

$$\begin{aligned} w_{n}^{i}=\sin \left( \frac{\theta _{n}^{i}}{2}\right) . \end{aligned}$$
(4.6)

We eventually define the order parameter of our problem as

$$\begin{aligned} z_{n}^{i}={\sqrt{\frac{2}{\delta _{n}}}}w_{n}^{i}. \end{aligned}$$
(4.7)

Note that, the above procedure defines \(T_{n}:u_{n}\mapsto z_{n}\) which associates to any given \(u_{n}\in C_{n}(I,S^{1})\) a piecewise-constant function \(z_{n}\in \tilde{C}_{n}(I,{\mathbb {R}})\) where

$$\begin{aligned} \tilde{C}_{n}(I,{\mathbb {R}})&:= \{z:[0,1)\rightarrow {\mathbb {R}}:z(x)=z^{i}_{n}, \hbox { if } x \in \lambda _{n}\{i+[0,1)\},\\&i=0,1,\ldots ,[1/\lambda _{n}]-1\} \end{aligned}$$

with \(z_{n}\) as in (4.7). We observe that if \(z_{n}=T_{n}(u_{n})=T_{n}(v_{n})\) then \(u_{n}\) and \(v_{n}\) differ by a constant rotation (possibly depending on \(n\)) so that \(H^{hf}_{n}(u_{n})=H^{hf}_{n}(v_{n})\). Therefore, with a slight abuse of notation, we now regard \(H^{hf}_{n}\) as a functional defined on \(z\in L^{1}(I,{\mathbb {R}})\) by

$$\begin{aligned} H^{hf}_{n}(z)={\left\{ \begin{array}{ll} H^{hf}_{n}(u),&{}\mathrm{if} \, z\in \tilde{C}_{n}(I,{\mathbb {R}})\\ +\infty &{}\mathrm{otherwise}. \end{array}\right. } \end{aligned}$$
(4.8)

Note that in the definition above, \(u\) is any function such that \(T_{n}u=z\). As a consequence, it will be natural to state the \(\Gamma \)-convergence theorem considering the convergence with respect to the order parameter \(z\).

Theorem 4.2

Let \(H_{n}^{hf}:L^1(I,{\mathbb {R}})\rightarrow [0,+\infty ]\) be the functional in (4.8). Assume that there exists \(l:=\lim _{n}\lambda _{n}/(2\delta _{n})^{1/2}\). Then \(H^{hf}(z):=\Gamma \hbox {-}\lim _{n}H_{n}^{hf}(z)/(\sqrt{2}\lambda _{n}\delta _{n}^{3/2})\) with respect to the \(L^{1}(I)\) convergence is given by one of the following formulas:

  1. (i)

    if \(l=0\)

    $$\begin{aligned} H^{hf}(z):={\left\{ \begin{array}{ll} \frac{8}{3}\#(S(z))&{}\mathrm{if} \, z\in BV(I,\{\pm 1\}), \\ +\infty &{}\mathrm{otherwise}. \end{array}\right. } \end{aligned}$$
    (4.9)
  2. (ii)

    if \(l\in (0,+\infty )\)

    $$\begin{aligned} H^{hf}(z):={\left\{ \begin{array}{ll} \frac{1}{l}\int _{I}(z^{2}(x)-1)^{2}\ \mathrm{d}x+{l}\int _{I}(z'(x))^{2}\ \mathrm{d}x &{}\mathrm{if}\, z\in W_{|per|}^{1,2}(I), \\ +\infty &{}\mathrm{otherwise}, \end{array}\right. } \end{aligned}$$
    (4.10)

    where we have set \(W^{1,2}_{|per|}(I):=\{z\in W^{1,2}(I),\ s.t.\ |z(0)|=|z(1)|\}\).

  3. (iii)

    if \(l=+\infty \)

    $$\begin{aligned} H^{hf}(z):={\left\{ \begin{array}{ll} 0&{}\mathrm{if} \, z=\mathrm{const}, \\ +\infty &{}\mathrm{otherwise}. \end{array}\right. } \end{aligned}$$
    (4.11)

In the following proposition, we consider an equibounded sequence of spins and obtain a first bound on the scalar product between neighbors.

Proposition 4.3

Let \(\mu _{n}\rightarrow 0\) and let \(u_{n}\) be such that

$$\begin{aligned} \sup _{n}H_{n}(u_{n})\le C\lambda _{n}\mu _{n}, \end{aligned}$$
(4.12)

then for all \(i\) we have that

$$\begin{aligned} \left| \frac{\alpha }{4}-(u_{n}^{i},u_{n}^{i+1})\right| \le \sqrt{C}\left( \frac{2}{\alpha }+\frac{1}{2}\right) \mu _{n}^{1/2} \end{aligned}$$
(4.13)

Proof

Since for all \(i\) we have that

$$\begin{aligned} \left| u^{i+2}-\frac{\alpha }{2}u^{i+1}+u^{i}\right| ^{2}\ge \left( \left| u^{i}-\frac{\alpha }{2}u^{i+1}\right| -1\right) ^{2}, \end{aligned}$$

by (4.12) and the definition of \(H_{n}\), we have that

$$\begin{aligned} \sum _{i}\lambda _{n}\left( \left| u^{i}-\frac{\alpha }{2}u^{i+1}\right| -1\right) ^{2}\le C\lambda _{n}\mu _{n}\end{aligned}$$

which implies that, for all \(i\),

$$\begin{aligned} \left( \left| u^{i}-\frac{\alpha }{2}u^{i+1}\right| -1\right) ^{2}\le C\mu _{n}. \end{aligned}$$

As a result, we have that

$$\begin{aligned} \left( \left| u^{i}-\frac{\alpha }{2}u^{i+1}\right| ^{2}-1\right) ^{2}\le C\left( 2+\frac{\alpha }{2}\right) ^{2}\mu _{n}. \end{aligned}$$

By an explicit computation, we finally get (4.13).\(\square \)

Proof of Theorem 4.2

We prove the theorem only in cases \((i)\) and \((ii)\); since the proof of \((iii)\) involves only minor changes of the arguments, we need in the other two cases.

Let us consider a sequence \(z_n\in \tilde{C}_{n}(I,{\mathbb {R}})\) such that \(\sup _{n}\frac{H_{n}^{hf}(z_{n})}{\lambda _{n}\delta _{n}^{3/2}}\le C <+\infty \). Equivalently there is a sequence \(u_{n}\in C_{n}(I,S^{1})\) satisfying \(\sup _{n}\frac{H_{n}^{hf}(u_{n})}{\lambda _{n}\delta _{n}^{3/2}}\le C <+\infty \). We claim that

$$\begin{aligned} \frac{H^{hf}_{n}(u_{n})}{\sqrt{2}\lambda _{n}\delta _{n}^{3/2}}&\ge \frac{\sqrt{2}\delta _{n}^{1/2}}{\lambda _{n}} \sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\left( (z_{n}^{i})^{2}\!-\!1\right) ^{2}\nonumber \\&+\,\frac{\lambda _{n}}{\sqrt{2}\delta _{n}^{1/2}}(1-\gamma _{n})\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\left( \frac{z_{n}^{i+1}-z_{n}^{i}}{\lambda _{n}}\right) ^{2} \end{aligned}$$
(4.14)

for some \(\gamma _{n}\rightarrow 0\). Associating to each \(u_{n}^{i}\) the angles \(\theta ^{i}_{n}\) and the functions \(w^{i}_{n}\) introduced in (4.6), by means of the trigonometric identity \(1-\cos (2x)=2\sin ^{2}(x)\) we can write that

$$\begin{aligned} 1-(u_{n}^{i},u_{n}^{i+1})&= 1-\cos (\theta _{n}^{i})=2\sin ^{2}\left( \frac{\theta _{n}^{i}}{2}\right) =2(w_{n}^{i})^{2}\\ 1-(u_{n}^{i},u_{n}^{i+2})&= 1-\cos (\theta _{n}^{i+1}+\theta _{n}^{i}). \end{aligned}$$

By Proposition 4.3 with \(\mu _{n}=\delta _{n}^{\frac{3}{2}}\), there exists a constant \(C'\) such that

$$\begin{aligned} 1-(u_{n}^{i},u_{n}^{i+1})\le C'\delta _{n}^{\frac{3}{4}}, \end{aligned}$$
(4.15)

so that in particular \(\theta _{n}^{i}\rightarrow 0\).

Introducing the function \(w_{n}\) and the angles \(\theta _{n}\), by(3.6) and (4.3) we may rewrite \(H^{hf}_{n}(u_{n})\) as follows

$$\begin{aligned} H^{hf}_{n}(u_{n})&= 4(1-\delta _{n})\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}(1-(u_{n}^{i},u_{n}^{i+1}))-\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}(1-(u_{n}^{i},u_{n}^{i+2}))\\&\quad +\,2\delta _{n}^{2}(1-c_{n}\lambda _{n})\\&= 8(1-\delta _{n})\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}(w_{n}^{i})^{2}-\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}(1-\cos (\theta _{n}^{i+1}+\theta _{n}^{i}))\\&\quad +\,2\delta _{n}^{2}(1-c_{n}\lambda _{n}). \end{aligned}$$

We further point out the following identities:

$$\begin{aligned}&4(w_{n}^{i})^{2}-\sin ^2(\theta _{n}^{i})=4(w_{n}^{i})^{4},\\&\displaystyle 2\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\sin ^{2}(\theta _{n}^{i})=\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}(\sin ^{2}(\theta _{n}^{i})+\sin ^{2}(\theta _{n}^{i+1})). \end{aligned}$$

The first one comes from the trigonometric identity \(4\sin ^{2}(x)-\sin ^2(2x)=4\sin ^4(x)\), while the second follows from the boundary condition (2.1). Moreover, the following limit holds true

$$\begin{aligned} \lim _{\begin{array}{c} (x,y)\rightarrow (0,0)\\ x\not =y \end{array}}\frac{\sin ^{2}(x)+\sin ^{2}(y)-(1-\cos (x+y))}{(\sin (x/2)-\sin (y/2))^{2}}=2 \end{aligned}$$
(4.16)

upon observing that

$$\begin{aligned} \sin ^{2}(x)+\sin ^{2}(y)-(1-\cos (x+y))=(\sin (x)-\sin (y))^{2}-(1-\cos (x-y)). \end{aligned}$$

We can therefore continue estimate \(H^{hf}_{n}(u_{n})\) as

$$\begin{aligned} H^{hf}_{n}(u_{n})&= \sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}(8(w_{n}^{i})^{2}-2\sin ^{2}(\theta _{n}^{i}))-8\delta _{n}\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}(w_{n}^{i})^{2}\\&\quad +\, 2\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\sin ^{2}(\theta _{n}^{i})-\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}(1-\cos (\theta _{n}^{i+1}+\theta _{n}^{i}))\\&\quad +\,2\delta _{n}^{2}(1-c_{n}\lambda _{n}) \\&= 8\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\left( (w_{n}^{i})^{4}-\delta _{n}(w_{n}^{i})^{2}+\frac{\delta _{n}^{2}}{4}\right) \\&\quad +\, \sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\left( \sin ^{2}(\theta _{n}^{i+1})+\sin ^{2}(\theta _{n}^{i})\right) \\&\quad -\,\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}(1-\cos (\theta _{n}^{i+1}+\theta _{n}^{i})) \\&\ge 8\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\left( (w_{n}^{i})^{2}-\frac{\delta _{n}}{2}\right) ^{2} + 2(1-\gamma _{n})\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}(w_{n}^{i+1}-w_{n}^{i})^{2}, \end{aligned}$$

for some \(\gamma _{n}\rightarrow 0\). The last inequality is a consequence of (4.16) once we recall that, by (4.15), \(\theta _{n}\rightarrow 0\) uniformly. In terms of \(z_{n}\), the inequality in (4.16) becomes:

$$\begin{aligned} H^{hf}_{n}(u_{n})\ge 2\delta _{n}^{2}\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\left( (z_{n}^{i})^{2}-1\right) ^{2} + (1-\gamma _{n})\delta _{n}\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}(z_{n}^{i+1}-z_{n}^{i})^{2}. \end{aligned}$$

The claim (4.14) is proved on dividing by \(\sqrt{2}\lambda _{n}\delta _{n}^{3/2}\).

The claim implies the liminf inequality both in case \((i)\) and \((ii)\). In case \((i)\), it is obtained applying Theorem 2.2 and Remark 2.3. For what concerns \((ii)\), it suffices to observe that piecewise affine interpolations of the sequence \(z_{n}\) associated with an equibounded \(u_{n}\) are, in this case, weakly compact in \(W_{|per|}^{1,2}(I)\) so that the lower bound follows by standard lower semicontinuity.

In order to prove the limsup inequality, we separately discuss cases \((i)\) and \((ii)\).

Case\((i)\). By the locality of the construction, it suffices to exhibit a recovery sequence for \(z=-\chi _{(0,1/2]}+\chi _{(1/2,1)}\). As it is well known (see for example Modica and Mortola 1977; Modica 1987), \(z_{\min }(t)=\tanh (t)\) is the solution of the following problem

$$\begin{aligned} \min \left\{ \int _{-\infty }^{+\infty }((z'(t))^{2}+(z(t)^{2}-1)^{2})\ \mathrm{d}t, z\in W^{1,2}({\mathbb {R}}),\ z(\pm \infty )=\pm 1\right\} =:m \end{aligned}$$
(4.17)

and, by a direct computation, the above minimum is \(m=\frac{8}{3}\). For all \(\varepsilon >0\), there exists \(R_{\epsilon }>0\) such that

$$\begin{aligned}&\max \left\{ \sup _{t\in (-\infty ,-R_{\varepsilon })}|z_{\min }(t)+1|,\sup _{t\in (R_{\varepsilon },+\infty )}|z_{\min }(t)-1|\right\} \le \varepsilon \nonumber \\&\quad \int _{-R_{\varepsilon }}^{+R_{\varepsilon }}((z_{\min }'(t))^{2}+(z_{\min }(t)^{2}-1)^{2})\le m+\varepsilon \end{aligned}$$
(4.18)

Let us define \(z_{\varepsilon }:{\mathbb {R}}\rightarrow {\mathbb {R}}\) as the odd \(C^{1}\) function such that

$$\begin{aligned} z_{\varepsilon }(t):={\left\{ \begin{array}{ll} z_{\min }(t)&{}\mathrm{if}\,t\in [0,R_{\varepsilon }],\\ p_{\varepsilon }(t)&{}\mathrm{if}\,t\in (R_{\varepsilon },R_{\varepsilon }+\varepsilon ),\\ 1&{}\mathrm{if}\,t\in (R_{\varepsilon }+\varepsilon ,+\infty ), \end{array}\right. } \end{aligned}$$

where \(p_{\varepsilon }\) is a suitable third-order interpolating polynomial that we may choose such that \(\Vert p_{\varepsilon }'\Vert _{\infty }\le 2\) (Fig. 3). Note that, by the definition of \(z_{\varepsilon }\) and by the properties (4.18) above, we have that there exists \(C>0\) such that

$$\begin{aligned} \int _{-\infty }^{+\infty }((z_{\varepsilon }'(t))^{2}+(z_{\varepsilon }(t)^{2}-1)^{2})\ \mathrm{d}t\le m+C\varepsilon . \end{aligned}$$
(4.19)

Let \(z_{n,\varepsilon }\in \tilde{C}_{n}(I,{\mathbb {R}})\) be defined as follows

$$\begin{aligned} z_{n,\varepsilon }^{i}=z_{\varepsilon }\left( \frac{\sqrt{2\delta _{n}}}{\lambda _{n}}\left( \lambda _{n}i-\frac{1}{2}\right) \right) . \end{aligned}$$
(4.20)

We have that \(z_{n,\varepsilon }\rightarrow z\) in \(L^{1}(I)\) as \(n\rightarrow +\infty \). If we set

$$\begin{aligned} i_{+}=\left[ \frac{1}{\lambda _{n}}\left( \frac{1}{2}+\frac{\lambda _{n}}{\sqrt{2\delta _{n}}}(R_{\varepsilon }+\varepsilon )\right) \right] +1\quad \hbox {and}\quad i_{-}=\left[ \frac{1}{\lambda _{n}}\left( \frac{1}{2}-\frac{\lambda _{n}}{\sqrt{2\delta _{n}}}(R_{\varepsilon }+\varepsilon )\right) \right] , \end{aligned}$$

then \(|z^i_{n,\varepsilon }|=1\) for all \(i\ge i_{+}\) or \(i\le i_{-}\). We now put \(w_{n,\varepsilon }^{i}=\sqrt{\frac{\delta _{n}}{2}}z_{n,\varepsilon }^{i}\), so that in particular for all \(i\) it holds that \(|w_{n,\varepsilon }^{i}|\le \sqrt{\frac{\delta _{n}}{2}}\). We can therefore define the angles

$$\begin{aligned} \varphi _{n,\varepsilon }^{i}=2\sum _{j=0}^{i}\arcsin (w_{n,\varepsilon }^{j}). \end{aligned}$$

Let us observe that \(\mathrm{sign}(\varphi _{n,\varepsilon }^{i+1}-\varphi _{n,\varepsilon }^{i})=\mathrm{sign}(w_{n}^{i})\) and that \(\varphi _{n,\varepsilon }^{1}-\varphi _{n,\varepsilon }^{0}=\varphi _{n,\varepsilon }^{[1/\lambda _{n}]}-\varphi _{n,\varepsilon }^{[1/\lambda _{n}]-1}\). As a consequence, upon defining \(u_{n,\varepsilon }^{i}=(\cos (\varphi _{n,\varepsilon })^{i}|\sin (\varphi _{n,\varepsilon }^{i}))\), we have that \(u_{n}\in \overline{{\mathcal U}}_{n}(I)\) and that \(T_{n}(u_{n,\varepsilon })=z_{n,\varepsilon }\). Using again the limit (4.16) and repeating the computation as in the proof of the lower bound, we obtain the existence of a sequence \(\eta _{n}\rightarrow 0\) such that

$$\begin{aligned} \frac{H^{hf}_{n}(u_{n,\varepsilon })}{\sqrt{2}\lambda _{n}\delta _{n}^{3/2}}&\le \frac{\sqrt{2}\delta _{n}^{1/2}}{\lambda _{n}} \sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\left( (z_{n,\varepsilon }^{i})^{2}-1\right) ^{2}\nonumber \\&\quad +\,\frac{\lambda _{n}}{\sqrt{2}\delta _{n}^{1/2}}(1+\eta _{n})\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\left( \frac{z_{n,\varepsilon }^{i+1}-z_{n,\varepsilon }^{i}}{\lambda _{n}}\right) ^{2}\!. \end{aligned}$$
(4.21)

Define now the piecewise-constant functions \(z^1_{\varepsilon ,n}(s)\) via

$$\begin{aligned} z^1_{\varepsilon ,n}(s):={\left\{ \begin{array}{ll} \left( \frac{z_{n,\varepsilon }^{i+1}\!-\!z_{n,\varepsilon }^{i}}{\sqrt{2}\delta _{n}^{1/2}}\right) &{}\hbox { if }s\in \left[ \frac{\sqrt{2}\delta _{n}^{1/2}}{\lambda _{n}}(\lambda _{n}i\!-\!\frac{1}{2}), \frac{\sqrt{2}\delta _{n}^{1/2}}{\lambda _{n}}(\lambda _{n}(i\!+\!1)\!-\!\frac{1}{2})\right) ,\quad i\!=\!0,\ldots ,[1/\lambda _{n}]\!-\!2\\ 0 &{}\hbox { otherwise.} \end{array}\right. } \end{aligned}$$

Notice that by construction \(z^1_{\varepsilon ,n}(s)=0\) when \(|s|\ge R_\varepsilon +\varepsilon +2\lambda _{n}\). Since each of the intervals \(\left[ \frac{\sqrt{2}\delta _{n}^{1/2}}{\lambda _{n}}(\lambda _{n}i-\frac{1}{2}), \frac{\sqrt{2}\delta _{n}^{1/2}}{\lambda _{n}}(\lambda _{n}(i+1)-\frac{1}{2})\right) \) has length \(\sqrt{2}\delta _{n}^{1/2} \rightarrow 0\), and since \(z_{\varepsilon }'\) is uniformly continuous in \({\mathbb {R}}\), we get that \(|z^1_{\varepsilon ,n}(s)-z_{\varepsilon }'(s)|\rightarrow 0\) uniformly with respect to \(s \in {\mathbb {R}}\). Being \(z^1_{\varepsilon ,n}(s)=0\) outside a compact set independent of \(n\), this implies

$$\begin{aligned} \lim _{n\rightarrow +\infty }\int _{-\infty }^{+\infty }(z^1_{\varepsilon ,n}(s))^2\,\mathrm{d}s=\int _{-\infty }^{+\infty }(z_{\varepsilon }'(s))^2\,\mathrm{d}s. \end{aligned}$$

On the other hand, by a direct computation, we get that

$$\begin{aligned}&\displaystyle \frac{\lambda _{n}}{\sqrt{2}\delta _{n}^{1/2}}(1\!+\!\eta _{n})\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\left( \frac{z_{n,\varepsilon }^{i+1}\!-\!z_{n,\varepsilon }^{i}}{\lambda _{n}}\right) ^{2}\!=\!(1\!+\!\eta _{n})\sum _{i=0}^{[1/\lambda _{n}]-2}\sqrt{2}\delta _{n}^{1/2}\left( \frac{z_{n,\varepsilon }^{i+1}-z_{n,\varepsilon }^{i}}{\sqrt{2}\delta _{n}^{1/2}}\right) ^{2}\\&\displaystyle \le (1+\eta _{n})\int _{-\frac{\sqrt{2}\delta _{n}^{1/2}}{2\lambda _{n}}}^{\frac{\sqrt{2}\delta _{n}^{1/2}}{2\lambda _{n}}}(z^1_{\varepsilon ,n}(s))^2\,\mathrm{d}s\le (1+\eta _{n})\int _{-\infty }^{+\infty }(z^1_{\varepsilon ,n}(s))^2\,\mathrm{d}s \end{aligned}$$

so that

$$\begin{aligned} \limsup _{n\rightarrow +\infty }\frac{\lambda _{n}}{\sqrt{2}\delta _{n}^{1/2}}(1+\eta _{n})\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\left( \frac{z_{n,\varepsilon }^{i+1}-z_{n,\varepsilon }^{i}}{\lambda _{n}}\right) ^{2}\le \int _{-\infty }^{+\infty }(z_{\varepsilon }'(s))^2\,\mathrm{d}s. \end{aligned}$$
(4.22)

To estimate the other term, we proceed in a similar way. We define the piecewise-constant functions \(\hat{z}_{\varepsilon ,n}(s)\) via

$$\begin{aligned} \hat{z}_{\varepsilon ,n}(s)\!:=\!{\left\{ \begin{array}{ll} z_{n,\varepsilon }^{i}&{}\hbox { if }s\in \left[ \frac{\sqrt{2}\delta _{n}^{1/2}}{\lambda _{n}}(\lambda _{n}i\!-\!\frac{1}{2}), \frac{\sqrt{2}\delta _{n}^{1/2}}{\lambda _{n}}(\lambda _{n}(i+1)-\frac{1}{2})\right) ,\quad i\!=\!0,\ldots ,[1/\lambda _{n}]\!-\!2\\ 0 &{}\hbox { otherwise.} \end{array}\right. } \end{aligned}$$

Notice that by construction \(\hat{z}_{\varepsilon ,n}(s)^2=1\) when \(|s|\ge R_\varepsilon +\varepsilon +2\lambda _{n}\). Since each of the intervals \(\left[ \frac{\sqrt{2}\delta _{n}^{1/2}}{\lambda _{n}}(\lambda _{n}i-\frac{1}{2}), \frac{\sqrt{2}\delta _{n}^{1/2}}{\lambda _{n}}(\lambda _{n}(i+1)-\frac{1}{2})\right) \) has length \(\sqrt{2}\delta _{n}^{1/2} \rightarrow 0\), and since \(z_{\varepsilon }\) is uniformly continuous in \({\mathbb {R}}\), we get that \(|\hat{z}_{\varepsilon ,n}(s)-z_{\varepsilon }(s)|\rightarrow 0\) uniformly with respect to \(s \in {\mathbb {R}}\). Being \(\hat{z}_{\varepsilon ,n}(s)^2=1\) outside a compact set independent of \(n\); this implies

$$\begin{aligned} \lim _{n\rightarrow +\infty }\int _{-\infty }^{+\infty }(\hat{z}_{\varepsilon ,n}(s)^2-1)^2\,\mathrm{d}s=\int _{-\infty }^{+\infty }(z_{\varepsilon }(s)^2-1)^2\,\mathrm{d}s. \end{aligned}$$

On the other hand, since by construction

$$\begin{aligned} \hat{z}_{\varepsilon ,n}\left( \frac{\sqrt{2}\delta _{n}^{1/2}}{\lambda _{n}}\left( t-\frac{1}{2}\right) \right) =z_{n,\varepsilon }^{i}\iff t\in [\lambda _{n}i, \lambda _{n}(i+1)) \end{aligned}$$

via the change of variables \(t-\frac{1}{2}= \frac{\lambda _{n}}{\sqrt{2}\delta _{n}^{1/2}}s\) we have

$$\begin{aligned}&\displaystyle \int _{-\infty }^{+\infty }(\hat{z}_{\varepsilon ,n}(s)^2-1)^2\,\mathrm{d}s \ge \int _{-\frac{\sqrt{2}\delta _{n}^{1/2}}{2\lambda _{n}}}^{\frac{\sqrt{2}\delta _{n}^{1/2}}{2\lambda _{n}}}(\hat{z}_{\varepsilon ,n}(s)^2-1)^2\,\mathrm{d}s\\&\quad \displaystyle = \frac{\sqrt{2}\delta _{n}^{1/2}}{\lambda _{n}} \int _0^1\left( \hat{z}_{\varepsilon ,n}\left( \frac{\sqrt{2}\delta _{n}^{1/2}}{\lambda _{n}}(t-\frac{1}{2})\right) ^2-1\right) ^2\,\mathrm{d}t\\&\quad \ge \frac{\sqrt{2}\delta _{n}^{1/2}}{\lambda _{n}} \sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\left( (z_{n,\varepsilon }^{i})^{2}-1\right) ^{2} \end{aligned}$$

so that

$$\begin{aligned} \limsup _{n\rightarrow +\infty }\frac{\sqrt{2}\delta _{n}^{1/2}}{\lambda _{n}} \sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\left( (z_{n,\varepsilon }^{i})^{2}-1\right) ^{2}\le \int _{-\infty }^{+\infty }(z_{\varepsilon }(s)^2-1)^2\,\mathrm{d}s. \end{aligned}$$
(4.23)

Combining (4.21), (4.22), and (4.23), we obtain

$$\begin{aligned} \limsup _{n\rightarrow +\infty }\frac{H^{hf}_{n}(u_{n,\varepsilon })}{\sqrt{2}\lambda _{n}\delta _{n}^{3/2}}\le \int _{-\infty }^{+\infty }((z_{\varepsilon }'(t))^{2}+(z_{\varepsilon }(t)^{2}-1)^{2})\ \mathrm{d}t\le m+C\varepsilon . \end{aligned}$$

This gives the required upper bound by arbitrariness of \(\varepsilon \).

Case \((ii)\). We argue by density. Let us consider \(z\in W^{1,2}_{|per|}(I)\cap C^{\infty }({\overline{I}})\). We define

$$\begin{aligned} z_{n}^{i}={\left\{ \begin{array}{ll} z(\lambda _{n}i)&{}\text {if } i=1,2,\ldots ,\left[ \frac{1}{\lambda _{n}}\right] -1,\\ z(1)&{}\text {if } i=\left[ \frac{1}{\lambda _{n}}\right] . \end{array}\right. } \end{aligned}$$
(4.24)

Note that, by taking the piecewise affine interpolation of such a \(z_{n}\), we have that

$$\begin{aligned}&\lim _{n}\left( \frac{\sqrt{2}\delta _{n}^{1/2}}{\lambda _{n}} \sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\left( (z_{n}^{i})^{2}-1\right) ^{2}\!+\!\frac{\lambda _{n}}{\sqrt{2}\delta _{n}^{1/2}}(1-\gamma _{n})\sum _{i=0}^{[1/\lambda _{n}]-2}\lambda _{n}\left( \frac{z_{n}^{i+1}-z_{n}^{i}}{\lambda _{n}}\right) ^{2}\right) \\&\quad =H^{hf}(z). \end{aligned}$$

To conclude, we construct \(u_{n}\) as in the proof of \((i)\) and observe that (4.21) still holds true.\(\square \)

Fig. 3
figure 3

In black the function \(\tanh (t)\). In red the function \(z_{\varepsilon }(t)\) in the limsup construction (Color figure online)

Full size image