FormalPara Suggested Prerequisites

This topic has elements of vector calculus, differential equations, scientific computation, computational fluid dynamics, physics, and biology in it. However, depending on the depth of the intended project, a student need not have experience in all of these things. A strong foundation in vector calculus and experience with programming are essential.

1 Biological Introduction

Cilia are generally small, slender fibers that serve a variety of biological functions. In some instances, cilia are immotile, fairly rigid, and may serve a sensory role. In others, cilia move and their primary function is to create fluid flow. For example, primary nodal cilia are rigid cilia that move in a conical fashion about a tilted axis. Primary nodal cilia are fairly sparsely packed and are critical in developing asymmetry in embryos before organ development [7, 8, 20]. Put another way, the conical motion of primary nodal cilia starts the biological signaling that puts your heart on the left side of your body rather than the right. When primary nodal cilia do not function properly, there is a chance that the signaling will get mixed up and the heart will form on the right side of the body in a condition known as situs inversus.

The pulmonary cilia that we are studying in this project are much more flexible and move in a different way than the previously described primary nodal cilia. Their primary function is fluid transport. Pulmonary cilia are flexible, densely packed, hair-like fibers that move with a coordinated whip-like motion that propels contaminants out of the lungs. The surface of the lung is lined with cells called epithelial cells. Patches of pulmonary cilia extend out from these epithelial cells into the airway surface liquid (ASL). The ASL is composed of two fluids: a periciliary liquid layer (PCL) and a mucus layer. The PCL is a water-like substance adjacent to the epithelial cells. The mucus layer is a thick, sticky fluid that sits on top of the PCL. The depth of the PCL is approximately the length of a cilium, but the thickness of the mucus layer can vary dramatically within a lung [9]. The mucus layer is responsible for trapping harmful contaminants from the airway above [19]. A sketch of the fluid surrounding the lung is shown in Fig. 1 (not to scale). Pulmonary cilia form a densely packed carpet on the surface of the lungs and the bulk effect of the cilia’s coordinated motion is a metachronal wave that travels along the carpet’s surface [19]. Recent studies have explored the formation of such metachronal waves [15, 18] as well as the efficiency of different wave configurations [9, 10, 24]. The metachronal wave helps propel the PCL and the contaminants trapped in the adjacent mucus layer above it out of the lungs. This process is known as mucociliary clearance, clearing contaminants and protecting the lungs from the effects of these pollutants [19].

Fig. 1
figure 1

Fluid layers above the pulmonary surface with cilia shown in red

Full size image

Our research draws motivation from a current subject of study in the biological community. Cystic fibrosis and primary ciliary dyskinesia (PCD) are two diseases with connections to the movement of cilia in the airway surface liquid in the lungs. Abnormalities caused by the cystic fibrosis gene lead to the depletion of the periciliary liquid and a thicker layer of mucus adhering to the airway surface [3]. Therefore, the coordinated beating of the cilia is inhibited in patients with cystic fibrosis because of the presence of unusually sticky mucus and the lack of periciliary liquid. This provides a favorable environment for infection [3]. A patient with primary ciliary dyskinesia suffers from impaired movement and possible immotility of the cilia, characterized by abnormalities in the beat, stroke, or coordination of cilia. This ultimately leads to reduced or absent mucociliary clearance [22]. Similar to the consequences of cystic fibrosis, without properly functioning cilia, the bacteria and contaminants remain in the mucus, leaving the lungs more susceptible to infection. Investigating the transport and activity of fluid tracers as a result of their interaction with healthy cilia will help further the biological study of cystic fibrosis, PCD, and other pulmonary or cilia-related diseases [4]. Research concerning properties of the PCL and mucus layers and their interaction with cilia is a subject of intense research because the mechanism by which the cilia cause clearance of the infected mucus remains uncertain.

There are competing theories as to the interaction between the cilia and the mucus layer. It is not known for certain whether or not the tips of the cilia penetrate the mucus layer during their beat cycle [16]. Given the variety and nature of questions regarding this physical scenario, creating a mathematical model of this fluid–structure interaction can provide insight into questions that might be difficult to explore with biological experiments. In our model, we choose to focus on the effects of a metachronal wave traveling through a patch of cilia on the surrounding periciliary liquid. As such, we make a simplifying assumption that there is no mucus layer for the cilia to directly interact with, which is consistent with the assumption that the cilia do not penetrate into the mucus and the entire length of the cilia is covered by the PCL. This decision is supported in [28]. Some models in the literature consider both the mucus and the PCL using different fluid modeling techniques and assumptions [9, 10].

The beat form of a single cilium is divided into two basic motions, shown in Fig. 2. The first is the power or effective stroke , where the cilium is nearly straight and in a plane perpendicular to the cell surface. Let us assume for discussion purposes in \(\mathbb {R}^3\) that the cilium is moving in the xz-plane during its power stroke, so in the view of Fig. 2, consider the plane of the page to be the xz-plane where y = 0 and the power stroke is in the positive x-direction when moving to the right. During the power stroke the cilium will move quickly, in an attempt to propel the mucus and PCL. This is followed by the recovery stroke, which propagates a bend from the base to the tip of the cilium, returning it to its original form and starting position [4]. For the recovery stroke, the cilium moves out of the xz-plane and has position values with y < 0 (out of the page) when the cilium is moving in the negative x-direction (to the left) as it returns to its original position. Different descriptions of the cilium beat form exist in the literature. Some are parameterizations of a flexible cilium [16] while others make simplifications by making the cilium more rigid [17]. As discussed further in Sect. 2.3, our model uses the latter approach.

Fig. 2
figure 2

Side view of the power stroke (black) and recovery stroke (gray) of a pulmonary cilium. Reproduced with permission of the ⒸERS 2019: European Respiratory Journal 44 (6) 1579–1588; DOI: 10.1183/09031936.00052014 Published 30 November 2014 [27]

Full size image

During a full beat cycle, the cilium quickly moves through its power stroke, propelling fluid forward and then makes a whip-like motion as it moves through its recovery stroke, back to the beginning of the next power stroke. The ratio of the recovery stroke duration to the power stroke duration is referred to as the temporal asymmetry, Rt. In pulmonary cilia, Rt > 1 because the power stroke is always faster than the recovery stroke [17]. Much research concerning pulmonary cilia has included a recovery stroke that is in the same plane as the effective stroke [14]. Our research introduces a model with an out-of-plane recovery stroke, which appears in biological studies [17], but is not present in all cilia instances [11].

Each cilium in a patch moves in coordination with the others, with neighboring cilia having a slight phase difference. The delay between beating cilia creates a metachronal wave affecting the propulsion of the PCL and mucus above. A metachronal wave is defined by its direction of movement relative to the power stroke direction. In our model, if a cilium’s power stroke is in the positive x-direction, the metachronal wave travels generally in the negative x-direction. A wave that is propagating somewhat parallel or antiparallel to the power stroke direction is labeled as symplectic or antiplectic, respectively [28]. In fact, our antiplectic metachronal wave travels backwards and to the left of the effective stroke direction, which is similar to Gheber and Priel’s model [17]. Sanderson and Sleigh observe an antiplectic wave in patches of rabbit tracheal cilia [28], so we implement various antiplectic metachronal waves in our model. Recent works explore the formation of the metachronal wave and explore properties of various configurations [9, 10, 24]. We are not exploring the formation of the metachronal waves in this project, rather focusing on the effects of the coordinated motion.

In the remainder of this chapter, we will introduce some mathematical foundations of computational fluid dynamics, specifically the method of regularized Stokeslets, that can be used to model biological fluids. We will also include an undergraduate project completed on this topic as well as suggestions for future studies.

2 Mathematical Model

We are interested in the factors influencing fluid flow of the PCL in healthy lungs, especially in the presence of a ciliary metachronal wave. To study this, we will focus on a technique in computational fluid dynamics referred to as the method of regularized Stokeslets (MRS). Our model approximates the body of a pulmonary cilium by placing a collection of 30 regularized Stokeslets along the centerline of that cilium, discretizing the continuous body. As will be discussed further in Sect. 2.2, a regularized Stokeslet is a regularized singularity that mathematically converts a force exerted on the fluid to a resulting velocity anywhere in the fluid. We then prescribe a beat form by specifying the location of the cilium at discrete time steps and implement that beat form for a patch of cilia representative of patches in the lungs. The MRS provides a linear relationship between velocities and forces that can be used to both calculate the forces the cilia are exerting on the fluid necessary to maintain the prescribed velocities of the beat form as well as the velocity anywhere in the fluid resulting from the ciliary motion. The regularization is necessary to ensure finite fluid velocities at the location of the forces, which is not the case when using singular, non-regularized Stokeslets.

Other studies of metachronal waves use adaptations of the immersed boundary method to model a one- or two-phase fluid flow, where both the mucus and PCL are considered [9, 10]. The MRS used in this work is a Lagrangian method, meaning that we calculate the fluid velocities only at the points in the fluid we are interested in studying and follow those points along their trajectories. Eulerian methods such as the immersed boundary method require the calculation of the fluid velocity at a grid that spans the entire fluid domain, which could be quite computationally expensive depending on the desired resolution. Imagine having one particular location that you want to watch evolve over time. The Lagrangian approach would take the fluid at the initial location of interest and follow it through its motion as it likely moves away from its initial position. The Eulerian approach would keep the initial position fixed and explore the fluid that flows past its fixed location. In this approach, to get a sense of the global behavior of the fluid, one would need to calculate fluid velocities at many locations throughout the fluid whereas with the Lagrangian approach, one would only need to calculate the velocity at one point at each time step.

The Lagrangian nature of the MRS saves in computational time when only interested in a few points in the fluid domain. The MRS also has flexibility in modeling problems with complicated geometries whereas some other methods struggle with that. For instance, boundary integral methods require integration over a closed surface, so the time-varying geometry of a beating cilium is unlikely to produce integrable surface integrals because there is no simple mathematical description of the surface. Section 2.1 provides an introduction to the Navier–Stokes equations, the governing equations of fluid dynamics. Section 2.2 introduces the method of regularized Stokeslets while Sects. 2.3 and 2.4 further describe the cilium beat form and patches, respectively.

2.1 Fluid Dynamics

While fluids in general encompass a variety of substances including liquids, gases, and plasmas, we will be focusing on the behavior of liquids in this project. The Navier–Stokes equations are a collection of nonlinear partial differential equations that describe the relationship between a fluid’s velocity, pressure, density, and viscosity. Viscosity is a fluid’s resistance to flow, or its thickness in the sense that honey is “thicker” and more resistant to flow than water, hence honey has a higher viscosity than water. Liquids are often categorized as Newtonian or non-Newtonian, depending on the relationship between the shear stress and local strain rate. The shear stress describes internal forces within the fluid while the local strain rate described the rate of deformation of the fluid. For Newtonian fluids, this relationship is linear while non-Newtonian fluids have a nonlinear relationship. Non-Newtonian fluids are often referred to as viscoelastic fluids because the nonlinear dependence between stress and strain rates provides some memory to the fluid, creating an elastic effect. Non-Newtonian fluids can also have shear-thinning or shear-thickening properties as a result of the nonlinearity. For instance, ketchup is shear-thinning in that it does not flow very readily unless the shear force of a knife is applied when spreading it on a hamburger bun. On the other hand, silly putty is shear-thickening. If you leave it in its storage container overnight, it will take the shape of its container indicating that it is indeed a fluid. However, if you roll it into a ball and bounce it on the ground, it will act like a solid. During the impact with the ground, the instantaneous forces from the collision cause a quick change in the properties of the fluid. The water-like PCL in the lung is considered a Newtonian fluid, so modeling Newtonian fluids will be the focus of this chapter. If one wants to expand consideration to include the mucus layer, then non-Newtonian effects would need to be taken into consideration.

While more general forms exist, the incompressible Navier–Stokes equations describe Newtonian fluids:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \rho \frac{\partial \mathbf{u}}{\partial t} + \rho \mathbf{u}\cdot \nabla\mathbf{u} &\displaystyle = &\displaystyle -\nabla p +\mu\nabla^2\mathbf{u} + \mathbf{F}{} \end{array} \end{aligned} $$
(1)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \nabla\cdot\mathbf{u} &\displaystyle =&\displaystyle 0,{} \end{array} \end{aligned} $$
(2)

where u represents the fluid velocity, ρ fluid density, p pressure, μ dynamic viscosity, and F external force. Note that bold variables represent vector quantities in \(\mathbb {R}^3\). When modeling fluid flow in three dimensions as we are here, Eq. (1) represents three equations due to the vector nature of velocity and these equations account for conservation of momentum in the system. Sometimes the left-hand side of Eq. (1) is represented as \(\rho \frac {D\mathbf {u}}{Dt}\), where \(\frac {D\mathbf {u}}{Dt}\) is a material derivative and encapsulates both the local acceleration term \(\frac {\partial \mathbf {u}}{\partial t}\) and the convective acceleration term u ⋅∇u that accounts for the fact that the fluid of interest is flowing to other areas of the fluid domain. The right-hand side of Eq. (1) brings in the effects of pressure, viscosity , and external forces. Equation (2) is sometimes referred to as the continuity equation and represents conservation of mass for an incompressible fluid whose density remains constant, which often means there are no large temperature variations within the fluid domain. Textbooks exploring fluid dynamics principles at the advanced undergraduate level or graduate school level include [2, 23, 25] and provide more detailed derivations and analysis of the incompressible Navier–Stokes equations, including further discussion of the physical interpretations of these equations as well as extensions to other fluid scenarios and models.

It is worth noting that while the Navier–Stokes equations are used to model many fluids, the proofs of existence and uniqueness of solutions are open mathematical problems, and are among the set of Millennium Prizes offered by the Clay Mathematics Institute [1]. Solving the Navier–Stokes equations exactly is challenging, so scholars often resort to either making simplifying assumptions that change the nature of the PDEs or using numerical methods to approximate solutions to Eqs. (1) and (2). In this work, we recognize that we can use characteristics of the biological system to make assumptions that will simplify the nonlinear time-dependent Navier–Stokes equations into the linear quasi-steady Stokes equations (namely the small length scale of cilia and low fluid velocities contribute to a low Reynolds number). The Reynolds number provides insight into the balance of inertial and viscous forces in a fluid and is given by

$$\displaystyle \begin{aligned} Re = \frac{UL\rho}{\mu},{}\end{aligned} $$
(3)

where U is a characteristic velocity, L is a characteristic length scale, ρ is the fluid density, and μ is the dynamic viscosity. The Reynolds number gives a sense of how the inertial forces and viscous forces balance in a given fluid flow. Notice that the Reynolds number is not a property of the fluid alone, but also includes information about the length scales and speed of the motion as well. Fluid flow that has very high speeds, large length scales, and low densities would have a high Reynolds number and inertial forces would dominate viscous forces. Flow in this regime is turbulent, so the flow around a flying airplane or water rushing out of a fire hydrant would be examples of high Reynolds number flow. In our case, the small size of the cilium coupled with the density and viscosity of water contributes to a low Reynolds number situation where flow is laminar rather than turbulent and inertial forces are negligible relative to viscous forces. You can often see the transition from high Reynolds number to low Reynolds number intuitively at some kitchen sink faucets. If you turn the water all the way on, the water flow often looks turbulent and bumpy, however if you reduce the amount of water coming out, there is often a point where the water becomes calm, smooth, and transparent, a sign of laminar flow. Note that the low Reynolds number assumption in this work (Re ≪ 1) is at a much smaller Reynolds number than the onset of laminar flow (on the order of 103).

The average velocity of our cilium over its beat cycle is U = 0.122 μm/s and the length scale we use is the length of a cilium, L = 6 μm. Discussion on cilia parameters can be found in [16, 29, 30]. We assume the density and viscosity of the PCL are the same as water [16], so ρ = 917 kg/m2 and μ = 1 kg/ms. This gives us a Reynolds number of Re = 6.75 × 10−5, which is sufficiently small so that the incompressible Navier–Stokes equations (1) and (2) can be simplified to the quasi-steady Stokes equations after nondimensionalization

$$\displaystyle \begin{aligned} \begin{array}{rcl} -\nabla p +\mu\nabla^2\mathbf{u} + \mathbf{F} &\displaystyle =&\displaystyle 0{} \end{array} \end{aligned} $$
(4)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \nabla\cdot\mathbf{u} &\displaystyle =&\displaystyle 0.{} \end{array} \end{aligned} $$
(5)

Notice the terms in the left-hand side of Eq. (1) become negligible in a low Reynolds number regime. Those terms represent acceleration terms in the Navier–Stokes equation, providing evidence that the inertial terms are no longer present in the quasi-steady Stokes equations. An example of the nondimensionalization and transition from the incompressible Navier–Stokes equations to the quasi-steady Stokes equations in low Reynolds flow can be found in [4].

Notice that the Navier–Stokes equations (1) and (2) are nonlinear PDEs with a time derivative (inertial term). The quasi-steady Stokes equations remove both the nonlinearity and the inertial term, meaning solutions to Eqs. (4) and (5) can be computed as a result of only considering the current force configuration since inertial effects are negligible. The previous force configuration is not needed to calculate fluid velocities. Since time is not immediately visible in Eqs. (4) and (5), any fluid flow in a low Reynolds number regime is reversible. That is, if one imposes a force on a fluid and calculates the resulting fluid flow at that instant in time, its motion will not persist to the next moment in time (because inertial effects have been ignored in the equations). Additionally, the fluid flow can be reversed by applying an equal and opposite force in the same location at another instant in time. Thus, small organisms that either want to generate fluid flow or to move themselves in a fluid environment need to move with motions that are not symmetric in the sense that if a cilium moves forward in a certain way and returns to its initial position in the same way but in the reverse direction, the fluid would have moved from the original motion, but would move back to its original state when the cilium returns to its original position. This is an instance of the scallop theorem introduced by Purcell [26] in reference to the idea that a scallop can open its shell slowly but close it quickly to move by forcing water out of it, but this does not occur in a low Reynolds number fluid regime. If the scallop were in a low Reynolds regime, the opening and closing of the shell (regardless of speed as long as the motion was low Reynolds number) will result in the scallop ending up where it started because the motion of the shell opening and closing have reciprocal motions. For cilia to generate fluid transport in a low Reynolds number regime, they must undergo a motion, described previously in this section, that breaks symmetry. The lack of time information in Eqs. (4) and (5) does not restrict our study only to steady flows, just flows whose parameters fall in a low Reynolds number regime.

2.2 Method of Regularized Stokeslets

Fundamental solutions play a role in solving linear partial differential equations. A fundamental solution or Green’s function F satisfies \( \mathcal {L}F = \delta (x)\), where \(\mathcal {L}\) is a linear differential operator and δ(x) is the Dirac delta function, whose value is 0 everywhere except when x = 0 where it is undefined. Solutions to a non-homogeneous differential equation \(\mathcal {L}f = g(x)\) can then be found through convolutions of F and g. Further discussions of fundamental solutions and convolutions can be found in various textbooks discussing differential equations, e.g., [21, 25]. When solving a linear differential equation, we can take advantage of superposition of solutions to find new solutions. In the case of solving the quasi-steady Stokes equations (4) and (5), boundary integral techniques rely on superimposing fundamental solutions. However, the fundamental solutions, or Stokeslets, are singular, meaning that they are not defined everywhere in the fluid domain. For some boundary integral calculations where you are integrating around a closed boundary and the singularities are separated from the fluid domain by the boundary, the singularity does not cause much concern. However, when using fundamental solutions to communicate forces directly on a fluid, there is not always a separation between the fluid domain and where the singularities exist, causing computational issues. This motivates the modification of the singular fundamental solutions (Stokeslets) to become regularized fundamental solutions (regularized Stokeslets).

The method of regularized Stokeslets (MRS), as developed by Cortez et al. [12, 13], uses Green’s functions to produce solutions to the quasi-steady Stokes equations (4) and (5) in free-space. The MRS computes the fluid velocity u at a location x resulting from a force F exerted on the fluid at a location x 0. We define the distance r between where the velocity is being calculated and a force is being exerted as \(r = \|\hat {\mathbf {x}}\|\), where \(\hat {\mathbf {x}} = \mathbf {x}-\mathbf {x_0}\) and ∥⋅∥ represents the L 2-norm. A Stokeslet is a fundamental solution to the singularly forced Stokes equations (4) and (5), where \(\mathbf {F} = \delta (\hat {\mathbf {x}})\mathbf {f}\) (e.g., see [25]). Alternatively, a regularized Stokeslet is a Green’s function to the Stokes equations when \(\mathbf {F} = \phi _\epsilon (\hat {\mathbf {x}})\mathbf {f}\). Here ϕ 𝜖 is a cutoff function that approximates a delta distribution as the regularization parameter 𝜖 → 0 and \(\mathbf {f} \in \mathbb {R}^3\) controls the direction and magnitude of the force. The Dirac delta function is radially symmetric and integrates to 1, so we typically use cutoff functions that have the same properties. In building an intuitive difference between these two fundamental solutions, imagine exerting a localized force by pushing on a fluid with a pencil. In the singular case, you are using the sharp point of the pencil to push the fluid and calculate the resulting flow. In the regularized case, you use the rounded eraser of the pencil to push the fluid and calculate the resulting flow. You might imagine that the flow locally will be different near the site of the force, but away from the site of the force, the difference will be negligible. The flow will be most different at the location of the force because in the regularized case, you can calculate the velocity there, but in the singular case you cannot. This feature is quite important in establishing the usefulness of the MRS.

In general, the choice of cutoff function is not unique, but rather is often motivated by the calculation details needed in a given problem. For instance,

$$\displaystyle \begin{aligned} \phi_\epsilon(r) = \frac{15 \epsilon^4}{8\pi (r^2 + \epsilon^2)^{3/2}}{} \end{aligned} $$
(6)

works well for our purposes [13]. This cutoff function produces the regularized Stokeslet \(S^{\phi _\epsilon }\):

$$\displaystyle \begin{aligned} S^{\phi_\epsilon}_{ij}(\hat{\mathbf{x}}) = \delta_{ij}\frac{r^2+2\epsilon^2}{(r^2+\epsilon^2)^{3/2}} + \frac{\hat{x}_i\hat{x}_j}{(r^2+\epsilon^2)^{3/2}}.{} \end{aligned} $$
(7)

As 𝜖 → 0, we recover the singular Stokeslet [25],

$$\displaystyle \begin{aligned} S_{ij}(\hat{x}) = \frac{\delta_{ij}}{r} + \frac{\hat{x}_i\hat{x}_j}{r^3}, \end{aligned} $$
(8)

which is undefined when r = 0 (when evaluating the velocity at the location of a force). Notice that \(S_{ij}^{\phi _\epsilon }\) in Eq. (7) does not have the same property when 𝜖 > 0. Velocities due to a regularized Stokeslet are found by

$$\displaystyle \begin{aligned} \mathbf{u^{\phi_\epsilon}}(\hat{\mathbf{x}}) = \frac{1}{8\pi\mu}S^{\phi_\epsilon}(\hat{\mathbf{x}})\mathbf{f}, {} \end{aligned} $$
(9)

which is sometimes helpful to express in terms of the ith component of the velocity

$$\displaystyle \begin{aligned} u_i^{\phi_\epsilon}(\hat{\mathbf{x}}) = \sum_{j=1}^{3n} \frac{1}{8\pi\mu}S^{\phi_\epsilon}_{ij}(\hat{\mathbf{x}})f_j, {} \end{aligned} $$
(10)

where n is the number of forces exerted on the fluid. Notice Eqs. (9) and (10) display a linear relationship between forces exerted on a fluid and resulting velocities calculated anywhere in the fluid. Similar relationships hold when replacing the regularized Stokeslet \(S^{\phi _\epsilon }\) with the singular Stokeslet S:

$$\displaystyle \begin{aligned} \mathbf{u}(\hat{\mathbf{x}}) = \frac{1}{8\pi\mu}S(\hat{\mathbf{x}}) \mathbf{f}. \end{aligned} $$
(11)

With this comes a natural question of the errors associated with calculating the same quantity with two different methods. There are errors due to regularization and quadrature (numerical approximation of integrals in both space and time), which are discussed in more detail in sources such as [4,5,6, 13], but will not be the focus of this discussion.

We use regularized Stokeslets to model a solid body (cilium) and do so by placing a collection of regularized Stokeslets along the centerline of the cilium. We select a value for the spreading parameter 𝜖 that spreads the force to approximately the radius of a pulmonary cilium [6, 29]. In our models we use the value 𝜖 = 0.1 μm. Using this value, we also calculate the number of regularized Stokeslets necessary to discretize the body of our cilia. Since each regularized Stokeslet has a diameter of 0.2 μm, it takes 30 to model a cilium at a length L = 6 μm.

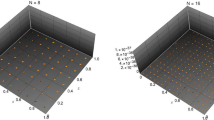
The regularized Stokeslets we are considering here are free-space solutions to the quasi-steady Stokes equations in three dimensions. However, the pulmonary cilia protrude from epithelial cells, and we are interested in modeling the PCL in three dimensions above the cell surface. To model the epithelial cells we implement a system of regularized image singularities that create a zero-velocity plane that emulates the no-slip cell surface. This creates a no-slip plane at z = 0 in \(\mathbb {R}^3\), and we only consider the fluid motion in \(\mathbb {R}^3\) where z > 0. To create a zero-velocity plane mathematically, we place a regularized Stokeslet as well as a collection of other regularized singularities (doublet, dipole, and two rotlets) at the image point reflected from the original regularized Stokeslet across the desired zero-velocity plane. These particular singularities were chosen because their net effect cancels that of the original regularized Stokeslet to create a plane within the fluid domain with no velocity that simulates the presence of a physical stationary boundary as the epithelial cells (at z = 0). The specific cutoff functions and form of the other singularities can be found in [4, 14] and a discussion of the singular (𝜖 = 0) versions of these can be found in [25]. Matlab code for the regularized singularities in both the free-space case and semi-infinite case (image singularities) can be found at https://github.com/ELBou21/FURM.

Figure 3 shows an example resulting from this combination of regularized singularities. Imagine two forces exerted in the xz-plane (shown in red). The resulting fluid flow is shown at a variety of tracking points, or tracer points, chosen in a grid pattern for velocity visualization purposes here. These are infinitesimally small, massless particles that move with the fluid, but do not affect the fluid itself. The blue arrows represent the fluid velocity in the xz-plane at the given locations resulting from the two red forces. Notice in the free-space solution on the left in Fig. 3a, there are visible blue velocity vectors where z = 0 indicating that there is fluid flow in that plane (the xy-plane that is perpendicular to the page). Contrast this with the velocity field shown in Fig. 3b that implements the system of image singularities. Notice that the net effect provides similar flow near the red forces, but now there are no visible blue arrows where z = 0, indicating that the velocities in the xy-plane are zero vectors. Since we are creating this zero-velocity plane with the intent of mimicking a no-slip plane that represents the cell surface, we would only consider the fluid domain above the no-slip plane where z > 0. Notice there is fluid flow generated below the plane in Fig. 3b, however, we disregard this in practice. It is shown here for the purposes of demonstrating the effects of the system of image singularities, but when using the MRS, one would only put tracking points at desired locations (not necessarily in a grid) in the feasible fluid domain where z > 0.

Fig. 3
figure 3

Fluid flow resulting from two regularized forces (shown in red) (a) in free-space and (b) with image singularities (not shown) to create a no-slip plane at z = 0 where the velocities vanish. In practice, only the fluid above the cell surface (where z > 0) would be studied

Full size image

The MRS provides a linear way to relate external forces exerted on the fluid into velocities anywhere in the fluid. Since the motion of the cilia is providing these external forces on the fluid, we must translate the beat form information into external forces exerted on the fluid. Often the beat form is known as a series of snapshots of the cilium’s position, which we use to calculate velocity. While the specifics of the beat form we use will be discussed in Sect. 2.3, consider x k to be the location of a regularized Stokeslet on a cilium’s centerline at time k. Using the discretized position information from the beat form in time intervals of length h, we implement a second order finite difference scheme with respect to time to calculate the velocity of each regularized Stokeslet at time k using information about the discretized position at four different (known) instances in time:

$$\displaystyle \begin{aligned} {\mathbf{u}}^k= \frac{{\mathbf{x}}^{k-2h} - 8{\mathbf{x}}^{k-h} + 8{\mathbf{x}}^{k+h} - {\mathbf{x}}^{k+2h}}{12h}. \end{aligned} $$
(12)

Note that because the cilium beat form is repeated and the position is known at each instance in time, there is no concern regarding how to initialize this velocity calculation. We arrange the information from each regularized singularity into a system of linear equations for each point of interest. We exploit the linear, homogeneous properties of the quasi-steady Stokes equations to create the system u = Af, where u is a 3m × 1 vector of velocities, f is a 3n × 1 vector of forces, and A is a 3m × 3n matrix containing the information of each regularized Stokeslet as well as the collection of regularized image singularities.Footnote 1 Here m is the number of velocity calculation points and n is the number of regularized Stokeslets or forcing points. Thus, the full solution superimposes solutions for each individual regularized Stokeslet and the collection of image singularities. To find the forces f that would recreate the desired ciliary motion, we iteratively solve the linear system created by imposing the velocities at each regularized Stokeslet given by the beat cycle using the generalized minimum residual method (GMRES) in MATLAB. In this case, we have the same number of tracking points, m, and forcing points, n, so A is a square matrix that we invert to solve. Note that this matrix becomes singular for large enough values of 𝜖 given a fixed spatial distribution [6].

After calculating the forces required to impose a cilium’s beat form, we can move on to calculating velocities at other points of interest anywhere in the fluid. We again use u = Af, but now m ≠ n and A is no longer a square matrix. The forces are already known from the previous calculation, but A and u are different in size because of the change in where the velocity is being calculated. Thus, we can solve for the fluid velocity at a given point through matrix multiplication as the net effect of each force we place in the fluid domain in the semi-infinite system. Once we have the velocity, we use Euler’s method to update the tracer’s new position.

2.3 Cilium Beat Form

Literature on modeling pulmonary cilia shows different approaches to modeling cilia and defining the beat form. Fulford and Blake parameterized a curved cilium that features a recovery stroke in the same plane as the power stroke [16]. The length of the cilium in their model’s recovery stroke is shorter than in the power stroke and patches of cilia are synchronized [16]. Gheber and Priel simplify a cilium into a straight line in the power stroke that sweeps out an arc of a circle and two lines connected at a bend point in an out-of-plane recovery stroke [17]. This model was created to study the transmission of light through a field of cilia. Consequently, their model’s recovery stroke does not build a full cilium, only the projection of the out-of-plane stroke onto the cell surface. Smith, Gaffney, and Blake model a line of cilia using the Fulford and Blake parameterization to represent each step in the beat form, but do not model the patches with metachronal waves we are interested in or an out-of-plane recovery stroke [30].

Taking beat parameters and inspiration for how to build a cilium in its recovery stroke from the model created by Gheber and Priel [17], we create and test a cilium beat cycle featuring an out-of-plane recovery stroke with a motile bend, motile bend angle, and a varying recovery angle. Top and side views of our power stroke are shown in Fig. 4a, b and the same views of our recovery stroke are shown in Fig. 4c, d. These features were selected to mimic the description of cilia in rabbit trachea given by Sanderson and Sleigh [28]. Our cilium’s beat cycle closely resembles Gheber and Priel’s [17], but we are concerned with more than the projection of the cilium onto the epithelial cells. We define a recovery stroke that has a similar projection to Gheber and Priel’s model but is comprised of the full length cilium moving in a three-dimensional fluid domain.

Fig. 4
figure 4

Stages of the (a, b) power and (c, d) recovery strokes. The power stroke moves from left to right while the recovery stroke moves from right to left. The same time step is used in all plots showing faster speeds during power stroke than during recovery stroke. (a) Top view of our cilium’s power stroke. (b) Side view of the power stroke beginning at θ i and ending at θ f. The effective stroke angle, θ e, is the angle between the most extreme cilium locations so that θ i + θ e + θ f = 180∘. (c) Top view of our cilium’s recovery stroke. (d) Side view of the recovery stroke

Full size image

To model a cilium of length L, we utilize parameters of a cilium’s temporal asymmetry and the arc of radius L of the power stroke from Gheber and Priel’s model [17]. They model the power stroke of a cilium by sweeping out an arc of radius L that begins at angle θ i and ends at angle θ f, both of which are measured from the cell surface, as shown in Fig. 4b. These angles can be calculated from the effective stroke angle θ e

$$\displaystyle \begin{aligned}\theta_i = \theta_f = (180^\circ - \theta_e)/2, \end{aligned} $$
(13)

as seen in [28]. We use θ e = 110∘, which makes θ i = θ f = 35∘. We define temporal asymmetry in the same manner as Gheber and Priel and choose the ratio of the recovery stroke to effective stroke to be Rt = 3 [17].

During the recovery stroke, we model the cilium as two lines connected at a bend point. This bend point propagates from L∕4 to L over the entire duration of the recovery stroke. The minimum bend angle of 135∘ is achieved halfway through the recovery stroke, where the angle is measured between the two lines of regularized Stokeslets. Thus, a smaller angle corresponds to a larger bend. The angle of the bend necessarily starts and ends at 180∘ to match the straight cilium at the beginning and end of the power stroke.

To match the projection described by Gheber and Priel [17], we instituted a parameter of the recovery stroke defining the elevation angle at the midpoint of the recovery stroke. This angle dictates how close the cilium gets to the xy-plane. An elevation angle of 0∘ corresponds to the recovery stroke sweeping through the xy- plane and an elevation angle of 90∘ would be completely vertical. To maintain the length of our cilium and match the projection given by Gheber and Priel [17], we elevate the cilium in the recovery stroke. Measured up from the xy-plane, our cilium progresses from the elevation angle of 35∘ at the end of the power stroke up to 55∘ at the midpoint of the recovery stroke when it is tilted over the negative y-axis (out of the page in Fig. 4d) and back down to 35∘ for the beginning of the next power stroke.

2.4 Patches of Cilia

After modeling a single cilium that includes characteristics that mimic the behavior of realistic cilia noted by Gheber and Priel [17], we copy an individual cilium to build a patch of cilia, spaced 1 μm apart in both the x- and y-directions. The power stroke moves in the positive x-direction and the recovery stroke circulates out in the negative y-direction, as shown in Fig. 4. To implement a phase difference as outlined by Gheber and Priel [17], we varied the starting stages of each cilium in the patch. While we refer to the phase difference as a delay, we actually implement the phase changes as a forward phase difference. Thus, the leading cilium that is farthest away from the initial cilium (located at the origin) is ahead of the initial cilium, as shown in Fig. 5. The initial cilium began at the first step of the power stroke, with each subsequent cilium in the x- or y-direction starting one step ahead of the previous one. Thus, in a 30 × 5 patch, with one time step “delay” in both the x- and y-directions, the leading cilium starts 33 steps ahead of the initial cilium. In our model, we use a time step of 50 steps per stroke with a temporal asymmetry of Rt = 3, meaning that the effective stroke completes in 13 steps and the recovery stroke completes in 37 steps. Therefore, the leading cilium and much of the surrounding cilia begin in a recovery stroke step. This observation will resurface when we begin our fluid flow analysis as it is central to the explanation of the trajectories of tracer points.

Fig. 5
figure 5

Starting stages of the initial cilium and the leading cilium

Full size image

3 Results

With a focus on fluid transport as a result of the metachronal wave, our research looked at the trajectories of a specific set of tracer points subject to different metachronal waves. Tracer points have no impact on the fluid and are only used for visualizing flow. They are massless infinitely small particles that move with the local fluid velocity. By following their position over a sequence of time snapshots, we can visualize their trajectories. We chose a set of 42 points to serve as our basis for comparison across the different cilia patches. Points were placed at a variety of locations with respect to the cilia. Locations below the cilia tips were less desirable to analyze because of near-field interactions with the cilia. However, points at z = 7 μm provided a good basis for analysis as they sat right above the tips of the cilia and did not experience the interactions with other cilia as significantly. As tracer points approached the edge of the patch, their motion changed as a result of moving away from the patch. For this project, we focused on the behavior due to the metachronal wave and were mainly interested in the behavior over the patch itself when edge effects were negligible. For future work, patches could be constructed with different dimensions depending on the scope of the problem of interest, but this does increase computational cost. Realistically, a patch in the lungs would be neighbored by other patches, but our model only focuses on a single patch.

We focused on several patches with different wave characteristics, including a synchronized patch, a patch with a “regular” metachronal wave, and two patches with compressed metachronal waves, outlined in Sect. 3.2. The size of the patches varies from a rectangular patch of 150 cilia (30 × 5) to a square patch of 100 cilia (10 × 10). These choices were made to balance computational cost and the ability to see the effects of the metachronal wave on particle trajectories before encountering edge effects. Modeling larger patches of cilia increases computational time, but depending on a particular project’s goals, this may be worth implementing.

3.1 No Metachronal Wave

As a first step in analyzing the effects of a metachronal wave, we modeled a synchronized patch of cilia without any phase delay, as seen in Fig. 6a, b. This facilitates analysis by emphasizing the influence of a delay on the trajectories of tracer points and ultimately the transport of fluid. Regardless of the tracer points’ starting positions, our synchronized patch, of size 30 × 5, caused only slight movement in the effective stroke direction, as shown by the blue paths in Fig. 7.

Fig. 6
figure 6

Synchronized (a, b), regular wave (c, d), and compressed wave (e, f) at the initial time step on a 30 × 5 patch. (a) Synchronized 30 × 5 patch of cilia. (b) Synchronized 30 × 5 patch of cilia. (c) Regular wave on a 30 × 5 patch of cilia. (d) Regular wave on a 30 × 5 patch of cilia. (e) Compressed wave on a 30 × 5 patch of cilia. (f) Compressed wave on a 30 × 5 patch of cilia

Full size image
Fig. 7
figure 7

Two views of trajectory comparisons between a synchronized patch of cilia and two metachronal waves for the tracer point beginning at (0, −2, 7). A single cilium is shown for perspective, but the red rectangular region shows the footprint of the 30 × 5 cilia patch. The implementation of a metachronal wave increases transport (magenta) over the synchronized case (blue) and the compressed wave (green) greatly reduces the loops caused by the recovery stroke, increasing transport. (a) Synchronized 30 × 5 patch of cilia with fluid trajectories shown. (b) Top view

Full size image

3.2 Various Metachronal Waves

Using the same tracer points discussed above, we examine the effects of a regular metachronal wave, beginning with a delay of one time step in both the x- and y-directions as discussed in Sect. 2.4 with the goal of finding the characteristics of a wave that influence fluid transport. This wave is shown in Fig. 6c, d. In comparison to the synchronized patch, the tracer points have much larger transport in the effective stroke direction. Looking at Fig. 7, we see that in the synchronized 30 × 5 patch the tracer point (blue) makes very little forward progress in the positive x-direction and instead loops back nearly to its starting location. In contrast, the tracer point from a patch with a one time-step delay in both directions (magenta) makes significant forward progress in the same time interval. From the top view in Fig. 7b, we see that the tracer’s path during the recovery stroke sweeps out a smaller arc in the metachronal wave case than in the synchronized case. Our interpretation of this movement is that the wave mitigates the backward motion of the cilia in the recovery stroke and increases the forward transport of the PCL.

The next patch of cilia we examine is a 30 × 5 field with a metachronal wave with a delay of one time step in the y-direction and two time steps in the x-direction. We will refer to this metachronal wave as a compressed wave because it decreases the wavelength of the metachronal wave as seen in Fig. 6e, f. The ability of the compressed wave to mitigate the effects of the recovery stroke is evident when viewing the trajectory of fluid tracers over the compressed wave in Fig. 7 (green). Since we have shortened the wavelength of the metachronal wave, we have more cilia in their power stroke in the same 30 × 5 patch in our model. Therefore, as the recovery stroke passes tracer points in the compressed patch, tracers are closer to the previous and upcoming power strokes than they were in the patch with the regular wave.

We also investigate compressing the wave in the y-direction by testing our model on a 10 × 10 patch with a delay of one time step in the x-direction and two in the y-direction. We chose to use a 10 × 10 patch to investigate y-compression so that there was a sufficient number of cilia in that direction to demonstrate the effects of that compression. Comparing tracer points over a synchronized patch, patch with a regular wave, and patches with compressed waves in the x- and y-directions shows that compression in either direction works to remove the effects of the recovery stroke, as shown in Fig. 8b. In the 10 × 10 patch we see that compression has less of an impact on transport in the x-direction, but this may be a factor of patch length. However, loops seen in the tracer trajectories are greatly reduced in size with both implementations of a compressed wave relative to the synchronized and regular wave patches, demonstrating its effectiveness at decreasing motion due to the recovery stroke.

Fig. 8
figure 8

Two views of trajectory comparisons between a synchronized patch of cilia and three metachronal waves for the tracer point beginning at (0, −4, 7). A single cilium is shown for perspective, but the rectangular region shows the footprint of the 10 × 10 cilia patch. The implementation of a metachronal wave increases transport and a compression in the x-direction reduces the loops caused by the recovery stroke, thus increasing transport. (a) Trajectory comparisons over a 10 × 10 patch of cilia with various metachronal waves. (b) Top view

Full size image

4 Conclusion

We sought to create a model of the carpet-like patches of pulmonary cilia found on the surface of the lungs, essential to the mucociliary clearance process. Using the method of regularized Stokeslets, we developed a model for pulmonary cilia that features an out-of-plane recovery stroke. By instituting a system of regularized singularities, we modeled the effects of the epithelial cells which act as a no-slip boundary for our fluid.

Our model uses many of the beat form parameters defined by Gheber and Priel. We also use their recovery stroke’s projection on the epithelial cells as a reference from which we develop our full length, out-of-plane recovery stroke [17]. In our models, we look at patches of pulmonary cilia and institute a metachronal wave moving in an antiplectic direction relative to the power stroke. We impose the beat form rather than letting it evolve from hydrodynamic interactions as other studies do to study the effects of the metachronal wave [15, 18]. By varying the time-step delay used to create these waves, we are able to investigate various compressions of the wave. These variations serve to shorten the wavelength of the metachronal wave and we show that this has a substantial effect on fluid transport over the patch of cilia. Tracer points over a 30 × 5 patch with a metachronal wave compressed in the x-direction travel farther than tracer points starting at the same location travel over a patch with a regular wave or the synchronized patch.

In the case where we compressed the wave in the y-direction, we observe less contribution by the recovery stroke, demonstrated through smaller loops in the tracer point trajectories over the 10 × 10 patches than in the synchronized and regular wave patches. The tracer points do not demonstrate a large difference in x-transport, however, we believe this is due to a smaller patch size in the x-direction.

5 Suggested Projects

There are many extensions of ideas in this project that can be investigated by undergraduates. The interests and experiences of a particular student might make some of these projects more suitable than others. As with the nature of academic research, this topic of biologically inspired computational fluid dynamics is a current topic of research and the scope of cutting edge papers is often larger and more involved than would be appropriate for an undergraduate project, however, the tools presented here are very valuable to use in a creative way to find new problems that are appropriate relative to the experiences and interests of a student.

Future research ideas from the project described here focus on improvements upon our current model. While we currently use two lines connected at a bend point to model the body of the cilium during the recovery stroke, our model would benefit from the creation of a smooth cilium body that includes the same, current out-of-plane recovery stroke.

Research Project 1

Create a model of a cilium that more accurately captures the features of the pulmonary cilium beat form. That is, create a smooth curve that has an out-of-plane recovery stroke and matches the physiological properties of the beat form [16, 27]. This may involve using parametric curves, interpolation, and/or splines in both time and space. Does the new beat form produce significantly different results in terms of transport when modeled with the method of regularized Stokeslets?

Since a regularized Stokeslet is a way to transmit local forces onto a fluid, we used collections of regularized Stokeslets to model slender solid objects (cilia) here, but that can be expanded to model objects or boundaries of any shape. The flexibility of the method allows a user to customize the regularized Stokeslet placement to model any desired geometry, as long as the flow conditions fall into the low Reynolds number regime. We used the idea of regularized image singularities to create a no-slip (zero-velocity) plane that emulates the epithelial cell surface, however other fluid geometries, either in biological contexts or in a laboratory setting, could use other techniques to model the flow. The flexibility of the MRS being able to adapt to irregular geometries is one of its main strengths over other computational methods, some of which require a mathematical formulation of the potentially complicated boundary. The fundamental idea here is that you can enforce a velocity condition anywhere you place a regularized Stokeslet (and use the linear relationship to translate that to the appropriate external forces as discussed in Sect. 2.2). In modeling our pulmonary cilia, we were enforcing non-zero velocities, but regularized Stokeslets can also be used to enforce stationary objects with zero velocity, like no-slip boundaries of irregular geometries.

Research Project 2

Use the method of regularized Stokeslets to model the geometry of primary nodal cilia. These cilia are more rigid, less densely spaced, and have a different motion than pulmonary cilia. The geometry of the biological setting is also different in that the cilia sit in a more enclosed region. Sources in the literature such as [7, 8, 20, 30] give more details about the flow induced by primary nodal cilia.

The system of regularized image singularities mentioned in Sect. 2.2 creates a no-slip plane at z = 0 in a three-dimensional fluid domain to create a semi-infinite fluid domain as shown in Fig. 3. In a laboratory setting, one may be interested in studying fluid flow in a tank where wall effects are not negligible. The tank floor would be modeled by the existing system of image singularities, but what if other tank walls need to be taken into account?

Research Project 3

Modify the system of image singularities to create the walls of a fluid tank. That is, for each regularized Stokeslet you place in the fluid domain, what collection of regularized singularities do you need to place outside the fluid domain to create five no-slip walls (the floor and four vertical sides)? Where do these singularities need to be placed?

Research Project 4

Can you attempt to achieve the same effect of creating a fluid tank with five walls without using a system of image singularities? Perhaps utilize the fact that regularized Stokeslets can be used to implement velocity conditions on the fluid. In the aforementioned work in this chapter, we used the known velocity of the cilium to solve for the forces needed to mimic that effect. Could you use the known velocity of a tank wall to mimic those wall effects without image singularities?

There are other boundary conditions that people are interested in beyond no-slip where velocity vanishes on the boundary (particularly a solid boundary). However, if you were looking at a multi-fluid model, you might have an interface between two fluids with different properties.

Research Project 5

Can you formulate conditions that would be appropriate to create a no-stress boundary condition that might appear at the interface of two fluids?

The model described in this work assumes the cilia are immersed in a semi-infinite water-like fluid to model the PCL. However, the biological system has a mucus layer sitting atop the PCL. Can you modify the MRS to incorporate more than one fluid? One step would be to explore adding a second Newtonian fluid layer. If you make the assumption that the second layer is non-Newtonian, the MRS may no longer be helpful because the linearity of the Stokes equations that we rely on breaks down.

Research Project 6

Explore the idea of implementing a two-phase fluid with the MRS. What challenges do you face? Can you come up with a creative way to approximate the effects of the second fluid that rests atop the first?

The literature involving metachronal waves includes work on the formation of the metachronal waves. Our discussion here imposes the waves and studies resulting flow, but modifications could be made to the technique to create the wave formation.

Research Project 7

Modify the techniques in this chapter to explore the formation of the metachronal waves instead of imposing them. Perhaps this involves treating different segments of the cilia differently so that adjacent regularized Stokeslets react to each other and the fluid instead of having their positions all enforced through the beat form. Since regularized Stokeslets transmit forces to the fluid, one might consider using external spring forces between nearby Stokeslets to create a flexible cilium that responds to the surrounding fluid.

When studying the motion of “particles” in the fluid in this project, the particles are actually infinitesimal passive fluid tracers that have no impact on the fluid. However, in the real world, the contaminants trapped in the mucus have physical dimensions and their presence affects the fluid around them. Their density affects their buoyancy; their size affects their drag forces. In mucociliary clearance, their size may impact their transport. In a different application, if one is trying to deliver drugs through an inhaled medication (like an asthma inhaler), the drug particles need to penetrate the fluid flow and get absorbed by the epithelial cells. Different drugs have different particle sizes that may present challenges to transport and absorption.

Research Project 8

Do the properties of the particles affect flow induced by a metachronal wave in a significant way? Can you model individual particles of a given radius or density to explore the effects of the particle’s physical presence on the flow? What particle properties are desirable for the case of contaminant transport out of the lung? What about in the case of a drug delivery system?

Since turbulence is not present in low Reynolds number systems, mixing can be an interesting topic. Some organisms use their motion to create mixing opportunities to find nutrients.

Research Project 9

Can you modify the cilia model presented here to study questions related to mixing of tracer particles in the fluid? If your goal was to create a low Reynolds fluid environment that is favorable to mixing near cilia, would you propose the cilia move in a metachronal wave or would you propose a different motion to enhance mixing? Can you find evidence that different motions are more adept at mixing the surrounding fluids?

The sizes of the cilia patches in this project were chosen to reduce computational time while still observing desired metachronal wave effects on fluid trajectories.

Research Project 10

Explore properties of the matrices involved in this system u = Af (both when A is square and when it is not). Do you have the same matrix characterization if A only contains regularized Stokeslets (in a free-space model) or if it also contains the systems of regularized image singularities (in a semi-infinite model)? Can you leverage any of these properties to explore ways of more efficiently calculating the forces when velocities are known or increasing computational speed when calculating velocities are calculated at tracer points from known forces?

While cilia are the foundation of the biological application focused on in this work, there is much research interest in biological fluid flows relating to transport of small flagellated organisms like bacteria and spermatozoa. Like cilia, flagella are slender objects immersed in a fluid, but they often serve the role of propelling a microorganism through a fluid.

Research Project 11

Explore other biological fluid flow scenarios to find an application of the MRS to suit your interests.