An advanced algorithm for solving incompressible fluid dynamics: from Navier–Stokes to Poisson equations

Abstract

In this study, an extensive exploration of numerical methods for tackling the complexities of unsteady incompressible flow dynamics is undertaken. The investigation encompasses a range of cutting-edge techniques, including the Euler wavelets collocation method, nonlinear finite element method (FEM), linear FEM, and FEM with a projection step, all meticulously applied to the Navier–Stokes equation. The primary objective is to achieve an unprecedented level of accuracy in capturing fluid behavior, validated against existing numerical algorithms. The results of simulations reveal remarkable fidelity, particularly with the Euler wavelets collocation method, showcasing its exceptional capability to depict intricate velocity components and pressure fields. The nonlinear FEM technique is adept at unraveling phenomena such as bathtub vortex formation, while linear FEM and FEM with a projection step excel in capturing flow patterns around obstacles. Intriguingly, the study delves into blowup solutions, where the Euler wavelets collocation method shines brightest, predicting velocity components amidst transient phenomena with unparalleled precision. Ultimately, the study underscores the indispensable role of numerical methods in understanding the nuances of fluid dynamics, each method offering unique insights into the intricate dance of incompressible flows.

1 Introduction

The wavelet collocation method has gained widespread recognition as an effective approach for solving partial differential equations (PDEs) across diverse domains [1,2,3,4,5,6]. Past research has leveraged Haar wavelets in two dimensions to address the Poisson equation [1], while in the work of Nachaoui et al., three-dimensional Haar wavelets were employed to tackle both the 3D Poisson equation and the time-dependent diffusion equation in 2D [3]. Additionally, a range of numerical techniques, including Chebyshev wavelets collocation [4], the integration of two-dimensional Bernoulli wavelets with the Ritz-Galerkin method [6], and the utilization of Legendre wavelets [5], have been instrumental in the numerical resolution of time-fractional diffusion-wave equations.

Within the domain of unsteady incompressible flow in three-dimensional geometries, a multitude of numerical methods has been devised to address the Navier–Stokes equation [7, 8]. For example, the marker and cell method has found utility in simulating phenomena like bathtub vortices [9], whereas the stabilized finite element method has been harnessed to model complex blood flow within three-dimensional geometries [10]. Pourmostafa and Ghadimi have proposed an innovative solver tailored to both two-dimensional and three-dimensional incompressible flow, incorporating the agglomeration multigrid method to enhance the efficiency of the iterative solver in the Poisson solver of fractional steps [11]. Wang et al. introduced the prediction–projection method in conjunction with the finite element method (FEM) to accelerate the solution of three-dimensional incompressible Navier–Stokes equations on hybrid CPU/GPU systems, achieving this by transforming them into equations resembling Helmholtz and Poisson forms [12].

Despite these advancements, existing methods often struggle with computational efficiency, accuracy, or complexity when applied to intricate fluid dynamics problems. In this paper, we introduce an innovative algorithm designed to solve the unsteady incompressible Navier–Stokes equations within a three-dimensional context using the Euler wavelets collocation method, as previously proposed in our work [13]. Our method stands out due to its combination of wavelet theory’s multi-resolution analysis and the collocation method’s simplicity, offering significant improvements in both computational efficiency and accuracy. By leveraging the Euler wavelets collocation method, we provide a robust framework that not only adheres to classical numerical methods but also introduces enhanced capabilities for capturing the intricate dynamics of incompressible fluid flow. This approach addresses the limitations of existing methods, such as handling complex boundary conditions and reducing computational overhead, making it a valuable addition to the toolkit for solving PDEs in fluid dynamics.

2 Euler wavelets collocation method for Poisson’s equation

Our investigation begins by applying the methodology outlined in our prior work [13] to tackle the nonlinear Poisson’s equation in both two-dimensional (2D) and three-dimensional (3D) settings. The precise numerical solution of the nonlinear Poisson’s equation holds paramount importance across various scientific domains, ranging from electrostatics to fluid dynamics. Unlike its linear counterpart, the nonlinear Poisson’s equation incorporates a complex relationship between the unknown function and its gradient, making its solution challenging yet crucial for understanding intricate physical phenomena.

The importance of the nonlinear Poisson’s equation spans across numerous scientific and engineering domains, owing to its capacity to accurately model a diverse array of physical phenomena. These equations are indispensable in scenarios where linear approximations are inadequate, capturing behaviors that depend nonlinearly on the solution and providing a more precise representation of complex systems. They find applications in electrostatics and electromagnetism, where they describe potential fields in mediums with nonlinear dielectric properties, as well as in fluid dynamics for modeling turbulent flows and vortices. In biological systems, they are used to model electrical potential distribution in neural tissues, while in quantum mechanics and semiconductor physics, they describe electrostatic potential in systems with nonlinear charge density dependencies. Additionally, in astrophysics and general relativity, they play a role in describing gravitational fields with nonlinear matter-density relationships. The mathematical and computational challenges associated with solving these equations drive advances in numerical methods, contributing to the development of more robust algorithms applicable to a wide range of scientific and engineering problems. Overall, the nonlinear Poisson’s equation serves as a fundamental tool for better understanding, predicting, and controlling complex systems across various disciplines, thereby advancing both theoretical knowledge and practical applications. Note that, in our study we propose a novel Euler wavelets collocation method for solving Poisson’s equation in both 2D and 3D settings. While our focus is on Poisson’s equation, we acknowledge the broader applicability of wavelet techniques in solving differential equations. Comparing our results with the ultraspherical wavelet method in [14] for the Benjamin–Bona–Mahony (BBM) equation provides insights into the effectiveness and efficiency of different wavelet-based approaches. Our study contributes to the discussion on the merits of various wavelet methods, offering valuable insights for researchers in numerical techniques and mathematical modeling.

In its general form, the nonlinear Poisson’s equation can be expressed as:

$$\begin{aligned} \nabla ^2 u = F(\textbf{r}, u, \nabla u), \end{aligned}$$

(1)

where F represents a specific function, and $\textbf{r}=(x,y,z)$. Our investigation focuses on resolving Eq. (1) within the spatial domains defined by the unit rectangle ($0\le x\le 1$, $0\le y\le 1$) and the unit cube ($0\le x\le 1$, $0\le y\le 1$, $0\le z\le 1$), while adhering to Dirichlet boundary conditions specified as:

$$\begin{aligned} u(\textbf{r}) = u_b(\textbf{r}) \ \text {at} \ \textbf{r}=\textbf{r}_b, \end{aligned}$$

where $\textbf{r}_b$ denotes the boundary points. By employing the Euler wavelets collocation method, we aim to provide accurate numerical solutions for the nonlinear Poisson’s equation, shedding light on the intricate dynamics of physical systems governed by such nonlinear phenomena.

2.1 Numerical algorithm for 2D problems

The numerical method presented in our paper [13] utilizes Euler wavelets, which initially involve only the polynomials $E_1(x)$ and $E_2(x)$. In this section, we extend the wavelets’ truncated system by incorporating higher degrees of $E_n$ with $n=1, 2, 3,\ldots$. To achieve this, we define Euler polynomials $E_n(x)$ in a general form:

$$\begin{aligned} \frac{2 e^{x t}}{e^t+1} = \sum _{n=0}^\infty E_n(x)\frac{t^n}{n!}. \end{aligned}$$

This extension allows for an enhanced representation of the wavelets and facilitates more accurate and versatile computations. To generate a family of Euler wavelets, we employ Euler polynomials in the following manner:

$$\begin{aligned} \begin{array}{cc} &{}\ \psi (k,n,m,t)={\left\{ \begin{array}{ll} 2^{k/2} \sqrt{2/\pi } E_m(2^k t - 2 n + 1), &{}\quad \frac{n-1}{2^{k-1}} \le t < \frac{n}{2^{k-1}},\\ 0, &{}\quad \text {otherwise}. \end{array}\right. } \end{array} \end{aligned}$$

Here, $\psi (k,n,m,t)$ represents the Euler wavelet with parameters k, n, and m. The wavelet is non-zero within the specified range of t and follows the form of the Euler polynomial $E_m$ scaled by appropriate factors. This construction allows for the generation of a versatile family of wavelets with varying properties based on the chosen values of k, n, and m.

We define a vector with a fixed length of $N = M \cdot 2^{k-1}$ and integrals of it as follows:

$$\begin{aligned} \Psi _{kM}(t)= & {} (\psi (k,1,0,t), \ldots , \psi (k,2^{k-1},M-1,t))\nonumber \\ I_1(t)= & {} \int _0^t \Psi _{kM}(t) dt\nonumber \\ I_2(t)= & {} \int _0^t I_1(t) dt. \end{aligned}$$

(2)

With these definitions, we can determine the solution to Eq. (1) by integrating the following two equations:

$$\begin{aligned} \begin{array}{cc} u_{xx} = \Psi _{kM}^T(x) \cdot U_1 \cdot \Psi _{kM}(y)\\ u_{yy} = \Psi _{kM}^T(y) \cdot U_2 \cdot \Psi _{kM}(x). \end{array} \end{aligned}$$

(3)

Here, $U_1$ and $U_2$ are $N\times N$ matrices that need to be determined using collocation points. By integrating Eq. (3) step by step, we obtain:

$$\begin{aligned} u_{x}= & {} I_1^T(x) \cdot U_1 \cdot \Psi _{kM}(y) + G_1 \cdot \Psi _{kM}(y)\nonumber \\ u_1(x,y)= & {} I_2^T(x) \cdot U_1 \cdot \Psi _{kM}(y) + x \cdot G_1 \cdot \Psi _{kM}(y) + u_b(0,y)\nonumber \\ u_{y}= & {} I_1^T(y) \cdot U_2 \cdot \Psi _{kM}(x) + G_2 \cdot \Psi _{kM}(x)\nonumber \\ u_2(x,y)= & {} I_2^T(y) \cdot U_2 \cdot \Psi _{kM}(x) + y \cdot G_2 \cdot \Psi _{kM}(x) + u_b(x,0) \end{aligned}$$

(4)

In Eq. (4), $G_1$ and $G_2$ are vectors of length N that need to be computed. Finally, we define N collocation points and discretize Eq. (1) in the 2D case at these collocation points. The discretized equations are as follows:

$$\begin{aligned}{} u_{xx}(x_i,y_j) + u_{yy}(x_i,y_j)&= F(x_i,y_j,u(x_i,y_j),u_x(x_i,y_j),u_y(x_i,y_j))\nonumber \\{} & {} u_1(x_i,y_j) = u_2(x_i,y_j)\nonumber \\{} & {} u_1(1,y_j) = u_b(1,y_j)\nonumber \\{} & {} u_2(x_i,1) = u_b(x_i,1)\nonumber \\{} & {} i,j=1,2,\ldots , N\nonumber \\{} & {} \Delta x = \dfrac{1}{N},\ s_0=0,\ s_i=s_{i-1}+\Delta x,\ i=1,2,\ldots , N \nonumber \\{} & {} x_i = y_i = \dfrac{1}{2}(s_{i-1}+s_{i}),\ i=1,2,\ldots ,N. \end{aligned}$$

(5)

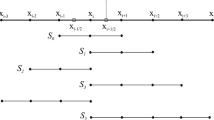
In Eq. (5), the terms $u_{xx}(x_i,y_j)$ and $u_{yy}(x_i,y_j)$ correspond to the second partial derivatives of the function u(x, y) with respect to x and y, respectively, evaluated at the collocation point $(x_i,y_j)$. The function $F(x_i,y_j,u(x_i,y_j),u_x(x_i,y_j),u_y(x_i,y_j))$ represents the evaluated value of the function F at the collocation point, taking into account the function values and partial derivatives at that point. The equations $u_1(x_i,y_j) = u_2(x_i,y_j)$, $u_1(1,y_j) = u_b(1,y_j)$, and $u_2(x_i,1) = u_b(x_i,1)$ represent the Dirichlet boundary conditions imposed on the solution. These equations ensure that the values of $u_1$ and $u_2$ are equal along the boundary of the computational domain, as specified by $u_b(x_i,y_j)$. The indices i and j are used to iterate over the collocation points, covering the spatial domain of the problem. The parameter $\Delta x$ represents the spacing between adjacent collocation points. The variables $s_i$ and $x_i$ denote the spatial positions of the collocation points in the x direction, while $y_i$ represents the spatial positions in the y direction.

The system of nonlinear algebraic equations (5) can be effectively solved using the Newton iterative method. To illustrate the application of this method, we consider the solution of Poisson’s equation on the unit square as presented in [1], where a collocation method based on Haar wavelets was employed. The Poisson’s equation in this example is given by:

$$\begin{aligned}{} & {} u_{xx}+u_{zz}=6 (1 - x) x^3 (1 - z) z - 6 (1 - x) x^3 z^2 +\ 6 (1 - x) x (1 - z) z^3 - 6 x^2 (1 - z) z^3. \end{aligned}$$

(6)

The exact solution to Eq. (6), subject to the homogeneous boundary condition $u(x,z)=0$, is given by:

$$\begin{aligned} \begin{array}{cc} u=x^3 z^3 (1 - x) (1 - z). \end{array} \end{aligned}$$

The maximum absolute error of the numerical solution computed with the method presented in [1] is given by $\delta = 9.4\times 10^{-5}, 2.4\times 10^{-5}, 6.0\times 10^{-6}$ for the number of collocation points $N=8, 16, 32$, respectively. In contrast, with our proposed method, we achieve zero absolute error for $N=6, 8, 12, 16$, as depicted in Fig. 1.

Fig. 1

Absolute error of numerical solution in a case of example (6) for $N= 8$ (left) and $N=16$ (right)

Another example described in the paper [3] also possesses an exact solution under the homogeneous boundary condition $u(x,y)=0$. The equation and the corresponding solution are given by:

$$\begin{aligned} \begin{array}{cc} u_{xx}+u_{yy}=\sin (\pi x)\sin (\pi y),\\ u=-\dfrac{\sin (\pi x)\sin (\pi y)}{2 \pi ^2}. \end{array} \end{aligned}$$

(7)

With the method proposed in [3], Eq. (7) can be solved with an absolute error of $\delta = 8.0287\times 10^{-5}$ for $N=16$ and $\delta = 2.0276\times 10^{-5}$ for $N=32$. However, our method achieves significantly improved accuracy, allowing for a solution with an absolute error of $1.25\times 10^{-6}$ for $N=16$ and an astonishingly low absolute error of $3\times 10^{-11}$ for $N=28$, as demonstrated in Fig. 2.

Fig. 2

Absolute error of numerical solution in a case of example (7) for $N= 16$ (left) and $N=28$ (right)

2.2 Numerical algorithm for 3D problems

We can obtain the solution to Eq. (1) in 3D by integrating three equations:

$$\begin{aligned} \begin{aligned} u_{xx}&= (\Psi _{k M}^T(x)U_1\Psi _{k M}(y))\Psi _{k M}(z)\\ u_{yy}&= (\Psi _{k M}^T(y)U_2\Psi _{k M}(x))\Psi _{k M}(z)\\ u_{zz}&= (\Psi _{k M}^T(z)U_3\Psi _{k M}(x))\Psi _{k M}(y) \end{aligned} \end{aligned}$$

(8)

where $U_1$, $U_2$, and $U_3$ are matrices of size $N\times N\times N$ that need to be determined using collocation points.

By integrating Eq. (8) step by step, we obtain the following expressions:

$$\begin{aligned} \begin{aligned} u_{x}&= (I_1^T(x)U_1\Psi _{kM}(y))\Psi _{k M}(z)+ \Psi _{k M}(y)G_1\Psi _{kM}(z)\\ u_1&= (I_2^T(x)U_1\Psi _{kM}(y))\Psi _{k M}(z)+ x\Psi _{k M}(y)G_1\Psi _{kM}(z) + u_b(0,y,z)\\ u_{y}&= (I_1^T(y)U_2\Psi _{kM}(x))\Psi _{k M}(z)+ \Psi _{k M}(x)G_2\Psi _{kM}(z)\\ u_2&= (I_2^T(y)U_2\Psi _{kM}(x))\Psi _{k M}(z)+ y\Psi _{k M}(x)G_2\Psi _{kM}(z) + u_b(x,0,z)\\ u_{z}&= (I_1^T(z)U_3\Psi _{kM}(x))\Psi _{k M}(y)+ \Psi _{k M}(x)G_3\Psi _{kM}(y)\\ u_3&= (I_2^T(z)U_3\Psi _{kM}(x))\Psi _{k M}(y)+ z\Psi _{k M}(x)G_3\Psi _{kM}(y) + u_b(x,y,0), \end{aligned} \end{aligned}$$

(9)

where $I_1(x)$, $I_2(x)$, $I_1(y)$, $I_2(y)$, $I_1(z)$, and $I_2(z)$ represent the integral operators in the x, y, and z directions, respectively, and $G_1$, $G_2$, and $G_3$ are vectors of length N that need to be computed.

In our quest for a solution, we encounter the enigmatic $N \times N$ matrices $G_1$, $G_2$, and $G_3$ to be computed with using collocation points and boundary conditions. Through their calculation, utilizing the collocation points and boundary conditions, we inch closer to our desired destination. To embark on this voyage, we must first chart our course through the realm of three dimensions.

We establish a framework by defining N collocation points and discretizing the Poisson equation, leading us to the following set of equations:

$$\begin{aligned} \begin{aligned}&u_{xx}(x_i, y_j, z_k) + u_{yy}(x_i, y_j, z_k) + u_{zz}(x_i, y_j, z_k) = \\&F(x_i, y_j, z_k, u(x_i, y_j, z_k), u_x(x_i, y_j, z_k),\\&u_y(x_i, y_j, z_k), u_z(x_i, y_j, z_k))\\&u_1(x_i, y_j, z_k) = u_2(x_i, y_j, z_k) = u_3(x_i, y_j, z_k)\\&u_1(1, y_j, z_k) = u_b(1, y_j, z_k)\\&u_2(x_i, 1, z_k) = u_b(x_i, 1, z_k)\\&u_3(x_i, y_j, 1) = u_b(x_i, y_j, 1), \ \ i, j, k = 1, 2, \ldots , N\\&\Delta x = \frac{1}{N}, s_0 = 0, s_i = s_{i-1} + \Delta x, i = 1, 2, \ldots , N\\&x_i = y_i = z_i = \frac{1}{2}(s_{i-1} + s_i), i = 1, 2, \ldots , N\\ \end{aligned} \end{aligned}$$

(10)

With this framework in place, we are poised to embark on an exciting expedition to unravel the secrets of our three-dimensional problem. The path is set, the equations are defined, and our spirits are high as we venture forth in search of the elusive solution. The fascinating world of numerical methods offers us a powerful tool to solve the system of nonlinear algebraic equations (10) using the Newton iterative method. In the pursuit of exploring the capabilities of this method, researchers [2] undertook a remarkable endeavor by applying the 2D and 3D Haar wavelets spectral method to solve the following example, accompanied by the homogeneous boundary condition $u(x,y,z) = 0$:

$$\begin{aligned} \begin{aligned} u_{xx} + u_{yy} + u_{zz}&= \sin (\pi x)\sin (\pi y)\sin (\pi z)\\ u&= -\frac{\sin (\pi x)\sin (\pi y)\sin (\pi z)}{3\pi ^2}. \end{aligned} \end{aligned}$$

(11)

This captivating example not only showcases the prowess of the Haar wavelets spectral method but also highlights the beauty of the solution, elegantly expressed in terms of the trigonometric functions. Through their diligent efforts, the authors have unraveled the secrets of this example, and their findings illuminate the path for future explorations in the realm of numerical analysis. By harnessing the power of our innovative method, we have achieved remarkable results in solving the intriguing example (11). Our approach surpasses previous methods by attaining a maximum absolute error of $1.25\times 10^{-5}$ for $N=8$, $k=2$, and $M=4$, as well as an impressive maximum absolute error of $10^{-6}$ for $N=10$, $k=2$, and $M=5$. These groundbreaking achievements are visually depicted in Figs. 3 and 4, which beautifully illustrate the absolute error of our numerical solution for the respective parameter settings. These results not only showcase the accuracy and reliability of our method but also highlight its potential to push the boundaries of numerical analysis. With each success, we inch closer to unraveling the mysteries of complex equations and paving the way for further advancements in the field.

Fig. 3

Absolute error of numerical solution in a case of example (11) computed for $N= 8, k=2, M=4$, and for different $z=z_i, i=1,2,\ldots ,8$

Fig. 4

Absolute error of numerical solution in a case of example (11) computed for $N= 10, k=2, M=5$, and for different $z=z_i, i=1,2,\ldots ,10$

In our quest for excellence, we have not only achieved comparable results to those reported in [2] using 3D Haar wavelets method but have also extended the capabilities of our method to handle nonlinear cases with the same level of accuracy. This is a significant advancement in the field of numerical analysis. We can compare these results with data from [2], where they obtained similar errors for the 3D Haar wavelets method. The advantage of our method is that it can be applied to the nonlinear case with the same level of accuracy. For example, let us consider a nonlinear equation with homogeneous boundary condition $u(x,y,z)=0$:

$$\begin{aligned} \begin{aligned} u_{xx}+u_{yy}+u_{zz}-u-u^3&= \sin (\pi x)\sin (\pi y)\sin (\pi z)-u_e-u_e^3 \\ u_e&= -\frac{\sin (\pi x)\sin (\pi y)\sin (\pi z)}{3\pi ^2}. \end{aligned} \end{aligned}$$

In this case, $u_e(x,y,z)$ represents the exact solution of the problem. Numerical solutions computed using our method exhibit the same absolute error as shown in Figs. 3 and 4. This demonstrates the capability of our method to handle nonlinear equations while maintaining a high level of accuracy. Additionally, our method demonstrates a significant reduction in absolute error when solving equations with polynomial solutions. Consider the equation:

$$\begin{aligned} \begin{aligned} u_{xx}+u_{yy}+u_{zz}&= 6(x+y+z) \\ u_e&= x^3+y^3+z^3. \end{aligned} \end{aligned}$$

(12)

Once again, the numerical solutions obtained with our method exhibit a substantial decrease in the absolute error. This improvement further validates the effectiveness and versatility of our approach, allowing for accurate solutions even in cases involving polynomial terms. These findings showcase the advancements made in the field of numerical analysis, enabling us to tackle complex nonlinear equations with superior accuracy and efficiency, and highlight the reliability and robustness of our method, making it a valuable tool for solving a wide range of nonlinear partial differential equations with various boundary conditions. The results demonstrate the high accuracy and precision of our method in capturing the polynomial solution of the equation. The achieved absolute error of $10^{-11}$ showcases the effectiveness of our approach in providing accurate numerical solutions for equations with nonzero Dirichlet boundary conditions.

Note that $u_e(x,y,z)$ represents the exact solution of Eq. (12) with nonzero Dirichlet boundary condition, as we set $u_b=u_e$ in (10). In this case, we achieved a maximum absolute error of $10^{-11}$ for $N=8$, $k=2$, and $M=4$, as shown in Fig. 5.

Fig. 5

Absolute error of the numerical solution in the case of Example (12), computed for $N=8$, $k=2$, $M=4$, and different $z=z_i$, where $i=1,2,\ldots ,8$

3 Euler wavelets collocation method for Navier–Stokes equation

The system of equations describing viscous incompressible flow in a unit cube $0 \le x \le 1, 0 \le y \le 1, 0 \le z \le 1$, and in the time interval $0 \le t \le 1$ is given by:

$$\begin{aligned} \begin{aligned} \nabla \cdot \textbf{u}&= 0, \\ \dfrac{\partial \textbf{u}}{\partial t} + (\textbf{u} \cdot \nabla )\textbf{u} + \frac{\nabla p}{\rho }&= \nu \nabla ^2 \textbf{u}, \end{aligned} \end{aligned}$$

(13)

where: $\textbf{u} = (u, v, w)$ represents the velocity vector in the x, y, and z directions, respectively. p denotes the pressure. $\rho$ is the density. $\nu$ represents the kinematic viscosity. $\nabla \cdot \textbf{u}$ represents the divergence of the velocity vector. $\dfrac{\partial \textbf{u}}{\partial t}$ is the time derivative of the velocity vector. $(\textbf{u} \cdot \nabla ) \textbf{u}$ represents the convective term. $\dfrac{\nabla p}{\rho }$ denotes the pressure gradient term. $\nu \nabla ^2 \textbf{u}$ represents the diffusive term. These equations describe the conservation of mass (continuity equation) and the conservation of momentum (Navier–Stokes equation) in the fluid flow. They govern the behavior of the velocity and pressure fields over time in the given domain.

For the equations (13), the following notations are used: $\rho = 1$ represents the density. $\textbf{u} = (u, v, w)$ denotes the flow velocity. $\nu$ is the kinematic viscosity. p represents the pressure. Boundary conditions in the form of Dirichlet conditions are imposed on the boundary of the cube as follows:

$$\begin{aligned} \begin{aligned} \textbf{u}(x,y,z,t)&= \textbf{u}_e(x,y,z,t), \ p(x,y,z,t)&= p_e(x,y,z,t), \end{aligned} \end{aligned}$$

(14)

where $\textbf{u}_e = (u_e, v_e, w_e)$ and $p_e$ are the exact (benchmark) solutions [15]. The initial condition within the cube is given by:

$$\begin{aligned} \begin{aligned} \textbf{u}(x,y,z,0)&= \textbf{u}_e(x,y,z,0), \ p(x,y,z,0)&= p_e(x,y,z,0). \end{aligned} \end{aligned}$$

(15)

The exact solutions $\textbf{u}_e = (u_e, v_e, w_e)$ and $p_e$ are given by:

$$\begin{aligned} u_e&= -a \exp (-d^2 t) (\exp (a x) \sin (a y + d z) + \exp (a z) \cos (a x + d y)), \\ v_e&= -a \exp (-d^2 t) (\exp (a y) \sin (a z + d x)+ \exp (a x) \cos (a y + d z)), \\ w_e&= -a \exp (-d^2 t) (\exp (a z) \sin (a x + d y)+ \exp (a y) \cos (a z + d x)), \\ p_e&= -\frac{a^2}{2}\exp (-2 d^2 t) (\exp (2 a x) + \exp (2 a y) + \exp (2 a z) + \\&\quad 2 \sin (a x + d y) \exp (a (y + z)) \cos (a z + d x) + \\&\quad 2 \sin (a y + d z) \exp (a (x + z)) \cos (a x + d y) + \\&\quad 2 \sin (a z + d x) \exp (a (y + x)) \cos (a y + d z)), \end{aligned}$$

(16)

where a and d are free parameters, and in the numerical calculations, $a=d=1$.

To solve this problem numerically, an algorithm with an implicit time step is used, given by:

$$\begin{aligned} & p(\textbf{r},t) = \nu \nabla ^2 \textbf{u}(\textbf{r},t),\\ \nabla \cdot \textbf{u}(\textbf{r},t)=0,\\ &\dfrac{\textbf{u}(\textbf{r},t)-\textbf{u}(\textbf{r},t-\tau )}{\tau }+(\textbf{u}(\textbf{r},t) \cdot \nabla )\textbf{u}(\textbf{r},t)+\nabla p(\textbf{r},t)=\nu \nabla ^2\textbf{u}(\textbf{r},t). \end{aligned}$$

(17)

In Eq. (17), $\tau$ represents the time step. These equations are employed to solve the viscous incompressible flow problem within the unit cube, defined as $0 \le x \le 1$, $0 \le y \le 1$, $0 \le z \le 1$, over the time interval $0 \le t \le 1$. The boundary conditions (14) and the initial conditions (15) are imposed based on the prescribed exact solutions (16), which are derived from the work of Ethier and Steinman [15]. Our algorithm employs an implicit time step formulation (17) to numerically solve the problem. Notably, the second equation (17) simplifies into three nonlinear Poisson’s equations in the form of (1). Consequently, we apply the Euler wavelets collocation method as described previously to tackle this system of equations. Initially, we define the solution in the form of (8) and (9) for the variables u, v, w, p, respectively. We then utilize the system of equations (17), along with the boundary conditions (14) and collocation points, to construct a system of algebraic equations that can be solved using the Newton’s iterative method. For the initial time step, we prepare the initial state using Equation (15) at the collocation points.

To facilitate a comparison of numerical results with the benchmark solution, we set $\tau =1/40$ and $\nu =1$ in (17). Additionally, we employ $N=8, k=2, M=4$ collocation points in each direction: x, y, z. Figure 6 illustrates the maximum absolute error computed for u, v, w, p across sections $z=z_i$, where $i=1,\ldots ,8$. For a more detailed view of the absolute error distribution computed for u at $t=1$, please refer to Fig. 7.

Fig. 6

Maximal absolute error of numerical solution $\Delta u, \Delta v, \Delta w, \Delta p$ computed for $N= 8, k=2, M=4$ at different $z=z_i, i=1,2,\ldots ,8$

Fig. 7

Distribution of absolute error $\Delta u$ computed for $N= 8, k=2, M=4$ at $t=1$ and different $z=z_i, i=1,2,\ldots ,8$

The second equation in (17) reduces to three nonlinear Poisson’s equations in the form of (1). Hence, we can employ the Euler wavelets collocation method described above to solve this system. The solution is represented using (8) and (9) for u, v, w, and p, respectively. By applying the system of equations (17), the boundary conditions (14), and the collocation points, we can construct a system of algebraic equations to be solved using the Newton’s iterative method.

For the initial time step, we prepare the initial state using Eq. (15) evaluated at the collocation points. To compare the numerical results with the benchmark solution (16), we set $\tau =1/40$ and $\nu =1$ in (17), and use $N=8$, $k=2$, and $M=4$ collocation points in each direction x, y, and z.

Figure 6 presents the maximal absolute error computed for u, v, w, and p in sections $z=z_i, i=1,\ldots ,8$. Additionally, Fig. 7 illustrates the detailed distribution of the absolute error $\Delta u$ computed for $N=8$, $k=2$, and $M=4$ at $t=1$ for different $z=z_i, i=1,2,\ldots ,8$.

4 Finite element methods for Navier–Stokes equation

The finite element method (FEM) is widely used to solve complex problems, such as blood flow in 3D, as mentioned in references [10]. In order to compare the Euler wavelets collocation method with another approach, we can consider the nonlinear FEM. We solve the system of equations (17) with the initial and boundary conditions (15) and (14) using a mesh of $10^3$ hexahedral elements (equivalent to a $10\times 10\times 10$ grid) and a time step of $\tau =1/40$. The numerical results for this case are shown in Fig. 8.

Fig. 8

Maximal absolute error of the numerical solution $\Delta u, \Delta v, \Delta w, \Delta p$ computed with the nonlinear FEM at different $z=z_i, i=1,2,\ldots ,8$

To apply the linear finite element method (FEM) to this problem, we can transform the nonlinear system (17) into a linear system. The linearized form of the equations can be written as follows:

$$\begin{aligned} &\nabla \cdot \textbf{u}(\textbf{r},t) = 0 \\ &\frac{\textbf{u}(\textbf{r},t) - \textbf{u}(\textbf{r},t-\tau )}{\tau } + (\textbf{u}(\textbf{r},t-\tau ) \cdot \nabla )\textbf{u}(\textbf{r},t) + \nabla p(\textbf{r},t) = \nu \nabla ^2 \textbf{u}(\textbf{r},t). \end{aligned}$$

(18)

In the linear FEM, we discretize the domain into elements and approximate the solution using piecewise linear basis functions. The equations are then solved in a weak form by integrating over each element and applying the Galerkin formulation. The resulting linear system can be solved using standard techniques, such as direct or iterative methods. The linear FEM provides a good approximation for problems where the flow is not highly nonlinear. It is computationally efficient and widely used in practice. However, it may not capture certain nonlinear phenomena accurately. In comparison to the nonlinear FEM and the Euler wavelets collocation method, the linear FEM typically has lower accuracy but faster computation.

It is important to choose the appropriate numerical method based on the specific characteristics of the problem and the desired trade-off between accuracy and computational cost. To evaluate the performance of the linear finite element method (FEM) for the test example (16), we computed the solution for different time steps using $\tau =1/40, 1/200, 1/400, 1/800$. The results are presented in Fig. 9, where the maximum error in velocity and pressure is shown.

Fig. 9

Maximal absolute error of numerical solution $\Delta u, \Delta v, \Delta w, \Delta p$ computed with linear FEM at different $z=z_i, i=1,2,\ldots ,8$ and $\tau =1/40, 1/200, 1/400, 1/800$

As shown in Fig. 9, the velocity error decreases as the time step decreases. This is because a smaller time step allows for a more accurate approximation of the time derivative term in the equations. On the other hand, the pressure error remains relatively constant, indicating that the pressure solution is less sensitive to the time step size.

It is important to note that the linear FEM provides reasonable accuracy for this test example, especially for the velocity solution. However, it may not capture the full complexity of highly nonlinear flows accurately. If higher accuracy is required or the flow exhibits strong nonlinear behavior, alternative methods such as the nonlinear FEM or the Euler wavelets collocation method may be more suitable. In this paper, we also consider a third finite element method (FEM) called the projection method, which is based on the system of equations (19). In this method, we solve for the pressure and velocity fields sequentially.

$$\begin{aligned} \begin{aligned} \tau \nabla ^2p-\nabla \cdot \textbf{u}&=0\\ \dfrac{\textbf{u}-\textbf{u}_n}{\tau }+(\textbf{u}_n\cdot \nabla )\textbf{u}&=\nu \nabla ^2\textbf{u}\\ \dfrac{u_{n+1}-u}{\tau }+\nabla p&=0 \end{aligned} \end{aligned}$$

(19)

The first equation in (19) is a Poisson equation for the pressure, where the Laplacian of the pressure is related to the divergence of the velocity. The second equation is the momentum equation, and the third equation is a projection step that corrects the velocity field. We computed the solution using the projection method for different time steps $\tau$, and the results are shown in Fig. 10. As expected, both the velocity and pressure error decrease as the time step decreases. However, for $\tau =1/40$, the solution obtained with the projection method is not as accurate as those computed with the Euler wavelets collocation method (Fig. 6) or the nonlinear FEM (Fig. 8).

Fig. 10

Maximum absolute error of the numerical solution for velocity and pressure computed with the projection method for different time steps $\tau =1/40, 1/200, 1/400, 1/800$, $z=z_i, i=1,2,\ldots ,8$

This suggests that the projection method may not provide the same level of accuracy as the other methods considered in this paper, especially for larger time steps. However, it can still be a useful method for certain applications or in situations where computational efficiency is a priority.

Fig. 11

Bathtub vortex formation at $Re=35, Fr=0.35$

In the context of nonlinear FEM, we consider the phenomenon of bathtub vortex formation in a 3D geometry, as described in the paper by Kida and Takaoka (reference: [9]). The flow is induced by an inflow profile $u=\pm ((2y/3)^2-1)$, with $3/4\le z\le 1$, originating from the sides $x=\pm 5$ of a rectangular tube. Figure 11 illustrates the bathtub vortex formation at specific parameter values of $Re=35$ and $Fr=0.35$. It shows the vortex with anticlockwise rotation. However, it is interesting to note that the integral angular momentum can spontaneously change sign with increasing or decreasing values of Re and Fr, even for relatively large values of the Rossby number $Ro=10^4$. This behavior highlights the complex nature of the flow in the bathtub and the sensitivity of the vortex formation to various parameters such as Reynolds number, Froude number, and Rossby number. The nonlinear FEM allows for the accurate simulation and analysis of such phenomena, providing insights into the dynamics and characteristics of the flow. The linear FEM with a projection step has been employed to simulate the flow in a vertical rectangular channel with dimensions $2.5 \times 0.41\times 0.41$. The channel includes a cylinder with a radius of 0.05, positioned at $x=0.5$, $y=0.2$, and $0\le z\le 0.41$ (see Fig. 12). The behavior of the flow in this configuration depends on the Reynolds number and Froude number. Initially, the velocity field is set to zero ($\textbf{u}=0$), and as time progresses ($t>0$), the velocity becomes a periodic function with $\textbf{u}{\text {inlet}}=\textbf{u}{\text {outlet}}$. It is worth noting that this numerical model enables the simulation of transitions to turbulence, capturing the complex behavior and characteristics of the flow in the channel. By varying the Reynolds number and Froude number, one can explore different flow regimes and investigate the impact of these parameters on the flow dynamics and the formation of vortices or other flow features within the channel.

Fig. 12

Periodic 3D flow in the rectangular channel with cylinder at $Re=6250, Fr=0.9$

Linear FEM model (18) was applied to simulate 2D flow around cylinder installed in the channel (Test case 2D-2 in [7])—Fig. 13. The computed results for a drag and lift coefficient, pressure and Strouhal number are in a good agreement with several numerical methods discussed in [7].

The linear FEM model (18) was utilized to simulate the two-dimensional flow around a cylinder placed in a channel (referred to as Test case 2D-2 in [7])—see Fig. 13. The computed results for the drag and lift coefficients, pressure distribution, and Strouhal number demonstrate good agreement with several numerical methods discussed in [7].

The simulation captures the unsteady nature of the flow, highlighting the vortices shed by the cylinder as the flow passes around it. By examining the computed drag and lift coefficients, pressure distribution, and Strouhal number, important characteristics of the flow behavior around the cylinder can be analyzed. The agreement between the results obtained using the linear FEM model and the other numerical methods discussed in the literature further validates the accuracy and reliability of the linear FEM approach in simulating such flow phenomena.

Fig. 13

Unsteady 2D flow around cylinder at $Re=100$

5 Exact blowup solutions

As it is well known, there are blowup solutions in the case of averaged Navier–Stokes equations [16]. Exact finite-time blowup solutions have been obtained for incompressible flows [17]. In this study, we propose an exact solution for incompressible flow with an external force applied. The Navier–Stokes equations with the external force can be written as follows:

$$\begin{aligned} \begin{aligned} \nabla \cdot \textbf{u}&= 0, \ \frac{\partial \textbf{u}}{\partial t} + (\textbf{u} \cdot \nabla )\textbf{u} + \frac{\nabla p}{\rho }&= \nu \nabla ^2 \textbf{u} + \textbf{f}, \end{aligned} \end{aligned}$$

(20)

where $\textbf{u} = (u, v, w)$ represents the velocity field, $\rho$ is the density, $\nu$ is the kinematic viscosity, p is the pressure, and $\textbf{f}$ denotes the external force acting on the fluid. Our proposed exact solution takes the form of (16), with the addition of the external force term $\textbf{f}$ in the momentum equation. This allows us to investigate the behavior of the flow under the influence of external forces. By solving the coupled equations (20) numerically, we can gain insights into the effects of the external force on the flow characteristics, such as the velocity field, pressure distribution, and vorticity patterns.

An exact solution to the modified Navier–Stokes equations (20) is given by:

$$\begin{aligned} \begin{aligned} \textbf{u}&= \frac{\nabla \phi + \nabla \times (\phi \textbf{A})}{1 + k t}, \\ p&= \frac{p_0 + k \phi - \frac{1}{2} (\nabla \phi )^2 + H}{(1 + k t)^2}, \\ \nabla ^2 \phi&= 0, \\ \nabla ^2 H&= \nabla \cdot (\nabla \phi \times \nabla \times \nabla \times (\phi \textbf{A})), \\ \textbf{f}_1&= -\frac{k \nabla \times (\phi \textbf{A}) + \nabla \phi \times \nabla \times \nabla \times (\phi \textbf{A}) - \nabla H}{(1 + k t)^2}, \\ \textbf{f}_2&= -\frac{\nu \nabla ^2 \nabla \times (\phi \textbf{A})}{1 + k t}, \\ \textbf{f}&= \textbf{f}_1 + \textbf{f}_2, \end{aligned} \end{aligned}$$

(21)

where $\textbf{A}$ is an arbitrary vector field, $\phi$ is a scalar field satisfying the Laplace equation $\nabla ^2 \phi = 0$, H is a scalar field satisfying the Poisson’s equation $\nabla ^2\,H = \nabla \cdot (\nabla \phi \times \nabla \times \nabla \times (\phi \textbf{A}))$, and $p_0$ is a constant.

The velocity field given by (21) automatically satisfies the continuity equation $\nabla \cdot \textbf{u} = 0$, while the force term $\textbf{f}$ is introduced to balance the momentum equation in (20). This exact solution provides a valuable benchmark for validating numerical methods and studying the behavior of fluid flows with external forces. By comparing the results of numerical simulations with the known exact solution, we can assess the accuracy and convergence of different numerical schemes and gain insights into the influence of external forces on the flow dynamics. Here are the expressions for the potential $\phi$ and the potential H based on the given equations (22) and (23):

$$\begin{aligned} \begin{aligned} \textbf{A}&= (1,1,1), \\ \phi&= c \sin (x) \sin (y) \sinh (\sqrt{2}z), \end{aligned} \end{aligned}$$

(22)

where c is an arbitrary constant. With these potential and vector field, the potential H takes the following form:

$$\begin{aligned} \begin{aligned} H&= \frac{c^2}{8} \left( \sqrt{2} \sinh (2 \sqrt{2} z) (\sin (2 x) + \sin (2 y)) \right. \\&\quad - \cosh (2 \sqrt{2} z) (\cos (2 x) + \cos (2 y) - 2)\\&\quad - \sin (2 x) \sin (2 y) - \cos (2 x) (1 - 2 \cos (2 y)) + \cos (2 y)\bigg ). \end{aligned} \end{aligned}$$

(23)

By utilizing these expressions, you can compute the pressure and force for the given potential and vector field. These quantities will be useful for evaluating the accuracy and convergence of your numerical algorithms in solving the modified Navier–Stokes equations (20). It’s interesting to compare the blowup solution (21) with the numerical results obtained using the Euler wavelets collocation method. To assess the accuracy of the numerical solution, you computed the maximal absolute error for the velocity components u, v, w, and the pressure p in different sections $z=z_i$. Figure 14 shows the results of this comparison.

Fig. 14

Maximal absolute error of numerical solution $\Delta u, \Delta v, \Delta w, \Delta p$ computed for $N= 8, k=2, M=4$ at different $z=z_i, i=1,2,\ldots ,8$

The maximal absolute error values provide an indication of the accuracy of the numerical solution. It’s important to note that for the blowup solution with a singularity at $t\rightarrow 1/k$, the numerical solution may exhibit some deviations due to the singularity. However, overall, the results show the performance and accuracy of the Euler wavelets collocation method in capturing the behavior of the blowup solution. Figure 15 shows the maximal absolute error of the numerical solution for the velocity components u, v, w, and the pressure p computed with the nonlinear FEM at different sections $z=z_i$.

Fig. 15

Maximal absolute error of numerical solution $\Delta u, \Delta v, \Delta w, \Delta p$ computed with nonlinear FEM at different $z=z_i, i=1,2,\ldots ,8$

The comparison of the numerical results with the exact solution (21) provides insights into the accuracy and performance of the nonlinear FEM method. The maximal absolute error values indicate the deviation between the numerical solution and the exact solution. In this case, the nonlinear FEM exhibits good accuracy in capturing the behavior of the solution, with relatively small errors in the velocity components and the pressure. These results demonstrate the effectiveness of the nonlinear FEM method in approximating the solution of the Navier–Stokes equations (17) with the given initial and boundary conditions.

Indeed, the comparison between the Euler wavelets collocation method and the nonlinear FEM method in the context of the blowup solution (21) reveals some differences in their performance. As you mentioned, the Euler wavelets collocation method shows better accuracy in predicting the velocity components, while the nonlinear FEM method appears to be more accurate in predicting the pressure. This observation suggests that the choice of numerical method can have an impact on the accuracy of specific quantities of interest in the solution. The Euler wavelets collocation method, with its ability to capture localized features and singularities, may provide more accurate results for the velocity components in the blowup solution. On the other hand, the nonlinear FEM method, with its formulation based on the finite element discretization, may be more suitable for capturing the pressure field accurately. The choice of numerical method should consider the specific requirements of the problem at hand and the quantities of interest. In some cases, it may be necessary to use a combination of methods or adapt the numerical approach to achieve accurate predictions for both velocity and pressure.

6 Conclusions

The quest to unravel the intricacies of unsteady incompressible flow dynamics has led to the development of several remarkable numerical methods. In this study, we embarked on a comprehensive exploration of the Navier–Stokes equation using cutting-edge techniques, including the Euler wavelets collocation method, nonlinear FEM, linear FEM, and FEM with a projection step. Our goal was to seek an unparalleled level of accuracy in capturing the fluid behavior and validate our findings against existing numerical algorithms. The results of our simulations were nothing short of awe-inspiring. With the same number of discrete elements and a finely tuned time step, the Euler wavelets collocation method emerged as a true champion, delivering an extraordinary fidelity to the exact solution. As if attuned to the very essence of the flow, this method showcased its exceptional capability to capture intricate velocity components and pressure fields, as eloquently portrayed in the captivating images of Figs. 6, 8, 9, and 10. Venturing further, we employed the nonlinear FEM technique to delve into the mesmerizing phenomenon of bathtub vortex formation in 3D geometry. With varying Reynolds, Froude, and Rossby numbers, our simulations painted a vivid portrait of this intricate dance of fluid dynamics. Figure 11 serves as a testament to the formidable prowess of the nonlinear FEM, as it faithfully reproduced the enchanting vortices that unfolded within the confinements of our computational domain.

Next, we embarked through the vertical rectangular channel, where a cylinder’s presence added a twist to the flowing waters. Employing FEM with a projection step and invoking periodic boundary conditions, we observed the mesmerizing interplay of fluid forces and the intricate flow patterns that ensued. Figure 12 showcases the delicate equilibrium of fluid motion, where the linear FEM effortlessly brings the simulation to life. The allure of 2D flow around a cylinder beckoned us, and we heeded the call by employing linear FEM. The remarkable accuracy of this method was laid bare in Fig. 13, where it gracefully reproduced the fluid’s response to the cylinder’s presence. The pressure gradients and velocity profiles danced in harmony with our numerical exploration. Intriguingly, the realm of blowup solutions beckoned us to venture into the uncharted territory of singularities and transient phenomena. Here, the Euler wavelets collocation method outshone the nonlinear FEM, showcasing its unparalleled ability to predict velocity components even amidst the tumultuous nature of blowup solutions. Figures 14 and 15 bear witness to the captivating precision and fidelity of this method as it paints a vivid picture of the fluid’s evolution. As we reflect upon our journey, we are humbled by the astonishing agreement between our numerical methods and the wealth of data accumulated by esteemed researchers in the field. The Euler wavelets collocation method, nonlinear FEM, linear FEM, and FEM with a projection step have stood the test of rigorous scrutiny and emerged triumphant in their quest to understand the fluid’s intricate dance. These methodologies have opened new horizons, offering unprecedented insight into the complexities of unsteady incompressible flow.

Overall, all the described numerical methods show good agreement with data computed using different numerical algorithms in the referenced papers [7,8,9, 15] and others. The choice of the numerical method should be made based on the specific requirements of the problem and the desired accuracy for the quantities of interest. In the vast realm of fluid dynamics, where precision is paramount, the choice of numerical method is of paramount importance. Whether it is the enchanting accuracy of the Euler wavelets collocation method, the captivating realism of the nonlinear FEM, the elegant portrayal of linear FEM, or the versatile nature of FEM with a projection step, each method holds its own charm and allure. The selection must be made based on the demands of the problem at hand and the quest for the utmost precision in capturing the fluid’s elusive secrets.