Abstract
Security monitors have been used to check for safety program properties at runtime, that is for any given execution trace. Such security monitors check a safety temporal property specified by a finite automaton or, equivalently, a regular expression. Checking this safety temporal specification for all possible execution traces, that is the program semantics, is a static analysis problem, more precisely a model checking problem, since model checking specializes in temporal properties. We show that the model checker can be formally designed by calculus, by abstract interpretation of a formal trace semantics of the programming language. The result is a structural sound and complete model checker, which proceeds by induction on the program syntax (as opposed to the more classical approach using computation steps formalized by a transition system). By Rice theorem, further hypotheses or abstractions are needed to get a realistic model checking algorithm.
Supported by NSF Grant CCF-1617717.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Model checking [9, 33] consists in proving that a model of a given program/computer system satisfies a temporal specificationFootnote 1. Traditionally, the model of the given program/computer system is a transition system and its semantics is the set of traces generated by the transition system. The temporal specification is usually one of the many variants of temporal logics such as the Linear Time Temporal logic (LTL), the Computation Tree Logic (CTL), or the combination CTL\({}^{*}\) of the two. The semantics of the temporal specification is a set of traces. The problem is therefore to check that the set of traces of the semantics of the given program/computer system is included in the set of traces of the semantics of the temporal specification. This is a Galois connection-based abstraction and so a model checking algorithm can be designed by calculus. To show that we consider a non-conventional temporal specification using regular expressions [25] and a structural fixpoint prefix-closed trace semantics which differs from the traditional small-step operational semantics specified by a transition system. There are properties of traces that are not expressible in temporal logic but are easily expressible using regular expressions [36].
2 Syntax and Trace Semantics of the Programming Language
Syntax Programs are a subset of C with the following context-free syntax.

A break exits the closest enclosing loop, if none this is a syntactic error. If
 is a program then
is a program then
 is a valid C program. We call “[program] component”
is a valid C program. We call “[program] component”
 either a statement, a statement list, or a program. We let
either a statement, a statement list, or a program. We let
 be the syntactic relation between immediate syntactic components. For example, if
be the syntactic relation between immediate syntactic components. For example, if
 then
then
 , and
, and
 .
.
Program labels Labels are not part of the language, but useful to discuss program points reached during execution. For each program component
 , we define
, we define

Prefix trace semantics Prefix traces are non-empty finite sequences
 of states where states
of states where states
 are pairs of a program label
are pairs of a program label
 designating the next action to be executed in the program and an environment
designating the next action to be executed in the program and an environment
 assigning values
assigning values
 to variables
to variables
 . A trace
. A trace
 can be finite
can be finite
 or infinite
or infinite
 (recording a non-terminating computation) so
(recording a non-terminating computation) so
 . Trace concatenation
. Trace concatenation
 is defined as follows
is defined as follows

In pattern matching, we sometimes need the empty trace
 . For example if
. For example if

 then
then
 and so
and so
 .
.
Formal definition of the prefix trace semantics The prefix trace semantics
 is given structurally (by induction on the syntax) using fixpoints for the iteration.
is given structurally (by induction on the syntax) using fixpoints for the iteration.
-
The prefix traces of an assignment statement
 (where
(where
 ) either stops in an initial state
) either stops in an initial state
 or is this initial state
or is this initial state
 followed by the next state
followed by the next state
 recording the assignment of the value
recording the assignment of the value
 of the arithmetic expression to variable x when reaching the label
of the arithmetic expression to variable x when reaching the label
 after the assignment.
after the assignment. 
The value of an arithmetic expression
 in environment
in environment
 is
is
 :
: 
-
The prefix trace semantics of a break statement
 either stops at
either stops at
 or goes on to the break label
or goes on to the break label
 (which is defined as the exit label of the closest enclosing iteration).
(which is defined as the exit label of the closest enclosing iteration). 
-
The prefix trace semantics of a conditional statement
 is
is
-
either the trace
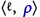 when the observation of the execution stops on entry of the program component for initial environment
when the observation of the execution stops on entry of the program component for initial environment
 ;
; -
or, when the value of the boolean expression
 for
for
 is false
is false
 , the initial state
, the initial state
 followed by the state
followed by the state
 at the label
at the label
 after the conditional statement;
after the conditional statement; -
or finally, when the value of the boolean expression
 for
for
 is true
is true
 , the initial state
, the initial state
 followed by a prefix trace of
followed by a prefix trace of
 starting
starting
 in environment
in environment
 (and possibly ending
(and possibly ending
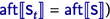 .
.

Observe that definition (4) includes the case of a conditional within an iteration and containing a break statement in the true branch
 . Since
. Since

 , from
, from
 and
and
 , we infer that
, we infer that
 .
.
-
The prefix traces of the prefix trace semantics of a non-empty statement list
 are the prefix traces of
are the prefix traces of
 or the finite maximal traces of
or the finite maximal traces of
 followed by a prefix trace of
followed by a prefix trace of
 .
. 
Notice that if
 then the last state of
then the last state of
 must be the first state of
must be the first state of
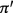 and this state is
and this state is
 and so the trace
and so the trace
 must be a maximal terminating execution of
must be a maximal terminating execution of
 i.e.
i.e.
 is executed only if
is executed only if
 terminates.
terminates. -
The prefix finite trace semantic definition
 (6) of an iteration statement of the form
(6) of an iteration statement of the form
 where
where
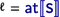 is the \(\subseteq \)-least solution
is the \(\subseteq \)-least solution
 to the equation
to the equation
 . Since
. Since
 is \(\subseteq \)- monotone (if
is \(\subseteq \)- monotone (if
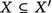 then
then
 and
and
 is a complete lattice,
is a complete lattice,
 exists by Tarski’s fixpoint theorem and can be defined as the limit of iterates [15]. In definition (6) of the transformer
exists by Tarski’s fixpoint theorem and can be defined as the limit of iterates [15]. In definition (6) of the transformer
 , case (6.a) corresponds to a loop execution observation stopping on entry, (6.b) corresponds to an observation of a loop exiting after 0 or more iterations, and (6.c) corresponds to a loop execution observation that stops anywhere in the body
, case (6.a) corresponds to a loop execution observation stopping on entry, (6.b) corresponds to an observation of a loop exiting after 0 or more iterations, and (6.c) corresponds to a loop execution observation that stops anywhere in the body
 after 0 or more iterations. This last case covers the case of an iteration terminated by a break statement (to
after 0 or more iterations. This last case covers the case of an iteration terminated by a break statement (to
 after the iteration statement).Footnote 2
after the iteration statement).Footnote 2

-
The other cases are similar.
Semantic properties As usual in abstract interpretation [16], we represent properties of entities in a universe
 by a subset of this universe. So a property of elements of
by a subset of this universe. So a property of elements of
 belongs to
belongs to
 . For example “to be a natural” is the property
. For example “to be a natural” is the property
 of the integers
of the integers
 . The property “n is a natural” is “
. The property “n is a natural” is “
 ”. By program component (safety) property, we understand a property of their prefix trace semantics
”. By program component (safety) property, we understand a property of their prefix trace semantics
 . So program properties belong to
. So program properties belong to
 . The collecting semantics is the strongest program property, that is the singleton
. The collecting semantics is the strongest program property, that is the singleton
 .
.
3 Specifying computations by regular expressions
Stephen Cole Kleene introduced regular expressions and finite automata to specify execution traces (called events) of automata (called nerve nets) [25]. Kleene proved in [25] that regular expressions and (non-deterministic) finite automata can describe exactly the same classes of languages (see [34, Ch. 1, Sect. 4]). He noted that not all computable execution traces of nerve nets can be (exactly) represented by a regular expression. The situation is the same for programs for which regular expressions (or equivalently finite automata) can specify a super-set of the prefix state trace semantics
 of program components
of program components
 .
.
Example 1 (Security monitors)
An example is Fred Schneider’s security monitors [29, 35] using a finite automata specification to state requirements of hardware or software systems. They have been used to check for safety program properties at runtime, that is for any given execution trace in the semantics
 . The safety property specified by the finite automaton or, equivalently, an regular expression is temporal i.e. links events occurring at different times in the computation (such as a file must be opened before being accessed and must eventually be closed). \(\square \)
. The safety property specified by the finite automaton or, equivalently, an regular expression is temporal i.e. links events occurring at different times in the computation (such as a file must be opened before being accessed and must eventually be closed). \(\square \)
Syntax of regular expressions Classical regular expressions denote sets of strings using constants (empty string
 , literal characters a, b, etc.) and operator symbols (concatenation
, literal characters a, b, etc.) and operator symbols (concatenation
 , alternation
, alternation
 , repetition zero or more times
, repetition zero or more times
 or one or more times
or one or more times
 ). We replace the literal characters by invariant specifications
). We replace the literal characters by invariant specifications
 stating that boolean expression
stating that boolean expression
 should be true whenever control reaches any program point in the set
should be true whenever control reaches any program point in the set
 of program labels. The boolean expression
of program labels. The boolean expression
 may depend on program variables
may depend on program variables
 and their initial values denoted
and their initial values denoted
 where
where
 .
.

We use abbreviations to designate sets of labels such as
 so that
so that
 is invariant,
is invariant,
 so that
so that
 is invariant at program label
is invariant at program label
 ,
,
 when
when
 holds everywhere but at program point
holds everywhere but at program point
 , etc.
, etc.
Example 2
 holds for any program.
holds for any program.
 states that the value of x is always positive or zero during program execution.
states that the value of x is always positive or zero during program execution.
 states that the value of x is always greater than or equal to its initial value
states that the value of x is always greater than or equal to its initial value
 during execution.
during execution.
 states that the value of x should be positive or zero and if program point
states that the value of x should be positive or zero and if program point
 is ever reached then x should be 0, and if computations go on after program point
is ever reached then x should be 0, and if computations go on after program point
 then x should be negative afterwards. \(\square \)
then x should be negative afterwards. \(\square \)
Example 3
Continuing Ex. 1 for security monitors, the basic regular expressions are names
 of program actions. We can understand such an action
of program actions. We can understand such an action
 as designating the set
as designating the set
 of labels of all its occurrences in the program. If necessary, the boolean expression
of labels of all its occurrences in the program. If necessary, the boolean expression
 can be used to specify the parameters of the action. \(\square \)
can be used to specify the parameters of the action. \(\square \)
There are many regular expressions denoting the language
 containing only the empty sequence
containing only the empty sequence
 (such that
(such that
 , etc.), as shown by the following grammar.
, etc.), as shown by the following grammar.

For specification we use only non-empty regular expressions
 since traces cannot be empty.
since traces cannot be empty.

We also have to consider regular expressions
 containing no alternative
containing no alternative
 .
.

Relational semantics of regular expressions The semantics (2) of expressions is changed as follows
 denotes the initial values
denotes the initial values
 of variables
of variables
 and
and
 their current value,
their current value,
 is the alternative denial logical operation)
is the alternative denial logical operation)

We represent a non-empty finite sequence
 of states
of states
 by a map
by a map
 (which is the empty sequence
(which is the empty sequence
 when \(n=0\)).
when \(n=0\)).
The relational semantics
 of regular expressions
of regular expressions
 relates an arbitrary initial environment
relates an arbitrary initial environment
 to a trace
to a trace
 by defining how the states of the trace
by defining how the states of the trace
 are related to that initial environment
are related to that initial environment
 .
.

Example 4
The semantics of the regular expression
 is
is
 . \(\square \)
. \(\square \)
4 Definition of regular model checking
Let the prefix closure
 of a set
of a set
 of stateful traces be
of stateful traces be

The following Def. 1 defines the model checking problem
 as checking that the semantics of the given program
as checking that the semantics of the given program
 meets the regular specification
meets the regular specification
 for the initial environment
for the initial environment
 Footnote 3.
Footnote 3.

The prefix closure
 allows the regular specification
allows the regular specification
 to specify traces satisfying a prefix of the specification only, as in
to specify traces satisfying a prefix of the specification only, as in

 . The extension of the specification by
. The extension of the specification by
 allows for the regular specification
allows for the regular specification
 to specify only a prefix of the traces, as in
to specify only a prefix of the traces, as in
 . Model checking is a boolean abstraction
. Model checking is a boolean abstraction

 .
.
5 Properties of regular expressions
Equivalence of regular expressions We say that regular expressions are equivalent when they have the same semantics i.e.
 .
.
Disjunctive normal form
 of regular expressions As noticed by Kleene [25, p. 14], regular expressions can be put in the equivalent disjunctive normal form of Hilbert—Ackermann. A regular expression is in disjunctive normal form if it is of the form
of regular expressions As noticed by Kleene [25, p. 14], regular expressions can be put in the equivalent disjunctive normal form of Hilbert—Ackermann. A regular expression is in disjunctive normal form if it is of the form
 for some \(n\geqslant 1\), in which none of the
for some \(n\geqslant 1\), in which none of the
 , for \(1 \leqslant i \leqslant n\), contains an occurrence of
, for \(1 \leqslant i \leqslant n\), contains an occurrence of
 . Any regular expression
. Any regular expression
 has a disjunctive normal form
has a disjunctive normal form
 defined as follows.
defined as follows.

The Lem. 1 below shows that normalization leaves the semantics unchanged. It uses the fact that
 where the
where the
 and
and
 do not contain any
do not contain any
 [23, Sect. 3.4.6, p.118]. It shows that normalization in (10) can be further simplified by
[23, Sect. 3.4.6, p.118]. It shows that normalization in (10) can be further simplified by
 and
and
 which have equivalent semantics.
which have equivalent semantics.
Lemma 1

.
 and
and
 of regular expressions Janusz Brzozowski [7] introduced the notion of derivation for regular expressions (extended with arbitrary Boolean operations). The derivative of a regular expression
of regular expressions Janusz Brzozowski [7] introduced the notion of derivation for regular expressions (extended with arbitrary Boolean operations). The derivative of a regular expression
 with respect to a symbol a, typically denoted as
with respect to a symbol a, typically denoted as
 or
or
 , is a regular expression given by a simple recursive definition on the syntactic structure of
, is a regular expression given by a simple recursive definition on the syntactic structure of
 . The crucial property of these derivatives is that a string of the form \(a\sigma \) (starting with the symbol a) matches an expression
. The crucial property of these derivatives is that a string of the form \(a\sigma \) (starting with the symbol a) matches an expression
 iff the suffix \(\sigma \) matches the derivative
iff the suffix \(\sigma \) matches the derivative
 [2, 7, 32].
[2, 7, 32].
Following this idea, assume that a non-empty regular expression
 has been decomposed into disjunctive normal form
has been decomposed into disjunctive normal form
 for some \(n\geqslant 1\), in which none of the
for some \(n\geqslant 1\), in which none of the
 , for
, for
 contains an occurrence of
contains an occurrence of
 . We can further decompose each
. We can further decompose each
 into
into
 such that
such that
-
 recognizes the first state of sequences of states recognized by
recognizes the first state of sequences of states recognized by
 ;
; -
the regular expression
 recognizes sequences of states after the first state of sequences of states recognized by
recognizes sequences of states after the first state of sequences of states recognized by
 .
.
We define
 for non-empty
for non-empty
 -free regular expressions
-free regular expressions
 by structural induction, as follows.
by structural induction, as follows.

The following Lem. 2 shows the equivalence of an alternative-free regular expression and its first and next decomposition.
Lemma 2
Let
 be a non-empty
be a non-empty
 -free regular expression and
-free regular expression and
 ,
,
 . Then
. Then
 is
is
 -free and
-free and
 .
.
6 The model checking abstraction
The model checking abstraction in Section 4 is impractical for structural model checking since e.g. when checking that a trace concatenation
 of a statement list
of a statement list
 for a specification
for a specification
 where
where
 is a trace of
is a trace of
 and
and
 is a trace of
is a trace of
 , we first check that
, we first check that
 satisfies
satisfies
 and then we must check
and then we must check
 for a continuation
for a continuation
 of
of
 which should be derived from
which should be derived from
 and
and
 . This is not provided by the boolean abstraction
. This is not provided by the boolean abstraction
 which needs to be refined as shown below.
which needs to be refined as shown below.
Example 5
Assume we want to check
 for the regular specification
for the regular specification
 by first checking the first statement and then the second. Knowing the boolean information that
by first checking the first statement and then the second. Knowing the boolean information that
 model checks for
model checks for
 is not enough. We must also know what to check the continuation
is not enough. We must also know what to check the continuation
 for. (This is
for. (This is
 that is if
that is if
 is equal to the initial value plus 1 at
is equal to the initial value plus 1 at
 , it is equal to this initial value plus 3 at
, it is equal to this initial value plus 3 at
 .) \(\square \)
.) \(\square \)
The model-checking
 of a trace
of a trace
 with initial environment
with initial environment
 for a
for a
 -free specification
-free specification
 is a pair
is a pair
 where the boolean
where the boolean
 states whether the specification
states whether the specification
 holds for the trace
holds for the trace
 and
and
 specifies the possible continuations of
specifies the possible continuations of
 according to
according to
 ,
,
 if none.
if none.
Example 6
For
 , we have
, we have

 and
and

 (we have ignored the initial empty statement list in
(we have ignored the initial empty statement list in
 to simplify the specification). \(\square \)
to simplify the specification). \(\square \)
The fact that
 returns a pair
returns a pair
 where
where
 is to be satisfied by continuations of
is to be satisfied by continuations of
 allows us to perform program model checking by structural induction on the program in Section 8. The formal definition is the following.
allows us to perform program model checking by structural induction on the program in Section 8. The formal definition is the following.


The model checking
 of a stateful trace
of a stateful trace
 in (11) returns a pair
in (11) returns a pair

 specifying whether
specifying whether
 satisfies the specification
satisfies the specification
 (when
(when
 ) or not (when
) or not (when
 ). So if
). So if
 in (12) then the trace
in (12) then the trace
 is a counter example to the specification
is a counter example to the specification
 specifies what a continuation
specifies what a continuation
 of
of
 would have to satisfy for
would have to satisfy for
 to satisfy
to satisfy
 (nothing specific when
(nothing specific when
 ).
).
Notice that
 checks whether the given trace
checks whether the given trace
 satisfies the regular specification
satisfies the regular specification
 for initial environment
for initial environment
 . Because only one trace is involved, this check can be done at runtime using a monitoring of the program execution. This is the case Fred Schneider’s security monitors [35] in Ex. 1 (using an equivalent specification by finite automata).
. Because only one trace is involved, this check can be done at runtime using a monitoring of the program execution. This is the case Fred Schneider’s security monitors [35] in Ex. 1 (using an equivalent specification by finite automata).
The set of traces model checking
 returns the subset of traces of
returns the subset of traces of
 satisfying the specification
satisfying the specification
 for the initial environment
for the initial environment
 . Since all program executions
. Since all program executions
 are involved, the model checking
are involved, the model checking
 of a program
of a program
 becomes, by Rice theorem, undecidable.
becomes, by Rice theorem, undecidable.
The regular specification
 is relational in that it may relate the initial and current states (or else may only assert a property of the current states when
is relational in that it may relate the initial and current states (or else may only assert a property of the current states when
 never refer to the initial environment
never refer to the initial environment
 ). If
). If
 is an execution trace satisfying the specification
is an execution trace satisfying the specification
 then
then
 in (15) determines a relationship between the initial environment
in (15) determines a relationship between the initial environment
 and the current environment
and the current environment
 . For example
. For example
 ,
,
 with
with
 expresses that the initial values of variables
expresses that the initial values of variables
 are denoted
are denoted
 would state that there is no constraint on the initial value of variables. The difference with the invariant specifications of is that the order of computations is preserved.
would state that there is no constraint on the initial value of variables. The difference with the invariant specifications of is that the order of computations is preserved.
 can specify in which order program points may be reached, which is impossible with invariantsFootnote 4.
can specify in which order program points may be reached, which is impossible with invariantsFootnote 4.
The model checking abstraction (12) which, given an initial environment
 and an
and an
 -free regular specification
-free regular specification
 , returns the set of traces satisfying this specification is the lower adjoint of the Galois connection
, returns the set of traces satisfying this specification is the lower adjoint of the Galois connection

If
 is a poset,
is a poset,
 is a complete lattice,
is a complete lattice,

 then
then
 where
where
 and
and
 , pointwise. This implies that
, pointwise. This implies that

To follow the tradition that model checking returns a boolean answer this abstraction can be composed with the boolean abstraction

where
 .
.
7 Soundness and completeness of the model checking abstraction
The following Th. 1 shows that the Def. 1 of model checking a program semantics for a regular specification is a sound and complete abstraction of this semantics.
Theorem 1
(Model checking soundness
 and completeness
and completeness
 .
.

At this point we know, by (15) and Th. 1 that a model checker
 is a sound and complete abstraction
is a sound and complete abstraction
 of the program component semantics
of the program component semantics
 which provides a counter example in case of failure. This allows us to derive a structural model checker
which provides a counter example in case of failure. This allows us to derive a structural model checker
 in Section 8 by calculational design.
in Section 8 by calculational design.
8 Structural model checking
By Def. 1 of the model checking of
 of a program
of a program
 for a regular specification
for a regular specification
 and initial environment
and initial environment
 , Th. 1 shows that a model checker
, Th. 1 shows that a model checker
 is a sound and complete abstraction
is a sound and complete abstraction
 of the program semantics
of the program semantics
 . This abstraction does not provide a model checking algorithm specification.
. This abstraction does not provide a model checking algorithm specification.
The standard model checking algorithms [10] use a transition system (or a Kripke structure variation [26]) for hardware and software modeling and proceeding by induction on computation steps.
In contrast, we proceed by structural induction on programs, which will be shown in Th. 2 to be logically equivalent (but maybe more efficient since fixpoints are computed locally). The structural model checking
 of the program
of the program
 proceeds by structural induction on the program structure:
proceeds by structural induction on the program structure:

where the transformer
 uses the results of model checking of the immediate components
uses the results of model checking of the immediate components
 and involves a fixpoint computation for iteration statements.
and involves a fixpoint computation for iteration statements.
The following Th. 2 shows that the algorithm specification is correct, that is
 for all program components
for all program components
 . So together with Th. 1, the structural model checking is proved sound and complete.
. So together with Th. 1, the structural model checking is proved sound and complete.
Theorem 2

 .
.
The proof of Th. 2 is by calculational design and proceeds by structural induction on the program component
 . Assuming
. Assuming
 for all immediate components
for all immediate components
 of statement, the proof for each program component
of statement, the proof for each program component
 has the following form.
has the following form.

For iteration statements,
 is a fixpoint, and this proof involves the fixpoint transfer theorem [16, Th. 7.1.0.4 (3)] based on the commutation of the concrete and abstract transformer with the abstraction. The calculational design of the structural model checking
is a fixpoint, and this proof involves the fixpoint transfer theorem [16, Th. 7.1.0.4 (3)] based on the commutation of the concrete and abstract transformer with the abstraction. The calculational design of the structural model checking
 is shown below.
is shown below.


Proof
— In case (19) of a program
 the calculational design is as follows.
the calculational design is as follows.


For the assignment
 in (23), case (a) checks the prefixes that stops at
in (23), case (a) checks the prefixes that stops at
 whereas (b) and (c) checks the maximal traces stopping after the assignment. In each trace checked for the specification
whereas (b) and (c) checks the maximal traces stopping after the assignment. In each trace checked for the specification
 the states are checked successively and the continuation specification is returned together with the checked trace, unless the check fails. Checking the assignment
the states are checked successively and the continuation specification is returned together with the checked trace, unless the check fails. Checking the assignment
 in (23) for
in (23) for

 consists in first checking
consists in first checking
 at
at
 and then checking on
and then checking on
 after the statement. In case (b),
after the statement. In case (b),
 is empty so trivially satisfied. Otherwise, in case (c),
is empty so trivially satisfied. Otherwise, in case (c),
 so
so
 is checked after the statement while
is checked after the statement while
 is the continuation specification.
is the continuation specification.
Proof
— In case (23) of an assignment statement
 , the calculational design is as follows.
, the calculational design is as follows.




— The model checking of an iteration statement
 in (27) checks one more iteration (after checking the previous ones as recorded by X) while the fixpoint (26) repeats this check for all iterations. Case (a) checks the prefixes that stops at loop entry
in (27) checks one more iteration (after checking the previous ones as recorded by X) while the fixpoint (26) repeats this check for all iterations. Case (a) checks the prefixes that stops at loop entry
 . (b) and (c) check the exit of an iteration when the iteration condition is false, (b) when the specification stops at loop entry
. (b) and (c) check the exit of an iteration when the iteration condition is false, (b) when the specification stops at loop entry
 before leaving and (c) when the specification goes further. (d), (e) and (f) check one more iteration when the iteration condition is true. In case (d), the continuation after the check of the iterates is empty so trivially satisfied by any continuation of the prefix trace. In case (e), the continuation after the check of the iterates just impose to verify
before leaving and (c) when the specification goes further. (d), (e) and (f) check one more iteration when the iteration condition is true. In case (d), the continuation after the check of the iterates is empty so trivially satisfied by any continuation of the prefix trace. In case (e), the continuation after the check of the iterates just impose to verify
 on iteration entry and nothing afterwards. In case (f) the continuation after the check of the iterates requires to verify
on iteration entry and nothing afterwards. In case (f) the continuation after the check of the iterates requires to verify
 at the loop entry,
at the loop entry,
 at the body entry, and the rest
at the body entry, and the rest
 of the specification for the loop body (which returns the possibly empty continuation specification
of the specification for the loop body (which returns the possibly empty continuation specification
 The cases (b) to (f) are mutually exclusive.
The cases (b) to (f) are mutually exclusive.
9 Notes on implementations and expressivity
Of course further hypotheses and refinements would be necessary to get an effective algorithm as specified by the Def. 3 of structural model checking. A common hypothesis in model checking is that the set of states
 is finite. Traces may still be infinite so the fixpoint computation (26) may not converge. However, infinite traces on finite states must involve an initial finite prefix followed by a finite cycle (often called a lasso). It follows that the infinite set of prefix traces can be finitely represented by a finite set of maximal finite traces and finite lassos. Regular expressions
is finite. Traces may still be infinite so the fixpoint computation (26) may not converge. However, infinite traces on finite states must involve an initial finite prefix followed by a finite cycle (often called a lasso). It follows that the infinite set of prefix traces can be finitely represented by a finite set of maximal finite traces and finite lassos. Regular expressions
 can be attached to the states as determined by the analysis, and there are finitely many of them in the specification. These finiteness properties can be taken into account to ensure the convergence of the fixpoint computation in (26).
can be attached to the states as determined by the analysis, and there are finitely many of them in the specification. These finiteness properties can be taken into account to ensure the convergence of the fixpoint computation in (26).
A symbolic representation of the states in finite/lasso stateful traces may be useful as in symbolic execution [24] or using BDDs [6] for boolean encodings of programs. By Kleene theorem [34, Theorem 2.1, p. 87], a convenient representation of regular expressions is by (deterministic) finite automata e.g. [28]. Symbolic automata-based algorithms can be used to implement a data structure for operations over sets of sequences [22].
Of course the hypothesis that the state space is finite and small enough to scale up and limit the combinatorial blow up of the finite state-space is unrealistic [11]. In practice, the set of states
 is very large, so abstraction and a widening/dual narrowing are necessary. A typical trivial widening is bounded model checking (e.g. widen to all states after n fixpoint iterations) [5]. Those of [30] are more elaborated.
is very large, so abstraction and a widening/dual narrowing are necessary. A typical trivial widening is bounded model checking (e.g. widen to all states after n fixpoint iterations) [5]. Those of [30] are more elaborated.
10 Conclusion
We have illustrated the idea that model checking is an abstract interpretation, as first introduced in [17]. This point of view also yields specification-preserving abstract model checking [18] as well as abstraction refinement algorithms [20].
Specifications by temporal logics are not commonly accepted by programmers. For example, in [31], the specifications had to be written by academics. Regular expressions or path expressions [8] or more expressive extensions might turn out to be more familiar. Moreover, for security monitors the false alarms of the static analysis can be checked at runtime [29, 35].
Convergence of model checking requires expressivity restrictions on both the considered models of computation and the considered temporal logics. For some expressive models of computation and temporal logics, state finiteness is not enough to guarantee termination of model checking [17, 21]. Finite enumeration is limited, even with symbolic encodings. Beyond finiteness, scalability is always a problem with model checking and the regular software model checking algorithm
 is no exception, so abstraction and induction are ultimately required to reason on programs.
is no exception, so abstraction and induction are ultimately required to reason on programs.
Most often, abstract model checking uses homomorphic/partitioning abstractions e.g. [4]. This is because the abstraction of a transition system on concrete states is a transition system on abstract states so model checkers are reusable in the abstract. However, excluding edgy abstractions as in [13], state-based finite abstraction is very restrictive [21] and do not guarantee scalability (e.g. SLAM [3]). Such restrictions on abstractions do not apply to structural model checking so that abstractions more powerful than partitioning can be considered.
As an alternative approach, a regular expression can be automatically extracted by static analysis of the program trace semantics that recognizes all feasible execution paths and usually more [19]. Then model-checking a regular specification becomes a regular language inclusion problem [27].
Notes
- 1.
- 2.
A definition of the form \(d(\vec {x})\triangleq \{f(\vec {x}\prime )\mid P(\vec {x}\prime ,\vec {x})\}\) has the variables \(\vec {x}\prime \) in \(P(\vec {x}\prime ,\vec {x})\) bound to those of \(f(\vec {x}\prime )\) whereas \(\vec {x}\) is free in \(P(\vec {x}\prime ,\vec {x})\) since it appears neither in \(f(\vec {x}\prime )\) nor (by assumption) under quantifiers in \(P(\vec {x}\prime ,\vec {x})\). The \(\vec {x}\) of \(P(\vec {x}\prime ,\vec {x})\) is therefore bound to the \(\vec {x}\) of \(d(\vec {x})\).
- 3.
We understand “regular model checking” as checking temporal specifications given by a regular expression. This is different from [1] model checking transition systems which states are regular word or tree languages.
- 4.
By introduction of an auxiliary variable
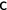 incremented at each program step one can simulate a trace with invariants. But then the reasoning is not on the original program
incremented at each program step one can simulate a trace with invariants. But then the reasoning is not on the original program
 but on a transformed program
but on a transformed program
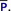 . Invariants in
. Invariants in
 holding for a given value of
holding for a given value of
 of
of
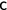 also hold at the position
also hold at the position
 of the traces in
of the traces in
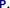 This king of indirect reasoning is usually heavy and painful to maintain when programs are modified since values of counters are no longer the same. The use of temporal specifications has the advantage of avoiding the reasoning on explicit positions in the trace.
This king of indirect reasoning is usually heavy and painful to maintain when programs are modified since values of counters are no longer the same. The use of temporal specifications has the advantage of avoiding the reasoning on explicit positions in the trace.
References
Abdulla, P.A., Jonsson, B., Nilsson, M., Saksena, M.: A survey of regular model checking. In: Gardner, P., Yoshida, N. (eds.) CONCUR 2004. LNCS, vol. 3170, pp. 35–48. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28644-8_3
Alur, R., Mamouras, K., Ulus, D.: Derivatives of quantitative regular expressions. In: Aceto, L., Bacci, G., Bacci, G., Ingólfsdóttir, A., Legay, A., Mardare, R. (eds.) Models, Algorithms, Logics and Tools. LNCS, vol. 10460, pp. 75–95. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63121-9_4
Ball, T., Levin, V., Rajamani, S.K.: A decade of software model checking with SLAM. Commun. ACM 54(7), 68–76 (2011)
Ball, T., Podelski, A., Rajamani, S.K.: Boolean and cartesian abstraction for model checking C programs. In: Margaria, T., Yi, W. (eds.) TACAS 2001. LNCS, vol. 2031, pp. 268–283. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45319-9_19
Biere, A., Cimatti, A., Clarke, E.M., Strichman, O., Zhu, Y.: Bounded model checking. Adv. Comput. 58, 117–148 (2003)
Bryant, R.E.: Graph-based algorithms for boolean function manipulation. IEEE Trans. Computers 35(8), 677–691 (1986)
Brzozowski, J.A.: Derivatives of regular expressions. J. ACM 11(4), 481–494 (1964)
Campbell, R.H., Habermann, A.N.: The specification of process synchronization by path expressions. In: Gelenbe, E., Kaiser, C. (eds.) OS 1974. LNCS, vol. 16, pp. 89–102. Springer, Heidelberg (1974). https://doi.org/10.1007/BFb0029355
Clarke, E.M., Emerson, E.A.: Design and synthesis of synchronization skeletons using branching time temporal logic. In: Kozen, D. (ed.) Logic of Programs 1981. LNCS, vol. 131, pp. 52–71. Springer, Heidelberg (1982). https://doi.org/10.1007/BFb0025774
Clarke, E.M., Henzinger, T.A., Veith, H., Bloem, R. (eds.): Handbook of Model Checking. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-10575-8
Clarke, E.M., Klieber, W., Nováček, M., Zuliani, P.: Model checking and the state explosion problem. In: Meyer, B., Nordio, M. (eds.) LASER 2011. LNCS, vol. 7682, pp. 1–30. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-35746-6_1
Cousot, P.: Méthodes itératives de construction et d’approximation de points fixes d’opérateurs monotones sur un treillis, analyse sémantique de programmes (in French). Thèse d’Étatès sciences mathématiques, Université de Grenoble Alpes, Grenoble, France, 21 March 1978
Cousot, P.: Partial completeness of abstract fixpoint checking. In: Choueiry, B.Y., Walsh, T. (eds.) SARA 2000. LNCS (LNAI), vol. 1864, pp. 1–25. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44914-0_1
Cousot, P., Cousot, R.: Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: POPL, pp. 238–252. ACM (1977)
Cousot, P., Cousot, R.: Constructive versions of Tarski’s fixed point theorems. Pac. J. Math. 81(1), 43–57 (1979)
Cousot, P., Cousot, R.: Systematic design of program analysis frameworks. In: POPL, pp. 269–282. ACM Press (1979)
Cousot, P., Cousot, R.: Temporal abstract interpretation. In: POPL, pp. 12–25. ACM (2000)
Crafa, S., Ranzato, F., Tapparo, F.: Saving space in a time efficient simulation algorithm. Fundam. Inform. 108(1–2), 23–42 (2011)
Cyphert, J., Breck, J., Kincaid, Z., Reps, T.: Refinement of path expressions for static analysis. PACMPL 3(POPL), 45 (2019)
Giacobazzi, R., Quintarelli, E.: Incompleteness, counterexamples, and refinements in abstract model-checking. In: Cousot, P. (ed.) SAS 2001. LNCS, vol. 2126, pp. 356–373. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-47764-0_20
Giacobazzi, R., Ranzato, F.: Incompleteness of states w.r.t. traces in model checking. Inf. Comput. 204(3), 376–407 (2006)
Heizmann, M., Hoenicke, J., Podelski, A.: Software model checking for people who love automata. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 36–52. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_2
Hopcroft, J.E., Motwani, R., Ullman, J.D.: Introduction to Automata Theory, Languages, and Computation - International Edition, 2nd edn. Addison-Wesley, Boston (2003)
King, J.C.: Symbolic execution and program testing. Commun. ACM 19(7), 385–394 (1976)
Kleene, S.C.: Representation of events in nerve nets and finite automata. In: Shannon, C.D., McCarthy, J. (eds.) Automata Studies, pp. 3–42. Princeton University Press, Princeton (1951)
Kripke, S.A.: Semantical considerations on modal logic. Acta Philosophica Fennica 16, 83–94 (1963). Proceedings of a Colloquium on Modal and Many-Valued Logics, Helsinki, 23–26 August 1962
Kupferman, O.: Automata theory and model checking. In: Clarke, E., Henzinger, T., Veith, H., Bloem, R. (eds.) Handbook of Model Checking, pp. 107–151. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-10575-8_4
Lichtenstein, O., Pnueli, A.: Checking that finite state concurrent programs satisfy their linear specification. In: POPL, pp. 97–107. ACM Press (1985)
Mallios, Y., Bauer, L., Kaynar, D., Ligatti, J.: Enforcing more with less: formalizing target-aware run-time monitors. In: Jøsang, A., Samarati, P., Petrocchi, M. (eds.) STM 2012. LNCS, vol. 7783, pp. 17–32. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38004-4_2
Mauborgne, L.: Binary decision graphs. In: Cortesi, A., Filé, G. (eds.) SAS 1999. LNCS, vol. 1694, pp. 101–116. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48294-6_7
Miller, S.P., Whalen, M.W., Cofer, D.D.: Software model checking takes off. Commun. ACM 53(2), 58–64 (2010)
Owens, S., Reppy, J.H., Turon, A.: Regular-expression derivatives re-examined. J. Funct. Program. 19(2), 173–190 (2009)
Queille, J.P., Sifakis, J.: Specification and verification of concurrent systems in CESAR. In: Dezani-Ciancaglini, M., Montanari, U. (eds.) Programming 1982. LNCS, vol. 137, pp. 337–351. Springer, Heidelberg (1982). https://doi.org/10.1007/3-540-11494-7_22
Sakarovitch, J.: Elements of Automata Theory. Cambridge University Press, Cambridge (2009)
Schneider, F.B.: Enforceable security policies. ACM Trans. Inf. Syst. Secur. 3(1), 30–50 (2000)
Wolper, P.: Temporal logic can be more expressive. Inf. Control 56(1/2), 72–99 (1983)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Cousot, P. (2019). Calculational Design of a Regular Model Checker by Abstract Interpretation. In: Hierons, R., Mosbah, M. (eds) Theoretical Aspects of Computing – ICTAC 2019. ICTAC 2019. Lecture Notes in Computer Science(), vol 11884. Springer, Cham. https://doi.org/10.1007/978-3-030-32505-3_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-32505-3_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-32504-6
Online ISBN: 978-3-030-32505-3
eBook Packages: Computer ScienceComputer Science (R0)





 (where
(where
 ) either stops in an initial state
) either stops in an initial state
 or is this initial state
or is this initial state
 followed by the next state
followed by the next state
 recording the assignment of the value
recording the assignment of the value
 of the arithmetic expression to variable
of the arithmetic expression to variable  after the assignment.
after the assignment. 
 in environment
in environment
 is
is
 :
: 
 either stops at
either stops at
 or goes on to the break label
or goes on to the break label
 (which is defined as the exit label of the closest enclosing iteration).
(which is defined as the exit label of the closest enclosing iteration). 
 is
is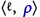 when the observation of the execution stops on entry of the program component for initial environment
when the observation of the execution stops on entry of the program component for initial environment
 ;
; for
for
 is false
is false
 , the initial state
, the initial state
 followed by the state
followed by the state
 at the label
at the label
 after the conditional statement;
after the conditional statement; for
for
 is true
is true
 , the initial state
, the initial state
 followed by a prefix trace of
followed by a prefix trace of
 starting
starting
 in environment
in environment
 (and possibly ending
(and possibly ending
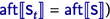 .
. are the prefix traces of
are the prefix traces of
 or the finite maximal traces of
or the finite maximal traces of
 followed by a prefix trace of
followed by a prefix trace of
 .
. 
 then the last state of
then the last state of
 must be the first state of
must be the first state of
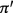 and this state is
and this state is
 and so the trace
and so the trace
 must be a maximal terminating execution of
must be a maximal terminating execution of
 i.e.
i.e.
 is executed only if
is executed only if
 terminates.
terminates. (6) of an iteration statement of the form
(6) of an iteration statement of the form
 where
where
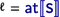 is the
is the  to the equation
to the equation
 . Since
. Since
 is
is 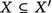 then
then
 and
and
 is a complete lattice,
is a complete lattice,
 exists by Tarski’s fixpoint theorem and can be defined as the limit of iterates [
exists by Tarski’s fixpoint theorem and can be defined as the limit of iterates [ , case (6.a) corresponds to a loop execution observation stopping on entry, (6.b) corresponds to an observation of a loop exiting after 0 or more iterations, and (6.c) corresponds to a loop execution observation that stops anywhere in the body
, case (6.a) corresponds to a loop execution observation stopping on entry, (6.b) corresponds to an observation of a loop exiting after 0 or more iterations, and (6.c) corresponds to a loop execution observation that stops anywhere in the body
 after 0 or more iterations. This last case covers the case of an iteration terminated by a break statement (to
after 0 or more iterations. This last case covers the case of an iteration terminated by a break statement (to
 after the iteration statement).
after the iteration statement).
 recognizes the first state of sequences of states recognized by
recognizes the first state of sequences of states recognized by
 ;
; recognizes sequences of states after the first state of sequences of states recognized by
recognizes sequences of states after the first state of sequences of states recognized by
 .
.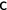 incremented at each program step one can simulate a trace with invariants. But then the reasoning is not on the original program
incremented at each program step one can simulate a trace with invariants. But then the reasoning is not on the original program
 but on a transformed program
but on a transformed program
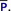 . Invariants in
. Invariants in
 holding for a given value of
holding for a given value of
 of
of
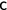 also hold at the position
also hold at the position
 of the traces in
of the traces in
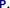 This king of indirect reasoning is usually heavy and painful to maintain when programs are modified since values of counters are no longer the same. The use of temporal specifications has the advantage of avoiding the reasoning on explicit positions in the trace.
This king of indirect reasoning is usually heavy and painful to maintain when programs are modified since values of counters are no longer the same. The use of temporal specifications has the advantage of avoiding the reasoning on explicit positions in the trace.