Abstract
The use of runtime verification has led to interest in deciding whether a property is monitorable: whether it is always possible for the satisfaction or violation of the property to be determined after a finite future continuation during system execution. However, classical two-valued monitorability suffers from two inherent limitations, which eventually increase runtime overhead. First, no information is available regarding whether only one verdict (satisfaction or violation) can be detected. Second, it does not tell us whether verdicts can be detected starting from the current monitor state during system execution.
This paper proposes a new notion of four-valued monitorability for \(\omega \)-languages and applies it at the state-level. Four-valued monitorability is more informative than two-valued monitorability as a property can be evaluated as a four-valued result, denoting that only satisfaction, only violation, or both are active for a monitorable property. We can also compute state-level weak monitorability, i.e., whether satisfaction or violation can be detected starting from a given state in a monitor, which enables state-level optimizations of monitoring algorithms. Based on a new six-valued semantics, we propose procedures for computing four-valued monitorability of \(\omega \)-regular languages, both at the language-level and at the state-level. Experimental results show that our tool implementation Monic can correctly, and quickly, report both two-valued and four-valued monitorability.
Supported by the Joint Research Funds of National Natural Science Foundation of China and Civil Aviation Administration of China (No. U1533130) and the Open Project of Shanghai Key Lab. of Trustworthy Computing.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Monitorability
- \(\omega \)-regular languages
- Linear temporal logic
- Multi-valued logics
- Runtime verification.
1 Introduction
Runtime Verification (RV) [6, 29, 32] is a lightweight formal technique in which program or system execution is monitored and analyzed. RV uses information extracted from an execution to check whether certain properties are satisfied or violated after a finite number of steps, possibly leading to online responses. In RV, properties are usually expressed using formalisms [26] such as Linear Temporal Logic (LTL) formulas [10, 17, 33, 36], Nondeterministic Büchi Automata (NBAs), and \(\omega \)-regular expressions, which represent \(\omega \)-regular languages [7, 15]. RV tools automatically synthesize monitors (i.e., code fragments) from formal specifications and then weave the code into the system through instrumentation [24, 25, 28]. The inserted code typically maintains a set of monitor objects that can detect property satisfaction or violation during system execution. Such approaches have been extended to parametric RV, in which properties are checked over every parameter instance (i.e., a combination of parameter values) by maintaining a monitor object for every parameter instance [11,12,13, 27, 34, 38].
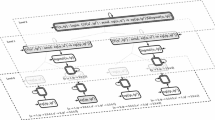
Figure 1 shows a monitor specification, written in the Movec language [13], for the parametric RV of an event-driven system that dispatches a variety of events (e.g., sensor status, keystrokes, program loadings etc.) to components (e.g., libraries, mobile apps, microservices etc.). Similar specifications can be written for other tools such as JavaMOP [11, 34] and TraceMatches [4, 5]. This specification defines a parametric monitor, named priority, which takes two parameters: a component ID c and an event ID e that should be instantiated with the values (i.e., actual arguments) generated by system execution. The specification body begins with four actions, which extract information regarding function calls: r records a component being registered to an event (it also creates a monitor object by instantiating the monitor parameters with the arguments of the call), u records an unregister, b records the broadcast of an event (the argument of the call) to all components, and n records a certain component being notified of a specific event. This specification is used to monitor system execution to check whether the property, specified as LTL formula  , is satisfied or violated after a finite number of steps, i.e., any infinite future continuation makes the property satisfied or violated, respectively. The property requires that if a component c registers to an event e and unregisters later, then before the unregister, the event e cannot be broadcasted until c has been notified (i.e., c has a higher priority than unregistered components).
, is satisfied or violated after a finite number of steps, i.e., any infinite future continuation makes the property satisfied or violated, respectively. The property requires that if a component c registers to an event e and unregisters later, then before the unregister, the event e cannot be broadcasted until c has been notified (i.e., c has a higher priority than unregistered components).
In practice, if the satisfaction or violation of a property is detected by a monitor object then an associated handler (i.e., a piece of code) is automatically triggered to perform some online response [11, 13, 34]. For example, Fig. 1 includes two handlers for the satisfaction (i.e., validation) and violation of the LTL formula: if the property is satisfied then a message is logged; if it is violated then an alarm is signaled and this prints the IDs of the component and the event. The two handlers may also be extended to more advanced operations, e.g., profiling and error recovery.
We may also monitor the system against other properties, e.g.,  that a component should receive notifications infinitely often after its registration,
that a component should receive notifications infinitely often after its registration,  that a component unregisters after its registration, and
that a component unregisters after its registration, and  that a registered component receives at least one notification before its deregistration. The developer may also write handlers for the satisfaction and violation of each property.
that a registered component receives at least one notification before its deregistration. The developer may also write handlers for the satisfaction and violation of each property.
When specifying properties, the developer is usually concerned with their monitorability [7, 10, 16, 37], i.e., after any number of steps, whether the satisfaction or violation of the monitored property can still be detected after a finite future continuation. When writing handlers for these properties, the developer might consider the following question: “Can the handlers for satisfaction and violation be triggered during system execution?” We say that a verdict and its handler are active if there is some continuation that would lead to the verdict being detected and thus its handler being triggered. This question can be partly answered by deciding monitorability (with the traditional two-valued notion). For example, \(\phi _2\) (above) is non-monitorable, i.e., there is some finite sequence of steps after which no verdict is active. Worse, \(\phi _2\) is also weakly non-monitorable [14], i.e., no verdict can be detected after any number of steps. Thus writing handlers for \(\phi _2\) is a waste of time as they will never be triggered. More seriously, monitoring \(\phi _2\) at runtime adds no value but increases runtime overhead. In contrast, \(\phi _1\), \(\phi _3\) and \(\phi _4\) are monitorable, i.e., some verdicts are always active. Thus their handlers must be developed as they may be triggered. However, this answer is still unsatisfactory, as the existing notion of monitorability suffers from two inherent limitations: limited informativeness and coarse granularity.
Limited Informativeness. The existing notion of monitorability is not sufficiently informative, as it is two-valued, i.e., a property can only be evaluated as monitorable or non-monitorable. This means, for a monitorable property, we only know that some verdicts are active, but no information is available regarding whether only one verdict (satisfaction or violation) is active. As a result, the developer may still write unnecessary handlers for inactive verdicts. For example, \(\phi _1\), \(\phi _3\) and \(\phi _4\) are monitorable. We only know that at least one of satisfaction and violation is active, but this does not tell us which ones are active and thus which handlers are required. As a result, the developer may waste time in handling inactive verdicts, e.g., the violation of \(\phi _3\) and the satisfaction of \(\phi _4\). Thus, the existing answer is far from satisfactory.
Limited informativeness also weakens the support for property debugging. For example, when writing a property the developer may expect that both verdicts are active but a mistake may lead to only one verdict being active. The converse is also the case. Unfortunately, these kinds of errors cannot be revealed by two-valued monitorability, as the expected property and the written (erroneous) property are both monitorable. For example, the developer may write formula \(\phi _4\) while having in mind another one  , i.e., what she/he really wants is wrongly prefixed by one
, i.e., what she/he really wants is wrongly prefixed by one  . These two formulas cannot be discriminated by deciding two-valued monitorability as both are monitorable.
. These two formulas cannot be discriminated by deciding two-valued monitorability as both are monitorable.
Coarse Granularity. The existing notion of monitorability is defined at the language-level, i.e., a property can only be evaluated as monitorable or not as a whole, rather than a notion for (more fine-grained) states in a monitor. This means that we do not know whether satisfaction or violation can be detected starting from the current state during system execution. As a result, every monitor object must be maintained during the entire execution, again increasing runtime overhead. For example,  is weakly monitorable, thus all its monitor objects (i.e., instances of the Finite State Machine (FSM) in Fig. 2), created for every pair of component and event, are maintained.
is weakly monitorable, thus all its monitor objects (i.e., instances of the Finite State Machine (FSM) in Fig. 2), created for every pair of component and event, are maintained.
Note that parametric runtime verification is NP-complete for detecting violations and coNP-complete for ensuring satisfaction [12]. This high complexity primarily comes from the large number of monitor objects maintained for all parameter instances [12, 13, 34]. For state-level optimizations of monitoring algorithms, if no verdict can be detected starting from the current state of a monitor object, then the object can be switched off and safely removed to improve runtime performance. For example, in Fig. 2, only satisfaction can be detected starting from states P1, P2 and T, whereas no verdict can be detected starting from state N. Thus a monitor object can be safely removed when it enters N. Unfortunately, the existing notion does not support such optimizations.
Our Solution. In this paper, we propose a new notion of four-valued monitorability for \(\omega \)-languages, and apply it at the state-level, overcoming the two limitations discussed above. First, the proposed approach is more informative than two-valued monitorability. Indeed, a property can be evaluated as a four-valued result, denoting that only satisfaction, only violation, or both are active for a monitorable property. Thus, if satisfaction (resp. violation) is inactive, then writing handlers for satisfaction (resp. violation) is not required. This can also enhance property debugging. For example, \(\phi _4\) and \(\phi _5\) can now be discriminated by their different monitorability results, as \(\phi _4\) can never be satisfied but \(\phi _5\) can be satisfied and can also be violated. Thus, additional developer mistakes can be revealed. Second, we can compute state-level weak monitorability, i.e., whether satisfaction or violation can be detected starting from a given state in a monitor. For example, in Fig. 2, N is weakly non-monitorable, thus a monitor object can be safely removed when it enters N, achieving a state-level optimization.
In summary, we make the following contributions.Footnote 1
-
We propose a new notion of four-valued monitorability for \(\omega \)-languages (Sect. 3), which provides more informative answers as to which verdicts are active. This notion is defined using six types of prefixes, which complete the classification of finite sequences.
-
We propose a procedure for computing four-valued monitorability of \(\omega \)-regular languages, given in terms of LTL formulas, NBAs or \(\omega \)-regular expressions (Sect. 4), based on a new six-valued semantics.
-
We propose a new notion of state-level four-valued weak monitorability and its computation procedure for \(\omega \)-regular languages (Sect. 5), which describes which verdicts are active for a state. This can enable state-level optimizations of monitoring algorithms.
-
We have developed a new tool, Monic, that implements the proposed procedure for computing monitorability of LTL formulas. We evaluated its effectiveness using a set of 97 LTL patterns and formulas \(\phi _1\) to \(\phi _6\) (above). Experimental results show that Monic can correctly report both two-valued and four-valued monitorability (Sect. 6).
2 Preliminaries
Let AP be a non-empty finite set of atomic propositions. A state is a complete assignment of truth values to the propositions in AP. Let \(\varSigma = 2^{AP}\) be a finite alphabet, i.e., the set of all states. \(\varSigma ^*\) is the set of finite words (i.e., sequences of states in \(\varSigma \)), including the empty word \(\epsilon \), and \(\varSigma ^\omega \) is the set of infinite words. We denote atomic propositions by p, q, r, finite words by u, v, and infinite words by w, unless explicitly specified. We write a finite or infinite word in the form \(\{p, q\}\{p\}\{q,r\}\cdots \), where a proposition appears in a state iff it is assigned true. We drop the brackets around singletons, i.e., \(\{p, q\}p\{q,r\}\cdots \).
An \(\omega \)-language (i.e., a linear-time infinitary property) L is a set of infinite words over \(\varSigma \), i.e., \(L \subseteq \varSigma ^\omega \). Linear Temporal Logic (LTL) [33, 36] is a typical representation of \(\omega \)-regular languages. LTL extends propositional logic, which uses boolean connectives \(\lnot \) (not) and \(\wedge \) (conjunction), by introducing temporal connectives such as  (next),
(next),  (until),
(until),  (release),
(release),  (future, or eventually) and
(future, or eventually) and  (globally, or always). Intuitively,
(globally, or always). Intuitively,  says that \(\phi \) holds at the next state,
says that \(\phi \) holds at the next state,  says that at some future state \(\phi _2\) holds and before that state \(\phi _1\) always holds. Using the temporal connectives
says that at some future state \(\phi _2\) holds and before that state \(\phi _1\) always holds. Using the temporal connectives  and
and  , the full power of LTL is obtained. For convenience, we also use some common abbreviations: true, false, standard boolean connectives \(\phi _1 \vee \phi _2 \equiv \lnot (\lnot \phi _1 \wedge \lnot \phi _2)\) and \(\phi _1 \rightarrow \phi _2 \equiv \lnot \phi _1 \vee \phi _2\), and additional temporal connectives
, the full power of LTL is obtained. For convenience, we also use some common abbreviations: true, false, standard boolean connectives \(\phi _1 \vee \phi _2 \equiv \lnot (\lnot \phi _1 \wedge \lnot \phi _2)\) and \(\phi _1 \rightarrow \phi _2 \equiv \lnot \phi _1 \vee \phi _2\), and additional temporal connectives  (the dual to
(the dual to  ),
),  (\(\phi \) eventually holds), and
(\(\phi \) eventually holds), and  (\(\phi \) always holds). We denote by \(L(\phi )\) the \(\omega \)-language accepted by a formula \(\phi \).
(\(\phi \) always holds). We denote by \(L(\phi )\) the \(\omega \)-language accepted by a formula \(\phi \).
Let us recall the classification of prefixes that are used to define the three-valued semantics and two-valued monitorability of \(\omega \)-languages.
Definition 1
(Good, bad and ugly prefixes [8, 31]). A finite word \(u \in \varSigma ^*\) is a good prefix for L if \(\forall w \in \varSigma ^\omega .uw \in L\), a bad prefix for L if \(\forall w \in \varSigma ^\omega .uw \not \in L\), or an ugly prefix for L if no finite extension makes it good or bad, i.e., \(\not \exists v\in \varSigma ^*. \forall w \in \varSigma ^\omega .uvw \in L\) and \(\not \exists v\in \varSigma ^*. \forall w \in \varSigma ^\omega .uvw \not \in L\).
In other words, good and bad prefixes satisfy and violate an \(\omega \)-language in some finite number of steps, respectively. We denote by good(L), bad(L) and ugly(L) the set of good, bad and ugly prefixes for L, respectively. Note that they do not constitute a complete classification of finite words. For example, any finite word of the form \(p \cdots p\) is neither a good nor a bad prefix for  , and also is not an ugly prefix as it can be extended to a good prefix (ended with q) or a bad prefix (ended with \(\emptyset \)).
, and also is not an ugly prefix as it can be extended to a good prefix (ended with q) or a bad prefix (ended with \(\emptyset \)).
Definition 2
(Three-valued semantics [10]). Let \(\mathbb {B}_3\) be the set of three truth values: true \(\top \), false \(\bot \) and inconclusive ?. The truth value of an \(\omega \)-language \(L \subseteq \varSigma ^\omega \) wrt. a finite word \(u \in \varSigma ^*\), denoted by \([u \models L]_3\), is \(\top \) or \(\bot \) if u is a good or bad prefix for L, respectively, and ? otherwise.
Note that the inconclusive value does not correspond to ugly prefixes. Although an ugly prefix always leads to the inconclusive value, the converse does not hold. For example,  = ? but \(p \cdots p\) is not an ugly prefix.
= ? but \(p \cdots p\) is not an ugly prefix.
Bauer et al. [10] presented a monitor construction procedure that transforms an LTL formula \(\phi \) into a three-valued monitor, i.e., a deterministic FSM that contains \(\top \), \(\bot \) and ? states, which output \(\top \), \(\bot \) and ? after reading over good, bad and other prefixes respectively. For example, in Fig. 2, state T is a \(\top \) state, whereas the remaining states are all ? states. This construction procedure requires 2ExpSpace. It has been shown that the three-valued monitor can be used to compute the truth value of an \(\omega \)-language wrt. a finite word [10], which is the output of the corresponding monitor after reading over this word.
Lemma 1
Let \(M = (Q\), \(\varSigma \), \(\delta \), \(q_0\), \(\mathbb {B}_3\), \(\lambda _3)\) be a three-valued monitor for an \(\omega \)-language \(L \subseteq \varSigma ^\omega \), where Q is a finite set of states, \(\varSigma \) is a finite alphabet, \(\delta : Q \times \varSigma \mapsto Q\) is a transition function, \(q_0 \in Q\) is an initial state, \(\mathbb {B}_3\) is an output alphabet and \(\lambda _3: Q \rightarrow \mathbb {B}_3\) is an output function. For any \(u \in \varSigma ^*\), \([u \models L]_3 = \lambda _3(\delta (q_0, u))\).
Definition 3
(Two-valued monitorability [7, 10, 37]). An \(\omega \)-language \(L \subseteq \varSigma ^\omega \) is u-monitorable for \(u \in \varSigma ^*\), if \(\exists v \in \varSigma ^*\) s.t. uv is a good or bad prefix, and monitorable if it is u-monitorable for every \(u \in \varSigma ^*\).
In other words, L is u-monitorable if u has a good or bad extension. L is monitorable if every finite word has a good or bad extension. Note that an ugly prefix can never be extended to a good or bad prefix. Thus, L is non-monitorable iff there exists an ugly prefix for L.
3 Four-Valued Monitorability
In this section, we propose a new notion of four-valued monitorability, to provide more informative answers to monitorability checking. As we promised, it can indicate whether only satisfaction, only violation, or both are active for a monitorable property. Two-valued monitorability cannot achieve this because its definition only requires that all finite words (i.e., u in Definition 3) can be extended to good or bad prefixes (which witness satisfaction or violation, respectively), but does not discriminate between them on the types and number of the verdicts that the extensions of each finite word can witness. To address this limitation, our approach aims to discriminate accordingly these finite words by inspecting which types of prefixes they can be extended to.
To achieve this objective, we first need to propose a new classification of prefixes, as the traditional classification (as the good, the bad and the ugly) is not satisfactory due to incompleteness, i.e., it does not include the finite words that are neither good nor bad but can be extended to good or bad prefixes. Thus we introduce the notions of positive, negative and neutral prefixes, in addition to good, bad and ugly prefixes, to complete the classification.
Definition 4
(Positive, negative and neutral prefixes). A finite word u is
-
a positive prefix for L if it is not good, but some finite extension makes it good but never bad, i.e., \(\exists w \in \varSigma ^\omega . uw \not \in L\), \(\exists v \in \varSigma ^*. \forall w \in \varSigma ^\omega . uvw \in L\), and \(\not \exists v \in \varSigma ^*. \forall w\in \varSigma ^\omega . uvw \not \in L\),
-
a negative prefix for L if it is not bad, but some finite extension makes it bad but never good, i.e., \(\exists w \in \varSigma ^\omega . uw \in L\), \(\exists v \in \varSigma ^*. \forall w \in \varSigma ^\omega . uvw \not \in L\), and \(\not \exists v \in \varSigma ^*. \forall w\in \varSigma ^\omega . uvw \in L\), or
-
a neutral prefix for L if some finite extension makes it good and some makes it bad, i.e., \(\exists v\in \varSigma ^*. \forall w \in \varSigma ^\omega .uvw \in L\) and \(\exists v\in \varSigma ^*. \forall w \in \varSigma ^\omega .uvw \not \in L\).
We denote by posi(L), nega(L) and neut(L) the set of positive, negative and neutral prefixes for L, respectively. It is easy to see that the three new sets of prefixes and the three traditional sets of good, bad and ugly prefixes are mutually disjoint. An interesting fact, as shown by the following theorem, is that the six sets of prefixes exactly constitute the complete set of finite words. Furthermore, the six types of prefixes directly correspond to the six-valued semantics (cf. Definition 5). This completes the classification of prefixes.
Theorem 1
\(good(L) \cup bad(L) \cup posi({L}) \cup nega({L}) \cup neut({L}) \cup ugly(L) = \varSigma ^*\).
The traditional three-valued semantics can identify only good and bad prefixes with the truth values \(\top \) and \(\bot \) respectively, whereas all the prefixes of the other four types are given the same value ?. To discriminate them, we further divide the value ? into four truth values.
Definition 5
(Six-valued semantics). Let \(\mathbb {B}_6\) be the set of six truth values: true \(\top \), false \(\bot \), possibly true  , possibly false ±, possibly conclusive \(+\) and inconclusive \(\times \). The truth value of an \(\omega \)-language \(L \subseteq \varSigma ^*\) wrt. a finite word \(u \in \varSigma ^*\), denoted by \([u \models L]_6\), is \(\top \), \(\bot \),
, possibly false ±, possibly conclusive \(+\) and inconclusive \(\times \). The truth value of an \(\omega \)-language \(L \subseteq \varSigma ^*\) wrt. a finite word \(u \in \varSigma ^*\), denoted by \([u \models L]_6\), is \(\top \), \(\bot \),  , ±, \(+\) or \(\times \) if u is a good, bad, positive, negative, neutral or ugly prefix for L, respectively.
, ±, \(+\) or \(\times \) if u is a good, bad, positive, negative, neutral or ugly prefix for L, respectively.
Note that the six-valued semantics models a rigorous correspondence between truth values and prefix types. Unlike the three-valued semantics, the inconclusive value now exactly corresponds to ugly prefixes.
The definition of four-valued monitorability is built on the following notion of four-valued u-monitorability which is used to discriminate finite words by inspecting which types of prefixes they can be extended to.
Definition 6
(Four-valued u -monitorability). An \(\omega \)-language \(L \subseteq \varSigma ^\omega \) is
-
weakly positively u-monitorable for \(u \in \varSigma ^*\), if \(\exists v \in \varSigma ^*\), s.t. uv is a good prefix.
-
weakly negatively u-monitorable for \(u \in \varSigma ^*\), if \(\exists v \in \varSigma ^*\), s.t. uv is a bad prefix.
-
positively u-monitorable if it is weakly positively, but not weakly negatively, u-monitorable. (u has only good extensions, thus u is a good/positive prefix.)
-
negatively u-monitorable if it is weakly negatively, but not weakly positively, u-monitorable. (u has only bad extensions, thus u is a bad/negative prefix.)
-
neutrally u-monitorable if it is both weakly positively and weakly negatively u-monitorable. (u has both good and bad extensions, thus u is a neutral prefix.)
-
not u-monitorable if it is neither weakly positively nor weakly negatively u-monitorable. (u has neither good nor bad extension, thus u is an ugly prefix.)
In other words, the traditional u-monitorability is split into two parts, i.e., weakly positive and weakly negative u-monitorability. As a result, L is u-monitorable iff L is positively, negatively or neutrally u-monitorable.
Definition 7
(Four-valued monitorability). An \(\omega \)-language \(L \subseteq \varSigma ^\omega \) is
-
positively monitorable if it is positively u-monitorable for every \(u \in \varSigma ^*\).
-
negatively monitorable if it is negatively u-monitorable for every \(u \in \varSigma ^*\).
-
neutrally monitorable if it is u-monitorable for every \(u \in \varSigma ^*\), and is neutrally \(\epsilon \)-monitorable for the empty word \(\epsilon \).
-
non-monitorable if it is not u-monitorable for some \(u\in \varSigma ^*\).
In other words, the set of monitorable \(\omega \)-languages is divided into three classes, i.e., positively, negatively and neutrally monitorable ones. Note that the definition of neutral monitorability consists of two conditions, of which the first ensures that L is monitorable while the second ensures that both of satisfaction and violation can be detected after some finite sequences of steps. We denote the four truth values (positively, negatively, neutrally and non-monitorable) by \(M_\top \), \(M_\bot \), \(M_+\) and \(M_\times \), respectively.
We can validate that four-valued monitorability indeed provides the informativeness we require, as described in Sect. 1, by showing the following theorem, that the truth values \(M_\top \), \(M_\bot \), and \(M_+\) indicate that only satisfaction, only violation, and both can be detected after some finite sequences of steps, respectively. This theorem can be proved by Definitions 7 and 6, in which u is substituted by the empty word \(\epsilon \).
Theorem 2
If an \(\omega \)-language \(L \subseteq \varSigma ^\omega \) is
-
\(M_\top \) then \(\exists u \in \varSigma ^*. \forall w \in \varSigma ^\omega . uw \in L\) and \(\not \exists u \in \varSigma ^*. \forall w \in \varSigma ^\omega . uw \not \in L\).
-
\(M_\bot \) then \(\exists u \in \varSigma ^*. \forall w \in \varSigma ^\omega . uw \not \in L\) and \(\not \exists u \in \varSigma ^*. \forall w \in \varSigma ^\omega . uw \in L\).
-
\(M_+\) then \(\exists u \in \varSigma ^*. \forall w \in \varSigma ^\omega . uw \in L\) and \(\exists u \in \varSigma ^*. \forall w \in \varSigma ^\omega . uw \not \in L\).
Let us consider some simple but essential examples regarding basic temporal connectives. More examples, such as the formulas used in Sect. 1, will be considered in Sect. 6.
-
Formula
 is positively monitorable, as any finite word can be extended to a good prefix (ended with p) but never a bad prefix. This means that only satisfaction, but no violation, of the property can be detected after some finite sequences of steps.
is positively monitorable, as any finite word can be extended to a good prefix (ended with p) but never a bad prefix. This means that only satisfaction, but no violation, of the property can be detected after some finite sequences of steps. -
Formula
 is negatively monitorable, as any finite word can be extended to a bad prefix (ended with \(\emptyset \)) but never a good prefix. This means that only violation, but no satisfaction, of the property can be detected after some finite sequences of steps.
is negatively monitorable, as any finite word can be extended to a bad prefix (ended with \(\emptyset \)) but never a good prefix. This means that only violation, but no satisfaction, of the property can be detected after some finite sequences of steps. -
Formula
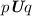 is neutrally monitorable, as it is monitorable and \(\epsilon \) (more generally, any finite word of the form \(p\cdots p\)) can be extended to both a good prefix (ended with q) and a bad prefix (ended with \(\emptyset \)). This means that both of satisfaction and violation of the property can be detected after some finite sequences of steps.
is neutrally monitorable, as it is monitorable and \(\epsilon \) (more generally, any finite word of the form \(p\cdots p\)) can be extended to both a good prefix (ended with q) and a bad prefix (ended with \(\emptyset \)). This means that both of satisfaction and violation of the property can be detected after some finite sequences of steps. -
Formula
 is non-monitorable, as any finite word can never be extended to a good or bad prefix, due to the infinite continuations \(\emptyset \emptyset \cdots \) and \(pp \cdots \) respectively. This means that neither satisfaction nor violation of the property can be detected.
is non-monitorable, as any finite word can never be extended to a good or bad prefix, due to the infinite continuations \(\emptyset \emptyset \cdots \) and \(pp \cdots \) respectively. This means that neither satisfaction nor violation of the property can be detected.
4 Computing Four-Valued Monitorability
In this section, we propose a procedure for computing the four-valued monitorability of \(\omega \)-regular languages, based on the six-valued semantics.
The first step is a monitor construction procedure that transforms an LTL formula into a six-valued monitor, i.e., a deterministic FSM which outputs \(\top \), \(\bot \),  , ±, \(+\) and \(\times \) after reading over good, bad, positive, negative, neutral and ugly prefixes respectively. For example, in Fig. 2, states P1, P2 and N are all ? states under the three-valued semantics. After refining the output function with the six-valued semantics, states P1 and P2 become
, ±, \(+\) and \(\times \) after reading over good, bad, positive, negative, neutral and ugly prefixes respectively. For example, in Fig. 2, states P1, P2 and N are all ? states under the three-valued semantics. After refining the output function with the six-valued semantics, states P1 and P2 become  states, whereas state N becomes a \(\times \) state.
states, whereas state N becomes a \(\times \) state.
The construction procedure first constructs a three-valued monitor, using the traditional approach which requires 2ExpSpace [10]. Then we refine its output function, assigning new outputs to ? states. Specifically, our procedure traverses all the states in the monitor, and for each state, starts another nested traversal to check whether a \(\top \) state or a \(\bot \) state is reachable. A ? state is assigned output  if \(\top \) states are reachable but no \(\bot \) state is, ± if \(\bot \) states are reachable but no \(\top \) state is, \(+\) if both \(\top \) and \(\bot \) states are reachable, or \(\times \) if neither is reachable. This refinement step can be done in polynomial time and NLSpace (using the three-valued monitor as the input). Thus, constructing a six-valued monitor requires also 2ExpSpace. Let us formalize the above construction procedure.
if \(\top \) states are reachable but no \(\bot \) state is, ± if \(\bot \) states are reachable but no \(\top \) state is, \(+\) if both \(\top \) and \(\bot \) states are reachable, or \(\times \) if neither is reachable. This refinement step can be done in polynomial time and NLSpace (using the three-valued monitor as the input). Thus, constructing a six-valued monitor requires also 2ExpSpace. Let us formalize the above construction procedure.
Definition 8
Let \(M = (Q\), \(\varSigma \), \(\delta \), \(q_0\), \(\mathbb {B}_3\), \(\lambda _3)\) be a three-valued monitor for an \(\omega \)-language \(L \subseteq \varSigma ^\omega \). The corresponding six-valued monitor \(M' = (Q\), \(\varSigma \), \(\delta \), \(q_0\), \(\mathbb {B}_6\), \(\lambda )\) is obtained by refining the output function \(\lambda _3\) of M as in Fig. 3.
We can show the following lemma, that the six-valued monitor can be used to compute the truth value of an \(\omega \)-language wrt. a finite word. This lemma can be proved by Definitions 5 and 2, Lemma 1 and Definition 8.
Lemma 2
Let \(M = (Q\), \(\varSigma \), \(\delta \), \(q_0\), \(\mathbb {B}_6\), \(\lambda )\) be a six-valued monitor for an \(\omega \)-language \(L \subseteq \varSigma ^\omega \). For any \(u \in \varSigma ^*\), \([u \models L]_6 = \lambda (\delta (q_0, u))\).
As a property of the six-valued monitor, the following theorem shows that each state in a monitor can be reached by exactly one type of prefixes (by Lemma 2 and Definition 5).
Theorem 3
Let \(M = (Q\), \(\varSigma \), \(\delta \), \(q_0\), \(\mathbb {B}_6\), \(\lambda )\) be a six-valued monitor for an \(\omega \)-language \(L \subseteq \varSigma ^\omega \). For a state \(q \in Q\), \(\lambda (q)\) equals \(\top \), \(\bot \),  , ±, \(+\) or \(\times \), iff it can be reached by good, bad, positive, negative, neutral or ugly prefixes, respectively.
, ±, \(+\) or \(\times \), iff it can be reached by good, bad, positive, negative, neutral or ugly prefixes, respectively.
Based on the six-valued monitor, the second step determines the four-valued monitorability of an \(\omega \)-language L by checking whether its monitor has some specific reachable states. The monitorability of L is \(M_\top \) iff neither \(\times \) nor \(\bot \) states are reachable (thus neither ± nor \(+\) states are reachable), \(M_\bot \) iff neither \(\times \) nor \(\top \) states are reachable (thus neither  nor \(+\) states are reachable), \(M_+\) iff no \(\times \) state is reachable but a \(+\) state is reachable (thus both \(\top \) and \(\bot \) states are reachable), and \(M_\times \) iff a \(\times \) state is reachable. These rules can be formalized:
nor \(+\) states are reachable), \(M_+\) iff no \(\times \) state is reachable but a \(+\) state is reachable (thus both \(\top \) and \(\bot \) states are reachable), and \(M_\times \) iff a \(\times \) state is reachable. These rules can be formalized:
Theorem 4
Let \(M = (Q\), \(\varSigma \), \(\delta \), \(q_0\), \(\mathbb {B}_6\), \(\lambda )\) be a six-valued monitor for an \(\omega \)-language \(L \subseteq \varSigma ^\omega \). The monitorability of L, denoted by \(\eta (L)\), is:
The above checking procedure can be done in linear time and NLSpace by traversing all the states of monitor. However, note that this procedure is performed after constructing the monitor. Thus, when an \(\omega \)-regular language L is given in terms of an LTL formula, the four-valued monitorability of L can be computed in 2ExpSpace; the same complexity as for two-valued monitorability. As we will see in Sect. 6, the small size of standard LTL patterns means that four-valued monitorability can be computed in very little time
Now consider other representations of \(\omega \)-regular languages. If L is given in terms of a Nondeterministic Büchi Automata (NBA), we first explicitly complement the NBA, and the rest of the procedure stays the same. However, the complement operation also involves an exponential blowup. If L is given in terms of an \(\omega \)-regular expression, we first build an NBA for the expression, which can be done in polynomial time, and the rest of the procedure is the same as for NBA. Hence, independent of the concrete representation, four-valued monitorability of an \(\omega \)-regular language can be computed in 2ExpSpace, by using the monitor-based procedure.
5 State-Level Four-Valued Weak Monitorability
In this section, we apply four-valued monitorability at the state-level, to predict whether satisfaction and violation can be detected starting from a given state in a monitor. Recall that the notions of monitorability (cf. Definitions 3 and 7) are defined using the extensions to good and bad prefixes. However, good and bad prefixes are defined for an \(\omega \)-language, not for a state. Thus such definitions cannot be directly applied at the state-level. Instead, we define state-level monitorability using the reachability of \(\top \) and \(\bot \) states, which are equivalent notions to good and bad prefixes according to Theorem 3.
Another note is that the resulting state-level monitorability is too strong to meet our requirements, because it places restrictions on all the states reachable from the considered state. For example, in Fig. 2, we require discriminating states P1 and P2 from state N, as satisfaction can be detected starting from P1 and P2, but neither satisfaction nor violation can be detected starting from N. However, P1, P2 and N are all non-monitorable as neither \(\top \) states nor \(\bot \) states are reachable from N (in turn, reachable from P1 and P2). To provide the required distinction, we should use a weaker form of state-level monitorability as follows.
Definition 9
(State-level four-valued weak monitorability). Let \(M = (Q, \varSigma , \delta , q_0, \mathbb {B}_6, \lambda )\) be a six-valued monitor. A state \(q \in Q\) is
-
weakly \(M_\top \) if a \(\top \) state but no \(\bot \) state is reachable from q.
-
weakly \(M_\bot \) if a \(\bot \) state but no \(\top \) state is reachable from q.
-
weakly \(M_+\) if both a \(\top \) state and a \(\bot \) state are reachable from q.
-
weakly \(M_\times \) if neither \(\top \) states nor \(\bot \) states are reachable from q.
A state is weakly monitorable, iff it is weakly positively, negatively or neutrally monitorable. For example, in Fig. 2, states P1, P2 and T are all weakly positively monitorable as T is a reachable \(\top \) state, while state N is weakly non-monitorable. Thus, states P1 and P2 can now be discriminated from state N.
We can validate that state-level four-valued weak monitorability can indeed predict whether satisfaction and violation can be detected starting from a given state, as anticipated in Sect. 1, by showing the following theorem, that the truth values \(M_\top \), \(M_\bot \), \(M_+\) and \(M_\times \) indicate that only satisfaction, only violation, both and neither can be detected, respectively. This theorem can be proved by Definition 9 and Theorem 3.
Theorem 5
Let \(M = (Q, \varSigma , \delta , q_0, \mathbb {B}_6, \lambda )\) be a six-valued monitor. Suppose a state \(q \in Q\) can be reached from \(q_0\) by reading \(u \in \varSigma ^*\), i.e., \(\delta (q_0, u) = q\). If q is
-
weakly \(M_\top \) then \(\exists v \in \varSigma ^*. \forall w \in \varSigma ^\omega . uvw \in L\) \(\wedge \) \(\not \exists v \in \varSigma ^*. \forall w \in \varSigma ^\omega . uvw \not \in L\).
-
weakly \(M_\bot \) then \(\exists v \in \varSigma ^*. \forall w \in \varSigma ^\omega . uvw \not \in L\) \(\wedge \) \(\not \exists v \in \varSigma ^*. \forall w \in \varSigma ^\omega . uvw \in L\).
-
weakly \(M_+\) then \(\exists v \in \varSigma ^*. \forall w \in \varSigma ^\omega . uvw \in L\) \(\wedge \) \(\exists v \in \varSigma ^*. \forall w \in \varSigma ^\omega . uvw \not \in L\).
-
weakly \(M_\times \) then \(\not \exists v \in \varSigma ^*. \forall w \in \varSigma ^\omega . uvw \in L\) \(\wedge \) \(\not \exists v \in \varSigma ^*. \forall w \in \varSigma ^\omega . uvw \not \in L\).
The four truth values can be used in state-level optimizations of monitoring algorithms:
-
If a state is weakly positively (resp. negatively) monitorable, then a monitor object can be safely removed when it enters this state, provided that only violation (resp. satisfaction) handlers are specified, as no handler can be triggered.
-
If a state is weakly neutrally monitorable, then a monitor object must be preserved if it is at this state as both satisfaction and violation can be detected after some continuations.
-
If a state is weakly non-monitorable, then a monitor object can be safely removed when it enters this state as no verdict can be detected after any continuation.
Besides, a monitor object can also be removed when it enters a \(\top \) state or a \(\bot \) state, as any finite or infinite continuation yields the same verdict.
Let us consider the relationship between the language-level monitorability and the state-level weak monitorability. The following lemma shows that the monitorability of an \(\omega \)-language depends on the weak monitorability of all the reachable states of its monitor. This means, if an \(\omega \)-language is non-monitorable, then its monitor contains a reachable weakly non-monitorable state.
Lemma 3
Let \(M = (Q\), \(\varSigma \), \(\delta \), \(q_0\), \(\mathbb {B}_6\), \(\lambda )\) be a six-valued monitor for an \(\omega \)-language \(L \subseteq \varSigma ^\omega \). L is monitorable iff every reachable state of M is weakly monitorable.
Let us consider how one can compute the state-level four-valued weak monitorability for each state in a six-valued monitor. We first formalize a mapping from truth values to weak monitorability, and then show that the state-level weak monitorability can be quickly computed from the output of the state.
Definition 10
(Value-to-weak-monitorability). Let \(\texttt {vtom}: \mathbb {B}_6 \mapsto \mathbb {M}_4\) be the value-to-weak-monitorability operator that converts a truth value in \(\mathbb {B}_6\) into the corresponding result of weak monitorability in \(\mathbb {M}_4 = \{ M_\top , M_\bot , M_+, M_\times \}\), defined as follows:  , \(\texttt {vtom}(\bot ) = \texttt {vtom}(\pm ) = M_\bot \), \(\texttt {vtom}(+) = M_+\) and \(\texttt {vtom}(\times ) = M_\times \).
, \(\texttt {vtom}(\bot ) = \texttt {vtom}(\pm ) = M_\bot \), \(\texttt {vtom}(+) = M_+\) and \(\texttt {vtom}(\times ) = M_\times \).
Theorem 6
Let \(M = (Q\), \(\varSigma \), \(\delta \), \(q_0\), \(\mathbb {B}_6\), \(\lambda )\) be a six-valued monitor for an \(\omega \)-language \(L \subseteq \varSigma ^\omega \). The four-valued weak monitorability of \(q \in Q\) equals \(\texttt {vtom}(\lambda (q))\).
6 Implementation and Experimental Results
We have developed a new tool, Monic, that implements the proposed procedure for computing four-valued monitorability of LTL formulas. Monic also supports deciding two-valued monitorability. We have evaluated its effectiveness using a set of LTL formulas, including formulas \(\phi _1\) to \(\phi _6\) (used in Sect. 1) and Dwyer et al.’s 97 LTL patterns [10, 18]. The tool implementation Monic and the dataset of LTL formulas are available at https://github.com/drzchen/monic. The evaluation was performed on an ordinary laptop, equipped with an Intel Core i7-6500U CPU (at 2.5GHz), 4GB RAM and Ubuntu Desktop (64-bit).
The result on formulas \(\phi _1\) to \(\phi _6\) shows that: \(\phi _1\) is neutrally monitorable, \(\phi _2\) is non-monitorable, \(\phi _3\) is positively monitorable, \(\phi _4\) is negatively monitorable, \(\phi _5\) is neutrally monitorable, and \(\phi _6\) is non-monitorable (but weakly monitorable). Thus, the violation of \(\phi _3\) and the satisfaction of \(\phi _4\) can never be detected, whereas both verdicts are active for \(\phi _1\) and \(\phi _5\). Further, \(\phi _4\) and \(\phi _5\) can be discriminated by their different monitorability results.
We also ran Monic on Dwyer et al.’s specification patterns [10, 18], of which 97 are well-formed LTL formulas. The result shows that 55 formulas are monitorable and 42 are non-monitorable. For those monitorable ones, 6 are positively monitorable, 40 are negatively monitorable and 9 are neutrally monitorable. Our result disagrees with the two-valued result reported in [10] only on the 6th LTL formula listed in the Appendix of [10]. More precisely, Monic reports negatively monitorable, whereas the result in [10] is non-monitorable. The formula is as follows (! for \(\lnot \), & for \(\wedge \),
 for \(\vee \),
for \(\vee \),
 for \(\rightarrow \), U for
for \(\rightarrow \), U for  ,
,
 for \(\mathbf{F} \), [] for
for \(\mathbf{F} \), [] for  ):
):

A manual inspection of its monitor (in Fig. 4) shows that our result is correct. Indeed, state F is a \(\bot \) state, and states N1 to N7 are all ± states that can reach the \(\bot \) state F.
Finally, the above results for \(\phi _1\) to \(\phi _6\) and the 97 LTL patterns were computed in 0.03 and 0.07 s, with 16 MB and 20 MB memory consumed, respectively (all reported by GNU time). To conclude, the results show that Monic can correctly report both two-valued and four-valued monitorability of typical formulas in very little time.
7 Related Work
Monitorability is a principal foundational question in RV because it delineates which properties can be monitored at runtime. The classical results on monitorability have been established for \(\omega \)-languages, especially for LTL [7, 10, 37]. Francalanza and Aceto et al. have studied monitorability for the Hennessy-Milner logic with recursion, both with a branching-time semantics [1, 21,22,23] and with a linear-time semantics [2]. There exist some variants of monitorability as well. For example, monitorability has been considered over unreliable communication channels which may reorder or lose events [30]. However, all of the existing works only consider two-valued notions of monitorability at the language-level.
Monitorability has been studied in other contexts. For example, a topological viewpoint [16] and the correspondence between monitorability and the classifications of properties (e.g., the safety-progress and safety-liveness classifications) [19, 20, 35] have been established. A hierarchy of monitorability definitions (including monitorability and weak monitorability [14]) has been defined wrt. the operational guarantees provided by monitors [3].
A four-valued semantics for LTL [8, 9] has been proposed to refine the three-valued semantics [10]. It divides the inconclusive truth value ? into two values: currently true and currently false, i.e., whether the finite sequence observed so far satisfies the property based on a finite semantics for LTL. Note that it provides more information on what has already been seen, whereas our six-valued semantics describes what verdicts can be detected in the future continuation.
8 Conclusion
We have proposed four-valued monitorability and the corresponding computation procedure for \(\omega \)-regular languages. Then we applied the four-valued notion at the state-level. To our knowledge, this is the first study of multi-valued monitorability, inspired by practical requirements from RV. We believe that our work and implementation can be integrated into RV tools to provide information at the development stage and thus avoid the development of unnecessary handlers and the use of monitoring that cannot add value, enhance property debugging, and enable state-level optimizations of monitoring algorithms.
Notes
- 1.
A longer version of this paper (with all proofs) is available at https://arxiv.org/abs/2002.06737.
References
Aceto, L., Achilleos, A., Francalanza, A., Ingólfsdóttir, A.: A framework for parameterized monitorability. In: Baier, C., Dal Lago, U. (eds.) FoSSaCS 2018. LNCS, vol. 10803, pp. 203–220. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89366-2_11
Aceto, L., Achilleos, A., Francalanza, A., Ingólfsdóttir, A., Lehtinen, K.: Adventures in monitorability: from branching to linear time and back again. In: Proceedings of the ACM on Programming Languages,(POPL 2019), vol. 3, pp. 52:1–52:29 (2019)
Aceto, L., Achilleos, A., Francalanza, A., Ingólfsdóttir, A., Lehtinen, K.: An operational guide to monitorability. In: Ölveczky, P.C., Salaün, G. (eds.) SEFM 2019. LNCS, vol. 11724, pp. 433–453. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-30446-1_23
Allan, C., et al.: Adding trace matching with free variables to AspectJ. In: Proceedings of OOPSLA 2005, pp. 345–364. ACM (2005)
Avgustinov, P., Tibble, J., de Moor, O.: Making trace monitors feasible. In: Proceedings of OOPSLA 2007, pp. 589–608. ACM (2007)
Bartocci, E., Falcone, Y., Francalanza, A., Reger, G.: Introduction to runtime verification. In: Bartocci, E., Falcone, Y. (eds.) Lectures on Runtime Verification. LNCS, vol. 10457, pp. 1–33. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-75632-5_1
Bauer, A.: Monitorability of \(\omega \)-regular languages. CoRR abs/1006.3638 (2010)
Bauer, A., Leucker, M., Schallhart, C.: The good, the bad, and the ugly, but how ugly is ugly? In: Sokolsky, O., Taşıran, S. (eds.) RV 2007. LNCS, vol. 4839, pp. 126–138. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-77395-5_11
Bauer, A., Leucker, M., Schallhart, C.: Comparing LTL semantics for runtime verification. J. Log. Comput. 20(3), 651–674 (2010)
Bauer, A., Leucker, M., Schallhart, C.: Runtime verification for LTL and TLTL. ACM Trans. Softw. Eng. Methodol. (TOSEM) 20(4), 14 (2011)
Chen, F., Rosu, G.: MOP: an efficient and generic runtime verification framework. In: Proceedings of OOPSLA 2007, pp. 569–588. ACM (2007)
Chen, Z.: Parametric runtime verification is NP-complete and coNP-complete. Inf. Process. Lett. 123, 14–20 (2017)
Chen, Z., Wang, Z., Zhu, Y., Xi, H., Yang, Z.: Parametric runtime verification of C programs. In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 299–315. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49674-9_17
Chen, Z., Wu, Y., Wei, O., Sheng, B.: Deciding weak monitorability for runtime verification. In: Proceedings of ICSE 2018, pp. 163–164. ACM (2018)
d’Amorim, M., Roşu, G.: Efficient monitoring of \(\omega \)-Languages. In: Etessami, K., Rajamani, S.K. (eds.) CAV 2005. LNCS, vol. 3576, pp. 364–378. Springer, Heidelberg (2005). https://doi.org/10.1007/11513988_36
Diekert, V., Leucker, M.: Topology, monitorable properties and runtime verification. Theor. Comput. Sci. 537, 29–41 (2014)
Drusinsky, D.: The temporal rover and the ATG rover. In: Havelund, K., Penix, J., Visser, W. (eds.) SPIN 2000. LNCS, vol. 1885, pp. 323–330. Springer, Heidelberg (2000). https://doi.org/10.1007/10722468_19
Dwyer, M.B., Avrunin, G.S., Corbett, J.C.: Patterns in property specifications for finite-state verification. In: Proceedings of ICSE 1999, pp. 411–420. ACM (1999)
Falcone, Y., Fernandez, J.-C., Mounier, L.: Runtime verification of safety-progress properties. In: Bensalem, S., Peled, D.A. (eds.) RV 2009. LNCS, vol. 5779, pp. 40–59. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04694-0_4
Falcone, Y., Fernandez, J.C., Mounier, L.: What can you verify and enforce at runtime? Int. J. Softw. Tools Technol. Transf. (STTT) 14(3), 349–382 (2012). https://doi.org/10.1007/s10009-011-0196-8
Francalanza, A.: A theory of monitors. In: Jacobs, B., Löding, C. (eds.) FoSSaCS 2016. LNCS, vol. 9634, pp. 145–161. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49630-5_9
Francalanza, A., et al.: A foundation for runtime monitoring. In: Lahiri, S., Reger, G. (eds.) RV 2017. LNCS, vol. 10548, pp. 8–29. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-67531-2_2
Francalanza, A., Aceto, L., Ingólfsdóttir, A.: Monitorability for the Hennessy-Milner logic with recursion. Formal Methods Syst. Design 51(1), 87–116 (2017). https://doi.org/10.1007/s10703-017-0273-z
Geilen, M.: On the construction of monitors for temporal logic properties. Electr. Notes Theor. Comput. Sci. 55(2), 181–199 (2001)
Havelund, K.: Runtime verification of C programs. In: Suzuki, K., Higashino, T., Ulrich, A., Hasegawa, T. (eds.) FATES/TestCom -2008. LNCS, vol. 5047, pp. 7–22. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-68524-1_3
Havelund, K., Reger, G.: Runtime verification logics a language design perspective. In: Aceto, L., Bacci, G., Bacci, G., Ingólfsdóttir, A., Legay, A., Mardare, R. (eds.) Models, Algorithms, Logics and Tools. LNCS, vol. 10460, pp. 310–338. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63121-9_16
Havelund, K., Reger, G., Thoma, D., Zălinescu, E.: Monitoring events that carry data. In: Bartocci, E., Falcone, Y. (eds.) Lectures on Runtime Verification. LNCS, vol. 10457, pp. 61–102. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-75632-5_3
Havelund, K., Roşu, G.: Synthesizing monitors for safety properties. In: Katoen, J.-P., Stevens, P. (eds.) TACAS 2002. LNCS, vol. 2280, pp. 342–356. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46002-0_24
Havelund, K., Roşu, G.: Runtime verification - 17 years later. In: Colombo, C., Leucker, M. (eds.) RV 2018. LNCS, vol. 11237, pp. 3–17. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03769-7_1
Kauffman, S., Havelund, K., Fischmeister, S.: Monitorability over unreliable channels. In: Finkbeiner, B., Mariani, L. (eds.) RV 2019. LNCS, vol. 11757, pp. 256–272. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-32079-9_15
Kupferman, O., Vardi, M.Y.: Model checking of safety properties. Formal Methods Syst. Design 19(3), 291–314 (2001). https://doi.org/10.1023/A:1011254632723
Leucker, M., Schallhart, C.: A brief account of runtime verification. J. Logic Algebraic Program. 78(5), 293–303 (2009)
Manna, Z., Pnueli, A.: The Temporal Logic of Reactive and Concurrent Systems: Specification. Springer, Heidelberg (1992). https://doi.org/10.1007/978-1-4612-0931-7
Meredith, P.O., Jin, D., Griffith, D., Chen, F., Rosu, G.: An overview of the MOP runtime verification framework. Int. J. Softw. Tools Technol. Transf. (STTT) 14(3), 249–289 (2012). https://doi.org/10.1007/s10009-011-0198-6
Peled, D., Havelund, K.: Refining the safety–liveness classification of temporal properties according to monitorability. In: Margaria, T., Graf, S., Larsen, K.G. (eds.) Models, Mindsets, Meta: The What, the How, and the Why Not?. LNCS, vol. 11200, pp. 218–234. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-22348-9_14
Pnueli, A.: The temporal logic of programs. In: Proceedings of FOCS 1977, pp. 46–57. IEEE Computer Society (1977)
Pnueli, A., Zaks, A.: PSL model checking and run-time verification via testers. In: Misra, J., Nipkow, T., Sekerinski, E. (eds.) FM 2006. LNCS, vol. 4085, pp. 573–586. Springer, Heidelberg (2006). https://doi.org/10.1007/11813040_38
Rosu, G., Chen, F.: Semantics and algorithms for parametric monitoring. Log. Methods Comput. Sci. 8(1), 1–47 (2012)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Chen, Z., Chen, Y., Hierons, R.M., Wu, Y. (2020). Four-Valued Monitorability of \(\omega \)-Regular Languages. In: Lin, SW., Hou, Z., Mahony, B. (eds) Formal Methods and Software Engineering. ICFEM 2020. Lecture Notes in Computer Science(), vol 12531. Springer, Cham. https://doi.org/10.1007/978-3-030-63406-3_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-63406-3_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-63405-6
Online ISBN: 978-3-030-63406-3
eBook Packages: Computer ScienceComputer Science (R0)






 . Each transition is labeled with a propositional formula denoting a set of satisfying states. For example, “!n” denotes
. Each transition is labeled with a propositional formula denoting a set of satisfying states. For example, “!n” denotes  is positively monitorable, as any finite word can be extended to a good prefix (ended with p) but never a bad prefix. This means that only satisfaction, but no violation, of the property can be detected after some finite sequences of steps.
is positively monitorable, as any finite word can be extended to a good prefix (ended with p) but never a bad prefix. This means that only satisfaction, but no violation, of the property can be detected after some finite sequences of steps. is negatively monitorable, as any finite word can be extended to a bad prefix (ended with
is negatively monitorable, as any finite word can be extended to a bad prefix (ended with 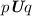 is neutrally monitorable, as it is monitorable and
is neutrally monitorable, as it is monitorable and  is non-monitorable, as any finite word can never be extended to a good or bad prefix, due to the infinite continuations
is non-monitorable, as any finite word can never be extended to a good or bad prefix, due to the infinite continuations 
