Districting Problems

Abstract

Districting is the problem of grouping small geographic areas, called basic units, into larger geographic clusters, called districts, such that the latter are balanced, contiguous, and compact. Balance describes the desire for districts of equitable size, for example with respect to workload, sales potential, or number of eligible voters. A district is said to be geographically compact if it is somewhat round-shaped and undistorted. Typical examples for basic units are customers, streets, or zip code areas. Districting problems are motivated by very diverse applications, ranging from political districting over the design of districts for schools, social facilities, waste collection, or winter services, to sales and service territory design. Despite the considerable number of publications on districting problems, there is no consensus on which criteria are eligible and important and, moreover, on how to measure them appropriately. Thus, one aim of this chapter is to give a broad overview of typical criteria and restrictions that can be found in various districting applications as well as ways and means to quantify and model these criteria. In addition, an overview of the different areas of application for districting problems is given and the various solution approaches for districting problems that have been used are reviewed.

1 Introduction

Most problems discussed in this book focus on the location of facilities: where to locate, how many to locate, when to locate, which type to locate, etc. However, although the driving force is the location of facilities, equally important is the second aspect of location problems that is usually not mentioned explicitly: the allocation of customers to facilities. Even if this task is trivial in many classical location problems such as the p-median or the p-center problem (see Chaps. 2 and 3), only after deciding about allocations can we evaluate a given facility configuration and, thus, try to find the optimal one. Hence, the allocations have a fundamental impact on the location of facilities and different rules of allocation will result in different evaluations of the same facility configuration. The focus of districting problems is now the other way around: we first find allocations—or, more generally, determine which customers should be served together—and then, if necessary, we find locations for the facilities serving the customers.

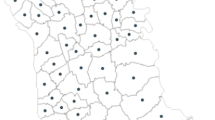
In general, districting is the problem of grouping small geographic areas, called basic units or basic areas, into larger geographic clusters, called districts or territories, in a way that the latter are acceptable according to relevant planning criteria. Typical examples for basic units are customers, streets, or zip code areas. Depending on the practical context, districting is also called territory design, territory alignment, zone design, or sector design. Three important criteria are balance, contiguity, and compactness. Balance describes the desire for districts of equitable size with respect to some performance measure for the districts. Depending on the context, this criterion can either be economically motivated, for example, equal sales potentials, workload, or number of customers, or have a demographic background, for example, the same number of inhabitants or eligible voters. A district is called contiguous if it is possible to travel between the basic units of the district without having to leave the district. Finally, a district is said to be geographically compact if it is somewhat round-shaped, undistorted, and without holes. Contiguous and compact districts usually reduce the travel time of the person responsible for servicing the district. Unfortunately, a rigid and concise mathematical definition of contiguity and compactness is often difficult and strongly depends on the available data. In addition, for each district often the location of a “facility” is either given or should be sought. This facility can be a branch office, a depot, or the home address of a sales person. Figure 25.1 shows an example of a districting plan for streets and for zip code areas.

Fig. 25.1

An example of a districting plan for streets and for zip-code areas

Districting problems are motivated by very diverse applications, ranging from political districting over the design of districts for schools, social facilities, waste collection, or winter services, to sales and service territory design. Looking at the literature, it is striking that only a few authors consider the districting problem independently from a practical background. Therefore, the aim of this chapter is to give a broad overview of typical criteria and restrictions that can be found in the various districting applications as well as ways and means to quantify and model these criteria. As most districting applications have a strong spatial component, it is natural to integrate the algorithms into a Geographic Information System (GIS). In a modern GIS, users can access and utilize the rich variety of maps, spatial databases, and geographical objects available to appropriately mark out the problem and display the solutions, see also Chap. 19.

The rest of the chapter is organized as follows. Section 25.2 reviews the broad range of districting applications and identifies and motivates the different planning restrictions. In Sect. 25.3, basic notations are introduced. This is followed by Sect. 25.4 that discusses the most common criteria found in districting applications and discusses possible approaches to quantify these criteria and to incorporate them into districting models. Finally, Sect. 25.5 presents an overview of the different solution techniques for solving districting problems.

2 Applications

There are four major areas of application for districting problems: political districting, sales territory design, service districting, and distribution districting, and this section provides a comprehensive but non-exhaustive overview. While sales is also a type of service, due to its dominant role in the literature, sales territory design will be discussed separately from service districting. But before we start, we mention a first “application” in the context of facility location that derives from the problem of aggregating demand points for location problems with the aim of reducing the complexity of the problem. Simchi-Levi et al. (2003) formulate the following guidelines (among others): aggregate demand points for 150–200 zones, make sure each zone has an approximately equal amount of total demand, and place aggregated points at the center of the zone. These guidelines read as a classical districting problem.

2.1 Political Districting

Political districting is the problem of dividing a governmental area, such as a city or a state, into constituencies from which political candidates are elected. Basic units typically correspond to census tracts, which are given as polygons, and the districts to the electoral constituencies. In general, the process of redistricting has to be periodically undertaken to account for population shifts. The length of these periods varies from country to country, e.g., in New Zealand every 5 years, in Canada and the U.S. every decade (after each census). In the past, political districting has often been flawed by manipulation aiming to favor some particular party or to discriminate against social or ethnic minorities. Since the responsibility for approving state and local districting plans usually falls to elected representatives, plans are likely to be shaped implicitly, if not overly, by political considerations, e.g., to keep them in power. A famous case arose in Massachusetts in the early nineteenth century when the state legislature proposed a salamander-shaped electoral district in order to gain electoral advantage. The governor of the state at that time was Elbridge Gerry, and this practice became known as gerrymandering. See Lewyn (1993) for an interesting description of gerrymandering cases.

To avoid political interference, many states have set up a neutral commission to determine political boundaries satisfying a number of legislative and common sense criteria. Depending on the country or jurisdiction involved, these criteria may be enforced by legislative directive, judicial mandate, or historical precedent. However, there is no consensus in political science, law, or geography on which criteria are legitimate for the districting process, i.e., satisfy the neutrality condition. Moreover, it is often unclear how they should be measured (Williams 1995). One important issue at stake is population equality. To respect the principle of “one man-one vote”, i.e., every vote has the same power, all districts should contain approximately the same number of voters, i.e., be balanced. In the U.S., population equality has been deemed by the courts to be very important, and as a result, the total deviation of congressional districts from perfect balance was less than 1% after the last census in 2000 (Webster 2013). In other countries, the allowed deviations are usually higher (Handley and Grofmann 2008). Two other important criteria always being mentioned are contiguity and compactness which both aim at preventing gerrymandering. While contiguity is generally undisputed and easy to verify, this is not the case for compactness. There is a broad discussion on how to quantify this criterion adequately (Horn et al. 1993), and whether it is relevant in the first place since an algorithm will never gerrymander on purpose as long as it is does not use political data (Garfinkel and Nemhauser 1970). Moreover, if an adequate minority representation is sought for, this may sometimes only be achieved through non-compact districts (Dixon 1968). Other—often disputed—criteria are the conformity to administrative boundaries, e.g., cities or counties, the preservation of communities of interest, socio-economic homogeneity or a fair representation of minority voters across the districts, the similarity with the previous electoral districts, or the consideration of topological obstacles such as mountain ranges, lakes, or rivers (cf. George et al. 1997; Parker 1990; Bozkaya et al. 2011). An excellent review on typical criteria for political districting and their eligibility is given in Webster (2013).

When discussing automated procedures in the literature, it is always noted that they are non-partisan and neutral as long as they do not use political data and, hence, prevent gerrymandering. However, even if the computer does not gerrymander on purpose, it may still do it accidentally, precisely because no political data is taken into account. Therefore, Puppe and Tasnádi (2008) recently introduced the notion of an (ex post) unbiased districting plan. In such a plan the number of districts won by each party respects the relative strength of the party in the population as close as possible. They focus on game theoretical aspects of the problem; see also Nagel (1965). However, one has to do a careful weighing up to avoid forthright politically biased criteria that lead, in spirit, to gerrymandering.

2.2 Sales Territory Design

The important but expensive task of designing sales territories is common to all companies that operate a sales force and need to subdivide the market area into regions of responsibility that are each attended to by one or more sales representatives. According to Zoltners and Sinha (2005), approximately every tenth full-time employee in the U.S. is working as a field and retail sales person and the expenditure for them is more than three trillion dollars every year. Territories with low sales potential, intense competition, or too many small accounts lead to low morale, poor performance, a high turnover rate, and an inability to assess the productivity of individual territories. Therefore, well-planned decisions enable an efficient market penetration and lead to decreased costs and improved customer service and sales. Zoltners and Sinha (2005) “guestimate” that a good territory alignment can increase sales by 2–7% compared to an average alignment. In the related literature, districts are predominantly called territories and districting is termed territory alignment or territory design.

In the classical problem, the task is to assign a given set of (prospective) customer accounts, each with a fixed market potential, to the individual members of the sales force such that each customer has a unique representative and each sales person faces equitable workload and travel time and has an equal income opportunity in terms of incentive pay (Zoltners and Sinha 2005). Thus, basic units correspond to accounts and are usually given as points. Concerning the travel time, if a sales person visits each customer every day, then the travel time is proportional to the length of a traveling salesman problem (TSP) tour. However, the workload of districts is usually balanced over 3–6 months and some customers may have to be visited only once during this time whereas others require weekly service. Moreover, customers may have time windows, tours may include overnight stays, and so on, which makes the actual computation of the travel times almost impossible. Hence, in most cases one has to rely on estimates. Typically, a sales person is exclusively responsible for all customers within a specific geographic region. However, in large companies sometimes a sales person is only responsible for a certain product segment or accounts of a particular size within his region. In such cases, sales territories may overlap. For practical examples of sales territory design see Fleischmann and Paraschis (1988), Zoltners and Sinha (2005), and López-Pérez and Ríos-Mercado (2013).

Three classical sales districting criteria are again balance, contiguity, and compactness. In contrast to political districting, typically more than one performance measure has to be balanced, for example workload and sales potential. A district with comparatively many small accounts or customers with low sales potential will yield lower sales and, hence, lower incentives for the responsible sales person than a district with an equitable workload but only high potential accounts. This disparity will lead to discontent among the sales persons and, in the long run, lower sales for the company. Having said that, only a few authors consider more than one balancing criterion: Deckro (1977), Zoltners and Sinha (1983), and Ríos-Mercado and Fernández (2009). Contiguous districts are desired to obtain clearly defined geographic areas of responsibility for each sales person, which should prevent them from competing for customers with a high sales potential. Unfortunately, customers are typically represented by their addresses, i.e., points on the map, and it is not clear how to assess contiguity in this case. Compactness describes the desire for districts that are geographically closely packed. Apart from the visual appeal of compact districts, the criterion often serves, together with contiguity, as a proxy for reducing the unproductive travel time of the sales force. The hope is that geographically compact and contiguous districts result in smaller travel times on a day-to-day basis than non-compact and/or non-contiguous districts.

As the main goal of most companies is to maximize profit, several authors relax the assumption that the sales potential of customers is fixed. Instead, they propose an integration of time-effort allocation and territory design methods to increase profit while maintaining the equitable workload criterion (cf. Lodish 1975; Glaze and Weinberg 1979; Zoltners and Sinha 1983). These models not only assign customers to sales people but also determine how much time should be invested in the customer. Some authors even object that equity is not the primary goal for most companies. Instead, the aim should be to maximize profits, regardless of any balancing aspect (Drexl and Haase 1999). However, in practice sales persons are typically reluctant to implement such detailed call plans resulting from pure profit maximizing approaches (Zoltners and Sinha 2005). Moreover, designing territories is a mid- or even long-term decision whereas time-effort allocation is an operational problem that is influenced by weather (especially in the beverage industry), sales promotions, etc. Thus, these two problems should be addressed separately.

Often, the number of districts to be designed is predetermined by the designated sales force size (Fleischmann and Paraschis 1988). If the size is not self-evident, methods based on the total workload involved in covering the entire market compared to the available time per sales person can be used. Another possibility is to follow the “decreasing returns” principle and add sales persons to the sales force as long as the expected increase in profit exceeds the expected increase in costs (Howick and Pidd 1990; Zoltners and Sinha 2005).

As sales persons have to visit their territories regularly, their home-base, e.g., office or residence, is an important factor to be considered in the alignment process. However, there is no consensus as to whether predetermined locations should be kept or be subject to the planning process. On the one hand, most sales persons have strong preferences for home-base cities. Hence, such locations should be respected or determined prior to the alignment to socialize them with the sales management (Zoltners and Sinha 2005). On the other hand, addresses and sales personnel frequently change and the management often does not want sales persons residences to overly influence the definition of territories (Fleischmann and Paraschis 1988).

One important, but only recently addressed aspect of sales territory design is that customers often require service with different frequencies. Some customers have to be visited weekly, while others require service only once per month. As a result, planners not only have to design the districts, but also schedule visits to customers within the planning horizon. For example, if the planning horizon is divided into weeks and days, then we also have to decide which customers should be visited in which week and on which day of that week. The criteria for scheduling customer visits are very similar to the ones for designing the sales territories. The total workload incurred by all customers served in each time period should be the same across all periods and the set of all customers visited in the same time period should be as compact as possible to reduce travel times during each period. While contiguity is still desirable, differing visiting frequencies will make it very difficult, or even impossible, to obtain contiguous sets of customers for each period. For more details, see Bender et al. (2016, 2018).

2.3 Service Districting

The problem of designing service districts appears in various contexts. One area of applications focuses on social facilities such as hospitals or public utilities. Sometimes districts are needed to define for each inhabitant which facility he should visit to obtain service, for example for preventive medical examinations, or to determine areas of responsibility of home-care visits by health-care personnel such as nurses or physiotherapists. The goal is to determine contiguous districts that have a good accessibility with respect to public transportation and have an equitable workload based on service and travel time or account for a high capacity utilization of the social facility (cf. Minciardi et al. 1981; Blais et al. 2003; Benzarti et al. 2013).

A second field of applications deals with providing service to streets. A classical problem concerns the design of districts for postal or leaflet delivery. Instead of considering each household separately, districts are composed of whole streets. Thus, basic units correspond to streets and each basic unit typically has two attributes: the times required to traverse the street with and without providing service. The task is to partition the streets into a given number of districts such that the required delivery time is approximately the same for all districts and does not exceed the working time restriction of the deliverer. The delivery time is proportional to the length of a Chinese postman tour through the district, which can be computed efficiently. Moreover, the delivery districts should be contiguous, incur little deadheading, and should not overlap, i.e., be geographically compact (Bodin and Levy 1991; Butsch et al. 2014; García-Ayala et al. 2016). A common characteristic of these applications is that the deliverer either walks through his district on foot or goes by bike so that one-way streets are no hindrance. If a street is too wide or has too much traffic to serve it in a zig-zag pattern, then each side of the street is modeled as a separate basic unit. A similar problem arises in the context of meter reading in power distribution networks (de Assis et al. 2014). Closely related are districting problems for solid waste disposal, salt spreading, and winter gritting (Hanafi et al. 1999; Muyldermans et al. 2002; Lin and Kao 2008). The criteria are almost identical to postal delivery. The only differences are that vehicles typically have to respect one-way streets and have difficulties making U-turns, and that their tours have to include a depot, e.g., to drop off the waste or refill salt. All these aspects make the computation of the travel times more difficult. Other applications deal with the design of patrol districts for police cars and primary response areas for ambulances, where the districts additionally should have an average response time and/or incident arrival rate below a given threshold (Baker et al. 1989; D’Amico et al. 2002; Camacho-Collados et al. 2015).

Other applications deal with the problem of assigning residential areas to schools (Ferland and Guénette 1990; Schoepfle and Church 1991). Criteria to be taken into account are capacity limitations and an equal utilization of the schools, maximal or average travel distances for students, good accessibility, and ethnic balance. Another aspect is to decide which students should walk to school and which should take the school bus. Districting problems also occur in electric power networks. According to Bergey et al. (2003), the World Bank regularly faces the challenge of helping developing countries to move from state owned, monopolistic electric utilities to a more competitive environment with multiple electricity service providers. At that, they face the task of partitioning the physical power grid into economically viable districts (distribution companies). The main aim is to determine non-overlapping and contiguous districts with approximately equal revenue potential (to foster competition) which are compact over a geographic region (to be easier to manage and more economical to maintain).

Fernández et al. (2010) study a very unique districting problem arising in the context of collection of waste electric and electronic equipment (WEEE) in Europe. The problem was motivated by a recycling directive adopted in the European Union which states, among other things, that each company selling electrical or electronic equipment in a European country has the responsibility to collect and recycle an amount of returned items proportional to the firm’s market share. A districting plan assigns basic units to companies; however, in contrast to classical districting problems, the territories should be as geographically dispersed as possible to avoid regional monopolies. The problem also involves particular balancing constraints and allows splitting basic units to balance territories with respect to different product types. They termed this the maximum dispersion territory design problem. In a related work, Fernández et al. (2013) introduce the maximum dispersion problem which is essentially a partition problem seeking to maximize a dispersion function. In this new problem, no split basic units are allowed, so it can be seen as a special case of the maximum dispersion territory design problem.

2.4 Distribution Districting

Another important field of applications is the design of pickup and delivery districts in logistics. Typically, such problems are modeled and solved as vehicle routing problems. However, if there exists considerable uncertainty in the demand of customers, several authors propose a two-phase approach. In the first phase, pickup and delivery districts are created based on uncertain demands. Once the districts are given, the uncertainty is revealed and the routing is done in the second phase on a day-to-day basis (Haugland et al. 2007). This conforms with the well-known “cluster first–route second” paradigm for vehicle routing problems. Hence, basic units correspond to potential customers, given as points, and the task is to partition the set of customers into districts, one for each driver, such that the districts satisfy certain planning criteria. A first advantage of these fixed customer assignments is that the driver becomes familiar with his district. This, in turn, increases the driver’s performance since he becomes quicker at finding customer addresses, localizing offices within buildings as well as organizing his routes (Zhong et al. 2007). A second advantage is that customers become familiar with their drivers, which increases customer satisfaction (Jarrah and Bard 2012). These advantages however have to be carefully weighed against flexible customer assignments on a daily basis which enable the planner to maximize the driver utilization and minimize the routing costs (Zhong et al. 2007).

Concerning the criteria for the districting process, districts should be contiguous and compact, and the workload should either be balanced or at least not exceed a given upper bound, e.g., the driver working time. The workload includes the service time at the customers and typically also an estimate of the average travel time within the district and to a centralized depot (Galvão et al. 2006; Zhong et al. 2007; Jarrah and Bard 2012; Lei et al. 2012, 2015).

A final application concerns the establishment of a distribution center which involves a considerable level of risk due to its enormous start-up investment and volatile customer demand patterns. One way of reducing this risk is to avoid both overcrowding and, especially, underutilization of centers by balancing the allocation of customers to them (Zhou et al. 2002).

3 Notations

This section introduces notations for the main components of districting problems.

3.1 Basic Units

A districting problem comprises a set J = {1, …, n} of basic units, sometimes also called sales coverage units, basic areas, or geographical units. Each basic unit represents a geometric object in the plane: a point, e.g., a geo-coded address, a line segment, e.g., a street, or a polygonal area, e.g., a zip-code area, county, or predefined company trading area. The distance between two basic units i, j ∈ J is denoted as d_ij = d(i, j). Typical examples for d_ij are Euclidean (cf. Fleischmann and Paraschis 1988) or road distances (cf. Ríos-Mercado and Salazar-Acosta 2011). The latter have the advantage that they can properly reflect obstacles such as rivers or mountain ranges. For non-point objects, distances are either computed between representative points, e.g., the midpoint of a street or the centroid of a polygon, or as the surface-to-surface distance.

Moreover, one or more quantifiable attributes, called activity measures, are associated with each basic unit. Typical examples are service times, estimated sales potential, or number of voters. Sometimes, they also include an estimate of the travel time for visiting the basic unit (Jarrah and Bard 2012). The activity measures are all assumed to be deterministic. Let $w_j^q$ denote the q-th activity measure of basic unit j ∈ J, 1 ≤ q ≤ Q, where Q is the number of different attributes to be considered. If Q = 1, the superscript is usually omitted.

If explicit neighborhood information is given for the basic units, then G = (V, E) denotes the neighborhood or contiguity graph where v_j ∈ V  corresponds to j ∈ J and {v_i, v_j}∈ E if and only if basic units i and j are neighboring. The length of edge {v_i, v_j} is d_ij. Finally, N(j) ⊆ V  denotes the set of basic units adjacent to v_j ∈ V .

3.2 Districts

A districtD_k, 1 ≤ k ≤ p, is a subset of basic units, where p is the total number of districts. The number of districts can either be fixed in advance, e.g., the number of political districts to create or the number of available nurses for elderly care, or be subject to planning, e.g., the minimal number of salespersons required to service all customers or the minimal number of patrol cars to ensure a certain response time. The q-th activity measure of a district is the sum of the activity measures of its basic units, i.e., $w^q(D_k) = \sum _{j \in D_k} w^q_j$. For Q = 1, w¹(D_k) is simply called the size of the district. Note that sometimes the size also includes an estimate of the (expected) travel time. However, as travel times are represented through the compactness criterion, we refrain from including them and just mention when this may change things.

In some applications the location c_k of a facility is associated with each district D_k. This may be some predefined site, e.g., a hospital providing preventive medical care, or be an outcome of the districting process, e.g., the optimal location of a sales office. In districting, this location is called the center of the district. One has to be aware of the ambiguity with the notion of a center in location theory, which is something different, see Chap. 4. Typically, the center coincides with a basic unit, i.e., c_k ∈ J. A predetermined set of centers is denoted by J_c.

Finally, a districting plan$\mathscr {D}$ is defined as a set of p districts $\mathscr {D}=\{D_1,\ldots ,D_p\}$.

3.3 Problem Formulation

The districting problem can now informally be described as follows: Partition all basic units J into a number of p districts that satisfy the planning criteria of balance, compactness, and contiguity and, if required, locate a center within each district. Unfortunately, in contrast to many other optimization problems, there does not exist the mathematical model for districting problems. This is mainly due to the considerable ambiguity on how to quantify the different planning criteria and in the motivation and relevance of some of them.

4 Districting Criteria

This section presents an overview over typical criteria employed in districting problems and various ways and means to quantify them. In the following, a measure for a criterion applied to a single district (the whole districting plan) is termed a local (global) measure. Moreover, if not explicitly stated otherwise, let Q = 1.

4.1 Complete and Exclusive Assignment

In most cases, each basic unit is assigned to exactly one district, i.e., the districts define a partition of the set J of basic units:

$$\displaystyle \begin{aligned} D_1 \,\cup\, \cdots \,\cup\, D_p \:=\: J \text{ and } D_l \,\cap\, D_k \:=\: \emptyset, \quad l \ne k,\, 1 \le l,\, k \le p. \end{aligned}$$

The requirement of exclusive assignment is sometimes also termed integrity. For political districting, these criteria are obvious. In sales territory design, unique allocations result in transparent responsibilities for the sales force avoiding contentions and allowing the establishment of long-term customer relations.

4.2 Balance

This criterion is one of the trademarks of districting problems. It expresses the desire for districts of equitable size with respect to the activity measure(s). In political districting, this criterion is employed to ensure the “one man–one vote” principle, and in sales territory design to avoid districting plans with large discrepancies in terms of workload, sales potential, or travel time.

Due to the discrete structure of the problem and the integrity assumption, perfectly balanced districts can generally not be accomplished. There exist different approaches in the literature to quantify imbalance and to incorporate the criterion into the districting process. The most common local measure is based on the relative deviation of the district size w(D_k) from the mean district size μ = w(J)∕p:

$$\displaystyle \begin{aligned} bal(D_k) \:=\: \left| \frac{w(D_k)-\mu}{\mu} \right|, \quad 1\le k\le p \end{aligned}$$

(cf. Forman and Yue 2003; Ríos-Mercado and Fernández 2009; de Assis et al. 2014). The larger this deviation is, the worse is the balance. A district D_k is perfectly balanced, if bal(D_k) = 0. If district sizes also include a solution dependent performance measure—in addition to the activity measure—, then this affects μ and the balance of one and the same district may be different for different districting plans. For example, in sales and service territory design, districts often have to be balanced with respect to workload; workload, in turn, usually consists of service times plus travel times. While the total sum of the former is solution independent, the latter depend on the actual district layout. Another approach concedes a priori a certain relative deviation α > 0 from perfect balance and only measures the imbalance exceeding this threshold (Bodin and Levy 1991; Bozkaya et al. 2011)

$$\displaystyle \begin{aligned} bal(D_k) \:=\: \frac 1{\mu} \max \{ w(D_k) - (1+\alpha)\mu,\, (1-\alpha)\mu - w(D_k),\, 0 \},\end{aligned} $$

i.e., the district is balanced if its size is between this lower and upper bound. Instead of determining the bounds based on the mean district size, they are sometimes directly motivated by the application, e.g., the working time restrictions of the mailman or the sales potential required to ensure a decent living for the sales person.

Using these local measures, the global balance of a districting plan is then typically computed as the maximal balance of a district

$$\displaystyle \begin{aligned} bal^{\max}(\mathscr{D}) \:=\: \max_{k=1,\ldots,p} bal(D_k).\end{aligned} $$

Less common are the sum over all districts (Bozkaya et al. 2003; Bodin and Levy 1991) or a convex combination of both (Butsch et al. 2014):

$$\displaystyle \begin{aligned} bal^{\text{sum}}(\mathscr{D}) \:=\: \sum_{k=1}^{p} bal(D_k) \quad \text{and} \quad bal^{\text{cv}}(\mathscr{D}) \:=\: \lambda\,bal^{\text{sum}}(\mathscr{D}) + (1-\lambda)\,bal^{\max}(\mathscr{D}),\end{aligned} $$

with λ ∈ (0, 1). The convex combination alleviates some of the weaknesses of bal^sum and $bal^{\max }$. The latter does not take into account the balance of all districts and sometimes yields rather poor solutions on average whereas the former allows a few highly unbalanced districts to be compensated by some well-balanced districts. A different global approach computes the range of district sizes (Tavares-Pereira et al. 2007)

$$\displaystyle \begin{aligned} bal^{\text{rng}}(\mathscr{D}) \:=\: \max_{k=1,\ldots,p} w(D_k) - \min_{k=1,\ldots,p} w(D_k). \end{aligned}$$

Mathematical Modelling

In districting models, there is no clear trend on whether to treat balance as a hard constraint (Hess et al. 1965; Fleischmann and Paraschis 1988; Zoltners and Sinha 2005) or to include it in the objective function (Blais et al. 2003; Ricca and Simeone 2008; de Assis et al. 2014). In the former case, the size of each district is required to lie between a given lower and upper bound. Some authors even do both (Bergey et al. 2003; Salazar-Aguilar et al. 2013b). All of the above measures easily give rise to linear expressions. While several different activity measures have been discussed in the literature, only a few authors consider more than one criterion simultaneously (Deckro 1977; Zoltners and Sinha 1983). In a recent series of papers, two activity measures have been considered simultaneously: the number of customers and the total demand per district (Salazar-Aguilar et al. 2011b, 2012, 2013b; Ríos-Mercado and Escalante 2016).

Concerning solution dependent performance measures, the most common addition is to include travel times in the district size. Due to the scale of realistic data sets, calculating the exact travel times within each district is usually too costly during optimization. Instead, most authors rely on estimates. A common way to approximate the total travel time (or distance) within a district is to use the Beardwood-Halton-Hammersley formula (Lei et al. 2012, 2015). This formula, however, has the downside that it is non-linear and therefore does not easily admit linear programming formulations. As an alternative, some authors propose to add to the service time of each basic unit a fixed estimate of the travel time to the “next basic unit in the district”. This estimate can, for example, be the average (expected) travel time to the k closest basic units, where k is a parameter that has to be tuned for each (set of) data instance(s) (Bard and Jarrah 2009; Jarrah and Bard 2012).

4.3 Contiguity

Almost all districting approaches require districts to be contiguous. In political districting, this criterion should prevent gerrymandering. For the other types of applications, contiguous districts reduce the day-to-day travel distances for sales persons, delivery vans, snow ploughs, mailmen, etc. Unfortunately, a rigid and concise mathematical formulation of contiguity is difficult for basic units representing points.

4.3.1 Graph-Based Measures

If basic units are lines or polygons, it is easy to derive explicit neighborhood information. For example, two zip-code areas are neighboring if they share a common border, or two streets if they meet in a crossroad. In the former case, sometimes an additional requirement is the existence of a direct road connection between the two basic units. In general, two basic units are called neighboring, if their geometric representations have a nonempty intersection. This information is stored in the neighborhood graph G = (V, E), and a district is contiguous if the basic units of the district induce a connected subgraph in G.

If basic units are represented by points, e.g., customer addresses, it is not clear how to assess contiguity. Over the years, different surrogate definitions for contiguity have been proposed. One approach is based on proximity graphs to estimate the adjacency of points. One such graph is the Gabriel graph, in which two nodes v_i and v_j are connected by an edge if and only if the disc with antipodal points v_i and v_j does not contain any other node in its interior (Gross and Yellen 2003). A second approach to construct a contiguity graph is based on the Voronoi diagram (Lei et al. 2012). Two basic units are defined to be adjacent, iff their Voronoi cells have a common link within the smallest axis-parallel rectangle enclosing all basic units (for a definition of Voronoi diagrams and cells, see Aurenhammar et al. 2013). A third construction of the proximity graph is to start with a complete graph and then sequentially go over all edges and delete for two intersecting edges in the planar representation of the graph the longer or more costly one (Haugland et al. 2007). All three graphs are planar. Moreover, by definition the Gabriel graph is a subset of the Voronoi-based graph.

Example 25.1

An example for these three proximity graphs for a point set with 26 basic units is depicted in Fig. 25.2. The Gabriel graph defines the most strict neighborhood relation. The graphs obtained by Lei et al. (2012) and Haugland et al. (2007) are fairly similar. The main difference is that the latter typically establishes more adjacencies along the boundary of the convex hull of the point set. Just by looking at the graphs it is difficult to decide which one is more suitable.

Fig. 25.2

Three different approximate contiguity graphs. (a) Point set of basic units. (b) Gabriel graph. (c) Voronoi-based graph. (d) Non-crossing edges graph

Finally, if the underlying road network is given, yet another possibility is to define two basic units as being adjacent, if the shortest path between the two does not contain another basic unit.

4.3.2 Geometric Measures

If no neighborhood information for basic units is given or can reasonably be derived, an alternative is to determine the overlap between the districts. For example, by computing the convex hull ch(D_k) around each district D_k and defining a district to be contiguous if no basic unit of another district lies in its convex hull, i.e., ch(D_k) ∩ ch(D_l) = ∅, ∀ l ≠ k (Kalcsics et al. 2005; Jarrah and Bard 2012). One advantage of this approach is that convex districts usually prevent the crossing of routes of different districts, a characteristic that typically implies inefficient routes.

4.3.3 Mathematical Modelling

In districting models, contiguity is always treated as a hard constraint (except in Hanafi et al. 1999). One possibility to include it in a mathematical programming formulation is due to Drexl and Haase (1999): Let c_k ∈ J_c be the predetermined center of district k and S ⊆ J ∖{N(c_k) ∪{c_k}} be a subset of basic units that are not adjacent to basic unit c_k. If all elements of S are assigned to district k (with center in unit c_k), i.e., S ⊂ D_k, then at least one basic unit not in S that is adjacent to an element of S must also be assigned to district k:

$$\displaystyle \begin{aligned} \sum_{j \in \bigcup_{i \in S}\, N(i) \setminus S}\, x_{c_k,j} - \sum_{j \in S}\, x_{c_k,j} \:\ge\: 1 - |S| \qquad \forall\, S \subseteq J \setminus \{ N(c_k) \cup \{c_k\} \}, \end{aligned}$$

where $x_{c_k,j}$ is 1 if j ∈ J is assigned to the district with center c_k and 0 otherwise. A clear drawback of this formulation is that it requires an exponential number of constraints. Nevertheless, this gives naturally rise to cut generation approaches, see Salazar-Aguilar et al. (2011a) and Ríos-Mercado and López-Pérez (2013). A second possibility that only needs a linear number of constraints is based on network flow constraints (Shirabe 2009). Each basic unit has one unit of supply, and the district centers act as sinks. District k is contiguous if and only if there exists a flow from each of its basic units to c_k that only passes through basic units in D_k:

$$\displaystyle \begin{aligned} \sum_{i \in N(j)}\, f_{ji} - \sum_{i \in N(j)}\, f_{ij} & \:=\: x_{c_k,j} && \forall\, j \in J \setminus \{c_k\} \qquad \\ \sum_{i \in N(j)}\, f_{ij} & \:\le\: (n-2)\,x_{c_k,j} && \forall\, j \in J \setminus \{c_k\} \qquad \\ \sum_{i \in N(c_k)}\, f_{i,c_k} & \:\le\: n-1, \end{aligned} $$

where f_ij is the flow from basic unit i to j and $f_{c_k,j}=0$, ∀ j ∈ N(c_k).

A simpler approach is to require that each district is a subtree of a shortest path tree T(c_k) rooted at the district center c_k, where the edge lengths typically correspond to road distances or are all assumed to be 1. Then, for each basic unit j of district k, at least one of the adjacent basic units i ∈ N(j) that immediately precedes j on some shortest path to the center c_k also has to be included in the district:

$$\displaystyle \begin{aligned} x_{c_k,j} \:\le\: \sum_{i \in S_j} x_{c_k,i} \qquad \forall j \in J \setminus \{c_k\}, \end{aligned} $$

where $S_j = \left \{i \in N(j) \mid \right .\text{{$i$} immediately precedes {$j$} on some shortest path from}$${j}\left . \text{ to } {c_k}\right \}$ (Zoltners and Sinha 1983; Mehrotra et al. 1998). Although this excludes some contiguous districts, these are unlikely to be compact, as they typically have large protrusions or indentations, or contain enclaves.

It is straightforward to extend all of the above constraints to the case where the choice of district centers is part of the optimization. For geometric contiguity measures obviously only informal mathematical formulations can be derived.

Remark 25.1

Only a few authors try to derive approximate neighborhood graphs for point-like basic units. The majority simply does not consider contiguity at all and tries to obtain districts with little overlap through an appropriate compactness measure, see also Example 25.2 (Fig. 25.3).

Fig. 25.3

Districting plans for two center-based compactness measures without contiguity. (a) Districts for cmp_ud(⋅). (b) Districts for $cmp_{\text{wd}^2}(\cdot )$

Remark 25.2

It is much easier to ensure strict contiguity if heuristics are used to solve the districting problem. Given a district D_k and the corresponding subgraph of G, it is possible to check in O(|D_k|) time whether D_k is connected or not. If the heuristic is based on local search, then adding a basic unit to a connected district will preserve connectivity. Likewise, removing a basic unit from a connected district will preserve connectivity if the removed basic unit does not coincide with a cut-vertex of the subgraph (Ricca et al. 2013). To reduce the computational effort in the latter case, King et al. (2012) have introduced the concept of geo-graphs for two-dimensional basic units that utilizes information from the planar dual graph of G.

4.4 Compactness

A district is said to be geographically compact if it is somewhat round-shaped and undistorted. The motivation for compact districts is almost identical to ensuring contiguity: to prevent gerrymandering or to reduce the day-to-day travel distances within the districts. Although being a very intuitive concept, a rigorous definition of compactness does not exist and, moreover, strongly depends on the geometric representation of basic units. In the context of political districting, typically measures based on the shape of districts are employed whereas in sales and distribution districting, distance-based measures are predominant. In the following, the most common ones for both approaches are presented.

4.4.1 Geometric Measures

If basic units are given as polygons, geometric approaches based on the area or perimeter of a district can be used to quantify compactness. Two common local measures are the Reock and Schwartzberg tests. The former calculates the ratio of the district area to the area of the smallest enclosing circle, while the latter determines the ratio of the districts perimeter length to the circumference of a circle with equal area

$$\displaystyle \begin{aligned} cmp(D_k) \:=\: \frac{A(D_k)}{\pi r_{enc}^2} \qquad \text{and} \qquad cmp(D_k) \:=\: \frac{P(D_k)}{2\sqrt{\pi\,A(D_k)}}, \end{aligned}$$

where A(⋅) and P(⋅) denote the area and the length of the perimeter, respectively, of a district and r_enc the radius of the smallest enclosing circle (Young 1988). For the Reock (Schwartzberg) test, larger (smaller) ratios indicate greater compactness. Other measures relate the activity of a district with the total activity of all basic units within the smallest enclosing circle (Ricca and Simeone 2008) or determine the ratio of the squared diameter of a district and its area (Garfinkel and Nemhauser 1970). A common global measure for the compactness of a districting plan is based on the length of the boundary between districts, i.e., the total length of the perimeter of the districts in the interior (Bozkaya et al. 2003; Lei et al. 2012)

$$\displaystyle \begin{aligned} cmp(\mathscr{D}) \:=\: \sum_{k=1}^p\, P(D_k) - P(J). \end{aligned}$$

Short inter-district boundaries typically result in compact districts. Numerous other measures have been discussed in the literature. Unfortunately, none of them is comprehensive; some fail to detect districts that are obviously noncompact, others assign a low rating to visibly compact districts (Niemi et al. 1990; Horn et al. 1993; Williams 1995).

To use geometric measures for basic units representing points or lines, one can try to give “shape” to the districts, for example through the smallest enclosing rectangle or circle, or through the convex hull. Instead of the convex hull, one can also use χ-shapes, which are polygons enclosing the point set that can provide a better fit to the points than the convex hull (Duckham et al. 2008). However, much more common are the following, distance-based measures:

4.4.2 Distance-Based Measures

Distance-based measures are used predominantly in applications where people have to travel within the districts, e.g., salesmen or mailmen. This confers with the motivation of compact districts in these applications: to reduce the day-to-day travel times. Moreover, in these applications basic units typically represent points or lines, making geometric measures unapplicable in the first place. The most common group of local measures is based on the sum of distances between the center of a district and its basic units. Variations exist in whether the distances are weighted with activity measures or not (w/u) and whether distances are squared or not (d²/d)

$$\displaystyle \begin{aligned} cmp_{\text{ud}}(D_k) \:=\: \sum_{j \in D_k}\, d_{c_k,j} \qquad & \quad cmp_{\text{ud}^2}(D_k) \:=\: \sum_{j \in D_k}\, d_{c_k,j}^2 \\ cmp_{\text{wd}}(D_k) \:=\: \sum_{j \in D_k}\, w_j\, d_{c_k,j} \qquad & \quad cmp_{\text{wd}^2}(D_k) \:=\: \sum_{j \in D_k}\, w_j\, d_{c_k,j}^2 \end{aligned} $$

(Bard and Jarrah 2009; Bergey et al. 2003; Hess and Samuels 1971; Zoltners and Sinha 2005). The second and fourth measure are also known as the (weighted) moment of inertia (Hess et al. 1965). Although the four local compactness measures follow the same idea, the resulting districts may look considerably different as the following example shows.

Example 25.2

Consider a point set of n = 75 basic units that has to be partitioned into p = 5 districts, each having a predetermined center. The allowed relative deviation in terms of balance from the mean district size μ is 5%, and contiguity is not explicitly imposed. Figure 25.3 shows the resulting districting plans that minimize the sum of the two center-based compactness measures cmp_ud(⋅) and $cmp_{\text{wd}^2}(\cdot )$ over all districts. The enlarged icons represent the district centers.

Having in mind that compactness acts as a proxy for travel times, the most natural measure is cmp_ud(⋅). However, we observe that there is a considerable overlap in the districts for this measure, especially between the districts represented by the diamond and pentagon shaped basic units. A much better visual separation is instead obtained for the weighted squared distance, $cmp_{\text{wd}^2}(\cdot )$, even if some district centers now lie outside their actual district (again, diamonds and pentagons). A large overlap between districts typically yields less efficient routes for sales persons. To underline this observation, we determine for each district the TSP tour through all basic units, including the center. The total lengths of the TSP tours for the two districting plans are: 92.78 and 73.56. The travel distances for the weighted squared distance are 20 % smaller than for cmp_ud(⋅). The results for cmp_wd(⋅) and $cmp_{\text{ud}^2}(\cdot )$ in terms of overlap and travel distances are between the other two measures, with the former being slightly better.

The situation is different if we try to enforce contiguity. Assume that an approximate neighborhood graph has been computed using the approach in Haugland et al. (2007). Using the contiguity constraints of Shirabe (2009), the resulting districting plans for cmp_ud(⋅) and $cmp_{\text{wd}^2}(\cdot )$ are shown in Fig. 25.4. The separation between the districts for cmp_ud(⋅) is clearer than before. However, even if the total length of the TSP tours reduces considerably (from 92.78 to 81.15), the districts consisting of the diamond, pentagon, and square shaped basic units are still distorted and will receive little approval from planners. (The square shaped district is connected since there exists an edge along the top of the point set.) For $cmp_{\text{wd}^2}(\cdot )$ the overlap is not much different from the previous plan, and the total travel distance even slightly decreased to 72.97. The main difference is that the centers are now all included in their districts, if only at the boundary.

Fig. 25.4

Districting plans for two center-based compactness measures with contiguity. (a) Districts for cmp_ud(⋅). (b) Districts for $cmp_{\text{wd}^2}(\cdot )$

This example illustrates the considerable differences between districting plans for different compactness measures and the influence of contiguity constraints. However, this is just a single example, and the observations cannot be generalized without further testing. Also, the length of a TSP tour is just an indicator for travel distances, as a sales person may not visit all customers on a single day.

The fact that squared distances produce compact but non-contiguous districts for fixed centers has been observed several times in the past (Hojati 1996; Schröder 2001). An important factor influencing the shape of districts is the spatial distribution of the district centers. If they are spread evenly, the differences between the measures in terms of district overlap will decrease, see Example 25.3. However, this uneven distribution is not unusual as sales force residences often concentrate in certain areas, e.g., larger cities, and sometimes even have the same address. Also the threshold for the allowed balance deviation has an impact on the compactness of solutions. The smaller the threshold value is, the larger the overlap between districts will get.

Instead of taking the sum, one could also take the maximum for each of the center-based measures (cf. Elizondo-Amaya et al. 2014; Ríos-Mercado and Fernández 2009; Muyldermans et al. 2003). However, this leaves considerable freedom for assignments below the maximal distance and typically increases the overlap. A slightly different approach is based on the maximal pairwise distance and the weighted sum of pairwise distances

$$\displaystyle \begin{aligned} cmp_{\text{mpw}}(D_k) \:=\: \max_{i,j \in D_k,\, i \neq j}\, d_{ij} \qquad & \quad cmp_{\text{spw}}(D_k) \:=\: \sum_{i,j \in D_k,\, i \neq j}\, w_i\,w_j\,d_{ij} \end{aligned} $$

(see Ríos-Mercado and Salazar-Acosta (2011), Ríos-Mercado and Escalante (2016) for the former and Blais et al. (2003) for the latter).

In case of measures based on the sum (maximum) of distances, the global compactness of a districting plan is then usually also computed as the sum (maximum) over all districts. But sometimes also a sum-max combination is used or a convex combination of sum and max (Muyldermans et al. 2003; de Assis et al. 2014; Butsch et al. 2014).

4.4.3 Mathematical Modelling

The majority of districting models has compactness as an objective function to be optimized. In addition, sometimes the maximal distance between a basic unit and its district center or between two basic unit of the same district is restricted (Benzarti et al. 2013). The appeal of distance-based measures is that they easily give rise to linear or, in case of pairwise distances, quadratic expressions. Therefore, these measures are sometimes also used for polygonal basic units, even if geometric measures could have been applied (Ríos-Mercado and Fernández 2009).

4.5 District Center

Strictly speaking, determining district centers is in most cases not an optimization criterion in itself. However, several measures for contiguity and compactness rely on district centers. Thus, if no centers are predefined for the districts, seeking district centers is part of the optimization process. Typically, a district center is the basic unit of the district that minimizes the respective compactness measure. But also the (weighted) center of gravity can be used to determine a district center. Note however that this center usually does not coincide with a basic unit, which is problematic if distance computations are based on road networks.

4.6 Other Criteria

There are a few other criteria for districting problems that are included from time to time in districting models. For example, for redistricting problems the changes in allocation from the old to the new districting plan should be kept small (de Assis et al. 2014). Especially in sales territory design, customers often have a preferred sales representative by whom they want to be serviced or vice-versa, i.e., customers have banned salesmen (Ríos-Mercado and López-Pérez 2013). Another criterion concerns the number of districts. Typically, p is predetermined such that, for example, the expected workload in a district neither exceeds the working time restriction of a deliverer nor renders him underutilized. If however travel times within a district account for a large portion of the total working time, then it is not always possible to fix p a priori since travel times strongly depend on the shape of districts, i.e., their compactness. Therefore, sometimes p is a design criterion (cf. Muyldermans et al. 2003). For instance, some applications in healthcare, in particular on the redistricting of liver allocation, attempt to minimize the disparity in liver availability among districts (Gentry et al. 2015). In other areas such as the location of Emergency Medical Service (EMS) the focus is to save lives and to minimize the effects of emergency health incidents. In that context, districting, or designing pre-determined response areas, allows an EMS system to reduce the response time of paramedic support to the incident. An important criterion for these applications is the patient survival probability. Thus, developing both dispatching and districting policies under uncertainty to improve the performance of EMS systems becomes very a very important issue (Mayorga et al. 2013).

5 Solution Approaches

As with most optimization problems also for districting many different solution approaches have been proposed in the literature over the years. These approaches can roughly be divided in those that utilize a mathematical programming model and those that depend merely upon heuristics. Among the former, location-allocation and set partitioning methods have been discussed. The latter mainly focus on geometric algorithms, simple construction methods, and classical metaheuristics such as GRASP, Tabu Search, Scatter Search, and Simulated Annealing. This section will present only a rough overview and description of the most common approaches. Detailed reviews can be found in Kalcsics et al. (2005) and Ricca et al. (2013).

5.1 Location-Allocation Methods

The first mathematical programming approach was proposed by Hess et al. (1965) for political districting. They had the idea to model the problem as a capacitated p-median facility location problem (see also Chap. 3). Basic units correspond to customers and their activity measure to their demand. The facilities to be located are the district centers, and the capacity of the facilities is chosen in such a way that the districts obtained by solving the problem are well balanced. Candidate locations for the facilities are all basic units. For an allowed relative deviation α > 0 of the district size from the mean district size μ, the formulation of Hess et al. (1965) is

$$\displaystyle \begin{aligned} \text{minimize} \quad &\; \sum_{i,j \in J}\, w_j\, d^2_{ij} x_{ij} {} \end{aligned} $$

(25.1)

$$\displaystyle \begin{aligned} \text{subject to} \quad &\; \sum_{i \in J} x_{ij} \:=\: 1 && \forall\, j \in J {} \end{aligned} $$

(25.2)

$$\displaystyle \begin{aligned} &\; \sum_{j \in J} w_j\, x_{ij} \:\ge \: (1-\alpha)\, \mu\, y_i && \forall\, i \in J {} \end{aligned} $$

(25.3)

$$\displaystyle \begin{aligned} &\; \sum_{j \in J} w_j\, x_{ij} \:\le \: (1+\alpha)\, \mu\, y_i && \forall\, i \in J {} \end{aligned} $$

(25.4)

$$\displaystyle \begin{aligned} &\; \sum_{i \in J} y_i \:=\: p && {} \end{aligned} $$

(25.5)

$$\displaystyle \begin{aligned} &\; y_i,\, x_{ij} \:\in\: \{0,1\} && \forall\, i,j \in J {}, \end{aligned} $$

(25.6)

where x_ij = 1 if basic unit j is assigned to district center i, 0 otherwise, and y_i = 1 if basic unit i is selected as district center, 0 otherwise. The objective function (25.1) maximizes the compactness of the districts using the center-based measure $cmp_{\text{wd}^2}(\cdot )$. Constraints (25.2), together with the integrality constraints on the x_ij-variables, model the unique and exclusive assignment criterion. Constraints (25.3) and (25.4) restrict the balance of the districts. Finally, Constraints (25.5) ensure that exactly p basic units are selected as district centers. As a result, all basic units allocated to the same basic unit i constitute a district with the basic unit as its center, i.e., there is a one-to-one correspondence between centers and districts. Note that the centers are just required to evaluate district compactness and have no meaning in itself.

Unfortunately, due to its NP-hardness, the practical use of this formulation is limited to instances with a few hundred basic units, which is rather small for typical sales districting problems. To this end, Hess et al. (1965) propose to use Cooper’s location-allocation heuristic to solve the problem. In this heuristic, the simultaneous location and allocation decisions of the underlying facility location problem are decomposed into two independent phases, a location and an allocation phase, which are alternatingly performed until a satisfactory result is obtained. In the location phase, a set J_c of district centers is determined. A fairly simple and commonly used method is to solve in each district resulting from the last allocation phase a single facility location problem with the respective compactness measure as objective function (cf. Fleischmann and Paraschis 1988; George et al. 1997). To obtain an initial set of centers, one can determine new centers based on the solution of a Lagrangian subproblem (Hojati 1996). Alternatively, one can use any of the heuristics for the (uncapacitated) p-median problem or one of the heuristics mentioned below.

Once the centers have been fixed, the allocation phase determines a balanced assignment of basic units to district centers. This can be done by fixing y_i = 1 for all i ∈ J_c in the above formulation. With present-day computers and mixed-integer linear programming (MILP) solvers, the resulting problem can be solved optimally even for large instances with 10,000 basic units or more within a short time. Even in the presence of contiguity constraints, several thousand basic units can be assigned in reasonable time (Ríos-Mercado and López-Pérez 2013). Alternatively, the allocation problem can be modeled as a minimum cost network flow problem allowing more flexibility for measuring and optimizing the balance and compactness of districts (George et al. 1997).

Example 25.3

Consider again the example depicted in Fig. 25.3, but assume now that the district centers are flexible and the current ones are just a starting point. Based on the districting plan for the measure $cmp_{\text{wd}^2}(\cdot )$, the new centers that minimize $cmp_{\text{wd}^2}(\cdot )$ over each district are shown on the left-hand side in Fig. 25.5. The subsequent allocation phase yields the new districts shown on the right-hand side. The districts are visually much more compact and there is no overlap between the convex hulls of the districts.

Fig. 25.5

Illustration of one iteration of the location-allocation procedure. (a) Location phase: new districts centers. (b) Allocation phase: new districts

In former times, when the exact solution of the allocation problem was unattainable for larger instances, the assignment problem was solved heuristically. Setting the tolerance α to zero and relaxing the integrality constraints on the assignment variables, i.e., x_ij ∈ [0, 1], the resulting linear program is a classical transportation problem that can be solved efficiently using specialized network algorithms. However, solving the relaxed problem yields districts that are perfectly balanced but usually assign portions of basic units to more than one district, i.e., ∃ i, i′∈ J_c, i≠i′, j ∈ J, such that $x_{ij},\, x_{i'j} > 0$. Such basic units are called splits. For an optimal basic feasible solution of the transportation problem, it is easy to prove that there are at most p − 1 splits (Hojati 1996). To restore the integrity of basic units, it is necessary to round for every split its fractional variables to one (one variable) or zero (the other variables). This yields disjoint districts but destroys their perfect balance. A simple split resolution rule is to assign a split to the district (center) that “owns” the largest share of the split (Hess and Samuels 1971). However, if there are just a few basic units per district, this rule may produce very unbalanced districts. An optimal split allocation with a minimal maximal percentage deviation can be obtained in polynomial time by using tree partitioning methods; unfortunately, the problem of finding a split resolution with a minimal total deviation is NP-hard; see Schröder (2001) for details.

5.2 Exact Methods

As districting is essentially a partitioning problem, classical set-partitioning approaches can be used to solve the problem. In a first step, balanced, contiguous, and compact candidate districts are generated in a heuristic fashion. In a second step, districts are selected from the set of candidates to optimize the overall balance of the district plan (Garfinkel and Nemhauser 1970; Mehrotra et al. 1998). Unfortunately, only small instances can be solved optimally with this approach. An advantage compared to location-allocation methods is however that almost any criterion can be applied on the generation of candidate districts.

More recently, Salazar-Aguilar et al. (2011a) introduced an exact method for handling districting problems subject to the connectivity constraints proposed by Drexl and Haase (1999). The authors present an exact solution framework based on a branch-and-bound algorithm combined with a cut generation strategy. First, the (exponentially many) connectivity constraints are relaxed and then the integer relaxation is solved by branch-and-bound. Afterwards, an easy separation problem is solved to find unconnected districts. The corresponding violated constraints are then added to the formulation and the iterative process starts again. When no more violated cuts are found, the algorithm stops with an optimal solution. Extensive empirical evidence is presented for several classes of districting models that include multiple balancing constraints and various compactness measures. Two MILP models are assessed: one based on a p-center compactness measure and the other based on a p-median function. The latter turns out to have a stronger linear programming relaxation and results in fewer violated connectivity constraints. The authors also propose two integer quadratic programming formulations for the center and median based compactness measure that result in a smaller number of variables than the linear formulations. These formulations are also solved within the same exact optimization framework. The empirical results show that the quadratic models allow solving larger instances than their linear counterparts. The former also require fewer iterations of the exact method to converge.

Ríos-Mercado and Bard (2019) present an exact optimization scheme for the maximum dispersion territory design problem introduced in Fernández et al. (2010). The exact algorithm takes full advantage of a tighter dual bound and a new reformulation embedded into a biased binary search scheme. Extensive testing indicates that the proposed exact algorithm is able to find optimal solutions to instances with up to 800 basic units and 12 companies and to instances with up to 1400 basic units and 8 companies. Previous to this research, the largest instances optimally solved with off-the-shelf branch-and-bound solvers had between 40 to 100 basic units and 4 companies. This work also extends the results for the maximum dispersion problem introduced by Fernández et al. (2013).

In the context of multi-objective districting, Salazar-Aguilar et al. (2011b) address a commercial districting problem. The authors propose a bi-objective programming model where compactness and balancing with respect to the number of customers are used as performance criteria. Constraints such as connectivity and balancing with respect to product demand are also considered in the model. They propose an improved epsilon-constraint method for generating the optimal Pareto front. Empirical evidence over a variety of instances shows that the improved method is well suited for finding optimal Pareto fronts with no more computational effort than the traditional method. Instances of up to 150 units and 6 territories are solved in relatively short amount of time. For this problem, the improved method finds practically the same fronts than those found by the traditional epsilon-constraint method. This is, to the best of our knowledge, the only exact method for multi-objective districting developed up to date.

5.3 Computational Geometry Methods

A very simple but efficient solution approach for basic units representing points is the successive dichotomies strategy (Kalcsics et al. 2005). The main idea is to recursively subdivide the problem geometrically using lines into smaller and smaller subproblems until an elementary level is reached, where the problem can be solved efficiently. Hence, the basic operation is to partition a subset J′ of basic units into two subsets $J^{\prime }_l$ and $J^{\prime }_r$ by drawing a line within this set of points. Given a number of line directions, for each direction the position of the line is determined in such a way that the two resulting subproblems are best balanced. For every direction, the line is evaluated by a convex combination of its balance and its compactness (evaluated through the length of inter-district boundaries), and the best line is then used to divide the problem into two subproblems. This procedure is repeated until every subset corresponds to a single district. The strategy quickly determines a well-balanced districting plan with no overlap between districts. However, as it does not explicitly account for (road) distances, the resulting districts sometimes lack compactness. Moreover, it is difficult to include neighborhood information. Instead of using lines, other geometric concepts can be used. Alternatively, the process of subdividing a point set J′ can be modeled and solved as a 2-facility location problem (Salazar-Aguilar et al. 2013a).

Example 25.4

Consider again the example in Fig. 25.3 and assume that the district centers are flexible. Figure 25.6 shows the districting plan obtained with the successive dichotomies algorithm using horizontal, vertical, and diagonal lines.

Fig. 25.6

Districting plan with the successive dichotomies algorithm

Another approach is based on weighted Voronoi diagrams on networks (for a definition of weighted Voronoi diagrams, see Aurenhammar et al. 2013). Assume that the neighborhood graph G is given. For center-based measures the most compact solution is obtained by assigning each basic unit to the closest center. If the distances $\{ d_{c_k,j} \mid c_k \in J_c \}$ are unique for each j ∈ J, then each district will also be connected. However, the resulting districts are often far from being balanced. To overcome this drawback, the idea is to modify the distances $d_{c_k,j}$ between basic units and centers in such a way that assignments to overly large districts are “penalized” and allocations to too small districts are “stipulated”. There are basically two options to modify distances. The first adds a real-valued weight $r_k \in \mathbb {R}$ to each distance $d_{c_k,j}$ (Zoltners and Sinha 1983) and the second multiplies $d_{c_k,j}$ by a positive weight $r_k \in \mathbb {R}^+$ (Ricca et al. 2008). Hence, basic unit j ∈ J is closer to center c_k than to center c_l ∈ J_c if $d_{c_k,j} + w_k < d_{c_l,j} + w_l$ or $w_k\,d_{c_k,j} < w_l\, d_{c_l,j}$, respectively. Increasing (decreasing) the weight for a specific center c_k while keeping the other weights unchanged, will reduce (increase) the number of basic units assigned to c_k under the closest assignment rule and thus reduce (increase) the size of the district. To obtain balanced districts, the weights have to be updated iteratively until a satisfactory result is obtained. During the update, care has to be taken since some districts may turn out empty under additive weights or become disconnected for multiplicative weights if the weights are too uneven. For details on the update procedures see Zoltners and Sinha (1983) and Ricca et al. (2008). The partitions of the graph induced by these weights are the so-called additively and multiplicatively weighted Voronoi diagrams. Note that the approach using additive weights is in fact a Lagrangian relaxation where the balancing constraints have been relaxed.

Most districting problems are solved using discrete models. However, these problems (and a number of other logistics problems as well) can be converted into problems with continuous demand functions. Continuous demand approximations models are based on the spatial density and distribution of demand rather than on precise information on every demand point. Given continuous approximations, one can for example use Voronoi diagrams to compute or to smooth existing districts (Galvão et al. 2006), or determine perfectly balanced districts (Carlsson and Delage 2013).

5.4 Construction Methods

There exist several easy approaches for constructing a districting plan from scratch. One of the most popular ones is based on the multi-kernel growth methodology first introduced in Vickrey (1961). The general idea of this methodology is to select a certain number of basic units as “seed centers” and then assign to each seed neighboring basic units in order of decreasing distance until the desired district size is reached. Variations exist with respect to the selection of seeds, whether districts grow simultaneously or sequentially around the seeds, and how to deal with enclaves of unassigned basic units which typically occur at the end of this greedy process (Bodin and Levy 1991; Williams 1995; Mehrotra et al. 1998; Bozkaya et al. 2003). The resulting districting plans are not always connected or balanced and typically serve as a starting point for a metaheuristic.

A different approach treats each basic unit initially as a single district and then merges iteratively pairs of districts until the prescribed number of districts is reached (Deckro 1977).

5.5 Metaheuristics

Given the NP-hardness of most of the districting problems, it is not surprising that moderate to large scale instances are intractable by exact optimization algorithms. The development of structured heuristic or metaheuristics has been a very important area of research over the past few years. Many interesting ideas and schemes have been developed with great success. A major advantage of these methods is their flexibility to include almost any practical criterion and measure for the design of districts and handle complex constraints. In this subsection we review some of the most relevant works on metaheuristics applied to districting problems in general.

5.5.1 Greedy Randomized Adaptive Search Procedure (GRASP)

In recent years, GRASP has been one of the most popular approaches to solve districting problems. An important reason for this is its flexibility to successfully handle connectivity constraints when constructing solutions from scratch.

The first GRASP implementation applied to a districting problem is due to Ríos-Mercado and Fernández (2009). In that work, the authors address a commercial districting problem with connectivity and multiple balancing constraints. They develop a reactive GRASP, where territories are built one at a time during the construction phase and reinsertion and swapping neighborhoods are explored during the improvement phase. The method is enhanced by a reactivity feature that automatically self-tunes the GRASP quality threshold parameter for accepting solutions from the restricted candidate list. The algorithm is tested on data sets coming from a commercial firm that range from 500 to 2000 basic units. It was observed that the algorithm was very robust under many different scenarios, providing solutions of significantly better quality than those from existing practice. In a follow-up work, Ríos-Mercado (2016) provides further experiments by applying the reactive GRASP for solving large scale instances ranging from 1000 to 2000 to basic units under different settings. An interesting finding is that the metaheuristic is able to obtain feasible designs with less than 3% balance deviation.

Fernández et al. (2010) present a GRASP approach for the maximum dispersion territory design problem with three different construction heuristics and several different neighbourhood topologies in its local search phase. Extensive computational testing shows the effectiveness of the proposed algorithm.

Ríos-Mercado and Salazar-Acosta (2011) address a commercial districting problem arising in the bottled beverage distribution industry where a set of city blocks has to be grouped into territories. As planning requirements, the grouping seeks to balance both the number of customers and the product demand across territories, maintain connectivity of territories, and limit the total cost of routing. This work addresses both district design and routing decisions simultaneously by considering a budget constraint on the total routing cost. A GRASP that incorporates advanced features such as adaptive memory and strategic oscillation is presented. Empirical evidence over a wide set of randomly generated test instances based on real-world data shows a very positive impact of these advanced components, significantly improving the solution quality.

Salazar-Aguilar et al. (2013b) study a commercial districting problem. Each territory must be compact, connected, and balanced according to two activity measures (number of costumers and product demand). Two GRASP heuristics (BGRASP and TGRASP) are proposed for this problem. For each of them two variants are studied: (1) keeping connectivity as a hard constraint during construction and post-processing phases and, (2) ignoring connectivity during the construction phase and adding this as a minimizing objective function during the post-processing phase. The main difference between BGRASP and TGRASP is the way they consider the planning criteria during the construction phase. In BGRASP, the construction attempts to find high quality solutions based on the optimization of two criteria: compactness and balance of the number of customers (product demand balance is treated as a constraint). The construction phase in TGRASP considers three objectives to be optimized: compactness and balance with respect to both activity measures. The proposed procedures are evaluated on a variety of problem instances, with 500 and 1000 basic units. An analysis of these procedures is carried out using different performance measures such as the number of non-dominated points, the k-distance, the size of the space cover (SSC), the coverage of two sets measure, and time. It is observed that SSC, coverage of two sets measure, and time exhibit significant variation depending on the GRASP procedure used. In contrast to that the number of points and k-distance measures did not show any significant variation over all evaluated procedures. BGRASP-I provides good frontiers in short time and BGRASP-II has the best coverage of the efficient points given by the others procedures.

A multi-objective capacitated redistricting problem (MCRP) arising from power meter reading is addressed by de Assis et al. (2014). Two objective functions are considered (compactness and homogeneity of districts) within a bi-objective optimization framework. The redistricting relies on the existence of an original set of districts. The goal of the problem is to partition power utility customers into new districts. The expansion of cities with new developments, population migration, and uneven changes of power demand in the suburbs are examples of forces that pressure the re-definition of districts. Each district refers to the working zone of a group of meter readers that perform readings of power consumption from the customers of that same district. The readings are performed in situ and feed the monthly invoice sent to each customer. The proposed solution method is based on a GRASP and multi-criteria scalarization technique to approximate the Pareto front. The approximate Pareto front is obtained iteratively by solving mono-objective problems in which the objective function is a weighted sum expression of the two criteria under consideration. The GRASP construction phase generates districts, one at a time, by using a greedy function that penalizes both a dispersion measure and district imbalance in weighted manner. If the resulting plan has more than p territories, a repair phase consisting of merging the smallest territories is carried out to ensure p territories are designed. As an improvement phase they use the reinsertion neighborhood. Computational tests are performed with a diverse set of 24 randomly generated instances with different sizes, demands and densities. A real-life network extracted from the city of São Paulo, Brazil, is also included in the tests. The results demonstrate the effectiveness of GRASP in producing high quality districts with respect to compactness and homogeneity. The results indicate the impact of conformity on the resulting trade-off curve, clearly showing a compromise between attaining compact solutions and maintaining allocations of customers to their current district. The authors conclude that the conformity is thus a relevant criterion and should be included in the optimization and decision making process regarding redistricting problems.

The existing literature reveals that practically all the works on commercial districting use center or median based compactness measures. While these measures yield mixed-integer programming models with some nice properties, they have the disadvantage of being very costly to be evaluated when used within heuristic frameworks. This is due to the center updating operations frequently needed throughout the heuristic search. Ríos-Mercado and Escalante (2016) propose a more robust dispersion measure based on the diameter of the formed territories, allowing for a more efficient heuristic search. For solving this particular territory design problem, they propose a GRASP that incorporates a novel construction procedure where territories are formed simultaneously in two main stages using different criteria. This also differs from previous literature where GRASP was used to build only one territory at a time. The procedure is further enhanced with two variants of forward-backward path relinking, namely static and dynamic. Path relinking is a sophisticated and very successful search mechanism. This idea is novel in any districting or territory design application to the best of our knowledge. The proposed algorithm and its components are extensively evaluated over a wide set of data instances. Experimental results reveal that the construction mechanism produces feasible solutions of acceptable quality, which are improved by an effective local search procedure. In addition, empirical evidence indicate that the two path relinking strategies have a significant impact on solution quality when incorporated within GRASP. The ideas and components of the developed method can be further extended to other districting problems under balancing and connectivity constraints.

5.5.2 Tabu Search (TS)

Blais et al. (2003) study a districting problem arising in a local community health clinic in Montreal, Canada, in which five districting criteria must be respected: indivisibility of basic units, respect for borough boundaries, connectivity, visiting personnel mobility, and workload balance. The last two criteria are combined into a single objective function. The authors present a tabu search heuristic considering two different neighborhood topologies. For the case study at hand, the design obtained by the heuristic was able to improve the then current solution in terms of workload balance and personnel mobility.

Bozkaya et al. (2003) propose a tabu search for a districting problem that considers the optimization of four different criteria in a single weighted objective function: population equality, territory compactness, socio-economic homogeneity, and similarity to the existing districting plan. Moreover, connectivity is treated as a hard constraint. The local search is based on a reinsertion and swap neighborhood. Concerning the tabu list, when a given basic unit is used in a move, it remains tabu for the next θ iterations, where θ is chosen randomly. Moreover, an adaptive memory procedure is employed. This procedure is based on the idea that components of high quality solutions can be used to construct other high quality solutions. The method therefore stores in a constantly updated pool a set of districts belonging to some of the best-known solutions. Then, disjoint districts can be extracted from the pool to serve as a basis for a new solution. Each district of the pool, or adaptive memory, is given a larger probability of being selected if it belongs to a better solution. In their empirical work, it was found that the proposed method is robust and powerful since it can easily incorporate a large number of criteria and produces feasible and high quality solutions. When tested on a real-world case study from Edmonton, Canada, the test results indicate that the algorithm can produce maps that dominate the existing districting map of Edmonton with respect to compactness and integrity of communities. It can also reduce the amount of deviation around the average district population from the current 25% to much lower levels (such as 1%), improving on the equality of representation.

Haugland et al. (2007) develop tabu search and multi-start metaheuristics for the problem of designing districts for vehicle routing problems with stochastic demands. In particular, demands are assumed to be uncertain at the time when the districts are made, and these are revealed only after the districting decisions are determined. They use the same neighbourhoods for the local search phase and the same tabu list implementation as in Bozkaya et al. (2003). The authors compare the two heuristics, finding out that tabu search outperforms multi-start.

Ríos-Mercado et al. (2017) present a tabu search metaheuristic as a follow-up to the work on the maximum dispersion territory design problem, first addressed by Fernández et al. (2010). In this paper, the authors significantly improve the previous GRASP approach by incorporating a strategic oscillation component within the tabu search.

5.5.3 Simulated Annealing (SA)

D’Amico et al. (2002) address the problem of re-drawing police command boundaries. They model this problem as a constrained graph-partitioning problem involving the partitioning of a police jurisdiction into command districts subject to constraints of contiguity, compactness, convexity and size. Since the districting affects urban emergency services, they also include quality-of-service constraints, which limit the response time (queue time plus travel time) to calls for service. Given the size of the problem, they propose a simulated annealing heuristic to search for good partitions of the police jurisdiction. At each iteration of the algorithm, they employ a variant of the well-known public domain software tool Patrol Car Allocation Model (PCAM) to optimally assign patrol cars to districts and assess the “goodness” of a particular district design with respect to some prescribed performance measures. For the neighbour topology, they consider moves that reassign a basic unit from a given district to an adjacent district. A computational case study using data from the Buffalo, NY, Police Department (BPD) is carried out revealing the merits of this approach. Among their main findings it was observed that under optimal car allocations, they are able to find an improved district design that lowers the disparity among officer workloads from 30% to only 14%. Also, the proportion of small workloads under 36% is greatly reduced. Hence, officer workloads are better balanced (primarily between 36% and 42%) across all districts and work shifts. At the same time, the response time feasibility constraints ensured no increase in the maximum response time of 29 min under current BPD operations.

5.5.4 Genetic Algorithm (GA)

Bação et al. (2005) solve a political districting problem using a genetic algorithm and apply it to a case study in Portugal. Their results indicate that the GA obtains better results when compared to the current practice.

Tavares-Pereira et al. (2007) study a multi-objective districting problem arising for Paris public transportation. The goal is to partition a territory into “homogeneous” zones without inclusions, where each zone is composed of a set of elementary territorial units. They propose a genetic algorithm to approximate the Pareto front based on an evolutionary algorithm with local search. The algorithm presents a new solution representation and new crossover/mutation operators. The algorithm can deal with multiple criteria, allows to solve large-size instances in a reasonable time, and generates high quality solutions. The algorithm is applied to the Paris region public transportation.

Steiner et al. (2015) address a health-care districting problem arising in Parana State, Brazil. The motivation for the problem is to develop a better system for patients by aggregating various health services offered in the municipalities of Parana into micro regions. The problem is formulated as a multi-objective graph partitioning problem, where the municipalities are represented by nodes, and roads connecting them are represented by edges. Their three-objective optimization problem considers maximizing the population homogeneity in the micro regions, maximizing the variety of medical procedures offered in the micro regions, and minimizing the inter-micro region distances to be traveled by patients. They develop a multi-objective genetic algorithm, which yields a significant improvement over the existing health-care system map of Parana State.

Forman and Yue (2003) present a genetic algorithm for a political districting problem, where the encoding of solutions and the genetic operators are based on the ones for Traveling Salesman Problems. This encoding forces near equality of district population and uses the fitness function to promote district contiguity and compactness. A post-processing step further refines district population equality. Results are provided for three states (North Carolina, South Carolina, and Iowa) using the 2000 census data.

5.5.5 Hybrid and Miscellaneous Approaches

Bergey et al. (2003) address an electrical power districting problem arising in the Republic of Ghana. Due to a variety of political, economic, and technological factors, many national electricity industries around the globe are transforming from non-competitive monopolies with centralized systems to decentralized operations with competitive business units. A key challenge faced by energy restructuring specialists at the World Bank is trying to simultaneously optimize the various criteria one can use to judge the fairness and commercial viability of a particular power districting plan. The authors propose a simulated annealing genetic algorithm for this problem. In their empirical work, they observe that the proposed method outperformed a well-known parallel simulated annealing heuristic.

Wei and Chai (2004) present a hybrid approach combining tabu search and scatter search for solving a multi-objective spatial zoning model. The problem considers a scalar function with three objectives: population unbalance, territory compactness, and socioeconomic homogeneity. The model also includes resource capacity constraints, but no connectivity constraints. Later, Bong and Wang (2006) tackle another multi-objective zoning model that optimizes four criteria: population equality, territory compactness, socio-economic homogeneity, and similarity of a solution with the existing plan. The model also includes resource capacity constraints. The authors propose a hybrid algorithm with elements from tabu search, scatter search, and path relinking. A comparative study between the results of multi-objective decision-making and single objective decision-making is conducted for the proposed multi-objective method with a selected single objective method called WAMCF. The empirical results show concrete evidence on two aspects that the proposed method can produce better results for the problem with lower values in the objectives achieved for the minimization problem. It was also observed that a more consistent result for the individual solution was delivered compared to the single objective approach because there is a big difference between the generated maximum and minimum best values.

Ricca and Simeone (2008) present a comparison of several local search metaheuristics for political districting considering territory connectivity, minimizing measures of population inequality, noncompactness, and nonconformity to administrative boundaries. Experiments on a set of medium to large real-life instances is carried out using descent search, tabu search, simulated annealing, and old bachelor acceptance algorithms. Except for descent, all local search methods show a very good performance. In particular, old bachelor acceptance produces the best results in the majority of the cases, especially when the objective function is focussing on compactness.

Salazar-Aguilar et al. (2012) propose a multi-objective scatter search heuristic for a bi-objective territory design problem. They consider a problem where compactness and balance with respect to product demand are sought. The problem includes also balancing territories with respect to workload and territory connectivity. The proposed scatter search-based framework contains a diversification step based on a greedy randomized adaptive search procedure, an improvement step based on a relinked local search strategy, and a combination step based on a solution of an assignment problem. The proposed metaheuristic is evaluated over a variety of instances taken from literature. This includes a comparison with two of the most successful multi-objective heuristics from literature such as the scatter tabu search procedure for multi-objective optimization by Molina et al. (2007), and the non-dominated sorting genetic algorithm by Deb et al. (2002). Experimental work reveals that the proposed procedure consistently outperforms both existing heuristics from literature on all instances tested.

5.6 Lower Bounding Schemes

To the best of our knowledge, the only work on lower bounds for districting problems is due to Elizondo-Amaya et al. (2014). In their work, the authors study a commercial districting problem that minimizes territory dispersion based on a p-center type of function subject to multiple balance constraints. Lower bounds are obtained using a binary search over a range of coverage distances. For each coverage distance a Lagrangian relaxation of a maximal covering model is effectively used. Their computational results indicate that the bounding scheme provides tighter lower bounds than those obtained by the linear programming relaxation.

6 Conclusions

In this chapter, we have given a broad overview of typical criteria and restrictions that can be found in various districting applications as well as ways and means to quantify and model these criteria. In addition, an overview of the different areas of application for districting problems was given and the various solution approaches for them that have been used were highlighted.

Despite the large number of publications, it is striking that only few authors consider the districting problem independently from a practical background. Moreover, there is no consensus on which criteria are eligible and important and, on how to measure them appropriately. Thus, instead of devising yet another (variant of a) metaheuristic for a districting model with yet another measure for compactness or additional constraint, research should first and foremost concentrate on a common and generic framework for districting problems. And it should try to categorize the suitability of criteria and measures based on the availability of data, the geometric representation of the basic units, and the different types of applications.