Abstract
In this paper, we propose a new leakage-resilient identity-based encryption (IBE) scheme that is secure against chosen-ciphertext attacks (CCA) in the bounded memory leakage model. It is the first CCA-secure leakage-resilient IBE scheme which does not depend on \(\mathtt {q}\)-type assumptions. More precisely, it is secure under the DLIN assumption for symmetric bilinear groups and under the XDLIN assumption for asymmetric bilinear groups, respectively.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
1.1 Background
Most of the encryption schemes known so far have been proven secure by assuming that the secret key is completely hidden. However, in the real world, a partial information of the secret key may leak by side-channel attacks [6, 14, 20] or a cold-boot attack [15]. In recent years, extensive research effort has been invested in providing encryption schemes which are provably secure even in this setting. Such schemes are said to be leakage-resilient.
Akavia et al. [2] introduced the bounded memory leakage model in which a bounded amount of information of the secret key is leaked to the adversary. Naor and Segev [26] showed how to construct leakage-resilient public-key encryption schemes from hash proof systems (HPS) in this model. (Other constructions were given by [4, 18, 22].) Qin et al. [28] showed a generic method to construct a CCA-secure leakage-resilient encryption scheme from any tag-based strongly universal\(_2\) HPS.
Regarding identity-based encryption (IBE) schemes, CPA-secure leakage-resilient IBE schemes were shown by Akavia et al. [2], Alwen et al. [3] and Chow et al. [8]. Furthermore, the scheme of Kurosawa and Phong [21] achieves the leakage rate \(1-o(1)\) under the DLIN assumption, where the leakage rate is defined as
On the other hand, CCA-secure leakage-resilient IBE schemes were shown by Alwen et al. [3], Sun et al. [30] and Li et al. [24]. Unfortunately, all these CCA-secure leakage-resilient IBE schemes rely on \(\mathtt {q}\)-type assumptions. Due to the Cheon attack [7], it is better to avoid such assumptions.
1.2 Our Contribution
In this paper, we propose the first CCA-secure leakage-resilient IBE scheme which does not depend on \(\mathtt {q}\)-type assumptions. More precisely, it is secure under the DLIN assumption for symmetric bilinear groups and under the XDLIN assumption for asymmetric bilinear groups. (See Sect. 2.1 for the types of bilinear groups.)
In fact, we construct a CCA-secure leakage-resilient IB-KEM. A CCA-secure leakage-resilient IBE scheme is obtained by combining our IB-KEM with any CCA-secure symmetric-key encryption scheme (which does not need to be leakage-resilient).
Our IB-KEM scheme is obtained by applying the technique of Qin et al. [28] to the CPA-secure leakage-resilient IBE scheme of Kurosawa and Phong [21]. Hereby, we can achieve the leakage rate 1/10. Our scheme will be able to generalize to k-linear assumption.
Table 1 shows a comparison of CCA-secure leakage-resilient IBE schemes.
1.3 Various Models for Leakage-Resilient
Several researchers consider some variants of leakage models to capture practical issues. We summarize some leakage models below.
Micali and Reyzin [25] considered the “only computation leak information” model to deal with physical observation via side-channel attacks. However, this model could not capture key leakage attacks, such as a cold-boot attack. To capture key leakage attacks, Akavia et al. [2] proposed the bounded memory leakage model, in which an adversary can get partial information on secret keys. Brakerski et al. [5] and Dodis et al. [9] presented a new model called continual memory leakage model, which allows leakage on the private key in many periods of time. In this model, the secret key is updated over time and the total leakage over the lifetime of the system is unbounded. Dodis et al. [10] invented the auxiliary input model, in which the entire secret could be leaked information-theoretically, provided that it is computationally infeasible to compute the secret.
All these leakage models only consider leakage occurring before the challenge ciphertext is given to the adversary. In response to this, Halevi and Lin [16] proposed the after-the-fact leakage model, in which an adversary can obtain leaked information after seeing the challenge ciphertext.
1.4 Organization
The rest of the paper is organized as follows. Section 2 introduces notations, some building blocks, and computational assumptions. Section 3 describes the definition of IB-KEM and the leakage-resilient CCA-security. We present the concrete construction of our CCA-secure leakage-resilient IB-KEM scheme in Sect. 4 and its security proof in Sect. 5. Finally, the conclusion of this paper is given in Sect. 6.
2 Preliminaries
2.1 Notations
We introduce some notations used in this paper. Let  denote the security parameter. We say that a function
denote the security parameter. We say that a function  is negligible in
is negligible in  if it is smaller than all polynomial fractions for a sufficiently large
if it is smaller than all polynomial fractions for a sufficiently large  . For a finite set \(\mathcal {S}\), we use
. For a finite set \(\mathcal {S}\), we use  to denote the process of sampling an element s from \(\mathcal {S}\) uniformly at random and let
to denote the process of sampling an element s from \(\mathcal {S}\) uniformly at random and let  denote its cardinality.
denote its cardinality.
Let \(\mathsf {GGen}\) be a probabilistic polynomial time (PPT) algorithm that on input the security parameter  returns a description
returns a description  of pairing groups, where
of pairing groups, where  ,
,  ,
,  are cyclic groups of a prime order q, \(g_1\) and \(g_2\) are generators of
are cyclic groups of a prime order q, \(g_1\) and \(g_2\) are generators of  and
and  , respectively, and
, respectively, and  is an efficiently computable (non-degenerated) bilinear map. Define
is an efficiently computable (non-degenerated) bilinear map. Define  , which is a generator of
, which is a generator of  .
.
We refer to [31] for a description of types of bilinear groups. There are three types of bilinear groups according to whether efficient isomorphisms exist or not between  and
and  [13]. In type 1, both the isomorphism \(\psi :\) and its inverse \(\psi ^{-1}:\) are efficiently computable, i.e., it can be regarded as
[13]. In type 1, both the isomorphism \(\psi :\) and its inverse \(\psi ^{-1}:\) are efficiently computable, i.e., it can be regarded as  . In type 2, the isomorphism
. In type 2, the isomorphism  is efficiently computable but its inverse is not. In type 3, there are no efficient isomorphisms between
is efficiently computable but its inverse is not. In type 3, there are no efficient isomorphisms between  and
and  . Type 1 pairing groups are called symmetric, and type 2 and 3 pairing groups are called asymmetric. We assume type 3 pairing groups in our scheme, but our scheme also works in type 1 and 2 setting under appropriate computational assumptions.
. Type 1 pairing groups are called symmetric, and type 2 and 3 pairing groups are called asymmetric. We assume type 3 pairing groups in our scheme, but our scheme also works in type 1 and 2 setting under appropriate computational assumptions.
We use implicit representation of group elements as introduced in [12]. For  and
and  we define
we define  as the implicit representation of a in
as the implicit representation of a in  . Similarly, for a matrix
. Similarly, for a matrix

we define

as the implicit representation of \(\mathbf {A}\) in  . Note that it is easy to compute \(\left[ \mathbf {A}\mathbf {B} \right] _s\) given \(\left( \left[ \mathbf {A} \right] _s,\mathbf {B}\right) \) or \(\left( \mathbf {A},\left[ \mathbf {B} \right] _s\right) \) with appropriate dimensions. We define
. Note that it is easy to compute \(\left[ \mathbf {A}\mathbf {B} \right] _s\) given \(\left( \left[ \mathbf {A} \right] _s,\mathbf {B}\right) \) or \(\left( \mathbf {A},\left[ \mathbf {B} \right] _s\right) \) with appropriate dimensions. We define  that can be efficiently computed given \(\left[ \mathbf {A} \right] _1\) and \(\left[ \mathbf {B} \right] _2\).
that can be efficiently computed given \(\left[ \mathbf {A} \right] _1\) and \(\left[ \mathbf {B} \right] _2\).
2.2 External Decisional Linear Assumption
We assume the following property.
Definition 1
(External Decisional Linear Assumption: XDLIN [1]). Let  . We say that the XDLIN assumption holds relative to \(\mathsf {GGen}\) in group
. We say that the XDLIN assumption holds relative to \(\mathsf {GGen}\) in group  if for any PPT adversary \(\mathsf {D}\), the following is negligible in
if for any PPT adversary \(\mathsf {D}\), the following is negligible in  :
:

where  ,
,  ,
,  , and
, and

This assumption is a variant of the standard decisional linear (DLIN) assumption [27] for asymmetric pairing groups. The XDLIN assumption is equivalent to the DLIN assumption in the generic group model.
2.3 Statistical Distance, Min-Entropy and Randomness Extractor
The statistical distance between random variables X, Y over a finite domain  is defined by
is defined by

The min-entropy of X is defined by

Furthermore, average min-entropy of X conditioned on Y is defined by

as defined in [11], which also proved the following lemma.
Lemma 1
([11, Lemma 2.2]). Let \(\ell \) be a positive integer. Let X, Y and Z be random variables. If Y has at most \(2^\ell \) possible values, then
One of main tools in our construction is a randomness extractor [11].
Definition 2
(Randomness Extractor). Let n be a positive integer, and \(\phi > n, \epsilon _\mathsf {Ext}\) be positive reals, and \(\mathcal {D}, \mathcal {S}\) be finite sets. A function  is called a \((\phi , \epsilon _\mathsf {Ext})\)-randomness extractor if for all pairs of random variables (X, I) such that X is a random variable over \(\mathcal {D}\) satisfying \(\tilde{H}_\infty (X \mid I) \ge \phi \),
is called a \((\phi , \epsilon _\mathsf {Ext})\)-randomness extractor if for all pairs of random variables (X, I) such that X is a random variable over \(\mathcal {D}\) satisfying \(\tilde{H}_\infty (X \mid I) \ge \phi \),
holds, where S is uniform over \(\mathcal {S}\) and R is uniform over  .
.
2.4 Hash Functions
Let  be a hash function, where \(\mathcal {D} = \mathcal {D}(\lambda )\) and \(\mathcal {R} = \mathcal {R}(\lambda )\) are sets. We require the following property of hash functions for our scheme.
be a hash function, where \(\mathcal {D} = \mathcal {D}(\lambda )\) and \(\mathcal {R} = \mathcal {R}(\lambda )\) are sets. We require the following property of hash functions for our scheme.
Definition 3
(Target Collision Resistance). We say a hash function  is target collision resistant if for any PPT adversary \(\mathsf {A}\),
is target collision resistant if for any PPT adversary \(\mathsf {A}\),

is negligible in  .
.
2.5 Useful Facts
Here, we introduce useful facts used in our security proof. We use the following lemmas to prove adaptive identity security of our scheme.
Lemma 2
(Programmable hash function [17, Theorem 7]). Let m, Q be integers. We choose  as follows: (1) set \(J = Q^2\), (2) sample
as follows: (1) set \(J = Q^2\), (2) sample  for \(i = 1,\ldots ,m\) and \(j = 1,\ldots ,J\), (3) set \(h_i = \sum _{j=1}^{J}u_{i,j}\). For \(h = (h_1,\ldots ,h_m)\), we define
for \(i = 1,\ldots ,m\) and \(j = 1,\ldots ,J\), (3) set \(h_i = \sum _{j=1}^{J}u_{i,j}\). For \(h = (h_1,\ldots ,h_m)\), we define

where  . Then, for any distinct
. Then, for any distinct  , we have
, we have
where the probability is taken over the choice of h.
Lemma 3
([32, Lemma 5]). Let  be reals such that
be reals such that

Furthermore, let  be reals such that \(0 < \delta _\mathrm {low}\le \delta _i \le \delta _\mathrm {up}\) for \(i = 1,\ldots ,l\). Then, we have
be reals such that \(0 < \delta _\mathrm {low}\le \delta _i \le \delta _\mathrm {up}\) for \(i = 1,\ldots ,l\). Then, we have

3 Identity-Based Key-Encapsulation Mechanism
In this section, we introduce the syntax, the correctness property, and the security notion for IB-KEM.
Syntax. An IB-KEM scheme  consists of four PPT algorithms.
consists of four PPT algorithms.
-
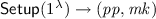 . The setup algorithm takes as input the security parameter
. The setup algorithm takes as input the security parameter  , outputs a public parameter \(\mathrm { pp }\) and a master key \(\mathrm { mk }\). We assume that \(\mathrm { pp }\) implicitly defines an identity space \(\mathcal {ID}\), a session key space \(\mathcal {K}\), and a secret key space \(\mathcal {SK}\).
, outputs a public parameter \(\mathrm { pp }\) and a master key \(\mathrm { mk }\). We assume that \(\mathrm { pp }\) implicitly defines an identity space \(\mathcal {ID}\), a session key space \(\mathcal {K}\), and a secret key space \(\mathcal {SK}\). -
 . The key generation algorithm takes as input the master key \(\mathrm { mk }\) and an identity \(\mathrm { id }\in \mathcal {ID}\), outputs a secret key \(\mathrm { sk }_\mathrm { id }\) for the \(\mathrm { id }\).
. The key generation algorithm takes as input the master key \(\mathrm { mk }\) and an identity \(\mathrm { id }\in \mathcal {ID}\), outputs a secret key \(\mathrm { sk }_\mathrm { id }\) for the \(\mathrm { id }\). -
\(\mathsf {Encap}(\mathrm { pp },\mathrm { id }) \rightarrow (\mathrm { ct },K)\). The encapsulation algorithm takes as input the public parameter \(\mathrm { pp }\) and an \(\mathrm { id }\in \mathcal {ID}\), outputs a session key \(K \in \mathcal {K}\) together with a ciphertext \(\mathrm { ct }\) with respect to identity \(\mathrm { id }\).
-
\(\mathsf {Decap}(\mathrm { sk }_\mathrm { id },\mathrm { ct }) \rightarrow K\) or \(\bot \). The decapsulation algorithm takes as input a secret key \(\mathrm { sk }_\mathrm { id }\) and a ciphertext \(\mathrm { ct }\), outputs a decapsulated key \(K \in \mathcal {K}\) or the rejection symbol \(\bot \).
Correctness. We require correctness of decapsulation: that is for all  , all pairs \((\mathrm { pp },\mathrm { mk })\) generated by
, all pairs \((\mathrm { pp },\mathrm { mk })\) generated by  , all identities \(\mathrm { id }\in \mathcal {ID}\), and all \((\mathrm { ct },K) \leftarrow \mathsf {Encap}(\mathrm { pp },\mathrm { id })\),
, all identities \(\mathrm { id }\in \mathcal {ID}\), and all \((\mathrm { ct },K) \leftarrow \mathsf {Encap}(\mathrm { pp },\mathrm { id })\),  .
.
Security. In this paper, we consider the IB-KEM variant of CCA-security for leakage-resilient IBE in the bounded memory leakage model [3]. Let \(\varPi \) be an IB-KEM scheme. We consider the IND-ID-lrCCA game between a challenger and an adversary \(\mathsf {A}\) as follows.
-
Setup phase: The challenger runs \(\mathsf {Setup}\) to generate \((\mathrm { pp }, \mathrm { mk })\), and sends \(\mathrm { pp }\) to \(\mathsf {A}\).
-
Query phase 1: The adversary \(\mathsf {A}\) makes queries of the following types:
-
Key generation query \(\mathrm { id }\in \mathcal {ID}\). The challenger computes and returns the secret key
 to \(\mathsf {A}\).
to \(\mathsf {A}\). -
Leakage query \((\mathrm { id },f)\), where
 is an efficiently computable function. The challenger returns \(f(\mathrm { sk }_\mathrm { id })\) to \(\mathsf {A}\).
is an efficiently computable function. The challenger returns \(f(\mathrm { sk }_\mathrm { id })\) to \(\mathsf {A}\). -
Decapsulation query \((\mathrm { id },\mathrm { ct })\). The challenger returns \(\mathsf {Decap}(\mathrm { sk }_\mathrm { id },\mathrm { ct })\) to \(\mathsf {A}\).
-
-
Challenge phase: \(\mathsf {A}\) sends the challenge identity \(\mathrm { id }^*\in \mathcal {ID}\) to the challenger. It must be that he has never queried \(\mathrm { id }^*\) as a key generation query. The challenger chooses a bit
 . The challenger runs \(\mathsf {Encap}(\mathrm { pp },\mathrm { id }^*)\) to generate \((\mathrm { ct }^*, K_0^*)\), and chooses a random session key
. The challenger runs \(\mathsf {Encap}(\mathrm { pp },\mathrm { id }^*)\) to generate \((\mathrm { ct }^*, K_0^*)\), and chooses a random session key  . Then, he sends \((\mathrm { ct }^*, K_b^*)\) to \(\mathsf {A}\).
. Then, he sends \((\mathrm { ct }^*, K_b^*)\) to \(\mathsf {A}\). -
Query phase 2: \(\mathsf {A}\) makes queries of the following types:
-
Key generation query \(\mathrm { id }\in \mathcal {ID}\), where it must be that \(\mathrm { id }\ne \mathrm { id }^*\).
-
Decapsulation query \((\mathrm { id },\mathrm { ct })\), where it must be that \((\mathrm { id }, \mathrm { ct }) \ne (\mathrm { id }^*, \mathrm { ct }^*)\).
-
-
Guess phase: Finally \(\mathsf {A}\) outputs a guess
 .
.
Note that, in query phase 1 and 2 the challenger computes \(\mathrm { sk }_\mathrm { id }\) the first time that \(\mathrm { id }\) is queried in a key generation, leakage, or decryption query, and responds to all future queries on the same \(\mathrm { id }\) with the same \(\mathrm { sk }_\mathrm { id }\).
Definition 4
(IND-ID-lrCCA security). An IB-KEM scheme \(\varPi \) is \(\ell \)-IND-ID-lrCCA (indistiguishability against adaptive identity leakage-resilient chosen-ciphertext attack) secure if for any PPT adversary \(\mathsf {A}\) that makes at most \(\ell \) leakage queries, the advantage

is negligible in  .
.
Remark: Challenge-Dependent Leakage. In the security definition, the adversary is not allowed to obtain the leakage \(f(\mathrm { sk }_\mathrm { id })\) after the challenge phase. We note that this restriction is indeed necessary: the adversary can encode the decapsulation algorithm for the challenge ciphertext \(\mathrm { ct }^*\) and the challenge identity \(\mathrm { id }^*\).
4 Construction
In this section, we propose a new CCA-secure leakage-resilient IB-KEM scheme.
Let  , n be the bit-length of a session key (i.e.,
, n be the bit-length of a session key (i.e.,  ), m be the bit-length of an identity (i.e.,
), m be the bit-length of an identity (i.e.,  ), \(\ell < \log _2{q}\) be any positive integer,
), \(\ell < \log _2{q}\) be any positive integer,  be a target collision resistant hash function,
be a target collision resistant hash function,  be a \((\log _2{q}-\ell ,\epsilon _\mathsf {Ext})\)-randomness extractor. We assume that m is independent of
be a \((\log _2{q}-\ell ,\epsilon _\mathsf {Ext})\)-randomness extractor. We assume that m is independent of  , \(\epsilon _\mathsf {Ext}\) is negligible in
, \(\epsilon _\mathsf {Ext}\) is negligible in  .
.
Our scheme  is described as follows.
is described as follows.
-
 : Choose
: Choose  and
and  uniformly at random and set
uniformly at random and set 
Output \(\mathrm { pp }= (\left[ \mathbf {A} \right] _1,\left[ \mathbf {B}_0 \right] _1,\left[ \mathbf {B}_1 \right] _1,\ldots ,\left[ \mathbf {B}_m \right] _1,\left[ \mathbf {D} \right] _1)\) and \(\mathrm { mk }= (a_1,a_2,\mathbf {B}_0,\mathbf {B}_1,\ldots ,\mathbf {B}_m,\mathbf {D})\).
For an identity
 , let
, let 
-
 : Compute a random matrix
: Compute a random matrix 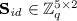 such that $$\begin{aligned} \mathbf {F}_\mathrm { id }\mathbf {S}_\mathrm { id }= \mathbf {D} \end{aligned}$$(1)
such that $$\begin{aligned} \mathbf {F}_\mathrm { id }\mathbf {S}_\mathrm { id }= \mathbf {D} \end{aligned}$$(1)as follows. Let

Choose
 at random, compute
at random, compute 
and set
$$ \mathbf {S}_{\mathrm { id }} = \begin{pmatrix} \mathbf {S}'' \\ \mathbf {S}' \end{pmatrix}. $$Output \(\mathrm { sk }_\mathrm { id }= \left[ \mathbf {S}_\mathrm { id } \right] _2\) as a secret key for the \(\mathrm { id }\).
-
\(\mathsf {Encap}(\mathrm { pp },\mathrm { id })\): Choose
 and
and  at random, compute
at random, compute 
Output \(\mathrm { ct }= (\left[ \mathbf {c} \right] _1,\left[ k_a \right] _T,\mathrm { sd })\) and \(K = \mathsf {Ext}(\left[ k_s \right] _T,\mathrm { sd })\).
-
\(\mathsf {Decap}(\mathrm { sk }_\mathrm { id },\mathrm { ct })\): On input \(\mathrm { sk }_{\mathrm { id }} = \left[ \mathbf {S}_\mathrm { id } \right] _2\) and \(\mathrm { ct }= (\left[ \mathbf {c} \right] _1,\left[ t \right] _T,\mathrm { sd })\), compute

Output \(\mathsf {Ext}(\left[ k_s \right] _T,\mathrm { sd })\) if \(\left[ t \right] _T = \left[ k_a \right] _T\), otherwise \(\bot \).
Correctness. Let \(\mathrm { sk }_\mathrm { id }= \left[ \mathbf {S}_\mathrm { id } \right] _2\), \(\mathrm { ct }= (\left[ \mathbf {c} \right] _1,\left[ t \right] _T,\mathrm { sd })\), and  . If \(\mathbf {c} = \mathbf {F}^\top _\mathrm { id }\mathbf {r}\) and \(t = \mathbf {r}^\top \mathbf {D} \left( {\begin{matrix} 1 \\ \alpha \end{matrix}}\right) \) then
. If \(\mathbf {c} = \mathbf {F}^\top _\mathrm { id }\mathbf {r}\) and \(t = \mathbf {r}^\top \mathbf {D} \left( {\begin{matrix} 1 \\ \alpha \end{matrix}}\right) \) then
in the \(\mathsf {Decap}\) procedure, and it is similar to \(k_s\). Therefore, our IB-KEM scheme \(\varPi \) satisfies correctness.
5 Security
In this section, we prove the IND-ID-lrCCA security of our scheme.
Theorem 1
Under the XDLIN assumption relative to \(\mathsf {GGen}\) in group  , our scheme \(\varPi \) is \(\ell \)-IND-ID-lrCCA secure for any positive integer \(\ell \) satisfying
, our scheme \(\varPi \) is \(\ell \)-IND-ID-lrCCA secure for any positive integer \(\ell \) satisfying
where  is a positive integer such that \(2^{-\eta }\) is negligible in
is a positive integer such that \(2^{-\eta }\) is negligible in  .
.
In particular, given an efficient adversary \(\mathsf {A}\) breaking the \(\ell \)-IND-ID-lrCCA secure of \(\varPi \) with advantage  , we can construct an adversary \(\mathsf {D}\) breaking the XDLIN assumption with advantage
, we can construct an adversary \(\mathsf {D}\) breaking the XDLIN assumption with advantage  such that
such that

holds for such  , where
, where  and
and  are the number of key generation queries and decapsulation queries made by \(\mathsf {A}\), respectively.
are the number of key generation queries and decapsulation queries made by \(\mathsf {A}\), respectively.
Remark
Our scheme works also on type 1 or 2 bilinear groups.
Proof
Let \(\mathsf {A}\) be an efficient adversary on the IND-ID-lrCCA security of \(\varPi \). Namely,  for infinitely many
for infinitely many  . We will consider a sequence of games, \(\text {Game}_{0},\ldots ,\text {Game}_{9}\) performed by a challenger and \(\mathsf {A}\). At the end of each game, the challenger outputs a bit
. We will consider a sequence of games, \(\text {Game}_{0},\ldots ,\text {Game}_{9}\) performed by a challenger and \(\mathsf {A}\). At the end of each game, the challenger outputs a bit  , which will be described below.
, which will be described below.
Let \(W_i\) be the event such that \(\gamma = 1\) in \(\text {Game}_i\).
-
Game\(_{0}\): This game is the IND-ID-lrCCA game. At the end of the game, the challenger outputs \(\gamma = 1\) if \(b' = b\), otherwise \(\gamma = 0\), where \(b'\) is \(\mathsf {A}\)’s guessing bit of b. Thus,
 (3)
(3)The challenge is \((\mathrm { ct }^*,K_b^*)\) where \(\mathrm { ct }^*= (\left[ \mathbf {c}^* \right] _1,\left[ k_a^* \right] _T,\mathrm { sd }^*)\). We denote by \(\mathbf {r}^*,\alpha ^*,k_s^*\) the corresponding intermediate values. The session key \(K_b^*\) is \(\mathsf {Ext}(\left[ k_s^* \right] _T,\mathrm { sd }^*)\) or random over
 , depending on the bit b.
, depending on the bit b. -
Game\(_{1}\) : This game is the same as \(\text {Game}_{0}\) except that the challenger changes the generation of the public parameter \(\mathrm { pp }\) and the ciphertext \(\mathrm { ct }^*\) as follows.
-
In the setup phase, choose
 uniformly at random. Set
uniformly at random. Set  , sample
, sample  for \(i = 1,\ldots ,m\) and \(j = 1,\ldots ,J\), and set
for \(i = 1,\ldots ,m\) and \(j = 1,\ldots ,J\), and set  . The public parameter is defined as $$\begin{aligned} \mathbf {B}_0&= \mathbf {A} \mathbf {R}_0 + \mathbf {I}_2, \\ \mathbf {B}_i&= \mathbf {A} \mathbf {R}_i + h_i \mathbf {I}_2 \text { for } i=1,\ldots ,m, \\ \mathbf {D}&= \mathbf {A} \mathbf {E}. \end{aligned}$$
. The public parameter is defined as $$\begin{aligned} \mathbf {B}_0&= \mathbf {A} \mathbf {R}_0 + \mathbf {I}_2, \\ \mathbf {B}_i&= \mathbf {A} \mathbf {R}_i + h_i \mathbf {I}_2 \text { for } i=1,\ldots ,m, \\ \mathbf {D}&= \mathbf {A} \mathbf {E}. \end{aligned}$$Output \(\mathrm { pp }= (\left[ \mathbf {A} \right] _1,\left[ \mathbf {B}_0 \right] _1,\left[ \mathbf {B}_1 \right] _1,\ldots ,\left[ \mathbf {B}_m \right] _1,\left[ \mathbf {D} \right] _1)\). The challenger holds \(\left( a_1,a_2,\mathbf {R}_0,\mathbf {R}_1,\ldots ,\mathbf {R}_m,\mathbf {E}\right) \) as a master key in this game.
In \(\text {Game}_{1}\), the \(\mathbf {F}_\mathrm { id }\) for
 can be written by
can be written by 
where \(\mathbf {R}_\mathrm { id }= \mathbf {R}_0 + \sum _{i = 1}^{m} \mathrm { id }[i] \mathbf {R}_i\) and \(\beta _h(\mathrm { id }) = 1 + \sum _{i = 1}^{m} \mathrm { id }[i] h_i\).
-
In the challenge phase, the challenger computes \(\left[ k_a^* \right] _T\) and \(\left[ k_s^* \right] _T\) as follows:
$$\begin{aligned} \left[ k_a^* \right] _T&= \left[ {\mathbf {c}^*}^\top \right] _1 \circ \left[ \mathbf {S}^*\left( {\begin{matrix} 1 \\ \alpha ^*\end{matrix}}\right) \right] _2, \\ \left[ k_s^* \right] _T&= \left[ {\mathbf {c}^*}^\top \right] _1 \circ \left[ \mathbf {S}^*\left( {\begin{matrix} 1 \\ 0 \end{matrix}}\right) \right] _2, \end{aligned}$$where \(\left[ \mathbf {S}^* \right] _2\) is the secret key for the \(\mathrm { id }^*\).
Note that this change does not affect the distributions of the public parameter \(\mathrm { pp }\) and the challenge \((\mathrm { ct }^*,K_b^*)\). Therefore, we have
$$\begin{aligned} \Pr [W_{0}] = \Pr [W_{1}]. \end{aligned}$$(4) -
-
Game\(_{2}\): Let \(\mathrm { id }^*\) be the challenge identity and \(\mathrm { id }_1,\ldots ,\mathrm { id }_Q\) be identities that \(\mathsf {A}\) queries in the key generation query and the decapsulation query, where
 . Define the event $$\begin{aligned} \mathcal {FORCEDABORT}: \bigvee _{i=1}^{Q}(\beta _h(\mathrm { id }_i) = 0) \vee \left( \beta _h(\mathrm { id }^*) \ne 0\right) , \end{aligned}$$
. Define the event $$\begin{aligned} \mathcal {FORCEDABORT}: \bigvee _{i=1}^{Q}(\beta _h(\mathrm { id }_i) = 0) \vee \left( \beta _h(\mathrm { id }^*) \ne 0\right) , \end{aligned}$$and

for \(\mathbf {id}_\mathsf {A}= (\mathrm { id }_1,\ldots ,\mathrm { id }_Q,\mathrm { id }^*)\), where the probability is taken over the choice of h. By Lemma 2, this probability has a minimum value greater than 0. Let \(\eta _\mathrm {low}\) be the minimum value of \(\eta (\mathbf {id}_\mathsf {A})\).
In the guess phase, \(\mathsf {A}\) outputs its guess
 for b. The challenger checks the event \(\mathcal {FORCEDABORT}\) occurs for \(\mathbf {id}_\mathsf {A}\). If yes, the challenger aborts the game and outputs a fresh random bit
for b. The challenger checks the event \(\mathcal {FORCEDABORT}\) occurs for \(\mathbf {id}_\mathsf {A}\). If yes, the challenger aborts the game and outputs a fresh random bit  . Otherwise, the challenger first estimates the probability \(\eta (\mathbf {id}_\mathsf {A})\) by sampling \((h_1,\ldots ,h_m)\) sufficiently large amount of times. Let \(\eta '(\mathbf {id}_\mathsf {A})\) be the estimation of \(\eta (\mathbf {id}_\mathsf {A})\). Depending on the estimate \(\eta '(\mathbf {id}_\mathsf {A})\) the challenger decides \(\gamma \) as follows:
. Otherwise, the challenger first estimates the probability \(\eta (\mathbf {id}_\mathsf {A})\) by sampling \((h_1,\ldots ,h_m)\) sufficiently large amount of times. Let \(\eta '(\mathbf {id}_\mathsf {A})\) be the estimation of \(\eta (\mathbf {id}_\mathsf {A})\). Depending on the estimate \(\eta '(\mathbf {id}_\mathsf {A})\) the challenger decides \(\gamma \) as follows:-
Case \(\eta '(\mathbf {id}_\mathsf {A}) \le \eta _\mathrm {low}\): The challenger outputs \(\gamma = [b=b']\).
-
Case \(\eta '(\mathbf {id}_\mathsf {A}) > \eta _\mathrm {low}\): With probability \(\eta _\mathrm {low}/\eta '(\mathbf {id}_\mathsf {A})\) the challenger outputs \(\gamma = [b=b']\). With probability \(1-\eta _\mathrm {low}/\eta '(\mathbf {id}_\mathsf {A})\) the challenger aborts the game and outputs a fresh random bit
 .
.
Lemma 4 in Appendix will show that

From Lemma 2, we have
 (5)
(5) -
-
Game\(_{3}\): In \(\text {Game}_{3}\), we make the following changes to the experiment. When \(\mathsf {A}\) queries an identity \(\mathrm { id }\) to the key generation oracle, the challenger checks whether \(\beta _h(\mathrm { id }) = 0\). If so, the challenger immediately aborts and returns a fresh random bit \(\gamma \). When \(\mathsf {A}\) outputs \(\mathrm { id }^*\) as a challenge identity, if \(\beta _h(\mathrm { id }^*) \ne 0\) the challenger immediately aborts and returns a fresh random bit \(\gamma \). Clearly, the above changes do not affect \(\mathsf {A}\)’s environment if \(\mathcal {FORCED}\mathcal {ABORT}\) dose not occur. Then, we have
$$\begin{aligned} \Pr [W_{2}] = \Pr [W_{3}]. \end{aligned}$$(6) -
Game\(_{4}\): This game is the same as \(\text {Game}_{3}\) except that the challenger changes the generation of the secret key \(\mathrm { sk }_\mathrm { id }= \left[ \mathbf {S}_\mathrm { id } \right] _2\) for \(\mathrm { id }\) as follows.
-
Case \(\beta _h(\mathrm { id }) \ne 0\): The challenger chooses
 , computes
, computes  satisfying $$\begin{aligned} \beta _h(\mathrm { id }) \mathbf {W}' = -\mathbf {A}\mathbf {W} + \mathbf {A}\mathbf {E}, \end{aligned}$$(7)
satisfying $$\begin{aligned} \beta _h(\mathrm { id }) \mathbf {W}' = -\mathbf {A}\mathbf {W} + \mathbf {A}\mathbf {E}, \end{aligned}$$(7)and sets
$$ \mathbf {S}_\mathrm { id }= \begin{pmatrix} \mathbf {W} - \mathbf {R}_\mathrm { id }\mathbf {W}' \\ \mathbf {W}' \end{pmatrix}. $$This \(\mathbf {S}_\mathrm { id }\) satisfies Eq. (1) because

Further, the above \(\mathbf {S}_\mathrm { id }\) has the same distribution as the secret key generated by
 , because 6 elements are chosen at random and the remaining are determined uniquely by Eq. (7).
, because 6 elements are chosen at random and the remaining are determined uniquely by Eq. (7). -
Case \(\beta _h(\mathrm { id }) = 0\): The challenger computes
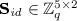 such that
such that 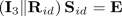 (8)
(8)as follows. The challenger computes
 where
where  , and sets $$ \mathbf {S}_{\mathrm { id }} = \begin{pmatrix} \mathbf {S}'' \\ \mathbf {S}' \end{pmatrix}. $$
, and sets $$ \mathbf {S}_{\mathrm { id }} = \begin{pmatrix} \mathbf {S}'' \\ \mathbf {S}' \end{pmatrix}. $$It is easy to see that \(\left[ \mathbf {S}_\mathrm { id } \right] _2\) is the correct secret key for \(\mathrm { id }\) by multiplying \(\mathbf {A}\) from the left to both hand sides of Eq. (8).
We show that the above \(\mathbf {S}_\mathrm { id }\) has the same distribution of the original
 as seen from \(\mathsf {A}\). Now, \(\mathbf {S}'\) is chosen randomly. Hence, we need to show that 2 elements in \(\mathbf {S}''\) e.g. \(\mathbf {e} \mathbf {S}''\) are also random where
as seen from \(\mathsf {A}\). Now, \(\mathbf {S}'\) is chosen randomly. Hence, we need to show that 2 elements in \(\mathbf {S}''\) e.g. \(\mathbf {e} \mathbf {S}''\) are also random where  . It suffices to prove
. It suffices to prove  is random even given \(\mathbf {A}\) and \(\mathbf {D} = \mathbf {A}\mathbf {E}\), since \(\mathbf {e} \mathbf {S}''= \mathbf {e} \mathbf {E} - \mathbf {e} \mathbf {R}_\mathrm { id }\mathbf {S}'\). It is easy to see that $$\begin{aligned} \begin{pmatrix} \mathbf {D} \\ \mathbf {u} \end{pmatrix} = \underbrace{\begin{pmatrix} \mathbf {A} \\ \mathbf {e} \end{pmatrix}}_{\mathbf {A}'} \mathbf {E}. \end{aligned}$$(9)
is random even given \(\mathbf {A}\) and \(\mathbf {D} = \mathbf {A}\mathbf {E}\), since \(\mathbf {e} \mathbf {S}''= \mathbf {e} \mathbf {E} - \mathbf {e} \mathbf {R}_\mathrm { id }\mathbf {S}'\). It is easy to see that $$\begin{aligned} \begin{pmatrix} \mathbf {D} \\ \mathbf {u} \end{pmatrix} = \underbrace{\begin{pmatrix} \mathbf {A} \\ \mathbf {e} \end{pmatrix}}_{\mathbf {A}'} \mathbf {E}. \end{aligned}$$(9)Because \(\mathbf {A}'\) is of full rank, the distribution of \(\mathbf {u}\) is random and independent from \(\mathbf {D}\) that \(\mathsf {A}\) knows. Hence, \(\mathbf {e} \mathbf {S}''\) is also random as seen from \(\mathsf {A}\).
Note that this change dose not affect the distribution of the secret key \(\mathrm { sk }_\mathrm { id }\) for \(\mathrm { id }\). Therefore, we have
$$\begin{aligned} \Pr [W_{3}] = \Pr [W_{4}]. \end{aligned}$$(10) -
-
Game\(_{5}\): This game is the same as \(\text {Game}_{4}\) except that \(\left[ \mathbf {c}^* \right] _1\) in the challenge is randomly chosen from
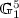 . Furthermore, the challenger chooses
. Furthermore, the challenger chooses  ,
,  , and computes
, and computes  at the beginning of the game. As we will show in Lemma 6, we have that there exists a PPT adversary \(\mathsf {D}\) such that
at the beginning of the game. As we will show in Lemma 6, we have that there exists a PPT adversary \(\mathsf {D}\) such that  (11)
(11)The decapsulation oracle in this game is depicted in Fig. 1. We define that a ciphertext \(\left[ \mathbf {c} \right] _1\) is valid for \(\mathrm { id }\) if there exists
 such that \(\left[ \mathbf {c} \right] _1 = \left[ \mathbf {F}^\top _\mathrm { id }\mathbf {r} \right] _1\). With \(\mathrm { pp }\) and \(\mathrm { mk }\), we can efficiently check whether \(\left[ \mathbf {c} \right] _1 = \left[ (c_1,c_2,c_3,c_4,c_5)^\top \right] _1\) is valid for \(\mathrm { id }\) by simply verifying $$ \left[ (c_3,c_4,c_5) \right] _1 = \left[ (c_1,c_2) \begin{pmatrix} a_1^{-1} &{} 0 \\ 0 &{} a_2^{-1} \end{pmatrix}\mathbf {F}'_{\mathrm { id }} \right] _1. $$
such that \(\left[ \mathbf {c} \right] _1 = \left[ \mathbf {F}^\top _\mathrm { id }\mathbf {r} \right] _1\). With \(\mathrm { pp }\) and \(\mathrm { mk }\), we can efficiently check whether \(\left[ \mathbf {c} \right] _1 = \left[ (c_1,c_2,c_3,c_4,c_5)^\top \right] _1\) is valid for \(\mathrm { id }\) by simply verifying $$ \left[ (c_3,c_4,c_5) \right] _1 = \left[ (c_1,c_2) \begin{pmatrix} a_1^{-1} &{} 0 \\ 0 &{} a_2^{-1} \end{pmatrix}\mathbf {F}'_{\mathrm { id }} \right] _1. $$ -
Game\(_{6}\): In this game, at line 6 in Fig. 1, the challenger returns \(\bot \). Then we have

Therefore, we obtain
 (12)
(12) -
Game\(_{7}\): In this game, at line 13 in Fig. 1, the challenger returns \(\bot \). As we will show in Lemma 7, we have
 (13)
(13) -
Game\(_{8}\): In this game, at line 8 in Fig. 1, the challenger returns \(\bot \). \((\left[ \mathbf {c} \right] _1,\mathrm { sd }) = (\left[ \mathbf {c}^* \right] _1,\mathrm { sd }^*)\) holds with probability
 before the challenge phase, since \(\mathsf {A}\) knows nothing about \((\mathbf {c}^*,\mathrm { sd }^*)\) chosen randomly. On the other hand, after the challenge phase \((\mathrm { id }^*,\mathrm { ct }^*= (\left[ \mathbf {c}^* \right] _1,\left[ k_a^* \right] _T,\mathrm { sd }^*))\) was already announced to \(\mathsf {A}\), any adversarial decapsulation query \((\mathrm { id }^*,(\left[ \mathbf {c}^* \right] _1,\left[ k_a \right] _T,\mathrm { sd }^*))\) with \(\left[ t \right] _T=\left[ k_a \right] _T\) is equal to \((\mathrm { id }^*,\mathrm { ct }^*)\). Hence, such adversarial decapsulation query is forbidden by the restriction of \(\mathrm {IND\text {-}ID\text {-}lrCCA}\) game. Thus we have
before the challenge phase, since \(\mathsf {A}\) knows nothing about \((\mathbf {c}^*,\mathrm { sd }^*)\) chosen randomly. On the other hand, after the challenge phase \((\mathrm { id }^*,\mathrm { ct }^*= (\left[ \mathbf {c}^* \right] _1,\left[ k_a^* \right] _T,\mathrm { sd }^*))\) was already announced to \(\mathsf {A}\), any adversarial decapsulation query \((\mathrm { id }^*,(\left[ \mathbf {c}^* \right] _1,\left[ k_a \right] _T,\mathrm { sd }^*))\) with \(\left[ t \right] _T=\left[ k_a \right] _T\) is equal to \((\mathrm { id }^*,\mathrm { ct }^*)\). Hence, such adversarial decapsulation query is forbidden by the restriction of \(\mathrm {IND\text {-}ID\text {-}lrCCA}\) game. Thus we have  (14)
(14) -
Game\(_{9}\): In this game, \(K_0^*\) is chosen at random from
 instead of using \(\mathsf {Ext}(\left[ k_s^* \right] _T, \mathrm { sd }^*)\). As we will show in Lemma 8, we have
instead of using \(\mathsf {Ext}(\left[ k_s^* \right] _T, \mathrm { sd }^*)\). As we will show in Lemma 8, we have  (15)
(15)In \(\text {Game}_{9}\), \(\mathsf {A}\) does not get any information about bit b because both \(K_0^*\) and \(K_1^*\) are random. Hence, we have
$$\begin{aligned} \Pr [W_{9}] = \frac{1}{2}. \end{aligned}$$(16)
From Eqs. (3)–(6) and (10)–(16), we have shown that given an adversary \(\mathsf {A}\) with advantage \(\epsilon _\mathsf {A}\), there exists an adversary \(\mathsf {D}\) with  such that
such that

Therefore, we have

The right side of the above inequality is non-negligible, since \(\epsilon _\mathsf {A}\) and  are non-negligible in
are non-negligible in  , other terms are negligible in
, other terms are negligible in  . Hence, this contradicts the XDLIN assumption. This completes the proof of Theorem 1. \(\square \)
. Hence, this contradicts the XDLIN assumption. This completes the proof of Theorem 1. \(\square \)
6 Conclusion
In this paper, we proposed the first CCA-secure leakage-resilient IB-KEM scheme which does not depend on \(\mathtt {q}\)-type assumptions. More precisely, it is secure under the DLIN assumption for symmetric bilinear groups and under the XDLIN assumption for asymmetric bilinear groups. A CCA-secure leakage-resilient IBE scheme is obtained by combining our IB-KEM with any CCA-secure symmetric-key encryption scheme (which does not need to be leakage-resilient). However, the leakage rate of our scheme is smaller than previous works [3, 24, 30].
References
Abe, M., Chase, M., David, B., Kohlweiss, M., Nishimaki, R., Ohkubo, M.: Constant-size structure-preserving signatures: generic constructions and simple assumptions. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 4–24. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_3
Akavia, A., Goldwasser, S., Vaikuntanathan, V.: Simultaneous hardcore bits and cryptography against memory attacks. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 474–495. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_28
Alwen, J., Dodis, Y., Naor, M., Segev, G., Walfish, S., Wichs, D.: Public-key encryption in the bounded-retrieval model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 113–134. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_6
Alwen, J., Dodis, Y., Wichs, D.: Leakage-resilient public-key cryptography in the bounded-retrieval model. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 36–54. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_3
Brakerski, Z., Kalai, Y.T., Katz, J., Vaikuntanathan, V.: Overcoming the hole in the bucket: public-key cryptography resilient to continual memory leakage. In: FOCS, pp. 501–510 (2010)
Brier, E., Clavier, C., Olivier, F.: Correlation power analysis with a leakage model. In: Joye, M., Quisquater, J.-J. (eds.) CHES 2004. LNCS, vol. 3156, pp. 16–29. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28632-5_2
Cheon, J.H.: Security analysis of the strong Diffie-Hellman problem. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 1–11. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_1
Chow, S.S., Dodis, Y., Rouselakis, Y., Waters, B.: Practical leakage-resilient identity-based encryption from simple assumptions. In: ACM CCS, pp. 152–161 (2010)
Dodis, Y., Haralambiev, K., López-Alt, A., Wichs, D.: Cryptography against continuous memory attacks. In: FOCS, pp. 511–520 (2010)
Dodis, Y., Kalai, Y.T., Lovett, S.: On cryptography with auxiliary input. In: STOC, pp. 621–630 (2009)
Dodis, Y., Ostrovsky, R., Reyzin, L., Smith, A.: Fuzzy extractors: how to generate strong keys from biometrics and other noisy data. SIAM J. Comput. 38(1), 97–139 (2008)
Escala, A., Herold, G., Kiltz, E., Ràfols, C., Villar, J.: An algebraic framework for Diffie-Hellman assumptions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 129–147. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_8
Galbraith, S.D., Paterson, K.G., Smart, N.P.: Pairings for cryptographers. Discret. Appl. Math. 156(16), 3113–3121 (2008)
Gandolfi, K., Mourtel, C., Olivier, F.: Electromagnetic analysis: concrete results. In: Koç, Ç.K., Naccache, D., Paar, C. (eds.) CHES 2001. LNCS, vol. 2162, pp. 251–261. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44709-1_21
Halderman, J.A., et al.: Lest we remember: cold boot attacks on encryption keys. In: USENIX, pp. 45–60 (2008)
Halevi, S., Lin, H.: After-the-fact leakage in public-key encryption. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 107–124. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_8
Hofheinz, D., Kiltz, E.: Programmable hash functions and their applications. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 21–38. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_2
Katz, J., Vaikuntanathan, V.: Signature schemes with bounded leakage resilience. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 703–720. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_41
Kiltz, E., Galindo, D.: Direct chosen-ciphertext secure identity-based key encapsulation without random oracles. Theor. Comput. Sci. 410(47–49), 5093–5111 (2009)
Kocher, P., Jaffe, J., Jun, B.: Differential power analysis. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 388–397. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_25
Kurosawa, K., Trieu Phong, L.: Leakage resilient IBE and IPE under the DLIN assumption. In: Jacobson, M., Locasto, M., Mohassel, P., Safavi-Naini, R. (eds.) ACNS 2013. LNCS, vol. 7954, pp. 487–501. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38980-1_31
Lewko, A., Rouselakis, Y., Waters, B.: Achieving leakage resilience through dual system encryption. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 70–88. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_6
Lewko, A., Waters, B.: New techniques for dual system encryption and fully secure HIBE with short ciphertexts. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 455–479. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_27
Li, J., Teng, M., Zhang, Y., Yu, Q.: A leakage-resilient CCA-secure identity-based encryption scheme. Comput. J. 59(7), 1066–1075 (2016)
Micali, S., Reyzin, L.: Physically observable cryptography. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 278–296. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_16
Naor, M., Segev, G.: Public-key cryptosystems resilient to key leakage. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 18–35. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_2
Okamoto, T., Takashima, K.: Fully secure functional encryption with general relations from the decisional linear assumption. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 191–208. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_11
Qin, B., Chen, K., Liu, S.: Efficient chosen-ciphertext secure public-key encryption scheme with high leakage-resilience. IET Inf. Secur. 9(1), 32–42 (2015)
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-39568-7_5
Sun, S.-F., Gu, D., Liu, S.: Efficient leakage-resilient identity-based encryption with CCA security. In: Cao, Z., Zhang, F. (eds.) Pairing 2013. LNCS, vol. 8365, pp. 149–167. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-04873-4_9
Tomida, J., Abe, M., Okamoto, T.: Efficient functional encryption for inner-product values with full-hiding security. In: Bishop, M., Nascimento, A.C.A. (eds.) ISC 2016. LNCS, vol. 9866, pp. 408–425. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-45871-7_24
Yamada, S.: Adaptively secure identity-based encryption from lattices with asymptotically shorter public parameters. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 32–62. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_2
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Proof of Lemmas
A Proof of Lemmas
To complete the proof of Theorem 1, we prove Lemmas 4, 6, 7, and 8.
Lemma 4

We introduce a lemma before proving Lemma 4.
Lemma 5
([19, Claim 6.7]). Let \(0< \rho < 1\) be a real. For a sequence of identities \(\mathbf {id}\in (\mathcal {ID})^{Q+1}\), and \(\mathcal {ABORT}\) be the event that the challenger aborts with added rules in \(\text {Game}_{2}\). For any fixed \(\mathbf {id}\),
Proof
(of Lemma 4). For a sequence of identities \(\mathbf {id}\in (\mathcal {ID})^{Q+1}\), we define \(\mathcal {Q}(\mathbf {id})\) as the event that \(\mathsf {A}\) uses the last entry in \(\mathbf {id}\) as the challenge and makes key generation queries and decapsulation queries for the remaining identities. Then, we have \(\sum _{\mathbf {id}\in (\mathcal {ID})^{Q+1}}\Pr [\mathcal {Q}(\mathbf {id})] = 1\). Let \(\delta (\mathbf {id}) = \Pr [\lnot \mathcal {ABORT}]\), and \(\delta _\mathrm {low}\) and \(\delta _\mathrm {up}\) be reals such that \(\delta _\mathrm {low}\le \delta (\mathbf {id}) \le \delta _\mathrm {up}\). Then, we have

The last inequality above follows from Lemma 3, since we have

and

From Lemma 5, we have \(\delta _\mathrm {up}- \delta _\mathrm {low}\le \eta _\mathrm {low}\rho /2\). Therefore, defining  , we obtain
, we obtain

\(\square \)
Lemma 6
For any PPT algorithm \(\mathsf {A}\), there exists a PPT algorithm \(\mathsf {D}\) such that

Proof
Let  be an XDLIN instance, where
be an XDLIN instance, where
Then, we build a PPT algorithm \(\mathsf {D}\) with input \((\left[ \mathbf {A} \right] _1,\left[ \mathbf {A} \right] _2,\left[ \mathbf {y} \right] _1)\) that simulates the IND-ID-lrCCA game with \(\mathsf {A}\) as follows.
-
Setup phase: \(\mathsf {D}\) generates \(\mathrm { pp }= \left( \left[ \mathbf {A} \right] _1,\left[ \mathbf {B}_0 \right] _1,\left[ \mathbf {B}_1 \right] _1,\ldots ,\left[ \mathbf {B}_m \right] _1,\left[ \mathbf {D} \right] _1\right) \) as same as the challenger, except that \(\mathsf {D}\) computes
$$\begin{aligned} \left[ \mathbf {B}_0 \right] _1&= \left[ \mathbf {A} \mathbf {R}_0 + \mathbf {I}_2 \right] _1, \\ \left[ \mathbf {B}_i \right] _1&= \left[ \mathbf {A} \mathbf {R}_i + h_i \mathbf {I}_2 \right] _1 \text { for } i = 1,\ldots ,m, \\ \left[ \mathbf {D} \right] _1&= \left[ \mathbf {A} \mathbf {E} \right] _1. \end{aligned}$$Finally \(\mathsf {D}\) sends \(\mathrm { pp }\) to \(\mathsf {A}\).
-
Query phase: \(\mathsf {D}\) answers for each query from \(\mathsf {A}\) as follows.
-
Key Generation query \(\mathrm { id }\). Assume that \(\beta _h(\mathrm { id }) \ne 0\). \(\mathsf {D}\) chooses
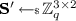 at random, computes
at random, computes 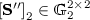 such that \(\left[ \beta _h(\mathrm { id }) \mathbf {S}'' \right] _2 = \left[ -\mathbf {A}\mathbf {S}' + \mathbf {A}\mathbf {E} \right] _2\), sets $$ \left[ \mathbf {S}_\mathrm { id } \right] _2 = \left[ \begin{pmatrix} \mathbf {S}' - \mathbf {R}_\mathrm { id }\mathbf {S}'' \\ \mathbf {S}' \end{pmatrix} \right] _2, $$
such that \(\left[ \beta _h(\mathrm { id }) \mathbf {S}'' \right] _2 = \left[ -\mathbf {A}\mathbf {S}' + \mathbf {A}\mathbf {E} \right] _2\), sets $$ \left[ \mathbf {S}_\mathrm { id } \right] _2 = \left[ \begin{pmatrix} \mathbf {S}' - \mathbf {R}_\mathrm { id }\mathbf {S}'' \\ \mathbf {S}' \end{pmatrix} \right] _2, $$and returns \(\mathrm { sk }_\mathrm { id }= \left[ \mathbf {S}_\mathrm { id } \right] _2\) to \(\mathsf {A}\).
-
Leakage query \((\mathrm { id }, f)\) and decapsulation query \((\mathrm { id }, \mathrm { ct })\). If \(\beta _h(\mathrm { id }) \ne 0\), then \(\mathsf {D}\) can generate \(\mathrm { sk }_\mathrm { id }\) as above. Furthermore, even in that case that \(\beta _h(\mathrm { id }) = 0\) (i.e., \(\mathrm { id }=\mathrm { id }^*\)), \(\mathsf {D}\) can generate \(\mathrm { sk }_\mathrm { id }\) by computing \(\mathbf {S}_\mathrm { id }\) such that
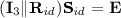 . Thus, \(\mathsf {D}\) can answer \(f(\mathrm { sk }_\mathrm { id })\) and \(\mathsf {Decap}(\mathrm { sk }_\mathrm { id }, \mathrm { ct })\) for any identity.
. Thus, \(\mathsf {D}\) can answer \(f(\mathrm { sk }_\mathrm { id })\) and \(\mathsf {Decap}(\mathrm { sk }_\mathrm { id }, \mathrm { ct })\) for any identity.
-
-
Challenge phase: \(\mathsf {D}\) generates the challenge \((\mathrm { ct }^*,K_b^*) = \left( (\left[ \mathbf {c}^* \right] _1,\left[ k_a \right] _T,\mathrm { sd }),K_b^*\right) \) as same as the challenger, except that \(\mathsf {D}\) computes
$$ \left[ \mathbf {c}^* \right] _1 = \left[ \begin{pmatrix} \mathbf {y} \\ \mathbf {R}_{\mathrm { id }^*}^\top \mathbf {y} \end{pmatrix} \right] _1 $$instead of \(\left[ \mathbf {c}^* \right] _1 = \left[ \mathbf {F}_{\mathrm { id }^*}^\top \mathbf {r} \right] _1\). Then, \(\mathsf {D}\) returns \((\mathrm { ct }^*,K_b^*)\) to \(\mathsf {A}\).
Finally, \(\mathsf {D}\) outputs \(\gamma = [b = b']\) where  is the output of \(\mathsf {A}\).
is the output of \(\mathsf {A}\).
We will show that the distribution of \((\mathrm { ct }^*, K_b^*)\) is the same as the challenge in \(\text {Game}_{4}\) if \(\mathbf {y} = \mathbf {A}^\top \mathbf {r}^*\), while if \(\mathbf {y}\) is a random it is the same as that in \(\text {Game}_{5}\) with overwhelming probability. First suppose that \(\mathbf {y} = \mathbf {A}^\top \mathbf {r}^*\). In this case,

showing that \((\mathrm { ct }^*, K_b^*)\) is the challenge in \(\text {Game}_{4}\). Next suppose that \(\mathbf {y}\) is random in  . It suffices to prove that
. It suffices to prove that  is also random in
is also random in  even given \(\mathbf {A}\),
even given \(\mathbf {A}\),  , and \(\mathbf {y}\). It is easy to see that
, and \(\mathbf {y}\). It is easy to see that
Therefore, \(\mathbf {z}\) is random because \(\mathbf {V}\) is of full rank with probability \(1-1/q\). Hence, \(\left[ \mathbf {c}^* \right] _1\) is random as expected.
Thus, \(\text {Game}_{4}\) and \(\text {Game}_{5}\) are indistinguishable under the XDLIN assumption, so that we have Eq. (17). \(\square \)
Lemma 7

Proof
We assume that all decapsulation queries are made after the challenge phase, but a similar (but slight simpler) argument can be used if \(\mathsf {A}\) makes queries before the challenge phase. Suppose that \((\mathrm { id }^*,\mathrm { ct }= (\left[ \mathbf {c} \right] _1,\left[ t \right] _T,\mathrm { sd }))\) is the first decapsulation query such that \(\mathrm { id }= \mathrm { id }^*\) and the condition at line 13 in Fig. 1 is evaluated. Let  , where
, where  . Then, we have
. Then, we have

where \(k_a\) is computed at line 11 in Fig. 1. From the supposition, we can assume that \(\alpha \ne \alpha ^*\), \(\mathbf {c}^*\) is chosen uniformly at random, and \(\left[ \mathbf {c} \right] _1\) is invalid for \(\mathrm { id }^*\). Hence, the matrix \(\mathbf {M}\) is of full rank with probability at least \(1-1/q\), that implies that the distribution of \(k_a\) is random and independent from \(\mathbf {D}\) and \(k_a^*\). In addition to \(\mathbf {D}\) and \(k_a^*\), \(\mathsf {A}\) knows at most \(\ell \) bit leakage  and n bit challenge session key \(K_b^*\) that is probable to provide information on the value of \(k_a\) to \(\mathsf {A}\). Let \(K_a\), F, and I denote random variables induced by \(k_a\),
and n bit challenge session key \(K_b^*\) that is probable to provide information on the value of \(k_a\) to \(\mathsf {A}\). Let \(K_a\), F, and I denote random variables induced by \(k_a\),  , and \(({\mathbf D}, k_a^*)\), respectively. Given \(k_a\),
, and \(({\mathbf D}, k_a^*)\), respectively. Given \(k_a\),  , and \(({\mathbf D}, k_a^*)\) that \(\mathsf {A}\) knows, we have
, and \(({\mathbf D}, k_a^*)\) that \(\mathsf {A}\) knows, we have
from Lemma 1 and the above discussion. Thus, for any \(k_a\), we have \(\Pr [K_a=k_a] \le 2^{\ell +n}/q\). Therefore, in the first evaluation of line 11, the condition \(t=k_a\) is satisfied with probability at most \({2^{\ell +n}}/{q}\). Now assuming \(t=k_a\) is not satisfied, the number of possible \(k_a\) decreases one. So, in the i-th evaluation of line 11, the probability that \(t=k_a\) holds is at most \(2^{\ell +n}/(q-i+1)\), in the case that \(t=k_a\) is not satisfied in all previous evaluations. From the above discussion, we have

From Eq. (2), we obtain Eq. (18). \(\square \)
Lemma 8

Proof
In \(\text {Game}_{9}\), the challenger returns \(\bot \) to \(\mathsf {A}\) at line 13 in Fig. 1. Hence, \(\mathsf {A}\) does not learn any information on \(k_s^*\) via the decapsulation oracle, since \(\mathsf {A}\) can only get decapsulation results of valid ciphertexts. Now, \(\mathsf {A}\) knows \(\mathbf {D}\), \(k_a^*\), and  as information about \(k_s^*\). Then, we show that the min-entropy of \(k_s^*\) is at least \(\log _2{q} - \ell \) with probability at least \(1-1/q\).
as information about \(k_s^*\). Then, we show that the min-entropy of \(k_s^*\) is at least \(\log _2{q} - \ell \) with probability at least \(1-1/q\).
First, we have
and then

The matrix \(\mathbf {N}\) is of full rank with probability at least \(1-1/q\), since \(\alpha ^*\ne 0\) and \(\left[ \mathbf {c}^* \right] _1\) is uniformly at random. Then, the distribution of \(k_s^*\) is random and independent from \(\mathbf {D}\) and \(k_a^*\). In addition to \(\mathbf {D}\) and \(k_a^*\), \(\mathsf {A}\) knows at most \(\ell \) bit leakage  that is probable to provide information on the value of \(k_s^*\) to \(\mathsf {A}\). Let \(K_a\), D, and F denote random variables induced by \(k_s^*\), \((\mathbf {D},k_a^*)\), and
that is probable to provide information on the value of \(k_s^*\) to \(\mathsf {A}\). Let \(K_a\), D, and F denote random variables induced by \(k_s^*\), \((\mathbf {D},k_a^*)\), and  respectively. Given \(k_s^*\), \((\mathbf {D},k_a^*)\), and
respectively. Given \(k_s^*\), \((\mathbf {D},k_a^*)\), and  that \(\mathsf {A}\) knows, we have
that \(\mathsf {A}\) knows, we have
from Lemma 1 and the discussion when ignoring  . Hence \(\mathsf {Ext}(K_s^*, \mathrm { sd }^*)\) is statistically indistinguishable from an n bits random string because \(\mathsf {Ext}\) is a \((\log _2{q} - \ell )\)-randomness extractor. Therefore, we have Eq. (19). \(\square \)
. Hence \(\mathsf {Ext}(K_s^*, \mathrm { sd }^*)\) is statistically indistinguishable from an n bits random string because \(\mathsf {Ext}\) is a \((\log _2{q} - \ell )\)-randomness extractor. Therefore, we have Eq. (19). \(\square \)
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Tomita, T., Ogata, W., Kurosawa, K. (2019). CCA-Secure Leakage-Resilient Identity-Based Key-Encapsulation from Simple (Not \(\mathtt {q}\)-type) Assumptions. In: Attrapadung, N., Yagi, T. (eds) Advances in Information and Computer Security. IWSEC 2019. Lecture Notes in Computer Science(), vol 11689. Springer, Cham. https://doi.org/10.1007/978-3-030-26834-3_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-26834-3_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-26833-6
Online ISBN: 978-3-030-26834-3
eBook Packages: Computer ScienceComputer Science (R0)




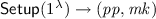 . The setup algorithm takes as input the security parameter
. The setup algorithm takes as input the security parameter  , outputs a public parameter
, outputs a public parameter  . The key generation algorithm takes as input the master key
. The key generation algorithm takes as input the master key  to
to  is an efficiently computable function. The challenger returns
is an efficiently computable function. The challenger returns  . The challenger runs
. The challenger runs  . Then, he sends
. Then, he sends  .
. : Choose
: Choose  and
and  uniformly at random and set
uniformly at random and set 
 , let
, let 
 : Compute a random matrix
: Compute a random matrix 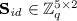 such that
such that 
 at random, compute
at random, compute 
 and
and  at random, compute
at random, compute 


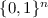 , depending on the bit b.
, depending on the bit b. uniformly at random. Set
uniformly at random. Set  , sample
, sample  for
for  . The public parameter is defined as
. The public parameter is defined as 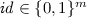 can be written by
can be written by 
 . Define the event
. Define the event 
 for b. The challenger checks the event
for b. The challenger checks the event  . Otherwise, the challenger first estimates the probability
. Otherwise, the challenger first estimates the probability  .
.

 , computes
, computes  satisfying
satisfying 
 , because 6 elements are chosen at random and the remaining are determined uniquely by Eq. (
, because 6 elements are chosen at random and the remaining are determined uniquely by Eq. (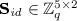 such that
such that 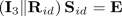
 where
where  , and sets
, and sets  as seen from
as seen from  . It suffices to prove
. It suffices to prove  is random even given
is random even given 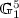 . Furthermore, the challenger chooses
. Furthermore, the challenger chooses  ,
,  , and computes
, and computes  at the beginning of the game. As we will show in Lemma
at the beginning of the game. As we will show in Lemma 
 such that
such that 



 before the challenge phase, since
before the challenge phase, since 
 instead of using
instead of using 
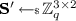 at random, computes
at random, computes 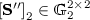 such that
such that 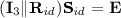 . Thus,
. Thus,