Second Order Differential Evolution for Constrained Optimization

Abstract

In this paper, second order differential evolution (SODE) algorithm is considered to solve the constrained optimization problems. After offspring are generated by the second order differential evolution, the ε constrained method is chosen for selection in this paper. In order to show that second order differential vector is better than differential vector in solving constrained optimization problems, differential evolution (DE) with the ε constrained method is used for performance comparison. The experiments on 12 test functions from IEEE CEC 2006 demonstrate that second order differential evolution shows better or at least competitive performance against DE when dealing with constrained optimization problems.

1 Introduction

Constrained optimization problems (COPs) are mathematical programming problems frequently encountered in the disciplines of science and engineering application. Evolutionary algorithm is usually used to deal with constrained optimization problems due to its excellent performance, but it is essentially an unconstrained optimization evolutionary algorithm, which must be combined with constraint handing technique to solve the constrained optimization problem. Evolutionary algorithm and an appropriate constraint handing technique are combined to form a complete constrained evolutionary optimization algorithm. Among all the evolutionary algorithms, differential evolution (DE) [1] is one of the most important problem solvers.

Differential evolution was introduced by Price and Storn in 1997 [1], and has numerous attractive advantages. First of all, its structure is simple. In addition, it includes few control parameters. More importantly, its search ability, such as, higher search efficiency, higher robustness and lower computational complexity, has been demonstrated in many real-world applications [2, 3].

Due to the above advantages, DE has been frequently applied to solve COPs. Many DE variants optimization have been tailored to tackle COPs [4]. However, few current studies investigate second order differential evolution (SODE) [5] for constrained optimization. To illustrate that second order differential vector is better than differential vector in solving constrained optimization problems, the ε constrained second order differential evolution (εSODE) is proposed in this paper.

The rest of the paper is organized as follows. In Sect. 2 some preliminary knowledge are presented. The proposed εSODE is shown in Sect. 3. The experimental and analytic results are presented in Sect. 4, and the last Section concludes the paper.

2 Preliminary Knowledge

2.1 Constrained Optimization Problems (COPs)

Without loss of generality, a COP can be described as follows:

$$ \begin{aligned}{\text{minimize}} & \quad f(\vec{x}),\vec{x} = (x_{1} , \ldots ,x_{D} ) \in S \\ {\text{subject}}\,{\text{to:}} & \quad {\text{g}}_{j} (\vec{x}) \le 0,j = 1, \ldots ,l \\ & \quad {\text{h}}_{j} (\vec{x}) = 0,j = l + 1, \ldots ,m \\ & \quad l_{i} \le x_{i} \le u_{i} ,i = 1, \ldots ,D \\ \end{aligned} $$

(1)

where $\vec{x} = (x_{1} , \ldots ,x_{D} )$ is an D dimensional vector, $f(\vec{x})$ is the objective function, ${\text{g}}_{j} (\vec{x}) \le 0$ and ${\text{h}}_{j} (\vec{x}) = 0$ are l inequality constraints and m − l equality constraints, respectively. $l_{i}$ and $u_{i}$ are the lower and upper bounds of the i-th decision variable $x_{i}$, respectively.

The decision space S is an D-dimensional rectangular space in ${\text{R}}^{n}$, in which every point satisfies the upper and lower bound constraints.

The feasible region $\Omega$ is defined by the l inequality constraints ${\text{g}}_{j} (\vec{x})$ and the (m − l) equality constraints ${\text{h}}_{j} (\vec{x})$. Any point $\vec{x} \in\Omega$ is called a feasible solution; otherwise, $\vec{x}$ is an infeasible solution. The aim of solving COPs is to locate the optimum in the feasible region.

Usually, the degree of constraint violation of individual $\vec{x}$ on the j-th constraint is calculated as follows:

$$ G_{j} (\vec{x}) = \left\{ {\begin{array}{*{20}l} {\hbox{max} (0,g_{j} (\vec{x})),} \hfill & {1 \le j \le l} \hfill \\ {\hbox{max} (0,\left| {h_{j} (\vec{x})} \right| - \delta ),} \hfill & {l + 1 \le j \le m} \hfill \\ \end{array} } \right. $$

(2)

$$ G(\vec{x}) = \sum\limits_{j = 1}^{m} {G_{j} (\vec{x})} $$

(3)

where ${\text{G}}_{j} (\vec{x})$ is the degree of constraint violation on the j-th constraint. $\delta$ is a positive tolerance value.

2.2 $\boldsymbol{\varepsilon}$ Constrained Method

The ε constrained method was proposed by Takahama and Sakai [6, 7]. The core idea of this method is to divide the individual-based constraint violation degree into different regions by artificially setting the ε value, and in different regions, the feasible solution and the infeasible solution adopt different evaluation methods respectively. The details on how to deal with the constraints, especially in constraint evolutionary optimization, can be found in the references [10, 11].

When comparing two individuals, say $\vec{x}_{\text{i}}^{k}$ and $\vec{x}_{j}^{k}$, $\vec{x}_{\text{i}}^{k}$ is better than $\vec{x}_{j}^{k}$ if and only if the following conditions are satisfied:

$$ \left\{ {\begin{array}{*{20}l} {f(\vec{x}_{i} ) < f(\vec{x}_{j} ),} \hfill & {if} \hfill & {G(\vec{x}_{i} ) \le \varepsilon \wedge G(\vec{x}_{j} ) \le \varepsilon } \hfill \\ {f(\vec{x}_{i} ) < f(\vec{x}_{j} ),} \hfill & {if} \hfill & {G(\vec{x}_{i} ) = G(\vec{x}_{j} )} \hfill \\ {G(\vec{x}_{i} ) < G(\vec{x}_{j} ),} \hfill & {} \hfill & {otherwise} \hfill \\ \end{array} } \right. $$

(4)

$$ \varepsilon ({\text{k}}) = \left\{ {\begin{array}{*{20}l} {\varepsilon (0)(1 - \frac{k}{{T_{c} }})^{cp} ,} \hfill & {0 < k < T_{c} } \hfill \\ {\quad 0,} \hfill & {k \ge T_{c} } \hfill \\ \end{array} } \right. $$

(5)

$$ cp = - \frac{\log \varepsilon \left( 0 \right) + \alpha }{{\log \left( {1 - \frac{k}{{T_{c} }}} \right)}} $$

(6)

where ε in Eq. (4) is controlled by Eqs. (5) and (6) and k is the current generation. $\varepsilon \left( 0\right)$ is the maximum degree of constraint violation of the initial population. $T_{c}$ is the maximum generation number. According to [8], $\alpha$ is set to 6.

2.3 Classical Differential Evolution

DE consists of four stages, i.e., initialization, mutation, crossover, and selection.

In the initialization stage, NP individuals are usually randomly generated from the decision space.

In the mutation operation stage, DE creates a mutant vector $\vec{v}_{i}$ for each sample $\vec{x}_{i}$. The two extensively used mutation operators (called DE/rand/1 and DE/best/1) are introduced as follows.

DE/rand/1:

$$ \vec{v}_{i} = \vec{x}_{{r_{1} }} + F(\vec{x}_{{r_{2} }} - \vec{x}_{{r_{3} }} ),\begin{array}{*{20}c} {} & {i = 1,2, \ldots ,NP} \\ \end{array} $$

(7)

DE/best/1:

$$ \vec{v}_{i} = \vec{x}_{best} + F(\vec{x}_{{r_{ 1} }} - \vec{x}_{{r_{ 2} }} ),\begin{array}{*{20}c} {} & {i = 1,2, \ldots ,NP} \\ \end{array} $$

(8)

where $r_{ 1} , r_{2} , r_{ 3}$ are three random and mutually different integers chosen from [1, NP], and F is a scaling factor and is used to control the amplification of the differential vector.

In the crossover operation stage, the crossover is applied to the parent individual $\vec{x}^{k}_{i}$ and its mutant vector $\vec{v}^{k}_{i}$. Then a trial vector $\vec{u}^{k}_{i}$ is produced.

$$ u^{k}_{{i , {\text{j}}}} = \left\{ {\begin{array}{*{20}l} {v^{k}_{{i , {\text{j}}}} ,} \hfill & {rand \le CR\quad or\quad j = j_{rand} } \hfill \\ {x^{k}_{{i , {\text{j}}}} ,} \hfill & {otherwise} \hfill \\ \end{array} } \right. $$

(9)

where rand is a uniformly distributed random number between 0 and 1. $j_{rand}$ is a random integer in [1, NP]. CR is the crossover probability.

In the selection operation stage, a comparison is conducted between parent individual $\vec{x}^{k}_{i}$ and trial vector $\vec{u}^{k}_{i}$ to select the better one among them.

$$ x_{i}^{k + 1} = \left\{ {\begin{array}{*{20}l} {u_{\text{i}}^{k} ,} \hfill & {f(u_{\text{i}}^{k} ) \le f(x_{\text{i}}^{k} )} \hfill \\ {x_{\text{i}}^{k} ,} \hfill & {otherwise} \hfill \\ \end{array} } \right. $$

(10)

2.4 Second Order Differential Evolution

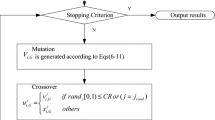
SODE is also composed of four stages, i.e., initialization, mutation, crossover, and selection. Except for the mutation stage, the other stages are the same as those of DE.

In the mutation operation stage, the usually and widely used mutation operations, DE/rand/1, is adopted as analytic model strategies in this paper. In order to efficiently utilize the direction information and the search status of the current population, the second order difference vector mechanism, which is based on the classical mutation strategies, is indicated as in Eqs. (11)–(15).

$$ d^{k} = x_{r1}^{k} - x_{r2}^{k} $$

(11)

$$ d_{1}^{k} = x_{r3}^{k} - x_{r4}^{k} $$

(12)

$$ d_{1}^{k} = x_{best}^{k} - x_{r4}^{k} $$

(13)

$$ d_{2}^{k} = x_{r5}^{k} - x_{{r_{6} }}^{k} $$

(14)

$$ d_{r}^{k} = d^{k} + \lambda (d_{1}^{k} - d_{2}^{k} ) $$

(15)

where r1, r2, r3, r4, r5, r6 are different random integers in [1, NP]. $\lambda$ is set as 0.1, which is discussed in reference [5]. $x_{best}^{k}$ is the best vector in generation k. $d_{1}^{k}$ in Eqs. (12) and (13) sets the same variable to different values, which is combined with Eq. (15) to produce different algorithms.

$(d_{1}^{k} - d_{2}^{k} )$ in Eq. (15) is the second order difference vector. The mutant vector $v_{i}^{k}$ is generated as follows:

$$ v_{i}^{k} = x_{{r_{7} }}^{k} + F \cdot d_{r}^{k} $$

(16)

where F is a scaling parameter and is set as 0.5. r7 is a random integer in [1, NP].

In this paper, two composing patterns of $d_{r}^{k}$ will be used. The first form of $d_{r}^{k}$ consists of Eqs. (12) and (14). The second form of $d_{r}^{k}$ consists of Eqs. (13) and (14). The first form and the second form based SODE, are denoted as SODErand and SODEbest, respectively.

3 The $\varepsilon$Constrained Second Order Differential Evolution

Evolutionary algorithm is a general optimization framework. In order to solve the constraint optimization problems, it must be combined with the appropriate constraint handing technique. Evolutionary algorithm and the constraint handing technique are combined to form a complete constrained evolutionary optimization algorithm. Therefore, while retaining the idea of SODE, this paper adds an $\varepsilon$ constrained method to select descendants, which is denoted as εSODErand and εSODEbest, respectively.

3.1 $\varepsilon$ SODErand

In this paper, εSODErand uses SODErand mentioned in Sect. 2 to combine with $\varepsilon$ constrained method. Its details is given in Algorithm 1.

3.2 A Subsection Sample

The difference between εSODEbest and εSODErand is the mutation operation stage. The former uses SODEbest mentioned in Sect. 2 to combine with $\varepsilon$ constrained method. Its details is given in Algorithm 2.

4 Experimental Results and Algorithmic Analysis

4.1 CEC2006 Benchmark Functions

In order to check the performance of the proposed algorithms εSODEbest and εSODErand, 12 functions are selected from IEEE CEC2006 [9] as the preliminary test suite, which is described in Table 1.

Table 1. CEC2006 benchmark functions.

Where D is the number of decision variables, LI is the number of linear inequality constraints, NI the number of nonlinear inequality constraints, LE is the number of linear equality constraints and NE is the number of nonlinear equality constraints, active is the number of active constraints at $\vec{x}$.

4.2 Experimental Settings

In order to show the performance of two proposed algorithms, εDE is chosen to compare with them. In this paper, εDE means to change SODErand in step6 of Algorithm 1 to DE. In addition to the special instructions, the parameters are set as follows.

• Independent running number: RUN = 25.

• Population size: NP = 50.

• Maximum number of function evaluations: maxFES = 240000.

Both parameters, F and CR are initialized to 0.5. Parameter $\lambda$ is set as 0.1.

It is noteworthy that the feasible rate, i.e., if the algorithm cannot consistently provide feasible solutions in all 25 runs, the running percentage of finding at least one feasible solution is recorded. So, based on the feasible rate, the experimental results are divided into two parts. One part is that the feasible rate of all three algorithms is 100%, and the other part is that there are some algorithms not 100% feasible. The former is called part 1, and the latter part is called part 2.

4.3 Experimental Comparison for Part 1

In the 12 functions, the solutions of 6 functions, include g₀₁, g₀₂, g₀₃, g₀₇, g₀₉, g₁₁, are consistent feasible over all 25 runs. All the final experimental results of the 6 functions over 25 runs, are statistically listed in Table 2, which includes the statistical items of the minimum final result (min), the median final result (median), the average final result (mean) and the standard deviation (std) in multiple runs.

Table 2. Comparison of the results based on CEC2006 functions.

Observed from Table 2 two proposed algorithms shows even better results in terms of reliability and accuracy when comparing with εDE. Comparatively speaking, εSODErand performs a little worse than that of εSODEbest. The fact of εSODErand and εSODEbest being better than εDE indicates that SODE has more information utilizing ability for solving constrained optimization problems than DE.

4.4 Boxplot Performance Comparison

To compare the performance of algorithms better, the boxplot analysis is taken for perusal. It can easily show the empirical distribution of all the final data in multiple runs pictorially. In order to better analyze the results, the functions are divided into two parts: Figs. 1 and 2.

Fig. 1.

Performance comparison on g₀₂, g₀₉, g₁₁.

Fig. 2.

Performance comparison on g₀₁, g₀₃, g₀₇.

Boxplots are shown in Fig. 1, which shows that both medians and interquartile range of εSODEbest are comparatively lower. The median of εSODErand is lower than that of εDE except for g02 function.

The performance comparison of g01, g03 and g07 are shown in Fig. 2. Observed from Fig. 2, the results of the three algorithms are relatively stable except for some outliers.

4.5 Experimental Comparison for Part 2

In the 12 functions, the solutions of 6 functions, include g₀₄, g₀₅, g₀₆, g₀₈, g₁₀, g₁₂, are inconsistent feasible. To get a more accurate solution, the 6 functions will be run 50 times to get results. The feasible rate, i.e., percentage of runs where at least one feasible solution is found, is recorded if an algorithm fails to consistently provide feasible solutions over all 50 runs. All the final experimental results of the 6 functions are statistically listed in Table 3.

Table 3. Comparison of the results based On CEC2006 functions.

Observed from Table 3, two proposed algorithms shows even better results in terms of feasible rate when comparing with εDE. Especially the functions g₀₆, g₀₈, g₁₀, the solutions obtained by εDE are not feasible, but two proposed algorithms significantly improve this phenomenon. This shows that SODE is more suitable for solving constrained optimization problems than DE.

5 Conclusions

A simple modification to SODE is proposed to solve COPs in this paper. The idea is that after producing offspring by the second order differential evolution, the ε constrained method is chosen for selection. εSODErand and εSODEbest on the basis of SODE are proposed. To test the effect of the proposed strategies, they are verified on CEC2006 Benchmark Functions. Experimental results show that second order difference vector has a certain role in dealing with constraint optimization problems. This idea can be hybridized with any DE variants, even for all the swarm intelligence and evolutionary computing methods. So, how to even better utilize the second order difference vector deserves further research.