An improved differential evolution algorithm for optimization including linear equality constraints

Abstract

A differential evolution algorithm (DE) is proposed to exactly satisfy the linear equality constraints present in a continuous optimization problem that may also include additional non-linear equality and inequality constraints. The proposed DE technique, denoted by DELEqC-II, is an extension of a previous method developed by the authors. In contrast to the previous approach, it uses both mutation and crossover strategies that maintain feasibility with respect to the linear equality constraints. Also, a procedure to correct numerical errors detected in the previous approach was incorporated in DELEqC-II. In the numerical experiments, scalable test-problems with linear equality constraints are used to analyze the performance of the new proposal.

1 Introduction

Most real world problems in areas such as management, physics, chemistry, and biology, involve finding optimal solutions to an optimization problem. Such solutions are not only optimal, they also must satisfy a set of constraints. Due to the growing complexity of the applications, leading to complex search spaces, it is clear that solving this kind of problems may be a challenging task. The difficulty level depends on the dimension of the problem, the number and complexity of equality and inequality constraints, the sparsity of the feasible space, and the location of the global optimum, among other features [1].

The general constrained optimization problem (COP) can be formulated as follows:

$$\begin{aligned} \begin{array}{ll} \min _x &{} f(x) \\ \text {s.t.} &{} g_i (x) \le 0 , i=1,\ldots ,p \\ &{} h_j (x) = 0 , j=1,\ldots ,m \end{array} \end{aligned}$$

(1)

where $x= \{x_1,\ldots ,x_n\}$ is the decision variable. The feasible region $\Omega$ is defined by the p inequality constraints $g_i(x)$, and the m equality constraints $h_j(x)$, with $m<n$.

Evolutionary algorithms (EAs) are increasingly popular for solving COPs, because of their robustness and adaptability to different kinds of problems. However, one of the greatest difficulties in EAs involves constraint handling. As they are unconstrained search techniques and lack an explicit mechanism to bias the search in constrained search spaces, they need additional mechanisms to deal with the constraints when solving COPs [2]. Furthermore, there are no guidelines to address the issue of handling unfeasible solutions, making this process a non trivial task.

The most common approach is the use of a penalty function which is considered easy to implement but usually requires extensive experimentation in order to set up the required parameter(s) of the method in a given problem [3]. Besides penalty methods, other approaches used in EAs include [4]: special representation schemes and move operators, that guarantee the generation of feasible solutions; repair techniques, to “correct” unfeasible solutions; handling constraints and objectives separately; and hybrid approaches. For additional literature on constraint handling, the reader is referred to [5, 6].

Linear equality constraints are extremely common in several areas such as Operations Research, Economics and Engineering, and we focus in this paper on obtaining solutions that automatically satisfy all linear equality constraints (in the form $Ex=c$, where $E \in \mathbb {R}^{m \times n}$, $x \in \mathbb {R}^{n}$ and $c \in \mathbb {R}^{m}$, with $m < n$). They are very hard to be satisfied when metaheuristics in general, and evolutionary computation in particular (differential evolution included), are adopted. Such constraints are usually approximated by inequality constraints (i.e. $| h_j(x) | \le \epsilon$) where the small tolerance value $\epsilon > 0$ is set by the user. This approach temporarily increases the feasible space, nevertheless, either feasible or good quality candidate solutions are still difficult to be obtained [7].

An interesting EA algorithm that handles linear equality constraints was proposed in [8]. The GENOCOP method, based on a genetic algorithm (GA), eliminates all linear equality constraints and writes the corresponding variables as a function of the remaining ones. Thus, the number of variables is reduced and the inequality constraints have to be appropriately modified.

In [9] two methods based on particle swarm optimization (PSO) were proposed to tackle linear equality constraints. The LPSO and the CLPSO methods start from a feasible initial population and the feasibility is maintained by modifications in the standard PSO formulas for velocity and position updates. This is done by only using linear combinations of other particle positions.

Another approach used in PSO was proposed in [10], where a technique called homomorphous mapping converts problems with linear equality constraints into unconstrained and lower-dimensional problems. This is a decoder-based approach that imposes a mapping between a feasible solution and a decoded solution, that is, it transforms an n-dimensional hypercube $[-1,1]^n$ into a feasible search space (which can be convex or non-convex). Then, standard evolution operations are performed in the hypercube.

In [9, 11] the Linear PSO was proposed as a constraint-preserving method, i.e., a method that preserves solutions satisfying all linear constraints. Starting from a set of feasible points, the idea is that the velocity updates are calculated as a linear combination of feasible position and velocity vectors, thus maintaining feasibility. This idea is closely related to the one proposed in this paper: by only using linear combinations among the members of the population, which is easy to implement in DE, the optimization method is capable of maintaining feasibility with respect to the linear equality constraints.

In our first attempt to maintain feasibility [12] with respect to linear equality constraints, a procedure for generating a random feasible initial population was proposed, and the algorithm developed, DELEqC, performed only mutation, avoiding the standard DE crossover operation. The results were compared with other procedures available in the literature [10, 11]. In addition, the proposed method was also compared with a DE using a tournament selection approach [3] and another DE using an adaptive penalty method [13] to enforce the linear equality constraints. The computational results indicate that DELEqC outperforms those few alternatives that were found in the literature. However, during further experiments, numerical errors were observed that allowed the population to drift away from the feasible set if the algorithm runs a higher number of generations. This is one of the issues that we intend to solve here.

Therefore, this paper is concerned with efficiently obtaining solutions that satisfy all linear equality constraints of an optimization problem by improving the previously developed algorithm. In contrast to DELEqC, the new proposal, DELEqC-II, allows for the utilization of both mutation and crossover operators, and provides a projection procedure to correct the solutions that “escape” from the feasible set. In this paper, scalable test-problems, both in the number of variables as in the number of constraints, are introduced and the performance of DELEqC-II is compared to that of the previous version.

The remainder of this paper is organized as follows: in Sect. 2 we briefly describe the differential evolution algorithm. Section 3 presents the proposed solution method, describing the procedure for generating a feasible initial population, the crossover and mutation operations, and the strategy for projecting the population back to the feasible space. In Sect. 4 we show some numerical results and comparisons on test problems containing only linear equality constraints, where the effectiveness and efficiency of DELEqC-II is studied. The test-problems are described in “Appendix A and B”. Finally, the conclusion and possible paths for future research are given in Sect. 5.

2 Differential evolution

Differential evolution (DE) [14, 15] is a simple and effective population-based stochastic algorithm originally designed for optimizing functions of continuous variables. DE utilizes $\mathtt{NP}$ members/vectors as a population for each generation $\mathtt{G}$. Each new vector is generated by adding the scaled difference between two members of the population to a third one. If the resulting vector yields a better objective function value, then it replaces the vector with which it was compared. The number of differences applied, the way individuals are selected, and the crossover operation define the different DE variants.

In the mutation process of the simplest DE variant (DE/rand/1/bin), for each vector $x_{i,j,G}$, $i=1,\ldots ,\mathtt{NP}$, $j=1,\ldots ,\mathtt{N}$ a vector v is generated according to

$$\begin{aligned} v_{i,j,G+1} = x_{r_1,j,G} + \mathtt{F} \times (x_{r_2,j,G} - x_{r_3,j,G}) \end{aligned}$$

(2)

where $r_1, r_2$ and $r_3$ are distinct and randomly selected indexes, different from index i. The scale parameter $\mathtt{F}$ controls the magnitude of the difference operation.

In addition, the crossover operation is controlled by the parameter $\mathtt{CR}$. According to a given probability $\mathtt{CR}$, the trial vector $u_{i,G+1}$ is generated from the elements of the target vector $x_{i,G}$ and the elements of the donor vector $v_{i,G+1}$, as follows

$$\begin{aligned}&u_{i,j,G+1} = \left\{ \begin{array}{ll} v_{i,j,G+1}, &{} \text{ if } \quad \mathtt{Rand}(0,1) < \mathtt{CR} \\ &{} \text{ or } \quad j = jRand \\ x_{i,j,G}, &{} \text{ otherwise } \end{array} \right. \\&i = 1,\ldots ,\mathtt{NP}; j = 1,\ldots ,\mathtt{N}. \nonumber \end{aligned}$$

(3)

where $\mathtt{Rand}(0,1)$ is a random real number from [0, 1] and jRand is a random integer from $[1,\ldots ,\mathtt{N}]$. Note that jRand ensures that $v_{i,G+1} \ne x_{i,G}$.

Then, the target vector $x_{i,G}$ is compared with the trial vector $u_{i,G+1}$ and the one with the better objective function value is selected to the next generation. Mutation, crossover and selection continue until a stopping criterion is reached.

As in most standard evolutionary methods, the move operators in DE are totally blind to the constraints, i.e., when applied to feasible members they do not necessarily generate feasible offspring. Keeping in mind that standard metaheuristics must be equipped with a constraint handling technique, here our focus is to obtain solutions automatically satisfying all linear equality constraints. The remaining constraints present in the problem can be dealt with constraint handling techniques available in the literature. The numerical experiments performed focus on optimization problems with linear equality constraints.

In this paper, four variants of the DE were tested:

DE/rand/1/bin: described in Eq. (2).

DE/best/1/bin

$$\begin{aligned} v_{i,j,G+1} = x_{best,j,G} + \mathtt{F} \times (x_{r_1,j,G} - x_{r_2,j,G}) \end{aligned}$$

(4)

DE/target-to-rand/1/bin

$$\begin{aligned} v_{i,j,G+1}&= x_{i,j,G} + \mathtt{F} \times (x_{r_1,j,G} - x_{r_i,j,G})\nonumber \\&\quad + \mathtt{F} \times (x_{r_2,j,G} - x_{r_3,j,G}) \end{aligned}$$

(5)

DE/target-to-best/1/bin

$$\begin{aligned} v_{i,j,G+1}&= x_{i,j,G} + \mathtt{F} \times (x_{best,j,G} - x_{r_i,j,G})\nonumber \\&\quad +\mathtt{F} \times (x_{r_2,j,G} - x_{r_3,j,G}) \end{aligned}$$

(6)

3 The proposed solution method

Although DELEqC-II can be applied to problems involving additional constraints, we will focus on optimization problems of the form

$$\begin{aligned} \begin{array}{ll} \min _x &{} f(x) \\ \text {s.t.} &{} Ex = c \end{array} \end{aligned}$$

(7)

where $f : \mathbb {R}^n \rightarrow \mathbb {R}$, $E \in \mathbb {R}^{m \times n}$, $x \in \mathbb {R}^{n}$ and $c \in \mathbb {R}^{m}$, with $m < n$. It is assumed that E has full rank, that is, the rows of E are linearly independent. Any additional constraints can be dealt with using standard constraint handling techniques from the evolutionary computation literature. A candidate solution $x \in \mathbb {R}^n$ is said to be feasible if $x \in \mathcal{S}$, where $\mathcal{S}$ denotes the feasible set

$$\begin{aligned} \mathcal{S} = \{ x \in \mathbb {R}^n : Ex=c\} \end{aligned}$$

(8)

A vector $d \in \mathbb {R}^n$ is said to be a feasible direction at the point $x \in \mathcal{S}$ if $x+d$ is feasible, that is, $E(x+d) = c$. It follows that d must satisfy $Ed = 0$ or, alternatively, that any feasible direction belongs to the null space of the matrix E, defined as

$$\begin{aligned} \mathcal{N}(E)= \{ x \in \mathbb {R}^n : Ex=0 \} \end{aligned}$$

(9)

Given two feasible vectors $x_1$ and $x_2$ it is clear that $d=x_1 - x_2$ is a feasible direction, as $E(x_1-x_2)=0$. As a result, the standard mutation operations adopted in DE (see Sect. 2) always generate feasible candidate solutions whenever the vectors involved in the differences are feasible, and no errors due to floating-point arithmetic are introduced.

3.1 Generating a feasible initial population

Algorithm 1, proposed in [12], is used to generate a feasible (with respect to the linear equality constraints) initial population of size $\mathtt{NP}$. The main idea is to start from a feasible vector $x_{0}$ and proceed by moving from $x_0$ along random feasible directions $d_i: x_i = x_0 + d_i; i = 1,2,\ldots ,\mathtt{NP}$. The feasible vector $x_0$ can be computed as $x_0= E^T (E E^T)^{-1} c$, where the superscript T denotes transposition. In fact, $Ex_0 = E E^T (E E^T)^{-1} c = c$.

Random feasible candidate solutions can then be generated as

$$\begin{aligned} x_i = x_0 + P_{\mathcal{N}(E)}v_i, \quad i=1,2,\ldots , \mathtt{NP} \end{aligned}$$

where $v_i \in \mathbb {R}^n$ is randomly generated (here, these values are randomly generated using a uniform distribution within a given hypercube) and the projection matrix [16] is given by

$$\begin{aligned} P_{\mathcal{N}(E)} = I - E^T (E E^T)^{-1} E. \end{aligned}$$

(10)

Also, in Algorithm 1, the matrix inversion in Eq. 10 is not actually performed.

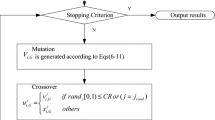
3.2 Mutation and crossover operators

At generation G, for each vector $x_{i,j,G}$, with $i=1,\ldots ,\mathtt{NP}$ and $j=1,\ldots ,\mathtt{N}$, the mutation scheme applied can be one of those described in Sect. 2 by Equations (2), (4), (5) or (6).

In the sequel, the crossover operation is performed:

$$\begin{aligned} u_{i,j,G+1} = (1 - \mathtt{CR}) \times x_{i,j,G} + \mathtt{CR} \times v_{i,j,G+1} \end{aligned}$$

(11)

The crossover operation is a linear combination of the target vector $x_{i,G}$ and the donor vector $v_{i,G+1}$. In fact, with CR$\in (0, 1]$, the proposed crossover (Eq. 11) is a convex combination of $x_{i,G}$ and $v_{i,G+1}$.

The two operators are thus able to maintain feasibility with respect to the linear equality constraints.

3.3 Projecting the population into the feasible space

Despite the good results obtained by DELEqC in [12], we observed that numerical errors can arise during mutation. All the mathematical operations of the proposal are theoretically designed so that feasibility with respect to $Ex=c$ is always maintained. This is equivalent to having $Ed=0$ for any vector d obtained as a difference of two feasible solutions from the population. However, floating-point arithmetic errors will occur in any finite arithmetic computer. Such errors will lead to a difference vector $d'$ slightly outside of the null space of the matrix E, that is, $Ed'$ is not exactly zero. As a result, an unfeasible individual is created in the population. From this point on, additional difference vectors not in the null space of E will appear. That is illustrated in Fig. 1.

An example of an optimization problem with an equality constraint is solved using DELEqC to illustrate the effect of the numerical error in the search. Consider the simple problem

$$\begin{aligned} \begin{array}{ll} \min &{} (x_{1}-2)^{2} + (x_{2}-1)^{2} \\ \text {s.t.} &{} x_{1} + x_{2} - 1 = 0. \end{array} \end{aligned}$$

(12)

Figure 1 shows the initial population (50 individuals) and the candidate solutions after 50, 100, 150, and 200 generations. One can see by this illustrative example that DELEqC (i) creates feasible individuals in the initial population, (ii) keeps all individuals feasible during up to 100 generations, and (iii) is able to find the solution of the problem.

However, after some generations, unfeasible candidate solutions appear in the population and the technique is no longer able to enforce the constraint of the problem.

Fig. 1

Illustration of DELEqC’s search behavior caused by numerical errors. In (a), values are randomly generated in ${[0,3]}\times {[0,3]}$ and, in (b), their projection onto the feasible domain. The solution of the problem is found in up to 50 generations, as presented in (c). However, after some generations e shows that floating-point errors from the mutation operation (Equations 2, 4, 5, and 6) are introduced. Such errors make individuals unfeasible and, eventually, all the population is unfeasible, and f converges to the solution of the unconstrained version of the problem

As pointed out, floating-point errors, such as loss of significant digits (in subtraction) and in the summation of numbers of very different magnitudes, may appear in any finite arithmetic computer. Although in Fig. 1 the unfeasible solutions appear when the candidate solutions became similar, this is only one example of the effect of floating-point errors. The adoption of diversity preservation techniques is not sufficient to avoid this issue. In fact, the floating-point errors may appear even when the candidate solutions are not close to each other in the search space. In order to demonstrate that, Fig. 2 shows the violation of the fittest individual (best objective function value) along the generations (i) when the selection pressure in DELEqC is removed (offspring always replace the target individuals), and (ii) adopting $F=0.3, 0.5, 0.7, 0.9$. Due to (i), the differences between the candidate solutions increase along the generations. It is also seen that as the values of F increase, the constraint violation of the best candidate solution also increases, in spite of the diversity of the population.

Fig. 2

Violation of the fittest individual along the evolution for different values of F

One way to fix the generation of unfeasible candidate solutions is to project the created individuals back into the feasible space. The lines 5–10 of the Algorithm 1 can be used to perform these projections. However, running these additional operations increases the computational cost of the search technique. In fact, for each candidate solution, two linear systems must be solved, but the time complexity is $O(m^{2})$, as the factorization ($O(m^{3})$) is performed only once (see Algorithm 1). Also, each modified (projected) candidate solution must be evaluated at this point.

3.4 DELEqC-II

In order to reduce the additional computational cost of projecting the candidate solutions back to the feasible region, we propose here to check the feasibility of the best (with respect to the objective function value) candidate solution in the population. If the best individual is unfeasible, then the population is projected onto the feasible region. Thus, the number of projections required is substantially reduced.

After projecting the population onto the feasible region, the best individual in the projected population can be worse than the best one from the previous generation. When this situation occurs, the best solution in generation G, $\overrightarrow{x}_{p_{best},G}$, is maintained in generation $G+1$. Thus, the quality of the best feasible solution never decreases along the generations and the best solution in each generation is feasible with respect to the linear equality constraints. That is performed in lines 26–30 of Algorithm 2.

An additional proposal is the incorporation to DELEqC of the crossover operator presented in Sect. 3.2. Thus, the proposed DELEqC-II performs both mutation and crossover, and keeps the generated candidate solutions feasible with respect to the linear equality constraints. Algorithm 2 presents a pseudo-code of DELEqC-II.

4 Computational experiments

Computational experiments were performed in order to (i) compare the results obtained by DELEqC-II with those found by DELEqC; (ii) examine the performance of DELEqC-II when different DE variants are used; (iii) analyze the sensitivity of DELEqC-II with respect to its parameter values; (iv) compare DELEqC-II to an approach where all the candidate solutions are projected to the feasible search space; and (v) inspect the quality of the results achieved by DELEqC-II in problems with different sizes, and with different ratios between the dimension of the problem and the number of linear equality constraints.

In [12], it was shown that DELEqC performed better than other techniques from the literature. Hence, the results found by DELEqC-II are compared only to those achieved by DELEqC.

Five test-problems from [10] (and also used in [12]) were adopted here; we used only the scalable functions from [12]. The test-problems and the procedure used to re-scale them are presented, respectively, in “Appendices A and B”. The pair (n, m) formed by dimension (n) and number of constraints (m) of the test-problems used here are $\{(10,5),(20,5),(20,10),(30,5),(30,15),(40,5), (40,20)\}$. Thus, the number of test-problems is $5 \times 7 = 35$. The original problems have $n=10$ and $m=5$. The new test-problems were generated increasing the dimension by 2, 3, and 4 times the original size. The number of constraints of the re-scaled test-problems are 5 (the original value) and n / 2. The vectors $v \in \mathbb {R}^n$ used to create the initial population are randomly sampled from a hypercube bounded in every dimension by $[-100, 100]$, $[-100, 100]$, [2.56, 5.12], $[-100, 100]$, and [300, 600], respectively, for the test-problems from 1 to 5 [12].

A maximum number of objective function evaluations is used here as the stop criterion. From the literature, no more than 5000, 20,000, 20,000, 40,000, and 20,000 objective function calls are allowed for the original versions of the test-problems 1-5, respectively. These limitations are modified for the scaled test-problems in view of the dimensionality of the problem. The budget is 5, 10 and 20 times that of the maximum original value for $n=20, 30, 40$, respectively. In Algorithm 2, GEN is defined as the maximum number of objective function evaluations allowed divided by the population size (NP). Also, the best solution is considered unfeasible when any of its constraints is violated by more than $10^{-6}$ (line 20 of Algorithm 2).

The source-code of DELEqC and DELEqC-II as well as all the data of the results presented in this paper are available on-line.¹ Also, a Supplementary Material is provided in order to support the analysis and conclusions presented here. There, boxplots of the parameter analysis, statistical values as well as non-parametric tests of the results found by DELEqC and DELEqC-II are included together with processing times and statistical results of DELEqC-II and of an approach in which all the candidate solutions are projected into the feasible search space.

4.1 Preliminary results

The first part of the computational experiments involves an analysis of DELEqC-II’s parameters and their performance when different DE variants are used.

We also tested the following parameter values: $\mathtt{F} = \{0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0\}$, $\mathtt{NP} = \{10, 20, 30, 40, 50, 60, 70, 80, 90, 100\}$, and $\mathtt{CR} = \{0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0\}$.

As handling the numerical issue discussed above is crucial to the application of DELEqC  [12] in practical situations, here we take DELEqC as being DELEqC-II with $\mathtt{CR}=1$. Hence, DELEqC can be recovered when using $\mathtt{CR}=1$ (no crossover) in DELEqC-II, and when the candidate solutions are not projected into the feasible region of the search space.

Five independent runs were performed for each parameter setup when solving each one of the 35 test-problems. Thus, a total of $4 \times 10 \times 10 \times 10 \times 35 \times 5 = 700000$ runs were preliminary performed.

Due to the large number of combinations, performance profiles [17] were used to identify the parameters which obtained the best results. Given a set A of algorithms to be tested on a set P of problems, the performance indicator (to be maximized) $t_{p,a}$ of algorithm $a\in A$ when applied to test-problem $p\in P$ is the median of the inverse of the minimum objective function value found by algorithm a in test-problem p. The performance ratio can be defined as $r_{p,a} = {t_{p,a}}/{\min \{ t_{p,a}: a \in A\}}$. Denoting cardinality of a set by $\left| . \right|$, performance profiles (PPs), are defined as $\rho _a(\tau ) = \frac{1}{n_p}\left| \{p\in P : r_{p,a}\le \tau \} \right|$. We used the normalized area under the performance profiles curves [18] as the performance indicator.

For each technique (DELEqC and DELEqC-II), we selected the best parameter settings for each DE variant presented in Sect. 2. The best performing techniques are: DELEqC-CR1.0-F0.6-rand-NP100 ($\mathtt{CR} = 1.0$, $\mathtt{F} = 0.6$, $\mathtt{NP} = 100$ using DE/rand/1/bin), DELEqC-CR1.0-F0.9-best-NP40 ($\mathtt{CR}=1.0$, $\mathtt{F}=0.9$, $\mathtt{NP}=40$ using DE/best/1/bin), DELEqC-CR1.0-F0.6-trand-NP100 ($\mathtt{CR}=1.0$, $\mathtt{F}=0.6$, $\mathtt{NP}=100$ using DE/target-to-rand/1/bin), DELEqC-CR1.0-F0.1-tbest-NP100 ($\mathtt{CR}=1.0$, $\mathtt{F}=0.1$, $\mathtt{NP}=100$ using DE/target-to-best/1/bin), DELEqC-II-CR0.7-F0.9-rand-NP100 ($\mathtt{CR}=0.7$, $\mathtt{F}=0.9$, $\mathtt{NP}=100$ using DE/rand/1/bin), DELEqC-II-CR0.1-F0.3-best-NP100 ($\mathtt{CR}=0.1$, $\mathtt{F}=0.3$, $\mathtt{NP}=100$ using DE/best/1/bin), DELEqC-II-CR0.7-F0.9-trand-NP100 ($\mathtt{CR}=0.7$, $\mathtt{F}=0.9$, $\mathtt{NP}=100$ using DE/target-to-rand/1/bin), and DELEqC-II-CR0.2-F0.1-tbest-NP100 ($\mathtt{CR}=0.2$, $\mathtt{F}=0.1$, $\mathtt{NP}=100$ using DE/target-to-best/1/bin).

In the next sections, additional independent runs were performed using these eight selected techniques. To make the further comparisons more robust, each test-problem was solved 100 times.

4.1.1 DELEqC variants

Here, the results obtained by DELEqC using different DE variants are analyzed. PPs are presented in Fig. 3 where DELEqC-CR1.0-F0.6-trand-NP100 outperformed the other combinations of DE variants and parameters. Thus, DELEqC-CR1.0-F0.6-trand-NP100 is used in Sect. 4.2 to compare DELEqC versus DELEqC-II.

The normalized area under the performance profiles curves (AUCs) are shown in Fig. 4, where it is possible to verify that (i) the variant target-to-rand obtained the largest AUC, and (ii) the variants with “target” obtained larger AUCs than those that do not include “target”.

Despite that, PPs indicate that DELEqC-CR1.0-F0.1-tbest-NP100 and DELEqC-CR1.0-F0.9-best-NP40 are more reliable than DELEqC-CR1.0-F0.6-rand-NP100, as they require a smaller $\tau$ to reach $\rho (\tau )=1$.

Fig. 3

Performance profiles for the best performing DELEqC techniques

Fig. 4

Normalized area under the performance profiles curves for the best performing DELEqC techniques

4.1.2 DELEqC-II variants

Here, the results obtained by DELEqC-II using different DE variants are analyzed. The performance profiles are presented in Fig. 5 and, similarly to DELEqC, DELEqC-II with target-to-rand variant (DELEqC-II-CR0.7-F0.9-trand-NP100) outperformed the other combinations of DE variants and parameters. In this manner, DELEqC-II-CR0.7-F0.9-trand-NP100 is used in Sect. 4.2 to compare DELEqC versus DELEqC-II.

In Fig. 6 one can observe that the variants rand and target-to-rand obtained larger AUCs than best and target-to-best. The variants rand and target-to-rand (i) reached the best results in a larger number of problems ($\rho (1)$), (ii) are more reliable (smaller $\tau$ such that $\rho (\tau )=1$), and (iii) have a best overall performance (larger AUCs). Thus, it is suggested to use these variants when using DELEqC-II.

Fig. 5

Performance profiles for the best performing DELEqC-II techniques

Fig. 6

Normalized area under the performance profiles curves for the best performing DELEqC-II techniques

Fig. 7

Performance profiles curves for results found by DELEqC (DELEqC-CR1.0-F0.6-trand-NP100) and DELEqC-II (DELEqC-II-CR0.7-F0.9-trand-NP100). The normalized area under the performance profiles curves are, respectively, 0.9977 and 1.0

Fig. 8

Boxplots of the results found by DELEqC and DELEqC-II when solving the test-problem 1. The maximum and minimum values are the same for all plots in the top while these limits vary in the remaining plots

Fig. 9

Boxplots of the results found by DELEqC and DELEqC-II when solving the test-problem 2

Fig. 10

Boxplots of the results found by DELEqC and DELEqC-II when solving the test-problem 3

Fig. 11

Boxplots of the results found by DELEqC and DELEqC-II when solving the test-problem 4

Fig. 12

Boxplots of the results found by DELEqC and DELEqC-II when solving the test-problem 5

4.2 Analysis of the results

The DELEqC and DELEqC-II variants were evaluated in the previous sections, and those with best general performance are, respectively, DELEqC-CR1.0-F0.6-trand-NP100 and DELEqC-II-CR0.7-F0.9-trand-NP100. In this section DELEqC-CR1.0-F0.6-trand-NP100 is referred to as DELEqC and DELEqC-II-CR0.7-F0.9-trand-NP100 as DELEqC-II for short. Two features are common in both cases: the DE variant (target-to-rand) and the population size (NP$=100$). As only mutation is present when CR$=1$, then one can observe that a smaller step size (F) is preferable in DELEqC. On the other hand, DELEqC-II achieves better results with a larger value of F than that used by DELEqC. Although good results are obtained with DELEqC-II when F$=0.9$, one can notice that an additional weighting (CR$=0.7$) is applied to the vectorial differences (see Equations 5 and 11). As a consequence, when choosing the parameter values which generate the best overall performance in DELEqC-II, the vectorial difference contributes with $0.7 \times 0.9 = 0.63$ to generate the new candidate solution. Thus, the main difference between DELEqC and DELEqC-II seems to originate in the participation of the target vector ($x_{i, j, G}$) in forming the new individual.

The contribution of the linear combination (crossover) is important as DELEqC-II achieved the best solution in general when compared to DELEqC.

This comparison can be shown in Fig. 7, where the performance profiles and the normalized area under these curves are presented. According to the performance profiles, DELEqC-II obtained the best results in most of the test-problems, and reached the best performance in general (normalized area under the performance profiles curves). On the other hand, DELEqC shows to be more reliable, as its performance profiles require a smaller $\tau$ in order to reach $\rho (\tau ) = 1$ (solve all problems). One can see in Fig. 10, with boxplots of the results found by both DELEqC and DELEqC-II techniques, that DELEqC-II achieves worse values when solving the test-problem 3 when $n=40$ and $m=20$.

A closer look at the results can be found in the boxplots in Figs. 8, 9, 10, 11 and 12. One can see that DELEqC-II obtained results better than or similar to those achieved by DELEqC in almost all tested cases. The exceptions are the test-problem 3, and the test-problem 1 when $n=10, 20$ and $m=5$. Also, it is important to highlight that DELEqC-II produces more stable results than DELEqC when the dimension n increases. This makes DELEqC-II more suitable than DELEqC for solving problems with a higher dimensionality. The behavior of both methods is similar when the ratio n / m increases.

In addition to the boxplots and the previous presented discussion, statistical results of DELEqC and DELEqC-II are presented in the Supplementary Material, where the Mann-Whitney non-parametric statistical test is also performed in order to evaluate when the results obtained by both techniques are similar. The results obtained by DELEqC-II are the best ones or statistically similar to the best ones with respect to the Mann-Whitney non-parametric statistical test (p-value $>0.5$) in 25 of the 35 test-problems. The best solution set with respect to each test-problem is assumed here as those with the best median value. Thus, we conclude that DELEqC-II performed in general better than DELEqC.

4.3 The effect of projecting all solutions

An additional experiment was conducted in order to verify the effect of projecting all solutions into the feasible space of the linear equality constraints. All test-problems were run with both approaches: DELEqC-II and a variant where all candidate solutions are projected. The results are presented in the Supplementary Material which shows that the convergence behavior is quite similar. The processing times were collected and it was observed that, as expected, DELEqC-II is faster. The ratio of the processing times of both variants ranged from 0.1 to 0.98. In fact, it was noted that, in about half of the cases, DELEqC-II uses less than half of the processing time. Thus, it is concluded that there is no reason to project all the individuals into the feasible space as the computing time is always higher and the median of the obtained solutions are quite similar.

4.4 Analysis of the parameters

DELEqC-II is analyzed here with respect to the performance obtained when varying the values of its parameters: NP, CR, and F. When a given parameter is varied, the other ones are fixed as those of DELEqC-II-CR0.7-F0.9-trand-NP100. The boxplots of the results for different values for NP, F, and CR are included in the Supplementary Material.

The performance of DELEqC-II decreases when smaller values are considered for the population size (NP). The best results are obtained in general using larger values for NP. The exception is the test-problem 3, where the best results are found using 50 or 60 individuals. Thus, it is suggested to apply DELEqC-II with no less than 50 individuals.

One can see in the boxplots that the performance of DELEqC-II decays when CR assumes lower or higher values. In fact, the performance of the technique can be substantially decreased when a wrong CR value is chosen. Middle-range values (CR$\in [0.5, 0.7]$) are preferable.

When the parameter F is analyzed, one can see that larger values result in a better performance of DELEqC-II. Values smaller than 0.8 can decrease the performance of the proposed technique in some test-problems.

One can notice that similarly to other metaheuristics, DELEqC-II is sensible to its parameter values. However, in general, the best parameter setting indicated here as DELEqC-II-CR0.7-F0.9-trand-NP100 tends to reach a good performance. It is also interesting to verify that the performance of DELEqC-II is different when looking only to the test-problem 3. In this case, smaller values of the parameters seem to perform better, as the Rastrigin function is highly multi-modal.

5 Conclusions

Dealing with constraints in Evolutionary Algorithms (EAs) is considered a hard task, specially the equality constraints. Although there are some alternatives to deal with constraints in EAs, in this paper we address the issue of exactly satisfying linear equality constraints. We propose here an improved differential evolution method capable of automatically satisfying liner equality constraints. The new method, DELEqC-II, is an extension of a previously developed algorithm, DELEqC.

The results show that DELEqC-II performed better in most of the test-problems and reached the best performance in general when compared to DELEqC. Particularly, DELEqC-II is more suitable than DELEqC for solving problems in higher dimensions. Also, a closer inspection in the parameter setting indicates that DELEqC-II is sensitive to its parameter values, a feature commonly observed in metaheuristics. On the other hand, we believe that a careful analysis will help those interested in using the approach proposed here to properly choose the parameter setting.

Fig. 13

Linear equality constraints of the feasible set $\mathcal{E}$

Finally, DELEqC-II can be easily combined with methods to handle the constraints other than the linear equality ones. As a result, those combinations, as well as DELEqC-II’s application to hard real-world optimization problems, are interesting research avenues.

Appendices

Appendix A: Test-problems

Test-problems 1–5 were taken from [10]. Also note that those problems are subject to the same set of linear constraints, described in Fig. 13. Following, the description and the optimal solution value of each problem.

Problem 1 (Sphere):

:

$$\begin{aligned} \min _{x \in \mathcal{E}} \quad \sum ^{n}_{i=1} x_i^2. \end{aligned}$$

The feasible set $\mathcal{E}$ is given by the linear equality constraints in Fig. 13 and $f(x^*) = 32.137$.

Problem 2 (Quadratic):

:

$$\begin{aligned}&\min _{x \in \mathcal{E}} \quad \sum ^{n}_{i=1}\sum ^{n}_{j=1} e^{-(x_i - x_j)^2}x_ix_j + \sum ^{n}_ {i=1}x_i\\&f(x^*) = 35.377 \end{aligned}$$

Problem 3 (Rastrigin):

:

$$\begin{aligned}&\min _{x \in \mathcal{E}} \quad \sum ^{n}_{i=1} x_i^2 + 10 - 10\cos (2\pi x_i)\\&f(x^*) = 36.975. \end{aligned}$$

Problem 4 (Rosenbrock):

:

$$\begin{aligned}&\min _{x \in \mathcal{E}} \quad \sum ^{n-1}_{i=1} 100(x_{i+1} - x_i^{2})^2 + (x_i - 1)^2\\&f(x^*) = 21485.3. \end{aligned}$$

Problem 5 (Griewank):

:

$$\begin{aligned}&\min _{x \in \mathcal{E}} \quad \dfrac{1}{4000}\sum ^{n}_{i=1} x_i^2 - \prod ^{n}_{i=10}\cos (\dfrac{x_i}{\sqrt{i}}) + 1\\&f(x^*) = 0.151. \end{aligned}$$

Appendix B: Scaling the test-problems

Problems 1–5 can be scaled by varying the number of variables (n) and the number of constraints (m). Let $G \in \mathbb {R}^{5 \times 10}$ and $p \in \mathbb {R}^{5}$ be the coefficient matrix and vector, respectively, associated to the set of linear equality constraints in Fig. 13. Hence

$$\begin{aligned} G = \begin{bmatrix} 0&-3&-1&0&0&2&-6&0&-4&-2 \\ -1&-3&-1&0&0&0&-5&-1&-7&-2 \\ 0&0&1&0&0&1&3&0&-2&2 \\ 2&6&2&2&0&0&4&6&16&4 \\ -1&-6&-1&-2&-2&3&-6&-5&-13&-4 \end{bmatrix} \end{aligned}$$

and $p^{T} = \begin{bmatrix} 3&0&9&-16&30 \end{bmatrix}$.

Now, let $0 \in \mathbb {R}^{5 \times 10}$ be a matrix with all values equal to zero. By varying n and m we can construct new sets of linear equality constraints for problems 1–5. Those sets are described as follow.

Constraint-set 1 In (7), setting $m = 5$ and $n = 20$ we obtain $x \in \mathbb {R}^{20}$ and $E = \begin{bmatrix} G&0 \end{bmatrix} \quad \text{ and } \quad c = \begin{matrix} p \end{matrix}$. The matrix $E \in \mathbb {R}^{5 \times 20}$ and the vector $c \in \mathbb {R}^{5}$ now describes the set of linear equality constraints, where E is of the special form $[G \quad 0]$, that is, its columns can be partitioned into two sets; the first 10 columns make up the original G matrix and the last 10 columns make up the 0 matrix. The next constraint-sets, follow the same construction rule.

Constraint-set 2 Setting $m = 10$ and $n = 20$ we obtain $E = \begin{bmatrix} G&0 \\ 0&G \end{bmatrix} \quad \text{ and } \quad c = \begin{bmatrix} p \\ p \end{bmatrix}$.

Constraint-set 3 Setting $m = 5$ and $n = 30$, we obtain $E = \begin{bmatrix} G&0&0 \\ \end{bmatrix} \quad \text{ and } \quad c = \begin{matrix} p \end{matrix}$.

Constraint-set 4 Setting $m = 15$ and $n = 30$, we obtain $E = \begin{bmatrix} G&0&0 \\ 0&G&0 \\ 0&0&G \\ \end{bmatrix} \quad \text{ and } \quad c = \begin{bmatrix} p \\ p \\ p \end{bmatrix}$.

Constraint-set 5 Setting $m = 5$ and $n = 40$, we obtain $E = \begin{bmatrix} G&0&0&0 \\ \end{bmatrix} \quad \text{ and } \quad c = \begin{matrix} p \end{matrix}$.

Constraint-set 6 Setting $m = 20$ and $n = 40$, we obtain $E = \begin{bmatrix} G&0&0&0 \\ 0&G&0&0 \\ 0&0&G&0 \\ 0&0&0&G \\ \end{bmatrix}$ and $c = \begin{bmatrix} p \\ p \\ p \\ p \end{bmatrix}$.