Evidence of Critical Transitions and Coexistence of Alternative States in Nature: The Case of Malaria Transmission

Abstract

Sometimes abrupt changes occur in nature. Examples of these phenomena exist in lakes, oceans, terrestrial ecosystems, climate, evolution, and human societies. Dynamical systems theory has provided useful tools to understand the nature of these changes. When certain non-linearities underlie system dynamics, rapid transitions may happen when critical thresholds for certain parameter values are overcome. Here we describe a malaria dynamical model that couples vector and human disease dynamics through mosquito infectious bites, with the possibility of super-infection, this is, the reinfection of asymptomatic hosts before they have cleared a prior infection. This key feature creates the potential for sudden transitions in the prevalence of infected hosts that seem to characterize malaria’s response to environmental conditions. This dynamic behavior may challenge control strategies in different locations. We argue that the potential for critical transitions is a general and overlooked feature of any model for vector borne diseases with incomplete, complex immunity.

This work was funded by the Spanish government through the Ramón y Cajal Fellowship program (DA).

1 Introduction

Critical transitions have received considerable attention in ecology, geophysics, hydrology and economics for the last decade [12]. They occur when natural systems drastically shift from one state to another. Comparatively less attention has been given to carefully characterize the underlying dynamic structure of the system under study. We believe the focus should change from describing, and understanding single transitions to characterizing the full dynamic behavior of the systems along with the environmental conditions in which these transitions occur. In epidemiology, critical transitions may underlie and potentially enhance (or undermine) attempts to control and eliminate infectious pathogens. Following an intervention, the trajectory of the host-pathogen system may cross a critical transition where pathogen prevalence drops to apparent eradication. However, the final success of eradication efforts depends strongly on dynamic underlying structure of the transition. Critical transitions are often associated to the coexistence of alternative equilibria. In that case, small changes in a driving parameter can lead to large shifts from low to high levels of prevalence (or vice versa). Continuous external pressure on critical transmission parameters, or seasonal variation in vector abundance, can also lead to hysteresis, whereby the inertial response of the system would effectively keep it trapped longer in either the endemic or disease-free state.

There is some (theoretical) evidence for the existence of alternative steady-states in infectious disease dynamics [3, 6, 7]. Here, we decribe one potentially important pre-condition for the existence of alternative steady states in malaria that stems from the complex immune response of the host to a highly diverse pathogen, the Plasmodium parasite. Humans are infected by concurrent multiple strains of the pathogen (superinfection). As as consequence, malaria infections are not fully immunizing, and multiplicity of infection is common in endemic regions. Under these conditions, rates of full recovery slow down. As a consequence, significant levels of superinfection create a positive feedback between infecting mosquitoes, which increase as humans remain infected longer, and disease prevalence, which also increases at the exposure to infecting mosquitoes increases. This loop has the potential to generate multiple alternative equilibria and associated tipping points.

We provide a model formulation of superinfection that explicitly allows infections to occur concurrently without interfering with each other. In addition, we present a semi-analytical, but general approach to identify alternative equilibria in models for vector-transmitted diseases. We then apply these methods to a vector-borne disease model (SECIR-LXVW) that has been successfully used to understand the origins of environmentally driven fluctuations of malaria, and the potential impact of increasing temperatures, in epidemic regions [1]. We demonstrate that irrespective of the details, superinfection consistently creates tipping points that can generate hysteresis in responses to control efforts (as well as seasonal variation in vector abundance). We argue that complex malaria immunity underlies abrupt transitions in response to control strategies or slight environmental variation. Models that fail to consider the complexity of malaria-induced immunity response may be misleading, and, therefore, their utility in practice is very limited when used to examine transitions towards low prevalence levels in response to different control strategies affecting the vectors as well as the pathogen.

2 The Model

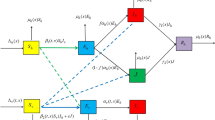
The model can be considering an extension of the standard Ross–McDonald model [8,9,10,11]. Details on model formulation and parameter definitions (including biologically reasonable parameter value ranges) are found in Alonso, Bouma and Pascual [1]). The model considers the dynamics of both humans and mosquitoes populations by means of two sub-models (Eqs. 1 and 2) that are coupled through mosquito bites; see Fig. 1b. The full ODE system can be written as:

$$\begin{aligned} \frac{dS}{dt}= & {} f_H\,N - \beta \,\,S + \sigma R -\delta \,S + \rho \,\,C \nonumber \\ \frac{dE}{dt}= & {} \beta \,S - \delta \,E -\gamma \,E\nonumber \\ \frac{dI}{dt}= & {} (1-\chi )\,\gamma \,E - \eta \,\beta \,\,I + \nu \,\,C - r\,\,I-\Psi \,\,I-\,\delta \,I \nonumber \\ \frac{dR}{dt}= & {} -\sigma R + r\,\,I -\delta \,R\nonumber \\ \frac{dC}{dt}= & {} \chi \,\gamma \,E + \eta \,\beta \,\,I -\nu \,\,C - \rho \,\,C-\alpha \,\,C -\delta \,C \end{aligned}$$

(1)

$$\begin{aligned} \frac{dL}{dt}= & {} f\,(X+V+W)\,\left( \frac{K_0-L}{K_0}\right) - \delta _L\,L - d_L\,L\nonumber \\ \frac{dX}{dt}= & {} -c\,a\,y\,X - \delta _M\,X +d_L\,L\nonumber \\ \frac{dV}{dt}= & {} +c\,a\,y\,X - \gamma _V\,V -\delta _M\,V\nonumber \\ \frac{dW}{dt}= & {} \gamma _V\,V - \delta _M\,W, \end{aligned}$$

(2)

where N is the total human population, which is assumed constant ($f_H=\delta$), y is the fraction of infectious humans ($y = (C+I)/N$) or disease prevalence, $\beta$ is the per capita rate of disease acquisition by humans through infectious bites ($\beta = a\,b\,W/N$), and r is a function of the number of infectious mosquitoes—see Eq. (3). This is a key point of our formulation: the way effective per capita recovery rates, r, behave as transmission intensity (the rate of infectious bites per human) change. Under the assumptions that (1) infectious bites arrive at a constant Poissonian rate, (2) the individual infections within a host progress independently, and (3) last a constant period, 1/$r_0$, Dietz, Molineax, and Thomas [4] derived the following expression for the effective per capita recovery rate,

$$\begin{aligned} r(\Lambda ) = \frac{\Lambda }{\exp (\Lambda /r_0)-1}, \end{aligned}$$

(3)

where $\Lambda$ denotes the rate of total infectious bites per human ($\Lambda = a\,W/N$), and $r_0$, is the basal recovery rate when disease transmission is very low (more precisely, in the limit of the infectious mosquito population tending to zero). Thus, the higher the rate of infectious bites per human host, $\Lambda$, the slower the disease clearance rate, and, therefore, the longer humans remain infectious. In vector-borne diesase models, the $\Lambda$ parameter is usually measured per year, and called the entomological inoculation rate (EIR).

Fig. 1

The human-mosquito SECIR-LXVW coupled model. Fluctuations in rainfall and temperature induce variability in malaria cases a through the dynamics of disease transmission represented in the model b including response functions that map temperature and rainfall onto certain mosquito model parameters. Model predictions capture real variability in cases including an abrupt shift to higher variability in the 2nd half of the time series (c) [1]. The model also predicts hysteresis (d)

3 Results

3.1 Saddle-Point Bifurcation

Stationary points of the coupled system are identifed by a semi-analytical method that consists of first finding the equilibria of the two submodels separately, this is, first, finding the expression for the number of infectious mosquitoes as a function of a given fraction of infectious humans (according to the mosquito submodel), and, second, the expression for the fraction of infectious humans for a given number of infecting mosquitoes (according to the human submodel). The fixed points should be, therefore, defined by the intersection of these two curves; see Fig. 2. The generality and feasibility of this method relies on the linearity of the human and mosquito submodels when considered separately. This means that both the human submodel (for a given number of infectious mosquitoes, $W^{\star }$), and the mosquito submodel (for a given fraction of infectious humans, y) are linear ODE systems.

Fig. 2

Saddle-node bifurcation and mosquito biting rates

Figure 2 shows that the intersection of the curves can produce more that one fixed point. As the biting rate a increases, the system undergoes two bifurcations. The first one corresponds to a transcritical bifurcation [5], and represents the transition from a free-disease situation ($R_0 < 1$) to an endemic stable equilibrium ($R_0 > 0$). The second one corresponds to a saddle node bifurcation (also called a tangential or fold bifurcation). The tangential intersection of the two curves defines a critical biting rate ($a_C=0.19089$). For $a > a_C$, there is the sudden appearance of a pair of resting points, a saddle node and a second stable point with a higher fraction of total infectious humans. The first stable point corresponding to a lower disease prevalence remains. As a result, two basins of attraction coexist, each consisting of initial conditions that lead to one of the two alternative stable states, separated by the existence, of an intermediate unstable state.

3.2 Hysteresis

Coexistence of stable equilibria give rise to a hysteretic behavior. When an external perturbation is applied through a gradual increase of a model parameter (for instance, the biting rate, a), the system responds with an abrupt, non-linear increase in disease prevalence. However, the symmetric gradual decrease of the same parameter is unable to drive the system back to the initial disease incidence levels. This involves an asymmetry in the temporal trajectories from endemicity to elimination, and from elimination to re-emergence. These hysteresis effects are illustrated in Fig. 1d. Although decreasing a back to its initial low values would eventually lead the system to settle down at the initial low incidence equilibrium, the transient trajectory to this state can take very long.

4 Conclusion

Our work demonstrates that inclusion of superinfection in malaria models, not only determines the lengthening of infectious periods [4], but is a key factor responsible for the coexistence of multiple stationary states, and the possibility of nonlinear regime shifts, including hysteresis. This has important implications [2]. Small changes in parameters (for instance, biting rate a or mosquitoes’ carrying capacity K) can give rise to large changes in disease incidence. Control efforts may see no progressive decrease of incidence until a sudden effect finally occurs. Conversely, the progressive relaxation of control efforts in endemic regions could generate sudden transitions from low to high incidence. Finally, concerning variability, as it is conjectured in Fig. 1c, since mosquito vital rates critically respond to temperature, sudden shifts from low to large fluctuations in incidence may follow in epidemic regions as average temperatures slowly increase due to global warming.