Disjoint Clustering in Combinatorial Circuits

Abstract

As the modern integrated circuit continues to grow in complexity, the design of very large-scale integrated (VLSI) circuits involves massive teams employing state-of-the-art computer-aided design (CAD) tools. An old, yet significant CAD problem for VLSI circuits is physical design automation. In this problem, one needs to compute the best physical layout of millions to billions of circuit components on a tiny silicon surface. The process of mapping an electronic design to a chip involves several physical design stages, one of which is clustering. Even for combinatorial circuits, there exists several models for the clustering problem. In particular, our primary consideration is the problem of disjoint clustering in combinatorial circuits for delay minimization (CN). The problem of clustering with replication for delay minimization has been well-studied and known to be solvable in polynomial time. However, replication can become expensive when it is unbounded. Consequently, CN is a problem worth investigating. We establish the computational complexities of several variants of CN. We also present a 2-approximation algorithm for an NP-hard variant of CN.

This research was supported in part by the Air Force Research Laboratory Information Directorate (AFRL/RI), through the Air Force Office of Scientific Research (AFOSR’s) Summer Faculty Fellowship Program, and the AFRL/RI Information Institute®, contract numbers FA9550-15-F-0001 and FA8750-16-3-6003.

1 Introduction

In this paper, we focus on the problem of disjoint clustering in combinatorial circuits for delay minimization (CN). Generally, it is not possible to place every circuit element in one chip because of various requirements and constraints. As a result, the circuit is partitioned into clusters, where each cluster represents a chip in the overall circuit design. While satisfying specific design constraints (e.g., cluster capacity), the circuit elements are assigned to clusters [11].

Gates and their interconnections usually have delays. The delays of the interconnections are determined by the way the circuit is clustered. Intra-cluster delays, d, are associated with the interconnections between gates in the same cluster. Inter-cluster delays, D, are associated with the interconnections between gates in different clusters. The delay along a path from an input to an output is the sum of the delays of the gates and interconnections on the path. The delay of the overall circuit, induced by a clustering, is the longest delay among all paths connecting an input to an output.

The problem of clustering combinatorial circuits for delay minimization when logic replication is allowed (CA) is well-studied [6, 11] and frequently arises in VLSI design. In CA, the goal is to find a clustering of a circuit that minimizes the delay of the overall circuit. CA is known to be solvable in polynomial time [6, 11]. With replication, circuit elements may be assigned to more than one cluster. Therefore, unbounded replication can be quite expensive. As systems grow in complexity, disjoint clustering (i.e., clustering without logic replication) becomes more necessary. It follows that there is a pressing need to study CN in VLSI design. In this paper, we consider several variants of CN and discuss their computational complexities. A more detailed discussion of related work can be found in the extended version of this paper.

The rest of this paper is organized as follows: The problems that we study are formally described in Sect. 2. In Sect. 3, we give some computational complexity results. In Sect. 4, we propose an approximation algorithm for an NP-hard variant of CN. We conclude the paper with Sect. 5, by summarizing our main results and identifying avenues for future work.

2 Statement of Problems

In this section, we define the main graph-theoretic concepts that are used in this paper.

Graphs considered in this paper do not contain loops or parallel edges. The degree of a vertex v of an undirected graph G is the number of edges of G that are incident with v. The maximum degree of G is denoted by $\varDelta (G)$ or simply $\varDelta$ when G is known from the context.

A directed path (or, just a path) of a directed graph G is a sequence $Q = v_0 e_1 v_1 \ldots e_l v_l$, where $v_0, v_1,\ldots , v_l$ are vertices of G, $e_1, \ldots , e_l$ are edges (also called arcs) of G, and $e_j=(v_{j-1}, v_j)$, $1\le j \le l$. We call l the length of the path Q, and sometimes we say that Q is an l-path of G. If $v_0=v_l$, then Q is called a directed cycle (or, just cycle). G is said to be a directed acyclic graph (DAG), if it contains no directed cycles. For further terminology on graphs and directed graphs, one may consult [1, 13].

A cluster is an arbitrary subset of the vertices of a DAG, and it does not have to be strongly connected. If C is a cluster in a DAG G, then an edge is said to be a cut-edge if it connects a vertex of C to a vertex from $V(G)\backslash C$. The degree of C is the number of cut-edges incident with a vertex in C.

The indegree and outdegree of a vertex are the number of arcs that enter and leave the vertex, respectively. A source (sink, resp.) is a vertex with indegree zero (outdegree zero, resp.). It is well-known that every DAG has a source and a sink [1].

2.1 Formulation of CN Using Combinatorial Circuits

A combinatorial circuit can be represented as a DAG $G=(V,E)$. In G, each vertex $v \in V$ represents a gate, and each edge $(u,v) \in E$ represents an interconnection between gates u and v. In general, each gate in a circuit has an associated delay [9]. In the model that we consider in this paper, each interconnection has one of the following types of delays: (1) an intra-cluster delay, d, when there is an interconnection between two gates in the same cluster, or (2) an inter-cluster delay, D, when there is an interconnection between two gates in different clusters.

The delay along a path from an input to an output is the sum of the delays of the gates and interconnections that lie on the path. The delay of the overall circuit is the maximum delay among all source to sink paths in the circuit.

A clustering partitions the circuit into disjoint subsets. A clustering algorithm tries to achieve one or both of the following goals, subject to one or more constraints:

• (1) The delay minimization through the circuit [3, 6, 9, 11].

• (2) The minimization of the total number of cut-edges [2, 4, 7, 8, 12].

In this paper, we study CN under the delay model described as follows:

• 1. Associated with every gate v of the circuit, there is a delay $\delta (v)$ and a size w(v).

• 2. The delay of an interconnection between two gates within a single cluster is d.

• 3. The delay of an interconnection between two gates in different clusters is D, where $D \gg d$.

The size of a cluster is the sum of the sizes of the gates in the cluster. The precise formulation of CN is as follows:

Given a combinatorial circuit, with each gate having a size and a delay, maximum degree $\varDelta$, intra- and inter-cluster delays d and D, respectively, and a positive integer M called cluster capacity, the goal is to partition the circuit into clusters such that

• 1. The size of each cluster is bounded by M,

• 2. The delay of the circuit is minimized.

2.2 Graph-Theoretic Formulation of CN

In the rest of the paper, we focus on a graph-theoretic formulation of CN. Given a clustering of a combinatorial circuit represented as a DAG $G=(V,E)$, the delays on the interconnections between gates induce an edge-delay function $\delta : E\rightarrow \{d, D\}$ of G. The weight of a cluster is the sum of the weights of the vertices in the cluster. The delay-length of a directed path $P=v_0e_1v_1\dots e_{l}v_l$ of G is $\sum ^l_{i=0}\delta (v_i) + \sum ^l_{i=1}\delta (e_i),$ where $\delta (e_i)$ is equal to d if $v_{i-1}$ and $v_i$ are inside the same cluster, or D, otherwise.

CN$\langle X, M, \varDelta \rangle$ is formulated (graph-theoretically) as follows: Given a DAG $G=(V,E)$, with vertex-weight function $w: V \rightarrow \mathbb {N}$, delay function $\delta : V \rightarrow \mathbb {N}$, maximum degree $\varDelta$, constants d and D, and a cluster capacity M, the goal is to partition V into clusters such that

• 1. The weight of each cluster is bounded by M,

• 2. The maximum delay-length of any path from a source to a sink of G is minimized.

The symbol X in our 3-tuple notation may represent some weighted set W of vertices or some unweighted set N of vertices. For some sets, $W=[n]$, where $[n]=\{1, 2, 3, \ldots , n\}$ with $n \in \mathbb {N}$. The symbol M is the cluster capacity.

A clustering of G, such that the weight of each cluster is bounded by M, is called feasible. Given a feasible clustering of G, one can consider the corresponding edge-length function $\delta : E\rightarrow \{d, D\}$ of G. A clustering of G is optimal if the maximum delay-length of any path from a source to a sink is the minimum among all clusterings.

The main contributions of this paper are as follows:

• 1. Establishing the computational complexities of several variants of CN$\langle X, M, \varDelta \rangle$ (Sect. 3).

• 2. Design and analysis of a 2-approximation algorithm for an NP-hard variant of CN$\langle X, M, \varDelta \rangle$ (Sect. 4).

3 Computational Complexities of Clustering Variants

In this section, we establish the computational complexities of several variants of CN.

In [5], CN is considered under area constraints and pin constraints, separately. The decision version of the area-constrained problem is formulated by them as follows: Given a directed acyclic graph $G=(V,E)$ representing a combinatorial circuit, a delay $\delta (v)$ and area $\alpha (v)$ for each $v \in V$, an inter-cluster delay constant $D \ge 0$, a cluster area bound M, and a maximum delay bound B, determine whether there exists a clustering with no replication so that in each cluster C, $\sum _{v \in C} \alpha (v) \le M$, and for any path $P=(p_1, p_2, \ldots , p_n)$ from a primary input to a primary output, $\sum _{i=1}^{n} \delta (p_i) + k \cdot D \le B$, where $k=|\{(p_i,p_{i+1}):(p_i,p_{i+1} \in P) \wedge (p_i,p_{i+1} \text { appear in different clusters})\}|$. Note that primary inputs and primary outputs represent sources and sinks of the DAG, respectively. The decision version of the pin-constrained problem has an analogous formulation. However, the area of each cluster C is not restricted, while the total number of I/O pins of each cluster must not exceed a given constant Q.

Fig. 1.

Gadgets used to represent variables and clauses.

We observe that the decision version of CN$\langle W, M, \varDelta \rangle$ belongs to NP. This follows from the observation that if we have an edge-weighted DAG, then we can compute a path of maximum edge-weight in polynomial time. Below, we will consider several restrictions of CN$\langle W, M, \varDelta \rangle$, which also belong to NP.

Our first result establishes NP-hardness and inapproximability of CN$\langle [4], 5, \varDelta \rangle$.

Theorem 1

CN$\langle [4], 5, \varDelta \rangle$ is NP-hard.

Proof

We recall CN$\langle [4], 5, \varDelta \rangle$ as follows: Given a DAG $G=(V,E)$, with vertex-weight function $w: V \rightarrow \{1,2,3,4\}$, $\delta (v)=0 \; \forall v \in V$, maximum degree $\varDelta$, constants d and D, and cluster capacity $M=5$, the goal is to partition V into clusters such that the weight of each cluster is bounded by M, and the maximum delay-length of any path from a source to a sink of G is minimized.

To show that CN$\langle [4], 5, \varDelta \rangle$ is NP-hard, we reduce from 3SAT (cf. Theorem 2.1 in [5]). For that purpose, we recall 3SAT as follows: Given a 3-CNF formula $\phi$ with n variables $x_1, \ldots , x_n$ and m clauses $C_1, \ldots , C_m$, the goal is to check whether $\phi$ has a satisfying assignment.

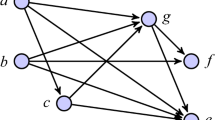
Let each variable $x_i$ $(1 \le i \le n)$ be represented by a variable gadget as shown in Fig. 1(a). Let each clause $C_j$ $(1 \le j \le m)$ be represented by a clause gadget as shown in Fig. 1(b). If a variable $x_i$ or its complement $\bar{x}_i$ is the pth literal of a clause $C_j$, where $p \in \{1,2,3\}$, then we add edges ($x_i, z_{jp}$) or ($\bar{x}_i, z_{jp}$), respectively. The resulting DAG G represents a combinatorial circuit. Let U denote the set of all vertices labeled $x_i$ or $\bar{x}_i$ $(1 \le i \le n)$. There are n sources labeled $T_i$ $(1 \le i \le n)$ and m sinks labeled $C_j$ $(1 \le j \le m)$. They are connected through some vertices in U and $3 \cdot m$ vertices labeled $z_{jp}$ $(1 \le j \le m, 1 \le p \le 3)$. Each $z_{jp}$ is connected to exactly one variable gadget. For every j, no two vertices in the set $\{z_{j1}, z_{j2}, z_{j3}\}$ are adjacent to both $x_i$ and $\bar{x}_i$ of the same variable gadget. In other words, $x_i$ and $\bar{x}_i$ cannot both be connected to the same clause gadget. Every $T_{i}$ and $C_j$ has a weight of 1, every $x_i, \bar{x}_i \in U$ has a weight of 4, and every $z_{jp}$ has a weight of 2. Let $d=0$ and let D be any positive integer. All vertices are given a delay of 0. The cluster capacity M is set to 5, and set $k=2\cdot D$. It is shown that an instance I of 3SAT is a “yes” instance if and only if an instance $I'$ of CN$\langle [4], 5, \varDelta \rangle$ is a “yes” instance.

Theorem 2

CN$\langle N, 2, 3 \rangle$ is NP-hard.

Proof

We recall CN$\langle N, 2, 3 \rangle$ as follows: Given a DAG $G=(V,E)$, with $w(v)=1 \; \forall v \in V$, $\delta (v)=0 \; \forall v \in V$, maximum degree $\varDelta =3$, constants d and D, cluster capacity $M=2$, and a positive integer k, the goal is to partition V into clusters such that the weight of each cluster is bounded by M, and the maximum delay-length of any path from a source to a sink of G is minimized.

In order to establish NP-hardness of CN$\langle N, 2, 3 \rangle$, we present a reduction from 3SAT$_{\le 3, \le 2}$. For that purpose, we recall 3SAT$_{\le 3, \le 2}$ as follows: Given a 3-CNF formula $\phi$ with n variables $u_1, \ldots , u_n$ and m clauses $C_1, \ldots , C_m$, such that each variable occurs at most three times and each literal occurs at most twice, the goal is to check whether $\phi$ has a satisfying assignment. Note that the requirement that each clause has exactly three literals is relaxed in this restriction of 3SAT. Any variable, say $u_i$, with q occurrences (for some $q > 3$) can be replaced with q new variables $w_1, \ldots , w_q$. The clauses $(\bar{w}_1 \vee w_2) \wedge (\bar{w}_2 \vee w_3) \wedge (\bar{w}_q \vee w_1)$ can then be added to $\phi$ to ensure that the q new variables retain the truth assignment of the original variable $u_i$ [10].

Given an instance I of 3SAT$_{\le 3, \le 2}$, we construct an instance $I'$ of CN$\langle N, 2, 3 \rangle$. Let each variable $u_i$ $(1 \le i \le n)$ be represented by a variable gadget as shown in Fig. 2(a), where the dashed arrows indicate possible successors. Note that since each variable $u_i$ occurs at most three times, then the size of the neighborhood of {$u_{i}, \bar{u}_{i}$} is at most three. Let each clause $C_j$ ($1 \le j \le m$) be represented by a clause gadget as shown in Fig. 2(b). A set of edges also connects clause gadgets to variable gadgets. For example, if the p-th literal of clause $C_j$ is the $\alpha$-th occurrence of some literal $u_a$, where $p \in \{1,2,3\}$, $\alpha \in \{1,2\}$ and $a \in \{1, \ldots , n\}$, then we add edge $(x_{jp}, u_{a\alpha }')$. Every vertex has a weight of 1. We set $d=0$ and let D be any positive integer. All vertices are given a delay of 0. The cluster capacity M is set to 2, and we set $k=3\cdot D$. The description of $I'$ is complete.

Fig. 2.

Gadgets used to represent variables and clauses.

Observe that $I'$ can be constructed from I in polynomial time. To complete the proof of the theorem, we show that I is a “yes” instance of 3SAT$_{\le 3, \le 2}$ if and only if $I'$ is a “yes” instance of CN$\langle N, 2, 3 \rangle$.

Suppose that I is a “yes” instance of 3SAT$_{\le 3, \le 2}$. This means that there exists an assignment of $\phi$ such that every clause has at least one true literal. If literal $u_i$ (or $\bar{u}_i$) is set to true, then we cluster the vertices as follows:

• 1. $t_i$ is clustered with $v_i$ and $f_i$ is clustered with $\bar{v}_i$ (or $t_i$ is clustered with $\bar{v}_i$ and $f_i$ is clustered with $v_i$).

• 2. For each $r \in \{1,2\}$, $\bar{u}_{ir}$ is clustered with $\bar{u}_{ir}'$ (or $u_{ir}$ is clustered with $u_{ir}'$).

• 3. If the r-th occurrence of literal $u_i$ (or $\bar{u}_i$) is the p-th literal of clause $C_j$, then $u_{ir}'$ (or $\bar{u}_{ir}'$) is clustered with clause gadget vertex $x_{jp}$, where $p \in \{1,2,3\}$.

• 4. For any p-th literal of clause $C_j$ that is set to true, then $x_{jp}$ is clustered with its successor.

• 5. The successors of the variable gadget vertex $f_i$, say $V_{f_i}$, are clustered in such a way that the edges of the underlying undirected graph of $G[V_{f_i}]$ form a perfect matching.

• 6. The clause gadget vertex $c_{j5}$ and its predecessors, say $V_{c_{j5}}$, are clustered in such a way that the edges of the underlying undirected graph of $G[V_{c_{j5}} \cup c_{j5}]$ form a perfect matching.

• 7. All other vertices are clustered alone.

Observe that the cluster capacity constraint is satisfied, and the maximum delay-length of any path from a source to a sink is $3\cdot D$. This means that $I'$ is a “yes” instance of CN$\langle N, 2, 3 \rangle$.

Conversely, suppose that $I'$ is a “yes” instance of CN$\langle N, 2, 3 \rangle$. This means that there is a way of partitioning the vertices of G into clusters of capacity $M=2$, such that the delay-length of any path from a source to a sink is at most $3\cdot D$. Observe that under any partitioning, the delay-length of any path from a source to a sink is at least $3\cdot D$. In any partitioning with delay-length equal to $3\cdot D$, we have that either $t_i$ is clustered with $v_i$ or $t_i$ is clustered with $\bar{v}_i$, for every $i \in \{1, \ldots , n\}$. Furthermore, in any partitioning with delay-length equal to $3\cdot D$, there is at least one $x_{jp}$ that must be clustered with its successor. If $t_i$ is clustered with $v_i$, then for each $r \in \{1,2\}$, $\bar{u}_{ir}$ must be clustered with $\bar{u}_{ir}'$. Set literal $u_i$ to true and consider each $u_{ir}'$ free. Otherwise, if $t_i$ is clustered with $\bar{v}_i$, then for each $r \in \{1,2\}$, $u_{ir}$ must be clustered with $u_{ir}'$. Set literal $\bar{v}_i$ to true and consider each $\bar{u}_{ir}'$ free. At least one $x_{jp}$ is clustered with its successor, namely some free vertex. This means that at least one true literal appears in every clause. Thus, a satisfying clustering for G yields a satisfying assignment for $\phi$. Hence, I is a “yes” instance of 3SAT$_{\le 3, \le 2}$.

In order to present our next results, we will need some definitions. We say that two edges of G are independent if they are not incident with the same vertex. A matching of G is a set of pairwise independent edges of G. A matching is maximal if it is not a subset of a larger matching.

Proposition 1

For any instance of CN$\langle N,2,\varDelta \rangle$ there exists an optimal clustering, such that the edges of G with delay d form a maximal matching of G.

Proof

Consider an optimal clustering of G. Since $M=2$, we have that any two edge with delay d are independent. Thus, they form a matching I. Now, if I is not maximal, then there is an edge e, such that $I\cup \{e\}$ is a matching. Put the end-vertices of e to the same cluster. Observe that the resulting clustering is feasible, moreover, its delay does not exceed the delay of the original clustering. Thus, the resulting clustering is again optimal. By continuing this process, we will end-up with a clustering such that the edges of delay d form a maximal matching. The proof is complete.

Our next proposition states that the clustering problem remains difficult even if we assume that the input DAG G contains a path which contains sufficiently many edges.

Proposition 2

For each fixed integer t, CN$\langle N,2,3 \rangle$ remains NP-hard even if we assume that G contains a path with at least t edges.

Proof

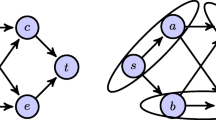
We present a reduction from CN$\langle N,2,3 \rangle$ to its restriction stated in the statement. Assume that the input DAG G of maximum degree 3 is given. Consider a component which is a directed 4-cycle, whose edges are directed from the left to right. Let $c_1$ be the source in it. Assume that $c_1$ is adjacent to $c_2$ and $c_3$, which are neither source nor a sink. Finally, let them be adjacent to the sink $c_4$ (Fig. 3).

Fig. 3.

The reduction with the directed 4-cycle.

Now, let the input DAG G be given which is of maximum degree three. Consider all edges of G which are incident to a source, and replace them with a 4-cycle (one 4-cycle per every edge), that is, if sw is an edge of G, then we replace it with a new 4-cycle, and connect s to $c_1$ and $c_4$ to w (Fig. 3). Let $G'$ be the resulting DAG. Observe that this procedure increases the length of any longest path by three. Thus, applying it sufficiently many times, we can get a DAG with desired lower bound for the length of the longest path. Moreover, observe that this process does not increase the maximum degree of the vertex, that is, the resulting graph is still of maximum degree three.

Let OPT(H) denote the optimal delay in a DAG H. We claim that

$$\begin{aligned} OPT(G')=OPT(G)+(d+2\cdot D). \end{aligned}$$

Consider an optimal clustering in G. Let $e=sw$ be an edge of G. If it is a d-edge in G, then declare the edges $sc_1$ and $c_4w$ of $G'$ as a d-edge. The rest of the edges of $G'$ in the part corresponding to e are declared as D-edges. On the other hand, if e is a D-edge, then declare the edges $c_1c_2$ and $c_3c_4$ as d-edges, and the rest of edges corresponding to e as D-edges. Now consider a critical path P. If it starts with a d-edge on P, then its delay d is replaced with $2\cdot (d+D)$ in $G'$. Thus the increase of the delay is $d+2\cdot D$. If it started with a D-edge, then its delay D becomes $d+3\cdot D$ in $G'$. Thus, the increase in the delay is again $d+2\cdot D$. Hence, we have the same increase in the delay. Clearly, this implies that

$$\begin{aligned} OPT(G')\le OPT(G)+(d+2\cdot D). \end{aligned}$$

To prove the converse inequality, let us show that we can always find an optimal clustering such that $sc_1$ and $c_4w$ are d-edges or D-edges at the same time. If $sc_1$ and $c_4w$ are d-edges then we are done. Thus, we can assume that one of them is a D-edge. Then we show that we can assume that the other one is also a D-edge. First, assume that $sc_1$ is a d-edge and $c_4w$ is a D-edge. Since we can always assume that the optimal clustering is a maximal matching (Proposition 1), we have that one of the edges of the 4-cycle incident to $c_4$ is a d-edge f. Now, if we consider a new clustering of $G'$ by replacing the edge $sc_1$ with the edge opposite to f (the unique edge of the 4-cycle that is not adjacent to f) in the 4-cycle as a d-edge. Clearly, the resulting clustering has the same delay as the original one. However, $sc_1$ now is a D-edge. Similarly, assume that $c_4w$ is a d-edge and $sc_1$ is D-edge. Since we can always assume that the optimal clustering is a maximal matching (Proposition 1), we have that one of the edges of the 4-cycle incident to $c_1$ is a d-edge f. Now, if we consider a new clustering of $G'$ by replacing the edge $c_4w$ with the edge opposite to f in the 4-cycle as a d-edge. Clearly, the resulting clustering has the same delay as the original one. However, $c_4w$ now is a D-edge. Thus, we can always find an optimal clustering such that $sc_1$ and $c_4w$ are d-edges or D-edges at the same time.

The proved property allows us to get a clustering in G simply by looking at $sc_1$ and $c_4w$. If they are d-edges at the same time, we declare sw as a d-edge in G. On the other hand, if they are D-edges, then we declare sw as a D-edge in G. Observe that the resulting clustering of G will have delay at most $OPT(G')-(d+2\cdot D)$. Thus,

$$\begin{aligned} OPT(G)\le OPT(G')-(d+2\cdot D) \end{aligned}$$

or

$$\begin{aligned} OPT(G')\ge OPT(G)+(d+2\cdot D). \end{aligned}$$

This completes the proof of the equality. The proved equality implies that optimizing the delay in $G'$ is the same that optimizing in G. Thus the above process is a reduction.

Let us say that a graph is cubic if any vertex is of degree 3. We are ready to obtain the final result of this section.

Theorem 3

For each fixed integer t, CN$\langle N,2,3 \rangle$ remains NP-hard even if we assume that G is a cubic graph that contains a path with at least t edges.

Proof

We get a reduction from the restriction of CN$\langle N,2,3 \rangle$ where we assume that G contains a path with at least 6 edges. Since $M=2$, we have that $OPT(G)\ge 3\cdot D$. As $\varDelta =3$, we have that the vertices of G are of degree 0, 1, 2 or 3. Now, we will show how to get rid of the vertices which have degree less than three. First, if we have a vertex of degree 0, we can remove it from G. In order to overcome the vertices of degree 1 and 2, we will make use of the following orientation of the complete graph $K_4$ on 4 vertices by removing an edge $e=uv$. Let the other two vertices of $K_4$ be $u'$ and $v'$. Direct the edges starting from $u'$ towards u and v. Direct the edges starting from $v'$ towards u and v. Finally, direct the edge $u'v'$ from $v'$ to $u'$ (Fig. 4).

Fig. 4.

The orientation of the edges of $K_4-e$.

Now, assume that our input DAG G contains a vertex w of degree one. Assume that w is a source. Take a copy of the above orientation of $K_4$ minus an edge, and join w to u and v with directed edges, so that w is a source, and u and v are sinks in resulting DAG $G'$. Observe that in the added part the maximum delay will be at most $2\cdot D$, which is less than OPT(G). Since w is a source, the added part will play no role. Similarly, one can overcome the case when w is a sink. One just needs to reverse the orientations of edges in the copy of $K_4$ minus an edge.

Next let us assume that we have a vertex w of degree two. First, let us assume that w is a source. We add a new vertex $w'$ and join w to $w'$ with a directed edge. Observe that w is of degree 3 and $w'$ is of degree one. Thus we can apply the trick from the previous paragraph. Similarly, if w is a sink, we will join $w'$ to the vertex w with a directed edge and again apply the trick from the previous paragraph.

Thus, we are left with the case when w-the degree two vertex, is neither a source nor a sink. Let x and z be the neighbors of w such that xw and wz are directed edges. We consider two cases. If z is a sink in G, then we add a new vertex $w'$ of degree 1 and join it to w with a directed edge $w'w$. Observe that in the optimal clustering $w'$ will not be on a path of optimal delay as it reaches only z and the delay of this path is at most $2\cdot D$. On the other hand, if we assume that G contains a path of length at least six, the optimal delay will be at least $3\cdot D$. Finally, if we assume that z is not a sink, then we add a new vertex $w'$ and join w to $w'$ with a directed edge $ww'$. Since z is not a sink and $M=2$, in any clustering z will be incident to at least one D-edge. Hence, there will be a path of optimal delay in $G'$ that will not terminate at $w'$. Thus, the addition of $w'$ will not play a role. Since $w'$ is a degree one vertex, we can overcome it via the trick mentioned above. Thus, without loss of generality, we can assume that the input graph in CN$\langle N,2,3 \rangle$ is a cubic graph.

4 A 2-approximation Algorithm

We now provide an integer program (IP) for CN$\langle W, M, \varDelta \rangle$.

4.1 An IP for CN$\langle W, M, \varDelta \rangle$

Let $w_j$ be the weight of vertex j. Define $x_{ij}$ to be an integer variable that is set to 1 if vertices i and j are in the same cluster, and 0 otherwise. We present the following IP:

Packing constraints

$$\begin{aligned} x_{ii}=1, \quad \forall i \in V \end{aligned}$$

(1)

$$\begin{aligned} \sum _{j=1}^{n}w_{j} \cdot x_{ij} \le M, \quad \forall i \in V \end{aligned}$$

(2)

Consistency constraints

$$\begin{aligned} x_{ij} = x_{ji}, \quad \forall i,j \in V \end{aligned}$$

(3)

$$\begin{aligned} x_{ik} \ge x_{ij}+x_{jk}-1, \quad \forall i,j,k \in V \end{aligned}$$

(4)

Condition (1) ensures that every vertex is clustered. Condition (2) ensures that every cluster has weight at most M. Condition (3) ensures that either i and j are in the same cluster or they are in different clusters. Likewise, condition (4) ensures that if i and j are in one cluster, and j and k are in one cluster, then i and k must be in the same cluster and all clusters are disjoint.

We now come to the objective function. For any vertex j, let $\delta _{j}$ be the delay at j in a clustering. This delay is completely dependent upon its predecessors. We can write

$$\begin{aligned} \delta _{j} = \max _{i: (i,j) \in E} \{\delta _{i}+d\cdot x_{ij}+D\cdot (1-x_{ij})\}. \end{aligned}$$

(5)

Hence the function to be minimized is $\delta _{t}$, where t is the sink of the circuit. Note that condition (5) can be easily linearized.

The correctness of reduction will be shown in the journal version of this paper.

4.2 An LP-rounding Algorithm for CN$\langle N, 2, \varDelta \rangle$

In this section, we present an LP-rounding algorithm for CN$\langle N, 2, \varDelta \rangle$.

Let LP$_{CN\langle N, 2, \varDelta \rangle }$ be the linear programming relaxation obtained from IP$_{CN\langle W, M, \varDelta \rangle }$ when vertices are unweighted and $M=2$ (i.e., the problem restricted to CN$\langle N, 2, \varDelta \rangle$), by replacing its 0-1 integrality constraints for $x_{ij}$ with $x_{ij} \in [0,1]$.

Theorem 4

Algorithm 1 is a 2-approximation algorithm.

Proof

Let Q be a path of G from a source to the sink t with maximum delay-length. Let OPT be the delay of an optimal clustering of G. This means that OPT is the sum of the fractional intra- and inter-cluster delays of the edges along Q. Let ALG be the delay of the clustering of G returned by Algorithm 1. Since the algorithm returns a solution with an integral delay, notice that for each intra-cluster edge $(i,j) \in Q$, the delay is increased by $d \cdot (1-\hat{x}_{ij})$. Moreover, for each inter-cluster edge $(i,j) \in Q$, the delay is decreased by $D \cdot (1-\hat{x}_{ij})$. Hence,

$$\begin{aligned} \frac{ALG}{OPT}&\le \dfrac{\sum _{(i,j) \in Q} d \cdot \hat{x}_{ij} + D \cdot (1-\hat{x}_{ij}) + \sum _{(i,j) \in Q} d \cdot (1-\hat{x}_{ij})- D \cdot (1-\hat{x}_{ij})}{\sum _{(i,j) \in Q} d \cdot \hat{x}_{ij} + D \cdot (1-\hat{x}_{ij})} \\&= 1 + \dfrac{\sum _{(i,j) \in Q} d \cdot (1-\hat{x}_{ij})- D \cdot (1-\hat{x}_{ij})}{\sum _{(i,j) \in Q} d \cdot \hat{x}_{ij} + D \cdot (1-\hat{x}_{ij})} \\&\le 1 + \dfrac{\sum _{(i,j) \in Q} d \cdot (1-\hat{x}_{ij})}{\sum _{(i,j) \in Q} d \cdot \hat{x}_{ij} + D \cdot (1-\hat{x}_{ij})} \\&\le 1 + \dfrac{\sum _{(i,j) \in Q} D \cdot (1-\hat{x}_{ij})}{\sum _{(i,j) \in Q} d \cdot \hat{x}_{ij} + D \cdot (1-\hat{x}_{ij})} \\&= 2 - \dfrac{\sum _{(i,j) \in Q} d \cdot \hat{x}_{ij}}{\sum _{(i,j) \in Q} d \cdot \hat{x}_{ij} + D \cdot (1-\hat{x}_{ij})} \\ \end{aligned}$$

5 Conclusion

In this paper, we studied the problem of disjoint clustering in combinatorial circuits for delay minimization (CN). We obtained the computational complexities of several variants of CN. We also proposed an approximation algorithm for a variant of CN and analyzed it.

We are interested in the following open problems:

• 1. Finding inapproximability bounds for variants of CN$\langle X, M, \varDelta \rangle$ using other assumptions.

• 2. Finding approximation, parameterized and exact exponential algorithms for other variants of CN$\langle X, M, \varDelta \rangle$.