Clustering without replication in combinatorial circuits

Abstract

The modern integrated circuit is one of the most complex products engineered to date. It continues to grow in complexity as years progress. As a result, very large-scale integrated (VLSI) circuit design now involves massive design teams employing state-of-the-art computer-aided design (CAD) tools. One of the oldest, yet most important CAD problems for VLSI circuits is physical design automation, where one needs to compute the best physical layout of millions to billions of circuit components on a tiny silicon surface (Lim in Practical problems in VLSI physical design automation, Springer, Dordrecht, 2008). The process of mapping an electronic design to a chip involves several physical design stages, one of which is clustering. Even for combinatorial circuits, there exists several models for the clustering problem. In particular, we consider the problem of clustering in combinatorial circuits for delay minimization, without permitting logic replication (CN). The problem of clustering for delay minimization when logic replication is allowed (CA) has been well-studied and is known to be solvable in polynomial time (Lawler et al. in IEEE Trans Comput 18(1):47–57, 1969; Rajaraman and Wong, in: 30th ACM/IEEE design automation conference, pp 309–314, 1993). However, unbounded logic replication can be quite expensive. It follows that CN is an important problem. We show that selected variants of CN are NP-hard. We also obtain approximability and inapproximability results for some of these problems. A preliminary version of this paper appears in Donovan et al. (in: 9th International conference on combinatorial optimization and applications, COCOA 2015, Proceedings, pp 334–347, 2015).

1 Introduction

In this paper, we consider the problem of clustering without replication in combinatorial circuits for delay minimization (CN). Combinatorial circuits implement Boolean functions and produce a unique output for every combination of input signals (Koshy 2004). The gates and their interconnections in the circuit represent implementations of one or more Boolean function(s). The Boolean functions are realized by the assignment of the gates to chips.

Due to manufacturing process requirements and capacity constraints, it is generally not possible to place all of the circuit elements in one chip. Consequently, the circuit is partitioned into clusters, where each cluster represents a chip in the overall circuit design. The circuit elements are assigned to clusters while satisfying specific design constraints (e.g., cluster capacity) (Rajaraman and Wong 1993).

Gates and their interconnections usually have delays. The delays of the interconnections are determined by the way the circuit is clustered. Intra-cluster delays are associated with the interconnections between gates in the same cluster. Inter-cluster delays are associated with the interconnections between gates in different clusters. The delay along a path from an input to an output is the sum of the delays of the gates and interconnections on the respective path. The delay of the overall circuit, with respect to a specific clustering, is the maximum delay among all paths that connect an input to any output in the clustered-circuit.

The problem of clustering combinatorial circuits for delay minimization when logic replication is allowed (CA) is well-studied (Lawler et al. 1969; Rajaraman and Wong 1993). It frequently arises in VLSI design. In CA, the goal is to find a clustering of a circuit that minimizes the delay of the overall circuit. CA has been shown to be solvable in polynomial time (Lawler et al. 1969; Rajaraman and Wong 1993). However, when replication is allowed, circuit elements may be assigned to more than one cluster. Thus, unbounded replication can be quite expensive. As systems become increasingly more complex, the need for clustering without logic replication is crucial. It follows that CN is an important problem in VLSI design.

In this paper, we consider several variants of CN and discuss their computational complexities. We design an approximation algorithm for one of these variants and obtain inapproximability results for other variants.

The rest of this paper is organized as follows: The problem is formally described in Sect. 2. We then examine the related work in Sect. 3. In Sect. 4, we give some hardness results for the clustering problem. We also show that our hardness results imply inapproximability below a certain threshold. In Sect. 5, we propose an approximation algorithm for solving the clustering problem, when the gates are unweighted and each cluster has at most two gates. We conclude the paper with Sect. 6, by summarizing our main results and identifying avenues for future work.

2 Statement of problems

In this section, we formally describe the problem studied in this paper. We start with graph preliminaries. Next, we formulate the problem using the language of combinatorial circuits. Finally, we represent such circuits as directed acyclic graphs and formulate the main problem using graph-theoretic terminology.

2.1 Graph preliminaries

In this subsection, we define the main graph-theoretic concepts that are used in the paper.

Graphs considered in this paper do not contain loops or parallel edges. The degree of a vertex v of an undirected graph G is the number of edges of G that are incident with v. The maximum degree of G is denoted by $\varDelta (G)$ or simply $\varDelta$ when G is known from the context.

Fig. 1

A DAG representing a combinatorial network with two sources and two sinks

A directed path (or, just a path) of a directed graph G is a sequence $Q = v_0 e_1 v_1 \ldots e_l v_l$, where $v_0, v_1,\ldots , v_l$ are vertices of G, $e_1, \ldots , e_l$ are edges (also called arcs) of G, and $e_j=(v_{j-1}, v_j)$, $1\le j \le l$. We call l the length of the path Q, and sometimes we say that Q is an l-path of G. If $v_0=v_l$, then Q is called a directed cycle (or, just cycle). G is said to be a directed acyclic graph (DAG), if it contains no directed cycles. For further terminology on directed graphs, one may consult (Bang-Jensen and Gutin 2010).

A cluster is an arbitrary subset of the vertices of a DAG, and it does not have to be strongly connected. If C is a cluster in a DAG G, then an edge is said to be a cut-edge if it connects a vertex of C to a vertex from $V(G)\backslash C$. The degree of C is the number of cut-edges incident with a vertex in C.

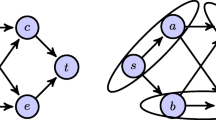
The indegree and outdegree of a vertex are the number of arcs that enter and leave the vertex, respectively. A source (sink, resp.) is a vertex with indegree zero (outdegree zero, resp.). It is well-known that every DAG has a source and a sink (Bang-Jensen and Gutin 2010). Let $\mathscr {I}$ and $\mathscr {O}$ be the set of sources and sinks of G, respectively. Notice that $\mathscr {I}=\{a, b\}$ and $\mathscr {O}=\{e,f\}$ in the DAG of Fig. 1; $C_1=\{a, c, g\}$ and $C_2=\{b, e, f\}$ represent a pair of disjoint clusters.

2.2 Formulation using combinatorial circuits

A combinatorial circuit can be represented as a DAG $G=(V,E)$. In G, each vertex $v \in V$ represents a gate, and each edge $(u,v) \in E$ represents an interconnection between gates u and v. In general, each gate in a circuit has an associated delay (Murgai et al. 1991). In the model that we consider in this paper, each interconnection has one of the following types of delays: (1) an intra-cluster delay, d, when there is an interconnection between two gates in the same cluster, or (2) an inter-cluster delay, D, when there is an interconnection between two gates in different clusters.

The delay along a path from an input to an output is the sum of the delays of the gates and interconnections that lie on the path. The delay of the overall circuit is the maximum delay among all source to sink paths in the circuit.

A clustering partitions the circuit into disjoint subsets. A clustering algorithm tries to achieve one or both of the following goals, subject to one or more constraints:

• (1) The delay minimization through the circuit (Rajaraman and Wong 1993).

• (2) The minimization of the total number of cut-edges (Hwang and Gamal 1995).

In this paper, we study CN under the delay model described as follows:

• 1. Associated with every gate v of the circuit, there is a delay $\delta (v)$ and a size w(v).

• 2. The delay of an interconnection between two gates within a single cluster is d.

• 3. The delay of an interconnection between two gates in different clusters is D, where $D \gg d$.

The size of a cluster is the sum of the sizes of the gates in the cluster. The precise formulation of CN is as follows:

Given a combinatorial circuit, with each gate having a size and a delay, maximum degree$\varDelta$, intra- and inter-cluster delaysdandD, respectively, and a positive integerMcalled cluster capacity, the goal is to partition the circuit into clusters such that

• 1. The size of each cluster is bounded byM,

• 2. The delay of the circuit is minimized.

2.3 Graph-theoretic formulation

In the rest of the paper, we focus on a graph-theoretic formulation of CN. Given a clustering of a combinatorial circuit represented as a DAG $G=(V,E)$, the delays on the interconnections between gates induce an edge-delay function$\delta : E\rightarrow \{d, D\}$ of G. The weight of a cluster is the sum of the weights of the vertices in the cluster. The delay-length of a directed path $P=v_0e_1v_1\dots e_{l}v_l$ of G is $\sum ^l_{i=0}\delta (v_i) + \sum ^l_{i=1}\delta (e_i),$ where $\delta (e_i)$ is equal to d if $v_{i-1}$ and $v_i$ are inside the same cluster, or D, otherwise.

We also employ the following notations and concepts. The symbol X below can be either W, which means that the vertices are weighted, or N, which means that the vertices are unweighted, the symbol M is the cluster capacity, and $\varDelta$ is the maximum number of arcs entering or leaving any vertex of the DAG (i.e., the maximum degree $\varDelta$ of the underlying undirected graph of the DAG).

CN$\langle X, M, \varDelta \rangle$ is formulated (graph-theoretically) as follows: Given a DAG $G=(V,E)$, with vertex-weight function$w: V \rightarrow \mathbb {N}$, delay function$\delta : V \rightarrow \mathbb {N}$, maximum degree$\varDelta$, constantsdandD, and a cluster capacityM, the goal is topartitionVinto clusters such that

• 1. The weight of each cluster is bounded byM,

• 2. The maximum delay-length of any path from a source to a sink ofGis minimized.

A clustering of G, such that the weight of each cluster is bounded by M, is called feasible. Given a feasible clustering of G, one can consider the corresponding edge-length function $\delta : E\rightarrow \{d, D\}$ of G. A clustering of G is optimal if the maximum delay-length of any path from a source to a sink is the minimum among all clusterings.

Fig. 2

An example of a DAG and clustering of the DAG

In Fig. 2, we consider a simple example of clustering a combinatorial circuit represented by a DAG, when logic replication is not allowed. In this example, the delays and weights of all vertices are equal to 0 and 1, respectively (i.e., $\delta (v)=0$ and $w(v)=1$ for all vertices v in the DAG), the cluster capacity is $M=2$, the intra-cluster delay is $d=0$; and, the inter-cluster delay is $D=1$. It can be easily seen that the partition $\Sigma =\{\{s,a\}, \{b,e\}, \{c,t\} \}$ forms a feasible clustering such that the longest delay-length of any path from s to t is 2. Moreover, we can quickly check to see that this clustering is optimal.

In this paper, we focus on a restriction of CN$\langle X, M, \varDelta \rangle$, when $\delta (v)=0$ for every vertex v of G.

The main contributions of this paper are as follows:

• 1. Establishing the NP-hardness of several variants of CN$\langle W, M, \varDelta \rangle$ (Sect. 4).

• 2. Proof of inapproximability for several variants of CN$\langle W, M, \varDelta \rangle$ (Sect. 4).

• 3. Design and analysis of a 2-approximation algorithm for CN$\langle N, 2, \varDelta \rangle$ (Sect. 5).

3 Related work

In this section, we describe some related work in the literature.

Lawler et al. (1969) were the first to present an exact polynomial time algorithm for CA. They also show that in the special case when the undirected underlying graph is a tree, CN is polynomial time solvable. We refer to the model under which the problems were studied in Lawler et al. (1969) as the “unit delay model” (Murgai et al. 1991), where $\delta (v)=0$, $\forall v \in V$ and $D=1$. A more general delay model is presented by Murgai et al. (1991), where $\delta (v) \ge 0$, $\forall v \in V$ and $D \ge 0$. As per Rajaraman and Wong (1993), this extension of the unit delay model is said to be more powerful and realistic. The algorithm for the general delay model proposed in Murgai et al. (1991) does not always return an optimal solution, although they specify the conditions under which their algorithm returns an optimum. Rajaraman and Wong (1993) consider CA under the more general delay model proposed in Murgai et al. (1991), and discuss an algorithm that returns an optimal clustering in polynomial time.

Yang and Wong (1997) extend the work done in Rajaraman and Wong (1993), and consider both area and pin constraints. Note that Murgai et al. (1991) and Rajaraman and Wong (1993) consider area constraints only. In Yang and Wong (1997), they propose an efficient clustering algorithm that achieves an optimal solution under either the area constraint only or the pin constraint only. However, when both constraints are present, the algorithm does not always return the optimal solution. They specify the rare condition under which the algorithm fails to do so.

Cong and Romesis extend the study of CA to multi-level circuit clustering, with application to hierarchical field programmable gate array (FPGA) architecture, where clustering is applied recursively in two stages (Cong and Romesis 2001). They show that the multi-level clustering problem for delay minimization with replication is NP-hard. They also propose an efficient heuristic for two-level clustering, providing a trade-off between area and delay by controlling the amount of replication.

Goldschmidt and Hochbaum (1988) studied the multiway partition problem, where the goal is to find a partition of an edge-weighted graph G into some non-empty clusters, such that the total edge weight between the clusters is minimum. This problem remains NP-hard, even when the input graph is unweighted, and there is no restriction on the cluster capacity. If the number of clusters is fixed (say r), then there is an algorithm that runs in time $O(n^{r^{2}})$ that solves this restriction exactly. Here n is the number of vertices of G. The case of the multiway partition problem, in which $r=2$, is frequently encountered in the literature. This case is called the bipartition problem. It is NP-hard for d-regular graphs (Bui et al. 1987), where $d\ge 3$ is a fixed constant. On the positive side, there is a dynamical programming based algorithm for solving this problem in the case of trees (Bui and Jones 1989; Goldberg and Miller 1988; MacGregor 1988).

Mak and Wong (1996) examine the amount of replication needed for clusterings that reduce the cut size. They focus on the bipartition problem with the goal of finding a minimum-cut that minimizes the size of the replication set. They present an efficient network-flow based algorithm that finds a min-cut partitioning which requires the least amount of replication to separate the gates of the circuit into two subsets. They also show how their algorithm applies to the problem of area-constrained min-cut partitioning with replication.

Kagaris (2003) considers CN under both area constraints and pin constraints, separately. Both area-constrained and pin-constrained problems are shown to be NP-hard, even for the unit delay model. Although not explicitly stated, the proof for the area-constrained problem establishes the NP-completeness of the decision version of CN$\langle \{1,2,3,4\}, 5, \varDelta \rangle$ – a restriction of CN$\langle W, M, \varDelta \rangle$. This implies that CN$\langle W, M, \varDelta \rangle$ is NP-hard (cf. Theorem 1). They present an efficient heuristic which makes use of the clustering algorithm described in Rajaraman and Wong (1993). Their experimental results show that the delay is about 1.5 times the optimum (on average) for small inter-cluster delays, but increases with large inter-cluster delays and large cluster capacities. However, they do not establish provable bounds.

Fig. 3

Reduction from Partition to ${CN}_{dec}\langle W, M, \varDelta \rangle$

4 Computational complexity of CN

In this section, we obtain the main results that deal with the computational complexity of CN. We prove theorems that establish the NP-hardness of some variants of CN. Our reductions imply that CN is inapproximable within a certain factor.

In order to formulate the results, we consider ${CN}_{dec}$, which is formulated as follows: Given a DAG$G=(V,E)$, with vertex-weight function$w: V \rightarrow \mathbb {N}$, delay function$\delta : V \rightarrow \mathbb {N}$, maximum degree$\varDelta$, constantsdandD, cluster capacityM, and a positive integerk, decide whether we can partitionVinto clusters such that

• 1. The weight of each cluster is bounded byM,

• 2. The longest delay-length of any path from a source to a sink ofGis at mostk.

It is not hard to see that ${CN}_{dec}$ is the decision version of CN$\langle W, M, \varDelta \rangle$. We make this correspondence explicit by writing ${CN}_{dec}$ as ${CN}_{dec}\langle W, M, \varDelta \rangle$. We use the same notation for restrictions of CN$\langle W, M, \varDelta \rangle$. If A is a subset of positive integers, then ${CN}_{dec}\langle A, M, \varDelta \rangle$ denotes the restriction of ${CN}_{dec}\langle W, M, \varDelta \rangle$, when the weights of verticies of the input DAG are from A.

Our first theorem establishes the NP-completeness of ${CN}_{dec}\langle W, M, \varDelta \rangle$. Clearly, this means that CN$\langle W, M, \varDelta \rangle$ is NP-hard.

Theorem 1

${CN}_{dec}\langle W, M, \varDelta \rangle$ is NP-complete.

Proof

We recall $CN_{dec}\langle W, M, \varDelta \rangle$ as follows: Given a DAG $G=(V,E)$, with vertex-weight function $w: V \rightarrow \mathbb {N}$, delay function $\delta (v)=0$, maximum degree $\varDelta$, constants d and D, cluster capacity M, and a positive integer k, decide whether we can partition V into clusters such that the weight of each cluster is bounded by M, and the longest delay-length of any path from a source to a sink of G is at most k.

It is clear that ${CN}_{dec}\langle W, M, \varDelta \rangle$ is in NP since it follows from the well-known fact that finding a maximum weighted path in an edge-weighted DAG is polynomial time solvable.

In order to establish NP-hardness of ${CN}_{dec}\langle W, M, \varDelta \rangle$, we present a reduction from Partition. For that purpose, we recall Partition as follows: Given a set $A=\{ a_{1}, a_{2}, \ldots , a_{n}\}$, the goal is to check whether there is a set $A_{1} \subset A$, such that $\sum _{a_i \in A_{1}} a_i = \sum _{a_i \in A \setminus A_{1}} a_i$, where $i \in \{1,2,\ldots , n\}$. Without loss of generality, we assume that $\sum _{a_i\in A} a_i = B$ is even, otherwise the problem is trivial.

We now construct an instance $I'$ of ${CN}_{dec}\langle W, M, \varDelta \rangle$ as shown in Fig. 3. There is a source s connected to a sink t through n vertices labeled $u_{1}$ through $u_{n}$. Let U denote the set of all vertices $u_i$ ($1 \le i \le n$). The vertices in U are pairwise nonadjacent. Each vertex $u_{i} \in U$ has a weight $a_{i}$, and both s and t have weight $\frac{B}{2}$. We set $d=0$ and let D be any positive integer. All vertices are given a delay of 0. The cluster capacity is set to B, and we set $k=D$. The description of $I'$ is complete.

Observe that $I'$ can be constructed from an instance I of Partition in polynomial time. In order to complete the proof of the theorem, we show that I is a “yes” instance of Partition if and only if $I'$ is a “yes” instance of ${CN}_{dec}\langle W, M, \varDelta \rangle$.

Assume that I is a “yes” instance of Partition. This means that there exists a partition of A into $A_{1}$ and $A \setminus A_{1}$ such that $\sum _{a_i \in A_{1}} a_i = \sum _{a_i \in A \setminus A_{1}} a_i = \frac{B}{2}$. Group the vertices corresponding to the elements in $A_{1}$ with s, and the remaining vertices with t. Observe that the cluster capacity constraint is met. Moreover, the longest delay-length of any path from s to t is D. This means that $I'$ is a “yes” instance of ${CN}_{dec}\langle W, M, \varDelta \rangle$.

For the proof of the converse statement, assume that $I'$ is a “yes” instance of ${CN}_{dec}\langle W, M, \varDelta \rangle$. This means that there is a way of partitioning the vertices of G into clusters such that the longest delay-length of any path from s to t is at most D. We observe that every vertex must be packed with either s or t, otherwise the longest delay-length must equal $2 \cdot D > k$. Let $U_s$ and $U_t$ denote the subsets of the vertices in U that are packed with s and t, respectively. Let w(s) and w(t) be the weights of vertices s and t, respectively. Let $w(U_{s})$ and $w(U_{t})$ be the sums of the weights of the vertices in U that are packed with s and t, respectively. Clearly, $w(s)+w(U_{s})+w(t) + w(U_{t}) = 2\cdot B.$ Since $w(s)+w(U_{s})\le B \text { and } w(t)+w(U_{t}) \le B,$ we have $w(U_{s}) \le \frac{B}{2} \text { and } w(U_{t}) \le \frac{B}{2}.$ This implies that $w(U_{s}) = \frac{B}{2} \text { and } w(U_{t}) = \frac{B}{2}.$ Thus, we have obtained the desired partition of A. Hence, I is a “yes” instance of Partition. $\square$

The proof of Theorem 1 implies NP-hardness of CN$\langle W, M, \varDelta \rangle$, even for planar networks and therefore, strengthens the result in Kagaris (2003). Moreover, we obtain the following inapproximability result.

Corollary 1

CN$\langle W, M, \varDelta \rangle$ does not admit a $(2-\varepsilon )$-approximation algorithm for each $\varepsilon >0$, unless $\mathbf{P}=\mathbf NP$.

Proof

By way of contradiction, suppose there exists a $(2-\varepsilon )$-approximation algorithm for CN$_{dec}\langle W, M, \varDelta \rangle$. We construct a polynomial time algorithm for Partition as follows:

Let OPT denote the delay of the optimal clustering of G. If I is a “yes” instance of Partition, then $OPT \le D$. Moreover, the maximum delay of any clustering solution of G returned by the $(2-\varepsilon )$-approximation algorithm for CN$_{dec}\langle W, M, \varDelta \rangle$ is at most $(2-\varepsilon ) \cdot D$. Otherwise, the maximum delay of any clustering solution of G must be at least $2 \cdot D$. Thus, the $(2-\varepsilon )$-approximation algorithm solves the instance I of Partition exactly. $\square$

The next theorem serves to strengthen Theorem 1.

Theorem 2

${CN}_{dec}\langle W, M, 3 \rangle$ is NP-complete.

Proof

We recall $CN_{dec}\langle W, M, 3 \rangle$ as follows: Given a DAG $G=(V,E)$, with vertex-weight function $w: V \rightarrow \mathbb {N}$, delay function $\delta (v)=0$, maximum degree $\varDelta =3$, constants d and D, cluster capacity M, and a positive integer k, decide whether we can partition V into clusters such that the weight of each cluster is bounded by M, and the longest delay-length of any path from a source to a sink of G is at most k.

It is clear that ${CN}_{dec}\langle W, M, 3 \rangle$ is in NP since it follows from the well-known fact that finding a maximum weighted path in an edge-weighted DAG is polynomial time solvable.

In order to establish NP-hardness of ${CN}_{dec}\langle W, M, 3 \rangle$, we present a reduction from Partition. For that purpose, we recall Partition as follows: Given a set $A=\{ a_{1}, a_{2}, \ldots , a_{n}\}$, the goal is to check whether there is a set $A_{1} \subset A$, such that $\sum _{a_i \in A_{1}} a_i = \sum _{a_i \in A \setminus A_{1}} a_i$, where $i \in \{1,2,\ldots , n\}$. Without loss of generality, we assume that $\sum _{a_i\in A} a_i = B$ is even, otherwise the problem is trivial.

We now construct an instance $I'$ of ${CN}_{dec}\langle W, M, 3 \rangle$ as shown in Fig. 4. Let U denote the set of all vertices $u_i$ ($1 \le i \le n$). The vertices in U are pairwise nonadjacent. Each vertex $u_{i} \in U$ belongs to a distinct path that connects the source s to the sink t. Let S denote the set of all vertices that are predecessors of the vertices in U. Let T denote the set of all vertices that are successors of the vertices in U. Note that in the underlying undirected graph, the subgraphs induced by S and T are isomorphic. Let m denote the size of S and T. Each vertex $u_{i} \in U$ has a weight of $a_{i}$. Every vertex in S and T has weight 1. We set $d=0$ and let D be any positive integer. Every vertex is given a delay of 0. The cluster capacity M is set to $\left( \frac{B}{2}+m \right)$, and we set $k=D$. The description of $I'$ is complete.

Fig. 4

Reduction from Partition to ${CN}_{dec}\langle W, M, 3 \rangle$

Observe that $I'$ can be constructed from an instance I of Partition in polynomial time. In order to complete the proof of the theorem, we show that I is a “yes” instance of Partition if and only if $I'$ is a “yes” instance of ${CN}_{dec}\langle W, M, 3 \rangle$.

Assume that I is a “yes” instance of Partition. This means that there exists a partition of A into $A_{1}$ and $A \setminus A_{1}$ such that $\sum _{a_i \in S_{1}} a_i = \sum _{a_i \in A \setminus A_{1}} a_i = \frac{B}{2}$. Group the vertices corresponding to the elements in $A_{1}$ with S, and the remaining vertices with T. Observe that the cluster capacity constraint is met. Moreover, the longest delay-length of any path from the source s to the sink t is D. This means that $I'$ is a “yes” instance of ${CN}_{dec}\langle W, M, 3 \rangle$.

Conversely, assume that $I'$ is a “yes” instance of ${CN}_{dec}\langle W, M, 3 \rangle$. This means that there is a way of partitioning the vertices of the DAG in Fig. 4 into clusters, such that the cluster capacity constraint is satisfied, and the longest delay-length of any path from s to t is at most D. Since S and T have the same underlying structure and $|S|=|T|$, then without loss of generality, we may assume that every vertex in S is clustered together, and every vertex in T is clustered together. Furthermore, each vertex $u_i \in U$ must be clustered with the vertices in either S or T. Otherwise, the delay-length of the path from s to t is strictly greater than D. Let $U_S$ and $U_T$ denote the subsets of the vertices in U that are packed with S and T, respectively. Observe that $U_S \cup U_T = U$. Notice that the delay-length of any path from s to a vertex in $U_S$ is 0, and the delay-length of any path from a vertex in $U_T$ to t is also 0. Let w(S) and w(T) denote the sum of the weights of all vertices in S and T, respectively. Notice that $w(S)=w(T)=m$. Let $w(U_{S})$ and $w(U_{T})$ denote the sum of the weights of all vertices in $U_S$ and $U_T$, respectively. Clearly, $w(U_{S})+w(U_{T})+w(S)+w(T) = B + 2 \cdot m.$ Since $w(U_{S})+w(S)\le \left( \frac{B}{2}+m \right)$ and $w(U_{T})+w(T) \le \left( \frac{B}{2}+m \right)$, then $w(U_{S}) \le \frac{B}{2}$ and $w(U_{T}) \le \frac{B}{2}$. This implies that $w(U_{S}) = \frac{B}{2} \text { and } w(U_{T}) = \frac{B}{2}.$ Thus, we have obtained the desired partition of A. Hence, I is a “yes” instance of Partition. $\square$

The proof of Theorem 2 implies an inapproximability result for CN$\langle W, M, 3 \rangle$.

Corollary 2

CN$\langle W, M, 3 \rangle$ does not admit a $(2-\varepsilon )$-approximation algorithm for each $\varepsilon >0$, unless $\mathbf{P} =\mathbf{NP}$.

Proof

By way of contradiction, suppose there exists a $(2-\varepsilon )$-approximation algorithm for CN$_{dec}\langle W, M, 3 \rangle$. We construct a polynomial time algorithm for Partition as follows:

Let OPT denote the delay of the optimal clustering of G. If I is a “yes” instance of Partition, then $OPT \le D$. Moreover, the maximum delay of any clustering solution of G returned by the $(2-\varepsilon )$-approximation algorithm for CN$_{dec}\langle W, M, 3 \rangle$ is at most $(2-\varepsilon ) \cdot D$. Otherwise, the maximum delay of any clustering solution of G must be at least $2 \cdot D$. Thus, the $(2-\varepsilon )$-approximation algorithm solves the instance I of Partition exactly.$\square$

The next theorem implies NP-hardness of CN$\langle \{1,2,3\}, 3, 3 \rangle$. In the proof, we use a 3SAT reduction modeled after the one presented in Kagaris (2003).

Theorem 3

${CN}_{dec}\langle \{1,2,3\}, 3, 3 \rangle$ is NP-complete.

Proof

We recall $CN_{dec}\langle \{1,2,3\}, 3, 3 \rangle$ as follows: Given a DAG $G=(V,E)$, with vertex-weight function $w: V \rightarrow \{1,2,3\}$, delay function $\delta (v)=0$, maximum degree $\varDelta =3$, constants d and D, cluster capacity $M=3$, and a positive integer k, decide whether we can partition V into clusters such that the weight of each cluster is bounded by M, and the longest delay-length of any path from a source to a sink of G is at most k.

It is clear that ${CN}_{dec}\langle \{1,2,3\}, 3, 3 \rangle$ is in NP since it follows from the well-known fact that finding a maximum weighted path in an edge-weighted DAG is polynomial time solvable.

In order to establish NP-hardness of ${CN}_{dec}\langle \{1,2,3\}, 3, 3 \rangle$, we present a reduction from 3SAT. For that purpose, we recall 3SAT as follows: Given a 3-CNF formula $\phi$ with n variables $x_1, \ldots , x_n$ and m clauses $C_1, \ldots , C_m$, the goal is to check whether $\phi$ has a satisfying assignment. Without loss of generality, for all $i \in \{1, \ldots , n\}$ we assume that each variable $x_i$ in $\phi$ appears at most three times and each literal at most twice. (Any 3SAT instance can be transformed to satisfy these properties in polynomial time (Papadimitriou 1994).)

Fig. 5

Gadgets used to represent variables and clauses

Let each variable $x_i$$(1 \le i \le n)$ be represented by a variable gadget as shown in Fig. 5a. Let each clause $C_j$$(1 \le j \le m)$ be represented by a clause gadget as shown in Fig. 5b. If a variable $x_i$ or its complement $\bar{x}_i$ is the 1st, 2nd, or 3rd literal of a clause $C_j$, then the corresponding vertex labeled $x_i$ (or $\bar{x}_i$) is connected to a sink labeled $C_j$ through a pair of vertices labeled {$y_{j1}, z_{j1}$}, {$y_{j2}, z_{j2}$}, or {$y_{j3}, z_{j3}$}, respectively. A simple example of the construction of an instance $I'$ is shown in Fig. 6, where $\phi = C_1 \wedge C_2$, with $C_1 = (x_1, \bar{x}_2, x_3)$ and $C_2 = (x_2, x_3, x_4)$.

Fig. 6

Simple example

Fig. 7

Reduction from the 3SAT problem to ${CN}_{dec}\langle \{1,2,3\}, 3, 3 \rangle$. The edges connecting variable gadgets to clause gadgets belong in the area with the shaded cloud

We now construct an instance $I'$ of ${CN}_{dec}\langle \{1,2,3\}, 3, 3 \rangle$ as shown in Fig. 7. The resulting DAG G represents a combinatorial circuit. Let U denote the set of all vertices labeled $x_i$ or $\bar{x}_i$$(1 \le i \le n)$. There are n sources labeled $T_i$$(1 \le i \le n)$ and m sinks labeled $C_j$$(1 \le j \le m)$. They are connected through some vertices in U and $3 \cdot m$ pairs of vertices labeled {$y_{jp}, z_{jp}$} $(1 \le j \le m, 1 \le p \le 3)$. Each $y_{jp}$ is connected to exactly one variable gadget. For every j, no two vertices in the set $\{y_{j1}, y_{j2}, y_{j3}\}$ are adjacent to both $x_i$ and $\bar{x}_i$ of the same variable gadget. In other words, $x_i$ and $\bar{x}_i$ cannot both be connected to the same clause gadget. Every $T_{i}$, $z_{jp}$, and $C_j$ has a weight of 1, every $x_i, \bar{x}_i \in U$ has a weight of 2, and every $y_{jp}$ has a weight of 3. We set $d=0$ and let D be any positive integer. All vertices are given a delay of 0. The cluster capacity M is set to 3, and we set $k=3\cdot D$. The description of $I'$ is complete.

Observe that $I'$ can be constructed from I in polynomial time. In order to complete the proof of the theorem, we show that I is a “yes” instance of 3SAT if and only if $I'$ is a “yes” instance of ${CN}_{dec}\langle \{1,2,3\}, 3, 3 \rangle$.

Suppose that I is a “yes” instance of 3SAT. This means that there exists an assignment of $\phi$ such that every clause has at least one true literal. If a literal $x_i$ is set to true, then the corresponding vertex $x_i$ (or $\bar{x}_i$) is clustered with $T_i$. However, if a literal $x_i$ is set to false, then the corresponding vertex $x_i$ is clustered alone. Since $M=3$, every $y_{jp}$ must be clustered alone. Since each clause $C_j$ has at least one true literal, the vertex $z_{jp}$ along the path of the vertex $x_i$ (or $\bar{x}_i$) corresponding to that true literal is clustered alone. The resulting delay-length of the corresponding source to sink path is $3\cdot D$. It is safe to cluster the remaining two $z_{jp}$ vertices with $C_j$, even if they both belong to paths corresponding to true literals. In this case, the resulting paths have delay-length $2\cdot D < 3\cdot D=k$. However, if either one these two $z_{jp}$ vertices belongs to a path corresponding to a false literal, then it must be clustered with $C_j$ to avoid exceeding the bound on the delay-length. Observe that the cluster capacity constraint is satisfied, and the longest delay-length of any path from a source $T_i$ to a sink $C_j$ is $3\cdot D$. This means that $I'$ is a “yes” instance of ${CN}_{dec}\langle \{1,2,3\}, 3, 3 \rangle$.

Conversely, suppose that $I'$ is a “yes” instance of ${CN}_{dec}\langle \{1,2,3\}, 3, 3 \rangle$. This means that there is a way of partitioning the vertices of G into clusters of capacity $M=3$, such that the longest delay-length of any path from a source to a sink is at most $3\cdot D$.

Since $M=3$, again notice that every $y_{jp}$ must be clustered alone. Each sink $C_j$ may be clustered with at most two vertices. This means that at least one $z_{jp}$ is clustered alone. Consider the vertex $x_i$ (or $\bar{x}_i$) along a path corresponding to a $z_{jp}$ clustered alone. Since any source to sink path with a $z_{jp}$ clustered alone has a delay-length of at least $3\cdot D$, then $T_i$ must be clustered with vertex $x_i$ (or $\bar{x}_i$). Otherwise, the delay-length of the path would be $4\cdot D > 3\cdot D = k$. Furthermore, since the cluster capacity is satisfied, either $x_i$ or $\bar{x}_i$ (but not both) can be clustered with $T_i$. Take each literal that corresponds to a vertex $x_i$ clustered with $T_i$, and set its value to true. Now, notice that any $z_{jp}$ along a path in which $x_i$ (or $\bar{x}_i$) is clustered alone, must be clustered with the sink $C_j$. Otherwise, the delay-length of the path would be $4\cdot D > 3\cdot D = k$. Take each literal that corresponds to a vertex $x_i$ not clustered with $T_i$ and set its value to false. Notice that at least one true literal appears in every clause. Thus, a satisfying clustering for G yields a satisfying assignment for $\phi$. Hence, I is a “yes” instance of 3SAT. $\square$

The proof of Theorem 3 implies an inapproximability result for CN$\langle \{1,2,3\}, 3, 3 \rangle$.

Corollary 3

CN$\langle \{1,2,3\}, 3, 3 \rangle$ does not admit a $(\frac{4}{3}-\varepsilon )$-approximation algorithm for any $\varepsilon >0$, unless $\mathbf{P} =\mathbf{NP}$.

Proof

By way of contradiction, suppose there exists a $(\frac{4}{3}-\varepsilon )$-approximation algorithm for CN$_{dec}\langle \{1,2,3\}, 3, 3 \rangle$. We construct a polynomial time algorithm for 3SAT as follows:

Let OPT denote the delay of the optimal clustering of G. If I is a “yes” instance of 3SAT, then $OPT \le 3 \cdot D$. Moreover, the maximum delay of any clustering solution of G returned by the $(\frac{4}{3}-\varepsilon )$-approximation algorithm for CN$_{dec}\langle \{1,2,3\}, 3, 3 \rangle$ is at most $(4-\varepsilon ) \cdot D$. Otherwise, the maximum delay of any clustering solution of G must be at least $4 \cdot D$. Thus, the $(\frac{4}{3}-\varepsilon )$-approximation algorithm solves the instance I of 3SAT exactly.$\square$

The next theorem implies NP-hardness of CN$\langle \{1,2\}, 2, 4 \rangle$ – a restriction of CN$\langle W, 2, \varDelta \rangle$.

Theorem 4

${CN}_{dec}\langle \{1,2\}, 2, 4 \rangle$ is NP-complete.

Proof

We recall $CN_{dec}\langle \{1,2\}, 2, 4 \rangle$ as follows: Given a DAG $G=(V,E)$, with vertex-weight function $w: V \rightarrow \{1,2\}$, delay function $\delta (v)=0$, maximum degree $\varDelta =4$, constants d and D, cluster capacity $M=2$, and a positive integer k, decide whether we can partition V into clusters such that the weight of each cluster is bounded by M, and the longest delay-length of any path from a source to a sink of G is at most k.

It is clear that ${CN}_{dec}\langle \{1,2\}, 2, 4 \rangle$ is in NP since it follows from the well-known fact that finding a maximum weighted path in an edge-weighted DAG is polynomial time solvable.

In order to establish NP-hardness of ${CN}_{dec}\langle \{1,2\}, 2, 4 \rangle$, we present a reduction from 3-Bounded Positive 1-in-3SAT (3-BP 1-in-3SAT). For that purpose, we recall 3-BP 1-in-3SAT as follows: Given a 3-CNF formula $\phi$ with n positive variables $x_1, \ldots , x_n$ and m clauses $C_1, \ldots , C_m$, such that each variable appears in at most three clauses, the goal is to check whether $\phi$ has a satisfying assignment such that every clause of $\phi$ has exactly one true literal (Denman and Foster 2009).

Let each variable $x_i$$(1 \le i \le n)$ be represented by a variable gadget as shown in Fig. 8a. Let each clause $C_j$$(1 \le j \le m)$ be represented by a clause gadget as shown in Fig. 8b. If a variable $x_i$ is the 1st, 2nd, or 3rd literal of a clause $C_j$, then the corresponding vertex labeled $x_i$ is connected to a sink labeled $C_j$ through a pair of vertices labeled {$y_{j1}, z_{j1}$}, {$y_{j2}, z_{j2}$}, or {$y_{j3}, z_{j3}$}, respectively.

Fig. 8

Gadgets used to represent variables and clauses

Fig. 9

Reduction from 3-BP 1-in-3SAT to ${CN}_{dec}\langle \{1,2\}, 2, 4 \rangle$. The edges connecting variable gadgets to clause gadgets belong in the area with the shaded cloud

We now construct an instance $I'$ of ${CN}_{dec}\langle \{1,2\}, 2, 4 \rangle$ as shown in Fig. 9. The resulting DAG G represents a combinatorial circuit. Let U denote the set of all vertices labeled $x_i$ or $\bar{x}_i$$(1 \le i \le n)$. There are n sources labeled $F_i$$(1 \le i \le n)$ and m sinks labeled $C_j$$(1 \le j \le m)$. They are connected through some vertices in U and $3\cdot m$ pairs of vertices labeled {$y_{jp}, z_{jp}$} $(1 \le j \le m, 1 \le p \le 3)$. Each $y_{jp}$ is connected to exactly one variable gadget. Every $x_i, \bar{x}_i \in U$, every $F_{i}$, $z_{jp}$, and $C_j$ has a weight of 1. Every $y_{jp}$ has a weight of 2. We set $d=0$ and let D be any positive integer. All vertices are given a delay of 0. The cluster capacity M is set to 2, and we set $k=3\cdot D$. The description of $I'$ is complete.

Observe that $I'$ can be constructed from I in polynomial time. In order to complete the proof of the theorem, we show that I is a “yes” instance of 3-BP 1-in-3SAT if and only if $I'$ is a “yes” instance of ${CN}_{dec}\langle \{1,2\}, 2, 4 \rangle$.

Suppose that I is a “yes” instance of 3-BP 1-in-3SAT. This means that there exists an assignment of $\phi$ such that every clause has exactly one true literal. If a literal $x_i$ is set to true, then the corresponding vertex $x_i$ is clustered alone. However, if a literal $x_i$ is set to false, then the corresponding vertex is clustered with $F_i$. Since $M=2$, every $y_{jp}$ must be clustered alone. Since each clause $C_j$ has exactly one true literal, the vertex $z_{jp}$ along the path of the vertex $x_i$ corresponding to that true literal is clustered with $C_j$. The resulting delay-length of the corresponding source to sink path is $3\cdot D$. The other two vertices belonging to the same clause gadget are clustered alone. Observe that the cluster capacity constraint is satisfied, and the longest delay-length of any path from a source $F_i$ to a sink $C_j$ is $3\cdot D$. This means that $I'$ is a “yes” instance of ${CN}_{dec}\langle \{1,2\}, 2, 4 \rangle$.

Conversely, suppose that $I'$ is a “yes” instance of ${CN}_{dec}\langle \{1,2\}, 2, 4 \rangle$. This means that there is a way of partitioning the vertices of G into clusters of capacity $M=2$, and the longest delay-length of any path from a source to a sink is at most $3\cdot D$.

Since $M=2$, again notice that every $y_{jp}$ must be clustered alone. Each sink $C_j$ is clustered with at most one vertex, so the remaining two $z_{jp}$ vertices are clustered alone. Consider a vertex $x_{i}$ along a path corresponding to a $z_{jp}$ that is clustered alone. Since such a source to sink path has a delay-length of at least $3\cdot D$, then the source $F_i$ must be clustered with vertex $x_i$. Otherwise, the delay-length of the path would be $4\cdot D > 3\cdot D=k$. Furthermore, since the cluster capacity is satisfied, $F_i$ can be clustered with either $x_i$ or $\bar{x}_i$ (but not both). Take each literal that corresponds to a vertex $x_i$ clustered with $F_i$ and set its value to false. Take each literal $x_i$ that corresponds to a vertex $x_i$ clustered alone and set its value to true. Notice that any $z_{jp}$ along a path in which vertex $x_i$ is clustered alone must be clustered with the sink $C_j$. Otherwise, the delay-length of the path would be $4\cdot D > 3\cdot D = k$. Observe that exactly one true literal appears in every clause. Thus, a satisfying clustering for G yields a satisfying assignment for $\phi$. Hence, I is a “yes” instance of 3-BP 1-in-3SAT. $\square$

The proof of Theorem 4 implies an inapproximability result for CN$\langle \{1,2\}, 2, 4 \rangle$.

Corollary 4

CN$\langle \{1,2\}, 2, 4 \rangle$ does not admit a $(\frac{4}{3}-\varepsilon )$-approximation algorithm for each $\varepsilon >0$, unless $\mathbf{P} =\mathbf{NP}$.

Proof

By way of contradiction, suppose there exists a $(\frac{4}{3}-\varepsilon )$-approximation algorithm for CN$_{dec}\langle \{1,2\}, 2, 4 \rangle$. We construct a polynomial time algorithm for 3-BP 1-in-3SAT as follows:

Let OPT denote the delay of the optimal clustering of G. If I is a “yes” instance of 3-BP 1-in-3SAT, then $OPT \le 3 \cdot D$. Moreover, the maximum delay of any clustering solution of G returned by the $(\frac{4}{3}-\varepsilon )$-approximation algorithm for CN$_{dec}\langle \{1,2\}, 2, 4 \rangle$ is at most $(4-\varepsilon ) \cdot D$. Otherwise, the maximum delay of any clustering solution of G must be at least $4 \cdot D$. Thus, the $(\frac{4}{3}-\varepsilon )$-approximation algorithm solves the instance I of 3-BP 1-in-3SAT exactly. $\square$

5 A 2-approximation algorithm for CN $\langle N, 2, \varDelta \rangle$

In this section, we present a 2-approximation algorithm for CN$\langle N, 2, \varDelta \rangle$. It is important to note that the computational complexity of this problem is unknown.¹ Our algorithm makes use of the fact that there is a polynomial time algorithm for finding a path with maximum edge-weight in DAGs. The algorithm tries to construct a so-called dominating matching of the input DAG G. If it succeeds, then the algorithm returns an optimal clustering of G. Otherwise, it returns some feasible clustering of G. We prove that this algorithm has a performance ratio of 2.

We start with the following:

Definition 1

A matching in a DAG G is a collection of edges that do not share a vertex. A matching of a DAG G is perfect if any vertex of G is incident to an edge from the matching.

Let $G=(V,A)$ be a DAG. Clearly, any perfect matching of G contains exactly $\frac{|V|}{2}$ edges. Let l be the length of a longest path in G.

Definition 2

A matching I in G is dominating, if every longest path of G contains more than $\frac{l}{2}$ edges of I.

It is easy to see that if G contains a dominating matching, then l has to be odd.

Lemma 1

Let $G=(V,A)$ be a DAG and let l be the length of a longest path in G. There is a polynomial algorithm which decides whether G has a dominating matching and finds one if it exists.

Proof

We may assume that G is connected, i.e., its undirected underlying graph is connected. If l is even, then there is no dominating matching. So we may assume that l is odd.

Let $I=\emptyset$. Construct a longest path P in G and add odd edges to I. Construct a set S initially consisting of the edges of P. Note that I is a perfect matching in G[S], the subgraph of G induced by S. This property of I in G[S] is maintained.

Consider an edge a in $A\backslash S$ such that only one end-vertex of a is in S. If there is not such an edge a, remove the edges of $A\backslash S$ from G. Also, remove the resulting isolated vertices of G. If a does not belong to a longest path of G, delete it from G and remove the resulting isolated vertices from G. Otherwise, let Q be a longest path of G passing through a. Add all odd edges of Q to I. If an edge of Q assigned to I is incident to an edge of I in G[S], then we have that G has no dominating matching. Otherwise, add all edges of Q to S and observe that I is a perfect matching in G[S]. Continue for as long as $A\ne S$.

Now we have that $A=S$ and I is a perfect matching in G[S]. Since every longest path of G must start from an edge in I and end with an edge of I, the only possibility for a longest path to contain at most $\frac{l}{2}$ edges of I is if it contains two consecutive edges that are not from I. Thus, we do the following. Consider every pair of edges not from I forming a directed path of length 2 and check whether the pair is on any longest path of G. If so, G has no dominating matching. Otherwise, I is a dominating matching.

The above proof is an algorithm which runs in polynomial time. The proof of the lemma is complete $\square$

Using Lemma 1, we obtain a 2-approximation algorithm for CN$\langle N, 2, \varDelta \rangle$.

Theorem 5

The problem CN$\langle N, 2, \varDelta \rangle$ admits a 2-approximation algorithm.

Proof

Consider Algorithm 5.1, which is a generic algorithm for the problem. For a path P, let l(P) be the length of P (i.e., the number of edges of P). Moreover, let l denote the length of a longest path of G.

The following shows a lower bound for OPT, where OPT is the delay of the optimal clustering of G when $M=2$.

$$\begin{aligned} OPT \ge \left\lceil \frac{l(P)}{2} \right\rceil \cdot d+ \left\lfloor \frac{l(P)}{2} \right\rfloor \cdot D. \end{aligned}$$

Since P represents any path, then the above inequality must also be true for the longest path. Thus,

$$\begin{aligned} OPT \ge \left\lceil \frac{l}{2} \right\rceil \cdot d+ \left\lfloor \frac{l}{2} \right\rfloor \cdot D. \end{aligned}$$

Now, let us estimate ALG, where ALG is the delay of the clustering found by the algorithm. We consider 2 cases.

Case 1G has no dominating matching. Then if l is even, we have

$$\begin{aligned} ALG&\le l\cdot D\\&\le 2\cdot \left( \left\lceil \frac{l}{2} \right\rceil \cdot d+ \left\lfloor \frac{l}{2} \right\rfloor \cdot D\right) \\&\le 2\cdot OPT. \end{aligned}$$

On the other hand, if l is odd, then since G has no dominating matching, we have

$$\begin{aligned} OPT \ge \left\lfloor \frac{l}{2} \right\rfloor \cdot d+\left\lceil \frac{l}{2}\right\rceil \cdot D. \end{aligned}$$

Hence

$$\begin{aligned} ALG&\le l\cdot D\\&\le 2\cdot \left( \left\lfloor \frac{l}{2} \right\rfloor \cdot d+ \left\lceil \frac{l}{2} \right\rceil \cdot D\right) \\&\le 2\cdot OPT. \end{aligned}$$

Case 2G has a dominating matching I. Then since any path of length l has an edge from I, we have

$$\begin{aligned} ALG&\le d+ (l-1)\cdot D\\&\le 2\cdot \left( \left\lceil \frac{l}{2} \right\rceil \cdot d+ \left\lfloor \frac{l}{2}\right\rfloor \cdot D\right) \\&\le 2\cdot OPT. \end{aligned}$$

The proof of the theorem is complete. $\square$

6 Conclusion

In this paper, we studied the problem of clustering without replication in combinatorial circuits for delay minimization (CN). We proved that several variants of CN$\langle W, M, \varDelta \rangle$ are NP-hard. We also showed that our results imply hardness of approximation within a certain factor for several variants of CN$\langle W, M, \varDelta \rangle$. On the positive side, there exists a 2-approximation algorithm for CN$\langle N, 2, \varDelta \rangle$. Our results are tabulated below in Table 1.

Table 1 Results

We are interested in the following open problems:

• 1. Finding approximation, parameterized, and exact exponential algorithms for several variants of CN$\langle X, M, \varDelta \rangle$.

• 2. Establishing the computational complexity of CN$\langle N, 2, \varDelta \rangle$ and finding an approximation algorithm for CN$\langle N, 2, \varDelta \rangle$ whose performance ratio is smaller than 2, if it exists.