Keywords

1 Introduction

The analysis of modern scientific literature shows that the stress state of cylindrical bodies with cracks under static loading has been studied sufficiently enough, but works with the analysis of the stress state under dynamic loading conditions is much smaller. As a rule, the researchers study cylinders of infinite length [1,2,3].

The complexity of theoretical studies of dynamic problems is due to the necessity of using the Laplace integral transform in time with subsequent numerical inversion. However, this task is not only mathematically complicated, but incorrect.

These difficulties can be avoided by use mixed numerical-experimental methods. In [4], the dynamic tension and in [5] the dynamic torsion of finite cylinders with ring cracks was investigated. But these methods, like all the experimental ones, are characterized by the disadvantages associated with the need to carry out experiments for each particular sample. This complicates the study of the impact of cylinder geometric dimensions on SIF values.

Recently, there have appeared works in which the modified method of finite difference in time is applied [6]. Using this method, in this paper, the problem of determining the SIN in the vicinity of a ring-shaped crack in a finite cylinder under the action of torque is solved. So far, such a problem has been considered only in a stationary formulation [7] and for a harmonic moment [8, 9].

2 Problem Formulation

Consider an isotropic finite elastic cylinder with height a and radius r0 (Fig. 1). The cylinder is related to the cylindrical coordinate system, whose centre coincides with the centre of the bottom end, and the axis Oz with the axis of the cylinder.

Fig. 1.
figure 1

Cylinder with outer ring-shaped crack.

Full size image

The bottom end of the cylinder is rigidly fixed and its top end is joined with a rigid plate with thickness d and the same radius. The plate suffers the action of a time-dependent torsional moment M(t). The cylinder contains a ring-shaped crack parallel to its ends and occupies the region \( z = c,b \le r \le r_{0} ,0 \le {\upvarphi } \le 2\uppi \). The lateral surface of the cylinder and the surface of the crack are free of stresses.

The cylinder is in state of the axisymmetric torsional deformation and only the angular displacement \( \bar{w}(r,z,t) \) will be nonzero. Next, to formulate the initial boundary value problem, we proceed to dimensionless quantities using the formulas:

$$ \begin{array}{*{20}c} {\bar{w}\left( {r,z,t} \right) = r_{0} \cdot w\left( {\upeta,\upzeta,\uptau} \right),\;\;\upgamma = a/r_{0} ,\;\;l = c/a,\;\upbeta = b/r_{0} } \\ {r = r_{0}\upeta,\quad 0 \le\upeta \le 1,\;\;z = a\upzeta,\;0 \le\upzeta \le 1,\;\;t = r_{0}\uptau/c_{2} ,\;\uptau \in \left( {0, + \infty } \right),\;\;c_{2}^{2} = G \cdot\uprho^{ - 1} } \\ \end{array} , $$

where \( \uprho,G \)—density and shear modulus for the cylinder material.

Then, dimensionless displacement will satisfy the equation with zero initial conditions:

$$ D_{{{\upeta \upzeta }}} w = \frac{{\partial^{2} w}}{{\partial\uptau^{2} }},\quad D_{{{\upeta \upzeta }}} = \frac{{\partial^{2} }}{{\partial\upeta^{2} }} + \frac{1}{\upeta}\frac{\partial }{{\partial\upeta}} - \frac{1}{{\upeta^{2} }} + \frac{1}{{\upgamma^{2} }}\frac{{\partial^{2} }}{{\partial\upzeta^{2} }}. $$
(1)

We formulate boundary conditions in relative dimensionless quantities.

On the cylinder ends, they have the form:

$$ \left. w \right|_{{\upzeta = 0}} = 0,\quad \left. w \right|_{{\upzeta = 1}} =\upalpha\left(\uptau \right)\upeta,\;\;0 \le\upeta \le 1,\;\;\uptau \in \left[ {0, + \infty } \right), $$
(2)

where α(τ)—unknown angle of rotation of the plate. It is determined from the equation of the motion of the plate:

$$ {\uppi \upgamma }m_{0} {\ddot{\upalpha }}\left(\uptau \right) = 2\left( {M_{0} \left(\uptau \right) - M_{R} \left(\uptau \right)} \right),\quad\upalpha\left( 0 \right) = 0,\;\;\upalpha\left( 0 \right) = 0, $$
(3)

where m0—a mass ratio of the plate and cylinder, M0, MR—dimensionless moments.

On the lateral surface of the cylinder, there must be fulfilled the equality:

$$ \uptau_{{{\upvarphi }r}} (1,\upzeta,\uptau) = 0, \quad 0 \le\upzeta \le 1,\;\;\uptau \in \left[ {0, + \infty } \right). $$
(4)

For the condition on the crack, we have:

$$ \uptau_{{{\upvarphi }z}} (\upeta,l,\uptau) =\upchi\left( {\upeta,\uptau} \right),\quad\uptau \in \left( {0, + \infty } \right),\;\;\upchi\left( {\upeta,\uptau} \right) = \overline{\upchi} \left( {r_{0}\upeta,r_{0}\uptau/c_{2} } \right), $$
(5)

where \( \upchi\left(\upeta \right) \equiv 0,\;\upbeta \le\upeta \le 1 \), and \( \overline{\upchi} \left( {r,t} \right) \)—unknown tangential stresses acting in the crack plane.

To solve the formulated initial boundary value problem (1)–(5), we apply a method based on the difference approximation of time derivatives, detailed in [6]. For this purpose, we create a time grid:

$$ \uptau_{k} = \sum\limits_{{\upnu = 1}}^{k} {h_{\upnu} } ,\;h_{\upnu} =\uptau_{k} -\uptau_{k - 1} ,\;(\uptau_{0} = 0),\quad k = 1,2,3, \ldots h_{i} \ne h_{j} $$

We introduce the designation \( w\left( {\upeta,\upzeta,\uptau_{k} } \right) = w_{k} \left( {\upeta,\upzeta} \right) \) and use the left-sided finite difference for time derivatives. Then, from zero initial conditions and Eq. (1), we find

$$ w_{0} = 0,\quad D_{{{\upeta \upzeta }}} w_{1} = \frac{{w_{1} }}{{h_{1}^{2} }},\;D_{{{\upeta \upzeta }}} w_{k} - \frac{{w_{k} }}{{h_{k}^{2} }} = \frac{{w_{k - 2} }}{{h_{k} h_{k - 1} }} - \frac{{w_{k - 1} }}{{h_{k} }}\left( {\frac{1}{{h_{k} }} + \frac{1}{{h_{k - 1} }}} \right),\;\;k = 2,3, \ldots $$
(6)

Next, according to [6], we write the angular displacement, the angle of rotation of the plate, the stresses in the cylinder and the moment in the form of a linear combination of new functions:

$$ \begin{aligned} w_{k} &= \sum\limits_{{\upnu = 1}}^{k} {C_{{k\upnu}} U_{\upnu} } ,\quad\upalpha_{k} = \sum\limits_{{\upnu = 1}}^{k} {C_{{k\upnu}} A_{\upnu} } ,\;\;\uptau_{{{\upvarphi }rk}} = \sum\limits_{{\upnu = 1}}^{k} {C_{{k\upnu}}\uptau_{{{\upvarphi }r\upnu}} } ,\;\;\uptau_{{{\upvarphi }zk}} = \sum\limits_{{\upnu = 1}}^{k} {C_{{k\upnu}}\uptau_{{{\upvarphi }z\upnu}} } ,\\M_{0k} &= \sum\limits_{{\upnu = 1}}^{k} {C_{{k\upnu}}\upmu_{{0\upnu}} } , \end{aligned}$$
(7)

where \( C_{k\nu } \) determined by the formulas:

$$ \begin{aligned} C_{kk} & = 1,\;k = 1,2,3, \ldots ,\quad C_{k,k - 1} = \frac{{h_{k - 1} }}{{h_{k - 1} - h_{k} }},\quad k = 2,3, \ldots \\ C_{{k,\upnu}} & = \frac{{h_{\upnu}^{2} }}{{h_{k}^{2} - h_{\upnu}^{2} }} \cdot \left( {\frac{{h_{k} }}{{h_{k - 1} }}C_{{k - 2,\upnu}} - \left( {1 + \frac{{h_{k} }}{{h_{k - 1} }}} \right)C_{{k - 1,\upnu}} } \right),\;\; k = 3,4, \ldots ;\;\;\upnu = 1,2, \ldots ,k - 2. \\ \end{aligned} $$

Then the functions \( U_{\upnu} \) satisfy the homogeneous Helmholtz equation

$$ D_{{{\upeta \upzeta }}} U_{\upnu} -\upkappa_{\upnu}^{2} U_{\upnu} = 0,\;\upnu = 1,2,3, \ldots ,\quad\upkappa_{\upnu} = h_{\upnu}^{ - 1} . $$
(8)

The boundary conditions on the cylinder surface for these functions can be written as follows:

$$ \left. {U_{\upnu} } \right|_{{\upzeta = 0}} = 0,\quad \left. {U_{\upnu} } \right|_{{\upzeta = 1}} = A_{\upnu}\upeta,\left. {\uptau_{{{\upvarphi }r\upnu}} } \right|_{{\upeta = 1}} = 0. $$
(9)

The conditions for the crack will take the form:

$$ \left. {\uptau_{{{\upvarphi }z\upnu}} } \right|_{{\upzeta = l}} =\upchi_{\upnu} \left(\upeta \right),\quad 0 \le\upeta \le 1,\;\;\upchi_{\upnu} \left(\upeta \right) \equiv 0,\;\;\upbeta \le\upeta \le 1,\;\;\upchi_{k} = \sum\limits_{{\upnu = 1}}^{k} {C_{k\nu }\upchi_{\nu } } . $$
(10)

And Eq. (3) takes the form:

$$ {\uppi \upgamma }m_{0} {\chi}_{\upnu}^{2} A_{\upnu} = 2\left( {\upmu_{{0\upnu}} -\upmu_{{R\upnu}} } \right),\quad\upmu_{{R\upnu}} \left(\uptau \right) = 2\uppi\int\limits_{0}^{1} {\upeta^{2} \left. {\uptau_{{{\upvarphi }z\upnu}} } \right|_{{\upzeta = 1}} d\upeta} , $$
(11)

where \( \upmu_{{0\upnu}} \) can be found from the recurrence relation.

3 Solution of the Problem

The solution of the boundary value problem (7)—(11) is represented in the form:

$$ U_{\upnu} (\upeta,\upzeta) = U_{\upnu}^{0} (\upeta,\upzeta) + U_{\upnu}^{1} (\upeta,\upzeta),\quad U_{\upnu}^{0} (\upeta,\upzeta) = A_{\upnu}\upeta\frac{{{\text{sh}}\left( {{\upgamma \upzeta \chi }_{\upnu} } \right)}}{{{\text{sh}}\left( {{\upgamma \upchi }_{\upnu} } \right)}}. $$
(12)

The first term is the solution to the problem in the absence of crack. The second term is the solution to Eq. (8). It satisfies the zero conditions on the cylinder ends and lateral surface and on the surface of the crack it satisfies the condition:

$$ \uptau_{{{\upvarphi }z\upnu}}^{1} (\upeta,l) =\upchi_{\upnu} \left(\upeta \right) -\uptau_{{{\upvarphi }z\upnu}}^{0} (\upeta,l),\quad 0 \le\upeta \le 1. $$
(13)

The functions \( U_{\upnu}^{1} \left( {\upeta,\upzeta} \right) \) are found separately for the parts of the cylinder separated by the crack plane:

$$ U_{\upnu}^{1} \left( {\upeta,\upzeta} \right) = U_{\upnu}^{ - } \left( {\upeta,\upzeta} \right),\quad\upzeta \in \left[ {0,l} \right),\;\; U_{\upnu}^{1} \left( {\upeta,\upzeta} \right) = U_{\upnu}^{ + } \left( {\upeta,\upzeta} \right),\;\upzeta \in \left( {l,1} \right]. $$
(14)

In order to find \( U_{\upnu}^{ \pm } \left( {\upeta,\upzeta} \right) \), it is necessary to solve Eq. (8) with boundary conditions:

$$ \begin{array}{*{20}c} {\left. {U_{\upnu}^{ - } } \right|_{{\upzeta = 0}} = 0,\quad \left. {U_{\upnu}^{ + } } \right|_{{\upzeta = 1}} = 0,\;\;\uptau_{{{\upvarphi }z\upnu}}^{ \pm } (\upeta,l) =\upchi_{\upnu} \left(\upeta \right) -\uptau_{{{\upvarphi }z\upnu}}^{0} (\upeta,l),\;0 \le\upeta \le\upbeta,} \\ {\uptau_{{{\upvarphi }r\upnu}}^{ - } (1,\upzeta) = 0,\quad 0 \le\upzeta \le l,\;\;\uptau_{{{\upvarphi }r\upnu}}^{ + } (1,\upzeta) = 0, = 0,\;\;l \le\upzeta \le 1.} \\ \end{array} $$
(15)

The solution to these boundary value problems is constructed by the integral transform method, similarly to [8]. It contains unknown tangential stresses acting in the crack plane. To find they, we obtain an integral equation for they by using the condition of continuity of angular displacements in the crack plane for \( \upeta \in \left[ {0,\upbeta} \right] \).

By using the procedure proposed in [8], we reduce this equation to a Fredholm equation of the second kind for an unknown function associated with tangential stresses acting in the crack plane:

$$ g_{\upnu} \left( s \right) + \frac{1}{{2\uppi}}\int\limits_{ - 1}^{1} {g_{\upnu} \left( y \right)\left[ {F\left( {y - s} \right) + Q\left( {y - s} \right)} \right]dy} = \frac{{A_{\upnu} s}}{{{\text{ch}}\left( {\upgamma \upkappa _{\upnu} \left( {1 - l} \right)} \right)}}, $$
(16)

where \( F\left( Y \right) \) and \( Q\left( Y \right) \) are expressed via uniformly convergence integrals and series, and \( A_{\upnu} \) determined from Eq. (11).

An approximate solution to Eq. (16), as in [8, 10], is sought in the form of an interpolation polynomial. To solve Eq. (16), we approximate its integrals according to the quadrature Gauss-Legendre formula and obtain a system of linear algebraic equations for the values of the unknown function in the interpolation nodes. As a result of the solution of the system, the unknown function is approximated by the interpolation polynomial.

The solution of Eq. (16) allowed us to obtain a formula for calculating the dimensionless SIF:

$$ K\left( {\uptau_{k} } \right) = \frac{{\overline{K} \left( {t_{k} } \right)}}{G\sqrt b },\quad K\left( {\uptau_{k} } \right) = \sum\limits_{{\upnu = 1}}^{k} {C_{{k\upnu}} K_{\upnu} } ,\;K_{\upnu} = \frac{\sqrt 2 }{\uppi}g_{\upnu} \left( 1 \right). $$
(17)

4 Numerical Results

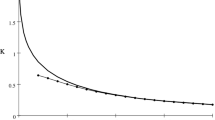
Using Formula (17), there was performed a numerical study of the dependence of the SIF on the dimensionless time \( \uptau \) for different load cases. The time grid nodes were condensed near the point \( \uptau = 0 \). The results of calculations are shown in Fig. 2 in the form of graphs of time dependencies of dimensionless SIFs. During these calculations it was considered that the relative thickness of the plate is δ = d/a = 0.1, the relative height of the cylinder is γ = a/r0 = 2, the crack is located in the middle plane of the cylinder l = c/r0 = 0.5, and the relative inner crack radius is b = b/r0 = 0.5.

Fig. 2.
figure 2

Time dependence of dimensionless SIFs for different types of load: \( M_{0} (\uptau) = H(\uptau) \) (left); \( M_{0} (\uptau) = H(\uptau) - H(\uptau - 1) \) (right).

Full size image

The charts have been constructed for the case of the action of a suddenly applied torsional load (Fig. 2 (left)), and the case of specifying the torsional load by a suddenly applied moment of the unit length (Fig. 2 (right)). Curve 1–4 correspond to different values of the relative plate density: \( {\bar{\uprho }} =\uprho_{\text{plate}} /\uprho_{\text{cyl}} :0.1;0.25;1;4 \).

From the graphs in Fig. 2 it can be seen that in all considered types of loading, during the transient process, the maximum SIF values are observed. When a sudden constant load is applied, this maximum is 1.5–2 times higher than the static value of SIF. Hence, it is most likely that the destruction of the cylinder will occur during the transient period. In addition, as can be seen from Fig. 2, an increase in the mass of the plate leads to an increase in the time until the SIF reaches its maximum value. However, it almost does not affect the maximum value itself, in the case of the action of a suddenly applied torsional load. In the case of the action of a load by a suddenly applied moment of the unit length, a decrease in the magnitude of the SIF maximum is observed. It can be explained by the fact that SIF does not have time to reach its maximum during the action of the load.

5 Conclusion

The paper proposes a method for solving the problem of determining the stress-strain state of an elastic finite cylindrical body with an outer ring-shaped crack that is under torsional loading. This technique is based on the differential approximation of the time derivative and use of a time grid with specially selected nodes. Numerical results demonstrate the effectiveness of such an approach when investigating the transient processes that occur immediately after load application. But arise some problems in applying this technique for large time intervals, due to the step-by-step accumulation of errors.