Chemical Oscillations and Spiral Waves

Abstract

Pattern formation is one of nature’s most fascinating phenomena. Starting with the evolution of life: cells and compartments start to differentiate such that they are able to undertake different tasks leading to life of complex organisms. Additionally, cells are able to release messenger substances, which may lead to an aggregation of cells as in the slime mold Dictyostelium discoideum. In this chapter, the formation of wave patterns, especially of spirals in non-equilibrium systems, is described. Starting with the revision of important aspects contributing to the historical development of synergetics, oscillating chemical reactions, such as the Belousov–Zhabotinsky reaction are described. Some theoretical aspects of reaction-diffusion systems and wave propagation in excitable media are outlined. The development and propagation of waves and thus, of spirals is described in such systems. At the end, the Belousov–Zhabotinsky reaction embedded in a compartmentalized system, namely an emulsion, is studied. Under the chosen conditions target patterns or spirals with segmented wave fronts evolve. These segmented waves (dashes) develop from a smooth one due to an instability. However, instead of forming a spiral turbulence, these dashes remain in an ordered configuration and form beautiful patterns.

1 Historical Remarks

Moving reaction waves occur in our everyday life even if we do not see them by eye. A remarkable example is our heart, in which waves trigger it to pump blood through our body (see chapter Spiral Waves in the Heart). The first person, who mentioned the existence of moving waves in a homogeneous medium was R. Luther in 1906 [1]. He already came to the conclusion that an autocatalytic reproduction of a chemical species must be involved. Furthermore, Luther was able to give an equation for the calculation of the wave velocity v:

$$\begin{aligned} v= a \sqrt{k D C}, \end{aligned}$$

(1)

where D represents the diffusion coefficient, k a rate constant of the chemical reaction, C a concentration and a a numerical constant. However, Luther gave no derivation for his equation.

Based on the work by Luther, B.P. Belousov started in 1951 to work on chemical oscillations in the catalyzed oscillatory bromate oxidation of citric acid. Since nobody believed in oscillating chemical reactions, Belousov was not able to publish his work before 1984 [2]. A.M. Zhabotinsky modified the reaction described by Belousov in 1961 in a fashion, which is still used today: the bromation of malonic acid, catalyzed by ferroin, which shows a color change from red to blue [3]. In 1974, Field and Noyes studied a semi-quantitative model of wave propagation in the reaction described by Belousov and Zhabotinsky. In their work, they were able to derive the equation given by Luther in 1906 [4]. Another remarkable aspect in the work of Luther was his comparison between chemical waves in a homogeneous medium and nerve impulses spreading over cell membranes, although he had no evidence for his suggestion [1]. In fact, there are structural analogies between both systems. The propagation velocity of a nerve pulse can be estimated using the Hodgkin–Huxley equation [5], which describes the propagation of stimuli throughout a nerve cell. They modeled the cell membrane as an electrical circuit, where the flow of ions can only be realized through ion selective channels and derived an equation which facilitate the calculation of the propagation of a nerve pulse over a membrane.

Oscillations in chemical systems were known much earlier than the propagating waves mentioned above. A brief summary of these historical experiments is given in the following: Already in 1829 F.F. Runge studied the contraction of a droplet of sulfuric acid on an area covered with mercury. He placed the acid on top of the mercury, where the droplet runs flat. Touching both with an iron wire, the acid contracts and forms a drop around the wire. Additionally, he observed that the mercury twitches slightly after touching. This system is nowadays known as the oscillating mercury heart [6]. At the end of the 19th century, R.E. Liesegang observed periodic precipitation patterns in gels (cf. Liesegang Rings, Spirals and Helices). In 1899 W. Ostwald observed the oscillating hydrogen production during the dissolution of chrome in acids. A theory of a hypothetical chemical reaction showing oscillations was given by A. Lotka in 1910. A more detailed description of his model is given in the next section. K.F. Bonhoeffer discovered in 1941 activity waves on passive iron wires. These wires were made passive by immersing them into sulfuric acid. Touching them with a piece of zinc, whereby it is locally cathodically polarized, an activity wave of local dissolution of the iron propagated along the wire [6].

2 Oscillations in Chemical Systems

The most prominent oscillating chemical reaction is the Belousov–Zhabotinsky (BZ) reaction. This reaction was first introduced by B.P. Belousov as a catalytic model for cancer cycles in which cerium ions are used instead of protein bounded metal ions, which are normally used by enzymes in living cells [6]. He described a periodic color change between colorless and yellow. In the default configuration, which is nowadays used, the color change in the BZ reaction is realized by the catalyst ferroin (Fe(1,10-phenanthrolin)$^{2+}_3$), which changes its color from red to blue upon oxidation. In its reduced state, it has a positive charge of two and in its oxidized state it has a positive charge of three. In the reaction, an organic substrate (usually malonic acid) is oxidized by bromate in an acidified milieu via the metal ion catalyst (ferroin) [7]. The ion Br$^-$ is playing the role of the inhibitor and HBrO$_2$ acts as the activator of the system since it is autocatalytically produced. The overall BZ reaction is governed by the oxidation of malonic acid due to bromination:

$$\begin{aligned} 3\, \text {H}^+ + 3\, \text {BrO}_3^-+5 \,\text {CH}_2\text {(COOH)}_2 \rightarrow 3 \,\text {BrCH(COOH)}_2 + 2\,\text {HCOOH} + 5 \,\text {H}_2\text {O} + 4\,\text {CO}_2. \end{aligned}$$

The entire reaction consists of a set of different chemical reactions that can be subdivided into three processes: First, the inhibitor Br$^-$ is consumed until its concentration falls below a certain concentration, which triggers the second process. This process contains the autocatalytic production of the activator HBrO$_2$. Furthermore, the metal catalyst ferroin is oxidized in this process, which is responsible for the color change to blue. When the reduced version (red color) of the catalyst is depleted, the third process sets in. Here, malonic acid is brominated and the metal catalyst is reduced and gets back its red color. Additionally, Br$^-$ is produced in the last process. Due to the increase of its concentration, the first process will be activated again [7]. If the above described system is stirred, it shows color oscillations in bulk. However, if it is performed in a Petri dish, it shows—depending on the initial concentrations of the reactants—spontaneously evolving patterns such as target patterns or spirals (see Sect. 4).

Another example of an oscillating reaction is the Briggs–Rauscher reaction, which is an oscillating iodine clock, cyclically changing its color from colorless to gold to blue. The reaction consist of the following ingredients: potassium iodate, hydrogen peroxide, perchloric acid, malonic acid, manganese(II)-sulfate and starch. This reaction works at room temperature, which makes it suitable for demonstrations (contrary to the Bray reaction, which is an early precursor of the Briggs–Rauscher reaction). The reaction shows visible concentration changes in iodine and the concentration of the iodine ion fluctuates. When the iodide concentration reaches a certain value, a starch complex is formed, which appears in blue color [8].

A theoretical analysis of a periodic reaction was given in 1910 by A. Lotka [6]. Nowadays it is referred to as Lotka–Volterra model. It represents a hypothetical chemical homogeneous system, which shows oscillations and is described by the following three reactions:

$$\begin{aligned} A + X_1 {\mathop {\longrightarrow }\limits ^{k_1}}2X_1, \nonumber \\ X_1 + X_2 {\mathop {\longrightarrow }\limits ^{k_2}}2X_2,\\ X_2 {\mathop {\longrightarrow }\limits ^{k_3}}F.\nonumber \end{aligned}$$

(2)

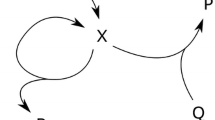
From the chemical point of view, the autocatalytic step (production of $X_2$) in the second equation does not make much sense, since the molecule $X_1$ must transform in presence of $X_2$ into $X_2$ as well. Thus, nowadays it is used to describe the relation between a predator and its prey. In this case, $X_1$ is referred to as rabbit, $X_2$ represents the predator (e.g., a lynx), A is the food of the rabbit and F quantity of the lynx having died of natural causes (with the death rate $k_3$).

The reactions from Eq. (2) result in a pair of nonlinear differential equations indicating the rates of change of the concentrations of the chemical species $X_1$ and $X_2$. The amount of food and the death rate (i.e., A and $k_3$) are assumed to be constant:

$$\begin{aligned} \begin{aligned} \text {d}[X_1]/\text {d} t = k_1 [X_1][A]-k_2[X_1][X_2] ,&\\ \text {d}[X_2]/\text {d} t = k_2[X_2][X_1]-k_3[X_2],&\end{aligned} \end{aligned}$$

(3)

where $k_i$ are constant reaction rates, and the values in brackets the concentrations of the corresponding species. Spoken in the predator-prey context, the oscillations occur in the amount of rabbits and lynx. If enough rabbits are present to feed on, the population of lynx will increase. However, this larger population will consume more rabbits, such that their population decreases and with this also the population of lynx.

3 Waves in Chemical Systems

3.1 Reaction-Diffusion Systems

Many patterns in nature arise in so-called reaction-diffusion!systems (cf. chapter Reaction-Diffusion Patterns and Waves). In these systems, a chemical reaction occurs locally and is transported in space by diffusion. A prominent reaction showing such patterns is the unstirred BZ reaction (Fig. 1). For a classical reaction-diffusion system, only one chemical component (here: u) is required:

$$\begin{aligned} \frac{\partial u}{\partial t} = D_u \frac{\partial ^2 u}{\partial x^2} + f(u). \end{aligned}$$

(4)

$D_u$ denotes the diffusion of the component u, x the spatial dimension, t the time and f the reaction term. This is a partial differential equations with diffusion. If a second component is involved in this process, one typically speaks of an activator-inhibitor system. In this case, one of the species is produced autocatalytically, whereas the other one inhibits this production. Thus, Eq. (4) extends to:

$$\begin{aligned} \begin{aligned} \frac{\partial u}{\partial t} = D_u \frac{\partial ^2 u}{\partial x^2} + f(u,w),&\\ \frac{\partial w}{\partial t} = D_w \frac{\partial ^2 w}{\partial x^2} + g(u,w).&\end{aligned} \end{aligned}$$

(5)

$D_u$ and $D_w$ represent the diffusion of the corresponding species u and w, respectively.

Fig. 1

(Image courtesy: S.C. Müller, personal communication)

Target patterns and spiral waves in the BZ reaction. The dark spots are small bubbles, since gas is produced during the reaction

In 1952 Alan Turing was the first, who described such systems mathematically. He showed that a chemical system will form stationary patterns, if some conditions for the diffusion constants are fulfilled, namely the diffusion of the activator must be much slower than that of the inhibitor [9]. The experimental observation of the patterns predicted by Turing took several decades, since the demanding conditions on the diffusion coefficients of activator and inhibitor in chemical solutions made it experimentally challenging. A “trick” was necessary to reduce the diffusion coefficient of the activator. In 1990 the first experimental observation of Turing patterns was realized by V. Castets et al. in the chlorine-dioxide-iodine-malonic acid reaction, as he trapped the activator in a gel matrix [10]. In nature, Turing patterns occur during morphogenesis, e.g., on animal skins.

In 1968 Prigogine and Lefever [11] formulated reaction-diffusion equations while they extended Turing’s equations, such that their equations could explain the differentiation of biological cells with the aid of reactions and substance exchange of two different types of molecules. They declared the role of diffusion in a system having two tasks: First, diffusion increases the stability of a system, but second, it also increases the variety of perturbations, which are compatible with the macroscopic equations of change.

3.2 Excitable Media

Excitability is an important concept in biology and chemistry. Common examples in nature are the brain and the heart (cf. chapter Spiral Waves in the Heart). Through these media electric pulses propagate forcing to change their state for a short time [12]. An important example from the chemical field represents the BZ reaction [13]. In such systems a perturbation is overdamped, if it is smaller than a certain threshold. A large perturbation, however, causes a response of the former. Due to the complete recovery of the system after the passage of an excitation wave, many of those can travel trough it. A single wave pulse is sketched in Fig. 2. The wave propagates towards the left. In its front, the medium is excitable. A perturbation induces a wave traveling through the system, where the wave front itself is in the excited regime. Behind the pulse, the medium must recover and is in the refractory state. When the system has fully recovered, a new perturbation can induce a new wave pulse. Within a spatially distributed excitable medium the excitation propagates from one point to the neighboring one by local coupling realized by diffusive transport [12]. Due to the interplay of diffusion and chemical reactions, waves of excitation can propagate through the medium, forming patterns like spiral waves in space or oscillations in time [13] (see Sect. 4).

Fig. 2

Sketch of a propagating concentration wave [u] over time. Before the system is perturbed, it is in the excitable regime (low concentration of u). After it has passed the excited regime, it must recover, since the concentration of u is lower than in the excitable state, which makes it immune to a new perturbation

4 Creation and Propagation of Spiral Waves

The propagation of waves in excitable media depends mainly on diffusion. Its velocity v can be calculated with the help of Eq. (1) with D, k and C being diffusion coefficient, rate coefficient and concentration of the activator u, respectively. When several waves emerge, such as concentric circles (see Fig. 1; also called target pattern)—induced by a pacemaker in the system (e.g., an impurity)—wave propagation is governed by the so-called dispersion relation of the system. It is defined as the velocity of a wave v divided by the distance between single waves, i.e., the wavelength $\lambda$. In general, this relation is positive in the BZ reaction, which means that the velocity of a wave decreases with decreasing distance between the waves [14]:

$$\begin{aligned} \frac{\text {d}v}{\text {d}\lambda } > 0. \end{aligned}$$

(6)

Additionally, the velocity of a wave depends on its curvature K (which is equal the inverse radius r of a wave). Plain waves are faster than curved ones. This fact is described by the following equation, which is called eikonal equation:

$$\begin{aligned} {v} = {v_0} - D {K} = {v_0} - D \frac{1}{r}. \end{aligned}$$

(7)

Here v describes the velocity of a curved wave in the normal direction, $v_0$ the velocity of a plain wave, and D is the diffusion coefficient. The eikonal equation describes, how the velocity of waves decrease with increasing curvature and it also places a stability condition on the wave front, since a uniform curvature of a wave is a stable solution of Eq. (7) [14]. This means that perturbations of the wave front, e.g., due to an obstacle balance out. Additionally, it is obvious that a critical curvature exists, where wave propagation fails:

$$\begin{aligned} K_{crit} = \frac{v_0}{D}. \end{aligned}$$

(8)

This plays a crucial role in the formation of spiral waves. At the tip of a spiral, the highest curvature that is possible in the system is adopted, and with this, the velocity is lowest there.

In Fig. 3 the process of the formation of a pair of counter-rotating spiral waves is depicted. The propagating wave front (1) reaches an obstacle (e.g., a region of lower excitability), which causes the break up of the wave front (2). After leaving the obstacle, the wave front remains broken and at the open wave ends an additional velocity component is present, which is perpendicular to its initial one (3). The wave starts to curl yielding a slower propagation velocity at the tips (cf. Eq. (7)). Each open end forms a spiral, having an opposite sense of rotation (i.e., opposite chirality) (4). In the end, spirals of Archimedean shape have formed, rotating around a fixed center, called the spiral core, which is the organizing center of the spiral. In the direct vicinity of the core, however, the shape differs slightly from the Archimedean [15] (see involute in chapter Spirals, Their Types and Peculiarities).

Fig. 3

Sketch of the formation of a pair of counter-rotating spiral waves. A plain wave (1) reaches an obstacle, which causes a breakup (2). At the open wave tips, the excitation can now propagate into the direction perpendicular to the direction of the plain excitation wave (3). Due to the slower propagation velocity of a curved wave, the wave tips can curl up to form a spiral (4)

The spiral tip is a singularity in the medium at which the spiral has the greatest curvature. This means that the normal velocity of a curved wave becomes zero ($\mathbf v = 0$, cf. Eq. (7)) and the tip moves tangentially along a circular trajectory, since the high curvature prohibits movement into the normal direction (Fig. 4) [16]. The area enclosed by the trajectory is called the spiral core and is not excitable. Spirals have the ability to organize an excitable medium, as they can take up the highest possible frequency in the medium. The value of this frequency is determined by the medium itself, as it depends, among other things, on its excitability. Higher frequencies do not exist, since otherwise, the excitation front would run into the refractory regime of its predecessor.

Fig. 4

(copyright by Hess, Markus, Müller, Plesser, Dortmund 1987)

Superposition of images of the spiral tip during one rotation around the core in pseudo-colors. The area never touched by the wave is colored in orange

In the two-dimensional (2D) BZ reaction, spiral waves, target patterns or simple oscillations can occur and run through the entire system. Target patterns can be induced by touching the medium in a single spot with a silver wire for a few seconds. On the surface of the wire bromide ions (which act as the inhibitor) are bound, which locally reduces the concentration of these ions in the reaction. This induces the autocatalytic formation of the activator HBrO$_2$ (cf. Sect. 2). Spiral waves emerge, when an enclosed wave front is disturbed, such that it ruptures (Fig. 3). This can be forced, if a wave front is treated with an air jet. Even an obstacle can force the wave front to break, if it is large enough (otherwise the wave fronts will merge behind the obstacle and no open wave end is created). With these methods, one gets always a pair of counter-rotating spirals as shown in the lower half of in Fig. 1. The initiation of a single spiral needs a little more experimental skills. Here a thin (quasi 2D) reaction container can be used, where a gel, in which the BZ reaction runs, is filled up to half. Then, a wave is initiated with a silver wire near one boundary. When one end of the wave reaches the boundary, the reaction container is filled up with the BZ gel and the wave can now propagate into the regime of the new gel. This method is described in detail in Ref. [17].

The wave propagation velocity v in the BZ reaction depends on the chemical composition of the reaction mixture, which determines the speed of the reaction and the transport processes. Especially, v is governed by the proton concentration [H$^+$] and bromate concentration [BrO$_3^-$] (cf. Eq. (1)) [18]:

$$\begin{aligned} v \sim \sqrt{k_uD_u[\text {H}^+][\text {BrO}_3^-]}, \end{aligned}$$

(9)

where $k_u$ is the reaction rate of the activator and $D_u$ its diffusion coefficient. If the initial concentrations of malonic acid, sulfuric acid and sodium bromate are high compared to the concentration of ferroin, homogeneous oscillations occur in the system. A comparable ratio between ferroin and the other three reactants yields reduction waves in the BZ medium.

The BZ reaction can be inhibited by oxygen, which diffuses up to 2 mm depth into the liquid layer. The inhibition occurs due to oxidation of malonic acid by ferroin. When atmospheric oxygen diffuses into the reaction, malonic acid is no longer available for the reaction, since its radicals are caught by oxygen [19]. Thus, it is advisable to perform experiments in a closed container.

5 Patterns in Microemulsions

The BZ reaction can be embedded on the one hand into a gel, which does not affect any properties of the reaction, such as diffusion of chemical species. On the other hand, the reaction can be loaded into an emulsion, which is a mixture of oil and water. In the system discussed here, only water-in-oil emulsions are considered (i.e., a little amount of water in much oil). The small water droplets are stabilized with a surfactant and have a size of a few nanometers, leading to the name microemulsion. They have certain physical properties, which are discussed in the following.

5.1 Physical Properties of Microemulsions

Almost everything in an emulsion is governed by the volume ratio between water and oil (cf. Fig. 5). Additionally the amount of surfactant is also important, since it is responsible for the stability of the system. Unless enough surfactant is available, the interface between water and oil cannot be fully covered with the surfactant and no defined structure is formed. In Fig. 5 (right) possible configurations of the water phase in a microemulsion are depicted, together with a phase diagram which shows how the ratio between water, oil and surfactant affects the emerging configurations. Here, mainly the L$_2$ phase is considered, i.e., spherical water droplets, surrounded by a monolayer of the surfactant diffusing through the oil phase. The droplets collide and merge, forming droplet clusters, which can split again. As the solvent, a saturated hydrocarbon is used, like octane or hexane. The used surfactant is sodium-bis(2-ethylhexyl) sulfosuccinate (AOT, Fig. 5 (left)), which shows the L$_2$ phase over a wide range of concentrations. AOT is an anionic surfactant consisting of a polar head group (SO$_{3}^-$) and two hydrophobic tails [20].

Fig. 5

Reprinted by permission from Springer: Patterns of Nanodroplets: The Belousov-Zhabotinsky-Aerosol OT-Microemulsion System, V. K. Vanag and I. R. Epstein [21], copyright 2008

Left: Sketch of the surfactant AOT with its polar head group SO$_{3}^-$. Right: Phase diagram of the water-AOT-oil system. The L$_2$ phase is a reverse microemulsion (water-in-oil microemulsion), in which most of the experiments in this work are performed. L$_H$ – hexagonal phase; LC – lamellar phase (liquid crystal).

The properties of an emulsion can be described with the help of two parameters: The molar ratio $\omega$ between water and AOT concentration [22]

$$\begin{aligned} \omega = \frac{[H_2O]}{[AOT]}, \end{aligned}$$

(10)

and the volume droplet fraction of the dispersed phase $\varphi _d$, which is the ratio of the sum of the individual volumes of water ($V_W$) and AOT ($V_{AOT}$) and the entire volume of the emulsion:

$$\begin{aligned} \varphi _d = \frac{V_W + V_{AOT}}{V_W + V_{AOT} + V_{oil}}. \end{aligned}$$

(11)

With the help of $\omega$, the droplet radius $R_{\omega }$ of the water core (without the AOT-molecule [23]) can be estimated with the empirical equation

$$\begin{aligned} R_w [nm] = 0.17 \omega . \end{aligned}$$

(12)

To calculate the radius of the droplet including the surfactant, the length of the AOT-molecule must be added ($\approx$ 1.1 nm) [24]. $\varphi _d$ acts as an order parameter of the system, since it determines the configuration of water, oil and AOT (cf. Fig. 5).

5.2 Percolation

When changing the amount of water, the droplets of the L$_2$ phase merge and form water channels pervading the entire medium. This process is called percolation. In general it means that components of a system form connected clusters. If a cluster reaches all ends of a system, the latter is percolated. Some practical examples are water in a coffee filter or forest fires and their models.

In a mircoemulsion, the first infinite droplet cluster is formed around a droplet fraction of 0.5, which is referred to as critical droplet fraction $\varphi _{cr}$ [24]. Due to this network of water channels, viscosity and electric conductivity increase as well. For $\varphi _d \ll \varphi _{cr}$, the droplets move nearly freely in the oil phase. The emulsion has a high viscosity due to the large amount of oil and its electric conductivity is close to that of pure oil. Above $\varphi _{cr}$ the number of such clusters increases rapidly [25] and with them the electric conductivity. In fact, the latter can be used to measure the critical droplet fraction, above which the system is percolated. Thus, percolation causes a threshold-like behavior of physical quantities.

5.3 BZ Reaction in Microemulsions

Embedding the BZ reaction in a microemulsion (referred to as BZ-AOT system), which shows the L$_2$ phase, changes the emerging patterns significantly compared to the aqueous BZ reaction. The reaction only runs within the water droplets, such that the diffusion coefficient of the activator is reduced. It diffuses with the same velocity as the droplet itself. Some products of the BZ reaction, such as molecular bromine Br$_2$ and the radical BrO$_2^{\bullet }$, which are inhibitors of the system, are soluble in the oil phase and can diffuse out of the droplets. Thus, their diffusion coefficient rises by 10–100 of the initial value. Hence, the conditions for Turing patterns are fulfilled (cf. Sect. 3) and the corresponding stationary patterns can occur in the BZ reaction [24]. Note that Turing patterns can only occur below the percolation threshold, due to the conditions on the diffusion coefficients of activator and inhibitor.

Fig. 6

Reprinted by permission from Springer: Patterns of Nanodroplets: The Belousov-Zhabotinsky-Aerosol OT-Microemulsion System, V. K. Vanag and I. R. Epstein [21], copyright 2008

Overview of patterns occurring in the BZ reaction embedded in a micro-emulsion. The patterns in the right column (above a chemical concentration relation of 0.1 M) are generated with another catalyst (bathoferroin).

Figure 6 shows an overview of patterns, which can occur in a microemulsion, depending on the ratio between the chemicals (sulfuric acid, sodium bromate and malonic acid), and the droplet fraction. Above the percolation transition, a bimodal distribution of the droplet radius is found (below the transition, only one radius is found) [21], favoring the formation of discontinuously propagating waves (like jumping, rotating and bubble waves) and dash waves (see Fig. 6, above a chemical concentration relation [H$_2$SO$_4$][NaBrO$_3$]/[MA] of 0.1 M). The latter develop from a smooth wave front, which splits up such that coherently moving wave segments separated by lateral gaps occur [21, 24]. These waves will be discussed briefly in the following section.

5.4 Segmented Waves

Segmented (or dash) waves occur mainly, when two pools of droplets exist, with radii of around 2 and 20 nm [21]. This is typical when using the catalyst bathoferroin, which is a derivate of the default catalyst ferroin. However, spirals cannot be induced in a controlled way as described in Sect. 4, but they have to form spontaneously (e.g., due to an impurity or small concentration differences). In the reaction with bathoferroin, dash waves or spirals, as well as discontinuously propagating waves, such as rotating and jumping waves evolve (Fig. 6).

Figure 7a shows dash waves in the upper left corner, with a negative (concave) curvature and (b) spiral waves with a positive (convex) curvature. Segmented waves evolve from ordinary (smooth) waves, which become unstable with time. They show so-called ripples, which means that some regions of the wave are propagating slower than their neighboring regions, and the curvature of these slow regimes becomes negative (box in Fig. 7b). In the course of time, the wave breaks in these regions, such that small segments of the original wave remain, which travel through the medium as if the wave front still exists. The instability occurs only, if the inhibitor diffuses fast (compared to the activator) and causes a wave break-up [26]. The former acts transverse to the wave front and it may occur through lateral inhibition or a kinetic interaction of the wave with a reactant in front of it [27, 28]. The segmentation of wave fronts always starts near the center of a spiral, since the curvature is highest there.

Dashes of one wave front propagate into the gaps of its precursor, which means that the dashes are displaced by the length of a dash relative to their precursor. In the dashes, the inhibitor is primarily generated, diffusing faster than the activator, and suppressing the autocatalytic reaction in the neighboring gaps. Additionally, this increases the time until the the medium has recovered when the subsequent wave front reaches it [21, 24]. The displacement of the dashes is visualized with the help of superposition of frames over time (Fig. 7c and d). The length of the dashes vary between 90 and 163 $\pm \,2\,\upmu$m and the length of the gaps from 40 to 104 $\pm \,2\,\upmu$m. Convex wave fronts show a splitting of dashes, when reaching 1.7 to 1.9 ± 0.1 times their initial length. This is depicted in Fig. 7d (red box), since the dashes propagate away from each other. For a concave curvature (as in Fig. 7c, black box) a merging of dashes can be found. The gaps get smaller, such that the dashes move closer together until they merge. Splitting or merging of the dashes was not found for a curvature K between −0.10 and 0.21 ± 0.1 mm$^{-1}$, i.e., for almost plain wave fronts—here, the dashes propagate straightforward without changing their length.

Fig. 7

Reprinted with permission from P. Dähmlow, V. K. Vanag, and S. C. Müller, Phys. Rev. E 89, 010902 (2014) [29]. Copyright 2014 by the American Physical Society

Snapshots of patterns in the bathoferroin-catalyzed BZ-AOT system with $\omega$ $=$ 12 ($\varphi _d$ $=$ 0.455) at t $=$ 224.8 min a in octane (size of images: 3 $\times$ 3 mm$^2$) and b in hexane (size of images: 5.9 $\times$ 6.1 mm$^2$). Superposition of binarized images c in octane between 180.0 and 189.2 min and d in hexane between 220.0 and 227.9 min with time interval of 40 s. Note that black lines in the superposition images represent the bright wave front.

Fig. 8

Histogram of the curvature K of a wave front for different experiments, in which a splitting of a dash occurs. The recipes are equal for all experiments: [MA] $=$ 0.242 M, [NaBrO$_3$] $=$ 0.174 M, [H$_2$SO$_4$] $=$ 0.194 M, $\omega$ $=$ 12 and $\varphi _d$ $=$ 0.455. 1 - dashed spiral in Fig. 7b, 2 - dashed spiral wave, 3 - dashed target pattern

The frequency distribution of the curvature, where splitting of dashes occurs, is shown in Fig. 8. For a mean curvature, the number of splitting dashes is much higher than that for small or large curvatures, since large curvatures occur only near the spiral core, where the number of dashes is much smaller than at the outer wave fronts.

The merging of wave fronts due to a decreasing distance between single segments is closely related to those studied in Ref. [30]. If the distance between the segments is smaller than the width of the wave front (i.e., the autocatalytic band), segments merge. An equal distance between both yields a constant length of single dashes. In our case, the distance between the dashes is also governed by the curvature of the initial wave. The segments are additionally forced to reduce their distance to each other at concave curvature of the initial wave front. A plain wave, where the distance between single dashes and the width of the wave front is equal shows a straight forward propagation of the segments, without any variations in length, as already described in Ref. [30].

6 Summary and Conclusion

Pattern formation in reaction-diffusion systems represents an important phenomenon in biological morphogenesis. In the early stages of the development of synergetics, people were fascinated by oscillatory chemical reactions, such as the mercury heart [6] or a periodic color change in the BZ reaction [2]. However, the scientific community doubted its existence, since self-organization of systems contradicted the increase in entropy and thus the second main theorem of thermodynamics. However, patterns can only form in systems, which are far away from thermodynamic equilibrium and have an energy- and/or mass transfer with their environment. This fact resolves the conflict.

In this chapter, the chronological sequence of important historical experiments contributing to the development of synergetics was given, especially in the context of pattern formation in reaction-diffusion systems. The most prominent example presents the BZ reaction, which shows both: periodic oscillations in a stirred solution and spatially expanding waves in an undisturbed system. The wave propagation in the spatially extended BZ reaction was studied in detail, and the influencing factors on the wave velocity (i.e., concentrations of reactants, reaction rate, diffusion, curvature of the wave front and dispersion relation) and the mechanism of the formation of spiral waves were described.

Additionally, it is possible to load the BZ reaction into a water-in-oil emulsion, which afflicts the relation of the diffusion coefficients of activator and inhibitor significantly. This enables the system to form a wide range of possible patterns such as Turing patterns, discontinuously propagating waves (such as bubble and jumping waves) and segmented waves (cf. Fig. 6). Segmented waves evolve from an ordinary wave (target pattern or spiral wave), due to an instability. These dashes split or merge, depending on the curvature of the initial wave front, such that their length remains within a certain interval. However, the length of the gaps play an important role. Single segments are either able to curl and form new spirals or propagate ahead (as shown in Fig. 7). Larger gaps between the dashes would mean that not the entire area between the segments will be inhibited, wave propagation will become possible and the segments can start to curl and a spiral turbulence will develop.

We find that spiral waves represent an interesting and fascinating pattern, which can be found in many biological and chemical systems, as described throughout this book. They organize the medium in which they occur and oust many other pattern with time.