Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

6.1 Introduction

Generally, the process of coordination arising out of the local interactions between smaller component parts of an initially disordered larger system is identified as self-organization . Such a principle is called “order from noise” as first formulated by the cyberneticist Heinz von Foerster in 1960 [1]. He noted that self-organization is facilitated by random perturbations (i.e. noise) that allow the system exploration throughout a variety of states in its state-space. This increases the chance of internal organization during the system influx into a set of certain (e.g. numerical) denominations towards which a system tends to evolve (called attractor ). It is often triggered by random fluctuations that are amplified by positive feedback, which would then allow entering the attractor stipulation itself.

A similar principle was formulated by the thermodynamists Ilya Prigogine and named “order out of chaos” [2]. Consequently, Georgi and Georgiev [3] utilized the stationary principle of least action within the concept of physics defining inner organization of a complex system as the state of the constraints determining the total action of the individual elements in such a system. There simultaneously emerges an elementary constant which value can be identified as the Planck quantum of action. The mechanism of such a mode of self-organization sustains the interaction between the elements and constrains leading to the minimization of constraints [2]. This is consistent with the Gauss’ principle of least constraint [4] saying that more elements minimize the constraints faster which is another aspect of the mechanism in the course of quantity accumulation. As a result, the paths of the elements are straightened, which is also consistent with the Hertz’s principle of least curvature [5] recently applied elsewhere [6].

In the 1940s, the forward-looking concept of self-organization was innovatory discussed by the cyberneticist Ashby [7]. In 1992, it was followed by above mentioned Förster [1] within his ides of cybernetics of second order as well as by Heylighen [8]. During the 1990s, the idea was picked up by physicists and chemists while studying phase transitions and other phenomena of spontaneous ordering of molecules and particles [9–12]. These include Ilya Prigogine [2, 13] who received a Nobel Prize for his investigation of self-organization of dissipative structures and Haken [14] who dubbed his approach as synergetics. In the 1980s, this tradition was cross-fertilized with the emerging mathematics of nonlinear dynamics and theory of chaos [2, 12, 13], producing such an investigation of complex systems that comes up quantitative, mathematical and predictable by physicists. However, the same period saw the appearance of a parallel approach, research into so-called complex adaptive systems [10] taking its inspiration more from biology and the social sciences than from physics and chemistry, thus helping to create another new disciplines of artificial life and social simulation, which falls beyond the scope of this chapter.

In the down-to-earth sphere of experimental chemistry, the naturally synchronized oscillating processes are among the most fascinating reactions [15, 16]. In one type of reaction, a mixture of chemicals goes through a sequence of colour changes, and this sequence repeats periodically; in another, the mixture periodically emits a burst of gas foaming up or even affects the stoichiometry of solid-state reactions. To many laypersons, these self-oscillating reactions are engaging examples of chemical magic; to others, having already some acquaintance with chemistry, these reactions still being the mystery and a challenge. Under a given set of conditions, experience tells us that chemical reactions go in only one direction rarely finding a chemical reaction that appears to reverse itself, much less to do so repeatedly. When we do encounter such a reaction, we may be inclined to draw an analogy to a simple physical oscillator such as a pendulum. A pendulum oscillates from side to another side through its equilibrium position, and these oscillations can be attributed to the inter-conversion between the potential and kinetic energy of the pendulum. Analogously to this physical process, the chemical oscillator may seems to swing through its equilibrium composition; but it contradicts to the second law of thermodynamics which asserts that, once a chemical system reaches equilibrium, it cannot deviate from that condition spontaneously. Therefore, oscillations in chemical reactions cannot be like the oscillations of a pendulum because chemical reactions cannot simply oscillate throughout the equilibrium condition. More links can be found between the oscillation processes and self-similar branching of dendrite arms resulting from unstable temperature and concentration gradients [17].

6.2 Self-Similarity and the Orderly Dendritic Growth

Rates of general processes are coupled with flows initiating growths, which associate off-equilibria subordinated with supersaturations, ΔC and undercoolings , ΔT. They are closely related by the functions whose forms depend upon the processes controlling transformation (atomic arrangement, heat and electrical conduction or mass and viscous flow) [17–20]. In each case, the growth rate increases with increasing degree of out-of-equilibrium and inherent perturbations on the reaction interface. The driving force for such an accelerated growth can be usually expressed by the negative value of the first derivative of the Gibbs energy change, ΔG, with respect to the reaction remoteness (from equilibrium), labelled as the distance, r. For small undercooling, we can still adopt the concept of constancy of the first derivatives, so that dΔG equals to the product of the entropy change, ΔS, and the temperature gradient, ΔT, which is the difference between the thermodynamic temperature gradient (associated with transformation) and the heat-imposed gradient at the reaction interface as a consequence of external and internal heat fluxes. Because ΔS is often negative, a positive driving force will exist to allow perturbations to grow, only if ΔT is positive [20]. At the critical wavelength linked to minimum undercooling at the solidification front depending on the surface tension thus lamellar eutectic oscillatory instability arises, leading to the formation of secondary arms called dendrites [17–20]. Illustrative view on self-similarity on the subject of such structures on gradual span ranking is best imagined by the sequential duplication of certain geometrical motives; see Fig. 6.1, simulating thus various natural objects.

Fig. 6.1
figure 1

Upperline growth of a snow crystal under near-constant weather conditions is primarily dependent on temperature, pressure, and vapour density and their interaction with environment. Growth [21] is based on a strong convexifying force up to micrometer size and three physically reasonable mechanisms: diffusion of water molecules off the crystal, exchange between attached and unattached molecules at the boundary and heat evolved interplay. Throughout dendritic crystallization, the lower vapour density first leads to lower frequency of side branches, then to sandwich instabilities and relatively thick plates. The melting rate regulates the ability of attached molecules at the boundary to detach. Other sketches and photos are described in the text

Full size image

Regimes displaying spatial or temporal order, we call dissipative structures [18], often associated with the formation of a dendrite which begins with the recurrent breakdown of an unstable planar solid/liquid interface. Perturbations are amplified until a marked difference in growth of the tips and depressions occurs. The temperature gradient must be deformed in the liquid as the tip increases, therefore, more heat will flow into the tip and less will flow out of it. Moreover, the equilibrium temperature at the interface, determined mainly by intermediate composition C, is changed as a consequence of the local interface curvature. Because the tip can also reject the solute in lateral direction, it will tend to grow more rapidly than a depression which tends to accumulate the excess solute rejected by the tips. Therefore, the form of the perturbation is no longer (initially) oscillatory but adopts the form of cells which are ellipsoid-like crystals growing anti-parallel to the net flux direction. If the growth conditions continue close to the limit of constitutional undercooling of the corresponding planar interface, tree-like formation occurs and the cells rapidly change to dendrites , which then exhibit secondary arms and crystallographic governing growth directions [17–20]. This pseudo-thermodynamic approach gives the same result as that deduced from the concept of zone constitutional undercooling. Its analysis, important for the manufacturing of advanced materials (such as fine-metals, nano-composed assets, formation of quantum dots and composite whiskers and growth of oriented biological structures) falls, however, beyond the scope of this chapter. Self-similarity is caused by periodic processes but the true sphere of the formation of oscillating reactions is, however, due to another nonequilibrium factors as will be shown later.

Self-similarity (and/or self-affinity) is exhibited, in various scales, by all natural plants (broccoli is a right example) and by crystals. It can be simulated upon a geometrical construction by repeating and duplicating patterns of various bifurcation processes known in vegetation, tree growth, etc. The typical feature of this growth is the so-called allometric scaling , the logarithms of the inverse compass setting (precision) as linearly dependent on logarithm of the length (e.g. measuring the circumference of leafs, live organs or more traditional length of the coast). The popular construction of Pythagorean tree starts by simple children-like drawing of a square with an attached right-angled triangle. Then two squares are attached along the free sides of triangle followed by repeating attachment of squares and triangles, see Fig. 6.1, middle line, inset of the left sketch. It certainly can be modified in various ways; the triangles need not be right-angled providing another degree of freedom. After as many as 50 iterations, the results cannot look more different: when the applied angle is greater than 90° (see middle line, the large sketch on left), we can envisage the structures like broccoli in comparison with a natural broccoli; cf. the middle line of Fig. 6.1, left photo; while right is electrodeposited metallic tantalum. Bottom left is a fern or even a pine tree. In other cases, it can remind us of a spiralling leaf or decorated coiled shell (Fig. 6.1, bottom middle), worth noting that the size of triangles in the bottom are the same in both exampled portrayals.

6.3 Chemical Swinging Clock and the Emergence of Planck Constant

In certain solute concentrations range (often from ~1020 to ~1023 ions per dm−3), the nonlinear coupling between chemical reaction and ionic diffusion leads under some circumstances to the appearance of succession of chemical waves. When a Russian scientist B.P. Belousov discovered in the year 1952 such an unpredictably spontaneous product of self-organization in the form of sequence changes of colour in some chemically reacting system; it took him several years to convince scientific officials to believe it. He was able to publish his finding in an obscure nonreviewed journal [22]. Belousov’s research was followed and enhanced by Zhabotinsky [22] and Tyson [23]. They discovered mostly inorganic reactions, which surprisingly deny the traditional view on chemical kinetics (characterized by the natural tendency to reach by the shortest way the state of equilibrium). They were interpreted even as a precursor of life processes [24–26] (cf. Bautrieb due to the Lebenskraft [25]).

A well-defined periodic precipitation patterns were traditionally obtained by chemists a long time ago. In early nineteenth century, Fechner published [27] a report on the regular swinging in a chemical system, describing an electrochemical cell that produced an oscillating current. Later in nineteenth century, Ord [28] prepared 1D precipitation patterns and Pringsheim [29] introduced the concept of osmotic pressure to this field late in eighties. Famous is Liesegang [30] who prepared various 2D patterns (often called Liesegang rings ) and Leduc [31] who developed the concept of osmotic pressure waves. There are many other researchers who contributed significantly better awareness of this subject. Creative incentive appeared already in middle of nineteenth century when Runge [32] shown substances interactions associated with various self-grown pictures; while in the 1930s, Nikiforov [33] proposed to characterize the spatial and temporal development of chemical waves by the Principle of the least action . It was expressed in 1744 by Maupertuis [34]: “when some change takes place in nature, the quantity of action necessary for the change is the smallest possible. The quantity of action is the product obtained by multiplying the mass of the bodies by their velocity and the distance travelled”, factually extending the earlier Fermat’s similarly attuned principle of least time [35–39].

Several research groups followed this approach and evaluated the quantities of action during the Liesegang rings formation [40–47]. They found that during the evolution of successive waves, the product of instantaneous propagation speed u and the wavelength λ converges to a constant value. It was found that this value depends on the type and the concentration of the used polymer. When trying to describe diffusing front of the process, a crucial role of a characteristic particle mass m was established. The product of the characteristic mass m, propagation speed u and the wavelength, λ, was termed as the diffusion action [37–39, 46, 47].

More than one hundred different combinations of cations and anions were utilized for the Liesegang rings formation from liquid phase, and the calculated values of their diffusion action, uλm, were in the order ~10−34 Js. Küster [40] and Schaafs [44] analyzed periodic structures in various biological materials by means of the principle of least action and approved a very surprising coincidence with the quantum of the least action [37–39], too. Recently, Stávek et al. [46] evaluated the diffusion action during the diffusion of 1D Belousov–Zhabotinsky waves and found the value of diffusion action of these chemical waves self-organized to fall close to the Planck constant .

Several physicists [48–51] contributed to this topic and several decades of long experimental and theoretical research can be condensed into the following equation [37–39, 46–53]:

$$\left( {K\kappa } \right)m\,\lambda \,u = h$$
(6.1)

where K is the diffusivity factor, κ is the tortuosity factor, m is the particle mass, λ is the wavelength, u is the propagation speed and h is a characteristic constant of the diffusion action lying close to the value of Planck constant. The parameter K (diffusivity factor) describes the geometrical arrangement of the experiment. For one-dimensional space (thin glass tubes) K = 1, for two dimensional space (thin layer in a Petri dish) K = 2, in case of the three-dimensional experiment the value K depends on the space angle available for the diffusion of Brownian particles from their source. If the whole space is available for the propagation of the chemical waves, then K = 4π. Many studies of the dispersion relations were performed in gels, membranes, resin beads, glasses in order to prevent hydrodynamic disturbances from the reacting media. These media help to localize the propagating bands; on the other hand, they modify the diffusion path of ions. The diffusion field in these restricted environments changes upon the tortuosity factor κ, characterizing thus the diffusivity in permeable (porous) media.

There is no consensus concerning relation (6.1) in scientific community at all [37–40, 44, 46, 47]. It was found by various scholars to be either accidental without any deeper physical meaning (pointing to the experimental difficulties in the estimation of mass of diffusing units) or enigmatic, with something very important on behind. Such diversity in opinions is partially due to the traditional, rather subjective discrimination between macroscopic and microscopic phenomena. The quantities u and λ on the left-hand side of Eq. (6.1) stay explicitly in contrast to m which is essentially macroscopic; they are accessible to the observation by unaided eye, while the Planck quantum of action h, on the right-hand side of Eq. (6.1) is regarded to be characteristic of tiny quantum processes on an atomic scale. There are several attempts for its explanation, cf. Fig. 6.2.

Fig. 6.2
figure 2

A schematic diagram showing the subcritical and critical oscillatory regimes

Full size image

For example, there is a very straightforward interpretation of relation (6.1) using a concept of the de Broglie wave known from elementary quantum mechanics [49–51] as a wave controlling the probability amplitude of a particle. Accordingly, we have reputedly to do with the de Broglie probability pilot wave of an abstract particle [49] of mass equal to the mass m of the end-product molecule moving with the speed of diffusion ≈u. It is further assumed ad hoc that the wavelength \(h / mu\) of this de Broglie-like wave [49] coincides with some integer multiple of the period of precipitation, what is just that meets the want. Such a simplistic exploitation of quantum ideas and quite formal approach to the problem, tolerable in pioneering works, together with the obscure concepts involved is, as we believe, the very reason which has led to the scepticism aimed against the quantum theoretical interpretation of Eq. (6.1) and for years effectively damped the activities in this interesting field.

6.4 Diffusion Action of Brownian Particles

Curiosity of self-organization attracted deserved attention in a wider analysis of time-symmetry breaking associated with the emergence of time-periodic solutions known as limit cycles whose period and amplitude are stable and independent of the initial conditions. The importance of self-organization was approved, as they can constitute models of rhythmic phenomena observed in nature, such as chemical clocks in more important biological or other evolution processes [54–57]. It became a model focus in generalized theory of chaos expressing its minute ordering [58–60]. Curiously even the attempt to imagine a self-organizing ether (primeval matter) became also source of a related reaction-diffusion model of space-time creation [50] based on 1887 Cu-t’ung subatomic wave theory. He proposed the subnuclear wave theory of ether based on Konfuciou’s idea of transmutation-bipolar ether of mutually transmuting states of “Jin” and “Jang”.

Let us turn our attention to the stable waves observed in this so-called yet-classical Belousov–Zhabotinsky [15, 22, 23] reactions resulting from the possibility of cascade splitting (called bifurcation [17]) which opens the way to gradual increase in complexity by a mechanism of successive transitions, leading either to the loss of stability of a primary branch and the subsequent evolution to a secondary solution displaying asymmetry in space and/or in time. It is worth mentioning that such transitions are sometimes accompanied by some remarkable trends, e.g. certain classes of reaction-diffusion systems under zero-flux boundary conditions may exhibit no net entropy production change when the system switches from the thermodynamic branch to a dissipative structure [37]. On the other hand, there is a systematic decrease in entropy in the vicinity of bifurcation points known in the associated fields, e.g. chaos [13, 17, 57–59, 61] or even traditional field of predicting weather.

A lot of research was given to the detailed observation of properties of these chemical waves, and a great number of theories were proposed in order to characterize the behaviour of these structures. There can be applied a very useful criterion enabling one to decide whether a particular physical problem belongs to the domain of classical and/or quantum physics [62–73]. Making use of A.J.W. Sommerfeld’s criterion [50, 51, 64, 68], we can assume that in every case where the quantity of type of action is relevant to a given physical problem occurring comparable with the Planck ’s quantum of action (~h), the problem can be solved consistently only within the frame of the quantum theory. There, however, is no further requirement put on the absolute scale of the system; it can be either of microscopic or macroscopic origin.

Assuming that the decisive process controlling the periodic precipitation or oscillating reactions is the diffusion of reactants (i.e. we consider the so-called Nernst–Brunner limit of chemical kinetics [51]); we need for the construction of the corresponding “relevant quantity of type action” the definition of something like the instant speed of diffusion. If we, for the sake of simplicity, confine ourselves only to one dimension, the diffusion can be described by the following differential equation (traditional Fick’s law) ∂n/∂t = D (∂2 n/∂x 2) leading to the relation for the position of extreme concentration x 2 = 2Dt which in time derivative is x u = D, where u = (∂x/∂t) has physical meaning of the instant speed of transfer of concentration maximum. It is quite reasonable just to call u the “instant speed of diffusion” [64–67].

These results can be identified as counterpart to random walk of a single Brownian particle (≈molecule) [68–73]. The only differences are that here is x no more the position of the concentration maximum but the mean square root \({\surd }\langle x^{2} \rangle\) of the position of a particular Brownian particle at time t and u has a meaning of its mean square root of stochastic speed \({\surd }\langle U^{2} \rangle\). For these quantities, the validity of the relation \({\surd }\langle x^{2} \rangle \,{\surd }\langle U^{2} \rangle\) ≥ D can be easily proved [51]. The diffusion constants D must naturally be identical for the microscopic as well as for the macroscopic cases and simultaneously the relations u = \({\surd }\langle U^{2} \rangle\) and x = \({\surd }\langle x^{2} \rangle\) must be valid. We can thus conclude that a typical “average” Brownian particle [51, 70–72] follows the position of the concentration maximum or in other words that the most significant packet of diffusing molecules consists of average Brownian particles. Therefore, if the microscopic movement of a Brownian particle of mass m would be controlled by a purely quantum process, where the diffusion constant in three dimensions should have Fürth ’s limiting value [69] of D = D Q  = h/ 4πm which can formally attain the same form as empirical Eq. (6.1), i.e. 4π m u x = h provided that the experimentally observed quantities u and λ are identified with u = \({\surd }\langle U^{2} \rangle\) (speed of diffusion) and x = \({\surd }\langle x^{2} \rangle\) (distance spanned by diffusion), respectively.

It seems thus plausible that to prove the quantum nature of Eq. (6.1), it is sufficient to make clear conditions under which the numerical value of diffusion constant D attains Fürth’s value D Q [51]. The key is provided by the close analogy between the diffusion equation and Schrödinger equation proposed by Fürth [69]. Accordingly, these equations may be mapped one onto another by substituting for diffusion coefficient the value

$${i}D_{Q} = {i}h/4\pi m$$
(6.2)

and/or identifying tentatively the universal noise source behind the assumed stochastic process with electromagnetic zero-point fluctuations of vacuum [63].

The fact that the Brownian and quantum diffusions are impossible to differentiate by intermittent examinations performed in configuration space which is just the equivalent of experimental techniques by means of which the periodic chemical reactions are investigated. It justifies the direct comparison of empirical diffusion coefficients with the Fürth ’s value D Q  = h/4π m. Assuming, namely, that the noise sources behind classical and quantum stochastic behaviour are independent, the resulting diffusion has to be given by a superposition of quantum and classical stochastic diffusions which are described by coefficients D Q and D S , respectively. Obviously, the diffusion coefficient attains its maximal value (theoretically D→∞) just if the ambient puts no constrains on the free movement of a particle, and consequently this quantity is formally analogous to working example of electric conductance [64]. Two simultaneous diffusion processes with coefficients D S and D Q are thus represented by a diffusion coefficient D corresponding to D S and D Q connected in series, i.e.:

$$D = D_{S} D_{Q} /\left( {D_{S} + D_{\text{Q}} } \right)$$
(6.3)

Then, it is easy to show by comparison with empirical data that there are numerous cases where D≈D Q (e.g. H+, Na+, Ca2+ and Ag+ ions in aqueous solutions at room temperature). Moreover, in accordance with formula (6.3), the accessibility of Fürth’s limit may be formally expressed as follows [51]: D S  > D Q . The very physical meaning of this condition is to provide a quantitative estimate for the partial decoupling of particle from the sources of classical noise, which is sufficient for reaching a quantum diffusion regime \(D_{S} = kT/6\pi \,\eta R > h/4\pi m\) in a real system.

Although somewhat formal, the application of correspondence principle in terms of diffusion constant provides the superposition of quantum and classical diffusion again. While D S is meaningful only to the mean-free path δ of the molecule

$$Mv_{F} \delta \le h/ 2\pi ,$$
(6.4)

if the mean-free path exceeds the de Broglie wavelength [49], the process is exclusively controlled by quantum effects only.

Very small Brownian particles (without observable persistency in motion) in medium of small viscosity, η, gives very high D S , in other words they decouple from the stochastic environment and their quantum-like behaviour starts to be apparently observable. Rough estimate is valid for the quantum performance

$$D_{S} = kT/6\pi \,\eta R > h/4\pi m$$
(6.5)

Evaluation for ball-like molecules of effective radius R within aqueous solutions at room temperature (T = 300 K) and viscosity η≈10−3 kg m−1 s−1provides estimate of quantum behaviour for 7.0 × 10−12 ≥ R/m. Supposing m = 1.67 × 10−27 kg multiplied by molecular weight of a given molecule we arrive to the same ion candidates of Na+, Ca2+ and Ag+ as above. Making an estimate for diffusion constant of H+ ions (protons) which are the most active and mobile particles in aqueous solutions and applying Eq. (6.5) for an effective proton radius in water (≈10−11 m) and for η (≈10−3 kg m−1 s−1), we obtain for the room temperature estimate of diffusion constant D S ≈ 2.2 × 10−8 m2s−1 which is within an error comparable with the numerical value of quantum diffusion constant for protons with m = 1.67 × 10−27 kg providing D Q ≈ 3.1 × 10−8 m2s−1. It indicates that diffusion of protons needs to be treated by more extended, fully quantum approach.

Based on the classical Einstein–von Smoluchowski description of diffusion as a particular case of the Brownian motion and on the fact that the Brownian and quantum movements are indistinguishable by intermitted measurements in configuration space, we have shown [51–53] that a certain class of self-organized periodic reactions characterized by the empirical dispersion relation (6.1) are to be very likely controlled by the Fürth ’s quantum diffusion of reactants.

To conclude this section and to further illustrate a validity of Eq. (6.1), let us consider a nice example of growth with an evident oscillatory character [53], a saw off slab from an old tree (cut down in Šesták’s owned forest), see Fig. 6.3. It is clear that we have to do with a special kind of Liesegang’s reaction with a cylindrical symmetry for which the following variation of the Eq. (6.1) is expected

Fig. 6.3
figure 3

Cross-section of a trunk of larch tree showing annual growth rings, reputedly showing a special kind of self-organized Liesegang’s rings [53]

Full size image
$$2m\lambda^{ 2} /\tau = h$$
(6.6)

where m is the molecular weight of precipitating cellulose, λ the distance between the neighbouring annual rings, τ the growth period and h = 6.63 × 10−34 Js is the Planck universal constant. Then, taking into account that the glucose-based polymer cellulose having empirical formula (C6H10O5) N is known to create, in wood, the chains of average polymerization degree N ≈ 400, its molecular weight may be determined immediately as m ≈ 400 × 162 × 1.67 × 10−27 = 1.08 × 10−22 kg. Admitting further for the distance between annual rings a value λ = 5 × 10−3 m and for the duration of the season an estimate τ = 8 × 106 s, we obtain an incredibly exact figure for the Planck constant , namely h = 6.7 × 10−34 Js.

6.5 Oscillation Processes in Chemistry and Biology: Systems Far from Equilibrium

We should also focus our attention to a specific case often encountered when an experimentalist faces chaotic trends in his resulting data while studying chemical reactions in an apparently closed system. Such results are frequently refused by reasoning that the experiment was not satisfactorily completed due to ill-defined reaction conditions, unknown disturbing effects from surroundings, etc. This attitude has habitual basis in traditional view common in classical thermodynamics that the associated dissipation of energy should be steadily decelerated to reach its minimum (often close to zero) at a certain stable state (adjacent to equilibrium). In many cases, however, the reaction is initiated to start far away from its equilibrium or external contributions are effectual (in a partly open system), or reaction intermediates play a role of doorway agents (i.e. feedback catalysis). In such a case, the seemingly chaotic (in fact oscillatory) behaviour is not an artefact but real scientific output worth of a more detailed inspection where the reaction mechanism should not only be understood in its traditional terms of time-continuous progress, but also as a reflection of reaction time-rejoinder which feedback character yields rather complex structure of self-organization . Statistics show that the stability of nonequilibrium steady state is reflected in the behaviour of the molecular/atomic fluctuations that became larger and larger as the steady state becomes more and more unstable, finally becoming cooperative on a long-range order. In many cases, this effect is hidden by our insensitive way of observations. Particularly it becomes apparent for those reactions that we let start far from equilibrium; which first exhibit nonequilibrium phenomena but later they either decay (disappear) close to their steady state or are abruptly stopped (freeze-in) by quenching phenomena (often forming the reinforced amorphous state of noncrystallites).

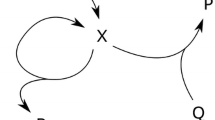
The oscillatory Belousov–Zhabotinsky processes [15, 22, 23] were also successfully simulated by the use of computers, and the most famous is a simple scheme known as “Brussellator” which is a theoretical model for a type of autocatalytic reaction proposed by Ilya Prigogine [2, 13] and his collaborators at the Université Libre de Bruxelles. It describes autocatalysis of the following variety: A → X; 2X + Y → 3X and B + X → Z + D; X → E which, however, can be simplified in the following scheme shown in Table 6.1 (left) as the so-called cross-catalytic reactions. It is involving two reactants A and B and two products Z and P with the intermediates X and Y. The catalytic loop is caused by multiplication of the intermediates X, well illustrating the input effect of reactant concentration within the given reaction mechanism (at the threshold concentration of A the steady subcritical region changes from the sterile to the fertile course of action capable of oscillations in supercritical region, see Fig. 6.2). Although first assumed hypothetically, it enabled to visualize the autocatalytic nature of many processes and gave to them the necessary practical dimension when applied to various reality situations: This scheme is typical for many biological systems such as the glycolytic energetic cycles where the oscillatory energy intermediates are adenosine-tri-phosphate (ATP) and adenosine-di-phosphate (ADP). It is also likely to explain the functioning of periodic flashes of the biogenic (cold) light produced by some microorganisms where the animated transformation is fed by oxygen whose energy conversion to light exhibit high efficiency [75]. Also the chromophore-assisted light inactivation offers the only method capable of modulating specific protein activities in localized regions and at particular times [76].

Table 6.1 Schematic portrait of the simplest self-organized reactions
Full size table

Another theoretical model is labelled “Oregonator” which is a simple realistic model of the chemical dynamics of the oscillatory processes [79–81]. The so-called Lotka–Volterra equations are known as the predator–prey equations in the form of a pair of first-order, nonlinear, differential equations frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. One of the basic schemas is the diffusional model, see the Table 6.1 right, which provides all-purpose source for oscillations [62, 64, 74].

Picturesque world of assorted bayaderes endowed with various seashells and other organized structures provided by different living organisms such as butterflies or animal skin ornamentation (zebra) was elaborated by cyberneticist Turing [81], formulating the hypothesis that such decorative patterns are, in general, the result of diffusion based reactions presented in Table 6.1 right, which are mostly functional at the early stages of the cell growth.

It is clear that the basic phenomenon of life [77–81] is a self-replicating mutable macro-molecular system capable to interact [77–80] inside itself as well as with its surroundings (supply of energy). It involves autocatalysis that is a process in which the given compound serves as a catalyst of its own synthesis. Certain biopolymers exhibit such an inquisitive property that is basis for self-reproduction, i.e. the feature enabling agglomerates of molecules (possessing similar starting capability—concentration) to develop preferentially for those molecules that grow to be dominant (morphogenesis [81]). It means that particular linear sequences of nucleotides must code for nonrandom sequences of amino acids having autocatalytic properties furthering their replication to a preferential reproduction. Other coding, providing less effective proteins, would have replicated more slowly. By mutual cooperative actions of autocatalytic reactions a larger self-regulating systems can be created by gastrulating to show the cyclic reproduction under its fixed repeating time—an important attribute of life. Most important role is played by enzymes that are big proteins molecules acting as biological catalysts and accelerating chemical reactions without being consumed themselves. Their activity is specific for a certain set of chemical substrates and it is dependent on various boundary conditions (concentration, acidity-pH, temperature, etc.). Such a system is again evidently far from equilibrium and its fertile behaviour cannot be explained by the classically viewed off-equilibrium thermodynamics that is sufficient to describe the formation of stable static structures (as crystals). Unlike standard equilibrium states, such self-catalysed states, that are far away from equilibrium, can be unstable because a small perturbation may lead precipitously to new states rich in their variety, seen not only within the above mentioned biologic systems, bust also in less known, but less significant physical and chemical systems of inorganic world. It is worth mentioning that such dynamic (dissipative) structures are linked with all kinds of flows shifting from linear (laminar) to nonlinear (turbulent) regimes, as for example, in fluid hydrodynamics (boundary friction), oscillations in electric gas discharges or in electron flow (local overheating known as the Kohler effect in resistors or mobility versus velocity control in semiconductors).

In order to find a best example in biology, the Ranvier nodes [82] (also known as myelin sheath gaps) can be exploited using the distance of the gap periodicity in the insulating myelin sheaths of myelinated axons where the axonal membrane is exposed to the extracellular space. This self-organization facilitates nerve conduction in myelinated axons, which is referred to as saltatory conduction (from the Latin saltare, to hop or leap) because of the manner in which the action potential comes out jumping from one node to the next along the length of the axon.

Beside the above discussion of quantum diffusion , further notes on relation between biology and quantum phenomena should be added. Quantum effects in biology do not seem bizarre at all. There is no additional strangeness, just quantum approach applied to minute biological processes from the bird navigation to photosynthesis. The actual questions of why we need quantum physics rather than classical physics can be explained exploring how a cell can maintain quantum coherence (i.e. preserve of a quantum state necessary for quantum effects) long enough to allow the process to complete when physics labs cannot maintain quantum coherence for nearly as long despite massive equipment. Such a minute events can have a profound influence on living beings which are vastly bigger despite a general expectation that something tinier than a hair on a dog’s tail could not possibly wag the dog. The recent innovative books [83, 84] show what is speculative and what has been supported by research conducted in labs around the world supporting ample reasoning to believe that quantum physics plays an important function in biological processes.

Quantum world represented by the Planck constant enters in chemistry and biology also when information aspect of the processes is considered. It is convenient to convert information coded, as usual, in binary units Γ 2 (bits) into the information Γ p expressed in physical units [52]. This relation obviously reads as follows:

$$\varGamma_{p} = \left( {k\,{\text{ln2}}} \right)\varGamma_{ 2}$$
(6.7)

where k is Boltzmann’s constant (k = 1.38 × 10−23 J K−1). We assume now that there is no information “an sich” or in other words information needs in all cases a material carrier [52]. From the point of view of macroscopic thermal physics there is, however, a fundamental difference between, e.g. genetic information inscribed in the DNA and information provided by a gravestone inscribed with personal data. Whereas in the former case for coding of information structural units on molecular level are used, which should be described by microscopic many-body formalism, to the latter case rather a macroscopic description in terms of boundary–value problem is adequate. To distinguish without ambiguity between these two extreme cases we need, however, a criterion which, having a sign of universality, specifies what the “molecular level” is. As far as we know, a good candidate for such a criterion is modified Sommerfeld’s condition [68] distinguishing between classical and quantum effects [51–55]. It reads as Ω = 2πℏ = h, where Ω is phase space occupied by a structural unit (qubit) where minimally 1 bit information is stored and h is the Planck universal constant again. Direct computation of the action Ω corresponding to one atom built in an ordinary crystal, liquid or gas confirms the validity of condition (7) in these cases. It proves the fact that every atom together with its nearest neighbourhood should be treated as a quantum structural unit responsible for information storage on a “molecular level”. Generalizing this result, we can conclude that the very nature of the entropy-like quantity, Carnot’s caloric [85] is the destructed information originally coded in occupied quantum states of structural units of which the macroscopic system under investigation consists.

6.6 Special Cases of Oscillation Processes: From Solid-State to Atmosphere

Oscillatory pattern can be found on various microscopic and mesoscopic cases of gemstones, shell ripening up to the macroscopic scale of geological sediment layers (see Fig. 6.4), and there arise a question why this separation is regular and what is its cause. Normally, we are looking for a reaction mechanism in the view of the processes sequences and its space distribution.

Fig. 6.4
figure 4

Self-organization in various scales from silica colloids in opals, to agates, from calcite in shells to geological layers (not in scale)

Full size image

In some cases, the authors use for the description of autocatalytic reactions overall phenomenological models and fractal geometry [17, 86, 87]. However, inorganic solid-state reactions are not often assumed to proceed via branching [88] or oscillations. In order to show a kind of self-organization in solid phase, let us assume a simple synthesis of cement as an illustration of ideal and real reactions, supposed to follow processes taking place during cement formation [89]. There are two starting solid reactants A (CaO) and B (SiO2) undergoing synthesis according the scheme below (left) to yield the final product AB (CaSiO3) either directly or via transient products A2B (CaSi2O4) and A3B (CaSi3O5). The formation of these intermediate products depends, beside the standard thermodynamic and kinetic factors, on the local concentrations. If A is equally distributed and so covered by the corresponding amount of B, the production of AB follows standard kinetic portrayal (arrows in Fig. 6.5). For a real mixture, however, the component A may not be statistically distributed everywhere so that the places rich in A may affect the reaction mechanism preferring the formation of A2B (or even A3B) the later decomposition of which is due to delayed reacting with deficient B that is becoming responsible for the time prolongation of reaction completion. If the component A tends to agglomerate the condition of synthesis of intermediates become more favourable taking thus the role of rate controlling process, and the entire course of reaction can consequently exhibit oscillation regime due to the temporary consumption of the final product AB. If intermediates act as the process catalyst, the oscillation course can even show a regular nature which localized micro-character is, however, difficult to be detected by direct macro-observations and can be assumed upon secondary characteristics of final morphology only. Introduction of diffusion is an important factor that may affect many of interface reaction (below scheme on right) to become oscillatory [88–91].

Fig. 6.5
figure 5

Portrayal of ideal and actual courses of a potential solid-state reaction where two reactants, A and B, undergo synthesis to the product, AB, via transient products, A2B and A3B (rights). Left: the characteristic plots of reaction progress. The creation of the intermediates depends, besides the standard thermodynamic and kinetic factors, on the local concentration (particle closeness) dependent to the degree of segregation. If the agglomeration is effective, the synthesis becomes helpful to produce intermediates, self-organizes, and the entire course of reaction becomes self-catalysed, possibly exhibiting oscillatory character

Full size image

The entire course of reaction can consequently exhibit an oscillation regime due to the temporary consumption of the final product AB, which is limited to small neighbouring areas. If the intermediates act as the process catalyst, the oscillation course is pronounced showing a more regular nature. Their localized fluctuation micro-character is, however, difficult to be detected by direct physical macro-observations and can be only believed upon secondary characteristics read-out from the resulting structure (final morphology).

Similarly, some glasses may exhibit a crystallization pendulum [92]: after proceeding very fast in certain direction(s), the growth often stops due to the changes in concentration and converts into dissolution while in the other direction(s), where the growth rate was initially lower, it never becomes negative even if it decelerates effectively. Hence, a competition between several simultaneous processes takes often place, typical for such a nonequilibrium system and leading to curious morphology (plate or needle-shaped crystals [92, 93]. Another working example is well known, resistor carrying large electrical current exhibiting negative differential resistance, i.e. currents that even decrease with increasing voltage supporting oscillations, rather than steady currents [39]. Instabilities also occur in thin wafers of certain semiconductors (GaAs, InP). If the electrical potential across the semiconductor exceeds a critical value the steady current that is stable at lower potentials, abruptly gives way to periodical changes in the current, often called Gunn oscillations [39, 94, 95]. There are other cases worth mentioning reaching the sphere of solid-state reactions [95–99].

Directional solidification of the PbCl2-AgCl eutectic [39, 100] provides swinging lamellar structure separated regularly at almost equal severance which can be compared with dynamic structures caused by Bernoulli instabilities well known in hydrodynamics [39, 101]. Atmosphere is another source of oscillatory effects when billow clouds are created from instability associated with air flows having marked vertical shear and weak thermal stratification. The common name for these fluctuations is Kelvin–Helmholtz instability often visualized as a row of horizontal eddies aligned within this layer of vertical shear.

The Kelvin–Helmholtz instability results from a turbulence of two air layers lying close to each other, which move with different speed and/or direction. According to Bernoulli’s principle, the pressure inside an air layer with the higher wind velocity is smaller than in the environment. Consequently, there is a force, which pulls the barrier shape (wave comb or hill summit) in the direction of the faster air flow [101]. Such an external perturbation may provide an oscillation of the vortex sheet where the pressure in concavities is higher than that in convexities. The amplitude of the oscillation grows up and the upper part of the sheet is carried by upper fluid instead the lower part of the sheet is carried by lower fluid. So a tautening of the front occurs, and there is a phenomenon of rolling up of the interface with a direction corresponding to the vorticity direction of the mixing layer. It is worth mentioning that such dynamic (dissipative) structures are linked with all kinds of flows shifting from linear (laminar) to nonlinear (turbulent) regimes; besides fluid hydrodynamics (boundary friction), they are oscillations in electric gas discharges or in electron flow (local overheating known as the Kohler effect in resistors or mobility versus velocity control efficient from semiconductors to traffic mentioned above [6, 94, 101–103]) (Fig. 6.6).

Fig. 6.6
figure 6

Humorous picture of self-organized perturbation of cigarette smoke oscillations showing general impact of Bernoulli–Kelvin–Helmholtz instabilities proficient on any scale

Full size image

This approach may even touches spheres of thermal analysis [39]. Often experimental trouble was a noisy heat flow signal obtained by flow differential scanning calorimetry that appeared random but dependent on the sample mass (internal heat production) and seemingly too low in frequency to be of electric in origin. For a high-resolution temperature derivative, there was found a straightforward match to the “noise” in the heat flow signal. Instead standard way of eliminating such a kind of “fluctuations” by more appropriate tuning of instrument, the advanced but also more logical approach was to deliberately incorporate such fluctuations in a controlled and regular way to entire experimentation, i.e. the temperature oscillation were imposed on the heating curve and the response was evaluated through a deconvolution. Thus, received cyclic reaction could be treated in a manner known before and applied for the method of DMA.

6.7 Thinkable Hypothesis of the Light Self-Organization

When talking on the subject of light let us first mention the Michelson and Morley’s article in the American Journal of Science which has been by some means portrayed as a most famous failed experiment in history instead providing insight into the properties of the aether. It compared the speed of light in perpendicular directions, in an attempt to detect the relative motion of matter through the stationary luminiferous aether. Although the small velocity was measured, it was considered far too small to be used as evidence of a speed relative to the aether, and it was understood to be within the range of an experimental error that would allow the speed to actually be zero [104, 105].

Now, we should first return to the previously noted Fermat Principle on least time, t [36–39] preceding the Maupertuis Principle of the least action [34]. It was already noticed by Galileo (1564–1642) who opened this problem by using formula t = d/√d v  × √(2/g) where d is direct distance, d v is vertical distance and g is gravitational acceleration (9.8 ms−2) aware that the cycloid curve yields the quickest descent. Historically this archetype problem introducing the calculus of variations is called “brachistochrone ” (from Ancient Greek βράχιστοςχρόνος—brakhistoskhrónos), meaning shortest time which is consistent with the Fermat’s principle. It interprets the actual path of a beam of light between two points taken by the one which is traversed in the least time. In 1697, Johann Bernoulli (1667–1748) already used this principle to derive the brachistochrone curve [106–110] by considering the trajectory of a beam of light in a medium where the speed of light increases following a constant vertical acceleration of gravity g. Supposing that a particle of mass m moves along some curve under the influence of gravity imagining that the mass point is like a bead that moves along a rigid wire without friction (Fig. 6.7).

Fig. 6.7
figure 7

Characteristic descending curves of a point mass free fall under the action of gravity (mg). Clearly, the straight line between the start A and the end B, the violet line, is the shortest distance, but it does not lead to the quickest descent. Below (orange) is parabola, below (green) is circle, yet below (black) is cycloid which has the fastest descent. At the bottom (blue) is a six order polynomial. Insert shows the characteristic (red) for the shortest time of travel along the brachistochrone on the Earth’s surface. Any solution is, therefore, a compromise between travelling further and travelling faster due to gravitational acceleration so that as helping the expression for the time of travel along the brachistochrone between two points on Earth’s surface [126, 127]

Full size image

The question is: What is the shape of the assumed wire for which the time to get from the start a to the end b is minimized? Whittaker [111] promoted the source of non-Euclidean geometry (e.g. Veričák’s theory [112]) capable to show how to express relativity formulas using hyperbolic function in 3D space namely employing the Bolyai–Lobachevski geometry of hyperbolic function for rapidity, i.e. the inverse tangent in the form [112–114]

$${\varphi } = \tan {\text{h}}^{ - 1} \left( {v/c} \right),$$
(6.8)

giving way to the access of general formulas [109]

$${\text{e}}^{{\varphi }} = \surd \left\{ {\left( { 1 { } + v/c} \right)/\left( { 1 { }{-}v/c} \right)} \right\}\,{\text{and}}\,{\text{e}}^{{ - {\varphi }}} = \surd \left\{{\left({ 1 { } - v/c} \right)/\left({ 1 { } + v/c} \right)} \right\},$$
(6.9)

where φ is the rapidity, v is the velocity and c is the limiting speed of light following the Latin word “celerites” meaning “swiftness”.

For the interpretation of the observed photon properties, the old concepts physics [109, 111, 115] is employed where the photon with mass m (Lavoisierian caloric mass m concept where v 2 /v 1 = m 1 /m 2 and c 2 /c 1 = m 1 /m 2 ) self-organizes its surroundings with the wavelength λ (Aristotelian space time t concept where v 2 /v 1 = t 2 /t 1 and c 2 /c 1 = λ 2 /λ 1) and the frequency f (Galilean time distance d concept where v 2 /v 1 = d 2 /d 1 and c 2 /c 1 = f 1 /f 2) assuming validity of c 2 /c 1 = (1 + v/c)/(1 − v/c). The so-called Doppler–Voigt–Einstein self-organization [109, 116, 117] transmits information about the relative velocity of the source and the observer. The photon as particle m moves simultaneously with its self-organized surroundings with wavelength λ and frequency f, and observable events are summarized in the Table 6.2.

Table 6.2 Three tuning mechanisms in the Doppler–Voigt–Einstein (DVE) self-organization [109, 116, 117]
Full size table

In the redshifted DVE self-organization, one should observe the diffusion of caloric mass from the photon mass to the surface of the moving object. In the blueshifted DVE self-organization, one should observe the diffusion of the caloric mass from the moving object to the photon mass (the radiation of the moving particle). The total energy of a moving particle which is the total sum of energies of the redshifted and blueshifted self-organizations gives the identical result as it was found by Einstein [118–120]. Presumably, his enthusiasm would have been even greater had he known that the same curve describes radial gravitational freefall versus proper time in general relativity. Entanglement plays a fundamental role in the brachistochrone evolution of composite quantum probability density. Brownian motion under brachistochrone-type of metrics [121], quantum adiabatic brachistochrone [109, 122, 123] as well as the situation of dry (~Coulomb) and viscous friction with the coefficient that arbitrarily depends on speed [124–127] and other solutions [128–130]. The subject discussed in this last section is still under the progress; the study shown here is more or less a curiosity that probably would not be publishable elsewhere but is worth of attention.