Comparison of Stochastic Frontier “Effect” Models Using Monte Carlo Simulation

Abstract

We used Monte Carlo simulations to compare the finite sample properties of three types of stochastic frontier models (KGMHLBC, RSCFG, and FE) that were designed to examine how observable characteristics of a company may influence its technical efficiency. RSCFG has a scaling property that gauges the effect of environmental factors on technical inefficiency but not on the inefficiency distribution. KGMHLBC does not have this scaling property. However, both RSCFG and KGMHLBC assume a specific distribution of technical inefficiency and are estimated using maximum likelihood analysis. On the other hand, FE does not impose any such distributional assumption of inefficiency and is estimated by the fixed effect treatment. Our simulation results reveal that FE is robust and insensitive to various specifications for the estimation of production technology and the marginal effect of environmental factors on efficiency, whereas RSCFG and KGMHLBC are likely sensitive to the a priori distribution of technical inefficiency. However, based on the rank correlations between inefficiency estimates and true inefficiency, FE produced the worst estimate of inefficiency.

The earlier draft of this paper was based on the second author’s thesis. The first author acknowledges that this work is supported by the National Research Foundation of Korea Grant funded by Korean Government (NRF-2013S1A3A2053312).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

8.1 Introduction

Since Aigner et al. (1977) and Meeusen and van den Broeck (1977) independently introduced stochastic frontier models, the literature has expanded not only quantitatively but also qualitatively. Stochastic frontier models that examine the technical efficiency of firms can be categorized into two groups: those that analyze production functions with input and output variables (Stevenson 1980; Greene 1990; Pitt and Lee 1981; Schmidt and Sickles 1984; Cornwell et al. 1990; Kumbhakar 1991; Battese and Coelli 1992; Lee and Schmidt 1993; Cuesta 2000; Lee 2006, 2010; Ahn et al. 2007), and those that examine the effects of observable characteristics of a firm on efficiency (so-called stochastic frontier “effect” models, SFEMs) (Reifschneider and Stevenson 1991; Caudill and Ford 1993; Caudill et al. 1995; Kumbhakar et al. 1991; Huang and Liu 1994; Battese and Coelli 1995; Wang 2002; Wang and Schmidt 2002).

This paper focuses on the second group, SFEMs. Although various SFEMs have been proposed, little is known about their comparative performances. This study applied Monte Carlo simulation techniques and compared three types of SFEMs. We focused particularly on the biases of the production function parameters, the marginal effects of exogenous factors on inefficiency, and the technical efficiency estimates in the presence of model misspecifications. Following the recommendation of Wang and Schmidt (2002), this paper uses a one-step approach¹ to examine the models. As explained by Wang and Schmidt (2002), the two-step approach can lead to biased estimates, including severe bias in Monte Carlo simulation results.

Alvarez et al. (2006) compared various SFEMs and categorized them based on the scaling property. This implies that firm characteristics affect the scale of technical inefficiency but not the shape of the inefficiency distribution. To be more specific, let u and z be random variables representing technical inefficiency and observable exogenous variables, respectively, and let u be influenced by z: u = u(z,δ). Different models specify different distributions of u. Models with the scaling property specify u as u = s(z,δ)u* where s(z,δ) is a scaling function and u ^* is a random variable with one-sided distribution and is independent of z. Therefore, z influences u only through a deterministic function of s(z,δ), but does not affect the distribution of u. More specifically, z influences u by changing the variance of u. The model of Reifschneider and Stevenson (1991), Caudill and Ford (1993), and Caudill et al. (1995; hereafter, RSCFG) includes the scaling property, whereas that of Kumbhakar et al. (1991), Huang and Liu (1994), and Battese and Coelli (1995; KGMHLBC) does not. In particular, Battese and Coelli (1995, BC) imposed additive decomposition in the inefficiency function u = zδ + w, where u was assumed to have a normal distribution truncated at zero, u ∼ N ⁺(zδ,σ ² _u ). Therefore, z changes the mean of the pre-truncation normal distribution of u and then affects u by changing the shape of the inefficiency distribution. RSCFG and KGMHLBC are identical in the way they require a specific distributional assumption of inefficiency and a normal distribution of a statistical disturbance term and then estimate a production function using a maximum likelihood (ML) method. In addition, both estimate technical inefficiency using the conditional expected value function on residual values originally derived by Jondrow et al. (1982).

Recently, Lee (2012) proposed an SFEM with panel data that estimates a production function and the effects of exogenous factors on inefficiency using the fixed effect (FE) treatment. This model is different from RSCFG and KGMHLBC in that it does not impose a distributional assumption of inefficiency or an uncorrelation assumption between inefficiency and input variables. The assumed additive specification of the inefficiency equation is the same as that of BC, u = zδ + w. In this specification, w ≥ − zδ because u ≥ 0. Hence, the w values are correlated to z. BC assumed a truncated normal distribution of w to free the model from the endogeneity problem. Lee (2012) took a different approach to escape from the endogeneity problem. In Lee’s (2012) model, w was treated as fixed, allowing for the correlation between w and z. Several specifications of w were proposed that were adopted by previous stochastic frontier models, including w _it  = α _i (Schmidt and Sickles 1984), w _it  = θ _t α _i (Lee and Schmidt 1993), and w _it  = θ _1t δ _1i  + θ _2t δ _2i  + … + θ _pt δ _pi (Ahn et al. 2007). The model becomes similar to the conventional panel data model with individual effects or multiplicative individual effects and time effects, and the estimation methods (e.g., the concentrated least squares and the generalized method of moments) are well developed.

Alvarez et al. (2006) compared KGMHLBC and RSCFG and presented several advantages of the scaling property. First, the coefficient of z, δ, can be interpreted independent of the distribution of inefficiency, and the marginal effect (ME) of z on inefficiency is simpler in RSCFG with the scaling property than in KGMHLBC without the property in which the ME equation is complicated and dependent upon the distribution of inefficiency. Second, it is possible for RSCFG to estimate a production function by nonlinear least squares analysis; then, no specific distributional assumption is required. Third, RSCFG may relax the unreasonable assumption that u|z is independent over time by re-specifying s(z,δ) and u*. For example, u _it  = s(z _it ,δ)u ^* _i where u* is time invariant, can be considered as a general form, as described by Battese and Coelli (1992).² Fourth, Alvarez et al. (2006) argued that it is intuitively appealing that the scaling property specifies that firms differ in their mean inefficiency but not in the shape of the inefficiency distribution.

FE also contains the above advantages of RSCFG over KGMHLBC (we will discuss the case of w _it  = α _i , but any other specification will follow the same rationale). The δ itself implies the ME of z on the conditional mean of u, δ = ∂E[u _it |z _it , α _i ]/∂z _it . Therefore, the relationship between z and u is straightforward in the specification of FE, which changes the impact of z on inefficiency in a linear fashion. FE does not require the assumption of uncorrelatedness of inputs and a part of inefficiency (w) or a specific distribution of the one-sided distribution of technical inefficiency. Unlike RSCFG and KGMHLBC, FE does not assume a distribution of statistical noise, v. Instead, it imposes the strict exogeneity assumption for consistency. As the ML estimation is sensitive to the distribution of technical inefficiency, this relaxation in FE is expected to yield robust estimates. Additionally, the independence assumption of u* in RSCFG or of w in KGMHLBC is practically unreasonable since the efficiency of an individual firm is likely to be more or less consistent over time. However, the inclusion of the time-invariant unobservable inefficiency α _i in FE allows for the time dependence of inefficiency. In other words, this unobservable inefficiency controls for heterogeneity of efficiency across different firms, as is observed in the real world.

However, there are two restrictions in FE: (i) z cannot include all or part of x, and thus input factors can influence output only through a production function. This restriction can be avoided if we specify a nonlinear inefficiency equation; and (ii) the time-invariant variables in z and x cannot be included as regressors because the within-transformation function eliminates all of the time-invariant variables. The second restriction can also be avoided if we adopt a different specification of w _it from w _it  = α _i . For example, the specification of w _it  = θ _t α _i presented by Lee and Schmidt (1993) allows for the ability to estimate the effect of a time-invariant regressor on a dependent variable.

The main purpose of this paper is to shed light on the finite sample properties of the aforementioned three models (KGMHLBC, RSCFG, and FE) using Monte Carlo simulations. SFEMs aim to analyze the effects of exogenous factors on efficiency and to precisely estimate technical efficiency based on the characteristics of firms. We used simulations to compare the estimation performances of the three models by examining the accuracy of the ME of z on the mean u as well as the rank correlation between the true inefficiency and inefficiency estimates. The effect parameter δ has different meanings in different models of KGMHLBC, RSCFG, and FE. For example, δ = ∂E[u|z, α]/∂z and is then the marginal effect in FE, whereas δ implies the degree of the effect of z on the variance of technical inefficiency in RSCFG. Thus, in our simulation, we compared the estimation performance of ME instead of δ. We extended the comparison of the three models to plausible cases in which (i) the variance of technical inefficiency differs, (ii) the forms of the true structure of inefficiency vary, and (iii) the input factors and environmental factors are allowed to have an arbitrary degree of correlation.

The remainder of this paper is organized as follows. Section 8.2 discusses the three different models. Section 8.3 describes the Monte Carlo simulation design and discusses the simulation results. Finally, Sect. 8.4 presents our conclusions.

8.2 Three Stochastic Frontier Models

The stochastic production frontier model for panel data is defined by

$$ {y}_{it}={\alpha}_0+{x}_{it}\beta +{v}_{it}-{u}_{it}, $$

(8.1)

where y _it is the dependent variable that represents the logarithm of output at the period t (t = 1, …, T) for firm i (i = 1, …, N), x _it is the 1 × k vector of functions of inputs, β is a k × 1 vector of coefficients, and v _it is an i.i.d. statistical noise term. The variable u _it is the non-negative “technical inefficiency” error, and the inefficiency equation is specified as

$$ {u}_{it}=u\left({z}_{it},\delta \right), $$

(8.2)

where the 1 × g vector z _it is a set of exogenous variables that affect technical inefficiency, and δ is a g × 1 vector of coefficients. The x _it and z _it can overlap in KGMHLBC and RSCFG but not in FE.

Because both KGMHLBC and RSCFG assume a truncated normal distribution of u _it , we note u _it  ∼ N ⁺(μ _it ,σ ² _it ) in a general form. Specifically, RSCFG assumesμ _it  = 0 and σ ² _it  = s(z _it ,δ), whereas KGMHLBC assumes μ _it  = h(z _it ,δ) and σ ² _it  = σ ² _u . RSCFG possesses the scaling property, and u _it can be expressed as

$$ {u}_{it}=s\left({z}_{it},\delta \right){u}_{it}^{*} $$

(8.3)

where the scaling function s(z _it , δ) is positive, and u ^* _it  ≥ 0 is i.i.d., and then is uncorrelated with z _it .

Caudill et al. (1995, CFG) assumed that u ^* _it follows a half-normal distribution and that s(z _it , δ) = exp  (z _it δ)^0.5. The random variable u ^* _it represents a firm’s intrinsic inefficiency level such as unobservable leadership, and s(z _it , δ) represents a firm’s inefficiency that can be explained by observable environmental factors. That is, the scaling property can be seen as a multiplicative decomposition of u _it into two independent parts. The i.i.d. assumption of u ^* _it does not seem to be reasonable because a firm’s intrinsic efficiency is likely to not be independent. However, the ML estimates are consistent if the model is correctly specified even though u ^* _it is not independent (Álvarez et al. 2006). The assumption of uncorrelation between the unobservable inefficiency u ^* _it and the observable efficiency determinants is also not appealing. BC specifies that μ _it  = h(z _it ,δ) and then u _it  = z _it δ + w _it , where w _it is normally distributed with truncation at − z _it δ. Because w _it  ≥ − z _it δ, w _it and z _it must be correlated.

The two different specifications of BC and CFG have different channels for the impact of z _it on inefficiency. If δ is positive, both models present a positive ME of z _it on inefficiency. An increase in z _it in CFG implies larger variance of the pre-truncation normal distribution of inefficiency, and then the half-normal distribution has a smaller density near zero and a larger density at a large value. Therefore, the mean inefficiency level increases. On the other hand, an increase in z _it in BC implies a larger mean of the pre-truncation normal distribution of inefficiency, and then the mean inefficiency moves toward the right side in the truncated normal at zero. Specifically, the MEs of the exogenous variable on the mean inefficiency can be summarized as follows for CFG and BC, respectively:

$$ \frac{\partial E\Big[{u}_{it}\left|{z}_{it}\Big]\right.}{\partial {z}_{it}}=\delta \frac{\sigma_{it}}{\sqrt{2\pi }}\kern0.36em =\delta \frac{\sqrt{ \exp \left({z}_{it}\delta \right)}}{\sqrt{2\pi }} $$

(8.4)

$$ \frac{\partial E\Big[{u}_{it}\left|{z}_{it}\Big]\right.}{\partial {z}_{it}}=\delta \left[1-{\lambda}_{it}\frac{\phi \left({\lambda}_{it}\right)}{\Phi \left({\lambda}_{it}\right)}-{\left(\frac{\phi \left({\lambda}_{it}\right)}{\Phi \left({\lambda}_{it}\right)}\right)}^2\right], $$

(8.5)

where λ _it  = z _it δ/σ _u and ϕ and Φ are the probability and cumulative density functions of a standard normal distribution, respectively. Equation (8.4) has the same sign as that of δ. Wang (2002) showed that the second term on the right-hand side of Eq. (8.5) is equal to the second moment of u _it divided by the variance of the pre-truncation normal, and then Eq. (8.5) also has the same sign as that of δ. However, the amount of the ME cannot be measured directly from δ.

As mentioned above, Lee (2012) proposed a stochastic frontier model that does not assume any distribution assumption and allows a correlation between inefficiency and input variables. The inefficiency equation is the same as that in BC:

$$ {u}_{it}={z}_{it}\delta +{w}_{it}. $$

(8.6)

Equation (8.6) splits the inefficiency into a part influenced by z _it and an unobservable random inefficiency. Lee also allowed for correlation between z _it and w _it by treating w _it as fixed. He proposed specifications for w _it to transform the model into the forms of previous models (Schmidt and Sickles 1984; Cornwell et al. 1990; Lee and Schmidt 1993; Lee 2006, 2010; Ahn et al. 2007), which are estimated by the FE treatment. The specifications of Kumbhakar (1991), Battese and Coelli (1992), and Cuesta (2000) were also accepted because they can also be estimated by the FE treatment as seen in Han et al. (2005). For example, w _it  = α _1i  + α _2i t + α _3i t ² is assumed, following Cornwell et al. (1990). Then, when substituting Eq. (8.6) for (8.1), the model becomes:

$$ {y}_{it}={\alpha}_0+{x}_{it}\beta +{v}_{it}-\left({z}_{it}\delta +{w}_{it}\right)={x}_{it}\beta -{z}_{it}\delta -\left({\alpha}_{1i}^{*}+{\alpha}_{2i}t+{\alpha}_{3i}{t}^2\right)+{v}_{it}, $$

(8.7)

where α ^*_1i  = α _1i  − α ₀. Following Schmidt and Sickles (1984), another example is w _it  = α _i . This represents unobservable time-invariant firm-specific inefficiency, and Eq. (8.7) is changed to

$$ {y}_{it}={\alpha}_0+{x}_{it}\beta +{v}_{it}-\left({z}_{it}\delta +{w}_{it}\right)={x}_{it}\beta -{z}_{it}\delta -{\alpha}_i^{*}+{v}_{it}, $$

(8.8)

where α ^* _i  = α _i  − α ₀. In this specification, the strict exogeneity assumption is imposed as E[v _it |x _i ,z _i ,α _i ] = 0,  t = 1, 2, …, T for the consistency of the estimator. Then, the within estimators of β and δ are consistent as NT → ∞. The inefficiency estimation also follows the same method of the maximum operator as the previous models. That is, the best firm in the sample is assumed to be a perfectly efficient one. In the case of w _it  = α _i , the inefficiency and efficiency are measured by

$$ {\overset{\frown }{u}}_{it}={ \max}_{i,t}\left(-{z}_{it}\overset{\frown }{\delta }+{\overset{\frown }{\alpha}}_i^{*}\right)-\left(-{z}_{it}\overset{\frown }{\delta }+{\overset{\frown }{\alpha}}_i^{*}\right),\kern0.5em \mathrm{and}\kern0.5em T{\overset{\frown }{E}}_{it}= \exp \left(-{\overset{\frown }{u}}_{it}\right). $$

(8.9)

Unlike CFG and BC, the ME of the exogenous variable on the mean inefficiency is calculated directly by δ because δ = ∂E[u _it |z _it ,α _i ]/∂z _it .

Theoretically, FE should be insensitive to the a priori distribution of inefficiency and statistical disturbance whereas KGMHLBC and RSCFG are not. However, how sensitive their estimation performances are to misspecification was examined next. We chose BC and CFG as representative models of KGMHLBC and RSCFG, respectively, and compared them to FE.

8.3 Monte Carlo Simulations

To examine the finite sample performance of the ML estimation of BC and CFG and the within estimation of FE, we conducted a series of Monte Carlo experiments for the panel data stochastic frontier model. Our simulations were based on a model with one input factor:

$$ {y}_{it}={\alpha}_0+{x}_{it}{\beta}_1+{v}_{it}-{u}_{it}. $$

(8.1)

Throughout, we set α ₀ = β ₁ = 1. We also had one exogenous factor (z _it  = c + ξ _zi  + s _zit ) in which s _zit was drawn from a normal distrivution of N(0,1), and one unobservable individual effect. ξ _zi was drawn from a uniform distrivution of U(0,1) and c = 4.0. The regressor x _it was generated in an additive form by the following process: x _it  = α _xz z _it  + ξ _xi  + s _xit , where α _xz  = (0, 0.5, 2), and the time-invariant components ξ _xi and time-varying components s _xit were drawn from U(0,1) and N(0,1), respectively.

We generated two error terms of u _it and v _it using several different data-generating processes (DGPs). The first DGP (DGP1) followed the BC specification. v _it was generated by N(0,σ ² _v ) with σ _v  = 1.0 and the inefficiency term u _it was generated by u _it  ∼ N ⁺(z _it δ ₁, σ ² _u ) where δ ₁ = 0.5 and σ _u take several different values of $\left(1,\sqrt{2},\sqrt{5}\right)$. These standard deviations of the pre-truncation normal imply the standard deviations of u _it as $\sqrt{ Var(u)}=\left(0.96,1.26,1.78\right).$ Note that the mean of the pre-truncation normal does not contain a constant. When a constant term is included in z _it , the BC estimation results revealed a severe identification problem between a constant coefficient in x _it and a constant in z _it . DGP2 followed the CFG specification. The inefficiency term u _it was generated by u _it  ∼ N ⁺(0, exp(δ ₀ + δ ₁ z _it )) where δ ₁ = 0.5 and δ ₀ takes several different values (−1, 0, 1) to examine the estimation performance of the three different models as variance of inefficiency changes. The (−1, 0, 1) of δ ₀ implies $\sqrt{ Var(u)}=$ (1.13, 1.86, 3.06). The error v _it followed the same DGP as in DGP1. DGP3 followed the FE specification as u _it  = δ ₁ z _it  + α _i where δ ₁ = 0.5 and α _i are drawn from a uniform distribution. DGP3 also included several different variances of inefficiency by changing the variance of α _i ; specifically, we used different intervals for uniform distribution such as σ _α  = (2, 4, 6), which implies $\sqrt{ Var(u)}=\left(0.57,1.15,1.73\right)\!.$ Because FE assumes neither an inefficiency distribution nor a statistical disturbance, we chose a uniform distribution of v _it instead of a normal distribution. We also generated additional data sets of DGP1-1 and 2-1, which had the same values of the inefficiency term u _it as DGP1 and 2, respectively, but v _it were generated using uniform distributions. DGP1-2 and 2-2 were generated to examine the estimation performance of BC and CFG when x _it and z _it overlap. They were the same as DGP1 and 2 but z _it δ = δ ₁ z _1it  + δ ₂ x _it for BC and z _it δ = δ ₀ + δ ₁ z _1it  + δ ₂ x _it for CFG with δ ₂ = 0.3.

Each of our experiments consisted of 1,000 independent replications. We considered approximately 50 different DGPs by varying the values of N, T, α _xz , and the variance of inefficiency. The basic settings were $({\alpha}_0,{\beta}_1,{\delta}_1,{\sigma}_v,$ ${\sigma}_u,{\alpha}_{xz},N,\;T)=(1,1,0.5,1,\sqrt{2},0.5,100,10)$ in the BC model, (α ₀, β ₁, δ ₀, δ ₁, σ _v ,α _xz , N, T)  =  (1, 1, 1, 0.5, 1, 0.5, 100, 10) in CFG, and (α ₀, β ₁, δ ₁, σ _v , σ _α , α _xz , N,  T) = (1, 1, 0.5, 1, 4, 0.5, 100, 10) in FE.

We begin by discussing the estimation of production technology and the effect of exogenous factors on efficiency. The results with DGP1, DGP2, and DGP3 are reported in Table 8.1 with different levels of correlation between x _it and z _it . Each table reports the biases and root mean squared errors (RMSE). The biases are 100 · (mean bias). So, for example, the first entry in Table 8.1, −2.480, indicates that the mean of ${\widehat{\alpha}}_0$ is 0.975. Because δ ₁ in the three different models do not have the same meaning, the estimates are not comparable. Therefore, we report estimates of all parameters only for a model that is consistent with the true specification. For example, we do not report estimates of δ ₁ in CFG or FE when DGP follows the BC specification. Instead, we present the estimation performance for the ME of an exogenous variable on mean inefficiency.

Table 8.1 The effect of the correlation between x and z

Panel A is relevant to the case that x _it and z _it are uncorrelated to each other. When the true data follow DGP1, BC is the true specification, and then is expected to produce the most precise estimates. In fact, BC estimates β ₁ the most precisely, but the intercept term is relatively inaccurate with a large RMSE, and ${\widehat{\sigma}}_u$ has a large mean bias of −0.065. CFG has a slightly smaller mean bias of β ₁ than does FE, but FE estimates ME quite accurately whereas CFG produces a large bias. Staying with DGP1 and moving to Panels B and C where α _xz  = 0.5 and α _xz  = 2, respectively, the ${\widehat{\beta}}_1$ in BC is closer to the true value, but the biases of ${\widehat{\delta}}_1$ and the ME estimator become moderately larger. The bias and RMSE of ${\widehat{\beta}}_1$ and the ME estimator in CFG begin to snowball as α _xz increases. FE shows the second best performance as its biases are slightly larger than those of BC but distinctively smaller than those of CFG. FE is perfectly insensitive to change in α _xz with respect to the production function estimation.

When the true data follow DGP2, the true specification is CFG. BC and CFG have a smaller bias of ${\widehat{\beta}}_1$ than does FE, and ${\widehat{\beta}}_1$ is slightly more accurate in BC than CFG when α _xz  = 0. However, the estimator of ME has a large mean bias in BC, whereas both CFG and FE have reasonably small values of bias, and CFG is a little more accurate than is FE. As α _xz increases, the bias of ${\widehat{\beta}}_1$ in BC increases rapidly, but ${\widehat{\beta}}_1$ in FE stays constant. Again, for the model with true specifications, CFG performs the best and FE does the second best in being close to CFG and separating itself from BC. One intriguing finding that we cannot explain is that under correct specifications, CFG produced a relatively large bias compared with BC and FE. As large biases for ${\widehat{\delta}}_0$ and ${\widehat{\delta}}_1$ in CFG were also observed, the inaccuracy in estimating ME in CFG may be due to difficulty with the correct identification of ${\widehat{\delta}}_0$ and ${\widehat{\delta}}_1$.

In the case of DGP3 where BC and CFG are misspecified, FE performs the best. The bias of ${\widehat{\beta}}_1$ in FE is unexpectedly larger than that in CFG as shown in Panel A even though the bias gaps are mild, but FE separates itself from BC and CFG with a distinctively small bias of the ME estimator. BC performs better in estimating ME than CFG, possibly because BC and FE share the common additive form of the inefficiency equation. Moving to Panel B and C, the ${\widehat{\beta}}_1$ in FE is insensitive to change in α _xz , but the bias of the ME estimator increases when α _xz  = 2. Again, BC produces relatively reasonable estimates, whereas CFG becomes wildly inaccurate as α _xz increases.

The results in Table 8.1 suggest the following. First, FE produces the most robust estimates of ME as well as production technology; this result is not surprising as FE is insensitive to the a priori distribution, whereas BC and CFG are very sensitive to misspecification. This implies that it would be good practice to utilize the three different models and compare their estimates to choose the correct specification among BC, CFG, and FE. If BC (or CFG) produces estimates that are similar to those produced by FE, then it is likely that BC (or CFG) is a correct specification. On the other hand, it is likely that neither BC nor CFG is a correct specification if all three models produce different estimates. Second, both BC and CFG estimate ME or the inefficiency equation inaccurately even when they are correctly specified if x _it and z _it are closely correlated. Therefore, FE is recommended in this case.

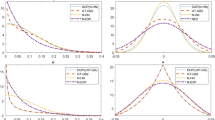
Table 8.2 displays how the different models perform in response to changes in the variance of inefficiency when we change σ _u , the variance of the pre-truncation normal for BC, δ ₀ for CFG, and σ _α for FE. Panels A and C show the estimation performances using the smallest and the largest variance of the inefficiency term, respectively. (Panel B shows that using an intermediate value). Discussing DGP1 first, we can see that the estimators for production technology parameters, β ₀ and β ₁, as well as the inefficiency equation parameter δ ₁, by BC, the true specification, do not show any particular trend, but the estimator of ME reduces the mean bias as the variance increases, whereas the RMSE remains constant. On the other hand, the other two models (CFG and FE) estimate the production function and ME more precisely as the variance increases. In particular, the performance of FE in both estimating production technology and ME surpasses that of BC in Panel C. Moving to DGP2, CFG with the true specification does not reveal any specific trend in estimating β = (β ₀,β ₁) ' and δ = (δ ₀,δ ₁) ', but both the mean bias and RMSE of the ME estimate expand as the variance of inefficiency increases. Unlike the case of DGP1, where a model with misspecification performs better when the inefficiency variance is large, the other models (BC and FE) perform worse as the inefficiency variance increases. BC in particular deteriorates rapidly. In the case of DGP3, which follows the FE specification, FE apparently performs better in estimating ME than BC and CFG, whereas BC is the next best. In practice, we have to consider the fact that CFG always estimates ME downward in every DGP as found in Tables 8.1 and 8.2, whereas BC also underestimates ME in most cases.

Table 8.2 The effect of the variance of u

Table 8.3 The effect of N

Table 8.4 The effect of T

Tables 8.3 and 8.4 show the results of cases with different sample sizes. We first changed the number of cross-sectional observations with a fixed time series (T = 10 and N = 25, 100, and 250; Table 8.3), and then we changed T with a fixed N (N = 100, T = 5, 25, and 50; Table 8.4). Panel A in Table 8.3 shows the estimation performance when the sample size is the smallest (N = 25 and T = 10). When the true data are generated by DGP1, BC is expected to perform the best. However, the ${\widehat{\beta}}_1$ of BC had a slightly larger bias than that of FE even though BC estimated ME a little more accurately than FE. As the sample became larger by increasing N, ${\widehat{\beta}}_0$ and ${\widehat{\sigma}}_u$ of BC started to have larger biases, but the core parameter, ME, was estimated more accurately with a smaller RMSE, whereas ${\widehat{\beta}}_1$ did not have a particular trend in its performance. The overall estimation performances of CFG and FE improved except for ${\widehat{\beta}}_1$ of FE as N increased. In the case of DGP2, CFG was expected to perform the best among the three models. In the small sample (N = 25 and T = 10), the bias of the ME estimator was the least in FE even though CFG had the smallest bias of the production function estimates. However, the performance of CFG improved more rapidly than did that of BC and FE as N increased. In fact, there was no significant improvement in BC and FE. Therefore, CFG had the least bias of ME when N was 250. Regarding DGP3, FE performed the best, and BC did the next best, as expected. As N grew, FE became more accurate, whereas BC and CFG were constant in their estimation performance. The same simulation evidence was found in the case of DGP1 and DGP2 in that the well-specified model performed better with a larger N, whereas the misspecified model performed equally poorly. Comparing the results in Table 8.4, there was not a significant trend in the estimation performances of the three models with DGP1. However, CFG improved in the case of DGP2 as T increased, whereas both BC and FE did not show a particular trend. With DGP3, FE as well as BC improved moderately as T increases, but CFG remained constant. In summary, FE is strongly recommended when the sample size is small given that FE outperformed BC and CFG in small samples independent of a prior distribution.

Table 8.5 The effect of the distribution of v and the correlation between x and z

Table 8.5 compares the estimation performances when DGP1 and 2 were modified in that the statistical noise v _it was generated by a uniform distribution instead of a normal distribution (denoted as DGP1-1 and DGP 2-1, respectively). It can be expected that the performances of BC and CFG will deteriorate because both impose a normal distribution assumption for statistical noise in their models, but the extent of deterioration in small samples is not known. First, we discuss the simulation results with DGP1 and DGP1-1. In DGP1-1, BC was no longer the best model. It had the least bias of ${\widehat{\beta}}_1$ only when α _xz  = 0, but the bias of ${\widehat{\delta}}_1$ was large, and the mean bias of the ME estimator was about five times as large as that in FE. When the correlation between x _it and z _it was increased to α _xz  = 2, FE outperformed BC significantly in both production function and ME estimation. Comparing the performances in DGP2 and 2-1, that of CFG was not significantly influenced by change in the distribution of statistical disturbance. We also conducted simulations with non-normal distributions of statistical noise for cases of different variances of inefficiency and different combinations of N and T, as shown in Tables 8.2, 8.3, and 8.4. To save space we will summarize the results (the detailed results are available upon request). The overall results are consistent with those in Table 8.5. As theory suggests, FE and CFG are insensitive to the distribution of v _it , but BC becomes worse when the true data of v _it do not come from a normal distribution. This property is another advantage of models with scaling properties. RSCFG is relatively insensitive to the a priori distribution of statistical noise.

Table 8.6 The case that x and z overlaps

BC and CFG may examine the effects of input factors on technical inefficiency by z _it including a part of x _it , but z _it and x _it cannot overlap in FE where input factors can influence output only through the production process. Therefore, it is a significant advantage of BC and CFG over FE if they are able to produce reasonably accurate estimates of the ME and production technology. Table 8.6 shows the estimation performance of BC and CFG when z _it and x _it overlap. That is, z _it δ = δ ₁ z _1it  + δ ₂ x _it for BC (DGP1-2) and z _it δ = δ ₀ + δ ₁ z _1it  + δ ₂ x _it for CFG (DGP2-2) with δ ₂ = 0.3. Beginning with the true specification of BC (DGP1 and 1-2), not only CFG but also BC produced large biases when an input factor was included as an exogenous efficiency determinant. For example, the mean value of ${\widehat{\beta}}_1$ in BC was close to the true value of one, and its RMSE was 0.05 when the sample was DGP1, but the bias and RMSE of ${\widehat{\beta}}_1$ increased to 0.11 and 0.35, respectively. The biases of ${\widehat{\delta}}_1$ and the ME_z estimator in BC also increased significantly. In particular, ${\widehat{\delta}}_2$ and the ME_x estimator were extremely inaccurate. The mean value of ${\widehat{\delta}}_2$ was 0.41 and its RMSE was 0.35 when the true value was 0.3. According to unreported simulation results, these problems were aggravated when z _it and x _it were more closely correlated. Turning our attention to DGP2 and 2-2, CFG also produced largely biased ${\widehat{\beta}}_1$ when z _it and x _it overlapped, even though the degree of aggravation was less severe than BC in DGP1-2. In summary, including some input variables in the environmental variable set does not seem to be an attractive choice for model specification.

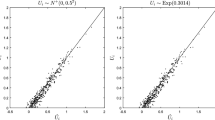
Hitherto, we have described the performances of BC, CFG, and FE with respect to the aim of stochastic frontier effect models that analyze the effects of observable environmental factors on technical inefficiency. Another aim is to estimate the level of technical efficiency by utilizing information on environmental factors. Both BC and CFG estimate ${\widehat{u}}_{it}$ by the conditional expectation of u _it on residuals, whereas FE estimates it by the maximum operator. This difference leads the properties of the estimators so that ${\widehat{u}}_{it}$ in BC and CFG are in absolute values, but ${\widehat{u}}_{it}$ values in FE are relative. Therefore, we compared the rank correlation between the true rank and the estimated rank; the results are shown in Table 8.7. Overall, FE was outperformed by BC and CFG in estimating the rank of inefficiency level in most DGPs. FE produced very high rank correlations following DGP3, but its inefficiency estimates were not closely correlated to the true rank of inefficiency in other DGPs. On the other hand, the rank correlations in BC and CFG remained constant in the range of [0.60, 0.95] in most DGPs. This may imply an advantage of the conditional expectation over the maximum operator. All three models (BC, CFG, and FE) produced more accurate estimates of inefficiency rank as the variance of inefficiency became larger. Generally, changing the correlation between z _it and x _it makes little difference in the accuracy of the inefficiency estimates of all three models. However, CFG deteriorated extremely quickly in its estimation performance for technical inefficiency when z _it and x _it were highly correlated and the inefficiency was misspecified. This result is consistent with our earlier finding in Table 8.1. CFG produced inaccurate estimates of the inefficiency equation parameters (δ ₀, δ ₁). Therefore, we would recommend against using CFG if z _it is closely correlated to x _it .

Table 8.7 Average rank correlation coefficients between true and estimated inefficiency

Non-normal distribution of statistical noise caused significant biases in BC estimates of production technology as well as the ME, but the estimation performance of technical inefficiency did not deteriorate significantly in BC. BC and CFG produced more or less equally precise estimates when z _it and x _it overlapped even though the rank correlation coefficients decreased when the variance of inefficiency was small.

8.4 Conclusion

We examined stochastic frontier models that analyze the effect of observable variables on inefficiency. There are three types of these models: KGMHLBC, RSCFG, and FE. KGMHLBC does not possess the scaling property and is estimated by ML analysis, and we chose BC as a representative of this model. RSCFG includes the scaling property in that environmental factors affect the scale of technical inefficiency but not the shape of the inefficiency distribution, and it is also estimated by ML. CFG was chosen to represent this model. The inefficiency equation specification in FE is similar to that in BC, but FE does not impose a distributional assumption for technical inefficiency or for statistical disturbance. By treating a time-invariant intrinsic inefficiency as fixed, FE did not have to assume correlation between efficiency factors (z) and intrinsic inefficiency (w).

We performed Monte Carlo simulations to examine the performances of the three models. For estimation of the production function and inefficiency equation, FE is the most robust and insensitive to various specifications. FE estimated the ME of environmental factors on technical inefficiency reasonably accurately in the presence of model misspecifications. On the other hand, BC and CFG are likely sensitive to the a priori distribution of technical inefficiency and produce large biases when a model is misspecified. Other notable findings point to practical advantages of FE: (1) FE showed the best estimation performance for ME when the sample size was small, (2) the disadvantage that FE cannot incorporate z to include a part of x was inconsequential because BC and CFG produced inaccurate estimates of the inefficiency equation when x and z overlapped, and (3) BC and CFG were also vulnerable when a statistical disturbance term did not follow a normal distribution. These results are somewhat consistent with those of Gong and Sickles (1989, 1992, GS), who recommended the within estimator as the preferred estimator for the stochastic frontier model. However, GS did not consider efficiency factors and presented only inefficiency estimates.

In the estimation performance of technical inefficiency, FE was the worst, whereas BC and CFG were the best. We may conclude that there is a slight superiority of BC over CFG because CFG deteriorated rapidly when the correlation between x and z was high. This result contrasts with the simulation results of GS. However, GS adopted the max operator proposed by Schmidt and Sickles (1984) for efficiency estimates in the ML estimation. A source of the disparity between our simulation and that of GS with respect to efficiency estimates may be the difference between the conditional expectation and the max operator approaches. In this case, using the conditional expectation as the efficiency estimation appears to produce more accurate estimates than the maximum operator.

We hope that the findings of our Monte Carlo simulation will be informative to applied researchers interested in the choice of legitimate models for efficiency analysis. We recommend FE if the research aim is to analyze production technology or the marginal effects of observable variables on efficiency. However, we recommend the ML estimations of BC and CFG over FE for the estimation of firm efficiency. We also found that models with and without the scaling property did not differ in terms of their estimation performance in our restricted simulation design.