Coordinating a Supply Chain with an EOQ Model

Abstract

In this paper, we consider a supply chain coordination scheme and issues in which a manufacturer supplies a product to a retailer. The retailer decides his optimal order quantity using an economic order quantity (EOQ) model which takes into consideration the shipment costs charged by the manufacturer. We show that under some circumstances, the manufacturer can offer a contract which includes a discount shipment fee per delivery and a shipment fee per unit to coordinate the supply chain and enhance the profits of both the manufacturer and the retailer. We also identify under which condition the manufacturer cannot coordinate the supply chain with shipment fees. This research highlights that the manufacturer needs to further investigate these conditions before offering and implementing a contract. Numerical examples are also included to illustrate the main results discussed in the paper.

Introduction

Classical economic order quantity (EOQ) model with different variations has been excelled by many researchers since it was first explored a century ago by Ford Whitman Harris in 1913. Several authors (for example, Clark 1972; Urgeletti Tinarelli 1983) have given comprehensive review for using an EOQ model. For instance, Cheng (1989) solved the EOQ model for a single product with demand related to unit price using a geometric programming method. By assuming that the demand declines exponentially over time, Wee (1995) examined an EOQ model with shortages. Khanra and Chaudhuri (2003) developed an EOQ model considering shortages over a finite-time horizon, by assuming a quadratic demand pattern. Sana and Chaudhuri (2008) considered an EOQ model for various types of deterministic demand when delay in payment is permitted by the retailer to the supplier. Chang and Dye (1999) considered the effect of the backlogging rate on the EOQ decision. Teng et al. (2003) extended Chang and Dye’s work by adding a non-constant purchase cost into the model. Some authors developed EOQ models that focused on deteriorating items with time-varying demand and shortages (for example, Benkherouf 1995; Hariga and Alyan 1997). Liao and Chung (2009) investigated EOQ for deteriorating items under the conditions of permissible delay in payments offered by the supplier. Salameh and Jaber (2000) developed models on lot sizing when procured items are of imperfect quality and Khan et al. (2011) summarized the current body of research that has extended the Salameh and Jaber (2000) EOQ model for imperfect items. Taleizadeh et al. (2013a) considered an EOQ problem under partial delayed payment and Taleizadeh et al. (2013b) developed EOQ models with multiple prepayments under no shortage, full backordering, and partial backordering. Pentico and Drake (2011) gave a comprehensive review on deterministic models that have been developed over the past 40 years with considerations, such as pricing, perishable, or deteriorating inventory, time-varying or stock-dependent demand, quantity discounts, or multiple-warehouses.

As the competition is intensified and more options in selecting distribution channels are available, many companies realize that the performance of their business is highly dependant upon the degree of collaboration and coordination across the supply chain. Extensive studies on a supply chain in which a manufacturer supplies a product to a retailer have been undertaken (e.g., Wang and Liu 2007; Lee and Rhee 2010). Coordination of the supply chain through a contract between the manufacturer and the retailer to incentivize both to accept the contract has attracted much attention of both academics and practitioners. Various contracts that can assist in the coordination of the supply chain have been widely studied, such as, quantity discount contract (Li and Liu 2006), returns policy (Pasternack 1985; Choi et al. 2004; Ai et al. 2012), revenue-sharing contract (Cachon and Lariviere 2005; Giannoccaro and Pontrandolfo 2009), returns with whole sale price discount (Chen 2011).

Chen et al. (2001) investigated a two-echelon system with set demand for multiple buyers, and used an optimization strategy to maximize total system-wide profits. Parlar and Weng (1997) explored the joint coordination between manufacturing and supply departments where the manufacturing department has random demands and a short product life. Furthermore, Weng (1995) analyzed the impact of joint decision policies on channel coordination in a system of a single supplier and a group of buyers and also addressed quantity discount on inventory and ordering policies. Consistent with Chen et al. (2001), he showed that quantity discounts alone cannot coordinate the supply chain. Lei et al. (2006) examined the optimal channel coordination policies for business processes that involve not only a supplier and buyer, but transportation partners as well.

Several authors have also discussed coordination schemes on EOQ models. For instance, Xia et al. (2008) examined the supply chain coordination issue for a supply chain with multiple buyers and multiple suppliers and found that matching buyers’ order profiles to suppliers’ cost structures is the main source of supply chain coordination. Chen and Chen (2005) considered a Multi-item inventory and production problem with joint setup costs for a single manufacturer and a single retailer where the retailer faces a deterministic demand and sells a number of products in the marketplace. Based on an EOQ policy, they determined the optimal replenishment policies for the retailer’s end-items and for the manufacturer’s raw materials to minimize the total cost of the supply chain. They proposed a profit sharing mechanism through a quantity discount scheme to achieve Pareto improvements among the participants of a coordinated supply chain.

More recently, Wahab et al. (2011) considered an EOQ model with defective items to examine the effects of imperfect items in a coordinated supply chain. They developed the optimal production-shipment policy by minimizing the total expected cost per unit time in a coordinated vendor–buyer supply chain with the return policy so that the defective items can be sent back to the vendor. Khan and Jaber (2011) developed the model for a two level multi-supplier, single-vendor supply chain where a vendor needs a number of components from different suppliers to make a single product. They optimized cycle time for three coordination mechanisms. Chan and Lee (2012) proposed a model that incorporates both incentive and coordination issues into a single coordination model for a single-vendor multi-buyer supply chain. They found that synchronizing ordering and production cycles while giving a price discount based on the buyers’ order intervals can achieve coordination. In addition, this coordination mechanism can be used as the incentive to motivate buyers to participate in the coordination. Mutlu and Cetinkaya (2011) studied a retailer-carrier channel for the purpose of long-term planning and coordination. Voigt and Inderfurth (2011) discussed the supply chain coordination on extending the standard framework of lot sizing decisions under asymmetric information by allowing investments in setup cost reduction. Duan et al. (2012) examined the coordination scheme that allows the buyer to delay the payment in compensation for altering the order size in a single-vendor, single-buyer supply chain system for fixed lifetime products.

Differing from papers on supply chain coordination using EOQ models, in this paper, we examine a manufacturer Stackelberg supply chain in which the manufacturer should decide the shipment fees to the retailer and the retailer should decide the optimal ordering quantity using an EOQ model which takes these shipment fees into consideration. We propose a contract offered by the manufacturer which consists of a discount shipment fee per delivery and a shipment fee per unit that can achieve supply chain coordination and ensure both the retailer and the manufacturer to be more profitable. We identify conditions under which such a contract can coordinate the supply chain and give the retailer incentives to accept it. This paper contributes the literature by proposing a new scheme using manufacturer’s shipment fees to coordinate the supply chain and ensure both the manufacturer and the retailer benefit.

The rest of the paper is organized as follows. We present the research framework in Sect. 2. Models, conditions that can coordinate the supply chain through a discount shipment fee per delivery, and conditions which result in a win–win situation for both the manufacturer and the retailer will be discussed in Sect. 3. In Sect. 4, we discuss situations in which the coordination conditions do not hold. Numerical examples that illustrate our results and insights are given in Sect. 5. Section 6 gives conclusions. Proofs are provided in the Appendix.

Framework

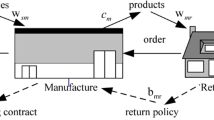
We consider a problem in a supply chain in which a manufacturer supplies a product to a retailer. We use the subscripts M and R to denote the manufacturer and the retailer, respectively. After the manufacturer produces the products, he delivers them to the retailer. The manufacturer is the Stackelberg leader and makes decision on its shipment charges (C _R , c _t ) to its retailer, where C _R is the fee per delivery (for the cost, such as the payment to the driver) and c _t is the cost per unit of product that is shipped to the retailer. Although for many major manufacturers, the transportation cost is a sunk cost, either because they have their own fleet or due to their long-term package contract with their third party transportation provider, this paper shows that the manufacturer can still leverage the shipment fees it charges to the retailer to coordinate the supply chain and eventually benefit itself and the retailer under certain conditions. The retailer, as the supply chain follower, determines the order quantity (Q). The ordering cost is s _R per order for the retailer.

The manufacturer first produces the products and then delivers the order amount to the retailer. The manufacturer’s production rate is p _M units per year and set-up cost per production run is s _M . Since shortages are not allowed in this model, we assume that the manufacturer has sufficient production capacity to ensure annual production rate p _M  ≥ D, where D is the retailer’s annual demand. The holding costs are h _M and h _R per unit annually at the manufacturer and the retailer, respectively. We also assume that the manufacturer’s production cost per unit is c and wholesale price per unit is w. The retailer sells the products at the price of p to the end customers.

In a traditional EOQ model, the retailer decides his ordering quantity based on its holding and ordering cost. In this paper, we consider the problem in the supply chain setting and focus on how the supply chain coordination scheme can enhance the supply chain efficiency. For simplicity, we assume that the manufacturer’s production cycle is the same as the retailer’s ordering cycle. The paper takes into consideration a number of special cases, such as a case in which the manufacturer’s holding cost is expensive as compared to his other costs, or that the retailer requires a slight change order by order. This assumption can be relaxed without altering our basic conclusions on the issues of supply chain coordination.

The following assumptions are used in this paper: (i) all parameters in the model are deterministic; (ii) the cost structure for the retailer (s _R and h _R ) is known by the manufacturer; (iii) replenishment at the retailer is instantaneous.

Models

The retailer’s total cost consists of ordering cost, holding cost, shipment cost that it pays to the manufacturer, and purchasing cost. The retailer’s revenue comes from selling the products to the customers. Let $\prod \nolimits_{R}$ and $\prod \nolimits_{M}$ be the profits of the retailer and the manufacturer, respectively. The retailer’s profit function is:

$$ \prod \nolimits_{R} = (p - w)D - \frac{{(s_{R} + C_{R} )D}}{Q} - \frac{{h_{R} }}{2}Q - c_{t} D. $$

(1)

The total cost of the manufacturer consists of set-up cost per run, holding cost if the retailer’s ordering quantity is lower than the run size and production cost. The manufacturer can collect the revenue from selling the products and charging shipment fees (per delivery and per unit shipped) to the retailer. Thus, the manufacturer’s profit function is:

$$ \prod \nolimits_{M} = (w - c)D - \frac{{s_{M} D}}{Q} - \frac{{h_{M} }}{2}Q - \left( {\frac{Q}{D} - \frac{Q}{{p_{M} }}} \right)h_{M} D + \frac{{C_{R} D}}{Q} + c_{t} D. $$

(2)

We first discuss the decisions in a decentralized supply chain and then examine under what conditions the manufacturer can set the optimal shipment fee per delivery ($C_{R}$). Then we discuss how the supply chain can achieve the coordination using $C_{R}$ in a contract by the manufacturer and under what conditions a contract consisting of $C_{R}$ and $c_{t}$ can enhance profits of the manufacturer and the retailer, as well as motivate the retailer to accept the contract. We also discuss the case if the manufacturer cannot set an optimal shipment fee per delivery ($C_{R}$) in a decentralized supply chain, how the manufacturer can incentivize the retailer so that the supply chain can achieve coordination and both of them are more profitable.

Decentralized Supply Chain Decision

In a decentralized supply chain, the retailer determines the ordering quantity (Q) to maximize its profit function in (1) by anticipating manufacturer’s shipment fee per delivery ($C_{R}$). The manufacturer anticipates the retailer’s interaction in order quantity (Q) and decides $C_{R}$. After the manufacturer announces $C_{R}$, the retailer decides Q.

From (1), we have the following result:

Proposition 1

For a given $C_{R}$ , there exists a unique optimal order quantity for the retailer (Q*), which is given by:

$$ Q^{*} = \sqrt {\frac{{(s_{R} + C_{R} )D}}{{ 2h_{R} }}} . $$

(3)

Equation (3) implies that the optimal order quantity (Q*) increases with the shipment fee per delivery (C _R ) and is independent of the shipment fee per unit ($c_{t}$). This suggests that when the retailer decides the order quantity based on its own interests, besides considering its own cost structure, it also needs to be aware of $C_{R}$ instead of the shipment fee per unit ($c_{t}$).

With the order quantity Q* in (3), the manufacturer maximizes his profit in (2) by determining $C_{R}$. Taking the partial derivative of (2) w.r.t. $C_{R}$:

$$ \frac{{\partial \prod \nolimits_{M} }}{{\partial C_{R} }} = \frac{{\sqrt 2 D^{2} h_{R} \left( {(s_{M} + 2s_{R} + C_{R} )h_{R} p_{M} - h_{M} (s_{R} + C_{R} )(3p_{M} - 2D)} \right)}}{{4p_{M} (h_{R} D(s_{R} + C_{R} ))^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }}. $$

(4)

With (4), we can show the following result:

Proposition 2

If $\frac{{h_{R} }}{{h_{M} }} < 3 - \frac{2D}{{p_{M} }} < \frac{{h_{R} }}{{h_{M} }}\frac{{(s_{M} + 2s_{R} )}}{{s_{R} }}$ , there exists a unique positive optimal shipment fee per order ( $C_{R}^{*}$ ) which is given by:

$$ C_{R}^{*} = \frac{{(h_{R} s_{M} - 3s_{R} h_{M} + 2h_{R} s_{R} )p_{M} + 2h_{M} s_{R} D}}{{(3h_{M} - h_{R} )p_{M} - 2h_{M} D}}. $$

(5)

Proposition 2 shows that if $\frac{{h_{R} }}{{h_{M} }} < 3 - \frac{2D}{{p_{M} }} < \frac{{h_{R} }}{{h_{M} }}\frac{{(s_{M} + 2s_{R} )}}{{s_{R} }}$, the manufacturer can set a positive optimal shipment fee per order. If $\frac{{h_{R} }}{{h_{M} }} < 3 - \frac{2D}{{p_{M} }} < \frac{{h_{R} }}{{h_{M} }}\frac{{(s_{M} + 2s_{R} )}}{{s_{R} }}$ does not hold, the manufacturer cannot have an optimal $C_{R}^{*}$. We will discuss this case in Sect. 4.

After the manufacturer announces $C_{R}^{*}$, the retailer makes the decision on Q*. Using (3), we have:

$$ Q^{*} = \sqrt {\frac{{ 2(s_{M} + s_{R} )p_{M} D}}{{(3h_{M} - h_{R} )p_{M} - 2h_{M} D}}} . $$

(6)

From (6) we see that a positive Q* requires $3 - \frac{2D}{{p_{M} }} \ge \frac{{h_{R} }}{{h_{M} }}$.

$\frac{{\partial Q^{*} }}{\partial D} = \frac{{(3h_{M} - h_{R} )(s_{M} + s_{R} )p_{M}^{2} }}{{[(3h_{M} - h_{R} )p_{M} - 2h_{M} D]\sqrt {2[(3h_{M} - h_{R} )p_{M} - 2h_{M} D](s_{M} + s_{R} )Dp_{M} } }} > 0$, implies that Q* increases with annual demand (D).

We now examine the decisions of the centralized supply chain. We will show how the manufacturer can use shipment fees (c _t , C _R ) to incentivize the retailer to order the amount of products that can maximize the supply chain’s profit through a contract between them so that both manufacturer and the retailer can gain more profit.

Centralized Supply Chain Decision

In a centralize supply chain, the retailer and the manufacturer collaborate to find an order quantity that maximizes chain-wide profit ($\prod$). Let $Q_{I}$ be this order quantity. With (1) and (2), the supply chain’s profit ($\prod$) is:

$$ \prod = (p - c)D - \frac{{s_{M} D}}{{Q_{I} }} - \frac{{h_{M} }}{2}Q_{I} - \left( {\frac{{Q_{I} }}{D} - \frac{{Q_{I} }}{{p_{M} }}} \right)h_{M} D - \frac{{s_{R} D}}{{Q_{I} }} - \frac{{h_{R} }}{2}Q_{I} . $$

(7)

With (7), we have the following result:

Proposition 3

There exists a unique optimal order quantity ( $Q_{I}^{*}$ ) that can maximize the supply chain profit, which is given by:

$$ Q_{I}^{*} = \sqrt {\frac{{2(s_{M} + s_{R} )Dp_{M} }}{{(3h_{M} + h_{R} )p_{M} - 2h_{M} D]}}} . $$

(8)

Since p _M  ≥ D, from Eq. (8), we have $Q_{I}^{*} = \sqrt {\frac{{2(s_{M} + s_{R} )Dp_{M} }}{{(3h_{M} + h_{R} )p_{M} - 2h_{M} D}}} \ge \sqrt {\frac{{2(s_{M} + s_{R} )D}}{{(3h_{M} + h_{R} ) - 2h_{M} }}}$ and $Q_{I}^{*} = \sqrt {\frac{{2(s_{M} + s_{R} )Dp_{M} }}{{(3h_{M} + h_{R} )p_{M} - 2h_{M} D}}} \le \sqrt {\frac{{2(s_{M} + s_{R} )p_{M} }}{{(3h_{M} + h_{R} ) - 2h_{M} }}}$, i.e., optimal order quantity ($Q_{I}^{*}$) is bounded by $\sqrt {\frac{{2(s_{M} + s_{R} )D}}{{(3h_{M} + h_{R} ) - 2h_{M} }}} \le Q_{I}^{*} \le \sqrt {\frac{{2(s_{M} + s_{R} )p_{M} }}{{(3h_{M} + h_{R} ) - 2h_{M} }}}$. Also, from Eq. (8), we have: $\frac{{\partial Q_{I}^{*} }}{\partial D} = \frac{{(3h_{M} + h_{R} )(s_{M} + s_{R} )p_{M}^{2} }}{{[(3h_{M} + h_{R} )p_{M} - 2h_{M} D]\sqrt {2[(3h_{M} + h_{R} )p_{M} - 2h_{M} D](s_{M} + s_{R} )Dp_{M} } }} > 0$, implying that $Q_{I}^{*}$ increases with annual demand (D). Comparing (6) to (8), we can see that the optimal ordering quantity (Q*) in the decentralized supply chain is higher than the optimal ordering quantity ($Q_{I}^{*}$) in the centralized supply chain.

From Eqs. (3) and (8), we see that the manufacturer can set a discount $C_{R}$ to have $Q^{*} = Q_{I}^{*}$. We denote this discount $C_{R}$ as $C_{R}^{d}$. We have the following result:

Proposition 4

If $3 - \frac{2D}{{p_{M} }} \le \frac{{h_{R} }}{{h_{M} }}\frac{{s_{M} }}{{s_{R} }}$ , the manufacturer can set a discount $C_{R}^{d}$ so that the retailer can order $Q_{I}^{*}$ and the supply chain can achieve the coordination , where $C_{R}^{d}$ is given by:

$$ C_{R}^{d} = \frac{{(h_{R} s_{M} - 3s_{R} h_{M} )p_{M} + 2h_{M} s_{R} D}}{{(3h_{M} + h_{R} )p_{M} - 2h_{M} D}}, $$

(9)

where $C_{R}^{d} < C_{R}^{*}$ in ( 5 ) for $h_{R} > 0$.

Proposition 4 shows that if the product of ratio $\frac{{h_{R} }}{{h_{M} }}$ and $\frac{{s_{M} }}{{s_{R} }}$ is sufficiently high ($\ge 3 - \frac{2D}{{p_{M} }}$), the manufacturer can set a discount shipment fee per order ($C_{R}^{d}$) which incentivizes the retailer to order the amount of products at $Q_{I}^{*}$. From the proof of Proposition 3, we have:

Corollary 1

If $3 - \frac{2D}{{p_{M} }} > \frac{{h_{R} }}{{h_{M} }}\frac{{s_{M} }}{{s_{R} }}$ , the supply chain cannot be coordinated using a discount $C_{R}^{d}$.

We now discuss how the manufacturer should incent the retailer to order the amount ($Q_{I}^{*}$) that can maximize chain-wide profit and ensure both are more profitable.

Coordinating the Supply Chain Through a (c ^d _t , C ^d _R ) Contract

Proposition 4 shows that a discount $C_{R}^{d}$ contract can induce the retailer to order ${Q_{I}}^{*}$. We now discuss a contract ($c_{t}^{d}$, $C_{R}^{d}$, $Q_{I}^{*}$) which consists of a new unit shipment cost ($c_{t}^{d}$) and a discount $C_{R}^{d}$ [given in Eq. (9)] that can enhance the retailer’s profit and ensure the retailer to accept this contract. With the discount $C_{R}^{d}$ in (9) and $Q_{I}^{*}$ in (8), the retailer’s profit and the manufacturer’s profit in (1) and (2) become:

$$ \prod \nolimits_{R} \left( {c_{t}^{d} ,C_{R}^{d} ,Q_{I}^{*} } \right) = (p - w)D - \frac{{(s_{R} + C_{R}^{d} )D}}{{Q_{I}^{*} }} - \frac{{h_{R} }}{2}Q_{I}^{*} - c_{t}^{d} D\quad {\text{and}} $$

(10)

$$ \prod \nolimits_{M} \left( {c_{t}^{d} ,C_{R}^{d} ,Q_{I}^{*} } \right) = (w - c)D - \frac{{s_{M} D}}{{Q_{I} *}} - \frac{{h_{M} }}{2}Q_{I}^{*} - \left( {\frac{{Q_{I}^{*} }}{D} - \frac{{Q_{I}^{*} }}{{p_{M} }}} \right)h_{M} D + \frac{{C_{R}^{d} D}}{{Q_{I}^{*} }} + c_{t}^{d} D. $$

(11)

With (1) and (10), we have when:

$$ c_{t}^{d} < \overline{{c_{t} }} = \frac{{h_{R} (Q^{*} - Q_{I}^{*} )}}{2D} - \frac{{s_{R} (Q^{*} - Q_{I}^{*} ) - C_{R}^{d} Q^{*} + C_{R}^{*} Q_{I}^{*} }}{{Q^{*} Q_{I}^{*} }} + c_{t} $$

(12)

$\prod \nolimits_{R} (c_{t}^{d} ,C_{R}^{d} ,Q_{I}^{*} ) > \prod \nolimits_{R} (c_{t} ,C_{R}^{*} ,Q^{*} )$, where $Q^{*}$, $C_{R}^{*}$, $Q_{I}^{*}$, and $C_{R}^{d}$ are given in (5), (6), (8), and (9), respectively.

From (12), we see that when $\frac{{h_{R} (Q^{*} - Q_{I}^{*} )}}{2D} > \frac{{s_{R} (Q^{*} - Q_{I}^{*} ) - C_{R}^{d} Q^{*} + C_{R}^{*} Q_{I}^{*} }}{{Q^{*} Q_{I}^{*} }}$, i.e., the annual holding cost difference for the retailer between the order size of $Q^{*}$ and $Q_{I}^{*}$ is sufficiently high ($> \frac{{s_{R} (Q^{*} - Q_{I}^{*} ) - C_{R}^{d} Q^{*} + C_{R}^{*} Q_{I}^{*} }}{{Q^{*} Q_{I}^{*} }}$), the manufacturer can set a $c_{t}^{d}$ that is higher than $c_{t}$ in a contract ($c_{t}^{d}$, $C_{R}^{d}$) to ensure the retailer enhanced profitability under this contract. However, when $\frac{{h_{R} (Q^{*} - Q_{I}^{*} )}}{2D} < \frac{{s_{R} (Q^{*} - Q_{I}^{*} ) - C_{R}^{d} Q^{*} + C_{R}^{*} Q_{I}^{*} }}{{Q^{*} Q_{I}^{*} }}$, the manufacturer should give the retailer a further discount in unit shipment cost ($c_{t}$) to incent the retailer to order $Q_{I}^{*}$ rather than $Q^{*}$. This raises a cautionary note for the management of the manufacturer. It should carefully examine whether $\frac{{h_{R} (Q^{*} - Q_{I}^{*} )}}{2D}$ is higher or lower than $\frac{{s_{R} (Q^{*} - Q_{I}^{*} ) - C_{R}^{d} Q^{*} + C_{R}^{*} Q_{I}^{*} }}{{Q^{*} Q_{I}^{*} }}$ before it makes the decision on unit shipment cost ($c_{t}^{d}$) to achieve supply chain coordination.

When the manufacturer offers a contract ($c_{t}^{d}$, $C_{R}^{d}$, $Q_{I}^{*}$), with (2) and (11), we have

$$ c_{t}^{d} > \underline{{c_{t} }} = \frac{{s_{M} (Q^{*} - Q_{I}^{*} ) + C_{R}^{*} Q_{I}^{*} - C_{R}^{d} Q^{*} }}{{Q^{*} Q_{I}^{*} }} - \frac{{h_{M} (Q^{*} - Q_{I}^{*} )(3p_{M} - 2D)}}{{2Dp_{M} }} + c_{t} , $$

(13)

$\prod \nolimits_{M} (c_{t}^{d} ,C_{R}^{d} ,Q_{I}^{*} ) > \prod \nolimits_{M} (c_{t} ,C_{R} ,Q^{*} )$, where $Q^{*}$, $C_{R}^{*}$, $Q_{I}^{*}$, and $C_{R}^{d}$ are given in (5), (6), (8), and (9), respectively.

From (13), we see that when $\frac{{h_{M} (Q^{*} - Q_{I}^{*} )(3p_{M} - 2D)}}{{2Dp_{M} }} < \frac{{s_{M} (Q^{*} - Q_{I}^{*} ) + C_{R}^{*} Q_{I}^{*} - C_{R}^{d} Q^{*} }}{{Q^{*} Q_{I}^{*} }}$, the manufacturer’s annual holding cost difference between the order size of $Q^{*}$ and $Q_{I}^{*}$ is sufficiently low, the manufacturer can set a $c_{t}^{d}$ that is higher than $c_{t}$ in a contract ($c_{t}^{d}$, $C_{R}^{d}$, $Q_{I}^{*}$) to ensure a profitability gain under this contract. However, when $\frac{{h_{M} (Q^{*} - Q_{I}^{*} )(3p_{M} - 2D)}}{{2Dp_{M} }} > \frac{{s_{M} (Q^{*} - Q_{I}^{*} ) + C_{R}^{*} Q_{I}^{*} - C_{R}^{d} Q^{*} }}{{Q^{*} Q_{I}^{*} }}$, the manufacturer should give the retailer further discount in unit shipment cost ($c_{t}$) to squeeze more profit under this contract.

From the above analysis, we see that when $\underline{{c_{t} }} < \overline{{c_{t} }}$ and $c_{t}^{d} > \underline{{c_{t} }}$, both the retailer and the manufacturer can earn more profit under the contract ($c_{t}^{d}$, $C_{R}^{d}$, $Q_{I}^{*}$). From (12) and (13), we see that $\underline{{c_{t} }} < \overline{{c_{t} }}$ requires

$$ 3 - \frac{2D}{{p_{M} }} > \frac{{2D(s_{R} + s_{M} )}}{{h_{M} Q^{*} Q_{I}^{*} }} - \frac{{h_{R} }}{{h_{M} }}. $$

(14)

Note that the condition in (14) only depends on parameters of the manufacturer and the retailer.

With Propositions 4 and (14), we summarize our above discussion in the following result:

Proposition 5

If $3 - \frac{2D}{{p_{M} }} \le \frac{{h_{R} }}{{h_{M} }}\frac{{s_{M} }}{{s_{R} }}$ , the manufacturer can offer a contract that consists of a discount shipment cost per delivery ( $C_{R}^{d}$ ), such that the supply chain can be coordinated ($Q^{*} = Q_{I}^{*}$). Further, a contract ( $c_{t}^{d}$, $C_{R}^{d}$, $Q_{I}^{*}$ ) that consists of unit shipment fee ( $c_{t}^{d}$ ) and a discount shipment fee per delivery ( $C_{R}^{d}$ ) can ensure that both the retailer and the manufacturer are more profitable if only if $3 - \frac{2D}{{p_{M} }} > \frac{{2D(s_{R} + s_{M} )}}{{h_{M} Q^{*} Q_{I} }} - \frac{{h_{R} }}{{h_{M} }}$ and $\underline{{c_{t} }} < c_{t}^{d} < \overline{{c_{t} }}$ , where $Q^{*}$, $C_{R}^{*}$, $Q_{I}^{*}$, $C_{R}^{d}$, $\overline{{c_{t} }}$ , and $\underline{{c_{t} }}$ are given by ( 5 ), ( 6 ), ( 8 ), ( 9 ), ( 12 ), and ( 13 ), respectively.

From Proposition 4 and (14), $\frac{{h_{R} }}{{h_{M} }}\frac{{s_{M} }}{{s_{R} }} > \frac{{2D(s_{R} + s_{M} )}}{{h_{M} Q^{*} Q_{I} }} - \frac{{h_{R} }}{{h_{M} }}$ requires:

$$ D < \frac{{h_{R} Q^{{^{*} }} Q_{I} }}{{2s_{R} }}. $$

(15)

Propositions 4 and 5, and (15) result in:

Proposition 6

When $\frac{{2D(s_{R} + s_{M} )}}{{h_{M} Q^{*} Q_{I} }} - \frac{{h_{R} }}{{h_{M} }} < 3 - \frac{2D}{{p_{M} }} \le \frac{{h_{R} }}{{h_{M} }}\frac{{s_{M} }}{{s_{R} }}$ , a contract ( $c_{t}^{d}$, $C_{R}^{d}$, $Q_{I}^{*}$ ) can ensure that both the retailer and the manufacturer are more profitable.

However, if $c_{t}^{d} > \underline{{c_{t} }} > \overline{{c_{t} }}$, i.e., $3 - \frac{2D}{{p_{M} }} < \frac{{2D(s_{R} + s_{M} )}}{{h_{M} Q^{*} Q_{I} }} - \frac{{h_{R} }}{{h_{M} }}$, the supply chain coordination cannot benefit the retailer, but can benefit the manufacturer. If $\prod \nolimits_{M} (c_{t}^{d} ,C_{R}^{d} ,Q_{I}^{*} ) + \prod \nolimits_{R} (c_{t}^{d} ,C_{R}^{d} ,Q_{I}^{*} ) > \prod \nolimits_{M} (c_{t}^{{}} ,C_{R}^{*} ,Q^{*} ) + \prod \nolimits_{R} (c_{t} ,C_{R}^{*} ,Q^{*} )$, the manufacturer should consider a side profit sharing contract ($c_{t}^{d}$, $C_{R}^{d}$, $\beta$) which would share the extra profit that is gained from setting $c_{t}^{d}$ and $C_{R}^{d}$ between the retailer and himself, such that $(1 - \beta )\left[ {\prod \nolimits_{M} (c_{t}^{d} ,C_{R}^{d} ,Q_{I}^{*} ) + \prod \nolimits_{R} (c_{t}^{d} ,C_{R}^{d} ,Q_{I}^{*} )} \right] > \prod \nolimits_{R} (c_{t} ,C_{R}^{*} ,Q^{*} )$, where $\beta$ is the profit share of the manufacturer and $(1 - \beta )$ is the profit share of the retailer.

The above analysis illustrates that when the retailer uses the EOQ model to determine an order quantity, the manufacturer can offer a discount shipment fee per delivery ($C_{R}^{d}$) to coordinate the supply chain to enhance chain-wide profit. The manufacturer also can offer a contract ($c_{t}^{d}$, $C_{R}^{d}$, $Q_{I}^{*}$) to enhance profit for both parties by setting $\underline{{c_{t} }} < c_{t}^{d} <\overline{{c_{t} }}$ if $\frac{{2D(s_{R} + s_{M} )}}{{h_{M} Q^{*} Q_{I} }} - \frac{{h_{R} }}{{h_{M} }} < 3 - \frac{2D}{{p_{M} }} \le \frac{{h_{R} }}{{h_{M} }}\frac{{s_{M} }}{{s_{R} }}$.

Discussion for Some Cases

We note that in Proposition 2, if the condition $\frac{{h_{R} }}{{h_{M} }} < 3 - \frac{2D}{{p_{M} }} < \frac{{h_{R} }}{{h_{M} }}\frac{{(s_{M} + 2s_{R} )}}{{s_{R} }}$ does not hold, the manufacturer cannot have an optimal positive shipment fee per order ($C_{R}^{*}$) in (5). In addition, Proposition 4 shows that only when $3 - \frac{2D}{{p_{M} }} \le \frac{{h_{R} }}{{h_{M} }}\frac{{s_{M} }}{{s_{R} }}$, the manufacturer can set a discount $C_{R}^{d}$ for the retailer to coordinate the supply chain. Now we discuss situations in which these conditions do not hold. There are two cases: ${{s_{M} } \mathord{\left/ {\vphantom {{s_{M} } {s_{R} }}} \right. \kern-0pt} {s_{R} }} > 1$, i.e., the manufacturer’s set-up cost per production run is higher than the retailer’s ordering cost per order, and ${{s_{M} } \mathord{\left/ {\vphantom {{s_{M} } {s_{R} }}} \right. \kern-0pt} {s_{R} }} < 1$. We illustrate the conditions of $3 - {{2D} \mathord{\left/ {\vphantom {{2D} {p_{M} }}} \right. \kern-0pt} {p_{M} }}$ for the optimal $C_{R}^{*}$ in the decentralized supply chain and the condition for the discount $C_{R}^{d}$ in the coordinated supply chain for cases ${{s_{M} } \mathord{\left/ {\vphantom {{s_{M} } {s_{R} }}} \right. \kern-0pt} {s_{R} }} > 1$ and ${{s_{M} } \mathord{\left/ {\vphantom {{s_{M} } {s_{R} }}} \right. \kern-0pt} {s_{R} }} < 1$ in Figs. 1 and 2, respectively.

Fig. 1

The condition of $3 - {{2D} \mathord{\left/ {\vphantom {{2D} {p_{M} }}} \right. \kern-0pt} {p_{M} }}$ for ${C_{R}}^{*}$ and $C_{R}^{d}$ when ${{s_{M} } \mathord{\left/ {\vphantom {{s_{M} } {s_{R} }}} \right. \kern-0pt} {s_{R} }} > 1$

Fig. 2

The condition of $3 - {{2D} \mathord{\left/ {\vphantom {{2D} {p_{M} }}} \right. \kern-0pt} {p_{M} }}$ for ${C_{R}}^{*}$ and $C_{R}^{d}$ when ${{s_{M} } \mathord{\left/ {\vphantom {{s_{M} } {s_{R} }}} \right. \kern-0pt} {s_{R} }} < 1$

From Figs. 1 and 2, we see that both have four ranges for $3 - {{2D} \mathord{\left/ {\vphantom {{2D} {p_{M} }}} \right. \kern-0pt} {p_{M} }}$. We now discuss the supply chain decisions for these ranges for two cases.

Case I: When $\frac{{s_{M} }}{{s_{R} }} > 1$

Range I: If $3 - \frac{2D}{{p_{M} }} < \frac{{h_{R} }}{{h_{M} }}$

This is the case of Range I in Fig. 1, implying that the demand level D is sufficiently high. From (4), we see that $\frac{{\partial \prod \nolimits_{M} }}{{\partial C_{R} }} > 0$, suggesting that a higher $C_{R}$ can enhance the manufacturer’s profit and the manufacturer cannot set an optimal $C_{R}^{*}$ in a decentralized supply chain. Equation (3) also shows that the retailer’s optimal order quantity increases with $C_{R}$ since the retailer can reduce its annual transportation cost by ordering more products per manufacturer’s delivery. In this case, let us assume that the manufacturer sets a $C_{R}$ based on the marketing price. Then, in a decentralized supply chain, the retailer can set the optimal order quantity using (3). From Proposition 4, we see that the manufacturer can coordinate the supply chain by setting a $C_{R}^{d}$ using (9). A $C_{R}^{d}$ contract should induce the retailer to order $Q_{I}^{*}$. We now discuss a contract ($c_{tt}^{{}}$, $C_{R}^{d}$) which consists of a unit transportation cost ($c_{tt}^{{}}$) and a $C_{R}^{d}$ that can enhance the retailer’s profit and ensure the retailer will accept this contract. Replacing $c_{t}^{d}$ with $c_{tt}^{{}}$ in (10) and comparing it to (1), we have when:

$$ c_{tt} < \overline{{c_{tt} }} = \frac{{h_{R} (Q^{*} - Q_{I}^{*} )}}{2D} - \frac{{s_{R} (Q^{*} - Q_{I}^{*} ) + C_{R}^{d} Q^{*} - C_{R} Q_{I}^{*} }}{{Q^{*} Q_{I}^{*} }} + c_{t} , $$

(16)

$\prod \nolimits_{R} (c_{tt} ,C_{R}^{d} ,Q_{I}^{*} ) > \prod \nolimits_{R} (c_{t} ,C_{R} ,Q^{*} )$, where $Q^{*}$, $Q_{I}^{*}$, and $C_{R}^{d}$ are given in (3), (5), and (9), respectively.

Replacing $c_{t}^{d}$ with $c_{tt}^{{}}$ in (11) and comparing it to (2), we have when:

$$ c_{tt} > \underline{{c_{tt} }} = \frac{{s_{M} (Q^{*} - Q_{I}^{*} ) + C_{R} Q_{I}^{*} - C_{R}^{d} Q^{*} }}{{Q^{*} Q_{I}^{*} }} - \frac{{h_{M} (Q^{*} - Q_{I}^{*} )(3p_{M} - 2D)}}{{2Dp_{M} }} + c_{t} , $$

(17)

$\prod \nolimits_{M} (c_{tt} ,C_{R}^{d} ,Q_{I}^{*} ) > \prod \nolimits_{M} (c_{t} ,C_{R} ,Q^{*} )$, where $Q^{*}$, $Q_{I}^{*}$, and $C_{R}^{d}$ are given in (3), (5), and (9), respectively.

From the above analysis, we see that when $\underline{{c_{tt} }} < c_{tt} < \overline{{c_{tt} }}$, both the retailer and the manufacturer can earn more profit under the contract ($c_{tt}^{{}}$, $C_{R}^{d}$). $\underline{{c_{tt} }} < \overline{{c_{tt} }}$ requires

$$ 3 - \frac{2D}{{p_{M} }} > \frac{{2D[(s_{R} - s_{M} )(Q^{*} - Q_{I}^{*} ) + 2C_{R}^{d} Q^{*} - 2C_{R} Q_{I}^{*} ]}}{{h_{M} Q^{*} Q_{I}^{*} (Q^{*} - Q_{I}^{*} )}} - \frac{{h_{R} }}{{h_{M} }}. $$

(18)

We summarize our above discussion in the following result:

Proposition 7

If $3 - \frac{2D}{{p_{M} }} < \frac{{h_{R} }}{{h_{M} }}$ , the manufacturer can offer a contract with $C_{R}^{d}$ , such that the supply chain can be coordinated ( $Q^{*} = Q_{I}^{*}$ ). Further, a contract ( $c_{tt}^{{}}$, $C_{R}^{d}$ ) that consists of a unit shipment cost ( $c_{tt}^{{}}$ ) and a shipment cost per shipment ( $C_{R}^{d}$ ) can ensure that both the retailer and the manufacturer gain more profits only if $3 - \frac{2D}{{p_{M} }}$ satisfies the condition given in ( 18 ).

However, if $c_{tt} > \underline{{c_{tt} }} > \overline{{c_{tt} }}$, i.e., $3 - \frac{2D}{{p_{M} }} < \frac{{2D[(s_{R} - s_{M} )(Q^{*} - Q_{I}^{*} ) + 2C_{R}^{d} Q^{*} - 2C_{R} Q_{I}^{*} ]}}{{h_{M} Q^{*} Q_{I}^{*} (Q^{*} - Q_{I}^{*} )}} - \frac{{h_{R} }}{{h_{M} }}$, the supply chain coordination cannot benefit the retailer, but can benefit the manufacturer. If $\prod \nolimits_{M} (c_{tt} ,C_{R}^{d} ,Q_{I}^{*} ) + \prod \nolimits_{R} (c_{tt} ,C_{R}^{d} ,Q_{I}^{*} ) > \prod \nolimits_{M} (c_{t} ,C_{R} ,Q^{*} ) + \prod \nolimits_{R} (c_{t} ,C_{R} ,Q^{*} )$, the manufacturer should consider a profit sharing contract ($c_{tt}^{{}}$, $C_{R}^{d}$, $\beta$) to share the extra profit gained from setting $c_{tt}^{{}}$ and $C_{R}^{d}$ with the retailer to coordinate the supply chain, such that $(1 - \beta )\left[ {\prod \nolimits_{M} (c_{tt} ,C_{R}^{d} ,Q_{I}^{*} ) + \prod \nolimits_{R} (c_{tt} ,C_{R}^{d} ,Q_{I}^{*} )} \right] > \prod \nolimits_{R} (c_{t} ,C_{R} ,Q^{*} )$, where $\beta$ is the profit share of the manufacturer and $(1 - \beta )$ is the profit share of the retailer.

Range II: $\frac{{h_{R} }}{{h_{M} }} < 3 - \frac{2D}{{p_{M} }} \le \frac{{h_{R} }}{{h_{M} }}\frac{{s_{M} }}{{s_{R} }}$

This is the case of Range II in Fig. 1, suggesting that the demand level D is moderately high. We have discussed this case in detail in Sect. 3.3.

Range III: $\frac{{h_{R} }}{{h_{M} }}\frac{{s_{M} }}{{s_{R} }} < 3 - \frac{2D}{{p_{M} }} < \frac{{h_{R} }}{{h_{M} }}\frac{{(s_{M} + 2s_{R} )}}{{s_{R} }}$

This is the case of Range III in Fig. 1, implying that the demand level D is moderately low. From Propositions 4 and 2, we can conclude that the manufacturer cannot coordinate the supply through setting a discount shipment fee $C_{R}^{d}$. Both the manufacturer and the retailer can operate in a decentralized supply chain. The manufacturer can first announce its optimal decision $C_{R}^{*}$ using Eq. (5). Then the retailer determines the optimal order quantity Q* that is given in (6).

Range IV: $3 - \frac{2D}{{p_{M} }} > \frac{{h_{R} }}{{h_{M} }}\frac{{(s_{M} + 2s_{R} )}}{{s_{R} }}$

This is the case of Range IV in Fig. 1, implying that the demand level D is sufficiently low. From (4) we see that $\frac{{\partial \prod \nolimits_{M} }}{{\partial C_{R} }} < 0$ suggesting that a lower $C_{R}$ can enhance the manufacturer’s profit and discourage the retailer to order more products (Eq. (3)). The manufacturer also cannot set an optimal $C_{R} *$ in a decentralized supply chain. Proposition 4 also shows that the manufacturer cannot coordinate the supply chain through setting the shipment fee $C_{R}^{d}$. The manufacturer needs to coordinate the supply chain using other mechanisms.

Case II: When $\frac{{s_{M} }}{{s_{R} }} < 1$

Range I: If $3 - \frac{2D}{{p_{M} }} \le \frac{{h_{R} }}{{h_{M} }}\frac{{s_{M} }}{{s_{R} }}$

This is the case of Range I in Fig. 2, implying that the demand level D is sufficiently high. It is the case in which the manufacturer can use a discount shipment fee per delivery ($C_{R}^{d}$) to coordinate the supply chain, but cannot set an optimal $C_{R}^{*}$ in a decentralized supply chain. The discussion for this range is similar to that of in Range I for the case when $\frac{{s_{M} }}{{s_{R} }} > 1$.

Range II: $\frac{{h_{R} }}{{h_{M} }}\frac{{s_{M} }}{{s_{R} }} < 3 - \frac{2D}{{p_{M} }} < \frac{{h_{R} }}{{h_{M} }}$

This is the case of Range II in Fig. 2, suggesting that the demand level D is moderately high. In this range, the manufacturer cannot either use a discount shipment fee per delivery ($C_{R}^{d}$) to coordinate the supply chain, no set an optimal $C_{R}^{*}$ in a decentralized supply chain. Since, in this paper, we focus on supply chain coordination, we will not discuss this case further.

Range III: $\frac{{h_{R} }}{{h_{M} }} < 3 - \frac{2D}{{p_{M} }} < \frac{{h_{R} }}{{h_{M} }}\frac{{(s_{M} + 2s_{R} )}}{{s_{R} }}$

This is the case of Range III in Fig. 2, implying that the demand level D is moderately low. Discussion for this range is similar to the discussion of Range III for the case when $\frac{{s_{M} }}{{s_{R} }} > 1$.

Range IV: $3 - \frac{2D}{{p_{M} }} > \frac{{h_{R} }}{{h_{M} }}\frac{{(s_{M} + 2s_{R} )}}{{s_{R} }}$

This is the case of Range IV in Fig. 2, implying that the demand level D is sufficiently low. Discussion for this range is similar to the discussion of Range IV for the case when $\frac{{s_{M} }}{{s_{R} }} > 1$.

The discussion in this section suggests that when the manufacturer makes a decision on whether or not to offer a contract to its retailer, it should first carefully examine the ratio of $\frac{{s_{M} }}{{s_{R} }}$, and then carefully examine the value of $3 - \frac{2D}{{p_{M} }}$ and the relationship between $3 - \frac{2D}{{p_{M} }}$and other costs $h_{R}$, $h_{M}$, $s_{M}$, and $s_{R}$.

Numerical Examples

In this section, we will illustrate our major results discussed above using numerical examples. We set $h_{R} = 6,h_{M} = 5,s_{R} = 100,s_{M} = 200$, and $p_{M} = 5000$ (the case $\frac{{s_{M} }}{{s_{R} }} > 1$), which gives $\frac{{h_{R} }}{{h_{M} }} = 1.2$, $\frac{{h_{R} }}{{h_{M} }}\frac{{s_{M} }}{{s_{R} }} = 2.4$, $\frac{{h_{R} }}{{h_{M} }}\frac{{(s_{M} + 2s_{R} )}}{{s_{R} }} = 4.8$, and $3 - \frac{2D}{{p_{M} }} < \frac{{h_{R} }}{{h_{M} }}\frac{{(s_{M} + 2s_{R} )}}{{s_{R} }}$ for any D. We see that when 4500 < D < 5000, then $3 - \frac{2D}{{p_{M} }} < \frac{{h_{R} }}{{h_{M} }}$, which is the Case I we discussed in Sect. 4.1.1. Also when 1500 ≤ D < 4500, then $\frac{{h_{R} }}{{h_{M} }} < 3 - \frac{2D}{{p_{M} }} \le \frac{{h_{R} }}{{h_{M} }}\frac{{s_{M} }}{{s_{R} }}$, which is the Case II we discussed in Sect. 3.3. In addition, when D < 1500, then $\frac{{h_{R} }}{{h_{M} }}\frac{{s_{M} }}{{s_{R} }} < 3 - \frac{2D}{{p_{M} }} < \frac{{h_{R} }}{{h_{M} }}\frac{{(s_{M} + 2s_{R} )}}{{s_{R} }}$, which is the Case III we discussed in Sect. 4.1.3. We also set p = 10, w = 10, c = 4 and c _t  = 1.

In the following numerical examples, we will focus the Case II discussed in Sect. 3.3, i.e., 1500 < D < 4500 resulting in $\frac{{h_{R} }}{{h_{M} }} < 3 - \frac{2D}{{p_{M} }} \le \frac{{h_{R} }}{{h_{M} }}\frac{{s_{M} }}{{s_{R} }}$.

The changes of $Q^{*}$, $C_{R}^{*}$, $Q_{I}^{*}$, and $C_{R}^{d}$ with the demand level D are illustrated in Table 1. Table 1 shows that as annual demand (D) increases, $Q^{*}$, $C_{R}^{*}$, $Q_{I}^{*}$, and $C_{R}^{d}$ increase. The manufacturer can use the shipment fee per delivery that is collected from the retailer to coordinate the supply chain and enhance the supply chain efficiency.

Table 1 The change of $Q^{*}$, $C_{R} ^{*}$, $Q_{I} ^{*}$, $C_{R}^{d}$, and profits of both decentralized and centralized supply chain with demand level D

When D = 1500, we have $\prod \nolimits_{M} (c_{t} ,C_{R}^{*} ,Q^{*} ) = 8176.3$ and $\prod \nolimits_{R} (c_{t} ,C_{R}^{*} ,Q^{*} ) = 3676.2$ while $\prod \nolimits_{M} (c_{t} ,C_{R}^{*} ,Q^{*} ) = 1 8 6 7 6$ and $\prod \nolimits_{R} (c_{t} ,C_{R}^{*} ,Q^{*} ) = 7 3 5 2. 3$ when D = 3000. Tables 2 and 3 show that the percent of enhancement in profits of the retailer and the manufacturer under a contract $(c_{t}^{d} ,C_{R}^{d} ,Q_{I}^{*} )$for different $c_{t}^{d}$, when D = 1500 and D = 3000, respectively.

Table 2 The percent of enhancement in profits of the retailer and the manufacturer under a contract $(c_{t}^{d} ,C_{R}^{d} ,Q_{I} ^{*})$for different $c_{t}^{d}$when D = 1500

Table 3 The percent of enhancement in profits of the retailer and the manufacturer under a contract $(c_{t}^{d} ,C_{R}^{d} ,Q_{I} ^{*})$for different $c_{t}^{d}$ when D = 3000

Tables 1 and 2 show that under a contract $(c_{t}^{d} ,C_{R}^{d} ,Q_{I}^{*} )$, the manufacturer sets $C_{R}^{d}$= 0 (free shipping per delivery for D = 1500 comparing to $C_{R}^{*}$= 200) to coordinate the supply chain. At the same time, the manufacturer charges a higher shipment fee per unit ($c_{t}^{d} > c_{t}^{{}} = 1$) so that both the retailer and the manufacturer can gain more profits.

Tables 1 and 3 show that under a contract $(c_{t}^{d} ,C_{R}^{d} ,Q_{I}^{*} )$, the manufacturer gives the retailer a significant discount in shipment fee per delivery ($C_{R}^{d}$= 20 comparing to $C_{R}^{*}$= 200 for D = 3000) to encourage the retailer to order $Q_{I}^{*}$ such that the supply chain can achieve coordination. At the same time, the manufacturer charges a slightly higher shipment fee per unit ($c_{t}^{d} > c_{t}^{{}} = 1$) so that both the retailer and the manufacturer can gain more profits. Comparing Tables 2 and 3, we see that as the retailer’s demand increases, contract $(c_{t}^{d} ,C_{R}^{d} ,Q_{I}^{*} )$ can significantly improve the profitability of both the retailer and the manufacturer, which motivates the manufacturer to offer such a contract while incenting the retailer to accept the contract.

Figure 3 shows that the boundaries of $c_{t}^{d}$($\overline{{c_{t} }}$ and $\underline{{c_{t} }}$) change with D in the contract $(c_{t}^{d} ,C_{R}^{d} ,Q_{I}^{*} )$ that can achieve the supply chain coordination and enhance both profits of the retailer and the manufacturer.

Fig. 3

$\overline{{c_{t} }}$ and $\underline{{c_{t} }}$ change with D in the contract $(c_{t}^{d} ,C_{R}^{d} ,Q_{I} ^{*})$

Figure 3 shows that as demand increases, the ranges of $c_{t}^{d}$ that can enhance both profits of the retailer and the manufacturer increase.

Conclusion

This research provides new insights for the retailer using the EOQ model to determine the optimal order quantity. We propose a coordination mechanism for the manufacturer who is the Stackelberg leader to coordinate the supply chain through offering a discount shipment fee per delivery that is collected from its retailer. We show that under certain circumstances, such a coordination mechanism through a contract between the manufacturer and the retailer can enable both to gain more profit.

In this paper, we show that based on the cost structure of both the manufacturer and retailer, as well as the production rate per year at the manufacturer, if the manufacturer knows the retailer’s demand information, the manufacturer can justify whether or not to offer a contract $(c_{t}^{d} ,C_{R}^{d} ,Q_{I}^{*} )$ to the retailer to incent the retailer to order $Q_{I}^{*}$ and, at the same time, enhance profitability for both parties. To know the demand information of the retailer, the manufacturer must maintain a good relationship with its retailer.

Our work shows the managers of the practitioners that they can easily determine whether or not a coordination contract could work for their supply chain by simply checking the coordination conditions presented in this paper. It also shows that supply chain coordination can enhance the profitability of both the manufacturer and the retailer if the coordination contract is well designed (the shipment fee per unit is set between the upper bound and lower bound given in this paper). The results obtained in this paper are helpful in structuring supply chain contracts involving shipment fees set by the manufacturer and the retailer’s optimal order quantity.

The research also discusses the case in which a manufacturer cannot have an optimal $C_{R}^{*}$in a decentralized supply chain and how the manufacturer can enhance the profits of both himself and the retailer. As discussed in Sect. 4.2.2, when the demand level D is moderately high, the manufacturer cannot use a discount shipment fee per delivery ($C_{R}^{d}$) to coordinate the supply chain, nor set an optimal $C_{R}^{*}$ in a decentralized supply chain. The direct extension of this study is to investigate other mechanisms (or contracts) that the manufacturer can use to coordinate the supply chain and incent the retailer to accept the contracts. In this paper we assume that the manufacturer, as a Stackelberg leader, knows the retailer’s demand information as well as cost information (holding cost and ordering cost). But if one or some of the retailer’s private information is not perfectly known by the manufacturer, it would be interesting to examine under which conditions the retailer would like to share this information with the manufacturer, how the manufacturer should incent the retailer to share this information, and how to design mechanisms to achieve supply chain coordination. This paper examines the coordination of a supply chain that consists of a manufacturer and a retailer. The present research could also be extended to consider how to design coordination contracts when the manufacturer supplies the products to multiple retailers who compete on retail price. A careful examination of whether the results and insights of this paper would still hold in a competitive environment might be very interesting and useful.

This research shows that the contract $(c_{t}^{d} ,C_{R}^{d} ,Q_{I}^{*} )$ can be a profit maximizing and coordinating contract under certain circumstances and highlights that need for the manufacturer to further investigate these conditions before offering the contract.

Appendix

Proof of Proposition 1

For a given $C_{R}$, taking partial derivatives of (1) w.r.t. Q:

$$ \begin{gathered} {{\partial \prod \nolimits_{R} } \mathord{\left/ {\vphantom {{\partial \prod \nolimits_{R} } {\partial Q}}} \right. \kern-0pt} {\partial Q}} = {{(s_{R} + C_{R} )D} \mathord{\left/ {\vphantom {{(s_{R} + C_{R} )D} {Q^{2} }}} \right. \kern-0pt} {Q^{2} }} - {{h_{R} } \mathord{\left/ {\vphantom {{h_{R} } 2}} \right. \kern-0pt} 2}\quad {\text{and}} \end{gathered}$$

(A1)

$\begin{gathered}\hfill \\ {{\partial^{2} \prod \nolimits_{R} } \mathord{\left/ {\vphantom {{\partial^{2} \prod \nolimits_{R} } {\partial Q^{2} }}} \right. \kern-0pt} {\partial Q^{2} }} = - {{2(s_{R} + C_{R} )D} \mathord{\left/ {\vphantom {{2(s_{R} + C_{R} )D} {Q^{ 3} }}} \right. \kern-0pt} {Q^{ 3} }} < 0. \hfill \\ \end{gathered}$Therefore, there exists a unique optimal ordering quantity for the retailer, which is given by setting ${{\partial \prod \nolimits_{R} } \mathord{\left/ {\vphantom {{\partial \prod \nolimits_{R} } {\partial Q}}} \right. \kern-0pt} {\partial Q}} = 0$.

Proof of Proposition 2

With Q ^* in (3), taking partial derivatives of (2) w.r.t. $C_{R}$:

$$ \frac{{\partial \prod \nolimits_{M} }}{{\partial C_{R} }} = \frac{{\sqrt 2 D^{2} h_{R} \left( {(s_{M} + 2s_{R} + C_{R} )h_{R} p_{M} - h_{M} (s_{R} + C_{R} )(3p_{M} - 2D)} \right)}}{{4p_{M} (h_{R} D(s_{R} + C_{R} ))^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }} $$

(A2)

$$ \frac{{\partial^{2} \prod \nolimits_{M} }}{{\partial C_{R}^{2} }} = - \frac{{\sqrt 2 \left[ { - h_{M} (3p_{M} - 2D)(s_{R} + C_{R} ) + h_{R} p_{M} (3s_{M} + 4s_{R} + C_{R} )} \right]h_{R}^{2} D^{3} }}{{8p_{M} (h_{R} D(s_{R} + C_{R} ))^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} }}. $$

(A3)

${{\partial \prod \nolimits_{M} } \mathord{\left/ {\vphantom {{\partial \prod \nolimits_{M} } {\partial C_{R} }}} \right. \kern-0pt} {\partial C_{R} }} = 0$ gives

$$ C_{R}^{*} = \frac{{(h_{R} s_{M} - 3s_{R} h_{M} + 2h_{R} s_{R} )p_{M} + 2h_{M} s_{R} D}}{{(3h_{M} - h_{R} )p_{M} - 2h_{M} D}} . $$

(A4)

With (A4), we see that $\left. {{{\partial^{2} \prod \nolimits_{M} } \mathord{\left/ {\vphantom {{\partial^{2} \prod \nolimits_{M} } {\partial C_{R}^{2} }}} \right. \kern-0pt} {\partial C_{R}^{2} }}} \right|_{{C_{R} = C_{R}^{*} }} < 0$, suggesting that there exists a unique optimal ordering quantity for the retailer, which is given by (A3). Also, a positive $C_{R}$ requires $\frac{{h_{R} }}{{h_{M} }} < 3 - \frac{2D}{{p_{M} }} < \frac{{h_{R} }}{{h_{M} }}\frac{{(s_{M} + 2s_{R} )}}{{s_{R} }}$.

Proof of Proposition 3

Taking partial derivatives of (7) w.r.t. $Q_{I}$:

$$ {{\partial \prod } \mathord{\left/ {\vphantom {{\partial \prod } {\partial Q_{I} }}} \right. \kern-0pt} {\partial Q_{I} }} = {{(s_{R} + s_{M} )D} \mathord{\left/ {\vphantom {{(s_{R} + s_{M} )D} {Q^{2} }}} \right. \kern-0pt} {Q^{2} }} - {{h_{R} } \mathord{\left/ {\vphantom {{h_{R} } 2}} \right. \kern-0pt} 2} - {{3h_{M} } \mathord{\left/ {\vphantom {{3h_{M} } 2}} \right. \kern-0pt} 2} + {{h_{M} D} \mathord{\left/ {\vphantom {{h_{M} D} {p_{M} }}} \right. \kern-0pt} {p_{M} }}\quad {\text{and}} $$

(A5)

${{\partial^{2} \prod} \mathord{\left/ {\vphantom {{\partial^{2} \prod} {\partial Q_{I}^{2} }}} \right. \kern-0pt} {\partial Q_{I}^{2} }} = - {{2(s_{R} + s_{M} )D} \mathord{\left/ {\vphantom {{2(s_{R} + s_{M} )D} {Q_{I}^{ 3} }}} \right. \kern-0pt} {Q_{I}^{ 3} }} < 0.$

Therefore, there exists a unique optimal ordering quantity for the supply chain, which is given by setting ${{\partial \prod} \mathord{\left/ {\vphantom {{\partial \prod} {\partial Q_{I} }}} \right. \kern-0pt} {\partial Q_{I} }} = 0$.

Proof of Proposition 4

Comparing Eqs. (3) to (8), we have that the manufacturer can set a discount in $C_{R}$ so that $Q^{*} = Q_{I}^{*}$, where $C_{R}^{d} = \frac{{(h_{R} s_{M} - 3s_{R} h_{M} )p_{M} + 2h_{M} s_{R} D}}{{(3h_{M} + h_{R} )p_{M} - 2h_{M} D}}$. A nonnegative $C_{R}^{d}$ requires $\frac{{h_{R} }}{{h_{M} }}\frac{{s_{M} }}{{s_{R} }} \ge 3 - \frac{2D}{{p_{M} }}$. Comparing (9) to (5), it is obvious that $C_{R}^{d} < C_{R}^{*}$ for $h_{R} > 0$.