Production and Remanufacturing Strategies in a Closed-Loop Supply Chain: A Two-Period Newsvendor Problem

Abstract

Effective and efficient closed-loop supply chain processes can constitute a significant competitive edge for companies. However, the integration of forward and reverse processes poses some challenges both on the supply side—e.g., availability of remanufacturable products—and on the demand side, e.g., cannibalization between new and remanufactured products. In this paper a two-period newsvendor-type approach is presented. The model is used to characterize the optimal production and remanufacturing policies. The main emphasis is on studying supply side interactions, in particular, the link between production and sales of new products and the resulting subsequent supply of used products. Further, the issue of storing excess production is addressed. The relationship between inventory and remanufacturing decisions is quantified.

1 Introduction

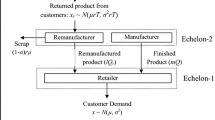
Over the last few years the design of closed-loop supply chain operations has attracted increasing attention in several industries including prominently, e.g., automotive or consumer electronics (Guide et al. 2006; Olugu et al. 2011). The term closed-loop refers to the fact that forward processes and reverse production or logistics processes are dealt with in an integrated fashion. The reverse processes may include some or all of the following stages: product acquisition, quality grading, repair, remanufacturing, recycling, or disposal (Guide and Van Wassenhove 2009).

In this paper, we study the production decisions of a firm for a single product with uncertain demand that can be supplied through manufacturing brand new products or remanufacturing returned cores from sales in previous periods. Specifically our model explicitly captures the fact that the supply of returned cores depends on manufacturing and supply decisions for brand new products in the past. Together with the demand uncertainty, this link gives rise to two interesting intertemporal phenomena. First, by increasing the supply in early periods the firm increases the availability of returned cores in the future. As remanufacturing returned cores is more efficient than producing brand new products this gives rise to reduced cost in later periods. However, this effect comes from an increase in first period cost and the trade-off has to be balanced. Second, given the demand uncertainty excess production in early periods not only increases the availability of returned cores in the future but also increases the overage in the early periods. Keeping this overage in stock for sale in future periods also influences the demand for remanufactured products. Thus, while the existence of both stocking excess production and remanufacturing returned cores should increase the incentives for excess production in early periods the two supply options are also to some extent substitutes and the main interesting question is under what conditions remanufacturing takes place at all and under what conditions it is the exclusive supply option chosen.

To answer these questions a stochastic single-product two-period model is formulated and analyzed. In a first step, the optimal remanufacturing policy is determined assuming that keeping inventories is not an option. This case can also be interpreted as a situation where the second period corresponds to the life cycle of a new generation of the product, e.g., smartphones, video game consoles. In such a setting, the stocked first period product could not be used toward the satisfaction of the second period demand (at least not without some rework). Then, this model is extended by allowing inventories and the main structural properties of this extended model are also analytically derived. Particularly, it is shown that when inventory cost is sufficiently small, no remanufacturing may take place even though returned cores are available. This setting can be observed, e.g., in the printer cartridge market.

The remainder of the paper is organized as follows. Section 9.2 presents related research and places the current model with respect to the existing scientific literature. Section 9.3 deals with the formal model definition and the theoretical results. The model is extended to include the possibility of inventories in Sect. 9.4. Section 9.5 concludes the paper with a short summary and an outlook on extensions of the presented work.

2 Related Work

We will split the discussion of the existing research in two parts. In the first part, we will cover the works on related topics in terms of product returns and remanufacturing, while in the second part we will focus on some of the recent works on two-period newsvendor models. Note that in neither part the review is meant to be exhaustive but rather should give a rough overview of some of the recent developments in these areas.

2.1 Product Returns and Remanufacturing

As mentioned in the introduction, there is a growing body of literature dealing with reverse logistics and closed-loop supply chains. There is a stream of literature dealing with game-theoretic models for analyzing competition and supply chain coordination in remanufacturing settings. A two-period model is used in Ferguson and Toktay (2006) to study possible competition on the remanufacturing market. They develop strategies on how to prevent a remanufacturing market entry of a competitor by collecting used items or collection and remanufacturing. Supply chains with different coordination mechanisms are studied in Bhattacharya et al. (2006) and Li et al. (2011). In Bhattacharya et al. (2006), the results show that the option to remanufacture increases order quantities and profits. It also leads to a higher service level for customers due to increased product availability. A higher cost difference between new and remanufactured products results in increased order quantities. In Li et al. (2011), a supply chain is studied under three different coordination settings (Stackelberg case, Nash case, inaccessible return information case). A retailer is confronted with stochastic demand and orders from a supplier who produces new and remanufactures used products. In the Nash case with simultaneous decisions concerning the manufacturing/order quantities, the quantities and profits are the lowest of the three cases.

Our model is most closely related to the stream of research dealing with (the quality of) product returns and the relationship between new and remanufactured products. The quality of product returns may be highly heterogeneous and there are several models that analyze the acquisition and/or grading process in remanufacturing. In a very simple setting without the possibility to grade goods before acquisition, in Galbreth and Blackburn (2006) the optimal acquisition quantity of used cores is shown to exceed the demand for remanufactured products. As remanufacturing cost depends on core quality, this strategy enables the remanufacturer to select only the high quality returns for actual remanufacturing and scrap the low quality returns. In Ferguson et al. (2009), the return of cores is given and a grading system is in place that categorizes these returns according to their quality. The decisions are how many cores of a particular quality class to remanufacture immediately, how many cores of a particular class to store for later remanufacturing, and how many cores to scrap. One of the main results is that the company always remanufactures the exact demand in each period. Moreover, the optimal strategies are intuitive in that it can be never optimal to store lower quality cores when higher quality ones are available. Analogously, it can be never optimal to scrap higher quality cores before all lower quality cores are scrapped. While these two (and related papers) provide insight into the acquisition and supply process for remanufacturing, they ignore the link with new products.

This link is addressed in Guide and Li (2010) where the influence of product and market characteristics on the potential cannibalization of new product sales by remanufactured products is derived through an empirical, field research. The main finding is that for the studied commercial product there seemed to be a potential for cannibalization, while for the consumer product the risk of cannibalization was small. The relationship between new and remanufactured products for demand satisfaction is also studied analytically in Ferrer and Swaminathan (2006, 2010), Inderfurth (2004), Kelle and Silver (1989), Li et al. (2010), Shi et al. (2011), Teunter and Flapper (2011), Wei et al. (2011), Zhou et al. (2011), and Zhou and Yu (2011).

In Li et al. (2010) and Wei et al. (2011), the focus is on the solution approach. In Li et al. (2010), a dynamic programming approach is developed for a multi-period production planning model including manufacturing, remanufacturing, and disposal decisions. The structure of the optimal control consists of two order-up-to levels for remanufacturing and manufacturing, respectively, and a threshold inventory level above which returned products are disposed of. Robust optimization is applied to an inventory-production planning model with remanufacturing and uncertain demand and supply of used products in Wei et al. (2011). Some numerical examples underpin the effectiveness of the approach and show the sensitivity of the key parameters concerning the solution. Particularly, holding and shortage costs are shown to have the strongest influence on the optimal production and remanufacturing decisions.

In Inderfurth (2004), a single-period, combined manufacturing/remanufacturing and inventory control problem is presented. The same capacity is used by manufacturing and remanufacturing processes, and stochastic demands for new and remanufactured products as well as stochastic returns of used products are considered. Downward substitution allows substitution of remanufactured items by new products but not vice versa. A main result is that the optimal solution deviates from the newsboy solution, particularly by a decreased inventory level of the remanufactured product and higher production of new products. In Shi et al. (2011), a stochastic model for deciding optimal production and remanufacturing quantities for a product portfolio is presented. Product demands are independent, for each product new and remanufactured units are perfect substitutes, the returns are of unknown quality and the amount of returned cores is a function of their acquisition price, which is also a decision variable. Even for the single-period case studied, the problem is hard to solve for larger sizes and so a Lagrangian relaxation-based approach is presented to obtain near-optimal solutions. The optimal strategy will always include (some) remanufacturing. The optimal acquisition and remanufacturing policies of a model with uncertain quality of returns are determined in Teunter and Flapper (2011). Considering stochastic demand, optimal newsboy-like solutions are derived and consequences of demand uncertainty are explored. Higher demands result in an increased optimal quantity of acquired cores and larger optimal remanufacturing-up-to levels. The value of quality information decreases when the demand uncertainty increases.

None of the above-mentioned papers addresses explicitly the link between previous sales and returns of used products. One of the first papers focusing on this link is Kelle and Silver (1989), where the case of planning reusable containers is considered. Returns are stochastic but depend on past sales, and due to loss sometimes new containers must be acquired. In Zhou et al. (2011), the different quality of returns is considered in a single-product, finite multi-period inventory model with stochastic demands. As a result, it is shown that the optimal policy for manufacturing, remanufacturing, and disposal has a simple form, represented by a sequence of constant control parameters. Numerical examples show significant cost reductions compared to two heuristics (pull policy with sorting, pull policy without sorting). In Zhou and Yu (2011), dynamic pricing allows to influence the uncertain supply of used products and random customer demands in a production–remanufacturing model. An exogenous selling price results in a simple policy, whereas considering the selling price as endogenous decision variable leads to an indecomposable state-dependent solution. In this case, the selling price decreases and the acquisition price increases with rising inventory of serviceable products but both decrease when the aggregate inventory level increases.

In Ferrer and Swaminathan (2006, 2010), the optimal supply quantities of new and remanufactured products are analyzed in similar settings as in our model. The case of perfect substitutability between new and remanufactured products is dealt with in a deterministic setting in Ferrer and Swaminathan (2006). Using a price-dependent demand function, it is shown that the possibility of remanufacturing induces the OEM to reduce early period prices for new products to stimulate sales and consequently provide a larger supply of returned cores for possible remanufacturing in later periods. Moreover, it is shown that in the given setting remanufacturing in later periods will always take place, either as an exclusive supply or jointly with the production of new products. In Ferrer and Swaminathan (2010), the model is extended to deal with imperfect substitutability of new and remanufactured products and the equilibrium prices and quantities of new and remanufactured products are derived under a simple demand competition setting. It is shown that in this setting, there may be market constellations where no remanufacturing takes place. As in Shi et al. (2011), the optimal strategy will always include (some) remanufacturing.

Our model differs from these approaches by the combined consideration of the following problem characteristics:

• Uncertain product demand

• Manufacturing and remanufacturing decision making, i.e., a closed-loop view

• Explicit link between sales in earlier periods and subsequent availability of returns for remanufacturing

• No market clearing and the possibility to store excess production for future use

2.2 Two-Period Newsvendor Models

In terms of our modeling approach, we follow a line of research utilizing variants and extensions of newsvendor-type models. Particularly, there is a recent interest in two-period newsvendor models for studying different types of flexibility for satisfying uncertain demands of product portfolios (see, e.g., accurate response in Cattani et al. 2008; Chung et al. 2008; Reimann 2011a; Zhang and Du 2009 and postponement strategies in Granot and Yin 2008 or Reimann 2011b). All of these models extend the classical newsvendor model by allowing (some) production after the demand revelation, i.e., during the selling season. In Cattani et al. (2008), the optimal levels of preseason and selling season capacity are determined under the assumption that the selling season capacity can be allocated to the different products upon demand realization. Contrary to that, the selling season capacity has to be pre-allocated to the different products before the selling season in Chung et al. (2008). The two settings are systematically compared in Reimann (2011a) to study the value of flexibility induced by delayed capacity allocation. Slightly deviating from the setting in these three studies, in Zhang and Du (2009) the value of outsourcing for supplementing limited in-house capacity is studied in two settings. In one setting, both in-house production and outsourcing decisions take place prior to the selling season. In the other setting, outsourcing can be used as an emergency option upon demand realization. Price and order postponement strategies to enhance effectiveness are studied in Granot and Yin (2008). Price postponement refers to the possibility of setting the price in reaction to the demand information, while order postponement is similar to the above-mentioned strategies and corresponds to adjusting supply quantities in response to demand revelation. Finally, in Reimann (2011b) accurate response and postponement strategies are combined in that prior to the selling season some standard component is produced, while during the selling season this standard component is then customized to the observed product demands.

In all of these models, the first period is only a preparatory phase and there is no demand in this period. Moreover, the possibility to utilize selling season capacity, i.e. to make decisions under certainty greatly enhances profitability and reduces the preseason production under uncertainty. In contrast to that, our current model deals with demands in both periods. Moreover, the first period demand and consequently the first period sales will influence (some of) the second period supply, namely, the one for remanufacturing. Consequently, it may be optimal to increase first period supply. In the remainder of the paper, we will show under which conditions this is the case.

3 The Model

We consider a two-period model. The manufacturer offers new products in the first period and has the opportunity to offer new and remanufactured products in the second period. Remanufactured products are made from customer returns of period 1 sales. The core collection yield is denoted by γ, i.e., a fraction 0 ≤ γ ≤ 1 of the units sold in period 1 are available for remanufacturing in period 2.

New and remanufactured products are perfect substitutes. The price in period t = 1, 2 is given by p _t , while the production cost for new products is c _t  < p _t . The cost savings associated with remanufacturing is δ ≥ 0, i.e., remanufacturing a collected core incurs cost of c ₂ − δ in period 2. Demand D _t in both periods is uncertain with known probability density and cumulative distribution functions ${f}_{{D}_{t}}$ and ${F}_{{D}_{t}}$, respectively. Throughout we will assume that the demand distributions are continuous and twice differentiable. Let d _t denote a demand realization in period t.

The expected sales quantity in the first period is a function of the first period production decision of new products q ₁ and denoted by ${S}_{{D}_{1}}({q}_{1})$. It is given by ${S}_{{D}_{1}}({q}_{1}) ={ \int \nolimits \nolimits }_{0}^{{q}_{1}}u\:{f}_{{D}_{ 1}}(u)\:\mathrm{d}u + {q}_{1}\:[1 - {F}_{{D}_{1}}({q}_{1})]$. Given the core collection yield γ defined above, $\gamma \:{S}_{{D}_{1}}({q}_{1})$ units will be returned by customers and are available for remanufacturing in the second period. However, the manufacturer may decide not to remanufacture all of them, and its remanufacturing decision variable is given by $\hat{{q}}_{2} \leq \gamma \:{S}_{{D}_{1}}({q}_{1})$. Moreover, the manufacturer can decide to manufacture q ₂ units of new products in period 2. Summarizing the total supply in period 2 is given by $\hat{{q}}_{2} + {q}_{2}$ and the associated expected sales are ${S}_{{D}_{2}}(\hat{{q}}_{2} + {q}_{2})$.

For formulating our intertemporal optimization problem, let us assume that second period cash flows are discounted with a factor 0 ≤ β ≤ 1. Then the objective of maximizing expected profits π is given by

$$\begin{array}{rcl} \mathop{\text{ max}}\limits_{{q}_{1},{q}_{2},\hat{{q}}_{2}}\pi = -{c}_{1}\:{q}_{1}+{p}_{1}\:{S}_{{D}_{1}}({q}_{1})+\beta \:\left [-{c}_{2}\:({q}_{2} +\hat{ {q}}_{2}) + \delta \:\hat{{q}}_{2} + {p}_{2}\:{S}_{{D}_{2}}({q}_{2} +\hat{ {q}}_{2})\right ],\ \quad & &\end{array}$$

(9.1)

while the constraints are

$$\hat{{q}}_{2} \leq \gamma \:{S}_{{D}_{1}}({q}_{1}),$$

(9.2)

$${q}_{1},{q}_{2},\hat{{q}}_{2} \geq 0.$$

(9.3)

Clearly, the constraints are convex and it is easy to verify that the objective function is concave. Consequently, the optimal solution is obtained by solving the set of KKT optimality conditions.

The structure of the optimal solution is summarized by the following result.

Proposition 1.

Depending on the shadow-price λ _R of the remanufacturing constraint (9.2), the three possible production scenarios are given by

• 1. λ _R = 0 (Exclusive, but limited remanufacturing in period 2): ${q}_{1} = {F}_{{D}_{1}}^{-1}(\frac{{p}_{1}-{c}_{1}} {{p}_{1}} )$ and $\hat{{q}}_{2} = {F}_{{D}_{2}}^{-1}(\frac{{p}_{2}-{c}_{2}+\delta } {{p}_{2}} )$ and q ₂ = 0

• 2. 0 < λ _R < βδ (Exclusive, full remanufacturing in period 2): ${q}_{1} = {F}_{{D}_{1}}^{-1}(\frac{{p}_{1}-{c}_{1}+\gamma \:{\lambda }_{R}} {{p}_{1}+\gamma \:{\lambda }_{R}} )$ and $\hat{{q}}_{2} = \gamma \:{S}_{{D}_{1}}({q}_{1}) = {F}_{{D}_{2}}^{-1}(\frac{\beta ({p}_{2}-{c}_{2}+\delta )-{\lambda }_{R}} {\beta \:{p}_{2}} )$ and q ₂ = 0

• 3. λ _R = βδ (Full remanufacturing and new production in period 2): ${q}_{1} = {F}_{{D}_{1}}^{-1}(\frac{{p}_{1}-{c}_{1}+\gamma \beta \delta } {{p}_{1}+\gamma \beta \delta } )$ and $\hat{{q}}_{2} = \gamma \:{S}_{{D}_{1}}({q}_{1})$ and ${q}_{2} = {F}_{{D}_{2}}^{-1}(\frac{{p}_{2}-{c}_{2}} {{p}_{2}} ) -\hat{ {q}}_{2}$

Proof.

All proofs are given in Appendix.

The optimal scenario and the associated production and remanufacturing quantities can be obtained easily through line-search for the optimal λ _R . Note that in the first case, the first period decision corresponds exactly to the well-known unconstrained, single-period newsvendor solution. There is no new production in period 2 and total second period supply is through remanufacturing. The second period supply quantity corresponds again to the unconstrained, single-period newsvendor quantity, this time subject to the remanufacturing cost (c ₂ − δ). Finally, in that scenario not all the collected cores are remanufactured.

In the second scenario, first period production exceeds the newsvendor quantity and all the returned cores are remanufactured and offered to the market in the second period. However, there is still no new production in period 2.

In the third scenario, there is again excess production in period 1 and all the returned cores are remanufactured and offered to the market in the second period. However, this supply is insufficient and consequently supplemented by new production. In this third scenario, the total supply in the second period corresponds exactly to the unconstrained, single-period newsvendor quantity under the manufacturing cost c ₂, i.e., the quantity that would also be produced if remanufacturing was not possible.

Thus, an interesting observation is that while in scenarios 2 and 3 there is excess period 1 production, it goes along with a reduction of the optimal total supply in period 2 compared to scenario 1. The excess production in period 1 is used only to narrow the gap between the optimal unconstrained remanufacturing supply and the optimal supply associated with the more costly new production.

Note that this result is in line with the results in Ferrer and Swaminathan (2006) where for the deterministic, but price-dependent demand case lower prices (and consequently larger supply quantities) in early periods are found when remanufacturing possibilities exist. An interesting new result provided by our approach is the link between excess production in period 1 and the remanufacturing quantity decision. Whenever excess production in period 1 occurs, this implies that all the returned cores are used for remanufacturing.

Using the results given by Proposition 1, the three different scenarios can be characterized as a function of the core collection yield γ and the remanufacturing cost savings δ. This is shown in the following lemma.

Lemma 1.

The existence of excess period 1 production and new production in period 2 is characterized by the following conditions.

• (a) Excess period 1 production occurs whenever

  $$\gamma \:{S}_{{D}_{1}}({q}_{1}^{\mathrm{NV}}) < {F}_{{ D}_{2}}^{-1}\bigg{(}\frac{{p}_{2} - {c}_{2} + \delta } {{p}_{2}} \bigg{)}.$$

  (9.4)

  Assuming uniform demand distributions D ₁ ∼ U(a ₁ ,b ₁ ) and D ₂ ∼ U(a ₂ ,b ₂ ) excess period 1 production occurs whenever

  $$\delta > \frac{{p}_{2}} {{b}_{2} - {a}_{2}}\Biggl[\gamma \biggl[E[{D}_{1}] - ({b}_{1} - {a}_{1})\frac{1} {2} \frac{{c}_{1}^{2}} {{p}_{1}^{2}}\biggl] - \biggl[ E[{D}_{2}] + ({b}_{2} - {a}_{2})\biggl(\frac{1} {2} -\frac{{c}_{2}} {{p}_{2}}\biggl)\biggl]\Biggl].$$

  (9.5)

• (b) New production in period 2 occurs whenever

  $$\gamma \:{S}_{{D}_{1}}({q}_{1}) < {F}_{{D}_{2}}^{-1}\bigg{(}\frac{{p}_{2} - {c}_{2}} {{p}_{2}} \bigg{)}.$$

  (9.6)

  Assuming uniform demand distributions D ₁ ∼ U(a ₁ ,b ₁ ) and D ₂ ∼ U(a ₂ ,b ₂ ) new production in period 2 occurs whenever

  • If $\gamma E[{D}_{1}] - \biggl[ E[{D}_{2}] + ({b}_{2} - {a}_{2})\bigl(\frac{1} {2} -\frac{{c}_{2}} {{p}_{2}}\bigl)\biggl]> 0$

    $$\delta < \sqrt{\frac{{b}_{1 } - {a}_{1 } } {2\gamma {\beta }^{2}} \frac{{c}_{1}^{2}} {\gamma E[{D}_{1}] -\biggl[ E[{D}_{2}] + ({b}_{2} - {a}_{2})\bigl(\frac{1} {2} -\frac{{c}_{2}} {{p}_{2}} \bigl)\biggl]}} - \frac{{p}_{1}} {\gamma \:\beta }$$

    (9.7)

  • If $\gamma E[{D}_{1}] -\biggl[ E[{D}_{2}] + ({b}_{2} - {a}_{2})\bigl(\frac{1} {2} -\frac{{c}_{2}} {{p}_{2}} \bigl)\biggl] \leq 0$

    $$\delta \geq 0.$$

Part (a) of Lemma 1 states that excess production in period 1 can only be optimal when the expected collection yield associated with the newsvendor quantity q ₁ ^NV is insufficient to cover the optimal unconstrained remanufacturing supply in period 2. This once again highlights the link between excess production in period 1 and reduced supply in period 2 described above. According to the second part (b) of Lemma 1 new production in period 2 can only occur when the collection yield associated with the optimal first period production is insufficient to cover even the optimal supply quantity associated with new production. It is easy to verify that the second part of Lemma 1 is more limiting on γ than the first. Whenever γ is large, i.e. condition (9.4) is violated, remanufacturing does not influence the first period decision and there is no excess production in period 1. We are in scenario 1. When γ is at an intermediate level, i.e. (9.4) is satisfied but (9.6) is violated, we are in scenario 2, while scenario 3 occurs for small values of γ which satisfy (9.6).

This provides an interesting insight into the strategic relationship between the collection efficiency/effectiveness and the manufacturing decision. Investing in a better return rate (e.g., by increasing the price paid for collected cores, or by improving the logistics network for collecting cores) reduces the necessity to produce excessive units in early periods just to ensure sufficient supply of remanufacturable cores in later periods.

For the special case of uniform demand distributions the lemma also provides explicit bounds on the remanufacturing cost savings δ. We first observe that when expected second period demand or demand uncertainty (given by the gap (b ₂ − a ₂)) increases, both excess period 1 production and new production in period 2 are more likely. When the market expands, i.e., in the early phases of the life cycle, it pays to provide a base for capitalizing on the remanufacturing opportunities. In the extreme case when $\gamma E[{D}_{1}] - [E[{D}_{2}] + ({b}_{2} - {a}_{2})(\frac{1} {2} -\frac{{c}_{2}} {{p}_{2}} )] \leq 0$ new production in period 2 occurs for all δ ≥ 0. Moreover, in that case the right-hand-side of condition (9.5) is smaller than zero and hence excess production occurs whenever δ ≥ 0. This can be easily understood. Observe first, that γE[D ₁] is the maximum possible expected sales quantity when q ₁ = b ₁. Observe further, that $E[{D}_{2}] + ({b}_{2} - {a}_{2})\bigl(\frac{1} {2} -\frac{{c}_{2}} {{p}_{2}} \bigl)$ is the minimum second period production corresponding to the newsvendor quantity associated with the cost of new production. Both excess production in the first period and new production in the second period need to take place if the returned cores induced by the maximum quantity produced in the first period are insufficient to satisfy the minimum second period production quantity.

Finally we also observe the inverse relationship between the core collection yield γ and the remanufacturing cost savings δ. When γ increases, the savings associated with remanufacturing need to be larger to induce additional excess production. Analogously, δ needs to be smaller, i.e., the cost savings need to be smaller to induce new production in period 2 when the core collection efficiency increases, i.e., γ. In both cases, the increased returns from the same first period sales quantity reduce the necessity of costly actions like excess production in period 1 and new production in period 2.

3.1 Illustrative Example

Let us consider a small illustrative example to support the theoretical findings above. For reasons of simplicity, we will assume that market prices and production costs are constant and given by ${p}_{1} = {p}_{2} = p = 10$, ${c}_{1} = {c}_{2} = c = 8$. The discount factor β = 0. 9. First period demand is given by a uniform distribution D ₁ ∼ U(a ₁, b ₁) with a ₁ = 25 and b ₁ = 75.

The main aim of the numerical study is to analyze variations in the core collection yield γ, the remanufacturing cost savings δ, and the expected second period demand E[D ₂] on the supply strategy and expected profitability.

For comparison, we will consider a base case setting, where D ₂ ∼ U(25, 75), γ = 0. 5, and δ = 1. Figures 9.1–9.3 all show the first period production of new products q ₁, the second period production of new products q ₂, and the second period remanufacturing of returned cores $\hat{{q}}_{2}$. Further, for ease of explanation the figures also show the optimal single-period newsvendor quantity q ₁ ^NV and the available supply of returned cores $\gamma \:{S}_{{D}_{1}}({q}_{1})$.

Fig. 9.1

Supply quantities under varying core collection yield γ

Fig. 9.3

Supply quantities under varying second period expected demand E[D ₂]

Figure 9.1 focuses on variations of γ from γ = 0. 05 to γ = 1 in steps of 0.05. We first observe that there is excess period 1 production, i.e., q ₁ > q ₁ ^NV for the entire range of γ. Thus, we are never in case 1 described above in Proposition 1. This can also be seen from the fact that $\hat{{q}}_{2} = \gamma \:{S}_{{D}_{1}}({q}_{1})$, i.e., all the returned cores are remanufactured. Moreover, except for the situation γ = 1 there is new production q ₂ > 0 implying that we are in case 3, while for γ = 1 we are in case 2.

Looking at the general effect of γ, we observe some intuitive results. When the core collection yield increases, remanufacturing increases and second period new production falls. Expected profits increase almost linearly from 115.53 to 145.64 when γ goes from 0.05 to 1. However, compared to variations in δ and E[D ₂], the profit effect of variations in γ is quite moderate.

Finally, we observe an interesting and at first sight counterintuitive phenomenon. When γ increases q ₁ first increases, and then drops again for γ = 1. When γ increases the same level of excess production yields a larger amount of returned cores. Thus, we would expect that costly excess production should go down. However, this is only true when γ increases from γ = 0. 95 to γ = 1 in which case no more new production in period 2 takes place. For smaller values of γ, the core collection yield and excess first period production move in the same direction to enable an extra reduction of the more costly new production in period 2.

The impact of variations in δ between δ = 0 and δ = c ₂ in steps of 0.5 are shown in Fig. 9.2. Here we observe very similar behavior as under variations of γ. When δ increases, and consequently remanufacturing gets less costly excess first period production increases, remanufacturing increases and new production in period 2 decreases. When δ = 0, we obtain a special—and trivial—case. When remanufacturing yields no cost advantage, the two periods are decoupled and the optimal decision in both periods is to supply the unconstrained single-period newsvendor quantities q ₁ ^NV and q ₂ ^NV, respectively. As the base case is stationary both in terms of demand and cost structure, we observe ${q}_{1} = {q}_{2} = {q}_{1}^{\mathrm{NV}} = {q}_{2}^{\mathrm{NV}}$. Finally, we observe a steep expected profit increase of about 120.75% between the cases of δ = 0 and δ = 8. Specifically, the expected profit rises almost linearly from 114.00 when there is no cost difference between new and remanufactured products (δ = 0), to 251.65, when the returned cores could directly be resold without any remanufacturing cost (i.e., δ = 8).

Fig. 9.2

Supply quantities under varying remanufacturing cost savings δ

Figure 9.3 shows the effects of different levels of second period demand. More precisely, we let D ₂ ∼ U(a ₂, b ₂), where a ₂ varies from 0 to 50 in steps of 5 and ${b}_{2} = {a}_{2} + 50$. Here we observe all three cases as described by Proposition 1. When second period demand is very small, i.e., E[D ₂] = 25, we are in case 1. There is no new production in period 2, no excess production in period 1 and not all the returned cores are remanufactured. Supplying the unconstrained single-period newsvendor quantity in period 1 is sufficient to ensure enough returned cores for satisfying the very low second period demand. For E[D ₂] = 30, there is still no new production in period 2, but all returned cores are remanufactured and first period production is already excessive. Thus, even on declining markets, excessive production and remanufacturing may be optimal when the decrease in demand from one period to the next is not too severe. Further, when E[D ₂] ≥ 35 full remanufacturing is supplemented by new production in period 2 to ensure sufficient second period supply. Finally, with increasing second period demand expected profits increase roughly linearly from 80.25 in the case of E[D ₂] = 25 to 174.61 when E[D ₂] = 75.

4 Inventory Carryover

In the previous section we have assumed that second period supply can only come from one of two sources, namely, production of new products or remanufacturing of returned cores in period 2. However, due to the demand uncertainty and pronounced through excess production in period 1, there may be unsold units of the product at the end of period 1. These could be carried over and used for demand satisfaction in period 2. This may not be a reasonable setting when the two periods correspond, e.g., to life cycles of two generations of a product. However, when the life cycle of a single product generation is considered inventories can play an important role. The interesting question is how these inventories will influence the optimal remanufacturing decision.

To answer this question, we will extend our model to deal with the possibility of inventory carryover. Given first period production q ₁ and sales ${S}_{{D}_{1}}({q}_{1})$, there is an expected inventory level ${I}_{{D}_{1}}({q}_{1})$ of unsold units at the end of period 1 which is given by ${I}_{{D}_{1}}({q}_{1}) = {q}_{1} - {S}_{{D}_{1}}({q}_{1})$. The manufacturer may be able to keep (some of) these excess units for sale as new products in period 2. The associated per-unit holding cost is given by h. To avoid the case where holding can never be optimal (which would take us back to our previous model), we assume that h < β c ₂. Further, to avoid the case where producing and holding units beyond the maximum demand in period 1 can be optimal we assume that c ₁ + h > β c ₂.

Holding excess production from period 1 is at the discretion of the manufacturer and the decision variable denoting the amount held is I ₁. Clearly, ${I}_{1} \leq {I}_{{D}_{1}}({q}_{1})$. The total supply in period 2 is given by ${I}_{1} +\hat{ {q}}_{2} + {q}_{2}$ and the associated expected sales are ${S}_{{D}_{2}}({I}_{1} +\hat{ {q}}_{2} + {q}_{2})$.

The modified model is given by

$$\begin{array}{rcl} \mathop{\text{ max}}\limits_{{q}_{1},{q}_{2},\hat{{q}}_{2},{I}_{1}}\pi & =& -{c}_{1}\:{q}_{1} + {p}_{1}\:{S}_{{D}_{1}}({q}_{1}) - h\:{I}_{1} \\ & & +\beta \:\left [-{c}_{2}\:({q}_{2} +\hat{ {q}}_{2}) + \delta \:\hat{{q}}_{2} + {p}_{2}\:{S}_{{D}_{2}}({I}_{1} + {q}_{2} +\hat{ {q}}_{2})\right ],\end{array}$$

(9.8)

while the constraints are

$$\begin{array}{rcl} \hat{{q}}_{2}& \leq & \gamma \:{S}_{{D}_{1}}({q}_{1}),\end{array}$$

(9.9)

$$\begin{array}{rcl}{ I}_{1}& \leq & {I}_{{D}_{1}}({q}_{1}),\end{array}$$

(9.10)

$$\begin{array}{rcl}{ q}_{1},{q}_{2},\hat{{q}}_{2},{I}_{1}& \geq & 0.\end{array}$$

(9.11)

As in the previous section, the model can be easily shown to be well behaved. The relationship between inventory and remanufacturing as supply sources is summarized in the following result.

Proposition 2.

There is a threshold holding cost ${h}^{{_\ast}} = \beta \:({c}_{2} - \delta )$ such that, if h > h ^∗ , remanufacturing is the primary supply for satisfying second period demand, while inventory as a secondary and new production as a third supply are only used to fill demand if necessary.

Specifically, depending on the shadow-price λ _R of the remanufacturing constraint the possible production scenarios are given by

• 1. λ _R = 0 (Exclusive, but limited remanufacturing in period 2): ${q}_{1} = {F}_{{D}_{1}}^{-1}(\frac{{p}_{1}-{c}_{1}} {{p}_{1}} )$ and $\hat{{q}}_{2} = {F}_{{D}_{2}}^{-1}(\frac{{p}_{2}-{c}_{2}+\delta } {{p}_{2}} )$ and I ₁ = 0 and q ₂ = 0

• 2. $0 < {\lambda }_{R} < h - \beta ({c}_{2} - \delta )$ (Exclusive, full remanufacturing in period 2): ${q}_{1} = {F}_{{D}_{1}}^{-1}(\frac{{p}_{1}-{c}_{1}+\gamma {\lambda }_{R}} {{p}_{1}+\gamma {\lambda }_{R}} )$ and $\hat{{q}}_{2} = \gamma \:{S}_{{D}_{1}}({q}_{1}) = {F}_{{D}_{2}}^{-1}(\frac{\beta ({p}_{2}-{c}_{2}+\delta )-{\lambda }_{R}} {\beta \:{p}_{2}} )$ and I ₁ = 0 and q ₂ = 0

• 3. ${\lambda }_{R} = h - \beta ({c}_{2} - \delta )$ (Full remanufacturing and limited use of inventory in period 2): ${q}_{1} = {F}_{{D}_{1}}^{-1}(\frac{{p}_{1}-{c}_{1}+\gamma (h-\beta ({c}_{2}-\delta ))} {{p}_{1}+\gamma (h-\beta ({c}_{2}-\delta ))} )$ and $\hat{{q}}_{2} = \gamma \:{S}_{{D}_{1}}({q}_{1})$ and ${I}_{1} = {F}_{{D}_{2}}^{-1}(\frac{\beta \:{p}_{2}-h} {\beta \:{p}_{2}} ) -\hat{ {q}}_{2}$ and q ₂ = 0

• 4. $h - \beta ({c}_{2} - \delta ) < {\lambda }_{R} < \beta \delta$ (Full remanufacturing and full use of inventory in period 2): ${q}_{1} = {F}_{{D}_{1}}^{-1}( \frac{{p}_{1}-{c}_{1}+\gamma {\lambda }_{R}} {{p}_{1}+\gamma {\lambda }_{R}-[\beta ({c}_{2}-\delta )-h+{\lambda }_{R}]})$ and $\hat{{q}}_{2} = \gamma \:{S}_{{D}_{1}}({q}_{1})$ and ${I}_{1} = {I}_{{D}_{1}}({q}_{1})$ and q ₂ = 0

• 5. λ _R = βδ (Full remanufacturing, full use of inventory, and new production in period 2): ${q}_{1} = {F}_{{D}_{1}}^{-1}( \frac{{p}_{1}-{c}_{1}+\gamma \beta \delta } {{p}_{1}+\gamma \beta \delta -(\beta \:{c}_{2}-h)})$ and $\hat{{q}}_{2} = \gamma \:{S}_{{D}_{1}}({q}_{1})$ and ${I}_{1} = {I}_{{D}_{1}}({q}_{1})$ and ${q}_{2} = {F}_{{D}_{2}}^{-1}(\frac{{p}_{2}-{c}_{2}} {{p}_{2}} ) -\hat{ {q}}_{2} - {I}_{1}$.

If h ≤ h ^∗ inventory is the primary supply for satisfying second period demand, while remanufacturing as a secondary and new production as a third supply are only used to fill demand if necessary.

Specifically, depending on the shadow-price λ _I of the inventory constraint the possible production scenarios are given by

• 6. λ _I = 0 (Exclusive, but limited use of inventory in period 2): ${q}_{1} = {F}_{{D}_{1}}^{-1}(\frac{{p}_{1}-{c}_{1}} {{p}_{1}} )$ and ${I}_{1} = {F}_{{D}_{2}}^{-1}(\frac{\beta \:{p}_{2}-h} {\beta \:{p}_{2}} )$ and $\hat{{q}}_{2} = 0$ and q ₂ = 0

• 7. $0 < {\lambda }_{I} < \beta ({c}_{2} - \delta ) - h$ (Exclusive, full use of inventory in period 2): ${q}_{1} = {F}_{{D}_{1}}^{-1}( \frac{{p}_{1}-{c}_{1}} {{p}_{1}-{\lambda }_{I}})$ and ${I}_{1} = {I}_{{D}_{1}}({q}_{1}) = {F}_{{D}_{2}}^{-1}(\frac{\beta \:{p}_{2}-h-{\lambda }_{I}} {\beta \:{p}_{2}} )$ and $\hat{{q}}_{2} = 0$ and q ₂ = 0

• 8. ${\lambda }_{I} = \beta ({c}_{2} - \delta ) - h$ (Full use of inventory and limited remanufacturing in period 2): ${q}_{1} = {F}_{{D}_{1}}^{-1}( \frac{{p}_{1}-{c}_{1}} {{p}_{1}-[\beta ({c}_{2}-\delta )-h]})$ and ${I}_{1} = {I}_{{D}_{1}}({q}_{1})$ and $\hat{{q}}_{2} = {F}_{{D}_{2}}^{-1}(\frac{{p}_{2}-{c}_{2}+\delta } {{p}_{2}} ) - {I}_{1}$ and q ₂ = 0

• 9. $\beta ({c}_{2} - \delta ) - h < {\lambda }_{I} < \beta \:{c}_{2} - h$ (Full use of inventory and full remanufacturing in period 2): ${q}_{1} = {F}_{{D}_{1}}^{-1}( \frac{{p}_{1}-{c}_{1}+\gamma [h-\beta ({c}_{2}-\delta )+{\lambda }_{I}]} {{p}_{1}+\gamma [h-\beta ({c}_{2}-\delta )+{\lambda }_{I}]-{\lambda }_{I}})$ and ${I}_{1} = {I}_{{D}_{1}}({q}_{1})$ and $\hat{{q}}_{2} = \gamma \:{S}_{{D}_{1}}({q}_{1})$ and q ₂ = 0

• 10. ${\lambda }_{I} = \beta \:{c}_{2} - h$ (Full use of inventory, full remanufacturing, and new production in period 2): ${q}_{1} = {F}_{{D}_{1}}^{-1}( \frac{{p}_{1}-{c}_{1}+\gamma \beta \delta } {{p}_{1}+\gamma \beta \delta -(\beta \:{c}_{2}-h)})$ and ${I}_{1} = {I}_{{D}_{1}}({q}_{1})$ and $\hat{{q}}_{2} = \gamma \:{S}_{{D}_{1}}({q}_{1})$ and ${q}_{2} = {F}_{{D}_{2}}^{-1}(\frac{{p}_{2}-{c}_{2}} {{p}_{2}} ) -\hat{ {q}}_{2} - {I}_{1}$.

The results in Proposition 2 can be summarized as follows. The possibility of keeping inventories never increases the first period excess production and never decreases total second period supply. Both effects can be easily understood. First period excess production not only leads to increased sales but also leads to increased overages. While increased sales induce increased core collection for possible remanufacturing, overages can be used directly as a second period supply. Thus, for the same first period production, the total available units for second period supply are larger when inventories are kept. Consequently, the same second period supply can be achieved with smaller first period excess production.

Further, remanufacturing may not take place at all. The conditions for this as well as excess period 1 production and new production in period 2 are given in the following lemma.

Lemma 2.

The existence of excess period 1 production, no remanufacturing, and new production in period 2 is characterized by the following conditions.

• (a) Excess period 1 production occurs whenever

  • If h > h ^∗

    $$\gamma \:{S}_{{D}_{1}}\left ({q}_{1}^{\mathrm{NV}}\right ) < {F}_{{ D}_{2}}^{-1}\bigg{(}\frac{{p}_{2} - {c}_{2} + \delta } {{p}_{2}} \bigg{)}$$

    (9.12)

  • If h ≤ h ^∗

    $${I}_{{D}_{1}}\left ({q}_{1}^{\mathrm{NV}}\right ) < {F}_{{ D}_{2}}^{-1}\bigg{(}\frac{\beta \:{p}_{2} - h} {\beta \:{p}_{2}} \bigg{)}.$$

    (9.13)

• (b) No remanufacturing takes place whenever

  $$h \leq {h}^{{_\ast}}\mbox{ and }{I}_{{ D}_{1}}({q}_{1}) > {F}_{{D}_{2}}^{-1}\bigg{(}\frac{{p}_{2} - {c}_{2} + \delta } {{p}_{2}} \bigg{)}.$$

  (9.14)

• (c) New production in period 2 takes place whenever

  $$\gamma \:{S}_{{D}_{1}}({q}_{1}) + {I}_{{D}_{1}}({q}_{1}) < {F}_{{D}_{2}}^{-1}\bigg{(}\frac{{p}_{2} - {c}_{2}} {{p}_{2}} \bigg{)}.$$

  (9.15)

  This is independent of the level of holding costs h.

Looking first at these results for h > h ^∗ we observe that the condition for excess period 1 production is identical to the one presented in Lemma 1. Moreover, remanufacturing will always take place as it is the primary supply option in period 2. Finally, the condition for new production in period 2 is more strict than the one given in Lemma 1. When inventories are possible, new production in period 2 can only occur when the sum of the collected cores and the inventory level associated with the optimal first period production is insufficient to cover the optimal supply quantity associated with new production. As the most costly new production only occurs when both inventory and remanufacturing are fully utilized, this condition also applies for h ≤ h ^∗ and is actually independent of the level of holding cost.

Turning now to the results for h ≤ h ^∗, the decision on excess period 1 production depends on whether or not the actual level of inventory from the unconstrained single-period newsvendor quantity in period 1 is sufficient to optimally supply the second period. Remanufacturing may not take place when inventory cost is low and the level of inventory exceeds the optimal second period supply associated with remanufacturing. From condition (9.14), we can see directly that remanufacturing is more likely when the associated cost savings δ or the second period price p ₂ increase, or the second period cost c ₂ decreases. Also an increase in second period demand will lead to more remanufacturing. The effect of first period characteristics is more implicit through the value of ${I}_{{D}_{1}}({q}_{1})$. ${I}_{{D}_{1}}({q}_{1})$ increases when the first period demand variance or service level (i.e., the optimal first period supply) increases. The latter increases when first period price increases or cost decreases. Consequently, in these cases it is more likely that no remanufacturing will occur.

Assuming uniform demand distributions, it is possible to derive closed-form expressions for the conditions on excess period 1 production, new production in period 2, and the occurrence of remanufacturing similar to those presented in Lemma 1. However, these expressions are more complex (third degree polynomials) and yield little explicit insight. Thus, we will now again turn to the numerical analysis of our illustrative example.

4.1 Illustrative Example

To show the effects of the possibility to keep inventories of unsold new production in period 1, we will return to our numerical setting from Sect. 9.3.1 and extend it by varying the holding cost h between 0 and 7.2 in steps of 1.2.

The results are shown in Fig. 9.4 for the basecase γ = 0. 5, δ = 1, and E[D ₂] = 50. Figure 9.4 provides the same information as Figs. 9.1–9.3 and additionally shows the available and utilized inventory at the end of period 1 ${I}_{{D}_{1}}({q}_{1})$ and I ₁, respectively. Let us first consider the settings that apply under different levels of h. In the numerical example ${h}^{{_\ast}} = \beta \:({c}_{2} - \delta ) = 6.3$. Thus, only for very high holding cost, in our case h = 7. 2, remanufacturing is the primary second period supply, while in all the other cases inventories are the primary second period supply. Second, the case h = 7. 2 implies that the manufacturer is indifferent between new production in period 2 and keeping unsold period 1 production in inventory for sale in period 2. Thus, while the figure shows some level of utilized inventory for h = 7. 2, the expected profit, optimal first period production q ₁ and optimal level of remanufacturing $\hat{{q}}_{2}$ are identical to the results from the base case without inventory. Keeping this in mind, we observe some interesting effects. As expected, reducing the holding cost increases the expected profit, in particular, from 129.61 when h = 7. 2 to 161.07 in the case of h = 0. Thus, whenever keeping inventories is possible and economically viable (i.e., the manufacturer is not indifferent to its utilization) the manufacturer increases its efficiency. The interesting fact is that this is achieved with increasing excessive new production in period 1. Thus, the manufacturer is willing to give up more and more period 1 profit in exchange for reduced cost in period 2. Finally, looking at period 2 supply one observes that remanufacturing and inventory complement each other in substituting the more costly new production in period 2. Thus, with decreasing holding cost h both the level of remanufacturing and the utilized inventory increase continuously.

Fig. 9.4

Supply quantities under varying holding cost h

To see whether this observation from the base case holds true in general and to study the effects of the possibility to store unsold period 1 production more thoroughly let us perform similar sensitivity analysis as in Sect. 9.3.1. To keep the unit gains from inventory at a comparable level with the remanufacturing cost savings we set h = 1. 2 for the following experiments.

Tables 9.1–9.3 show the results of varying γ, δ, and E[D ₂] under both the model without inventories and the model with inventories. Note that for the model without inventories, the tables reproduce the results from Figs. 9.1–9.3, respectively.

Table 9.1 Supply quantities and expected profits with and without inventories under varying core collection yield γ and holding cost h = 1. 2

Table 9.3 Supply quantities and expected profits with and without inventories under varying expected second period demand E[D ₂] and holding cost h = 1. 2

Concerning the relationship between inventories and remanufacturing, we first observe from Table 9.1 that the result discussed above does not hold in general. When γ is small, I ₁ and $\hat{{q}}_{2}$ both increase with increasing core collection yield. This is in line with the findings from above. However, when γ is large inventories start to drop as γ increases further, while $\hat{{q}}_{2}$ keeps increasing. This happens when q ₂ = 0. In that case—as described above—q ₁ starts to fall. While this fall translates directly into a fall in available and utilized inventory, the increasing core collection yield outweighs the reduction in q ₁ and $\hat{{q}}_{2}$ increases.

Comparing in more detail the cases with and without inventories, we find that profits increase in both cases when γ increases. More interestingly, the gap between the expected profits with and without inventory increase first and then decreases. Thus, the gain from the possibility to hold inventories is largest when γ is around 0.5. Further, first period excess production is much larger when inventories are possible. This is clear as excess production increases expected sales and expected inventory at the same time. Another interesting finding is that for small levels of γ, remanufacturing is larger with inventories, while for large values of γ the opposite is true. This can be understood by the fact that for h = 1. 2 inventories are the primary supply and their utilization reduces the need for remanufacturing. Particularly, for large γ there are no longer all returned cores used for remanufacturing when inventories are possible.

Looking at Table 9.2, we observe some more interesting facts. The positive effect of increasing remanufacturing cost savings δ is actually pronounced by the possibility of keeping inventories, as indicated by the widening gaps between the expected profits with and without inventories. Concerning the relationship between I ₁ and $\hat{{q}}_{2}$ we observe the same effect as already discussed for variations of h. When δ increases, both remanufacturing and utilized inventories increase throughout.

Table 9.2 Supply quantities and expected profits with and without inventories under varying remanufacturing cost savings δ and holding cost h = 1. 2

Finally, looking at Table 9.3 we find that expected second period demand has the strongest impact on new production in period 2 q ₂. While I ₁ and $\hat{{q}}_{2}$ also increase when the second period market size increases, once expected second period demand exceeds expected first period demand the additional demand is met exclusively through new production. Thus, in that case the cost savings associated with keeping inventories and remanufacturing do not outweigh the first period profit decrease due to increased excess production.

When looking at $\hat{{q}}_{2}$, we observe a similar effect as discussed above for variations of γ. When expected second period demand is small, $\hat{{q}}_{2}$ is smaller in the model with inventories than in the model without inventories. This effect is reversed when the expected second period demand increases—and in our numerical case exceeds E[D ₂] = 35. The driver for this is again that for small expected second period demand not all of the returned cores are used. Specifically, we observe, e.g., for E[D ₂] = 25 that the optimal second period supply in both models is 15. Without inventories this comes exactly from remanufacturing, while in the model with inventories this supply is split between inventories and remanufacturing. The most interesting observation is that even though the market is clearly declining—from E[D ₁] = 50 to E[D ₂] = 25—there is significant increased excess production in period 1 when inventories are possible. Yet this still leads to a considerable increase in expected profits.

5 Conclusion

In this paper, we have presented a stochastic single-product two-period newsvendor model to analyze the optimal production and remanufacturing decisions of a firm under uncertain demand. Our model extends previous research by jointly considering demand uncertainty, the possibility of keeping inventories of first period production and the fact that the supply of returned cores depends on manufacturing and supply decisions for brand new products in the past.

We analytically derive conditions on the optimality of strategies like excessive first period production, new production in period two, and remanufacturing. Using a numerical analysis we present sensitivity analysis, of the results with respect to model parameters like core collection yield, remanufacturing cost savings, and second period expected demand.

One of our main results is that contrary to some findings in the existing literature remanufacturing may not take place when costs for storage are relatively low.

Further we find that depending on the particular characteristics of the scenario studied, inventories and remanufacturing may either be substitutes or complements. The former effect is observed when the core collection yield γ is large, while the latter effect occurs when core collection yield γ is small.

Finally, a third interesting observation is that excess first period production first increases and then decreases when the core collection yield γ increases. This is due to two opposite effects. First an increase in γ lowers the level of excess first period production necessary to obtain the same level of returned cores. Second, an increase in returned cores enables increased remanufacturing to substitute the more costly new production in period 2. Obviously, the latter effect explains the increase in excess new production in period 1 for small levels of γ when new period 2 production is necessary to achieve a sufficient second period supply. The former effect takes over, when the level of remanufacturing is already sufficient to substitute all new production in period 2.

Our work can be extended in several interesting directions. First, the core acquisition process seems to be an interesting area to study in detail. Following some models in the literature the amount of returned cores can be linked to an acquisition price function.

Second, in the same context it should be promising to include the quality of returned cores to allow for a more comprehensive analysis of the remanufacturing profitability. Third, following some of the literature, an extension toward a setting where manufacturers compete for the market of new and/or remanufactured products is interesting to focus on the strategic decisions whether and how to set up the closed-loop supply chains under different market environments.

6 Appendix

Let λ^R correspond to the lagrangian multiplier of the remanufacturing constraint, while ${\lambda }^{{q}_{2}}$ and ${\lambda }^{\hat{{q}}_{2}}$ correspond to the lagrangian multipliers of the nonnegativity constraints for q ₂ and $\hat{{q}}_{2}$, respectively. Note that we do not need the nonnegativity constraint for first period production q ₁ since this will be trivially q ₁ ≥ 0 due to our assumption p ₁ > c ₁ and the nonnegativity of demand. Then the system of Karush-Kuhn-Tucker (KKT) conditions is given by

$$\begin{array}{rcl} & & -{c}_{1} + ({p}_{1} + {\lambda }^{\mathrm{R}}\:\gamma )\:[1 - {F}_{{ D}_{1}}({q}_{1})] = 0,\end{array}$$

(9.16)

$$\begin{array}{rcl} & & -\beta \:{c}_{2} + \beta \:{p}_{2}\:[1 - {F}_{{D}_{2}}({q}_{2} +\hat{ {q}}_{2})] + {\lambda }^{{q}_{2} } = 0,\end{array}$$

(9.17)

$$\begin{array}{rcl} & & -\beta \:{c}_{2} + \beta \:\delta + \beta \:{p}_{2}\:[1 - {F}_{{D}_{2}}({q}_{2} +\hat{ {q}}_{2})] - {\lambda }^{\mathrm{R}} + {\lambda }^{\hat{{q}}_{2} } = 0,\end{array}$$

(9.18)

$$\begin{array}{rcl} & & {\lambda }^{\mathrm{R}}\:[\hat{{q}}_{ 2} - \gamma \:{S}_{{D}_{1}}({q}_{1})] = 0,\end{array}$$

(9.19)

$$\begin{array}{rcl} & & \hat{{q}}_{2} \leq \gamma \:{S}_{{D}_{1}}({q}_{1}),\end{array}$$

(9.20)

$$\begin{array}{rcl} & & {q}_{2}\:{\lambda }^{{q}_{2} } = 0,\end{array}$$

(9.21)

$$\begin{array}{rcl} & & -{q}_{2} \leq 0,\end{array}$$

(9.22)

$$\begin{array}{rcl} & & \hat{{q}}_{2}\:{\lambda }^{\hat{{q}}_{2} } = 0,\end{array}$$

(9.23)

$$\begin{array}{rcl} & & -\hat{{q}}_{2} \leq 0,\end{array}$$

(9.24)

$$\begin{array}{rcl} & & {\lambda }^{C} \geq 0,\end{array}$$

(9.25)

$$\begin{array}{rcl} & & {\lambda }^{{q}_{2} },{\lambda }^{\hat{{q}}_{2} } \geq 0.\end{array}$$

(9.26)

Case 1. Exclusive, but limited remanufacturing in period 2:

This case implies that ${\lambda }^{\hat{{q}}_{2}} = 0$ and ${\lambda }^{{q}_{2}} > 0$. Further, since $\hat{{q}}_{2} < \gamma \:{S}_{{D}_{1}}({q}_{1})$ it follows from (9.19) that λ^R = 0.

Consequently, (9.17) leads to

$${F}_{{D}_{2}}(\hat{{q}}_{2}) = \frac{\beta \:({p}_{2} - {c}_{2}) + {\lambda }^{{q}_{2}}} {\beta {p}_{2}},$$

(9.27)

while (9.18) leads to

$${F}_{{D}_{2}}(\hat{{q}}_{2}) = \frac{\beta \:({p}_{2} - {c}_{2} + \delta )} {\beta {p}_{2}} = \frac{{p}_{2} - {c}_{2} + \delta } {{p}_{2}}.$$

(9.28)

From (9.27) and (9.28), we obtain ${\lambda }^{{q}_{2}} = \beta \:\delta > 0$. Finally, (9.16) leads directly to

$${F}_{{D}_{1}}({q}_{1}) = \frac{{p}_{1} - {c}_{1}} {{p}_{1}}.$$

(9.29)

This completes the proof of case 1.

Case 2. Exclusive, full remanufacturing in period 2:

In this case, λ^C > 0 whereas ${\lambda }^{\hat{{q}}_{2}} = 0$ and ${\lambda }^{{q}_{2}} > 0$. While (9.17) again gives rise to (9.27), (9.18) now yields

$${F}_{{D}_{2}}(\hat{{q}}_{2}) = \frac{\beta \:({p}_{2} - {c}_{2} + \delta ) - {\lambda }^{\mathrm{R}}} {\beta {p}_{2}},$$

(9.30)

which—together with (9.27)—gives

$${\lambda }^{\mathrm{R}} = \beta \:\delta - {\lambda }^{{q}_{2} }.$$

(9.31)

Since ${\lambda }^{{q}_{2}} > 0$, the upper boundary λ^R < β δ follows directly. Finally, (9.16) leads directly to

$${F}_{{D}_{1}}({q}_{1}) = \frac{{p}_{1} - {c}_{1} + {\lambda }^{\mathrm{R}}\:\gamma } {{p}_{1} + {\lambda }^{\mathrm{R}}\:\gamma }.$$

(9.32)

This completes the proof of case 2.

Case 3. Full remanufacturing and new production in period 2:

This case is induced by λ^R > 0 as well as ${\lambda }^{{q}_{2}} = {\lambda }^{\hat{{q}}_{2}} = 0$. Then, (9.17) yields

$${F}_{{D}_{2}}({q}_{2} +\hat{ {q}}_{2}) = \frac{\beta \:({p}_{2} - {c}_{2})} {\beta {p}_{2}} = \frac{{p}_{2} - {c}_{2}} {{p}_{2}},$$

(9.33)

while (9.18) once again gives rise to

$${F}_{{D}_{2}}({q}_{2} +\hat{ {q}}_{2}) = \frac{\beta \:({p}_{2} - {c}_{2} + \delta ) - {\lambda }^{\mathrm{R}}} {\beta {p}_{2}}$$

(9.34)

and (9.16) leads to (9.32). From (9.33) and (9.34), it follows that λ^R = β δ and as a result (9.32) can be rewritten as

$${F}_{{D}_{1}}({q}_{1}) = \frac{{p}_{1} - {c}_{1} + \gamma \:\beta \:\delta } {{p}_{1} + \gamma \:\beta \:\delta },$$

(9.35)

which concludes the proof of this third case.

The proof of (9.4) follows directly from Proposition 1 and its proof. Consider the case λ^R = 0. In that case, we observe from (9.29) that the optimal first period decision corresponds to the well-known single-period newsvendor quantity, denoted by q ₁ ^NV. Moreover, the optimal second period supply comes exclusively from remanufacturing and is given by (9.27). We will denote this quantity by $\hat{{q}}_{2}^{\max }$. Since λ^R = 0, this second period supply is unconstrained, which implies that $\hat{{q}}_{2}^{\max } \leq \gamma \:{S}_{{D}_{1}}({q}_{1}^{\mathrm{NV}})$. On the other hand, whenever λ^R > 0 we know from (9.19) that $\hat{{q}}_{2} = \gamma \:{S}_{{D}_{1}}({q}_{1})$. Further, from (9.32) we observe that q ₁ > q ₁ ^NV which implies that ${S}_{{D}_{1}}({q}_{1}) > {S}_{{D}_{1}}({q}_{1}^{\mathrm{NV}})$, while (9.30) yields $\hat{{q}}_{2} <\hat{ {q}}_{2}^{\max }$. These conditions jointly hold only if $\hat{{q}}_{2}^{\max } > \gamma \:{S}_{{D}_{1}}({q}_{1}^{\mathrm{NV}})$ which concludes the proof of this part of Lemma 1.

The proof of (9.6) follows directly from the proof of case 3 in Proposition 1. To prove (9.5) and (9.7), we need to consider the explicit formulae of ${S}_{{D}_{1}}({q}_{1})$ and ${F}_{{D}_{t}}^{-1}({q}_{t})$ associated with the uniform demand distributions. The expected sales are given by ${S}_{{D}_{1}}({q}_{1}) = {q}_{1} -\frac{{({q}_{1}-{a}_{1})}^{2}} {2\:({b}_{1}-{a}_{1})}$. The supply quantity is given by ${q}_{t} = {F}_{{D}_{t}}^{-1}({q}_{t}) = {a}_{t} + ({b}_{t} - {a}_{t})\:{F}_{{D}_{t}}({q}_{t})$. The rest is achieved by simple algebra.

Let λ^R and λ^I correspond to the lagrangian multipliers of the remanufacturing and inventory constraint, respectively. Further let λ^I1, ${\lambda }^{{q}_{2}}$ and ${\lambda }^{\hat{{q}}_{2}}$ correspond to the lagrangian multipliers of the non-negativity constraints for I ₁, q ₂ and $\hat{{q}}_{2}$, respectively. Note that we do not need the nonnegativity constraint for first period production q ₁ since this will be trivially q ₁ ≥ 0 due to our assumption p ₁ > c ₁ and the nonnegativity of demand. Then the system of KKT conditions is given by

$$\begin{array}{rcl} & & -{c}_{1} + ({p}_{1} + {\lambda }^{\mathrm{R}}\:\gamma - {\lambda }^{\mathrm{I}})\:[1 - {F}_{{ D}_{1}}({q}_{1})] + {\lambda }^{\mathrm{I}} = 0,\end{array}$$

(9.36)

$$\begin{array}{rcl} & & -h + \beta \:{p}_{2}\:[1 - {F}_{{D}_{2}}({q}_{2} +\hat{ {q}}_{2} + {I}_{1})] - {\lambda }^{\mathrm{I}} + {\lambda }^{{I}_{1} } = 0,\end{array}$$

(9.37)

$$\begin{array}{rcl} & & -\beta \:{c}_{2} + \beta \:{p}_{2}\:[1 - {F}_{{D}_{2}}({q}_{2} +\hat{ {q}}_{2} + {I}_{1})] + {\lambda }^{{q}_{2} } = 0,\end{array}$$

(9.38)

$$\begin{array}{rcl} & & -\beta \:{c}_{2} + \beta \:\delta + \beta \:{p}_{2}\:[1 - {F}_{{D}_{2}}({q}_{2} +\hat{ {q}}_{2} + {I}_{1})] - {\lambda }^{\mathrm{R}} + {\lambda }^{\hat{{q}}_{2} } = 0,\end{array}$$

(9.39)

$$\begin{array}{rcl} & & {\lambda }^{\mathrm{R}}\:[\hat{{q}}_{ 2} - \gamma \:{S}_{{D}_{1}}({q}_{1})] = 0,\end{array}$$

(9.40)

$$\begin{array}{rcl} & & \hat{{q}}_{2} \leq \gamma \:{S}_{{D}_{1}}({q}_{1}),\end{array}$$

(9.41)

$$\begin{array}{rcl} & & {\lambda }^{\mathrm{I}}\:[{I}_{ 1} - {q}_{1} +\: {S}_{{D}_{1}}({q}_{1})] = 0,\end{array}$$

(9.42)

$$\begin{array}{rcl} & & {I}_{1} \leq {q}_{1} -\: {S}_{{D}_{1}}({q}_{1}),\end{array}$$

(9.43)

$$\begin{array}{rcl} & & {q}_{2}\:{\lambda }^{{q}_{2} } = 0,\end{array}$$

(9.44)

$$\begin{array}{rcl} & & -{q}_{2} \leq 0,\end{array}$$

(9.45)

$$\begin{array}{rcl} & & \hat{{q}}_{2}\:{\lambda }^{\hat{{q}}_{2} } = 0,\end{array}$$

(9.46)

$$\begin{array}{rcl} & & -\hat{{q}}_{2} \leq 0,\end{array}$$

(9.47)

$$\begin{array}{rcl} & & {I}_{1}\:{\lambda }^{{I}_{1} } = 0,\end{array}$$

(9.48)

$$\begin{array}{rcl} & & -{I}_{1} \leq 0,\end{array}$$

(9.49)

$$\begin{array}{rcl} & & {\lambda }^{C} \geq 0,\end{array}$$

(9.50)

$$\begin{array}{rcl}{}^{{q}_{2} },{\lambda }^{\hat{{q}}_{2} },{\lambda }^{{I}_{1} } \geq 0.& &\end{array}$$

(9.51)

Case 1.  Exclusive, but limited remanufacturing in period 2:

This case implies that ${\lambda }^{\hat{{q}}_{2}} = 0$, ${\lambda }^{{q}_{2}} > 0$, and ${\lambda }^{{I}_{1}} > 0$. Further, since $\hat{{q}}_{2} < \gamma \:{S}_{{D}_{1}}({q}_{1})$ it follows from (9.41) that λ^R = 0. Finally, λ^I = 0 since ${I}_{1} = 0 \leq {q}_{1} -\: {S}_{{D}_{1}}({q}_{1})$.

Consequently, (9.36), (9.38), and (9.39) lead again to (9.27), (9.28), and (9.29) while (9.37) gives rise to

$${F}_{{D}_{2}}(\hat{{q}}_{2}) = \frac{\beta \:{p}_{2} - h + {\lambda }^{{I}_{1}}} {\beta \:{p}_{2}}.$$

(9.52)

From (9.28) and (9.52), it follows that $h = \beta \:({c}_{2} - \delta ) + {\lambda }^{{I}_{1}}$. Since ${\lambda }^{{I}_{1}} > 0$, this implies that h > β (c ₂ − δ) which concludes the proof of this part.

Case 2.  Exclusive, full remanufacturing in period 2:

In this case, λ^C > 0 whereas λ^I = 0, ${\lambda }^{\hat{{q}}_{2}} = 0$, ${\lambda }^{{q}_{2}} > 0$ and ${\lambda }^{{I}_{1}} > 0$. Once again the first part of the proof is identical to the proof of case 2 in Proposition 1. Further, (9.37) again gives rise to (9.52). Thus, from (9.30) and (9.52) we get

$${\lambda }^{\mathrm{R}} = h - \beta \:({c}_{ 2} - \delta ) - {\lambda }^{{I}_{1} } > 0,$$

(9.53)

which implies h > β (c ₂ − δ) and completes the proof of case 2.

Case 3.  Full remanufacturing and limited use of inventory in period 2:

This case is induced by λ^R > 0, ${\lambda }^{{q}_{2}} > 0$ as well as ${\lambda }^{\mathrm{I}} = {\lambda }^{\hat{{q}}_{2}} = {\lambda }^{{I}_{1}} = 0$. In this case, (9.36) gives rise to (9.32), while (9.38) leads to

$${F}_{{D}_{2}}(\hat{{q}}_{2} + {I}_{1}) = \frac{\beta \:({p}_{2} - {c}_{2}) + {\lambda }^{{q}_{2}}} {\beta {p}_{2}}.$$

(9.54)

From (9.39), we obtain

$${F}_{{D}_{2}}(\hat{{q}}_{2} + {I}_{1}) = \frac{\beta \:({p}_{2} - {c}_{2} + \delta ) - {\lambda }^{\mathrm{R}}} {\beta {p}_{2}}$$

(9.55)

and (9.37) gives rise to

$${F}_{{D}_{2}}(\hat{{q}}_{2} + {I}_{1}) = \frac{\beta \:{p}_{2} - h} {\beta \:{p}_{2}}.$$

(9.56)

Together, (9.54)–(9.56) yield ${\lambda }^{\mathrm{R}} = h - \beta \:({c}_{2} - \delta )$ and λ^R > 0 implies that h > β (c ₂ − δ) which concludes the proof of this part.

Case 4.  Full remanufacturing and full use of inventory in period 2:

In this case λ^R > 0, λ^I > 0 and ${\lambda }^{{q}_{2}} > 0$ while ${\lambda }^{\hat{{q}}_{2}} = {\lambda }^{{I}_{1}} = 0$. Consequently, from (9.36) we obtain

$${F}_{{D}_{1}}({q}_{1}) = \frac{{p}_{1} - {c}_{1} + {\lambda }^{\mathrm{R}}\:\gamma } {{p}_{1} + {\lambda }^{\mathrm{R}}\:\gamma - {\lambda }^{\mathrm{I}}}.$$

(9.57)

From (9.38) and (9.39) we once again obtain (9.54) and (9.55), respectively. Equation (9.37) now gives

$${F}_{{D}_{2}}(\hat{{q}}_{2} + {I}_{1}) = \frac{\beta \:{p}_{2} - h - {\lambda }^{\mathrm{I}}} {\beta \:{p}_{2}}.$$

(9.58)

From (9.54) and (9.55), we get ${\lambda }^{\mathrm{R}} = \beta \:\delta - {\lambda }^{{q}_{2}}$ which—due to ${\lambda }^{{q}_{2}} > 0$—implies λ^R < β δ. Moreover, from (9.55) and (9.58) we obtain ${\lambda }^{\mathrm{R}} = h - \beta \:({c}_{2} - \delta ) + {\lambda }^{\mathrm{I}}$. Since λ^I > 0, it follows that ${\lambda }^{\mathrm{R}} > h - \beta \:({c}_{2} - \delta )$, which concludes the proof of this case.

Case 5.  Full remanufacturing, full use of inventory and new production in period 2.

This case is characterized by λ^R > 0 and λ^I > 0, while ${\lambda }^{{q}_{2}} = {\lambda }^{\hat{{q}}_{2}} = {\lambda }^{{I}_{1}} = 0$. As in case 4 above, (9.36) gives rise to (9.57). From (9.37), we get

$${F}_{{D}_{2}}({q}_{2} +\hat{ {q}}_{2} + {I}_{1}) = \frac{\beta \:{p}_{2} - h - {\lambda }^{\mathrm{I}}} {\beta \:{p}_{2}},$$

(9.59)

(9.38) yields

$${F}_{{D}_{2}}({q}_{2} +\hat{ {q}}_{2} + {I}_{1}) = \frac{\beta \:({p}_{2} - {c}_{2})} {\beta \:{p}_{2}} = \frac{{p}_{2} - {c}_{2}} {{p}_{2}},$$

(9.60)

while (9.38) gives

$${F}_{{D}_{2}}({q}_{2} +\hat{ {q}}_{2} + {I}_{1}) = \frac{\beta \:({p}_{2} - {c}_{2} + \delta ) - {\lambda }^{\mathrm{R}}} {\beta \:{p}_{2}}.$$

(9.61)

From (9.60) and (9.61), we get λ^R = β δ. Further from (9.59) and (9.60), we obtain ${\lambda }^{\mathrm{I}} = \beta \:{c}_{2} - h$ which implies h < β c ₂ since λ^I > 0. Finally, note that using the expressions for λ^I and λ^R and our assumption c ₁ + h > β c ₂ we get $0 \leq {F}_{{D}_{1}}({q}_{1}) \leq 1$ which concludes the proof of case 5.

Case 6.  Exclusive, but limited use of inventory in period 2:

This case implies that ${\lambda }^{\hat{{q}}_{2}} > 0$, ${\lambda }^{{q}_{2}} > 0$ and ${\lambda }^{{I}_{1}} = 0$. Further, since $0 =\hat{ {q}}_{2} < \gamma \:{S}_{{D}_{1}}({q}_{1})$ it follows from (9.19) that λ^R = 0. Finally, λ^I = 0 since ${I}_{1} \leq {q}_{1} -\: {S}_{{D}_{1}}({q}_{1})$.

Consequently, (9.36) leads again to (9.29). Further, (9.37) gives rise to

$${F}_{{D}_{2}}({I}_{1}) = \frac{\beta \:{p}_{2} - h} {\beta \:{p}_{2}},$$

(9.62)

(9.38) yields

$${F}_{{D}_{2}}({I}_{1}) = \frac{\beta \:({p}_{2} - {c}_{2}) + {\lambda }^{{q}_{2}}} {\beta \:{p}_{2}},$$

(9.63)

and from (9.39), we obtain

$${F}_{{D}_{2}}({I}_{1}) = \frac{\beta \:({p}_{2} - {c}_{2} + \delta ) + {\lambda }^{\hat{{q}}_{2}}} {\beta \:{p}_{2}}.$$

(9.64)

Finally, together (9.62) and (9.64) imply that $h = \beta \:({c}_{2} - \delta ) - {\lambda }^{\hat{{q}}_{2}}$. Since ${\lambda }^{\hat{{q}}_{2}} > 0$, this implies that h ≤ β (c ₂ − δ) which concludes the proof of this part.

Case 7.  Exclusive, full use of inventory in period 2:

In this case, ${\lambda }^{\mathrm{R}} = {\lambda }^{{I}_{1}} = 0$ while λ^I > 0, ${\lambda }^{{q}_{2}} > 0$, and ${\lambda }^{\hat{{q}}_{2}} > 0$. Thus, (9.36) gives

$${F}_{{D}_{1}}({q}_{1}) = \frac{{p}_{1} - {c}_{1}} {{p}_{1} - {\lambda }^{\mathrm{I}}},$$

(9.65)

while (9.37) leads to

$${F}_{{D}_{2}}({I}_{1}) = \frac{\beta \:{p}_{2} - h - {\lambda }^{\mathrm{I}}} {\beta \:{p}_{2}}.$$

(9.66)

From (9.38) and (9.39), we obtain once again (9.63) and (9.64), respectively. As a result, it follows from (9.64) and (9.66) that ${\lambda }^{\mathrm{I}} = \beta \:({c}_{2} - \delta ) - h - {\lambda }^{\hat{{q}}_{2}}$. Since ${\lambda }^{\hat{{q}}_{2}} > 0$, this gives the upper bound of λ^I. Further, by rewriting this term we get $h = \beta \:({c}_{2} - \delta ) - {\lambda }^{\mathrm{I}} - {\lambda }^{\hat{{q}}_{2}}$. Clearly, this implies that h ≤ β (c ₂ − δ) which concludes the proof of this case.

Case 8.  Full use of inventory and limited remanufacturing in period 2:

In this case, ${\lambda }^{\mathrm{R}} = {\lambda }^{{I}_{1}} = {\lambda }^{\hat{{q}}_{2}} = 0$ while λ^I > 0 and ${\lambda }^{{q}_{2}} > 0$. From (9.36), we once again obtain (9.65) while (9.37) leads to

$${F}_{{D}_{2}}({I}_{1} +\hat{ {q}}_{2}) = \frac{\beta \:{p}_{2} - h - {\lambda }^{\mathrm{I}}} {\beta \:{p}_{2}},$$

(9.67)

(9.38) yields

$${F}_{{D}_{2}}({I}_{1} +\hat{ {q}}_{2}) = \frac{\beta \:({p}_{2} - {c}_{2}) + {\lambda }^{{q}_{2}}} {\beta \:{p}_{2}},$$

(9.68)

and from (9.39) we obtain

$${F}_{{D}_{2}}({I}_{1} +\hat{ {q}}_{2}) = \frac{\beta \:({p}_{2} - {c}_{2} + \delta )} {\beta \:{p}_{2}}.$$

(9.69)

From (9.67) and (9.69), we get ${\lambda }^{\mathrm{I}} = \beta \:({c}_{2} - \delta ) - h$. Since λ^I > 0, this implies that h ≤ β (c ₂ − δ) which concludes the proof of this case.

Case 9.  Full use of inventory and full remanufacturing in period 2:

This case is identical to case 4. From (9.54) and (9.58), we get ${\lambda }^{\mathrm{I}} = \beta \:{c}_{2} - h - {\lambda }^{{q}_{2}}$, which given that ${\lambda }^{{q}_{2}} > 0$ yields the upper bound on λ^I. Further, from (9.55) and (9.58) we obtain ${\lambda }^{\mathrm{I}} = \beta \:({c}_{2} - \delta ) - h + {\lambda }^{\mathrm{R}}$ which—given that λ^R > 0—directly yields the lower bound on λ^I and concludes the proof of this case.

Case 10.  Full use of inventory, full remanufacturing, and new production in period 2:

This case and its proof is identical to case 5.

For h > h ^∗, the proof of (9.12) is identical to the proof of the first part of Lemma 1. For h ≤ h ^∗, consider the case λ^I = 0. In that case, we observe from (9.29) that the optimal first period decision corresponds to the well-known single-period newsvendor quantity, denoted by q ₁ ^NV. Moreover, the optimal second period supply comes exclusively from inventory and is given by (9.62). We will denote this quantity by I ₁ ^max. Since λ^I = 0, this second period supply is unconstrained, which implies that ${I}_{1}^{\max } \leq {q}_{1} - {S}_{{D}_{1}}({q}_{1}^{\mathrm{NV}})$. On the other hand, whenever λ^I > 0 we know from (9.42) that ${I}_{1} = {q}_{1} - {S}_{{D}_{1}}({q}_{1})$. Further, from (9.65) we observe that q ₁ > q ₁ ^NV which implies that ${S}_{{D}_{1}}({q}_{1}) > {S}_{{D}_{1}}({q}_{1}^{\mathrm{NV}})$. Since at most the complete additional production can be sold we get ${q}_{1} - {S}_{{D}_{1}}({q}_{1}) \geq {q}_{1}^{\mathrm{NV}} - {S}_{{D}_{1}}({q}_{1}^{\mathrm{NV}})$. Further, (9.66) yields I ₁ < I ₁ ^max. These conditions jointly hold only if ${I}_{1}^{\max } > {q}_{1} - {S}_{{D}_{1}}({q}_{1}^{\mathrm{NV}}) = {I}_{{D}_{1}}({q}_{1}^{\mathrm{NV}})$ which concludes the proof of this part of Lemma 2.

Let us now turn to the proof of condition (9.14). From the proof of Proposition 2, we know that no remanufacturing can only occur if h > h ^∗. Whenever h ≤ h ^∗, we observe from (9.28) and (9.62) that ${I}_{1}^{\max } \geq \hat{ {q}}_{2}^{\max }$. From case 7 of Proposition 2, we know that whenever inventory is fully used ${I}_{1} = {F}_{{D}_{2}}^{-1}(\frac{\beta \:{p}_{2}-h-{\lambda }^{\mathrm{I}}} {\beta \:{p}_{2}} ) = {I}_{{D}_{1}}({q}_{1}) \leq {I}_{1}^{\max }$. From case 8 of Proposition 2, we observe that remanufacturing occurs as soon as ${\lambda }^{\mathrm{I}} \geq \beta \:({c}_{2} - \delta ) - h$ which implies that the associated inventory level ${I}_{{D}_{1}}({q}_{1}) \leq \hat{ {q}}_{2}^{\max }$. Thus no remanufacturing occurs whenever ${I}_{{D}_{1}}({q}_{1}) >\hat{ {q}}_{2}^{\max }$.

The proof of (9.15) follows directly from the proof of case 5 of Proposition 2.