Growing Networks Driven by the Evolutionary Prisoner’s Dilemma Game

Abstract

In this chapter, we present a model of growing networks in which the attachment of nodes is driven by the dynamical state of the evolving network. In particular, we study the interplay between form and function during network formation by considering that the capacity of a node to attract new links from newcomers depends on a dynamical variable: its evolutionary fitness. The fitness of nodes are governed in turn by the payoff obtained when playing a weak Prisoner’s Dilemma game with their nearest neighbors. Thus, we couple the structural evolution of the system with its evolutionary dynamics. On the one hand, we study both the levels of cooperation observed during network evolution and the structural outcome of the model. Our results point out that scale-free networks arise naturally in this setting and that they present non-trivial topological attributes such as degree-degree correlations and hierarchical clustering. On the other hand, we also look at the long-term survival of the cooperation on top of these networks, once the growth has finished. This mechanism points to an evolutionary origin of real complex networks and can be straightforwardly applied to other kinds of dynamical networks problems.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

It is well established that the pattern of interactions among the constituents of many complex systems can not be accurately described neither by lattices or other uniformly distributed spatial models, nor using mean-field formulations. Instead, they need to be characterized by what is generally known as a complex network [1,  2]. In many of these networks, the distribution of the number of interactions, that is the degree k, that an individual shares with the rest of the elements of the system, it is to say, P(k), is found to follow a power-law, P(k) ∼ k ^− γ, with an exponent 2 < γ < 3 in most cases. This implies a high heterogeneity in the degree distribution. The ubiquity in Nature of these so-called scale-free (SF) networks has led scientists to propose many models aimed at reproducing the SF degree distribution [1,  2]. Nonetheless, most of the existing approaches are based on growth rules that depend solely on the topological properties of the network and therefore neglect the connection between the structural evolution and the particular function of the network or the dynamics that takes place on it. This is the case of the well-known Barabási–Albert (BA) model [3], based on two fundamental ingredients: growth and preferential attachment. In this model, the new nodes are sequentially added to the network attaching preferentially to those who have the highest connectivity. However, it is important to recall that accumulated evidences suggest that form follows function [4] and that the formation of a network is also related to the dynamical states of its components through a feedback mechanism that shapes its structure. Taking these facts into consideration, one should not ignore the particular dynamics evolving on top of a network when trying to propose a model for its growth. On the contrary, the outcome of that dynamics should affect somehow the development of the structure.

A paradigmatic case study of the structure and dynamics of complex systems is that of social networks. In these systems, it is particularly relevant to understand how cooperative behavior emerges. The mathematical approach to model the cooperative versus defective interactions is usually addressed under the general framework of Evolutionary Game Theory [5,  6,  7] through diverse social dilemmas [8]. In the general case, it is the individual benefit rather than the overall welfare what drives the system evolution. The emergence of cooperation in natural and social systems has been the subject of intense research recently [9,  10,  11,  12,  13,  14,  15,  16,  17,  18,  19]. (see also the recent reviews [20,  21]). These works are based either on the assumption of an underlying, given static network (or two static, separate networks for interaction and imitation, respectively) or on a coevolution and rewiring process, starting from a fully developed network that already includes all the participating elements [22,  23,  24,  25,  26,  27] (see also the recent review [28]). As we already know, it has been shown that if the well-mixed population hypothesis is abandoned, so that individuals only interact with their neighbors, cooperation is promoted by heterogeneity, specifically on SF networks. However, the main questions remain unanswered: Are cooperative behavior and structural properties of networks related or linked in any way? If so, how? Moreover, if SF networks are best suited to support cooperation, then, where did they come from? What are the mechanisms that shape the structure of the system?

To contribute answering those questions, in this chapter we analyze the growth and formation of complex networks by coupling the network formation rules to the dynamical states of the elements of the system. As we have already mentioned, many mechanisms have been proposed for constructing complex scale-free networks similar to those observed in natural, social, and technological systems from purely topological arguments (for instance, using a preferential attachment rule or any other rule available in the literature [1,  2]). As those works do not include information on the specific function or origin of the network, it is very difficult to discuss the origin of the observed networks on the basis of those models, hence motivating the question we are going to address. The fact that the existing approaches consider separately the two directions of the feedback loop between the function and form of a complex system demands a new mechanism where the network grows coupled to the dynamical features of its components. Our aim here is to discuss a recent attempt in this direction, by linking the growth of the network to the dynamics taking place among its nodes.

The model combines two ideas in a novel manner: preferential attachment and evolutionary game dynamics. Indeed, with the problem of the emergence of cooperation as a specific application in mind, we consider that the nodes of the network are individuals involved in a social dilemma and that newcomers are preferentially linked to nodes with high fitness, the latter being proportional to the payoffs obtained in the game. In this way, the fitness of an element is not imposed as an external constraint [29,  30], but rather it is the result of the dynamical evolution of the system. At the same time, the network is not exogenously imposed as a static and rigid structure on top of which the dynamics evolves, but instead it grows from a small seed and acquires its structure during its formation process.

Finally, we stress that this is not yet another preferential attachment model, since the quantity that favors linking of new nodes has no direct relation with the instantaneous topology of the network. In fact, as we will see, the main result of this interplay is the formation of homogeneous or heterogeneous networks (depending on the values of the parameters of our system) that share a number of topological features with real world networks such as a high clustering and degree-degree correlations. Thus, the model we propose not only explains why heterogeneous networks are appropriate to sustain cooperation, but also provides an evolutionary mechanism for their origin. On the other hand, we will find that there are some important and quite surprising differences between the networks we build using this model, and SF topologies. In particular, we will show that the microscopic organization of cooperation is quite different from that observed when studying the Prisoner’s Dilemma game in static networks. This new organization of cooperation appears during network growth and its fingerprint is still observed when analyzing again the microscopic patterns formed by cooperators when the network has ceased its growth.

2 The Model

Our model naturally incorporates an intrinsic feedback between dynamics and topology. In this way, the growth of the network starts at time t = 0 with a core of m ₀ fully connected nodes. New elements are incorporated to the network and attached to m of the existing nodes with a probability that depends on the dynamical states of these nodes. In particular, the growth of the network proceeds by adding a new node at equally spaced time intervals (denoted by τ_T), and the probability that a node i in the network receives one of the m new links is

$${\Pi }_{i}(t) = \frac{1 - \epsilon + \epsilon {f}_{i}(t)} {{\sum \nolimits }_{j=1}^{N(t)}(1 - \epsilon + \epsilon {f}_{j}(t))},$$

(5.1)

where f _i (t) accounts for the dynamical state of a node i, namely its instant fitness [37] (see below), and N(t) is the size of the network at time t. The parameter ε ∈ [0, 1) controls the weight that newcomers assign to the fitness f _i (t) of the existing nodes in order to decide the attachment probabilities. Therefore, when ε > 0 those nodes with large fitness f _i (t) are preferentially chosen.

How does the dynamical fitness of nodes change in time? The fitness of a node at time t, f _i (t), is defined by the payoffs obtained when playing the Prisoner’s Dilemma (PD) game [31] with its k _i (t) neighbors (note that the connectivity k _i of a node i depends on time since it increases due to the attachment of the nodes as the network grows). In particular, each of the nodes present in the network play a round of the PD game at equally spaced time intervals (denoted by τ_D). Each of these rounds consist in playing once with each of its k _i (t) neighbors. The sum of the payoffs obtained in the last round of the game constitutes its instant evolutionary fitness, f _i (t), that appears in the attachment probability (5.1). Obviously, when a new round of the PD game is played the fitness changes, so that f _i (t) is updated every τ_D time steps.

What is the payoff obtained by a node after playing with a neighbor? The payoff that a node receives when playing with one of its neighbors depends on their instant strategies. The strategy of a node can take two values: Cooperation (C) or Defection (D). According to the PD game there are three possible situations for each pair of nodes linked together in the network, as far as the payoffs obtained by them are concerned:

• If two cooperators meet, both receive R (Reward).

• If two defectors play, both receive P (Punishment).

• If a cooperator and a defector compete, the former receives S (Sucker’s payoff) and the latter obtains T (Temptation).

In the PD game, the ordering of the four payoffs (T, R, P and S) is the following: T > R > P > S. In the following, we will fix the value of three of these parameters to R = 1 and $P = S = 0$, and we will leave the Temptation payoff as the unique free parameter T = b > 1 of the game [9,  32,  33]. With this choice we are considering the so-called weak PD game.

Are the strategies of nodes fixed or do they change in time? After playing a round of the PD game (at each τ_D time steps), every node i compares its evolutionary fitness with that corresponding to a randomly chosen neighbor j. Then, if f _i (t) ≥ f _j (t), node i will keep its strategy for the next round of the game, but if f _j (t) > f _i (t) node i will adopt the strategy of player j with a probability proportional to the payoff difference, f _j (t) − f _i (t) [6,  34,  9,  35,  7,  36,  11]. The specific form of this probability is given by

$${P}_{i} = \frac{{f}_{j}(t) - {f}_{i}(t)} {b \cdot \max \left [{k}_{i}(t),{k}_{j}(t)\right ]}.$$

(5.2)

Note that the denominator of the above expression provides a proper normalization so that 0 ≥ P _i  ≤ 1. To this aim, the denominator, b ⋅maxk _i (t), k _j (t), is the maximum possible fitness difference between two nodes of degree k _i and k _j .

To complete the description of our model we have to set the initial strategy of the initial core of m ₀ nodes and newcomers. Those nodes in the initial core are initially set as cooperators. Therefore, our model can be seen as a test for the survival of this small initial core of cooperation. On the other hand, newcomers adopt with the same probability one of the two available strategies, cooperation or defection, since these nodes have not played any round of the game before being added to the network.

Having introduced how the network grows (at each τ_T time steps) and how the fitness of nodes evolve (at each τ_D time steps) we have settled the basis of a model in which both processes evolve entangled. In other words, the growth of the network as defined above is coupled to the evolutionary dynamics of the PD game that simultaneously evolves in the system. The strength of this coupling is controlled by the parameter ε and by the two associated time scales (τ_T and τ_D). Therefore, (5.1) can be viewed as an “Evolutionary Preferential Attachment” (EPA) mechanism. Depending on the value of ε, we can have two extreme situations:

• (1) When ε ≃ 0, referred to as the weak selection limit [16], the network growth is independent of the evolutionary dynamics as all nodes have roughly the same probability of attracting new links.

• (2) Alternatively, in the strong selection limit, ε → 1, the fittest players (highest payoffs) are much more likely to attract the links from newcomers.

Between the above two situations there is a continuum of intermediate values that will give rise to a wide range of in-between behaviors.

We have carried out numerical simulations of the model exploring the (ε, b)-space. It is worth mentioning that we have also explored different time relations τ_D − τ_T, but we will focus on the results obtained when τ_D ∕ τ_T > 1, that is when the network growth is faster than the evolutionary dynamics. Since τ_D > τ_T, the linking procedure is done with the payoffs obtained after the last round of the game. All results reported have been averaged over at least 10² realizations, and the number of links of a newcomer is taken to be m = 2 whereas the size of the initial core is m ₀ = 3. Note that, since a fixed number of m links are added with each new node, during network growth the average degree of the nodes remains constant to ⟨k⟩ = 2m.

3 Degree Distribution and Average Level of Cooperation

The dependence of the degree distribution on ε and b is shown in Fig. 5.1. As it can be seen, the weak selection limit produces homogeneous networks characterized by a tail that decays exponentially fast with k. Alternatively, when ε is large, scale-free networks arise. Although this might a priori be expected from the definition of the growth rules, this needs not be the case: indeed, it must be taken into account that in a one-shot PD game (i.e. when the PD game is played only once), defection is the best strategy regardless of the opponent’s choice. However, if the network dynamics evolves into a state in which all players (or a large part of the network) are defectors, they will often play against themselves and their payoffs will be reduced (we recall that P = 0). The system’s dynamics will then end up in a state close to an all-D configuration (i.e. with all the nodes playing as defectors) rendering f _i (t) = 0 ∀i ∈ [1, N(t)] in (5.1). From this point on, new nodes would attach randomly to other existing nodes (see (5.1)) and therefore no hubs can come out. This turns out not to be the case, which indicates that for having some degree of heterogeneity, a nonzero level of cooperation is needed. Conversely, the heterogeneous character of the system provides a feedback mechanism for the survival of cooperators that would not overcome defectors otherwise.

Fig. 5.1

Degree distribution of the topologies created for fixed values of b = 1. 5 (Top left) and b = 2. 5 (Top right), and fixed values of ε = 0. 3 (Bottom left) and ε = 0. 99 (Bottom right). The networks are made up of N = 10³ nodes, with ⟨k⟩ = 4, and τ_D = 10τ_T. Every point is the average of 300 independent realizations

In Fig. 5.1, we also show the dependence of the degree of heterogeneity of the networks with the temptation to defect, and we found out that only in the strong selection limit, it depends slightly on b. On the other hand, for small values of ε, there is not any dependence of the degree distribution on b, because in this scenario the dynamics does not play a relevant role on the attachment, on the contrary, it is almost random.

Regarding the outcome of the dynamics, we have also studied the average level of cooperation ⟨c⟩. The average level of cooperation is defined as the fraction of nodes that play as cooperators in the stationary state of the evolutionary dynamics. We have checked that, although the network keeps growing, the fraction of nodes that play as cooperators reaches a stationary value after a transient time. The Fig. 5.2 shows the dependence of ⟨c⟩, as a function of the two model parameters ε and b. As shown in the figure, for a fixed value of b ≳ 1, the level of cooperation increases with ε. In particular, in the strong selection limit ⟨c⟩, the system attains its maximum value. This is a somewhat counterintuitive result as in the limit ε → 1, new nodes are preferentially linked to those with the highest payoffs, which for the PD game, should correspond to defectors. However, the population achieves the highest value of ⟨c⟩. On the other hand, higher levels of cooperation are achieved in heterogeneous rather than in homogeneous topologies, which is consistent with previous findings [9,  10,  11].

Fig. 5.2

Color-coded average level of cooperation in the system ⟨c⟩ right at the end of the EPA procedure, it is to say, when the final size is achieved as a function of the temptation to defect b and the selection pressure ε. The networks are made up of 10³ nodes with ⟨k⟩ = 4 and τ_D = 10τ_T. Reprinted from [38]

4 Degree Distribution Among Cooperators

In this section we want to study the dependence between strategy and degree of connectivity, comparing the results with those obtained for the static SF scenario, where we recall that cooperators occupy always the highest and medium classes of connectivity, while defectors are not stable when seating on the hubs ( [39]). As we will show, the interplay between the local structure of the network and the hierarchical organization of cooperation seems to be highly nontrivial, and quite different to what has been reported for static scale-free networks [9,  11]. In Fig. 5.3 one can see that, surprisingly enough, as the temptation to defect increases, the likelihood that cooperators occupy the hubs decreases. Indeed, during network growth, cooperators are not localized neither at the hubs nor at the lowly connected nodes, but in intermediate degree classes. It is important to realize that this is a new effect that arises from the competition between network growth and the evolutionary dynamics. In particular, it highlights the differences between the microscopic organization in the steady state for the PD game in static networks and that found when the network is evolving.

Fig. 5.3

Probability P _c (k) that a node with connectivity k plays as a cooperator for different values of b in the strong selection limit (ε = 0. 99) at the end of the growth of a network with N = 10³ nodes and ⟨k⟩ = 4. Reprinted from [38]

To address this interesting and previously unobserved phenomenon, we have developed a simple analytical argument that can help understand the reasons behind it. Let k _i ^c be the number of cooperator neighbors of a given node i. Its fitness is f _i ^d = bk _i ^c, if node i is a defector, and f _i ^c = k _i ^c, if it is a cooperator. The value of k _i ^c is expected to change because of two factors. On the one hand, due to the network growth (node accretion flow, at a rate of one new node each time unit τ_T) and on the other hand, due to imitation processes dictated by (5.2), that take place at a pace τ_D. As it has been mentioned before, we will focus on the case in which τ_D is much larger than τ_T, for now. Thus, the expected increase of fitness is

$$\Delta {f}_{i} = {\Delta }_{\mathrm{flow}}{f}_{i} + {\Delta }_{\mathrm{evol}}{f}_{i},$$

(5.3)

where Δ _flow f _i means the variation of fitness in node i due to the newcomers flow, and Δ _evol f _i stands for the change in fitness due to changes of neighbors’ strategies. Note that both Δ _flow f _i and Δ _evol f _i are related to the change of k _i ^c (the former due to the attachment of new cooperator neighbors to node i and the latter due to the old neighbors that changed their strategy). Therefore, the above expression leads to an expected increase in k _i ^c given by

$$\Delta {k}_{\mathrm{i}}^{\mathrm{c}} = {k}_{\mathrm{ i}}^{\mathrm{c}}(t + {\tau }_{\mathrm{ D}}) - {k}_{\mathrm{i}}^{\mathrm{c}}(t) = {\Delta }_{\mathrm{ flow}}{k}_{\mathrm{i}}^{\mathrm{c}} + {\Delta }_{\mathrm{ evol}}{k}_{\mathrm{i}}^{\mathrm{c}}.$$

(5.4)

On the other hand, the expected increase of degree of node i in the interval of time (t, t + τ_D) only has the contribution from newcomer flow, and recalling that new nodes are generated with the same probability to be cooperators or defectors, i.e, ρ₀ = 0. 5, it will take the form

$$\Delta {k}_{i} = {\Delta }_{\mathrm{flow}}{k}_{i} = 2{\Delta }_{\mathrm{flow}}{k}_{\mathrm{i}}^{\mathrm{c}}.$$

(5.5)

If the fitness (hence connectivity) of node i is high enough to attract a significant part of the newcomer flow, the first term in (5.3) dominates at short time scales, and then the hub degree k _i increases exponentially. Connectivity patterns are then dominated by the growth by preferential attachment, ensuring, as in the BA model  [3], that the network will have a SF degree distribution. Moreover, the rate of increase of the connectivity:

$${\Delta }_{\mathrm{flow}}{k}_{\mathrm{i}}^{\mathrm{c}} = \frac{1} {2}m{\tau }_{\mathrm{D}} \frac{{f}_{i}} {{\sum \nolimits }_{j}{f}_{j}}$$

(5.6)

is larger for a defector hub by a factor b, because of its larger fitness, and then one should expect hubs to be mostly defectors, as confirmed by the results shown in Fig. 5.3. This small set of most connected defector nodes attracts most of the newcomer flow.

On the contrary, for nodes of intermediate degree, say of connectivity m ≪ k _i  ≪ k _max, the term Δ _flow f _i in (5.3) can be neglected, in other words, the arrival of new nodes is a rare event, so for a large time scale, we have that $\dot{{k}}_{i} = 0$. Note that if $\dot{{k}}_{i}(t) = 0$ for all t in an interval t ₀ ≤ t ≤ t ₀ + T, the size of the neighborhood is constant during that whole interval T, and thus the evolutionary dynamics of strategies through imitation is exclusively responsible for the strategic field configuration in the neighborhood of node i. During these periods, the probability distribution of strategies in the neighborhood of node i approaches that of a static network. Thus, recalling that the probability for this node i of intermediate degree to be a cooperator is large in the static regime [11], we then arrive to the conclusion that for these nodes the density of cooperators must reach a maximum, in agreement with Fig. 5.3. Of course, it is clear that this scenario can be occasionally subject to sudden avalanche-type perturbations following “punctuated equilibrium” patterns in the rare occasions in which a new node arrive.

Furthermore, our simulations show that these features of the shape of the curve P _c (k) are indeed preserved as time goes by, giving further support to the above argument based on time scale separation and confirming that our understanding of the mechanisms at work in the model is correct.

5 Clustering Coefficient and Degree–Degree Correlations

Apart from the degree distribution, we are also interested in exploring other topological features emerging from the interaction between network growth and the evolutionary dynamics in our EPA networks. Namely, we will focus on two important topological measures that describes the existence of nontrivial two-body and three-body correlations: the degree–degree correlations and the clustering coefficient respectively. We will show that the networks generated by the EPA model display both hierarchical clustering and disassortative degree–degree correlations.

5.1 Clustering Coefficient

The clustering coefficient of a given node i, cc _i , expresses the probability that two neighbors j and m of node i, are also connected. The value of cc _i is obtained by counting the actual number of edges, denoted by e _i , in ${\mathcal{G}}_{i}$, the subgraph induced by the k _i neighbors of i, and dividing this number by the maximum possible number of edges in ${\mathcal{G}}_{i}$:

$$c{c}_{i} = \frac{2{e}_{i}} {{k}_{i}({k}_{i} - 1)}.$$

(5.7)

The clustering coefficient of a given network, CC is calculated by averaging the individual values {cc _i } across the network nodes, $CC ={ \sum \nolimits }_{i}c{c}_{i}/N$. Therefore, the clustering coefficient CC measures the probability that two different neighbors of a same node, are also connected to each other. In the left panel of Fig. 5.4, we show the value of CC as a function of b and ε. In this figure, we observe that it is in the strong selection limit where the largest values of CC are obtained. Therefore, in this regime, not only highly heterogeneous networks are obtained but the nodes also display a large clusterization into neighborhoods of densely connected nodes. In the right panel of Fig. 5.4 we show the scaling of the clustering with the network size CC(N) in the strong selection limit. In this case, we observe that for b ≥ 2. 5 the value of CC is stationary while when b < 2. 5 the addition of new nodes in the network tends to decrease its clustering.

Fig. 5.4

(Left) Clustering coefficient CC as a function of b and ε. (Right) Scaling of CC with the network size for several values of b in the strong selection limit (ε = 0. 99). The networks are made up of N = 10³ nodes and have ⟨k⟩ = 4

We now focus on the dependence of the clustering coefficient CC with the degree of the nodes, k, in the strong selection limit (ε = 0. 99). Interestingly enough, we show in Fig. 5.5 that the dependence of CC(k) is consistent with a hierarchical organization expressed by the power law CC(k) ∼ k ^− β, a statistical feature found to describe many real-world networks [2]. The behavior of CC(k) in Fig. 5.5 can be understood by recalling that in scale-free networks, cooperators are not extinguished even for large values of b if they organize into clusters of cooperators that provide the group with a stable source of benefits [11]. To understand this feature in detail, let’s assume that a new node j arrives to the network: since the attachment probability depends on the payoff of the receiver, node j may link either to a defector hub or to a node belonging to a cooperator cluster. In the first scenario, it will receive less payoff than the hub, so it will sooner or later imitate its strategy, and therefore will get trapped playing as a defector with a payoff equal to f _j  = 0. Thus, node j will not be able to attract any links during the subsequent network growth. On the other hand if it attaches to a cooperator cluster and forms new connections with m elements of the cooperator cluster, two different outcomes are possible, depending on its initial strategy: if it plays as a defector, the triad may eventually be invaded by defectors and may end up in an state where the nodes have no capacity to receive new links. But if it plays as a cooperator, the group will be reinforced, both in its robustness against defector attacks and in its overall fitness to attract new links.

Fig. 5.5

Dependence of the clustering coefficient CC(k) ∼ k ^− β with the nodes’ degree for different values of b in the strong selection limit (ε = 0. 99). The networks are made up of N = 10³ nodes and have ⟨k⟩ = 4. The straight line is an eye guide that corresponds to k ^− 1. Reprinted from [38]

To sum up, playing as a cooperator while taking part in a successful (high fitness) cooperator cluster reinforces its future success, while playing as a defector undermines its future fitness and leads to dynamically and topologically frozen structures (it is to say, with f _i  = 0), so defection cannot take long-term advantage from cooperator clusters. Therefore, cooperator clusters that emerge from cooperator triads to which new cooperators are attached can then continue to grow if more cooperators are attracted or even if defectors attach to the nodes whose connectivity verifies k > mb. Moreover, the stability of cooperator clusters and its global fitness grow with their size, specially for their members with higher degree, and naturally favors the formation of triads among its components. Thus, it follows from the above mechanism that a node of degree k is a vertex of (k − 1) triangles, and then

$$CC(k) = \frac{k - 1} {k(k - 1)/2} = 2/k,$$

(5.8)

which is exactly the sort of functional form for the clustering coefficient we have found (Fig. 5.5).

5.2 Degree–Degree Correlations

Now we turn the attention to the degree–degree correlations of EPA networks. Degree–degree correlations are defined by the conditional probability, P(k ^′ | k), that a node of degree k is connected with a node of degree k ^′. However, since the computation of this probability yields very noisy results, it is difficult to assess whether degree–degree correlations exist in a given network topology. A useful measure to overcome this technical difficulty is to compute the average degree of the neighbors of nodes with degree k, K _nn(k), that is related with the probability P(k | k ^′) as

$${K}_{\mathrm{nn}}(k) ={ \sum \nolimits }_{{k}^{^\prime}}{k}^{'}P({k}^{'}\vert k).$$

(5.9)

In networks without degree–degree correlations the function K _nn(k) is flat whereas for degree–degree correlated networks the function is approximated by K _nn ∼ k ^ν and the sign of the exponent ν reveals the nature of the correlations. For assortative networks ν > 0 and nodes are connected to neighbors with similar degrees. On the other hand, for disassortative networks ν < 0, high degree nodes tend to be surrounded by low degree nodes.

In Fig. 5.6, we plot several functions K _nn(k) corresponding to different values of b in the strong selection limit. We observe that for all the cases there exist negative correlations that make highly connected nodes to be more likely connected to poorly connected nodes and viceversa. Therefore, the EPA topologies are disassortative while this behavior is enhanced as the temptation to defect, b, increases as observed from the slope of the curves in the log-log plot. This disassortative nature of EPA networks will be of relevance when analyzing the results presented in the following section.

Fig. 5.6

Degree–degree correlations among the nodes of the EPA networks. We plot the average nearest-neighbors degree K _nn(k) of a node of degree k for several values of the parameter b used to generate the networks. The networks are generated with ε = 0. 99, and have N = 4. 10³ nodes and ⟨k⟩. Note that negative correlations imply that hubs are not likely to be connected to each other

6 Dynamics on Static Networks Constructed Using the EPA Model

Up to this section we have analyzed the topology and the dynamics of the EPA networks while the growing process takes place. Now we adopt a different perspective by considering the networks as static substrates while studying the evolutionary dynamics of the nodes. This approach will be done in different ways allowing us to have a deeper insight on the EPA networks and their robustness.

6.1 Stopping Growth and Letting Evolutionary Dynamics Evolve

To confirm the robustness of the networks generated by Evolutionary Preferential Attachment, let us consider the realistic situation in which after incorporating a large number of participants, the network growth stops when a given size N is reached, and after that, only evolutionary dynamics takes place. The question we aim to address here is: will the cooperation observed during the coevolution process resist?

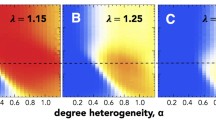
In Fig. 5.7, we compare the average level of cooperation ⟨c⟩ when the network just ceased growing with the same quantity computed after allowing the evolutionary dynamics to evolve many more time steps without attaching new nodes, ⟨c⟩ _∞ . The green area indicates the region of the parameter b where the level of cooperation increases with respect to that at the moment the network stops growing. On the contrary, the red zone shows that beyond a certain value, b _c , of the temptation to defect the cooperative behavior does not survive and the system dynamics evolves to an all-D state. Surprisingly, the cooperation is enhanced by the growth stop for a wide range of b values pointing out that the cooperation levels observed during growth are very robust. Moreover, the value of b _c appears to increase with the intensity of selection ε in agreement with the increase of the degree heterogeneity of the substrate network. These results highlight the phenomenological difference between playing the PD game simultaneously to the growth of the underlying network and playing on fixed static networks.

Fig. 5.7

Degree of cooperation when the last node of the network is incorporated, ⟨c⟩, and the average fraction of cooperators observed when the system is time-evolved ⟨c⟩ _∞ after the network growth ends. The four panels show these measures for several values of ε. From top to bottom and left to right we show ε = 0. 5, 0. 75, 0. 9, and 0. 99 (strong selection limit). The networks are made up of N = 10³ nodes with ⟨k⟩ = 4 and τ_D = 10τ_T. Every point is the average over 10³ realizations

6.2 Effects of Randomizations in the Evolutionary Dynamics

Now, in order to gain more insight in the relation between network topology and the supported level of cooperation, we study the evolution of cooperation when network growth is stopped and we make different randomizations of both the local structure and the strategies of the nodes. In particular, in Fig. 5.8, we show the asymptotic level of cooperation when the following randomizations are made after the growth is stopped: (1) the structure of the EPA network is randomized by rewiring its links while preserving the degree of each node; (2) the structure of the network is kept intact but the strategies of the nodes are reassigned while preserving the global fraction of cooperation (strategy randomization); and (3) when the two former randomization procedures are combined. Note that the randomization of the network structure is made by interchanging pair of links. This randomization, although preserves the degree distribution of the network destroys the degree correlations of the original EPA network and decreases significantly its clustering coefficient.

Fig. 5.8

Cooperation levels at the end of the growth process and after letting the network relax as a function of b. The original network was grown up to N = 4. 10³ nodes with ε = 0. 99 and ⟨k⟩ = 4, and the asymptotic cooperation levels are computed 10⁷ time steps afterwards. Full circles show the cooperation level when the network stops growing. The other curves show the asymptotic cooperation when the structure of the network has been randomized (triangles), when the strategies of the nodes have been reassigned randomly (squares) and with both randomizations processes (diamonds). Reprinted from [40]

As it can be seen from Fig. 5.8, the crucial factor for the cooperation increment during the size-fixed period of the dynamics is the structure of these EPA networks, since its randomization leads to an important decrease of cooperation at levels far away from those of the original one. This drop of cooperation when randomizing the structure is in good agreement with previous findings in complex topologies, specifically, for static BA networks [35,  41]. On the other hand, the strategy randomization procedure does not prevent high levels of cooperation, thus confirming that the governing factor of the network behavior is the structure arising from the co-evolutionary process. Moreover, the asymptotic level of cooperation in this case (squares in Fig. 5.8) is larger that those observed when the network is simply let to evolve without any randomization (C _∞ in Fig. 5.7). This result points out that using a random initial condition for the strategies differs strongly from starting from a configuration where degrees and strategies are correlated as a result of the EPA model (Fig. 5.3). We will come back to this point in Sect. 5.8.

6.3 EPA Networks as Substrates for Evolutionary Dynamics

The high levels of cooperation observed when applying a random initial configuration for the strategies to EPA networks motivate the question on whether EPA networks are best suited to support cooperative behavior than other well-known models. In order to answer this question, we consider our EPA networks when used as static substrates for the evolutionary dynamics and compare with the cases of both Barabási–Albert [3] and Erdős–Reńyi (ER) [42] graphs. To this aim, we take a particular example of our model networks, grown with b = 2. 1 and ε = 0. 99, and run the evolutionary dynamics starting from an initial configuration with 50% cooperators and defectors placed at random. The average level of cooperation as a function of the temptation to defect is represented in Fig. 5.9 together with the diagrams for BA and ER networks. Surprisingly, the plot shows that the EPA network remarkably enhances the survival of cooperation for all the values of b studied. Therefore, the attachment process followed by EPA networks is seen to be more efficient than the BA preferential attachment model studied in [9,  11,  14]. Obviously, the roots of this behavior cannot be found in the degree distribution, P(k), but in the high levels of clustering [43] and the disassortative mixing [44] shown above.

Fig. 5.9

Cooperation levels in ER, BA, and our Evolutionary Preferential Attachment network models, as a function of the temptation parameter b. The EPA network is built up using the model described in the main text for b = 2. 1 and ε = 0. 99. All networks are made up of N = 10³ nodes, with ⟨k⟩ = 4, and every point shown is the average over 10³ independent realizations. Reprinted from [40]

7 Time Evolution of the P _{{ c}} (k) After Network Growth

As we have already mentioned, it is widely known that SF topologies are able to sustain higher levels of cooperation than random structures, due to the microscopical organization of the strategies [9,  11]. In particular, it has been shown that in those heterogeneous settings the hubs always play as cooperators being surrounded by a unique cluster of cooperators, while defectors cannot take advantage of high connectivity, and thus occupy medium and low degree classes. Nonetheless, in our EPA structures, we have observed (Sect. 5.4) that during network grows, some hubs play as defectors, thus implying a very different scenario than that of static heterogeneous networks.

In this section, we turn again to the situation in which the network growth is stopped (and no randomization is made) to study the roots of the increment of the asymptotic level of cooperation observed in Fig. 5.7. To this aim, we look at the temporal evolution of the probability that a node of degree k is a cooperator, P _c (k), once the network growth has ceased. As we have observed in Sect. 5.4, the growth process leads to a concentration of cooperators at intermediate degree nodes, explained from the fact that while the network is growing, newcomers join in with the same probability of being cooperators or defectors. In this situation, defectors have an evolutionary advantage as they get higher payoffs from cooperator newcomers. Although these cooperators will subsequently change into defectors and stop providing payoff to the original defector, the stable source of fresh cooperator nodes entering the network compensates for this effect. However, when the growth stops while the dynamics continues, we observe from Fig. 5.10 that low degree nodes are rapidly taken over by cooperators, and after 10⁴ time steps they are mainly cooperators. On the contrary, hubs are much more resistant to change, and even after 10⁷ time steps not all of them have changed into cooperators (revealed by those values P _c (k) = 0 in Fig. 5.10).

Fig. 5.10

Probability of being a cooperator as a function of the degree at the end of the Evolutionary Preferential Attachment process, 10⁴ time steps later, and 10⁷ time steps later, for b = 2. 2 and ε = 0. 99. Reprinted from [40]

The persistence of hub defectors is a very striking observation, in contrast with previous findings in static SF networks [9,  41,  11], for which hubs are always cooperators or, in other words, a defector hub is unstable. This occurs because a defector seating on a hub will rapidly convert its neighbors to defectors, which in turn leaves it with zero payoff; subsequently, if one of its neighbors turns back to cooperation, the hub will eventually follow it. It seems, however, that the coupling of evolutionary game dynamics with the network growth leads to a structural configuration that stabilizes defection on hubs. The unexpected result that Fig. 5.10 shows is that defector hubs can also be asymptotically stable once the network growth has ceased. Indeed, we have observed in our simulations that hubs are defectors for as long as the dynamics continues (at least, t = 10⁷ generations after finishing growing the network). However, it is important to stress that not all realizations of the process end up with defector hubs. For low values of b, this is practically never the case and almost no realizations produce defectors at the hubs, but, as b increases, the percentage of realizations where this phenomenon is observed increases rapidly.

In Sect. 5.4, we have discussed why a hub can be a defector while the network is growing, because it takes advantage of the newcomer flow, getting high benefits from them. Nevertheless, the surprising fact that defector hubs may have very long lives on the static regime, may be the relevant feature for the cooperative behavior of the network resulting from the growth process, and thus it is important to fully understand the reason for such a slow dynamics. We next analyze this in detail.

8 Microscopic Roots of Cooperation After Network Growth

Having identified the coexistence of cooperator and defector hubs, we next study why this configuration seems to be asymptotically stable and why the hubs are not invaded by opposite strategies. In Fig. 5.11, we present the payoffs of cooperators and defectors as a function of their degree. This plot is taken from a single realization of the dynamics in which defector and cooperator hubs coexist asymptotically. As can be seen, the payoff grows approximately as a power law, f _k  ∼ k ^α; however, the key point here is not this law but the fact that the payoffs for defectors and cooperators of the same degree are very similar. In view of the strategy update rule (5.2), it becomes clear that the evolution must be very slow. Moreover, if we take into account the role of the degree in that expression, we see that hubs have a very low probability to change their strategies, whatever they may be.

Fig. 5.11

Average payoffs of cooperators and defector nodes at the end of network growth (t = 0) as a function of their degrees, k, for a realization of the Evolutionary Preferential Attachment model with b = 1. 8. Note that the similarity between cooperators’ and defectors’ payoffs implies that imitation events take place on a long time scale. Reprinted from [40]

Considering now the disassortative nature of the degree–degree correlations (Fig. 5.6) we can explain how these dynamical configurations can be promoted by the structure of the network. The large dissasortativity of EPA networks suggests that hubs are mostly surrounded by low degree nodes and not directly connected to other hubs. Instead, the connection with hubs is made in two steps (i.e. via a low degree node). This local configuration resembles that of the so-called Dipole Model [45], a configuration in which two hubs (not directly connected) are in contact with a large amount of common neighbors which in turn are low degree nodes. In this configuration, it can be shown analytically that the two hubs can coexist asymptotically with opposite strategies, provided that the hub playing as cooperator is in contact with an additional set of nodes playing as cooperators, for this will provide the hubs with a stable source of benefits. On the contrary, defector hubs are only connected to the set of nodes that are also in contact with the cooperator hubs. In this setting, the low degree individuals attached to both hubs experience cycles of cooperation and defection (we call them fluctuating individuals, because their strategies can never get fixed) due to the high payoffs obtained by the hubs. If such a local configuration for the strategies of hubs and their leaves arises, neither of the two hubs will take over the set of fluctuating individuals, nor the latter will invade the hubs as they are mainly lowly connected nodes with small payoffs.

In order to test if the grown networks exhibit local dipole-like structures, we have measured the connectivity of the neighbors of defector and cooperator hubs, which we represent in Fig. 5.12. The figure undoubtedly shows that highly connected nodes playing as defectors are mainly connected to poorly connected cooperators (acting as the set of fluctuating strategists), whereas cooperator hubs are connected to each other and also to a significant fraction of lowly connected nodes. This fully confirms that, in contrast to all previous results, there is a structure allowing the resilience of defector hubs, and moreover, it gives rise to a situation quite similar to that described by the Dipole Model.

Fig. 5.12

Connectivity matrix of cooperators with defectors (Left) and of cooperators with themselves (Right). The element (i, j) is set to 1 (black square in the figure) when a link between a defector (cooperator) of degree i and a cooperator (cooperator) of degree j exists, respectively. Reprinted from [40]

9 Conclusions

In this chapter we have presented a model in which the rules governing the formation of the network are linked to the dynamics of its components. This model provides an evolutionary explanation for the origin of the two most common types of networks found in natural systems: when the selection pressure is weak, homogeneous networks arise, whereas strong selection pressure gives rise to scale-free networks. A remarkable fact is that the proposed evolution rule gives rise to complex networks that share some topological features with those measured in real systems, such as the power law dependence of the clustering coefficient with the degree of the nodes. Interestingly, our results shows that the microscopic dynamical organization of strategists in EPA networks is very different from the case in which the population evolves on static networks. Namely, there can be hubs playing as defectors during network growth, while cooperators occupy mainly the middle classes. It is worth stressing that the level of cooperation during network growth reach the largest values for the strong selection limit in which the newcomers launch their links to those fittest elements of the system.

Furthermore, the generated networks are robust in the sense that after the growth process stops, the cooperative behavior remains. Moreover, we have shown that for most cases the cooperative behavior increases when network growth is stopped. We have also shown that the non-trivial topological patterns of EPA networks are the roots for such enhancement of the cooperation. In particular, we have shown that rewiring the links while keeping the degree distribution (thus destroying any kind of correlations between nodes) yields a dramatic decrease of the levels of cooperation. On the other hand, a randomization of the strategies does not affect the asymptotic levels of cooperation. Therefore, the ability of EPA networks to promote the resilience of cooperation is rooted in the correlations created during network formation via the coevolution with evolutionary dynamics.

Maybe the most important difference we have found between the evolutionary dynamics on top of EPA networks and that on top of well-known model networks is the dynamic stabilization of defectors on hubs, long after the growth has finished. We have shown that these defector hubs can be extremely long-lived due to the similarity of payoffs between cooperators and defectors arising from the co-evolutionary process. Moreover, we have been able to link the payoff distribution to the network structure. In particular, we show that the disassortative nature of EPA networks together with the formation of local dipole-like structures during network growth is responsible for the fixation of defection in hubs.

Finally, the coevolutionary perspective presented in this chapter has focused on the formation of a complex system rather than being applied to the rewiring of links in already formed systems. Given the simplicity of the formulation presented here we thus expect that the model will contribute to explain other realistic scenarios in which the dynamical states of the constituents of a complex system coevolve with its formation.