1 Introduction

The evolution of cooperation has been a long-standing open question in the fields of economics, biology, and social science [5, 13, 21, 33]. Evolutionary Game Theory (EGT) since its birth [28, 29], has been developed as one of the most suitable tools in the study of the emergence of cooperation within a group of selfish players. Traditionally, EGT is studied mostly under the context of well-mixed populations. Nonetheless, as the study and applications of network theory have been arising overwhelmingly in the literature as well as in industry recently, following the seminal work of [23], evolutionary games on networks start to receive a significant amount of attention from researchers of various disciplines [1, 2, 10, 11, 14, 18, 22, 24,25,26, 30, 31]. Specifically, as social networks are often modeled as complex networks such as small-world networks [34] and scale-free networks [7], EGT on complex networks has also drawn massive research interest in recent years [4, 15, 27, 32]. A considerable amount of the research effort has been extensions of models that exist for well-mixed populations to the case of populations with spatial structure, especially for simpler spatial structures such as lattice and regular graph [10, 23,24,25, 31], and are typically frequency-based and aim at finding conditions and mechanisms that promotes cooperation [2, 4, 15, 17].

Moreover, the players are often considered homogeneous, or in other cases the player heterogeneity is typically reflected by the types or the update strategies of players that are often exogenous and pre-defined [3, 36]. Heterogeneous population was introduced by [26] as a notion opposed to well-mixed populations, and the heterogeneity only affects the selection of interacting players but not the payoff of the player involved. [3] discussed the evolutionary dynamics of a heterogeneous population in the sense that the population is split into several portions, each of which maintains a distinct updating process. [36]considered the case where each player is associated with an updating strategy that is selected from a finite set of pre-defined strategies.

On the other hand, focusing on the influence of network itself, [35] revealed the relationship between some network characteristics and the distribution of player actions in a specific subset of game types. Besides, [16] investigated the relation between fixation probability and degree under weak selection and concluded that a crucial factor affecting the fixation probability is the degree of the invader. It should be noted that such perspective is rarely highlighted in the literature where the impact of structural characteristics on evolutionary dynamics is emphasized. Typically, the heterogeneity of players is described as an exogenous property instead of a property coming from the network structure, and the study on the affect of such heterogeneity on the payoffs received by the players is also lacking.

Nonetheless, numerous examples can be found in real-world networks that show implications of the impact of structural heterogeneity on evolutionary dynamics. For instance, in social networks an individual with a large amount of links (e.g., followers as in twitter or facebook) are quite often considered celebrities. The interaction or cooperation between two celebrities more likely brings greater consequences to themselves compared to the case of one celebrity and one non-celebrity player or two one non-celebrity players. In this case, the prestige of player is represented by the number of connections that directly link to it, or its degree in the network.

In this paper, we attempt to emphasize on the structural heterogeneity of players in evolutionary dynamics. We propose a model for evolutionary games on networks with the help of adjacency matrix. The heterogeneity of each player inherited from network structure is characterized by the so-called centrality measures, which can be calculated using adjacency matrix. The impact of centrality of invader on evolutionary dynamics is analyzed through the fixation probability of a single cooperator theoretically as well as in simulations. In simulation, several different centrality measures are compared under different game types, network types, and selection strengths. Results show that the fixation probability of cooperation largely depends on the centrality of the invader, regardless of other factors. Additionally, for each centrality measure the relation between centrality and fixation probability shows a distinct pattern, and this pattern varies for different network types and game types.

Among the findings, the most notable one is that while using the proposed adapted payoff, for all three game types we tested (Prisoner’s Dilemma, coexistence game and coordination game), in both scale-free networks and small-world networks, choosing the player with maximum betweenness centrality as invader significantly increases the fixation probability of cooperation. This not only reveals the important role of structural heterogeneity in evolutionary dynamics in complex networks, but also potentially gives us a structural explanation of how cooperation emerges in human society. Furthermore, it also leads us to possible directives that can help promote cooperation in various human economical, political and social networks.

2 Model

Consider a network \(G = (N, E)\) with \(N=\{1, \ldots , n\}\) being the set of vertices and E being the set of edges. Each vertex in N represents a player, and each edge in E indicates that the two linked players can engage in a 2-player symmetric game. We use ij to denote an edge between i and j for any distinct \(i, j \in N\). Then i and j are called neighbors of each other if the edge ij exists. The set of neighbors of any vertex \(i \in N\) is denoted \(N_i\), and hence \(n_i = |N_i|\) is the degree of i. In this paper, we assume \(n_i >0\) for all \(i \in N\), since otherwise there exist some isolated players that neither have any interaction with any other player, nor have any impact on the game dynamics.

The adjacency matrix of G, denoted A, is then defined as \(A = [a_{ij}]\) such that

$$\begin{aligned} a_{ij} = \left\{ \begin{array}{ll} 1,&{} \quad \text {if }ij \in E, \\ 0,&{} \quad \text {otherwise.} \end{array} \right. \end{aligned}$$

Note that G is assumed to be simple and undirected, thus \(a_{ii} = 0\) for any \(i \in N\) and \(a_{ij}=a_{ji}\) for any \(i,j\in N\).

Consider a 2-player symmetric game where players can be one of two types in \(S= \{C, D\}\), in which C represents cooperation and D represents defection. A \(2 \times 2\) payoff matrix U is defined as follows

$$\begin{aligned} \begin{array}{c|cc} &{} \hbox {C} &{} \hbox {D}\\ \hline \hbox {C} &{} u_{CC} &{} u_{CD}\\ \hbox {D} &{} u_{DC} &{} u_{DD} \end{array} \end{aligned}$$

where \(u_{s_1s_2}\) represents the payoff a player of type \(s_1\) gets playing against a player of type \(s_2\), for \(s_1, s_2 \in S\). Let \(\mathbf {s}: N \rightarrow S\) be types of players in N. Particularly, we use \(s_i\) to denote the type of player \(i \in N\).

Traditionally, the payoff that player i receives while playing against another player j is

$$\begin{aligned} f'_{ij} = a_{ij}u_{s_i s_j}. \end{aligned}$$
(1)

The coefficient \(a_{ij}\) here guarantees that they can only interact if they are neighbors. The accumulated payoff of player i is then

$$\begin{aligned} f'_i = \sum \limits _{j=1}^n a_{ij}u_{s_i s_j}. \end{aligned}$$

Alternatively, as shown in many real-world instances, the scale of the result of interaction is usually related to the scale of the entities involved in the interaction. In other words, interaction between large or powerful entities tends to have a more impactful result, regardless of the result being positive or negative. Examples of such mechanics can be easily found in the economic or political world. For instance, the interaction of two large corporations or political entities will naturally produce larger economic or political consequences compared to two smaller ones.

Therefore, in order to incorporate player prestige and network structure into games as well as evolutionary dynamics, each vertex is given a parameter, namely centrality, that is a measure of importance of vertices within a graph. Generally, centrality can be denoted as

$$\begin{aligned} \mathbf {c}: N \rightarrow {\mathbb {R}}. \end{aligned}$$

As the definition of ‘importance’ heavily depends on the actual application, many different centrality measures have been introduced in the literature for different application purposes [6, 8, 9, 19, 20]. In fact, degree is often considered the conceptually simplest centrality measure, as we can define the degree centrality \(\mathbf {c}^d\) as in the following equation.

$$\begin{aligned} c^d_i = n_i \quad \text { for } i \in N. \end{aligned}$$

Besides degree, in this paper we consider three other centrality measures, betweenness centrality, closeness centrality and eigenvector centrality.

Betweenness centrality \(\mathbf {c}^b\) is defined based on the shortest paths in the graph.

$$\begin{aligned} c^b_i = \sum \limits _{j\ne i \ne k}\frac{\sigma _{jk}(i)}{\sigma _{jk}}\quad \text {for } i \in N, \end{aligned}$$

where \(\sigma _{jk}\) is the total number of shortest paths from vertex j to vertex k and \(\sigma _{jk}(i)\) is the number of those paths that pass through i. Intuitively, betweenness centrality ranks vertices by the number of shortest paths that pass through each of them.

Closeness centrality \(\mathbf {c}^c\) is defined based on the distance between vertices. The closeness centrality is then

$$\begin{aligned} c^c_i = \frac{1}{\sum \limits _{j\ne i}d_{ij}}\quad \text {for } i \in N, \end{aligned}$$

where \(d_{ij}\) is the distance between i and j and is equal to the edge number of the shortest path between i and j. As it can be seen from its definition, closeness centrality ranks a vertex by the distances of the given vertex to all other vertices.

Eigenvector centrality is defined as a vector \(\mathbf {c}^e\) that satisfies

$$\begin{aligned} A\mathbf {c}^e = \lambda _1\mathbf {c}^e, \end{aligned}$$

where \(\lambda _1\) is the largest eigenvalue of the adjacency matrix A. Generally, a vertex with high eigenvector centrality means that it is connected to many other vertices who have high eigenvector centralities.

Based on centrality \(\mathbf {c}\), we propose the following adapted payoff

$$\begin{aligned} f_{ij} = a_{ij}c_ic_j u_{s_i s_j}. \end{aligned}$$
(2)

Intuitively, the payoffs of two interacting players not only depend on their types but also depend on their combined prestige in the form of the product of their centralities. Accordingly, for each centrality measure, the adapted payoff is denoted by \(f^b, f^c, f^d, f^e\), each of which corresponds to \(\mathbf {c}^b, \mathbf {c}^c, \mathbf {c}^d, \mathbf {c}^e\), respectively.

As a result, the adapted accumulated payoff of any player i with centrality \(\mathbf {c}\) is

$$\begin{aligned} f_i = c_i\sum \limits _{j=1}^n a_{ij}c_j u_{s_i s_j}. \end{aligned}$$
(3)

In order to distinguish from the adapted payoff, hereafter the payoff defined in (1) is referred to as the traditional payoff.

In this work, through computational simulation on complex networks, the impact of the incorporation of centrality on the evolutionary dynamics is evaluated. The performance of the aforementioned centrality measures is also compared.

3 Imitation Dynamics

In this paper we consider an imitation process, where in each round a focus player is selected uniformly at random, and its imitation target is selected uniformly at random among its neighbors. The focus player imitates its target with the probability calculated from the following Fermi function

$$\begin{aligned} q_{ij} = \frac{1}{1+e^{-\beta (f_j - f_i)}}, \end{aligned}$$

where \(\beta \ge 0\) is the selection strength, and \(f_i\) and \(f_j\) are calculated using (3). Intuitively, a player of lower accumulated payoff (or fitness in biological context) tends to imitate a player of higher accumulated payoff.

Assuming that the underlying network remains unchanged, the state of the evolutionary game can be described by the vector that consists of types of each player,

$$\begin{aligned} \mathbf {s}=\{s_i\in S: i\in N\}. \end{aligned}$$

The state space is then denoted by \(\chi =S^n\). Hereafter, the two types C and D are assigned with scalars as \(S=\{0, 1\}\), where 0 represents D and 1 represents C. Since it is a Moran process and the transition is time independent, the transition probability between any two states \(\mathbf {s}, \mathbf {s}'\in \chi \) is nonzero only if the Euclidean distance between the two vectors is less than or equal to 1 as is stated by the following equation

$$\begin{aligned} P_{\mathbf {s} \rightarrow \mathbf {s}'} = 0 \quad \text { if } d(\mathbf {s}, \mathbf {s}') > 1, \end{aligned}$$

where \(d(\mathbf {s}, \mathbf {s}')\) is the Euclidean distance between \(\mathbf {s}\) and \(\mathbf {s}'\), i.e.,

$$\begin{aligned} d(\mathbf {s}, \mathbf {s}')=\sqrt{\sum _{i\in N}(s_i-s'_i)^2 }. \end{aligned}$$

Given a state \(\mathbf {s} \in \chi \), let \(\mathbf {s}^i\) be the state where player i switching its type while others remaining the same, i.e.,

$$\begin{aligned}&d(\mathbf {s}, \mathbf {s}^i)=1,\\&s_i+s^i_i=1. \end{aligned}$$

Analogically, \(\mathbf {0}^i\) is used to denote the state where the type of player i is 1 and all other players have type 0. The transition probability from \(\mathbf {s}\) to \(\mathbf {s}^i\) can be calculated as

$$\begin{aligned} P_{\mathbf {s}\rightarrow \mathbf {s}^i} = \frac{1}{nn_i}\sum _{j\in N_i}|s_i-s_j|q_{ij} = \frac{1}{nn_i}\sum _{j\in N}|s_i-s_j|a_{ij}q_{ij}. \end{aligned}$$

One can then derive the transition probability of a state \(\mathbf {s}\) to itself as follows.

$$\begin{aligned} P_{\mathbf {s} \rightarrow \mathbf {s}}= 1- \sum \limits _{i\in N}P_{\mathbf {s}\rightarrow \mathbf {s}^i}. \end{aligned}$$

An important note is that, for the states of all defection (\(\mathbf {0}\)) and all cooperation (\(\mathbf {1}\)), one has

$$\begin{aligned} P_{\mathbf {1} \rightarrow \mathbf {1}}&= 1,\\ P_{\mathbf {0} \rightarrow \mathbf {0}}&= 1. \end{aligned}$$

Notably, this process can be described as an absorbing Markov chain [12] with \(2^n-2\) transient states and two absorbing states \(\mathbf {0}\) and \( \mathbf {1}\). Hence P is a \(2^n \times 2^n\) transition matrix for the said absorbing Markov chain. Alternatively, one can write P in the form of

$$\begin{aligned} P= \begin{pmatrix} Q &{}R\\ \mathbf {0} &{}I_r \end{pmatrix}, \end{aligned}$$

where Q is a \((2^n-2)\times (2^n-2)\) matrix, R is a \((2^n-2)\times 2\) matrix, \(\mathbf {0}\) is a \(2 \times (2^n-2)\) zero matrix, and \(I_r\) is the \(2 \times 2\) identity matrix. Specifically, Q contains the transition probabilities among transient states, R contains the transition probabilities from transient states to the two absorbing states \(\mathbf {0}\) and \(\mathbf {1}\).

Consequently, the probability of transitioning from the i-th transient state to the j-th transient state in exactly k steps is the (i, j)-entry of \(Q^k\). The fundamental matrix M is defined as the summation of \(Q^k\) for all possible k,

$$\begin{aligned} M=\sum \limits _{k=0}^{\infty }Q^k = (I_t-Q)^{-1}, \end{aligned}$$

where \(I_t\) is the \((2^n-2) \times (2^n - 2)\) identity matrix. The (i, j)-entry of matrix M is the expected number of times the absorbing Markov chain is in the j-th transient state, given that the chain started in the i-th transient state.

As we mainly focus on the fixation probability of cooperation, without loss of generality, we assume that the first n rows/columns of P correspond to the states \(\mathbf {0}^1, \ldots , \mathbf {0}^n\), respectively, and the \(2^n\)-th row/column corresponds to the absorbing state \(\mathbf {1}\). One can also rewrite R as

$$\begin{aligned} R= \begin{pmatrix} R^{\mathbf {0}}&\quad R^{\mathbf {1}} \end{pmatrix}, \end{aligned}$$

where \(R^{\mathbf {0}}\) and \(R^{\mathbf {1}}\) are column vectors of length \(2^n-2\) that consists of transition probabilities from transient states to the two absorbing states \(\mathbf {0}\) and \(\mathbf {1}\), respectively. The fixation probability of cooperation can then be calculated via the following vector

$$\begin{aligned} B^{\mathbf {1}}=MR^{\mathbf {1}}. \end{aligned}$$

The first n elements of \(B^{\mathbf {1}}\) corresponds to the fixation probability of cooperation starting with the states \(\mathbf {0}^1, \ldots , \mathbf {0}^n\), respectively. In other words, if player i is chosen as the invader, the fixation probability, or the probability of the absorbing Markov chain ending in the state of all cooperation (i.e., \(\mathbf {1}\)) is then

$$\begin{aligned} p_i=B^{\mathbf {1}}_i\quad \text {for }i \in \{1, \cdots , n\}. \end{aligned}$$

As a result, the average fixation probability of cooperation is

$$\begin{aligned} \overline{p}=\frac{1}{n}\sum \limits _{i=1}^nB^{\mathbf {1}}_i. \end{aligned}$$

In the next section, the fixation probability is evaluated through intensive computational simulations. We explore whether there is a correspondence between the centrality of the invader \(c_i\) and the fixation probability \(p_i\), and if yes how does such correspondence change as different aspects of the evolutionary game change. Besides, as centrality measures are best at identifying the most important vertices in a network, it is also worth investigating what is the difference between the average fixation probability of invaders with maximum centrality (denoted \(\overline{p}_m\) hereafter) and average fixation probability \(\overline{p}\).

4 Simulation Results

We vary six aspects of the evolutionary game in the simulation, including payoff type, game type, network type, selection strength, network size and centrality scale. Firstly the performances of traditional payoff and adapted payoff are compared briefly. Then we test on two types of complex networks including scale-free networks and small-world networks. Three different types of game configuration are considered, including Prisoner’s Dilemma, coexistence game, and coordination game. Particularly, the utility matrix is set as

$$\begin{aligned} \begin{array}{c|cc} &{} \hbox {C} &{} \hbox {D}\\ \hline \hbox {C} &{} 1 &{} 0\\ \hbox {D} &{}2 &{} 0.8 \end{array} \end{aligned}$$

for Prisoner’s Dilemma,

$$\begin{aligned} \begin{array}{c|cc} &{} \hbox {C} &{} \hbox {D}\\ \hline \hbox {C} &{} 1 &{} 1.6\\ \hbox {D} &{}2 &{} 1 \end{array} \end{aligned}$$

for coexistence game, and

$$\begin{aligned} \begin{array}{c|cc} &{} \hbox {C} &{} \hbox {D}\\ \hbox {C} &{} 2 &{} 1.2\\ \hbox {D} &{}1.6 &{} 2 \end{array} \end{aligned}$$

for coordination game.

Additionally, the model is tested under six different selection strengths including 0.001, 0.01, 0.1, 1, 10 and 100, and in populations of size 100, 300, 500 and 700. More than \(10^4\) runs are executed per graph in order to obtain the fixation probability.

4.1 On Scale-Free Networks

Scale-free networks are generated according to the preferential attachment model proposed by [7]. The generation process starts with a complete graph of \(m_0\) vertices and then adds one vertex that connects with m existing vertices until the number of vertices reaches the desired value. The probability of the new vertex connecting with an “old” vertex is depending on the number of neighbors the old vertex already has. Hence, it is called the preferential attachment, as vertices with higher degrees have higher probability to be selected as the neighbors of new vertex, which in turn will increase their degrees. This results in the phenomenon of “the rich gets richer”, which eventually leads to the power law distribution of degree in the scale-free network. In our simulation, we set \(m_0=4\), \(m=2\).

Figure 1 shows an example run on one graph that showcases the relation between fixation probability and centrality of invader on scale-free networks under selection strength \(\beta =0.01\) and with population size of 100. We study the relation between centrality of the invader and the fixation probability in different games with traditional payoff and adapted payoff. The relation between centrality of the invader and the fixation probability shows similar patterns across all three game types. Rather, the said relation varies as the payoff changes from the traditional payoff (1) to the adapted payoff (2).

Fig. 1
figure 1

Fixation probability and centrality of invader on scale-free networks with \(n=100\) and \(\beta =0.01\) in an example run. a, c, e are with traditional payoff; b, d, f are with adapted payoff; a, b are results with Prisoner’s Dilemma; c, d are with coexistence game; e, f are with coordination game; Centrality is normalized between 0 and 1 for all centrality measures

Full size image

While using traditional payoff, for all four aforementioned centrality measures \(\mathbf {c}^b, \mathbf {c}^c, \mathbf {c}^d, \mathbf {c}^e\), the fixation probability and centrality of invader showed a positively linear relationship approximately. On the other hand, using adapted payoff has yielded a different pattern. For closeness centrality and eigenvector centrality, the relation between the fixation probability and centrality of invader remains linear. However, for betweenness centrality and degree, the fixation probability exhibits an exponential growth with regard to centrality in most cases.

Table 1 displays the average fixation probability \(\overline{p}\) and the fixation probability of the players of maximum centrality \(\overline{p}_m\) on scale-free networks for the adapted payoff with all four centrality measures. All the data are averaged over test results on 100 different graphs. For all four cases using adapted payoff, the fixation probability \(\overline{p}_m\) is significantly larger than the average fixation probability \(\overline{p}\), especially for the cases with betweenness centrality and degree.

Table 1 Average fixation probability \(\overline{p}\) and fixation probability for the player of maximum centrality \(\overline{p}_m\) on scale-free networks with \(n=100\) and \(\beta =0.01\)
Full size table

Next we investigate the difference between \(\overline{p}\) and \(\overline{p}_m\) under different selection strengths and population sizes. The result is generally consistent in different settings of selection strengths and population sizes, as it is shown in Fig. 2. Similar to the example in Fig. 1, the fixation probability of the players with maximum centrality is significantly higher than average for all four centrality measures. Nonetheless, with the adapted payoff using betweenness centrality and degree the gap between \(\overline{p}\) and \(\overline{p}_m\) is even larger than thereof closeness centrality and eigenvector centrality. Moreover, with the adapted payoff using betweenness centrality and degree, the fixation probability \(\overline{p}_m\) maintains at a very high level throughout all the cases that have been tested.

Fig. 2
figure 2

Fixation probability under different selection strengths and population sizes on scale-free networks. a, c, e compare the average fixation probability and the fixation probability of maximum centrality player in three game types under different selection strengths; b, d, f serve the same purpose but under different network sizes, where the selection strength is fixed at 0.01. Note that the axes are in logarithmic scale

Full size image
Fig. 3
figure 3

Fixation probability and centrality of invader on small-world networks with \(n=100\) and \(\beta =0.01\) in an example run. Same setup is used as for scale-free networks. a, c, e are with traditional payoff; b, d, f are with adapted payoff; a, b are results with Prisoner’s Dilemma; c, d are with coexistence game; e, f are with coordination game; centrality is normalized between 0 and 1 for all centrality measures

Full size image

4.2 On Small-World Networks

Small-world networks used in this paper are generated using the method as described in [34]. The generation process starts with a ring lattice with each vertex having 2K neighbors, then for each vertex, it precedes to rewire each of its incident edges according to probability \(\alpha \in [0, 1]\). Here \(\alpha \) can also be deemed as the randomness of the generated small-world network, and \(\alpha =1\) indicates that a random network is generated. In this paper, \(K = 3\) and \(\alpha = 0.4\) is used for the simulation if it is unspecified. Besides, we also run simulations to see if the rewiring probability \(\alpha \) or the average degree 2K has a significant impact on the fixation probability.

Figure 3 demonstrates the result of an example run on a small-world network. Using traditional payoff, the relation between fixation probability and centrality of invader is vaguer comparing to the case of scale-free network. However, in a few cases, an ascending trend of fixation probability can still be observed when centrality of invader increases. Using adapted payoff, we obtained similar results to the case of traditional payoff except for the one using betweenness centrality. Using betweenness centrality, the fixation probability is significantly higher if the invader has the maximum centrality than in any other case.

This trend is further validated by the follow-up tests on multiple graphs using adapted payoff, as shown in Table 2.

Table 2 Average fixation probability and fixation probability for the player of maximum centrality on small-world networks with \(n=100\) and \(\beta =0.01\)
Full size table

For betweenness centrality, \(\overline{p}_m\) retains its superior performance over the average fixation probability \(\overline{p}\). Besides, for eigenvector centrality, \(\overline{p}_m\) also holds a slight advantage over \(\overline{p}\). Notably, for the adapted payoff using degree as centrality measure, in the test runs we performed, the invader never succeeded in taking over the network, regardless of its centrality. This pattern shifts only when the selection strength increases to a relatively high level, which is shown in Fig. 4. Other than that, the result is mostly consistent through the changes made on selection strength and network size according to Fig. 4. It is worth noting that the decreasing trend of \(\overline{p}_m\) as the network size increases can be deemed reasonable and intuitive, in reference to the case of well-mixed population.

Fig. 4
figure 4

Fixation probability under different selection strengths and population sizes on small-world networks with \(n=100\). a, c, e compare the average fixation probability and the fixation probability of maximum centrality player in three game types under different selection strengths; b, d, f serve the same purpose but under different network sizes, where the selection strength is fixed at 0.01

Full size image

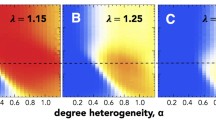
Additionally, adjusting the rewiring probability \(\alpha \) in the construction of small-world networks can give us a series of networks that ranging from regular graphs to random graphs. Thus, it is also interesting to evaluate how the rewiring probability affects the simulation results. Besides, we also provide simulation results for small-world networks with different average degrees. Figure 5 shows the simulation results for different rewiring probabilities and average degrees, where the small-world networks have 100 nodes and selection strength is fixed at 0.01. Notably, both \(\overline{p}\) and \(\overline{p}_m\) remain at a very low level for the three centrality measures other than betweenness centrality, except for the case of degree centrality with average degree being 12. Besides, with rewiring probability changing from 0.2 to 0.4, or average degree changing from 4 to 6, there is a significant increase for the fixation probability of \(\overline{p}_m\) in the case of betweenness centrality in all three game types.

Fig. 5
figure 5

Fixation probability under different rewiring probabilities and average degrees on small-world networks with \(n=100\). a, c, e compare the average fixation probability and the fixation probability of maximum centrality player in three game types under different rewiring probabilities, where the average degree is 6; b, d, f serve the same purpose but under different average degrees, and rewiring probability is fixed at 0.4

Full size image

4.3 Discussion

To summarize, our simulation attempts to investigate the relationship between centrality of invaders and fixation probability under imitation dynamics on complex networks from four different angles, payoff function, centrality measure, game type, and graph type.

Using traditional payoff, the fixation probability of cooperation has a positively linear relation to the centrality of the invader, in all cases for all four aforementioned centrality measures and for both scale-free and small-world networks.

Using the proposed adapted payoff, the relation between the fixation probability of cooperation and the centrality showed different patterns. For scale-free networks, the fixation probability of the players of max centrality \(\overline{p}_m\) is significantly higher than the average fixation probability \(\overline{p}\), for all four centrality measures. Among them, betweenness centrality and degree have much higher level of fixation probability and the gap between \(\overline{p}_m\) and \(\overline{p}\) is much larger. Such relation holds consistently under different selection strengths and network sizes.

Fig. 6
figure 6

Centrality distribution in a scale-free network with 100 nodes. The red line in each graph indicates the corresponding average centrality

Full size image
Fig. 7
figure 7

Centrality distribution in a small-world network with 100 nodes, rewiring probability of 0.4, and average degree of 6. The red line in each graph indicates the corresponding average centrality

Full size image
Fig. 8
figure 8

Fixation probability under different scales of normalized centrality on scale-free and small-world networks with \(n=100\). a, c, e compare the average fixation probability and the fixation probability of maximum centrality player in three game types under different scales of normalized centrality on scale-free networks. Analogously, b, d, f are the results for small-world networks

Full size image

On small-world networks, \(\overline{p}_m\) only displays superiority over the average fixation probability \(\overline{p}\) for betweenness centrality. For other three centrality measures, there is no significant advantage in choosing players of max centrality as invaders in terms of fixation probability. Such result is also proved to be generally consistent under different selection strengths and network sizes, and under most part of the range of rewiring probabilities and average degrees that has been tested.

The simulation results obtained on scale-free and small-world networks have raised some questions on the patterns of the difference between \(\overline{p}\) and \(\overline{p}_m\). It is particularly interesting that why \(\overline{p}_m\) is significantly larger than \(\overline{p}\) in the cases of betweenness centrality on both scale-free networks and small-world networks, and degree centrality on scale-free networks. One common trait these three cases have is that the absolute values of centrality are larger than the other cases, and there is a relatively larger disparity between the maximum centrality and the average centrality, as shown in Figs. 6 and 7.

Therefore, it is worth to compare the previous results with the performance of the centrality measures that are normalized to the same range. Moreover, as the scale of the normalized centrality may have an impact on the fixation probability as well. Particularly, the centralities of nodes in a network are normalized to the range of [0, C], where the maximum centrality is normalized to C. In this case, we call C the scale of the normalization, and consider three different scales, 1, 10, 100. The results are presented in Fig. 8. Results show that an increase in the scale of normalization mostly likely results in an increase of \(\overline{p}_m\). For \(\overline{p}\), it is only seen significant increase in the case of coexistence game on small-world networks as the scale increases. Potentially, it means that only when there is a large difference between maximum centrality and average centrality, \(\overline{p}_m\) would have a dominant advantage over \(\overline{p}\). Intuitively, the selected centrality measure should create a sufficiently large disparity between the most prestigious nodes and the average, to be able boost the fixation probability when they are the invaders.

5 Conclusion

This paper studied the impact of player heterogeneity from network structure on evolutionary dynamics in complex networks. Player heterogeneity is described by centrality measures which can be calculated using the adjacency matrix of the underlying network. An evolutionary game model is proposed which incorporates centrality. Essentially, the model highlights the effect of player heterogeneity in evolutionary dynamics by proposing an adapted payoff function that is not only related to the utility matrix but also related to the centrality of its opponent and itself.

Via computational simulation, we showed that using traditional payoff, the fixation probability and the centrality of the invading player generally have a positive linear relationship regardless of which centrality measure is used. However, when using the proposed adapted payoff that incorporates centrality, results vary for distinct centrality measures and network types. For closeness centrality and eigenvector centrality on scale-free networks, the results are similar to the case using traditional payoff. For betweenness centrality and degree on scale-free networks, the relation between fixation probability and centrality exhibits an exponential pattern, where the fixation probability of players with maximum betweenness centrality is significantly higher than the average fixation probability. For small-world networks, the relation between fixation probability and centrality is not as clear as in the case of scale-free networks. However, the fixation probability of players with maximum betweenness centrality still holds a significant advantage over the average. In order to have a better understanding of the simulation results, further test on the scale of normalization of the centrality has been executed. Results show that the increase of the scale of the centrality generally causes the fixation probability to increase, especially for the fixation probability of the players with maximum centrality.

The characteristic of complex networks, adapted payoff and imitation dynamics can shed some light on the emergence of cooperation in human society, or potentially be applied in real world practices.

It provides a new perspective on how cooperation is formed in society that is composed mostly of selfish individuals. As most social networks have scale-free or small-world property, potentially the heterogeneity from network structure played an important role in the evolution of cooperation in the said networks, in a way such that the players with high (e.g., betweenness) centrality started the trend of cooperation as a result of some external factors, and the rest of the society just followed through.

Besides, the results might provide valuable directive instructions for the promotion of cooperation in applications that align with our model. For instance, in certain complex networks (economical or political), if the administrator needs to promote cooperation, then according to our results one should always prioritize the players with higher centrality. Moreover, if the player with maximum betweenness centrality can be targeted in a scale-free or small-world network, cooperation is heavily favored by selection assuming other factors are omitted or insignificant. Knowing that, when one needs to promote cooperation in a social network, it is generally much more beneficial to prioritize the players with maximum centrality than some random players, although the centrality measure should be carefully selected depending on the application, and the disparity represented by the centrality measure should be sufficiently large.