Chain Sampling

Abstract

A brief introduction to the concept of chain sampling for quality inspection is first presented. The chain sampling plan of type ChSP-1 selectively chains the past inspection results. A discussion on the design and application of ChSP-1 plans is presented in the second section of this chapter. Various extensions of chain sampling plans such as ChSP-4 plan are discussed in the third part. Representation of the ChSP-1 plan as a two-stage cumulative results criterion plan and its design are discussed in the fourth part. The fifth section relates to the modification of ChSP-1 plan which results in sampling economy. The sixth section of this chapter is on the relationship between chain/dependent sampling and deferred sentencing type of plans. A review of sampling inspection plans that are based on the ideas of chain or dependent sampling or deferred sentencing is also made in this section. A large number of recent publications based on the idea of chaining past and future lot results are also reviewed. The economics of chain sampling when compared to the two-plan quick switching system is discussed in the seventh section. The eighth section extends the attribute chain sampling rule to variables inspection. In the ninth section, chain sampling is compared with the well-known CUSUM approach for attribute data. The tenth section gives several other interesting extensions such as chain sampling for mixed inspection and process control. The final section gives the concluding remarks.

1 Introduction

Acceptance sampling is the methodology that deals with procedures by which decision to accept or not accept lots of items is based on the results of the inspection of samples. Special purpose acceptance sampling inspection plans (shortly special purpose plans) are tailored for special applications as against general or universal use. Prof. Harold F. Dodge, who is regarded as the father of acceptance sampling, introduced the idea of chain sampling in [1]. Chain sampling inspection can be viewed as a protocol or plan based on a cumulative results criterion (CRC), where related batch information is chained or cumulated. The phrase chain sampling is also used in sample surveys to imply snowball sampling for collection of data. It should be noted that this phrase was originally coined in the acceptance sampling literature and should be distinguished from its usage in other areas.

Chain sampling is extended to two or more stages of cumulation of inspection results with appropriate acceptance criteria for each stage. The theory of chain sampling is also closely related to the various other methods of sampling inspection such as dependent-deferred sentencing, tightened-normal-tightened sampling, quick switching inspection, etc. In this chapter, we provide an introduction to chain sampling and discuss briefly various generalizations of chain sampling plans. We also review a few sampling plans which are related to or based on the methodology of chain sampling. The selection or design of various chain sampling plans is also briefly presented.

2 ChSP-1 Chain Sampling Plan

A single sampling attributes inspection plan calls for acceptance of a lot under consideration if the number of nonconforming units found in a random sample of size n is less than or equal to the acceptance number Ac. Whenever the operating characteristic (OC) curve of a single sampling plan is required to pass through a prescribed point, the sample size n will be an increasing function of the acceptance number Ac. This fact can be verified from the table of np or unity values given in [2] for various values of the probability of acceptance P_a(p) of the lot under consideration whose fraction nonconforming units is p. The same result is true when the OC curve has to pass through two predetermined points, usually one at the top and the other at the bottom of the OC curve (see [3]). Thus, for situations where small sample sizes are preferred, only single sampling plans with Ac =  0 are desirable (see [4]). However, as observed by Dodge [1] and several authors, the Ac =  0 plan has a “pathological” OC curve in that the curve starts to drop rapidly even for a very small increase in the proportion or fraction nonconforming. In other words, the OC curve of the Ac =  0 plan has no point of inflection. Whenever a sampling plan for costly or destructive testing is required, it is common to force the OC curve to pass through a point, say (LQL, β), where LQL is the limiting quality level for ensuring consumer protection and β is the associated consumer’s risk. All other sampling plans such as double and multiple sampling plans will require more sample size for a one-point protection such as (LQL, β). Unfortunately, the Ac =  0 plan has the following two disadvantages:

• 1. The OC curve of the Ac =  0 plan has no point of inflection and hence it starts to drop rapidly even for a smallest increase in the fraction nonconforming p.

• 2. The producer dislikes an Ac =  0 plan because a single occasional nonconformity will call for the rejection of the lot.

The chain sampling plan ChSP-1 of [1] is an answer to the question whether anything can be done to improve the “pathological” shape of the OC curve of a zero acceptance number plan. A production process, when in a state of statistical control, maintains nearly a constant but unknown fraction nonconforming p. If a series of lots formed from such a stable process is submitted for inspection, known as a Type B situation, then the samples drawn from the submitted lots are simply random samples drawn directly from the production process. Hence, it is logical to allow a single occasional nonconforming unit in the current sample whenever the evidence of good past quality, as demonstrated by the i preceding samples containing no nonconforming units, is available. Alternatively, we can chain or cumulate the results of past lot inspections to take a decision on the current lot without increasing the sample size.

The operating procedure of the chain sampling plan of type ChSP-1 is formally stated below:

• 1. From each of the lots submitted, draw a random sample of size n and observe the number of nonconforming units d.

• 2. Accept the lot if d is zero. Reject the lot if d > 1. If d = 1, the lot is accepted provided all the samples of size n each drawn from the preceding i lots are free from nonconforming units; otherwise, reject the lot.

Thus the ChSP-1 plan has two parameters, namely, the sample size n and i, the number of preceding sample results chained for making a decision on the current lot. It is also required that the consumer has confidence in the producer, and the producer will not deliberately pass a poor-quality lot taking advantage of the small samples used and the utilization of preceding samples for taking a decision on the current lot.

The ChSP-1 plan always accepts the lot if d = 0 and conditionally accepts if d = 1. The probability of preceding i samples of size n to be free from nonconforming units is $P_{0,n}^i$. Hence, the OC function is $P_a(p)=P_{0,n}+P_{1,n}P_{0,n}^i$ where P_d,n is the probability of getting d nonconforming units in a sample of size n. Figure 12.1 shows the improvement in the shape of the OC curve of the zero acceptance number single sampling plan by the use of chain sampling. Clark [5] provided a discussion on the OC curves of chain sampling plans, a modification, and some applications. Liebesman and Hawley [6] argued in favor of chain sampling because the attribute international sampling standards suffer from the small or fractional acceptance numbers. Liebesman and Hawley [6] also provided necessary tables and examples for the chain sampling procedures. Most textbooks on statistical quality control also contain a section of chain sampling and provide some applications.

Fig. 12.1

Comparison of OC curves of Ac = 0 and ChSP-1 plans

Soundararajan [7, 8] constructed tables for the selection of chain sampling plans for given acceptable quality level (AQL, denoted as p₁), producer’s risk α, LQL (denoted as p₂), and β. ChSP-1 plans found from this source are approximate, and a more accurate procedure that also minimizes the sum of actual producer’s and consumer’s risks is given in [9]. Table 12.1, adapted from [9], is based on the binomial distribution for OC curve of the ChSP-1 plan. This table can also be used to select ChSP-1 plans for given LQL and β which may be used in place of zero acceptance number plans.

Table 12.1 ChSP-1 plans indexed by AQL and LQL (α = 0.05, β = 0.10) for fraction nonconforming inspection

Ohta [10] investigated the performance of ChSP-1 plans using the Graphical Evaluation and Review Technique (GERT) and derived measures such as OC, average sample number (ASN) for the ChSP-1 plan. Raju and Jothikumar [11] provided a ChSP-1 plan design procedure based on Kullback-Leibler information and necessary tables for the selection of the plan. Govindaraju [12] discussed the design ChSP-1 plan for minimum average total inspection (ATI). There are a number of other sources where the ChSP-1 plan design is discussed. This chapter provides additional references on designing chain sampling plans, inter alia, discussing various extensions and generalizations.

3 Extended Chain Sampling Plans

Frishman [13] extended the ChSP-1 plan and developed ChSP-4 and ChSP-4A plans which incorporate a rejection number greater than 1. Both ChSP-4 and ChSP-4A plans are operated like a traditional double sampling attributes plan but use (k − 1) past lot results instead of actually taking a second sample from the current lot. Table 12.2 is a compact tabular representation of Frishman’s ChSP-4A plan.

Table 12.2 ChSP-4A plan

ChSP-4 plan restricts r to b + 1 which means that the same rejection number is used for both stages. Conditional double sampling plans of [14] and the partial and full link sampling plans of [15] are actually particular cases of the ChSP-4A plan when k = 2 and k = 3, respectively. However the fact that the OC curves of these plans are the same as the ChSP-4A plan is not reported in both papers (see [16]).

Extensive tables for the selection of ChSP-4 and ChSP-4A plans under various selection criteria were constructed by Raju [17, 18], Raju and Murthy [19, 20], and Raju and Jothikumar [21]. Raju and Jothikumar [21] provided a complete summary of various selection procedures for ChSP-4 and ChSP-4A plans and also discussed two further types of optimal plans: the first one involving minimum risks and the second one based on Kullback-Leibler information. Unfortunately, the tables given in [17,18,19,20,21] for the ChSP-4 or ChSP-4A design require the user to specify the acceptance and rejection numbers. This serious design limitation is not an issue with the procedures and computer programs developed by Vaerst [22] who discussed the design of ChSP-4A plans involving minimum sample sizes for given AQL, α, LQL, and β without assuming any specific acceptance numbers. Raju [17, 18], Raju and Murthy [19, 20], and Raju and Jothikumar [21] considered a variety of design criteria, while [22] discussed only the (AQL, LQL) criterion. The ChSP-4 and ChSP-4A plans were obtained from [17,18,19,20,21]. The procedure given in [21] can be used in any Type B situation of a series of lots from a stable production process, not necessarily when the product involved costly or destructive testing. This is because the acceptance numbers covered are well over zero. The major disadvantage of [13] extended ChSP-4 and ChSP-4A plans is that the neighboring lot information is not always utilized. Vidya [23] considered the variance of the outgoing quality limit (VOQL) criterion for designing ChSP-4 plans. Even though ChSP-4 and ChSP-4A plans require smaller sample size than the traditional double sampling plans, these plans may not be economical to other comparable conditional sampling plans.

Bagchi [24] presented an extension of the ChSP-1 plan, which calls for additional sampling only when one nonconforming unit is found. The operating procedure of Bagchi’s extended chain sampling plan is given below:

• 1. At the outset, inspect n₁ units selected randomly from each lot. Accept the lot if all the n₁ units are conforming; otherwise, reject the lot.

• 2. If i successive lots are accepted, then inspect only n₂ < n₁ items from each of the submitted lots. Accept the lot as long as no nonconforming units are found. If two or more nonconforming units are found, reject the lot. In the event of one nonconforming unit is found in n₂ inspected units, then inspect a further sample (n₁ − n₂) units from the same lot. Accept the lot under consideration if no further nonconforming units are found in the additional (n₁ − n₂) inspected units; otherwise, reject the lot.

Representing Bagchi’s plan as a Markov chain, [25] derived the steady-state OC function and few other performance measures.

Gao [26] considered the effect of inspection errors on a chain sampling plan with two acceptance numbers and also provided design procedures. Application of chain sampling for a reliability acceptance test for exponential life times is also given in [26].

4 Two-Stage Chain Sampling

Dodge and Stephens [27] viewed the chain sampling approach as a cumulative result criterion (CRC) applied in two stages and extended it to include larger acceptance numbers. Their approach calls for the first stage of cumulation of a maximum of k₁ consecutive lot results, during which acceptance is allowed if the maximum allowable nonconforming units is c₁ or less. After passing the first stage of cumulation (i.e., when consecutive lots are accepted), the second stage cumulation of k₂ (> k₁) lot results begins. In the second stage of cumulation, an acceptance number of c₂ (> c₁) is applied. Stephens and Dodge [28] presented a further generalization of the family of “two-stage” chain sampling inspection plans by using different sample sizes in the two stages. The complete operating procedure of a generalized two-stage chain sampling plan is stated below:

• 1. At the outset, draw a random sample of n₁ units from the first lot. In general, a sample of size n_j (j = 1, 2) will be taken while operating in jth stage of cumulation.

• 2. Record d the number of nonconforming units in each sample, as well as D the cumulative number of nonconforming units from the first and up to, and including, the current sample. As long as D_i ≤ c₁ (1 ≤ i ≤ k₁), accept the ith lot.

• 3. If k₁ consecutive lots are accepted, continue to cumulate the number of nonconforming units D in the k₁ samples plus additional samples up to but no more than k₂ samples. During this second stage of cumulation, accept the lots as long as D_i ≤ c₂ (k₁ < i ≤ k₂).

• 4. After passing the second stage of k₂ lot acceptances, start cumulation as a moving total over k₂ consecutive samples (by adding the current lot result and dropping the preceding k₂th lot result). Continue to accept lots as long as D_i ≤ c₂ (i > k₂).

• 5. In any stage of sampling, reject the lot if D_i > c_i and return to Step 1 (a fresh restart of the cumulation procedure).

Figure 12.2 shows how the cumulative result criterion is used in a two-stage chain sampling plan for k₁ = 3 and k₂ = 5.

Fig. 12.2

Operation of a two-stage chain sampling plan with k₁ = 3 and k₂ = 5

An important subset of the generalized two-stage chain sampling plan is when n₁ = n₂, and this subset is designated as ChSP-(c₁, c₂), which has five parameters n, k₁, k₂, c₁, and c₂. The original chain sampling plan ChSP-1 of [1] is a further subset of the ChSP-(0,1) plan with k₁ = k₂ − 1, that is, the OC curve of the generalized two-stage chain sampling plan is equivalent to the OC curve of the ChSP-1 plan when k₁ = k₂ − 1. Dodge and Stephens [27] derived the OC function of ChSP-(0,1) plan as

$$\displaystyle \begin{aligned}P_a(p) = \frac{P_{0,n}(1-P_{0,n})+P_{0,n}^{k_1} P_{1,n} \left(1-P_{0,n}^{k_2-k_1}\right) }{1-P_{0,n}+P_{0,n}^{k_1} P_{1,n} \left(1-P_{0,n}^{k_2-k_1}\right)}, ~~~k_2>k_1. \end{aligned} $$

Both the ChSP-1 and ChSP-(0,1) plans overcome the disadvantages of the zero acceptance number plan mentioned earlier. The operating procedure of the ChSP-(0,1) plan can be succinctly stated as follows:

• 1. A random sample of size n is taken from each successive lot, and the number of nonconforming units in each sample is recorded, as well as the cumulative number of nonconforming units found so far.

• 2. Accept the lot associated with each new sample as long as no nonconforming units are found.

• 3. Once k₁ lots have been accepted, accept subsequent lots as long as the cumulative number of nonconforming units is no greater than one.

• 4. Once k₂ > k₁ lots have been accepted, cumulate the number of nonconforming units over the most k₂ lots, and continue to accept as long as this cumulative number of nonconforming units is one or none.

• 5. If, at any stage, the cumulative number of nonconforming units becomes greater than one, reject the current lot and return to Step 1.

Procedures and tables for the design of ChSP-(0,1) plan are available in [29, 30]. Govindaraju and Subramani [31] showed that the choice of k₁ = k₂ − 1 is always forced on the parameters of the ChSP-(0,1) plan when a plan is selected for given AQL, α LQL, and β, that is, a ChSP-1 plan will be sufficient, and one need not opt for a two-stage cumulation of nonconforming units.

In various technical reports of the Statistics Center, Rutgers University (see [32] for a list), Stephens and Dodge formulated the two-stage chain sampling plan as a Markov chain and evaluated its performance. The performance measures considered by them include the steady-state OC function, ASN, average run length (ARL), etc. For comparison of chain sampling plans with the traditional or noncumulative plans, two types of ARLs are used. The first type of ARL, i.e., ARL₁, is the average number of samples to the first rejection after a sudden shift in the process level, say from p₀ to p_s. The usual ARL, i.e., ARL₂, is the average number of samples to the first rejection given the stable process level p₀. The difference (ARL₁ −ARL₂) measures the extra lag due to chain sampling. However, this extra lag may be compensated by the gains in sampling efficiency as explained in [33].

Stephens and Dodge [34] summarized the Markov chain approach to evaluate the performance of some selected two-stage chain sampling plans, while more detailed derivations were published in their technical reports. Based on the expressions for the OC function derived by Stephens and Dodge in their various technical reports listed in [32]. Raju and Murthy [35] and Jothikumar and Raju [36] discussed various design procedures for the ChSP-(0,2) and ChSP-(1,2) plans. Raju [37] extended the two-stage chain sampling to three stages and evaluated the OC performances of few selected chain sampling plans fixing the acceptance numbers for the three stages. The three-stage cumulation procedure becomes very complex and will play only a limited role for costly or destructive inspections. The three-stage plan will however be useful for general Type B lot by lot inspections.

5 Modified ChSP-1 Plan

In [1], chaining of past lot results does not always occur. It occurs only when a nonconforming unit is observed in the current sample. This means that the available historical evidence of quality is not utilized fully. Govindaraju and Lai [38] developed a modified chain sampling plan (MChSP-1) that always utilizes the recently available lot quality history. The operating procedure of the MChSP-1 plan is given below.

• 1. From each of the submitted lots, draw a random sample of size n. Reject the lot if one or more nonconforming units are found in the sample.

• 2. Accept the lot if no nonconforming units are found in the sample provided the preceding i samples also contained no nonconforming units except in one sample which may contain at most one nonconforming unit. Otherwise, reject the lot.

A flow chart showing the operation of the MChSP-1 plan is in Fig. 12.3. MChSP-1 plan allows a single nonconforming unit in any one of the preceding i samples, but the lot under consideration is rejected if the current sample has a nonconforming unit. Thus, the plan gives a “psychological” protection to the consumer in that it allows acceptance only when all the current sample units are conforming. Allowing one nonconforming unit in any one of the preceding i samples is essential to offer protection to the producer, i.e., to achieve an OC curve with a point of inflection. In MChSP-1 plan, rejection of lots would occur until the sequence of submissions advances to a stage where two or more nonconforming units were no longer included in the sequence of i samples. In other words, if two or more nonconforming units are found in a single sample, it will result in i subsequent lot rejections. In acceptance sampling, one has to look at the OC curve to have an idea of the protection to the producer as well as to the consumer, and what happens in an individual sample or for a few lots is not very important. If two or more nonconforming units are found in a single sample, it does not mean that the subsequent lots need not be inspected since they will be automatically rejected under the proposed plan. It should be noted that results of subsequent lots will be utilized continuously and the producer has to show an improvement in quality with one or none nonconforming unit in the subsequent samples in order to permit future acceptances. This will act as a strong motivating factor for quality improvement.

Fig. 12.3

Operation of the MChSP-1 plan

The OC function P_a(p) of the MChSP-1 plan is derived by Govindaraju and Lai [38] as $P_a(p) = P_{0,n}\left (P_{0,n}^i+iP_{0,n}^{i-1}P_{1,n}\right )$. Figure 12.4 compares the OC curves of ChSP-1 and MChSP-1 plans. From Fig. 12.4, we observe that the MChSP-1 plan decreases the probability of acceptance at poor-quality levels but maintains the probability of acceptance at good-quality levels when compared to the OC curve of the zero acceptance number single sampling plan. The ChSP-1 plan, on the other hand, increases the probability of acceptance at good-quality levels but maintains the probability of acceptance at poor-quality levels. In order to compare the two sampling plans, we need to match them. That is, we need to design sampling plans whose OC curves approximately pass through two prescribed points such as (AQL, 1 − α) and (LQL, β). Figure 12.5 gives such a comparison and establishes that MChSP-1 plan is efficient in requiring a very small sample size compared to the ChSP-1 plan. A two-stage chain sampling plan would generally require a sample size equal to or more than the sample size of a zero acceptance single sampling plan. The MChSP-1 plan will however require a sample size smaller than the zero acceptance number plan.

Fig. 12.4

Comparison of OC curves of ChSP-1 and MChSP-1 plans

Fig. 12.5

OC curves of matched ChSP-1 and MChSP-1 plans

6 Chain Sampling and Deferred Sentencing

Like chain sampling plans, there are other plans that use the results of neighboring lots for taking a conditional decision of acceptance or rejection. Plans that make use of past lot results are either called chain or dependent sampling plans. Similarly plans that make use of future lot results are known as deferred sentencing plans. These plans have a strategy of accepting the lots conditionally based on the neighboring lot quality history and hence referred to as conditional sampling plans. We will briefly review several such conditional sampling plans available in the literature.

Contrary to chain sampling plans that make use of past lot results, deferred sentencing plans use future lot results. The idea of deferred sentencing was first published in a paper by Anscombe et al. [39]. The first simplest type deferred sentencing scheme of [39] requires the produced units be split into small size lots, and one item is selected from each lot for inspection. The lot sentencing rule is that whenever Y  nonconforming units are found out of X or fewer consecutive lots tested, all such cluster of consecutive lots starting from the lot that resulted the first nonconforming unit to the lot that resulted the Y th nonconforming unit are rejected. Lots not rejected by this rule are accepted. This rule is further explained in the following sentences. A run of good lots of length X will be accepted at once. If a nonconforming unit occurs, then the lot sentencing or disposition will be deferred until either further (X − 1) lots have been tested or (Y − 1) further nonconforming items are found, whichever occurs the sooner. At the outset, if the (X − 1) succeeding lots result in fewer than (Y − 1) nonconforming units, the lot that resulted the first nonconforming unit and any succeeding lots clear of nonconforming units will be accepted. As soon as Y  nonconforming units occur in no more than X lots, all lots not so far sentenced will be rejected. Thus the lot disposition will sometimes be made at once and sometimes with a delay not exceeding (X − 1) lots. Some of the lots to be rejected according to the sentencing rule may already have been rejected through the operation of the rule on a previous cluster of Y  nonconforming units partly overlapping the one being considered. The actual number of new lots rejected under the deferred sentencing rule can be any number from 1 to X. Anscombe et al. [39] also considered modifications of the above deferred sentencing rule, including inspection of a sample of size more than one from each lot. Anscombe et al. [39] originally presented their scheme as an alternative to [40] continuous sampling plan of type CSP-1 which is primarily intended for the partial screening inspection of produced units directly (when lot formation is difficult).

The deferred sentencing idea was formally tailored into an acceptance sampling plan by Hill et al. [41]. The operating procedure of [41] scheme is described below:

• 1. From each lot, select a sample of size n. The lots are accepted as long as no nonconforming units are found in the samples. If one or more nonconforming units are found, the disposition of the current lot will be deferred until (X − 1) succeeding lots are inspected.

• 2. If the cumulative number of nonconforming units for X consecutive lots is Y  or more, then a second sample of size n is taken from each of the lots (beginning with the first lot and ending with the last batch that showed a nonconforming unit in the sequence of X nonconforming units). If there are less than Y  nonconforming units in the X, accept all lots from the first up to but not including the next batch that showed a nonconforming unit. The decision on this batch will be deferred until (X − 1) succeeding lots are inspected.

Hill et al. [41] also evaluated the OC function of some selected schemes and found them very economical when compared to the traditional sampling plans, including the sequential attribute sampling plan.

Wortham and Mogg [42] developed a dependent stage sampling plan which is operated under steady state as follows:

• 1. For each lot, draw a sample of size n and observe the number of nonconforming units d.

• 2. If d ≤ r, accept the lot; if d > r + b, reject the lot. If r + 1 ≤ d ≤ r + b, accept the lot if the (r + b + 1 − d)^th previous lot was accepted; otherwise, reject the current lot.

Govindaraju [43] has observed that the OC function of DSSP(r, b) is the same as the OC function of the repetitive group sampling (RGS) plan of [44]. This means that the existing design procedures for the RGS plan can also be used for the design of DSSP(r, b) plan. The deferred state sampling plan of [45] has a similar operating procedure except in Step 2 in which when the current lot is accepted if the forthcoming (r + b + 1 − d)^th lot is accepted. The steady-state OC function of the dependent (deferred) stage sampling plan is given by

$$\displaystyle \begin{aligned} P_a(p)= \frac{P_{a,r}(p)}{1-P_{a,r+b}(p)+P_{a,r}(p)}\end{aligned}$$

where P_a,r(p) is the OC function of the single sampling plan with acceptance number r and sample size n. Similarly P_a,r+b(p) is the OC function of the single sampling plan with acceptance number r + b and sample size n. A procedure for

the determination of plan for given AQL, α, LQL, and β was also developed by Vaerst [22].

Wortham and Baker [46] extended the dependent (deferred) state sampling into a multiple dependent (deferred) state (MDS) plan MDS(r, b, m). The operating procedure of the MDS(r, b, m) plan is given below:

• 1. For each lot, draw a sample of size n and observe the number of nonconforming units d.

• 2. If d ≤ r, accept the lot; if d > r + b, reject the lot. If r + 1 ≤ d ≤ r + b, accept the lot if the consecutive m preceding lots were all accepted (consecutive m succeeding lots must be accepted for the deferred MDS(r, b, m) plan).

The steady-state OC function of the MDS(r, b, m) plan is given by the recursive equation

$$\displaystyle \begin{aligned} P_a(p)= P_{a,r}(p)+ \left[ P_{a,r+b}(p)- P_{a,r}(p) \right ]\left( P_{a}(p) \right)^m\end{aligned}$$

Vaerst [47], Soundararajan and Vijayaraghavan [48], Kuralmani and Govindaraju [49], and Govindaraju and Subramani [50] provided detailed tables and procedures for the design of MDS(r, b, m) plans for various requirements. Afshari and Gildeh [51] provided a procedure to design the MDS plan in a fuzzy environment such when testing is imperfect.

Vaerst [22, 47] modified the MDS(r, b, m) plan to make it on par with the ChSP-1 plan. The operating procedure of the modified MDS(r, b, m) plan, called MDS-1(r, b, m), is given below:

• 1. For each lot, draw a sample of size n and observe the number of nonconforming units d.

• 2. If d ≤ r accept the lot; if d > r + b, reject the lot. If r + 1 ≤ d ≤ r + b, accept the lot if r or less nonconforming units are found in each of the consecutive m preceding (succeeding) lots.

When r = 0, b = 1, and m = i, MDS-1(r, b, m) plan becomes the ChSP-1 plan. The OC function of the plan is given by recursive equation

$$\displaystyle \begin{aligned} P_a(p)= P_{a,r}(p)+ \left[ P_{a,r+b}(p)- P_{a,r}(p) \right] \left( P_{a, r}(p) \right)^m\end{aligned}$$

Vaerst [47, 52], and [53] provided detailed tables and procedures for the design of plans for various requirements. The major but an obvious shortcoming of the chain sampling plans is that since they use sample information from past lots for disposing the current lot, there is a tendency to reject the current lot of given good quality when the process quality is improving or accept the current lot of given bad quality when the process quality is deteriorating. Similar criticisms (in reverse) can be leveled against the deferred sentencing plans. As mentioned earlier, [33] recognizing this disadvantage of chain sampling defined the ARL performance measures ARL₁ and ARL₂. Recall that ARL₂ is the average number of lots that will be accepted as a function of the true fraction nonconforming. ARL₁ is the average number of lots accepted after an upward shift in the true fraction nonconforming occurred from the existing level. Stephens and Dodge [54] evaluated the performance of the two-stage chain sampling plans comparing the ARLs with matching single and double sampling plans having approximately the same OC curve. It was noted that the slightly poorer ARL property due to chaining of lot results is well compensated by the gain in sampling economy. For deferred sentencing schemes, [41] investigated trends as well as sudden changes in quality. It was found that the deferred sentencing schemes will discriminate better between fairly constant quality at one level and fairly constant quality at another level than will a lot-by-lot plan scheme with the same sample size. However, when quality varies considerably from lot to lot, the deferred sentencing scheme found to operate less satisfactorily, and in certain circumstances the discrimination between good and bad batches may even be less than for the traditional unconditional plans with the same sample size. Further the deferred sentencing scheme may pose problems of flow, supply storage space, and uneven workload (which is not a problem with chain sampling).

Cox [55] provided a more theoretical treatment and considered one-step forward and two-step backward schemes. The lot sentencing rules and inspection are modeled as a stochastic process and applied Bayes’s theorem for the sentencing rule. He did recognize the complexity of modeling a multistage procedure. When the submitted lot fraction nonconforming vary, say when a trend exists, both chain and deferred sentencing rules have disadvantages. But this disadvantage can be overcome by combining chain and deferred sentencing rules into a single scheme. This idea was first suggested by Baker [56] in his dependent deferred state (DDS) plan. Osanaiye [57] provided a complete methodology of combining chain and deferred sentencing rules and developed the chain-deferred (ChDP) plan. The ChDP plan has two stages for lot disposition and its operating procedure is given below:

• 1. From lot numbered k, inspect n units and count the number of nonconforming units d_k. If d_k ≤ c₁, accept lot numbered k. If d_k > c₂, reject lot numbered k. If c₁ < d_k ≤ c₂, then combine the number of nonconforming units from the immediate succeeding and preceding samples, namely, d_k−1 and d_k+1.

• 2. If d_k ≤ c, accept the kth lot provided d_k + d_k−1 ≤ c₃ (chain approach). If d_k > c, accept the lot provided d_k + d_k+1 ≤ c₃ (deferred sentencing).

One possible choice of c is the average of c₁ and c₃ + 1. Osanaiye [57] also provided a comparison of ChDP with the traditional unconditional double sampling plans as the OC curves of the two types of plans are the same (but the ChDP plan utilizes the neighboring lot results). Shankar and Srivastava [58] and Shankar and Joseph [59] provided a GERT analysis of ChDP plans taking the approach of [10]. Shankar and Srivastava [60] discussed the selection ChDP plans using tables. Osanaiye [61] provided a multiple sampling plan extension of the ChDP plan (called MChDP plan). MChDP plan uses several neighboring lot results to achieve sampling economy.

Osanaiye [62] provided a practically useful discussion on the choice of conditional sampling plans considering autoregressive processes, inert processes (constant process quality shift), and linear trends in quality. Based on a simulation study, it was recommended that the chain-deferred schemes are the cheapest if either the cost of 100% inspection or sampling inspection is high. He recommended the use of the traditional single or double sampling plans only if the opportunity cost of rejected items is very high. Osanaiye and Alebiosu [63] considered the effect of inspection errors on dependent and deferred double sampling plans vis-à-vis ChDP plans. They observed that the chain-deferred plan in general has a greater tendency to reject nonconforming items than any other plans irrespective of the magnitude of any inspection error.

Many of the conditional sampling plans, which follow either the approach of chaining or deferring or both, have the same OC curve of a double (or a multiple) sampling plan. Exploiting this equivalence, [64] provided a general selection procedure for conditional sampling plans for given AQL and LQL. The plans considered include the conditional double sampling plan of ChSP-4A plans of [13], conditional double sampling plan of [14], link sampling plan of [15], and ChDP plan of [57]. A perusal of the operating ratio LQL/AQL of [64] tables reveal that these conditional sampling plans apply in all Type B situations because a wide range of discrimination between good and bad qualities is achievable. However, the sample sizes, even though smaller than the traditional unconditional plans, will not be as small as the zero acceptance number single sampling plans. This limits the application of the conditional sampling plans to this special purpose situation, where ChSP-1 or MChSP-1 plan suits the most.

Govindaraju [65] developed a conditional single sampling (CSS) plan, which has desirable properties for general applications as well as for costly or destructive testing. The operating procedure of the CSS plan is as follows:

• 1. From lot numbered k, select a sample of size n and observe the number of nonconforming units d_k.

• 2. Cumulate the number of nonconforming units observed for the current lot and the related lots. The related lots will be either past lots, future lots, or a combination depending on whether one is using dependent sampling or deferred sentencing. The lot under consideration is accepted if the total number of nonconforming units in the current lot and the m related lots is less than or equal to the acceptance number, Ac. If d_k is the number of nonconforming units recorded for the kth lot, the rule for disposition for the kth lot is as follows:

  • a. For dependent or chain sampling, accept the lot if $\left (d_{k-m}+ \dots +d_{k-1}+d_k \right ) \le Ac$; otherwise, reject the lot.

  • b. For deferred sampling, accept the lot if $\left (d_{k} +d_{k+1}+\right .$ $\left .\dots + d_{k+m} \right ) \le Ac$; otherwise, reject the lot.

  • c. For dependent-deferred sampling, where m is desired to be even, accept the lot if $\left (d_{k-\frac {m}{2}}+ \dots + d_{k}+ \dots +\right .$ $\left .\le d_{k+\frac {m}{2}} \right ) \le Ac$; otherwise, reject the lot.

Thus, the CSS plan has three parameters, the sample size n, acceptance number Ac, and number of related lot results used, m. As in the case of any dependent sampling procedure, dependent single sampling takes full effect only from the (m + 1)^st lot. In order to maintain equivalent OC protection for the first m lots, additional sample mn units can be taken from each lot and the lot can be accepted if the total number of nonconforming units is less than or equal to Ac or additional samples of size (m + 1 − i)n can be taken for the ith lot (i = 1, 2, …, m) and the same decision rule be applied. In either case, the results of the additional samples should not be used for lot disposition from lot (m + 1). Govindaraju [65] has shown that the CSS plans require much smaller sample sizes than all other conditional sampling plans. In case of trends in quality, the CSS plan can also be operated as a chain-deferred plan, and this will ensure that the changes in lot qualities are somewhat averaged out.

7 Comparison of Chain Sampling with Switching Systems

Dodge [66] first proposed the quick switching sampling (QSS) system which basically consists of two intensities of inspection, i.e., normal (N) and tightened (T) plans. Romboski [67] investigated the QSS system and introduced several modifications of the original QSS system. Under the QSS system, if a lot is rejected under the normal inspection, a switch tightened inspection will be made; otherwise, normal inspection shall continue. If a lot is accepted under the tightened inspection, then the normal inspection will be restored; otherwise, tightened inspection will be continued. For a review of quick switching systems, see [68] or [69].

Taylor [68] introduced a new switch number to the original QSS-1 system of [67] and compared it with the chain sampling plans. When the sample sizes of normal and tightened plans are equal, the quick switching systems and the two-stage chain sampling plans were found to give nearly identical performance. Taylor’s comparison is only valid for a general situation where acceptance numbers of greater than zero are used. For costly or destructive testing, acceptance numbers are kept at zero for achieving minimum sample sizes. In such situations, both ChSP-1 and ChSP-(0,1) plans will fare poorly against other comparable schemes when the incoming quality is at AQL. This fact is explained in the following paragraph using an example.

For costly or destructive testing, a quick switching system employing zero acceptance number was studied in [70] and [71]. Under this scheme, the normal inspection plan has a sample size of n_N units, while the tightened inspection plan has a higher sample size n_T (> n_N). The acceptance number is kept at zero for both normal and tightened inspections. The switching rule is that a rejection under the normal plan (n_N, 0) will invoke the tightened plan (n_T, 0). An acceptance under the (n_T, 0) plan will revert back to normal inspection. This QSS system, designated as of type QSS-1(n_N, n_T;0), can be used in place of the ChSP-1 and ChSP-(0,1) plans. Let AQL =  1%, α =  5%, LQL =  15%, and β =  10%. The ChSP-1 plan for the prescribed AQL and LQL conditions is found as n =  15 and i =  2 (from Table 12.1 of this chapter). The matching QSS-1 system for the prescribed AQL and LQL conditions can be found as QSS-1(n_N = 5, n_T = 19) from the tables given in [70] or [72]. At good-quality levels, the normal inspection plan will require sampling only 5 units. Only at poor-quality levels, 19 units will be sampled under the QSS system. Hence, it is obvious that Dodge’s chain sampling approach is not truly economical at good-quality levels but fares well at poor-quality levels. However, if the modified chain sampling plan MChSP-1 plan of [38] is used, then the sample size needed will be only 3 units (and i, the number of related lot results to be used is fixed at 7 or 8). The other alternative is to use the chained quick switching system proposed in [73]. For a detailed discussion of this approach, consult [74].

A more general two-plan system having zero acceptance numbers for the tightened and normal plans was studied by Calvin [75], Soundararajan and Vijayaraghavan [76], and Subramani and Govindaraju [77]. Calvin’s TNT scheme uses zero acceptance numbers for normal and tightened inspection and employs the switching rules of [78], which is also roughly employed in [79]. The operating procedure of the TNT scheme, designated as TNT(n_N, n_T;0), is given below:

• 1. Start with the tightened inspection plan (n_T, 0). Switch to normal inspection (Step 2) when t lots in a row are accepted; otherwise, continue with the tightened inspection plan.

• 2. Apply the normal inspection plan (n_N, 0). Switch to the tightened plan if a lot rejection is followed by another lot rejection within the next s lots.

Using the tables of [80], the zero acceptance number TNT(n_N, n_T;0) plan for given AQL =  1%, α =  5%, LQL =  15%, and β =  10% is found as TNT(n_N = 5, n_T = 16;Ac = 0). We again find that the MChSP-1 plan calls for a smaller sample size when compared to Calvin’s zero acceptance number TNT plan.

Skip-lot sampling plans of [81] and [82] are based on skipping of sampling inspection of lots on the evidence of good-quality history. For a detailed discussion of skip-lot sampling, [32] may be consulted. In skip-lot sampling plan of type SkSP-2 of [82], once m successive lots are accepted under the reference plan, the chosen reference sampling plan is applied only for a fraction of the time. Govindaraju [83] studied the employment of the zero acceptance number plan as a reference plan (among several other reference sampling plans) in the skip-lot context. For given AQL =  1%, α =  5%, LQL =  15%, and β =  10%, the SkSP-2 plan with a zero acceptance number reference plan is found as n = 15, m = 6, and f ≈ 1∕5. Hence, the matching ChSP-1 plan n =  15 and i =  2 is not economical at good-quality levels when compared to the SkSP-2 plan n = 15, m = 6, and f ≈ 1∕5. This is because the SkSP-2 plan requires the zero acceptance number reference plan with a sample of size 15 to be applied only to one in every five lots submitted for inspection once six consecutive lots are accepted under the reference single sampling plan (n = 10, Ac = 0). However, the modified MChSP-1 plan is more economical at poor-quality levels when compared to the SkSP-2 plan. Both plans require about the same sampling effort at good-quality levels.

8 Chain Sampling for Variable Inspection

The main assumption made for the various types of chain sampling plans and other attribute schemes such as deferred-dependent plans and quick switching systems is that the fraction nonconforming p in a series of lots roughly remains a constant. No other distributional assumptions are made for attribute sampling inspection plans. If the assumption of constant p for a series of lots is violated, there can be a delay in detection of a change in p. This delay is measured using the difference (ARL₁ −ARL₂) (see Sect. 12.4). However, if the rule of chaining lot inspection results is modified as a chain-deferred rule, the overall producer’s and consumer’s risk will remain the same even if there is a linear trend in p in a series of lots (see the discussion in Sect. 12.5). If the distribution of the quality characteristic of interest is known, variable inspection becomes feasible. Govindaraju and Balamurali [84] extended the idea of chain sampling to variable inspection assuming normality. This approach is particularly useful when testing is costly or destructive provided the quality variable is measurable on a continuous scale and known to be normally distributed. It is well known that the variable plans do call for a very low sample sizes when compared to the attribute plans. However, not all variable plans possess a satisfactory OC curve as shown by Govindaraju and Kuralmani [85]. Often, a variable plan is unsatisfactory if the acceptability constant is too large particularly when the sample size is small. Only in such cases, it is necessary to follow the chain sampling approach to improve upon the OC curve of the variable plan. Table 12.3 is useful for deciding whether a given variables sampling plan has a satisfactory OC curve or not. If the acceptability constant k_σ of a known sigma variables plan exceeds k_σl, then the plan is deemed to have an unsatisfactory OC curve like an Ac = 0 attribute plan.

Table 12.3 Limits for deciding unsatisfactory variable plans

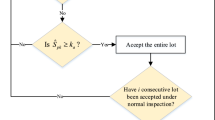
The operating procedure of the chain sampling plan for variables inspection is as follows:

• 1. Draw a random sample of size n_σ, say $\left ( x_1, x_2, \dots , x_{n_{\sigma }} \right )$, and then compute $\nu = (U-\bar {X})/\sigma$ where $\bar {X} = \sum \limits _{i=1}^{n_\sigma } x_i/n_\sigma$.

• 2. Accept the lot if ν ≥ k_σ and reject if $\nu < k^\prime _\sigma$. If $k^\prime _\sigma \le \nu < k_\sigma$, accept the lot provided the preceding i lots were accepted on the condition that ν ≥ k_σ.

Thus the variable chain sampling plan has four parameters, namely, the sample size n_σ; the acceptability constants k_σ and $k^\prime _\sigma$ (< k_σ); and i, the number of preceding lots used for conditionally accepting the lot. The OC function of this plan is given by $P_a(p) = P_V+ (P^\prime _V-P_V)P_V^i$ where $P_V=\Pr (\nu \ge k_\sigma )$ is the probability of accepting the lot under the variables plan (n_σ, k_σ) and $P^\prime _V=\Pr (\nu \ge k^\prime _\sigma )$ is the probability of accepting the lot under the variables plan $(n_\sigma , k^\prime _\sigma )$. Even though the above operating procedure of the variables chain sampling plan is of a general nature, it would be appropriate to fix $k^\prime _\sigma =k_{\sigma l}$. For example, suppose that a variable plan with n_σ = 5 and k_σ = 2.46 is currently under use. From Table 12.3, the limit for the undesirable acceptability constant k_σl for n_σ = 5 is obtained as 1.1278. Since the regular acceptability constant k_σ = 2.26 is greater than $k^\prime _\sigma = 1.1278$, the variable plan can be declared to possess an unsatisfactory OC curve. Hence, it is desirable to chain the results of neighboring lots to improve upon the shape of the OC curve of the variable plan (n_σ = 5, k_σ = 2.26), that is, the variable plan currently under use will be operated as a chain sampling plan fixing i as four. A more detailed procedure on designing chain sampling for variable inspection, including the case when sigma is unknown, is available in [84]. The chain sampling for variables will be particularly useful when inspection costs are prohibitively high, and the quality characteristic is measurable on a continuous scale.

Luca [86] extended the modified chain sampling plan MChSP-1 of [38] for variable inspection. The main advantage of the MChSP-1 is the reduction of sample size compared to the ChSP-1 plan. While the variable chain sampling approach reduces the amount inspection substantially, the variable inspection based on the modified chain sampling plan rule can achieve some marginal gains.

The idea of using chain sampling rules for variables inspection proved popular in the recent years, and a large number of plans using conditional lot disposition rules appeared in the literature. Balamurali and Jun [87] extended the variable chain sampling idea to MDS sampling plans based on the normal distribution. Balamurali et al. [88] employed the Weibull distribution so that the plans can be used for lifetime assurance (see [89] and [90]). Aslam et al. [91] extended the MDS rule to a lifetime characteristic following the Burr XII distribution.

Arizono et al. [92] first coined the idea of employing the process capability index for the design of a variables inspection plan. Wu et al. [93] extended the work of [87] to MDS sampling plan using the capability index C_pk for normally distributed processes with two-sided specification limits (see [94] who also developed a variables MDS sampling plan for lot sentencing based on the process capability index) (also see [95]). Wu et al. [96] employed the quick switching rules and presented variable quick switching sampling (VQSS) system based on the C_pk index. There are numerous papers employing rules based on chaining lot results which employ various process capability indices, and the reader is suggested to refer to the review given in [96]. Kurniati et al. [97] employed the TNT plan rules with a unilateral specification limit based on one-sided capability indices. Yan et al. [98] extended the MDS rules to assure protection of coefficient of variation of a normally distributed quality characteristic.

9 Chain Sampling and CUSUM

In this section, we will discuss some of the interesting relationships between the cumulative sum (CUSUM) approach of [99, 100] and chain sampling approach of [1]. As explained in [101], the CUSUM approach for Gaussian processes is largely popular in the area of statistical process control (SPC), but [99] proposed it to be used with attribute (binomial) inspection problems arising in acceptance sampling as well. Page [99] compares the CUSUM-based inspection scheme with the deferred sentencing schemes of [39] and the continuous sampling plan CSP-1 of [40] for evaluating their relative performance. In fact Dodge’s CSP-1 plan forms the theoretical basis for the ChSP-1 chain sampling plan. A more formal acceptance sampling scheme based on the one-sided CUSUM for lot-by-lot inspection was proposed in [102]. Beattie’s plan calls for drawing a random sample of size n from each lot and observing the number of nonconforming units d. For each lot, a CUSUM value is calculated for a given slack parameter k. If the computed CUSUM is within the decision interval (0, h), then the lot is accepted. If the CUSUM is within the return interval (h, h^′), then the lot is rejected. If the CUSUM falls below zero, it is reset to zero. Similarly, if the CUSUM exceeds h + h^′, it is reset to h + h^′. In other words, for the jth lot, the plotted CUSUM can be succinctly defined as $S_j=\min \left (h+h^\prime ,~\max (d_j-k+S_{j-1}) \right )$ with S₀ = 0. Beattie’s plan is easily implemented using the typical number of nonconforming units CUSUM chart for lot-by-lot inspection (see Fig. 12.6).

Fig. 12.6

Beattie’s CUSUM acceptance sampling plan

Prairie and Zimmer [103] provided detailed tables and nomographs for the selection of Beattie’s CUSUM acceptance sampling plan. An application is also reported in [104].

Beattie [105] introduced a “two-stage” semicontinuous plan where the CUSUM approach is followed and the product is accepted as long as the CUSUM S_j is within the decision interval (0, h). For product falling in the return interval (h, h^′), an acceptance sampling plan such as the single or double sampling plan is used for lot disposition. Beattie [105] compared the “two-stage” semicontinuous plan with the ChSP-4A plan of [13] and the deferred sentencing scheme of [41]. It is also remarked in [105] that chain sampling plans (ChSP-4A type) call for steady rate of sampling and simple to administer. The two-stage semicontinuous sampling plan achieved some gain in the average sample number at good-quality levels but is more difficult to administer. The two-stage semicontinuous plan also requires more sample size than ChSP-4A plans when the true quality is poorer than acceptable levels.

We will now explore an interesting equivalence between the ChSP-1 plan and a CUSUM scheme intended for high-yield or low-fraction nonconforming production processes for which the traditional p or np control charts are not useful. Lucas [106] gave a signal rule for lack of statistical control if there are two or more counts within an interval of t samples. In case of low-process fraction nonconforming, this means that if two or more nonconforming units are observed in any t consecutive samples or less, a signal for an upward shift in the process fraction level is obtained. It should be noted that if two or more nonconforming units are found even in the same sample, a signal for lack of statistical control will be obtained. Govindaraju and Lai [107] discussed the design given in [106] and provided a method of obtaining the parameters n (the subgroup or sample size) and t (the maximum number of consecutive samples considered for a signal). Lucas [106] has shown that his signal rule is equivalent to a CUSUM scheme having a reference value k = 1∕t and decision interval (0, h = 1) for detecting an increase in the process count level. It was also shown that a fast initial response (FIR) feature can be added to the CUSUM scheme (see [108]) with an additional subrule of signaling lack of statistical control if the first count occurs before the tth sample. This FIR CUSUM scheme has a head start of S₀ = 1 − k with k = 1∕t and h = 1. Consider the ChSP-1 plan of [1] which rejects a lot if two or more counts (of nonconformity or nonconforming units) occur but allows acceptance of the lot if no counts occur or a single count is preceded by t (the symbol i was used before) lots having samples with no counts. If the decision of rejecting a lot is translated as the decision of declaring the process to be not in statistical control, then it is seen that Lucas’s scheme and the ChSP-1 plan are the same. This equivalence will be further clearer if one considers the operation of two-stage chain sampling plan ChSP-(0,1) of [27] given in Sect. 12.4. When k₂ = k₁ + 1, the ChSP-(0,1) plan is equivalent to the ChSP-1 plan with t = k₁. Hence, it can also be noted that the subrule of not allowing any count for the first t samples suggested for the FIR CUSUM scheme of [106] is an inherent feature of the two-stage chain sampling scheme. This means that the ChSP-1 plan is equivalent to the FIR CUSUM scheme with the head start (1 − k) with k = 1∕t and h = 1.

10 Other Interesting Extensions

If homogeneous lot formation is difficult, and random sampling from the lot is harder, the binomial assumption may not be valid. Gao and Tang [109] considered the chain sampling rule when testing for conformance status which exhibits correlation between successive units. A two-state Markov chain model for the correlation within each sample was assumed as against a two-state Markov chain model for the fraction nonconforming p. In acceptance sampling, random samples are taken; hence, the correlation within the sample is not an issue. The proposal given in [109] may only apply when random samples are difficult to obtain.

Mixed sampling plans are two-phase sampling plans in which both variable quality characteristics and attribute quality measures are used in deciding the acceptance or rejection of the lot. Baker and Thomas [110] reported the application of chain sampling for acceptance testing for armor packages. Their procedure uses chain sampling for testing structural integrity (attributes inspection), and a variable sampling plan is used for testing penetration depth quality characteristic. Baker and Thomas [110] also suggested the simultaneous use of control charts along with their proposed acceptance sampling procedures. Suresh and Devaarul [111] proposed a more formal mixed acceptance sampling plan where a chain sampling plan is used for the attribute phase. Suresh and Devaarul [111] also obtained the OC function for their mixed plan and discussed various selection procedures. For controlling multidimensional characteristics, [112] developed multidimensional mixed sampling plans (MDMSP). This plan handles several quality characteristics during the variable phase of the plan, while the attribute sampling phase can be based on chain sampling or other attribute plans. Aslam et al. [113] presented mixed multiple dependent state sampling plans based on the popular process capability index. Balamurali [114] and Usha and Balamurali [115] extended the mixed chain sampling approach using the process capability index C_pk. In a similar vein, another form of mixed modified chain sampling plan is given in [116]. Balamurali et al. [117] generalized the mixed sampling incorporating the multiple dependent state sentencing rule. Balamurali and Usha [118] also extended the mixed sampling incorporating the quick switching system rules. These approaches would further reduce the sampling effort but no investigation was done on the delay in detection of a shift.

In some situations, it is desirable to adopt three attribute classes where items are classified into three categories, namely, good, marginal, and bad (see [119]). Shankar et al. [120] developed three class chain sampling plans and derived various performance measures through GERT approach and also discussed their design.

Suresh and Deepa [121] provided a discussion on formulating a chain sampling plan given a gamma or beta prior distribution for product quality. Tables are for the selection of the plans and examples are also provided by Suresh and Deepa [121]. Latha and Jeyabharathi [122] considered the beta-binomial process for the operation of the ChSP-1 plan. The main limitation of this approach is that the assumption of nearly constant process fraction nonconforming needed for chain sampling is not fulfilled. As a result, the (ARL₁ −ARL₂) delay will be higher. A number of other lot chaining rules were also proposed such as the rule given in [123] where the number of preceding lot results employed depends on the number of nonconforming results found in the current sample.

Tang and Cheong [124] extended the idea of the chain inspection procedure to enhance its sensitivity in detecting a process shift while monitoring high-quality processes with low fraction nonconforming. The MDS plan rules are also used in control charting (see [125] and [126]).

11 Concluding Remarks

Chain sampling attribute inspection plans for a series of lots can be implemented without any distributional assumption. The main requirement is that the fraction nonconforming p in the series of lots submitted for inspection is fairly constant. If there is any linear trend in p, the chain sampling inspection can be modified as a chain-deferred inspection procedure so that the producer’s and consumer’s risks are maintained the same for the series of lots inspected. If the chain sampling rule is applied for variable inspection, distributional assumptions such as a normality must be met. For costly and destructive testing, the sample size must be kept small. Small sample sizes such as five can be effective when lot results are chained under variable inspection. If the normality assumption is suspect, it is desirable to employ the regular attribute chain sampling in order to assure the set risks.

This chapter largely reviewed the methodology of chain sampling inspection of quality in a series of lots. Various extensions of the original chain sampling plan ChSP-1 of [1] and modifications are briefly reviewed. Chain sampling approach is primarily useful for costly or destructive testing, where small sample sizes are preferred. Chain sampling achieves greater sampling economy when it is combined with the approach of deferred sentencing so that the combined plan can be used for any general situations. This chapter does not cover designing of chain sampling plans in any great detail. One may consult textbooks such as [74] or [32, 127] for detailed tables. A large number of papers primarily dealing with the design of chain sampling plans are available only in journals, and some of them are listed as references. It is often remarked that designing sampling plans is more of an art than a science. There are statistical, engineering, and other administrative aspects that are to be taken into account for successful implementation of any sampling inspection plan, including the chain sampling plans. For example, the sample size may be fixed due to administrative and other reasons. Given this limitation, what sampling plan should be used requires careful consideration. Several candidate sampling plans, including chain sampling plans, must be sought first, and then the selection of a particular type of plan must be made based on the performance measures such as the OC curve, etc. Sampling plans that make use of related lot results must also be investigated for their performance against trend in the submitted lot quality as well as sudden jumps. The effectiveness of a chosen plan or a sampling scheme must be monitored over time for a series of batches. The severity of inspection is reduced with the chaining-related lot results, but consumer protection should receive more attention by way of minimizing the delay in detection of a poor-quality lot submission.