Analysis of Mixed Loss-Delay M/M/m/K Queueing Systems with State-Dependent Arrival Rates

Abstract

An M/M/m queue with mixed loss and delay calls was analyzed by J. W. Cohen half a century ago (1956) where the two types of calls had identical constant arrival and service rates. It is straightforward to extend his analysis to an M/M/m/K queue. In this chapter, we further generalize the model such that the call arrival rates can depend on the number of calls present in the system at the arrival time. This model includes the balking and the finite population size models as special cases. We present a method of calculating the blocking probability for loss calls as well as the distribution of the waiting time for accepted delay calls. We solve a set of linear simultaneous equations for the state probabilities by numerical computation. The effects of loss calls on the mean waiting time of delayed calls are discussed based on the numerical results.

Introduction

In the traditional basic modeling of teletraffic engineering, an M/M/m loss system is used as a model of circuit-switched traffic leading to the Erlang-B formula for the blocking probability [1, p. 106]. An M/M/m delay system with an infinite waiting room is used as a model of packet-switched traffic leading to the Erlang- C formula for the waiting probability [1, p. 103]. Such models are actually used in the methodology for the spectrum requirement calculation for the International Mobile Telecommunication-2000 (IMT-2000) in third-generation wireless communication systems [2]. Cohen [3] analyzed an M/M/m queueing system with mixed loss and delay calls with different arrival rates and identical service rates (see [9], pp. 304–305).

The mixed loss-delay system could be used as a model for the performance evaluation of a communication channel shared by circuit-switched traffic and packet- switched traffic. Cohen's analysis was recently extended to an M/M/m/K queueing system with a finite waiting room by Takagi [5], who derives explicit formulas for the blocking probability of loss calls, the blocking probability of delay calls, and the waiting time distribution of delay calls.

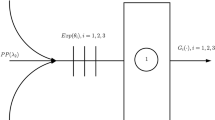
In this chapter, we consider a mixed loss-delay M/M/m/K queueing system in which the arrival rates of loss and delay calls can depend on the number of those calls in the system at their arrival times and the constant service rates can be different between the loss and delay calls. More specifically, when there are j loss calls and k delay calls in the system, the two types of calls arrive in an independent Poisson process with rates λ₁(j,k) and λ₂(j,k), respectively. Their service times are independent of each other and exponentially distributed with constant rates μ₁ and μ₂, respectively. The number of servers is denoted by m. The loss calls are lost if all servers are busy when they arrive. The delay calls wait in the waiting room unless the total number of calls present in the system exceeds K when they arrive. Namely, K is the capacity of the system including m calls in service (m ≤ K). The assumption of state-dependent arrival rates allows us to handle a wide range of customer arrival processes. An example is the balking such that the arrival rate decreases as the number of customers present in the system increases. Another example is a queue with a finite population of customers. Figure 10.1 shows a schema of our system.

Fig. 10.1

Mixed loss-delay M/M/m/K queueing system.

The rest of the chapter is organized as follows. In Sect. 10.2, we present a set of linear simultaneous equations for the equilibrium state probabilities. These equations are assumed to be solved numerically. In Sect. 10.3, we calculate the blocking probabilities for both loss and delay calls, the waiting and nonwaiting probabilities, as well as the waiting time distribution for accepted delay calls. Numerical examples are shown in Sect. 10.4. We conclude in Sect. 10.5 with a summary of present work and a plan for future study.

Equilibrium State Probability Equations

Let us denote the equilibrium state probability by

$$\begin{array}{r} P_{j,k}: = P\left\{{\rm{The\ number\ of\ the\ calls\ of\ loss\ system\ in\ the\ system}} = j,\right.\\ \left.{\rm{The\ number\ of\ the\ calls\ of\ delay\ system\ in\ the\ system}} = k\right\},\\ 0 \le j \le m,0 \le j + k \le k.\\ \end{array}$$

(10.1)

The number of states is

$$\left({K + 1} \right)\left({m + 1} \right) - \frac{{m\left({m + 1} \right)}}{2} = \left({m + 1} \right)\left({K + 1 - \frac{m}{2}} \right).$$

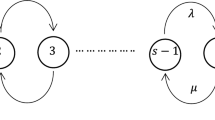
Figure 10.2 shows the state transition rate diagram for the mixed loss-delay M/M/m/K system we analyze now.

Fig. 10.2

State transition rate diagram for the mixed loss-delay M/M/m/K system.

Considering the number of loss and delay calls present in the system simultaneously, we can write the balance equations for the equilibrium state probabilities as follows:

First, we consider the empty state (0,0). The system goes out of this state when a call arrives, and comes into this state when the service finishes at state (1,0) and (0,1). Thus we have

$$\left[ {\lambda _1 \left({0,0} \right) + \lambda _2 \left({0,0} \right)} \right]P_{0,0} = \mu _1 P_{1,0} + \mu _2 P_{0,1}.$$

(10.2)

Second, we consider the state (j,k) such that 0 ≤ j ≤ m − 1, 1 ≤ j+k ≤ m − in which there are calls being served and some free servers, and find

$$\left[ {\lambda _1 \left({0,k} \right) + \lambda _2 \left({0,k} \right) + k\mu _2} \right]P_{0,k} = \lambda _2 \left({0,k - 1} \right)P_{0,k - 1} + \mu _1 P_{1.k} + \left({k + 1} \right)\mu _2 P_{j,1},1 \le k \le m - 1,$$

(10.3)

$$\begin{array}{r} \left[ {\lambda _1 \left({j,k} \right) + \lambda _2 \left({j,k} \right) + j\mu _1 + k\mu _2} \right]P_{j,k} = \lambda _1 \left({j - 1,k} \right)P_{j - 1,k} + \lambda _2 \left({j,k - 1} \right)P_{j,k - 1}\\ + \left({j + 1} \right)\mu _1 P_{j + 1,k} + \left({k + 1} \right)\mu _2 P_{j,k + 1}\\ 1 \le j \le m - 1,1 \le k \le m - 1,2 \le j + k \le m - 1,\\ \end{array}$$

(10.4)

$$\left[ {\lambda _1 \left({j,0} \right) + \lambda _2 \left({j,0} \right) + j\mu _1} \right]P_{j,0} = \lambda _1 \left({j - 1,0} \right)P_{j - 1,0} + \left({j + 1} \right)\mu _1 P_{j + 1,0} + \mu _2 P_{j,1,} 1 \le j \le m - 1.$$

(10.5)

Third, we consider the state (j,k) such that 0 ≤ j ≤ m,j+k = m in which all servers are busy and all waiting positions are available for delay calls, and find

$$\left[ {\lambda _2 \left({0,m} \right) + m\mu _2} \right]P_{0,m} = \lambda _2 \left({m - 1} \right)P_{0,m - 1} + \mu _1 P_{1,m} + m\mu _2 P_{0,m + 1},$$

(10.6)

$$\begin{array}{r} \left[ {\lambda _2 \left({j,k} \right) + j\mu _1 + k\mu _2} \right]P_{j,k} = \lambda _1 \left({j - 1,k} \right)P_{j - 1,k} + \lambda _2 \left({j,k - 1} \right)P_{j,k - 1}\\ + \left({j + 1} \right)\mu _1 P_{j + 1,k} + \left({m - j} \right)\mu _2 P_{j,k + 1,}\\ 1 \le j \le m - 1,1 \le k \le m - 1,j + k = m,\\ \end{array}$$

(10.7)

$$\left[ {\lambda _2 \left({m,0} \right) + m\mu _1} \right]P_{m,0} = \lambda _1 \left({m - 1,0} \right)P_{m - 1,0}.$$

(10.8)

Fourth, we consider the state (j,k) such that 0 ≤ j ≤ m,m+1 ≤ j + k ≤ K − 1 in which all servers are busy and there is at least one waiting position available for a delay call, and find

$$\left[ {\lambda _2 \left({0,k} \right) + m\mu _2} \right]P_{0,k} = \lambda _2 \left({0,k - 1} \right)P_{0,k - 1} + \mu _1 P_{1,k} + m\mu _2 P_{0,k + 1},m + 1 \le k \le K - 1,$$

(10.9)

$$\begin{array}{r} \left[ {\lambda _2 \left({j,k} \right) + j\mu _1 + \left({m - j} \right)\mu _2} \right]P_{j,k} = \lambda _2 \left({j,k - 1} \right)P_{j,k - 1}\\ + \left({j + 1} \right)\mu _1 P_{j + 1,k} + \left({m - j} \right)\mu _2 P_{j,k + 1},\\ 1 \le j \le m - 1,m + 1 \le j + k \le - 1,\\ \end{array}$$

(10.10)

$$\left[ {\lambda _2 \left({m,k} \right) + m\mu _1} \right]P_{m,k} = \lambda _2 \left({m,k - 1} \right)P_{m,k - 1} \;\;1 \le k \le K - m - 1.$$

(10.11)

Finally, we consider the state (j,k) such that 0 ≤ j ≤ m, j + k = K in which all servers are busy and all waiting positions are occupied, and find

$$m\mu _2 P_{0,k} = \lambda _2 \left({0,K - 1} \right)P_{0,K - 1,} $$

(10.12)

$$\left[ {j\mu _1 + \left({m - j} \right)\mu _2} \right]P_{j,k} = \lambda _2 \left({j,k - 1} \right)P_{j,k - 1,} 1 \le j \le m - 1,j + k = K,$$

(10.13)

$$m\mu _1 P_{m,k - m} = \lambda _2 \left({m,K - m - 1} \right)P_{m,K - m - 1.} $$

(10.14)

The total number of equations is given by

$$\begin{array}{l} 1 + \left({m - 1} \right) + \frac{{\left({m - 1} \right)\left({m - 2} \right)}}{2} + \left({m - 1} \right) + 1 + \left({m - 1} \right) + 1 + \left({K - m - 1} \right)\\ + \left({K - m - 1} \right)\left({m - 1} \right) + \left({K - m - 1} \right) + 1 + \left({m - 1} \right) + 1 = \left({m + 1} \right)\left({k + 1 - \frac{m}{2}} \right),\\ \end{array}$$

which equals the number of all states. One of the equations is redundant. The normalization condition is given by

$$\sum\limits_{j = 0}^m {\sum\limits_{k = 0}^{K - j} {P_{j,k} = 1.}} $$

(10.15)

Hence we have a set of linear simultaneous equations with respect to the unknowns {P _j,k ; 0 ≤ j ≤ m, 0 ≤ j + k ≤ K}. It is assumed that they are solved numerically.

Analysis of Blocking Probability and Waiting Time

We are now in a position to calculate the blocking probability of loss calls, the blocking probability of delay calls, the waiting and nonwaiting probabilities of accepted delay calls, and the waiting time distribution of accepted delay calls.

Blocking Probability of Loss Calls

Loss calls are blocked if all servers are busy upon their arrival. If the population of loss calls is infinite, the blocked loss calls are simply lost for good. If the population of loss calls is finite, the blocked loss calls are assumed to return to their source without being served.

Let us consider a long time г. The mean number of loss calls that arrive in г is given by product of the arrival rate λ₁(j,k) of loss calls and the time interval P _j,k г in which the system is in state (j,k) during г summed over all possible states as follows:

$$\sum\limits_{j = 0}^m {\sum\limits_{k = 0}^{K - j} {\lambda _1 \left({j,k} \right)P_{j,k} \tau.}}$$

(10.16)

The mean number of loss calls blocked during г is given by the product of the arrival rate λ₁(j,k) of loss calls and the time interval P _j,k гsummed over all states in which all servers are busy:

$$\sum\limits_{j = 0k = m - j}^m {\sum\limits_{}^{K - j} {\lambda _1 \left({j,k} \right)P_{j,k} \tau.}} $$

(10.17)

Thus the blocking probability P _B of loss calls is given by the ratio of the above two equations:

$$P_B = \frac{{\sum\limits_{j = 0k = m - j}^m {\sum\limits_{}^{K - j} {\lambda _1 \left({j,k} \right)} P_{j,k}}}}{{\sum\limits_{j = 0}^m {\sum\limits_{k = 0}^{K - j} {\lambda _1 \left({j,k} \right)P_{j,k}}}}}$$

(10.18)

Blocking Probability of Delay Calls

Delay calls are blocked if all servers are busy and all waiting positions are occupied upon their arrival. If the population of delay calls is infinite, the blocked delay calls are simply lost. If the population of delay calls is finite, the blocked delay calls are assumed to return to their source without being served. The mean number of arrivals of delay calls during time г is given by

$$\sum\limits_{j = 0}^m {\sum\limits_{k = 0}^{K - j} {\lambda _2 \left({j,k} \right)P_{j,k\tau.}}} $$

(10.19)

The mean number of delay calls blocked during г is given by the product of the arrival rate λ₂(j,k) of delay calls and the time interval P _j,k−j г summed over all states 0 ≤ j ≤ m in which all servers are busy and all waiting positions are occupied:

$$\sum\limits_{j = 0}^m {\lambda _2 \left({j,K - j} \right)P_{j,k - j\tau.}} $$

(10.20)

Thus the blocking probability P′_B of delay calls is given by the ratio of the two:

$$P'_B = \frac{{\sum\limits_{j = 0}^m {\lambda _2 \left({j,K - j} \right)P_{j,k - j}}}}{{\sum\limits_{j = 0}^m {\sum\limits_{k = 0}^{K - j} {\lambda _2 \left({j,k} \right)P_{j,k}}}}}$$

(10.21)

Waiting and Nonwaiting Probabilities of Accepted Delay Calls

We now consider the delay calls that are accepted upon arrival. The mean number of delay calls accepted during г is given by the product of the arrival rate λ₂(j,k) of delay calls and the time interval P _j,k г summed over all states 0 ≤ j ≤ m, 0 ≤ j+k ≤ K − 1 in which there is at least one waiting position available:

$$\sum\limits_{j = 0}^m {\sum\limits_{k = 0}^{K - j - 1} {\lambda _2 \left({j,k} \right)P_{j,k\tau.}}} $$

(10.22)

Therefore the probability that there are j loss calls and k delay calls present in the system immediately before the arrival of an arbitrary delay call that is to be accepted is given by

$$\hat P_{j,k} = \frac{{\lambda _2 \left({j,k} \right)P_{j,k}}}{{\sum\limits_{j = 0}^m {\sum\limits_{k = 0}^{K - j - 1} {\lambda _2 \left({j,k} \right)P_{j,k}}}}}, \quad 0 \le j \le m,\quad 0 \le j + k \le K - 1.$$

(10.23)

Let us denote by W the waiting time of an accepted delay call. The probability that accepted delay calls do not wait is given by the probability that there is at least one server available upon their arrival:

$$P\left\{{W = 0} \right\} = \sum\limits_{j = 0}^{m - 1} {\sum\limits_{k = 0}^{m - j - 1} {\hat P_{j,k}}} = \frac{{\sum\limits_{j = 0}^{m - 1} {\sum\limits_{k = 0}^{m - j - 1} {\lambda _2 \left({j,k} \right)P_{j,k}}}}}{{\sum\limits_{j = 0}^m {\sum\limits_{k = 0}^{K - j - 1} {\lambda _2 \left({j,k} \right)P_{j,k}}}}}.$$

(10.24)

The probability that accepted delay calls wait is given by the probability that all the servers are busy but that there is at least one waiting position available upon their arrival:

$$P\left\{{W > \;0} \right\} = \sum\limits_{j = 0}^m {\sum\limits_{k = m - j}^{K - j - 1} {\hat P_{j,k}}} = \frac{{\sum\limits_{j = 0}^m {\sum\limits_{k = m - j}^{K - j - 1} {\lambda _2 \left({j,k} \right)P_{j,k}}}}}{{\sum\limits_{j = 0}^m {\sum\limits_{k = 0}^{K - j - 1} {\lambda _2 \left({j,k} \right)P_{j,k}}}}}.$$

(10.25)

Waiting Time Distribution of Accepted Delay Calls

Let us denote by R( _{j,k, j+k−m} (s) the Laplace—Stieltjes transform (LST) of the distribution function (DF) of the waiting time of a delay call that arrives when there are j loss calls and k delay calls in the system, where j+k = m. This is the time until the total number of calls in the system decreases to m−1, at which point the service to that call is started. Then the LST of the DF for the waiting time W (>0) of accepted delay calls that are to wait is given by

$$F_W^* \left({s\left| {W > 0} \right.} \right) = \frac{{\sum\limits_{j = 0}^m {\sum\limits_{k = 0}^{k - j - 1} {\lambda _2 \left({j,k} \right)P_{j,k}} R_{j,k,j + k - m}^* \left(s \right)}}} {{\sum\limits_{j = 0}^m {\sum\limits_{k = m - j}^{k - j - 1} {\lambda _2 \left({j,k} \right)P_{j,k}}}}}.$$

(10.26)

The LST of the DF for the waiting time W (=0) of all accepted delay calls is given by

$$\begin{array}{rl} F_W^* \left(s \right) & = P\left\{{W = 0} \right\} + F_W^* \left({s\left| {W > 0} \right.} \right)P\left\{{W = 0} \right\} \\ {} & = \frac{{\sum\limits_{j = 0}^m {\left[ {\sum\limits_{k = 0}^{m - j - 1} {\lambda _2 \left({j,k} \right)P_{j,k}} + \sum\limits_{k = m - j}^{k - j - 1} {\lambda _2 \left({j,k} \right)P_{j,k} R_{j,k,j + k - m}^* \left(s \right)}} \right]}}} {{\sum\limits_{j = 0}^m {\sum\limits_{k = 0}^{k - j - 1} {\lambda _2 \left({j,k} \right)P_{j,k}}}}}. \\ \end{array} $$

(10.27)

We can obtain R( _j+k−m(s) (m j + k≤K − 1) as follows. Note that the third subscript of R( _j+k−m(s) denotes the number of calls present in the waiting room. We start with

$$R_{j,k,0}^* \left(s \right) = r_{j,k} \left(s \right) + \hat r_{j,k} \left(s \right)$$

(10.28)

for j+k = m, where

$$r_{j,k} \left(s \right) = \frac{{j\mu _2}} {{j\mu _1 + k\mu _2}} \times \frac{{j\mu _1 + k\mu _2}} {{s + j\mu _1 + k\mu _2}} = \frac{{j\mu _2}} {{s + j\mu _1 + k\mu _2}}$$

(10.29)

is the LST of the DF for the transition time from state (j,k) to state (j − 1, k), and

$$\hat r_{j,k} \left(s \right) = \frac{{k\mu _2}} {{j\mu _1 + k\mu _2}} \times \frac{{j\mu _1 + k\mu _2}} {{s + j\mu _1 + k\mu _2}} = \frac{{k\mu _2}} {{s + j\mu _1 + k\mu _2}}$$

(10.30)

is the LST of the DF for the transition time from state (j,k) to state (j,k − 1). For j+k = m + l, we have

$$R_{j,k,l}^* \left(s \right) = r_{j,k} \left(s \right)R_{j - 1,k,l - 1}^* \left(s \right) + \hat r_{j,k} \left(s \right)R_{j,k - 1,l - 1}^* \left(s \right).$$

(10.31)

Therefore, we can calculate R( _j,k,l (s) recursively for l = 1,2,...,K -m−1 by starting with R( _j,k,0(s) given in (10.28).

Numerical Examples

Using the method of analysis given in Sect. 10.3, we present numerical examples of the blocking probabilities for loss and delay calls and the mean waiting time for accepted delay calls. The latter can be obtained from the LST of the DF for the waiting time given in (10.27). We consider the cases of fixed arrival rates, balking of delay calls, and the finite population size.

Equilibrium State Probabilities

Let us first confirm that our generalization in the above yields the same results as the analysis in [5] for the M/M/m/K queue with constant arrival rates and identical service rates. To do so numerically, we consider the mixed loss-delay M/M/3/5 queue with λ₁ = ₂, λ₂ = 3, and μ₁ = μ₂ = 3. Table 10.1 shows the equilibrium state probabilities we have computed with the above method. We have confirmed that these values are identical with those calculated by using the formulas in [5].

Table 10.1 Equilibrium state probabilties in the mixed loss-delay M/M/3/5 queue with λ₁ = 2, λ₂ = 3, and μ₁ = μ₂ = 3.

Blocking Probabilities of Loss and Delay Calls

We now consider the M/M/m/K queues with constant arrival rates in the case in which the service rates are different for loss and delay calls. Figure 10.3 shows the blocking probabilities of loss and delay calls in the M/M/4/7 queue with μ₁ = 2, μ₂ = 1, λ₁ = 0.005 for 0 ≤ λ₂ ≤ 20. As the arrival rate of delay calls increases, both blocking probabilities increase. The blocking probability of loss calls increases faster than that of delay calls.

Fig. 10.3

Blocking probabilities of loss and delay calls in the M/M/4/7 queue with fixed arrival and service rates (μ₁ = 2,μ₂ = 1, λ₁ = 0.005, and 0 ≤ λ₂ ≤ 20).

Mean Waiting Time

We evaluate the mean waiting times of accepted delay calls for several cases of state-dependent arrival rates in the M/M/4/7 queue.

Fixed Arrival Rates

Figure 10.4 shows numerical examples of the mean waiting time of delay calls when μ₁ = 2, μ₂ = 1, λ₁ = {500,0.005} for 0 ≤ λ₂ ≤ 20. The mean waiting time of delay calls increases as their arrival rate λ₁ increases. When λ₂ is small, the mean waiting time increases quickly. When λ₂ is large, the mean waiting time increases slowly. We can also observe the effects of sharing the servers with loss calls on the mean waiting time.

Fig. 10.4

Mean waiting time of delay calls in the M/M/4/7 queue with fixed arrival and service rates (μ₁ = 2, μ₂ = 1, λ₁ = {500,0.005}, and 0 ≤ λ₂ ≤ 20).

Balking

Balking in the arrival process means that the arrival rate of calls decreases as the number of calls present in the system increases. We consider three models of balking for delay calls in which their arrival rates λ₂(j,k) for j+k m are given as follows: Model 1:

$${\text{Model}}\,{\text{1:}}\lambda _2 \left({j,k} \right) = V_2 \left({\frac{{K - j - k}} {{K - m}}} \right)^\alpha,\,\,\,0 \leq V_2 \leq 20,$$

Model 2:

$${\text{Model}}\,{\text{2:}}\lambda _2 \left({j,k} \right) = \frac{{V_2}} {{\left({j + k - m + 1} \right)^\alpha}},\,\,\,0 \leq V_2 \leq 20,$$

Model 3:

$${\text{Model}}\,{\text{3:}}\lambda _2 \left({j,k} \right) = V_2 e^{- \alpha \left({j + k - m} \right)},\,\,\,0 \leq V_2 \leq 20,$$

where α > 0. It is assumed that λ₂(j,k) = V₂ for 0 ≤j + k ≤ m in the three models. Model 1 is the case in which the arrival rate of delay calls decreases in power law with the occupancy ratio of waiting positions. Model 2 is the case in which the arrival rate of delay calls decreases in power law with the number of occupied waiting positions. Model 3 is the case in which the arrival rate of delay calls decreases exponentially with the number of occupied waiting positions. See Fig. 10.5 for dependence of λ₂(j,k) on the total number of calls, j + k, present in the system.

Fig. 10.5

Three models of the arrival rate of delay calls with balking (m = 4, K = 7, α = 2, ?₂ = 0.3).

In Figs. 10.6-10.8, we plot the mean waiting time of delay calls with balking for models 1-3, respectively, by assuming μ₁ = 2, μ₂ = 1, α = 2, λ₁ = {500,0.005} for 0 ≤ V₂ ≤ 20.

Fig. 10.6

Mean waiting time of delay calls in the M/M/4/7 queue with balking of model 1

Fig. 10.7

Mean waiting time of delay calls in the M/M/4/7 queue with balking model 2 (μ₁ =2, μ₁ = 1, μ₁ = {500, 0.005}, α = 2, and 0 ≤ V₂ ≤ 20).

Fig. 10.8

Mean waiting time of delay calls in the M/M/4/7 queue with balking model 3

Finite Population Size

M/M/m/K queues with finite population of loss and delay calls can be handled with our model of state-dependent arrival rates by assuming that

$$\begin{array}{*{20}c} {\lambda _1 \left({j,k} \right) = \left({n_1 - j} \right)V_1,\,\,\,\,\,\,0 \leq j \leq n_1,} \\ {\lambda _2 \left({j,k} \right) = \left({n_2 - j} \right)V_2,\,\,\,\,\,\,0 \leq j \leq n_2,} \\ \end{array} $$

where n ₁ and n ₂ are the fixed total numbers of loss and delay calls, respectively. The call arrivals then form pseudo-Poisson processes.

In Fig. 10.9, we show the mean waiting time of delay calls in the finite population model with μ₁ = 2, μ₂ = 1, n ₁ = n ₂ = 20, α = 2, V₁ = {25, 0.00025} for 0 ≤ v₂≤ 1.

Fig. 10.9

Mean waiting time of delay calls in the M/M/4/7 queue with finite population (μ₁ = 2, μ₂ = 1, n ₁ = n ₂ = 20, α = 2, V₁ = {25, 0.00025}, and 0 ≤ V₂ ≤ 1).

Concluding Remarks

In this chapter, we have shown the analysis of a mixed loss-delay M/M/m/K queue- ing system with state-dependent arrival rates and different constant service rates. We have first presented a set of linear simultaneous equations for the equilibrium state probabilities and the normalization condition. We have then evaluated the blocking probabilities for loss and delay calls and the mean waiting time for accepted delay calls.

For numerical examples, we have considered the cases of fixed arrival rates, balking of delay calls, and finite population size in the M/M/4/7 queueing system. In these examples, we have observed how the mean waiting time of accepted delay calls increases as their arrival rate increases when they share the servers with loss calls.

It is our future work to extend the model to allow multiple classes of both loss and delay calls with some scheduling discipline among them. Such a model would be closer to the channel sharing by circuit- and packet-switched traffic in the next- generation wireless communication systems.