On first-come, first-served queues with three classes of impatient customers

Abstract

In this article, we study queuing systems with three classes of impatient customers which differ across the classes in their distribution of service times and patience times. The customers are served on a first-come, first-served (FCFS) policy independent of their classes. Such systems are common in customer call centers, which often segment their arrivals into classes of callers whose requests differ in complexity and criticality. First of all, we consider an $M/G/1 + M$ queue and then analyze the $M/M/m + M$ system. Using the virtual waiting time process, we obtain performance measures such as the percentage of customers receiving service in each class, the expected waiting times of customers in each class, and the average number of customers waiting in the queue. We use our characterization to perform a numerical analysis of the $M/M/m + M$ system. Finally, we compare the performance of a system based on numerical solution with the steady-state performance measures of a comparable $M/M/m + M$ system.

1 Introduction

In this article, we consider a queue system with three different classes of impatient customers which are independent in their arrival and service time distributions. As the customers have limited patience, customers may abandon the system whenever their waiting time exceeds the patience time. In a call center, such situations (abandonment without service) are frequent which motivates us to categorize the customers into the three different classes, as it may lead to improved performance of the system. For example, credit card call center service requests can be categorized into credit limit, pin change, and fraudulent activity on a credit card holder’s account. Here customer representatives can respond to credit limit inquiries quickly, for pin change they might ask for verification details, effectively it may take a few minutes. But on the other hand, the representative who responds to a fraudulent activity call needs more time as compared to other categories. Customer’s requests vary; therefore, call centers train their subset of employees to handle only a certain type of service requests. Based on the customer’s request, the automatic call distributor will divert their call to a suitable representative. Depending on the type of service requests, each class of customers is independent of each other with respect to their distribution of patience times and service times. Therefore, a subset of employees may serve a queue that receives arrivals from different classes that vary from each other in their service requirements and their callers’ patience levels. Here, note that call centers sometimes may assign tags to their customers like most valued, valued, or ordinary to priorities the customers. However, we have to consider the callers’ request on a first-come, first-served (FCFS) basis independent of their class. In this paper, we analyzed the performance of the FCFS queue system with three classes of customers that may differ from each other in both their distribution of patience times and their distribution of service times.

Studies for describing the performance of queue systems with a single class of “impatient customers” have included analytical characterizations (Daley [10], Baccelli and Hebuterne [3], Stanford [16]) and approximations to performance (Garnett et al. [11], Zeltyn and Mandelbaum [18], Iravani and Balcıoğlu [13]). Literature has many studies of two-class systems, where most of the systems have prioritized one customer over the other. Choi et al. [9] study the underlying Markov process of an M/M/1 queue with impatient customers of higher priority. Brandt and Brandt [5] extend the approach in [9] for the generally distributed first-class customers in two-class M/M/1 system. Iravani and Balcıoğlu [14] use the level-crossing technique proposed by Brill and Posner [7, 8] to study two M/GI/1 systems, where they consider a preemptive-resume discipline where customers’ classes have exponentially distributed patience times and then consider a non-preemptive discipline where customers in the first class have exponentially distributed patience times, but customers in the other class have patience. Iravani and Balcıoğlu [13] obtain the waiting time distributions for each class and the probability that customers in each class will abandon them. Adan et al. [1] design heuristics to determine the staffing levels required to meet target service levels in an overloaded FCFS multiclass system with impatient customers. Van Houdt [12] considers a MAP/PH/1 multiclass queue where customers in each of the classes have a general distribution of patience times. Van Houdt [12] derive a numerical method for analyzing the performance of the system by reducing the joint workload and arrival processes to a fluid queue and expresses the steady-state measures using matrix analytical methods. His method provides an exact characterization of the waiting time distribution and abandonment probability under a discrete distribution of patience times, and approximations of the same performance measures under a continuous distribution of patience times. Sakuma and Takine [15] study the M/PH/1 system and assume that customers in each class have the same deterministic patience time.

Our work is mainly focused on the system in which three classes of impatient customers are served on an FCFS basis, independent of their class. Ivo Adan et.al. [2] study a similar system with two classes of impatient customers, they analyze this process to obtain performance measures such as the percentage of customers receiving service in each class, the expected waiting times of customers in each class, and the average number of customers waiting in the queue. We consider two systems ($M/M/1+M,~ M/M/m+M$) with three classes of impatient customers, which are served according to an FCFS discipline. To analyze the performance of these systems, we used the virtual waiting time process, see Benes [4], Takács et al. [17] and Ivo Adan et al. [2]. In a virtual waiting time process, the service times of customers who will eventually abandon the system are not considered. By analyzing this process, we find performance characteristics such as the percentage of customers who receive service in each class, the expected waiting times of customers in each class, and the average number of customers waiting in the queue from each class. A related formula for the virtual waiting time in a single class $M/G/1+PH$ queue is given by Brandt and Brandt [6], it is not suitable for direct computation as it consists of an exponentially growing number of terms. We next perform a numerical analysis of the $M/M/m+M$ system under many arrival rates, mean service times, and mean patience times. Our analysis explains that accounting for differences across classes in the distribution of customers’ service times and patience times is critical, as the performance of our system differs considerably from a system where only the service time distribution varies across classes. The results of our numerical analysis have several administrative implications including service level forecasting, revenue management, and the evaluation of server productivity. Finally, we compare the performance of a system based on numerical results of a comparable $M/M/m+M$ system.

This article is organized as follows: In Sect.2, we study the $M/G/1+M$ queue. In Sect. 3, we study the $M/M/m+M$ queue system, including a special case where the three classes have the same mean service time. In Sect. 4, we derive steady-state performance measures. In Sect. 5, we present our numerical analysis, and in Sect. 6, conclusion is given.

2 $M/G/1+M$ system

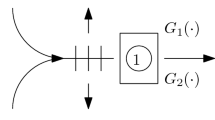
Firstly we consider a single-server queueing system with three classes of impatient customers; see Figure 1. Assume that the arrival of Class $i \,(i=1,2,3)$ customers is according to the independent Poisson process with rate $\lambda _i$ and needs independent and identically distributed (iid) service times with CDF $G_i(.)$ and mean $\tau _i$. The customers are impatient, and the patience time distribution for Class $i\,(i=1,2,3)$ customers is exponential with parameter $\theta _i$ and are independent. That is customers from Class i abandon the system after an exponential amount of time with parameter $\theta _i$ if their queuing time is longer than their patience time. For this system, our main aim is to determine performance characteristics such as the long-run fraction of customers entering service, server utilization, and the expected waiting time for the service. Since the customers are impatient in each class, the system will always be stable even if the total arrival rate exceeds the service rate.

Fig. 1

Single-server model

It is natural to analyze this system through its queue length process. However, keeping the information of the number of customers from each class is not enough. We would also require the information of the class of each customer at each position in the queue since patience times depend on customer class. This provides the Markov process intractable. Therefore, we used the virtual queueing time process below as in [2].

Let W(t) be the virtual queueing time at time t. W(t) decreases with a rate 1 at all times, provided that it is positive. If an arrival from Class i customers occurs at time t and $W(t)= w$, the arrival leaves the system without service with probability $1-{\mathrm {{e}}^{-\theta _i w}}$ , or enters for the service with probability ${\mathrm {{e}}}^{-\theta _i w}$, and require a random amount of service with CDF $G_i(\cdot )$. Hence, the distribution of $S_i(t)$, the size of the upward jump at time t due to an arrival from Class i customers, given $W(t)=w$, is given by

$$\begin{aligned} P(S_i(t) \le y|W(t) = w) = 1-{\mathrm {{e}}}^{-\theta _i w} + {\mathrm {{e}}}^{-\theta _i w}G_i(y), \end{aligned}$$

(1)

and thus

$$\begin{aligned} E(\mathrm {{e}}^{-s S_i(t)}|W(t)=w)=&{} 1-{\mathrm {{e}}}^{-\theta _i w} + {\mathrm {{e}}}^{-\theta _i w} {\tilde{G}}_i(s) , \end{aligned}$$

where ${\tilde{G}}_i(\cdot )$ is the Laplace-Stieltjes transform (LST) of $G_i(\cdot )$. Let

$$\begin{aligned} \psi (s,t)=&\, {} E(\mathrm {{e}}^{-s W(t)}), \\ p_0(t)=&\, {} P(W(t)=0), \\ \phi (s,t)=&\, {} \psi (s,t) - p_0 (t), \end{aligned}$$

and

$$\begin{aligned} \psi (s)=&\lim _{t \rightarrow \infty } \psi (s,t) = E{\mathrm {e}^{-sW}} ,\\p_0=&\lim _{t \rightarrow \infty } p_0(t) = {} P(W=0), \\ \phi (s)=&\, \psi (s) - p_0, \end{aligned}$$

where W is the limit (in distribution) of W(t) as $t \rightarrow \infty$. In the interval $(t,t+h]$, an arrival of type i occurs with probability $\lambda _ih + o(h)$ , and no event occurs with probability $1 - (\lambda _1 + \lambda _2+\lambda _3)h + o(h)$ as $h \rightarrow 0$. Then, we obtain

$$\begin{aligned} \psi (s,t+h)=&\, {} (1-\lambda _1 h-\lambda _2 h-\lambda _3h) \phi (s,t) {\mathrm {{e}^{sh}}} \\&+ (1-\lambda _1 h-\lambda _2 h-\lambda _3h) p_0(t) \\&+ \sum _{i=1}^3 \lambda _i h (\phi (s,t) - \phi (s+\theta _i,t) \\&+ \psi ( s+\theta _i,t) {\tilde{G}}_i(s) ) + o(h). \end{aligned}$$

putting${\mathrm {{e}}}^{sh} = 1 + sh + o(h)$ and rearranging terms and dividing by h, and then letting $h \rightarrow 0$, we find

$$\begin{aligned} \frac{d}{dt}\psi (s,t)=&{} s\phi (s,t) - \sum _{i=1}^3 \lambda _i \psi (s+\theta _i,t) (1- {\tilde{G}}_i(s)). \end{aligned}$$

Now let $t\rightarrow \infty$. Then, $\frac{d}{dt}\psi (s,t) \rightarrow 0,\psi (s,t) \rightarrow \psi (s)$ and $\phi (s,t) \rightarrow \phi (s)$,so

$$\begin{aligned} 0=&{} s\phi (s) - \sum _{i=1}^3 \lambda _i \psi (s+\theta _i) (1-{\tilde{G}}_i(s)) . \end{aligned}$$

Dividing by s and using

$$\begin{aligned} {H}_i(s) = \lambda _i \frac{1-{\tilde{G}}_i(s)}{ s}, \end{aligned}$$

we finally get

$$\begin{aligned} \varvec{\psi } (s) = p_0 + \sum _{i=1}^3 \varvec{\psi } (s+\theta _i) {H}_i(s). \end{aligned}$$

(2)

Note that, the LST of the equilibrium distribution of the service times of customers from Class i is ${H}_i(s)/(\lambda _i \tau _i)$.

Repeated application of (2) shows that its solution can be written as

$$\begin{aligned} \varvec{\psi } (s) = p_0 c(s), \end{aligned}$$

(3)

where

$$\begin{aligned} c(s) = \sum _{i=0}^\infty \sum _{j=0}^\infty \sum _{k=0}^\infty c_{i,j,k}(s). \end{aligned}$$

The terms $c_{i,j,k}(s)$ satisfy the recurrence relation

$$\begin{aligned} c_{i,j,k}(s) ={}&{H}_1(s+(i-1)\theta _1+j\theta _2+k\theta _3)c_{i-1,j,k}(s) \\ {}&+ {H}_2(s+ i\theta _1+(j-1)\theta _2+k\theta _3)c_{i,j-1,k}(s)\\ {}&+ {H}_3(s+ i\theta _1+j\theta _2+(k-1)\theta _3)c_{i,j,k-1}(s), \end{aligned}$$

with $c_{0,0,0}(s)=1$ and $c_{i,j,k}(s)=0$ if $i<0$ or $j<0$ or $k<0$. The recursive procedure to obtain equation (3) as well as convergence properties of the series c(s) will be explained in detail in Sect. 3, where we analyze the multi-server system with three classes. Now, to find $p_0$, we use $\psi (0)=1$ in equation (2), we get

$$\begin{aligned} p_0&= 1 - \sum _{i=1}^3 \psi (\theta _i)\lambda _i \tau _i = 1 - p_0 \sum _{i=1}^3 c(\theta _i) \lambda _i \tau _i , \\ \Rightarrow p_0&= \left[ 1+\sum _{i=1}^3 c(\theta _i) \lambda _i \tau _i \right] ^{-1}. \end{aligned}$$

In Sect. 4, we shall see that many performance measures can be computed in terms of $\psi (\theta _i)$.

3 $M/M/m+M$ system

Now we consider a FCFS multi-server system with m servers serving 3 classes of impatient customers; see Figure 2.

3.1 Model

Unlike in Section 2, we assume that customers from Class i arrive according to a Poisson process with rate $\lambda _i$, need iid ${\mathrm {Exp}}(\mu _i)$ service times, and have iid ${\mathrm {Exp}}(\theta _i)$ patience times $( i=1,2,3 )$. Whenever service does not begin before the patience time expires, the customer leaves without service.

Fig. 2

m-server model

3.2 Virtual queueing time process

We assume that W(t) be the virtual queueing time at time t in this system. This is the queueing time that would be experienced by a virtual customer arriving at time t. Let $N_i(t)$ be the number of servers serving a Class i customer just after time $t+W(t)$ but before the next customer (if there is one) entering service at time $t+W(t)$. This tells that $N_i(t)$ is the number of servers busy with a Class i customer just before a customer arriving at time t enters for service. So we observe that $N_1(t)+N_2(t)+N_3(t)$ is always at most $m-1$.

The above definition allows us to determine the size of the upward jump of the virtual queuing time if an arriving customer at time t decides to join the queue (since his patience exceeds W(t)). The jump is the minimum of the service time of the arriving customer and the residual service times of the customers in service at the moment he enters service at time $t+W(t)$. As we will explain below, $\{(W(t), N_1(t), N_2(t),N_3(t)), t \ge 0\}$ is a Markov process with upward jumps, the size of which depends on W(t), and a continuous downward deterministic drift of rate 1 between jumps.

Assume that $W(t)=0$ and $(N_1(t),N_2(t),N_3(t)) = (i,j,k).$ Then, (i, j, k) is the number of busy servers of classes 1, 2 and 3 at time t. For $0\le i+j+k \le m-1,$ the transition rates of services in state (0, i, j, k) are given by

$$\begin{aligned} q_{(0,i,j,k),(0,i-1,j,k)}=&\, i\mu _1,\\ q_{(0,i,j,k),(0,i,j-1,k)}=&\, j\mu _2,\\ q_{(0,i,j,k),(0,i,j,k-1)}=&\, k\mu _3, \end{aligned}$$

and for $0\le i+j+k<m-1$, the transitions rates of arrivals are

$$\begin{aligned} q_{(0,i,j,k),(0,i+1,j,k)}=&\, \lambda _1,\\ q_{(0,i,j,k),(0,i,j+1,k)}=&\, \lambda _2,\\ q_{(0,i,j,k),(0,i,j,k+1)}=&\, \lambda _3. \end{aligned}$$

Now we have all transitions from states $(0,i,j,k),\,0\le i+j+k \le m-1,$ except for the transition rates of arrivals in states with $i+j+k = m-1.$ These transition rates are explained below

Now assume that the state of the quad-variate process at time t is (w, i, j, k) with $w\ge 0$ and $i+j+k=m-1.$ This explains that just after time $t+w$ we will have i busy servers of Class 1 , j busy servers of Class 2 and k busy servers of Class 3. Consider an arrival from Class 1 at time t. This customer has to wait w amount of time for service to begin. He abandons the system before his service starts with probability $1-e^{-\theta _1w}$, in which case the state does not change, and he enters for service at time $t+w$ with probability $e^{-\theta _1w}$. Then, the next departure occurs after an ${\mathrm {Exp}((i+1)\mu _1}+j\mu _2+k\mu _3)$ time X and the departure at time $t+w+X$ is from Class 1 with probability $(i+1)\mu _1/((i+1)\mu _1+j\mu _2+k\mu _3)$, from Class 2 with probability $j\mu _2/((i+1)\mu _1+j\mu _2+k\mu _3)$ and from Class 3 with probability $k\mu _3/((i+1)\mu _1+j\mu _2+k\mu _3)$. In the first case, the state jumps at time t from (w, i, j, k) to $(w+X,i,j,k)$. In the second and third cases, the state jumps to $(w+X,i+1,j-1,k)$ and $(w+X,i+1,j,k-1)$, respectively. In the case of a Class 2 and 3 arrival, the process is similar.

Hence, we get the following transition rates from states (w, i, j, k) with $w\ge 0$ and $i+j+k=m-1;$

$$\begin{aligned}&q_{(w,i,j,k),\,([w+x,w+x+dx),i+1,j-1,k)}\\&\quad = \, \lambda _1 {\mathrm {{e}}^{-\theta _1 w}}((i+1) \mu _1 + j \mu _2 +k \mu _3) \\&\qquad \times\mathrm {e}^{-((i+1)\mu _1+j\mu _2+k \mu _3)x}dx\\&\ \qquad\times \,\frac{j \mu _2}{(i+1) \mu _1 + j \mu _2+k \mu _3 }\\&\quad = \, \lambda _1{\mathrm {{e}}^{-\theta _1 w}} j\mu _2 \\&\qquad \times {\mathrm {{e}}^{-((i+1)\mu _1+j\mu _2+k \mu _3)x}}dx ,\end{aligned}$$

similarly;

$$\begin{aligned}&q_{(w,i,j,k),\,([w+x,w+x+dx),i,j,k)}\\&\quad = \, \lambda _1 {\mathrm {{e}}^{-\theta _1 w} (i+1) \mu _1 \mathrm {{e}}^{-((i+1) \mu _1 +j \mu _2+k \mu _3)x}}dx\\&\qquad +\, \lambda _2 {\mathrm {{e}}^{-\theta _2 w} (j+1) \mu _2 \mathrm {{e}}^{-(i\mu _1+(j+1)\mu _2+k \mu _3)x}}dx\\&\qquad +\, \lambda _3 {\mathrm {{e}}^{-\theta _3 w} (k+1) \mu _2 \mathrm {{e}}^{-(i\mu _1+j\mu _2+(k+1) \mu _3)x}}dx ,\\& q_{(w,i,j,k),\,([w+x,w+x+dx),i+1,j,k-1)} \\&\quad= \, \lambda _1 {\mathrm {{e}}^{-\theta _1 w} k \mu _3 \mathrm {{e}}^{-((i+1)\mu _1}+j\mu _2+k \mu _3)x}dx .\\&q_{(w,i,j,k),\,([w+x,w+x+dx),i-1,j+1,k)}\\&\quad = \, \lambda _2 {\mathrm {{e}}^{-\theta _2 w} i \mu _1 \mathrm {{e}}^{-(i\mu _1+(j+1)\mu _2+k \mu _3)x}}dx .\\&q_{(w,i,j,k),\,([w+x,w+x+dx),i-1,j,k+1)}\\&\quad = \, \lambda _3 {\mathrm {{e}}^{-\theta _3 w} i \mu _1 \mathrm {{e}}^{-(i\mu _1+j\mu _2+(k+1) \mu _3)x}}dx .\\& q_{(w,i,j,k),\,([w+x,w+x+dx),i,j+1,k-1)}\\&\quad = \, \lambda _2 {\mathrm {{e}}^{-\theta _2 w} k \mu _3 \mathrm {{e}}^{-(i\mu _1+(j+1)\mu _2+k \mu _3)x}}dx .\\& q_{(w,i,j,k),\,([w+x,w+x+dx),i,j-1,k+1)}\\&\quad = \, \lambda _3 {\mathrm {{e}}^{-\theta _3 w} j \mu _2 \mathrm {{e}}^{-(i\mu _1+j\mu _2+(k+1) \mu _3)x}}dx . \end{aligned}$$

Between upward jumps, the virtual waiting time process W decreases continuously and deterministically at a rate 1, while it is positive. When W reaches 0 in state (0, i, j, k), the process will stay in this state until either an service completion or arrival occurs.

3.3 Steady-state analysis

We first begin with the following notations. Let

$$\begin{aligned}\psi _{i,j}(s,t)&= \,E(e^{-sW(t)}; N_1(t) =i,N_2(t)=j, \\&\quad \ N_3(t) = m-1-i-j) , \ 0 \le i+j \le m-1,\\p_{i,j,k} (t)&= \, P(W(t) = 0, \ N_1(t) = i, \ N_2(t) = j,\\&\quad N_3(t)=k), \ \quad 0\le i+j+k \le m-1,\\ \phi _{i,j}(s,t)&= \, \psi _i (s,t) \\&\quad -p_{i,j,m-1-i-j}(t), \ 0 \le i+j \le m-1, \end{aligned}$$

and is the identity matrix where $(W(t),N_1(t),N_2(t),N_3(t))$ converges to $(W,N_1,N_2,N_3)$ in distribution as $t\rightarrow \infty$. We begin with the balance equations for the steady-state probabilities $p_{i,j,k}$. Let

$$\begin{aligned} {\varvec{p}}_n = [p_{i,j,k}] , \quad 0\le i,j,k\le n,\, i+j+k=n, \,{\text {and}}\, 0\le n<m . \end{aligned}$$

where

$$\begin{aligned}&{\varvec{p}}_0=[p_{0,0,0}],\\&\quad {\varvec{p}}_1= [p_{0,0,1} ~p_{0,1,0}~ p_{1,0,0}],\\&\quad {\varvec{p}}_2=[p_{0,0,2} ~p_{0,1,1}~ p_{0,2,0}~p_{1,0,1}~ p_{1,1,0}~ p_{2,0,0}],\\&\quad {\varvec{p}}_3=[p_{0,0,3} ~p_{0,1,2}~ p_{0,2,1}~\\&\quad p_{0,3,0}~p_{1,0,2}~ \\&\quad p_{1,1,1}~ p_{1,2,0}~ p_{2,0,1}~ p_{2,1,0}~ p_{3,0,0}],\\&\quad \vdots \\&\quad {\varvec{p}}_n=[p_{0,0,n} ~p_{0,1,n-1}~ \cdots ~ p_{0,n,0}~p_{1,0,n-1}~p_{1,1,n-2}~ \cdots ~ \\&\quad p_{1,n-1,0}~\cdots p_{n-1,0,1}~ p_{n-1,1,0}~ p_{n,0,0}]\\ \end{aligned}$$

Then, the balance equations can be written in vector-matrix form as

$$\begin{aligned}&{\varvec{p}}_0 (\lambda _1+\lambda _2+\lambda _3)\nonumber \\&\quad = \, {\varvec{p}}_1 \varvec{M}_1,\nonumber \\&\quad {\varvec{p}}_n (\lambda _1+\lambda _2+\lambda _3)\nonumber \\&\quad + {\varvec{p}}_n \varvec{\Delta } _{n}\nonumber \\&\quad = \, {\varvec{p}}_{n-1} \varvec{\Lambda } _{n-1} + {\varvec{p}}_{n+1} \varvec{M}_{n+1},\nonumber \\&\quad 1 \le n < m-1, \end{aligned}$$

(4)

where the $\frac{(n+1)(n+2)}{2}\times \frac{(n+1)(n+2)}{2}$ matrix $\Delta _n=diag[(n-i-j)\mu _3+j\mu _2+i\mu _1]$, $0\le i+j\le n$ (here i, j as in the $\phi (s)$), the matrix of the order $\frac{(n+1)(n+2)}{2}\times \frac{(n+2)(n+3)}{2},$ $\Lambda _n=[\lambda _{n,u,v}]$ and the matrix $M_n=[\mu _{n,i,j,k}]$ of the order $\frac{(n+1)(n+2)}{2}\times \frac{n(n+1)}{2}$ is given by

$$\begin{aligned} \lambda _{{n,u,v}} & = \left\{ {\begin{array}{*{20}l} {\lambda _{1} ,} \hfill & {v = u + m} \hfill \\ {\lambda _{2} ,} \hfill & {v = u + 1,\;1 \le u \le (m - 1),} \hfill \\ {} \hfill & {v = u + 2,\;m \le u \le (m - 1) + (m - 2),} \hfill \\ {} \hfill & \vdots \hfill \\ {} \hfill & {v = u + (m - 1),\;u = (m - 1) + (m - 2) + \cdots + 2 + 1} \hfill \\ {\lambda _{3} ,} \hfill & {v = u,\;1 \le u \le (m - 1),} \hfill \\ {} \hfill & {v = u + 1,\;m \le u \le (m - 1) + (m - 2),} \hfill \\ {} \hfill & \vdots \hfill \\ {} \hfill & {v = u + (m - 2),\;u = (m - 1) + (m - 2) + \cdots + 2 + 1} \hfill \\ \end{array} } \right., \\ & \quad \mu _{{n,(i,j,k),(i - 1,j,k)}} = i\mu _{1} ,\quad 1 \le i \le n, \\ & \quad \mu _{{n,(i,j,k),(i,j - 1,k)}} = j\mu _{2} ,\quad 0 \le j \le n, \\ & \quad \mu _{{n,(i,j,k),(i,j,k - 1)}} = k\mu _{3} ,\quad 0 \le k \le n. \\ \end{aligned}$$

Further, we can write above balance equations as

$$\begin{aligned} \varvec{p_n}=\varvec{p}_{n+1}\varvec{R}_{n+1}, \quad 0\le n < m-1. \end{aligned}$$

(5)

The $\frac{(n+2)(n+1)}{2}\times \frac{(n+1)n}{2}$ matrices $\varvec{R}_{n}$, recursively written as

$$\begin{aligned}&\varvec{R}_1=~ \varvec{M}_1(\lambda _1\\&\quad +\lambda _2+\lambda _3)^{-1}\\&\quad \varvec{R}_{n+1}=~\varvec{M}_{n+1}((\lambda _1+\lambda _2+\lambda _3)I\\&\quad +\varvec{\Delta }_n-\varvec{R}_n\varvec{\Lambda }_{n-1})^{-1},1\le n < m-1 \end{aligned}$$

where ${\mathrm {I}}$ is the identity matrix.

Now we shall derive differential equations for the time-dependent LSTs $\psi _{i,j}(s,t)$ and then take t to $\infty$ to obtain the steady state equations. For small $h>0,$ we have

$$\begin{aligned}&\psi _{i,j}(s,t+h)= {} (1-\lambda _1 h-\lambda _2 h-\lambda _3 h) \phi _{i,j} (s,t) {\mathrm {{e}}^{sh}}\\&\quad +\, (1-\lambda _1 h-\lambda _2 h -\lambda _3 h-(i\mu _1 + j\mu _2+(m-1-i-j)\mu _3)h) p_{i,j,m-1-i-j} (t) \\ {}&\quad +\, \lambda _1 h (\phi _{i,j} (s,t) - \phi _{i,j}(s+\theta _1,t)) \\ {}&\quad +\, \lambda _2 h (\phi _{i,j}(s,t) - \phi _{i,j}(s+\theta _2,t)) \\ {}&\quad +\,\lambda _3 h (\phi _{i,j} (s,t) - \phi _{i,j}(s+\theta _3,t)) \\ {}&\quad +\, \lambda _1 h \psi _{i,j} ( s+\theta _1,t) \frac{(i+1)\mu _1}{s+(i+1)\mu _1 + j\mu _2+(m-1-i-j)\mu _3} \\ {}&\quad +\, \lambda _1 h \psi _{i,j} ( s+\theta _1,t) \frac{j\mu _2}{s+(i+1)\mu _1 + j\mu _2+(m-1-i-j)\mu _3} \\ {}&\quad +\, \lambda _1 h \psi _{i-1,j} ( s+\theta _1,t) \frac{(m-i-j)\mu _3}{s+i\mu _1 + j\mu _2+(m-i-j)\mu _3} \\ {}&\quad +\, \lambda _2 h \psi _{i,j} ( s+\theta _2,t) \frac{i\mu _1}{s+i\mu _1 + (j+1)\mu _2+(m-1-i-j)\mu _3} \\ {}&\quad +\, \lambda _2 h \psi _{i,j} ( s+\theta _2,t) \frac{(j+1)\mu _2}{s+i\mu _1 + (j+1)\mu _2+(m-1-i-j)\mu _3} \\ {}&\quad +\, \lambda _2 h \psi _{i,j-1} ( s+\theta _2,t) \frac{(m-i-j)\mu _3}{s+i\mu _1 + j\mu _2+(m-i-j)\mu _3} \\ {}&\quad +\, \lambda _3 h \psi _{i+1,j} ( s+\theta _3,t) \frac{(i+1)\mu _1}{s+(i+1)\mu _1 + j\mu _2+(m-1-i-j)\mu _3}\\ \\ {}&\quad +\, \lambda _3 h \psi _{i,j+1} ( s+\theta _3,t) \frac{(j+1)\mu _2}{s+i\mu _1 + (j+1)\mu _2+(m-1-i-j)\mu _3} \\ {}&\quad +\, \lambda _3 h \psi _{i,j} ( s+\theta _3,t) \frac{(m-i-j)\mu _3}{s+i\mu _1 + j\mu _2+(m-i-j)\mu _3} \\ {}&\quad +\, \lambda _1 h p_{i-1,j,m-1-i-j} (t) \\ {}&\quad +\, \lambda _2 h p_{i,j-1,m-1-i-j} (t) \\ {}&\quad +\, \lambda _3 h p_{i,j,m-2-i-j} (t)+ o(h), \end{aligned}$$

where $p_{i,j,k}(t)=0, ~{\mathrm {if}} ~ i<0~{\mathrm {or}}~j<0~{\mathrm {or}}~k<0$. Also substituting $e^{sh}=1+sh+o(h)$, rearranging terms, dividing by h and then taking limit as $h\rightarrow 0$, we get

$$\begin{aligned}&\frac{d}{dt}\psi _{i,j}(s,t)=~ s\phi _{i,j}(s,t)\\&\quad -\lambda _1\psi _{i,j}{(s+\theta _1,t)} -\lambda _2\psi _{i,j}{(s+\theta _2,t)}\\&\quad -\lambda _3\psi _{i,j}{(s+\theta _3,t)}\\&\quad -(i\mu _1 + j\mu _2+(m-1-i-j)\mu _3)h) p_{i,j,m-1-i-j} (t) \\ {}&\quad +\, \lambda _1 \psi _{i,j} ( s+\theta _1,t) \frac{(i+1)\mu _1}{s+(i+1)\mu _1 + j\mu _2+(m-1-i-j)\mu _3} \\ {}&\quad +\, \lambda _1 \psi _{i,j} ( s+\theta _1,t) \frac{j\mu _2}{s+(i+1)\mu _1 + j\mu _2+(m-1-i-j)\mu _3} \\ {}&\quad +\, \lambda _1 \psi _{i-1,j} ( s+\theta _1,t) \frac{(m-i-j)\mu _3}{s+i\mu _1 + j\mu _2+(m-i-j)\mu _3} \\ {}&\quad +\, \lambda _2 \psi _{i,j} ( s+\theta _2,t) \frac{i\mu _1}{s+i\mu _1 + (j+1)\mu _2+(m-1-i-j)\mu _3} \\ {}&\quad +\, \lambda _2 \psi _{i,j} ( s+\theta _2,t) \frac{(j+1)\mu _2}{s+i\mu _1 + (j+1)\mu _2+(m-1-i-j)\mu _3} \\ {}&\quad +\, \lambda _2 \psi _{i,j-1} ( s+\theta _2,t) \frac{(m-i-j)\mu _3}{s+i\mu _1 + j\mu _2+(m-i-j)\mu _3} \\ {}&\quad +\, \lambda _3 \psi _{i+1,j} ( s+\theta _3,t) \frac{(i+1)\mu _1}{s+(i+1)\mu _1 + j\mu _2+(m-1-i-j)\mu _3} \\ {}&\quad +\, \lambda _3 \psi _{i,j+1} ( s+\theta _3,t) \frac{(j+1)\mu _2}{s+i\mu _1 + (j+1)\mu _2+(m-1-i-j)\mu _3} \\ {}&\quad +\, \lambda _3 \psi _{i,j} ( s+\theta _3,t) \frac{(m-i-j)\mu _3}{s+i\mu _1 + j\mu _2+(m-i-j)\mu _3} \\ {}&\quad +\, \lambda _1 p_{i-1,j,m-1-i-j} (t) \\ {}&\quad +\, \lambda _2 p_{i,j-1,m-1-i-j} (t) \\ {}&\quad +\, \lambda _3 p_{i,j,m-2-i-j} (t) \end{aligned}$$

For the steady state, as $t\rightarrow \infty$ the system attains steady state so that $\frac{d}{dt}\psi _{i,j}(s,t)\rightarrow 0,\,\psi _{i,j}(s,t)\rightarrow \,\psi _{i,j}(s),\,\phi _{i,j}(s,t)\rightarrow \phi _{i,j}(s)$ and $p_{i,j,k}(t)\rightarrow p_{i,j,k}$. Therefore, we have

$$\begin{aligned} 0= &\;s\phi _{i,j}(s)-\lambda _1\psi _{i,j}{(s+\theta _1)} -\lambda _2\psi _{i,j}{(s+\theta _2)}-\lambda _3\psi _{i,j}{(s+\theta _3)} \nonumber \\ {}&-(i\mu _1 + j\mu _2+(m-1-i-j)\mu _3) p_{i,j,m-1-i-j} \nonumber \\ {}&+\, \lambda _1 \psi _{i,j} ( s+\theta _1) \frac{(i+1)\mu _1}{s+(i+1)\mu _1 + j\mu _2+(m-1-i-j)\mu _3} \nonumber \\ {}&+\, \lambda _1 \psi _{i,j} ( s+\theta _1) \frac{j\mu _2}{s+(i+1)\mu _1 + j\mu _2+(m-1-i-j)\mu _3} \nonumber \\ {}&+\, \lambda _1 \psi _{i-1,j} ( s+\theta _1) \frac{(m-i-j)\mu _3}{s+i\mu _1 + j\mu _2+(m-i-j)\mu _3} \nonumber \\ {}&+\, \lambda _2 \psi _{i,j} ( s+\theta _2) \frac{i\mu _1}{s+i\mu _1 + (j+1)\mu _2+(m-1-i-j)\mu _3} \nonumber \\ {}&+\, \lambda _2 \psi _{i,j} ( s+\theta _2) \frac{(j+1)\mu _2}{s+i\mu _1 + (j+1)\mu _2+(m-1-i-j)\mu _3} \nonumber \\ {}&+\, \lambda _2 \psi _{i,j-1} ( s+\theta _2) \frac{(m-i-j)\mu _3}{s+i\mu _1 + j\mu _2+(m-i-j)\mu _3} \nonumber \\ {}&+\, \lambda _3 \psi _{i+1,j} ( s+\theta _3) \frac{(i+1)\mu _1}{s+(i+1)\mu _1 + j\mu _2+(m-1-i-j)\mu _3} \nonumber \\ {}&+\, \lambda _3 \psi _{i,j+1} ( s+\theta _3) \frac{(j+1)\mu _2}{s+i\mu _1 + (j+1)\mu _2+(m-1-i-j)\mu _3} \nonumber \\ {}&+\, \lambda _3 \psi _{i,j} ( s+\theta _3) \frac{(m-i-j)\mu _3}{s+i\mu _1 + j\mu _2+(m-i-j)\mu _3} \nonumber \\ {}&+\, \lambda _1 p_{i-1,j,m-1-i-j} \nonumber \\ {}&+\, \lambda _2 p_{i,j-1,m-1-i-j} \nonumber \\ {}&+\, \lambda _3 p_{i,j,m-2-i-j} \end{aligned}$$

(6)

The above equations can be written in vector-matrix form. For this, let

$$\begin{aligned}&\varvec{\psi }(s)=\,[\psi _{0,0},\psi _{0,1},\psi _{0,2},\cdots ,\\&\qquad \psi _{0,m-1},\psi _{1,0},\cdots ,\psi _{1,m-2},\cdots ,\psi _{m-1,0}]\\&\varvec{\phi }(s)=\,\varvec{\psi }(s)-\varvec{p}_{m-1}\\&\varvec{\phi }(s)=\,[\phi _{0,0},\phi _{0,1},\phi _{0,2},\cdots ,\\&\qquad \phi _{0,m-1},\phi _{1,0},\cdots ,\phi _{1,m-2},\cdots ,\phi _{m-1,0}] \end{aligned}$$

Here matrix $\varvec{\psi }(s)$ is of the order $1\times \frac{m(m+1)}{2}.$ Then for $\frac{m(m+1)}{2}\times \frac{m(m+1)}{2}$ matrices $A_l(s),~(l=1,2,3)$ we have

$$\begin{aligned} s\varvec{\phi }(s)=\varvec{p}_{m-1}\Delta _{m-1}-\varvec{p}_{m-2}\Lambda _{m-2}+\sum _{l=1}^3\varvec{\psi }(s+\theta _l)A_l(s)\nonumber \\ s\varvec{\phi }(s)=\varvec{p}_{m-1}\Delta _{m-1}-\varvec{p}_{m-1}R_{m-1}\Lambda _{m-2}+\sum _{l=1}^3\varvec{\psi }(s+\theta _l)A_l(s) \end{aligned}$$

(7)

where nonzero entries of the matrix $A_l(s)=[a_{l,u,v}]$ for $l=1,2,3$ are given by

$$\begin{aligned} A_{1,u,u}:=\lambda _1\frac{s+(m-1-i-j)\mu _3}{s+(i+1)\mu _1+j\mu _2+(m-1-i-j)\mu _3}, \\ A_{1,u,v}:= -\lambda _1\frac{(m-i-j)\mu _3}{s+i\mu _1+j\mu _2+(m-i-j)\mu _3}, \end{aligned}$$

that is,

where i and j as in the vth entry of $\varvec{\psi (s)}$ or $\varvec{\phi (s)}.$ Consider next

$$\begin{aligned} D(s)&:=I+\frac{\Delta _{m-1}-R_{m-1}\Lambda _{m-2}}{s},\nonumber \\\quad H_l(s)&:=\frac{A_l(s)}{s},\quad s>0,\, l=1,2,3 \end{aligned}$$

(8)

For $s>0$, we can divide (7) by s, and using (8), we obtain

$$\begin{aligned} \varvec{\psi }(s)=\varvec{p}_{m-1}D(s)+\sum _{l=1}^3\varvec{\psi }(s+\theta _l)H_l(s). \end{aligned}$$

(9)

Let

$$\begin{aligned} D_{i,j,k}(s)=&\,D(s+i\theta _1+j\theta _2+k\theta _3)\\ \psi _{i,j,k}(s)=&\,\psi (s+i\theta _1+j\theta _2+k\theta _3) \end{aligned}$$

Then (9) gives us for $i,j,k\ge 0$

$$\begin{aligned}&\varvec{\psi }_{i,j,k}(s)\nonumber \\&\quad =\, \varvec{p}_{m-1}D_{i,j,k}(s)+\varvec{\psi }_{i+1,j,k}(s)H_1(s+i\theta _1+j\theta _2+k\theta _3)\nonumber \\&\quad +\varvec{\psi }_{i,j+1,k}(s)H_2(s+i\theta _1+j\theta _2+k\theta _3)\nonumber \\&\quad +\varvec{\psi }_{i,j,k+1}(s)H_3(s+i\theta _1+j\theta _2+k\theta _3) \end{aligned}$$

(10)

To obtain $\psi (s)=\psi _{0,0,0}(s)$, we apply equation (10):

$$\begin{aligned}&\varvec{\psi }_{0,0,0}(s)\\&\quad =\, \varvec{p}_{m-1}D_{0,0,0}(s)+\varvec{\psi }_{1,0,0}(s)H_1(s)\\&\quad +\varvec{\psi }_{0,1,0}(s)H_2(s)+\varvec{\psi }_{0,0,1}(s)H_3(s)\\&\quad =\, \varvec{p}_{m-1}(D_{0,0,0}(s)+D_{1,0,0}(s)H_1(s)\\&\quad +D_{0,1,0}(s)H_2(s)+D_{0,0,1}(s)H_3(s))\\&\quad \,+ \varvec{\psi }_{2,0,0}(s)H_1(s+\theta _1)H_1(s)+\varvec{\psi }_{0,2,0}(s)H_2(s+\theta _2)H_2(s)\\&\quad \,+\varvec{\psi }_{0,0,2}(s)H_3(s+\theta _3)H_3(s)\\&\quad \,+ \varvec{\psi }_{1,1,0}(s)(H_2(s+\theta _1)H_1(s)+H_1(s+\theta _2)H_2(s))\\&\quad \,+ \varvec{\psi }_{1,0,1}(s)(H_3(s+\theta _1)H_1(s)+H_1(s+\theta _3)H_3(s))\\&\quad \,+ \varvec{\psi }_{0,1,1}(s)(H_3(s+\theta _2)H_2(s)+H_2(s+\theta _3)H_3(s)) \end{aligned}$$

Therefore, after n iterations we get

$$\begin{aligned} \varvec{\psi (s)}=\varvec{p}_{m-1}\sum _{i+j+k<n} D_{i,j,k}(s)C_{i,j,k}(s)+\sum _{i+j+k=n} \psi _{i,j,k}(s)C_{i,j,k}(s) \end{aligned}$$

(11)

The $\frac{m(m+1)}{2}\times \frac{m(m+1)}{2}$ matrices $C_{i,j,k}(s)$ are defined as follows: A sequence of grid points ${\mathbf{p }}=\{(i_0,j_0,k_0),(i_1,j_1,k_1),\cdots (i_n,j_n,k_n)\}$ is called path from $(i_0,j_0,k_0)$ to $(i_n,j_n,k_n)$ if each of steps $(i_{l+1},j_{l+1},k_{l+1})-(i_l,j_l,k_l),l=0,1\cdots ,(n-1)$, is either (1, 0, 0), (0, 1, 0) or (0, 0, 1). For the path ${\mathbf{p}}$

Fig. 3

Path p

$$\begin{aligned}&C_p(s)=H_{(i_{n-1},j_{n-1},k_{n-1})}(s)\cdots H_{(i_1,j_1,k_1)}(s)H_{(i_0,j_0,k_0)}(s) \\&\quad H_{(i_l,j_l,k_l)} = \left. {\left\{ \begin{array}{ll} H_1(s+i_l\theta _1+j_l\theta _2+k_l\theta _3), & {\text {if}} (i_{l+1},j_{l+1},k_{l+1})-(i_l,j_l,k_l)=(1,0,0)\\ H_2(s+i_l\theta _1+j_l\theta _2+k_l\theta _3), & {\text {if }} (i_{l+1},j_{l+1},k_{l+1})-(i_l,j_l,k_l)=(0,1,0)\\ H_3(s+i_l\theta _1+j_l\theta _2+k_l\theta _3), &{} {\text {if}} (i_{l+1},j_{l+1},k_{l+1})-(i_l,j_l,k_l)=(0,0,1) \end{array}\right. }\right. \end{aligned}$$

For the path ${\mathbf{p}}=\{i_0,j_0,k_0\}$, set $C_p(s)=1$. Let ${{\mathcal {P}}}(i,j,k)$ be the set of all paths from (0, 0, 0) to (i, j, k). Then $C_{i,j}(s)$ is defined by

$$\begin{aligned} C_{i,j,k}(s)=\sum _{p\in {{\mathcal {P}}}(i,j,k)} C_p(s) \end{aligned}$$

For $i+j+k>0,$ the $\frac{m(m+1)}{2}\times \frac{m(m+1)}{2}$ matrices $C_{i,j,k}(s)$ can be recursively calculated from

$$\begin{aligned}C_{i,j,k}(s)&=\sum _{p\in {{\mathcal {P}}}(i-1,j,k)} H_{i-1,j,k}C_p(s)\nonumber \\&\quad +\sum _{p\in {{\mathcal {P}}}(i,j-1,k)} H_{i,j-1,k}C_p(s)\nonumber \\&\quad +\sum _{p\in {{\mathcal {P}}}(i,j,k-1)} H_{i,j,k-1}C_p(s)\nonumber \\&\quad = \quad H_1(s+(i-1)\theta _1+j\theta _2+k\theta _3)C_{i-1,j,k}(s)\nonumber \\&\quad +H_2(s+i\theta _1+(j-1)\theta _2+k\theta _3)C_{i,j-1,k}(s)\nonumber \\&\quad +H_3(s+i\theta _1+j\theta _2+(k-1)\theta _3)C_{i,j,k-1}(s) \end{aligned}$$

(12)

where $C_{0,0,0}(s)=I$ and $C_{i,j,k}(s)$ is all zero matrix if $i<0$ or $j<0$ or $k<0$.

Lemma 3.1

For each $\delta >0,$ the series $\sum _{i=0}^\infty \sum _{j=0}^\infty \sum _{k=0}^\infty C_{i,j,k}(s)$ is absolutely and uniformly convergent for all $s>\delta .$

Proof

Fix $\delta >0.$ It suffices to prove that there are constants M and $r<1$ such that for all $s>\delta$ and $i+j+k\ge 0$,

$$\begin{aligned} |C_{i,j,k}(s)|\le Mr^{i+j+k}E, \end{aligned}$$

(13)

where E is the all-one matrix and the inequality is component-wise. In this bound $s\ne 0$, since $H_1(s)$ and $H_2(s)$, thus by (12) also $C_{i,j,k}(s)$, are unbounded as s approaches to 0. Now fix $r<1$. Since $H_l(s)\le \frac{\lambda _lE}{s} \,(l=1,2,3)$, there exists an $N\ge 0$ such that, for $s>\delta$ and $i+j+k\ge N,$

$$\begin{aligned} |H_l(s+i\theta _1+j\theta _2+k\theta _3)|\le \frac{2r}{3(m)(m+1)}E,\quad l=1,2,3 \end{aligned}$$

(14)

Recurrence relation (12) implies that, for each $i,j,k\ge 0,\,C_{i,j,k}(s)$ is bounded for $s>\delta .$ Hence, there is a (sufficiently large) M such that (13) is valid for $s>\delta$ and the finitely many $i+j+k\le N$. By induction we now prove that (13) is valid for all $i+j+k\ge N$. Suppose it holds for all $i+j+k=n$ (also true for $n=N$). From (12) and (14), we get, for $s>\delta$ and $i+j+k=n+1$,

$$\begin{aligned}&|C_{i,j,k}(s)| \\&\quad \le \, |H_1(s+(i-1)\theta _1+j\theta _2+k\theta _3)||C_{i-1,j,k}(s)|\\&\quad +|H_2(s+i\theta _1+(j-1)\theta _2+k\theta _3)||C_{i,j-1,k}(s)|\\&\quad +|H_3(s+i\theta _1+j\theta _2+(k-1)\theta _3)||C_{i,j,k-1}(s)|\\&\quad \le \, \frac{2r}{3m(m+1)}E(|C_{i-1,j,k}(s)|+|C_{i,j-1,k}(s)|+|C_{i,j,k-1}(s)|)\\&\quad \le \, \frac{2r}{3m(m+1)}3Mr^n E^2=Mr^{n+1}E, \end{aligned}$$

where the last inequality follows from the induction hypothesis. $\square$

Since $D_{i,j,k}(s)$ are uniformly bounded for every $s>\delta >0$ and $i+j+k\ge 0$, we get the following.

Corollary 3.1.1

The series $\sum _{i=0}^\infty \sum _{j=0}^\infty \sum _{k=0}^\infty D_{i,j,k} (s) C_{i,j,k}(s)$ is absolutely and uniformly convergent for all $s>\delta >0$.

Proof

Using that $|\psi _{i,j,k}(s)|\le 1$, the second term in (11) is bounded and given by

$$\begin{aligned} \left| \sum _{i+k+k=n}\psi _{i,j,k}(s)C_{i,j,k}(s)\right| \le \sum _{i+k+k=n}|C_{i,j,k}(s)| \end{aligned}$$

Therefore it vanishes as $n\rightarrow \infty$ by virtue of the absolute convergence of the series of $C_{i,j,k}(s)$. Hence, taking as $n\rightarrow \infty$ in (11), we get, from Corollary 3.1.1,

$$\begin{aligned} \varvec{\psi (s)}=\varvec{p_{m-1}}\varvec{C(s)}, \end{aligned}$$

(15)

where

$$\begin{aligned} \varvec{C(s)}=\sum _{i=0}^\infty \sum _{j=0}^\infty \sum _{k=0}^\infty D_{i,j,k} (s) C_{i,j,k}(s). \end{aligned}$$

(16)

in particular, we have

$$\begin{aligned} \varvec{\psi (\theta _l)}=\varvec{p_{m-1}}\varvec{C(\theta _l)},\quad l=1,2,3. \end{aligned}$$

(17)

To complete the LST of the virtual queueing time, we need to evaluate $\varvec{p_{m-1}}$. For this, first we set $s=0$ in (7), and we obtain

$$\begin{aligned} 0&=\varvec{p}_{m-1}\Delta _{m-1}-\varvec{p}_{m-1}\varvec{R}_{m-1}\Lambda _{m-2}+\sum _{l=1}^3\varvec{\psi }(\theta _l)A_l(0)\nonumber \\&=\, {} \varvec{p}_{m-1}\Delta _{m-1}-\varvec{p}_{m-1}\varvec{R}_{m-1}\Lambda _{m-2}+\varvec{p}_{m-1}\sum _{l=1}^3\varvec{C}(\theta _l)A_l(0) \end{aligned}$$

(18)

where the second equality follows from (17). To uniquely determine $\varvec{p}_{m-1}$, we finally need the normalizing equation

$$\begin{aligned} \sum _{n = 0}^{m-1} {\varvec{p}}_{n}{\varvec{e}}+ \varvec{\phi }(0) {\varvec{e}}= 1, \end{aligned}$$

(19)

where $\varvec{e}$ is the vector of all-one and ${\varvec{p}}_{n}$ is given by (5) for $0\le n<m-1$. However, equation (19) requires the computation of $\varvec{\phi }(0)$, which is the complicated step. Taking the derivatives on both sides of (7) and setting $s=0$, we get

$$\begin{aligned} \varvec{\phi }(0) = \sum _{l=1}^3 \left( \varvec{\psi }(\theta _l)A_l'(0) + \varvec{\psi }'(\theta _l)A_l(0) \right) . \end{aligned}$$

(20)

Here, prime indicates derivative with respect to s. Thus, to calculate $\varvec{\phi (0)}$ we need $\varvec{\psi '(s)}$ at $s=\theta _1,s=\theta _2$ and $s=\theta _3.$ For this, we can use (15,16). After differentiating (15), we obtain

$$\begin{aligned} \varvec{\psi }'(s) = {\varvec{p}}_{m-1} C'(s) = {\varvec{p}}_{m-1} \sum _{i=0}^\infty \sum _{j=0}^\infty \sum _{k=0}^\infty \left( D'_{i,j,k} (s) C_{i,j,k} (s) + D_{i,j,k} (s) C'_{i,j,k}(s) \right) . \end{aligned}$$

(21)

The terms $C_{i,j,k} (s)$ can be recursively computed by taking the derivative of (12):

$$\begin{aligned} C_{i,j,k}'(s) =&\quad H_1'(s+(i-1)\theta _1+j\theta _2+k\theta _3)C_{i-1,j,k}(s)\\&+ H_1(s+(i-1)\theta _1+j\theta _2+k\theta _3)C_{i-1,j,k}'(s)\\&+H_2'(s+i\theta _1+(j-1)\theta _2+k\theta _3)C_{i,j-1,k}(s)\\&+H_2(s+i\theta _1+(j-1)\theta _2+k\theta _3)C_{i,j-1,k}'(s)\\&+H_3'(s+i\theta _1+j\theta _2+(k-1)\theta _3)C_{i,j,k-1}(s)\\&+H_3(s+i\theta _1+j\theta _2+(k-1)\theta _3)C_{i,j,k-1}'(s), \end{aligned}$$

where $C_{i,j,k}'(s)$ is all zero matrix if $i=j=k=0$ or if $i<0$ or $j<0$ or $k<0$. Term-by-term differentiation of (16) is justified by the following two lemmas. $\square$

Lemma 3.2

For each $\delta >0,$ the series $\sum _{i=0}^\infty \sum _{j=0}^\infty \sum _{k=0}^\infty C'_{i,j,k}(s)$ is absolutely and uniformly convergent for all $s>\delta .$

Proof

The proof is similar to the proof of Lemma 3.1. It is sufficient to show that there are constants M and $r<1$ such that, for all $s>\delta$ and $i+j+k\ge 0,$

$$\begin{aligned} |C_{i,j,k}'(s)|\le Mr^{i+j+k}E, \end{aligned}$$

(22)

Now fix $r<1$. Since $H_l(s)\le \lambda _lE/s(l=1,2,3)$, and $H_l'(s)\le \lambda _lE/s^2(l=1,2,3)$ there is an $N\ge 0$ such that, for $s>\delta$ and $i+j+k\ge N,$

$$\begin{aligned} |H_l(s+i\theta _1+j\theta _2+k\theta _3)|\le \frac{2r}{6(m)(m+1)}E,\quad l=1,2,3 \end{aligned}$$

(23)

and

$$\begin{aligned} |H_l'(s+i\theta _1+j\theta _2+k\theta _3)|\le \frac{2r}{6(m)(m+1)}E,\quad l=1,2,3 \end{aligned}$$

(24)

Recursions (12)) and (22) imply that, for each $i,j,k\ge 0$ $C_{i,j,k}(s)$ and $C_{i,j,k}'(s)$ are bounded for $s>\delta$. Hence, there is a (sufficiently large) M such that both (13) and (22) are valid for $s>\delta$ and the finitely many $i+j+k\le N$. Following the induction steps in the proof of Lemma 3.1, it follows that (13) is valid for all $i+j+k\ge N$. We now show that (22) also holds for all $i+j+k\ge N$. Suppose that (22)) holds for all $i+j+k= N$ (also holds for $n=N$). From (22), (23) and (24), we get, for $i+j+k= n+1$,

$$\begin{aligned} |C_{i,j,k}(s) \le&\quad |H_1'(s+(i-1)\theta _1+j\theta _2+k\theta _3)||C_{i-1,j,k}(s)|\\&+ |H_1(s+(i-1)\theta _1+j\theta _2+k\theta _3)||C_{i-1,j,k}'(s)|\\&+|H_2'(s+i\theta _1+(j-1)\theta _2+k\theta _3)||C_{i,j-1,k}(s)|\\&+|H_2(s+i\theta _1+(j-1)\theta _2+k\theta _3)||C_{i,j-1,k}'(s)|\\&+|H_3'(s+i\theta _1+j\theta _2+(k-1)\theta _3)||C_{i,j,k-1}(s)|\\&+|H_3(s+i\theta _1+j\theta _2+(k-1)\theta _3)||C_{i,j,k-1}'(s)|\\ \le&\frac{2r}{6m(m+1)}E(|C_{i-1,j,k}(s)|+|C_{i-1,j,k}'(s)|+|C_{i,j-1,k}(s)|\\&+|C_{i,j-1,k}'(s)|+|C_{i,j,k-1}(s)|+|C_{i,j,k-1}'(s)|)\\ \le&\frac{2r}{6m(m+1)}6Mr^nE^2=Mr^{n+1}E, \end{aligned}$$

where the last inequality follows from the mathematical induction hypothesis. $\square$

Lemma 3.3

For each $s>0,$ the derivative of C(s) exists and is equal to

$$\begin{aligned} C'(s)=\sum _{i=0}^\infty \sum _{j=0}^\infty \sum _{k=0}^\infty \left( D_{i,j,k}'(s) C_{i,j,k}(s)+D_{i,j,k}(s)C_{i,j,k}'(s)\right) . \end{aligned}$$

Proof

Fix $s>0$. First note that the series converges by Lemmas 3.1-3.2 and the fact that $D_{i,j,k}$ and $D_{i,j,k}'$ are uniformly bounded for all $i+j+k\ge 0$. It suffices to prove that, for each sequence $\{h_n\}$ converging to 0 such that $s+h_n>0$ for all n,

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{C(s+h_n)-C(s)}{h_n}=\sum _{i=0}^\infty \sum _{j=0}^\infty \sum _{k=0}^\infty B_{i,j,k}'(s) \end{aligned}$$

where $B_{i,j,k}(s)=D_{i,j,k}(s) C_{i,j,k}.$ Let $h_n$ be a sequence. Thus, there is a $\delta >0$ such that $s+h_n>\delta$ for all n. According to (13) and (22) and that the fact that $D_{i,j,k}(s+h_n)$ and $D_{i,j,k}'(s+h_n)$ are uniformly bounded for all n and $i+j+k\ge 0,$ there are constants M and $r<1$ such that, for all n and $i+j+k\ge 0,$

$$\begin{aligned} |B_{i,j,k}'(s)|\le {} Mr^{i+j+k}E. \end{aligned}$$

(25)

We need to show that for each $\epsilon >0$ there is an N such that, for $n>N$,

$$\begin{aligned}&\left| \frac{C(s+h_n)-C(s)}{h_n} - \sum _{i=0}^\infty \sum _{j=0}^\infty \sum _{k=0}^\infty B'_{i,j,k}(s) \right| \nonumber \\&\quad = \left| \sum _{i=0}^\infty \sum _{j=0}^\infty \left( \frac{B_{i,j,k}(s+h_n)-B_{i,j,k}(s)}{h_n} - B'_{i,j,k}(s) \right) \right| < \epsilon . \end{aligned}$$

(26)

Let $\epsilon >0$. For given n and $i,j,k\ge 0$, it follows from the mean value theorem that there is an $0<\eta <1$ such that $(B_{i,j,k}(s+h_n)-B_{i,j,k}(s))/h_n = B'_{i,j,k} (s + \eta h_n)$. Hence by (25)

$$\begin{aligned}&\left| \frac{B_{i,j,k}(s+h_n)-B_{i,j,k}(s)}{h_n} - B'_{i,j,k}(s) \right| \\&\quad \le {}|B'_{i,j,k} (s + \eta h_n)| + |B'_{i,j,k}(s)| \\&\quad \le {} 2 M r^{i+j+k} E. \end{aligned}$$

Note that M and r do not depend on n, i, j, k. So there is a constant K such that, for all n,

$$\begin{aligned} \sum _{i+j+k\ge K} \left| \frac{B_{i,j,k}(s+h_n)-B_{i,j,k}(s)}{h_n} - B'_{i,j,k}(s) \right| < \frac{\epsilon }{2} . \end{aligned}$$

(27)

Further, for given $i,j,k\ge 0,(B_{i,j,k}(s+h_n)-B_{i,j,k}(s))/h_n$ converges to $B_{i,j,k}'(s)$ as an tends to infinity. Hence, there is an N such that, for $n>N$

$$\begin{aligned} \sum _{0\le i+j+k< K} \left| \frac{B_{i,j,k}(s+h_n)-B_{i,j,k}(s)}{h_n} - B'_{i,j,k}(s) \right| < \frac{\epsilon }{2} . \end{aligned}$$

(28)

Combining (27) and (28) yields (26).

Substituting (17) and (21) with $s=\theta _l$ in (20) gives

$$\begin{aligned} \begin{aligned} \varvec{\phi }(0) = {\varvec{p}}_{m-1} \sum _{l=1}^{3} \left( C(\theta _l) A'_l (0) + C'(\theta _l) A_l (0) \right) \end{aligned} \end{aligned}$$

and the normalization equation (19) can be rewritten as

$$\begin{aligned} \sum _{n = 0}^{m-1} {\varvec{p}}_{n}{\varvec{e}}+ {\varvec{p}}_{m-1} \sum _{l=1}^{3} \left( C(\theta _l) A'_l (0) + C'(\theta _l) A_l (0) \right) {\varvec{e}}= 1. \end{aligned}$$

(29)

$\square$

The following theorem summarizes the above findings.

Theorem 3.4

The steady-state LST $\psi (s)$ of the virtual queuing time satisfies

$$\begin{aligned} \varvec{\psi }(s)=\varvec{p}_{m-1}\varvec{C}(s) \end{aligned}$$

where $\varvec{C}(s)$ is defined by (16) and the probability vectors $\varvec{p}_n$ for $0\le n \le m-1$ are the solution to the system of linear equations (5), (18) and (29).

3.4 Special case $\mu _{1}=\mu _{2}=\mu _{3}=\mu$

We now suppose $\mu _1=\mu _2=\mu _3=\mu$. Now we are dealing with easy problem, since we do not need to keep track of $N_1(t),N_2(t)$ and $N_3(t)$ separately, only $N(t)=N_1(t)+N_2(t)+N_3(t)$. Define

$$\begin{aligned} \begin{aligned} \psi (s)=&{} \lim _{t \rightarrow \infty } E(s^{-sW(t)};N(t) = m-1)\\ =&{} E(s^{-sW};N = m-1), \\ p_{i}=&{} \lim _{t \rightarrow \infty } P(W(t) = 0, N(t)=i) \\ =&{} P(W=0, N = i), \quad 0 \le i \le m-1,\\ \phi (s)=&{} \psi (s) - \varvec{p}_{m-1} . \end{aligned} \end{aligned}$$

Then the balance equation (4) can be written as

$$\begin{aligned} \varvec{p}_{n-1} (\lambda _1+\lambda _2+\lambda _3) = \varvec{p}_n n \mu , \quad 1 \le n \le m-1, \end{aligned}$$

(30)

and (9) reduces to

$$\begin{aligned}&\varvec{\psi } (s) = \varvec{p}_{m-1} + \varvec{\psi } (s+\theta _1) \frac{\lambda _1 }{s+m\mu } + \varvec{\psi } (s+\theta _2) \frac{\lambda _2 }{s+m\mu }\\&\quad +\varvec{\psi } (s+\theta _3) \frac{\lambda _3 }{s+m\mu } . \end{aligned}$$

The solution of this equation is given by (15)

$$\begin{aligned} \varvec{\psi } (s) = \varvec{p}_{m-1} \varvec{c}(s), \end{aligned}$$

where

$$\begin{aligned} c(s)=\sum _{i=0}^\infty \sum _{j=0}^\infty \sum _{k=0}^\infty c_{i,j,k}(s) \end{aligned}$$

For $i+j+k>0,$ the terms $c_{i,j,k}(s)$ are determined from recursion

$$\begin{aligned}&{c_{i,j,k}(s)} = \frac{\lambda _1}{s+(i-1)\theta _1+j\theta _2 + k\theta _3+m\mu }{c_{i-1,j,k}(s)} \\&\quad + \frac{\lambda _2}{s+ i\theta _1+(j-1)\theta _2+k\theta _3+\mu }{c_{i,j-1,k}(s)} \\&\quad + \frac{\lambda _3}{s+ i\theta _1+j\theta _2+(k-1)\theta _3+\mu }{c_{i,j,k-1}(s)}, \end{aligned}$$

with $c_{0,0,0}=1$ and $c_{i,j,k}=0$, if $i<0$ or $j<0$ or $k<0$. The normalization equation becomes

$$\begin{aligned} 1 = \sum _{n=0}^{m-1} \varvec{p}_n + \phi (0) = \sum _{n=0}^{m-1} p_n + \varvec{\psi } (\theta _1) \frac{\lambda _1 }{k\mu } + \varvec{\psi } (\theta _2) \frac{\lambda _2 }{k\mu }+ \varvec{\psi } (\theta _3) \frac{\lambda _3 }{k\mu }. \end{aligned}$$

Together with (30), this yields, for $n=0,1,\cdots ,m-1,$

$$\begin{aligned} \varvec{p_n}=\left( 1-\psi (\theta _1) \frac{\lambda _1 }{k\mu } - \psi (\theta _2) \frac{\lambda _2 }{k\mu }- \psi (\theta _3) \frac{\lambda _3 }{k\mu }\right) \frac{\frac{\rho ^n}{n!}}{\sum _{j=0}^{m-1} \frac{\rho ^j}{j!}} \end{aligned}$$

where $\rho =\frac{\lambda _1+\lambda _2+\lambda _3}{\mu }$.

4 Performance measures

Now we show how many useful performance measures in steady-state can be computed in terms of the LST evaluated at $\theta _1,\theta _2$ and $\theta _3$. Suppose the $M/M/m+M$ system is in a steady state. An arrival faces a queuing time of W. If the arrival is from Class i, the customer will enter service if his/her impatience time $T_i$ is longer than W. For Class 1, this probability is given by the following (and similarly for Class 2 and 3, by replacing $\theta _1$ by $\theta _2$ and $\theta _3$, respectively):

$$\begin{aligned}&P(T_1 > W)= {} E(\mathrm {{e}}^{-\theta _1 W}) \\&\quad = \sum _{i+j+k \le m-1} E(\mathrm {{e}}^{-\theta _1W};N_1 = i, N_2 = j,N_3=k)\\&\quad = {} \sum _{n < m-1} {\varvec{p}}_n {\varvec{e}}\\&\quad + \varvec{\psi }(\theta _1) {\varvec{e}}. \end{aligned}$$

Here, we are using that W=0 and $E(e^{\theta W};N_1 = i, N_2 = j,N_3=k)=p_{ijk}$ when $i+j+k<m-1.$ Next, using Little’s law, we see that the expected number of servers busy serving Class 1 customers is given by

$$\begin{aligned} \lambda _1 P(T_1 > W) \frac{1}{\mu _1} = \frac{\lambda _1}{\mu _1} \left( \sum _{n < m-1} {\varvec{p}}_n {\varvec{e}}+ \varvec{\psi }(\theta _1) {\varvec{e}}\right) \end{aligned}$$

and the steady state throughput equals

$$\begin{aligned} \sum _{i=1}^3 \lambda _i P(T_i > W)=&{} \sum _{i=1}^3 \lambda _i \left( \sum _{n < m-1} {\varvec{p}}_n {\varvec{e}}+ \varvec{\psi } (\theta _i) {\varvec{e}}\right) . \end{aligned}$$

Now we compute the expected time of a Class 1 customer waiting for service. This is given by

$$\begin{aligned} E(\min (W,T_1))=&{} E(E(\min (W,T_1)|W))\; = \; E\left( \frac{1-\mathrm {{e}}^{-\theta _1 W}}{\theta _1}\right) \\=&{} \frac{1-E(\mathrm {{e}}^{-\theta _1 W})}{\theta _1} \; = \; \frac{1-P(T_1 > W)}{\theta _1}. \end{aligned}$$

By Little’s law, we get the following for the expected number of Class i customers waiting for service

$$\begin{aligned} E(L_i^q) = \lambda _i E(\min (W,T_i)) = \frac{\lambda _i}{\theta _i} (1-P(T_i > W)). \end{aligned}$$

At last, we compute the expected conditional waiting time of Class i customers entering service follows from

$$\begin{aligned} E(W| T_i> W) = \frac{E(W; T_i> W)}{P(T_i > W)}, \end{aligned}$$

where

$$\begin{aligned} E(W; T_i > W) = E(W {\mathrm {{e}}^{-\theta _i W}}) = -\left. \frac{d}{ds} E({\mathrm {{e}}^{-s W}})\right| _{s=\theta _i} = -\varvec{\psi }'(\theta _i) {\varvec{e}}. \end{aligned}$$

These formulae simplify significantly when applied to the $M/G/1+M$ system. In particular, the probability that the server is busy serving a Class i customer is given by

$$\begin{aligned} \rho _i = \lambda _i\tau _i\psi (\theta _i), \end{aligned}$$

where $\psi (s)$ is as defined in Eq. (2). The probability that the server is busy is given by

$$\begin{aligned} \rho = \psi (\theta _1)\lambda _1\tau _1 + \psi (\theta _2)\lambda _2\tau _2+\psi (\theta _3)\lambda _3\tau _3. \end{aligned}$$

In steady state, the throughput is equal to

$$\begin{aligned} \psi (\theta _1)\lambda _1 + \psi (\theta _2)\lambda _2+\psi (\theta _3)\lambda _3. \end{aligned}$$

and the reneging rate by

$$\begin{aligned} (1-\psi (\theta _1))\lambda _1 + (1-\psi (\theta _2))\lambda _2+(1-\psi (\theta _3))\lambda _3. \end{aligned}$$

The expected number of Class $i,\, (i=1,2,3)$ customers waiting for service in a steady state is given by

$$\begin{aligned} E(L_i^q) = \frac{\lambda _i}{\theta _i}(1-\psi (\theta _i)). \end{aligned}$$

The expected number of Class $i,\, (i=1,2,3)$ customers in the system in steady state is given by

$$\begin{aligned} E(L_i) = E(L_i^q) + \lambda _i\tau _i\psi (\theta _i). \end{aligned}$$

This implies that, in the special case when $\tau _i=\frac{1}{\theta _i}$

$$\begin{aligned} E(L_i)=\frac{\lambda _i}{\theta _i}. \end{aligned}$$

This is expected since in this case, the system behaves like an infinite server queue for each class of customers.

5 Numerical analysis

For numerical analysis we have considered three different systems based on their patience time distribution as follows:

System 1: In this system, we considered the distribution of patience time across the classes are same that is $\frac{2}{3}$ unit ($\theta _1=\theta _2=\theta _3=1.5$).

System 2: In this system, we considered the distribution of patience time are different across the classes. For Class 1 patience time is 1 unit ($\theta _1=1$), Class 2 patience time is $\frac{2}{3}$ unit $\theta _2=1.5$ and for Class 3 it is $\frac{1}{2}$ unit $\theta _3=2.$

System 3: In system 3, we considered that patience time distribution for Class 1 and Class 2 customers are same but differs from Class 3. Here taking $(\theta _1=1.5\,,\theta _2=1.5,\theta _3=2)$.

In all of the systems, we consider requests from Class 1 have a mean service time of 1 unit $\mu _1=1$, requests from Class 2 have a mean service time of $\frac{3}{2}$ units $(\mu _2=1.5)$, and requests from Class 3 have a mean service time of $\frac{1}{2}$ units $(\mu _3=2)$. The arrival rate of customers across the classes remain same ($\lambda _1=\lambda _2=\lambda _3$) and vary from 6 to 20 throughout the calculations. And we hold number of servers in the system for this analysis is 5.

In Table [1,2,3], we present three steady state performance measures from the above systems. The measures include the percentage of customers who receive service, the system throughput, and the mean waiting time of all customers. We discuss each of these measures:

• Percentage all customers receiving service: The percentage of all customers who receive service is highest in System 2 while lowest in System 1; see Table  1. We observe that when the arrival rate is high, all systems are approximately equally efficient. Also recall that patience time in System 1 for Class 3 is higher than that is in System 2 and System 3. Consequently, a higher number of Class 3 customers are served in System 1 compared to System 2 and System 3. Since the patience time of Class 1 customers is highest in System 2, a maximum number of customers from Class 1 will be served in System 2. Also for Class 3 customers the patience time is the same in System 2 and System 3; approximately equal proportion of customers from Class will be served in these two systems. That means the manager of the system can decide for which class of customers should be served at priority.

• System throughput: We observed in Table 2 that the percentage of all customers receiving service is highest (lowest) in System 2 (System 1). Therefore, it is not surprising at all that the system throughput is highest (lowest) in System 2 (System 1). Initially, increasing the arrival rate in the system increases server utilization and hence system throughput. However, the gains in throughput due to an increase in server utilization diminish and are eventually offset by a reduction in the effective service rate of the system. The service rate of the system is decreasing, as the number of Class 1 customers are increasing and taking longer time to serve. The result has potential implications for systems with limited service capacity that generate revenue based on system throughput.

• Mean waiting time of all customers: We observed that the mean waiting time is lowest in System 3 while highest in System 2; see Table 3. This is because the patience time of Class 1 customer is highest in System 2 which needs a longer time to serve. At the low arrival rate, all systems serve in approximately equal time, while at the higher arrival rate System 3 has significantly less waiting time for service. Here it is interesting that in System 3, the percentage of all customers receiving service is lesser than that is in System 2 while having a lesser mean waiting time. This result again has ramifications for service level forecasting as the average waiting time of all customers is another common measure of service level.

Table 1 Percentage of all customers receiving service

Table 2 System throughput

Table 3 Mean waiting time—all customers

6 Conclusion

In this article, we analyzed a queuing system with three classes of impatient customers who arrive according to $PP(\lambda _i)\,(i=1,2,3)$ and are served on the basis of FCFS. We also determine the performance measures such as the percentage of all customers receiving service in each class, the mean waiting time of customers in each class and the expected conditional waiting time for each class of customers. After numerical analysis, we found that it may very effective in call centers since in call centers usually patience time of customers differs from each other. And a subset of servers can be trained to handle a class of customers. Overall this system has many managerial implications.